DOI:
https://doi.org/10.14483/23448393.2374Published:
2008-11-30Issue:
Vol. 14 No. 2 (2009): July - DecemberSection:
Science, research, academia and developmentAnálisis de la impedancia de salida en lazo cerrado de inversores funcionando en modo isla, utilizando esquemas droop
Output Impedance Analysis In A Closed Loop Of Inverters Connected In Parallel Operating In Island Mode.
Keywords:
Esquemas droop, inversor, modo isla, impedancia de salida, microrred. (es).Downloads
References
REN21 Steering Committee. "Renewable 2009, Global Status Report". Worldwatch Institute Washington, DC. 2009.
R.H. Lasseter, et al. "White paper on integration of distributed energy resources. The CERTS microgrid concept". Consortium for Electric Reliability Technology Solutions. 2002, pp. 1-27.
PSIM 7.0 User´s Guide (2006), Powersim Inc.
N. Mohan, T.M. Underland, W.P. Robbins, "Power electronics: converters, applications, and design". 3th ed. International. John Wiley & Sons. 2003.
Y. S. Jung, et. al. "A new small signal modeling of average current mode control". Power Electronics Specialists Conference, 1998. PESC 98 Record. 29th Annual IEEE, vol. 2. 1998, pp.1118-1124.
D. M. Sable, R.B. Ridley, "Comparison of performance of singleloop and current-injection control for PWM converters that operate in both continuous and discontinuous modes of operation". Power Electronics, IEEE Transactions on, vol. 7, No.1, Jan 1992, pp.136-142.
D. N. Zmood, D.G. Holmes, "Stationary frame current regulation of PWM inverters with zero steady-state error". Power Electronics, IEEE Transactions on, vol.18, No.3, May 2003, pp. 814-822.
R. W. Erickson, "Fundamental of power electronics". Norwell, MA: Kluwer. 1997.
J. Grainger, W. Stevenson, "Power System Analysis". McGraw-
Hill. 1994.
M. C. Chandorkar, et. al. "Control of parallel connected inverters in standalone AC supply systems". Industry Applications, IEEE Transactions on, vol. 29, No.1, 1993, pp.136-143.
J. M. Guerrero, et. al. "Decentralized Control for Parallel Operation of Distributed Generation Inverters Using Resistive Output Impedance". Industrial Electronics, IEEE Transactions on, vol. 54, No.2, April 2007, pp.994-1004.
J.M. Guerrero, et. al. "Output Impedance Design of ParallelConnected UPS Inverters With Wireless Load-Sharing Control". Industrial Electronics, IEEE Transactions on, vol. 52, No.4, Aug. 2005, pp. 1126-1135.
J. F. Chen, C.L. Chu, C.L. Huang, "The parallel operation of two UPS by the coupled-inductor method". Industrial Electronics. Proceedings of the IEEE International Symposium on, May 1992, pp.733-736.
C. C. Hua, et. al., "Parallel operation of inverters for distributed photovoltaic power supply system". Power Electronics Specialists Conference, 2002. pesc 02. 2002 IEEE 33rd Annual, vol. 4, 2002, pp. 1979-1983.
K. De Brabandere, et. al. "A Voltage and Frequency Droop Control Method for Parallel Inverters". Power Electronics, IEEE Transactions on, vol. 22, No.4, July 2007, pp.1107-1115.
J. M. Guerrero, et. al. "A wireless controller for parallel inverters in distributed online UPS systems". Industrial Electronics Society, 2003. IECON '03. The 29th Annual Conference of the IEEE, vol. 2, 2003, pp. 1637-1642.
S. J. Chiang, et. al. "A multimodule parallelable series-connected PWM voltage regulator". Industrial Electronics, IEEE Transactions on, vol. 48, No.3, Jun. 2001, pp.506-516.
J. M. Guerrero, "A wireless controller to enhance dynamic performance of parallel inverters in distributed generation systems". Power Electronics, IEEE Transactions on, vol. 19, No.5, Sept. 2004, pp. 1205-1213.
E. A. A. Coelho, P.C. Cortizo, P.F.D. Garcia, "Small-signal stability for parallel-connected inverters in stand-alone AC supply systems". Industry Applications, IEEE Transactions on, vol.38, no.2, Mar/Apr 2002, pp.533-542.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Ciencia, Investigación, Academia y Desarrollo
Ingeniería, 2009-00-00 vol:14 nro:2 pág:4-12
Análisis de la impedancia de salida en lazo cerrado de inversores funcionando en modo isla, utilizando esquemas droop
OUTPUT IMPEDANCE ANALYSIS IN A CLOSED LOOP OF INVERTERS CONNECTED IN PARALLEL OPERATING IN ISLAND MODE.
César Leonardo Trujillo Rodríguez
Profesor de la Facultad de Ingeniería, Universidad Distrital.
David Velasco de la Fuente
Candidato a Doctor Universidad Politécnica de Valencia.
Emilio Figueres Amorós
Profesor Departamento de Ingeniería Electrónica, Universidad Politécnica de Valencia.
Gabriel Garcerá Sanfeliú
Profesor Departamento de Ingeniería Electrónica, Universidad Politécnica de Valencia.
Rubén Ortega González
Profesor Escuela Superior de Computo, Instituto Politécnico Nacional de México.
Resumen
En este artículo se analiza la condición en modo isla, es decir cuando una microrred no se encuentra conectada a la red eléctrica y por ende los inversores que hacen parte de la microrred deben operar como fuentes de tensión en paralelo, con otros equipos de similares características. La temática se centra en la forma de interconectar los inversores sin utilizar ningún tipo de comunicación, a través de esquemas droop. En primera instancia se analiza cómo obtener una impedancia de salida determinada a partir de un lazo de realimentación de impedancia; posteriormente, se plantea la forma de aprovechar las características físicas tanto del inversor, como del controlador, con el fin de alcanzar resultados similares a los que se logran utilizando la técnica de lazo de realimentación de impedancia. Para validar dicho análisis, se realizan simulaciones de inversores conectados en paralelo alimentando una carga y se dan conclusiones.
Palabras clave:
Esquemas droop, inversor, modo isla, impedancia de salida, microrred.
Abstract
In this paper the island mode condition is analysed. The island mode refers to a microgrid that is not connected to the electrical grid and the inverters have to operate as a voltage source in parallel with others equipments of similar characteristics. This study focuses on how to interconnect the inverters without using any type of communication, by using droop schemes. First, an analisys is performed on how to obtain a certain value of output impedance by using an impedance loop. Then, we propose to use physical characteristics of the inverter and the type of controller to achieve results similar to those obtained by the impedance loop. In order to validate this analysis, simulations on parallel connection of several inverters supplying power to load are performed. Lastly some conclusions are presented.
Key words:
Droop schemes, inverter, island mode, output impedance, microgrid.
1. INTRODUCCIÓN
En los últimos años, una de las grandes prioridades a escala mundial es el desarrollo de fuentes alternativas de generación de energía eléctrica, y en especial de fuentes renovables las cuales producen una baja contaminación ambiental. Opciones como la energía eólica, solar, biomasa renovable e hidrógeno jugarán un papel importante en el largo plazo, produciendo cambios substanciales en el perfil tecnológico ambiental y organizacional del sistema energético global [1].
La dinámica de cogeneración energética empleando energías renovables, así como la ausencia de energía eléctrica en lugares remotos u apartados de las grandes urbes hace factible el implementar interfaces denominadas microrredes [2], los cuales son pequeños sistemas inteligentes de distribución eléctrica y térmica auto gestionados localmente, capaces de conectarse tanto a la red eléctrica pública de distribución como aislados de la misma (condición en modo isla). En este artículo se analiza la condición en modo isla, donde los inversores, los cuales adaptan la energía proveniente de una fuente de energía primaria por la carga, hacen parte de la microrred y deben operar como fuentes de tensión en paralelo con otros equipos. Aunque existen diferentes alternativas para conectar en paralelo los inversores, este artículo se centra en la forma de interconectar los inversores sin utilizar ningún tipo de comunicación, a través de esquemas droop. Para ello se ha implementado un inversor monofásico (sección 2).
El artículo se ha esquematizado de la siguiente manera: en la sección 2 se hace una descripción del sistema implementado. En la sección 3 se hace una breve síntesis de los esquemas droop, se aborda el análisis de la impedancia de salida del sistema y se implementa el esquema droop correspondiente. En la sección 4 se presentarán los resultados de la simulación realizada en PSIM [3] y finalmente se presentan las conclusiones.
2. DESCRIPCIÓN DEL INVERSOR MONOFÁSICO IMPLEMENTADO
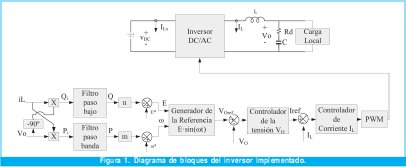
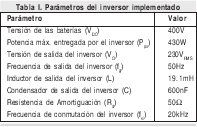
La figura 1 muestra el diagrama de bloques de la estructura de control del inversor implementado, el cual consiste de un inversor monofásico de 440W, que conmuta a una frecuencia de 20kHz, utiliza modulación bipolar sinusoidal por ancho de pulso SPWM [4] y cuyos parámetros se listan en la Tabla 1.
El inversor controla la corriente y la tensión de salida (230VRMS a 50Hz), para lo cual se implementó un control modo corriente media (ACC) [5], el cual presenta la ventaja comparativa de poseer una respuesta más plana de la función de transferencia de corriente en el inductor, respecto de la tensión de referencia. Además, exhibe menos distorsión que el control de corriente pico (CIC) [6] para generar corriente alterna.
El control modo de corriente opera de la siguiente forma: la tensión de referencia del controlador de tensión de salida es suministrada por los esquemas droop (sección 3.), que se basan en el hecho de emular el comportamiento de los generadores de potencia, los cuales disminuyen su frecuencia y/o amplitud de tensión cuando la potencia consumida, activa y/o reactiva, se incrementa [4].
El control de la tensión de salida del inversor se realiza a través de un controlador PI, cuya salida impone la referencia de corriente al controlador de corriente de salida, implementado a través de un controlador resonante (o controlador armónico) [7].
Los controladores resonantes tienen la ventaja de introducir en el lazo una alta ganancia a la frecuencia de la señal de consigna y proveer a la salida la contribución necesaria para anular el efecto causado por las perturbaciones de la red eléctrica.
Para el diseño de los controladores es necesario identificar las funciones de transferencia de las variables a controlar. Las funciones de transferencia se extraen siguiendo la técnica de modelado del conmutador PWM [8].
2.1 Modelo de pequeña señal del inversor implementado
Para realizar un control realimentado lineal a partir de un circuito inherentemente no lineal como es un convertidor conmutado, hay que linealizar la etapa de potencia. Ante pequeñas perturbaciones en torno a un punto de trabajo el convertidor conmutado tiene un modelo lineal de pequeña señal, a partir del cual se pueden diseñar reguladores lineales para cerrar lazos de control de diferentes características [8].
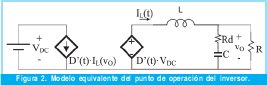

En la figura 2 se presenta el modelo equivalente del punto de operación del inversor implementado; la carga del inversor es de tipo resistivo.
Donde, D(t) es el ciclo de trabajo en el punto de operación y D'(t)=2•D(t)-1.
La ecuación 1, muestra las relaciones establecidas para la corriente en el inductor, IL(t), y el ciclo de trabajo, D(t), en el punto de operación.
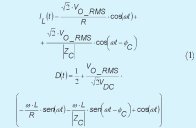
Siendo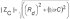 y
y 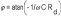
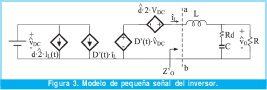
Con base en las pequeñas perturbaciones en torno al punto de operación se establece el modelo en pequeña señal (figura 3) [5].
En la figura 3 las magnitudes 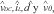 , denotan que son términos de pequeña señal.
, denotan que son términos de pequeña señal.
A partir del modelo la figura 3, se obtiene la función de transferencia que relaciona la corriente en el inductor al ciclo de trabajo, GIL_d(s) y la función de transferencia que relaciona la tensión de salida del inversor a la corriente en el inductor, GVo_IL(s), esto con el fin de aplicar el control modo corriente media. Dicho control plantea la existencia de un lazo interno de corriente y un lazo externo de tensión que fija la referencia del primer lazo. En la Tabla 2 se muestran los parámetros (función de transferencia, frecuencias de cruce y márgenes de fase) de los controladores de corriente y tensión seleccionados para este estudio.
3. ESQUEMAS DROOP
Los esquemas droop se basan en el concepto ampliamente conocido para el manejo del flujo de potencia en sistemas a gran escala, que consiste en disminuir la frecuencia de los generadores AC cuando su potencia de salida se incrementa [9]. La idea fundamental es emular a través del inversor el comportamiento de la dinámica de los generadores AC.
A manera de ejemplo se aborda el estudio del flujo de potencia en estado estable a través de una línea de transmisión entre los puntos A y B de un sistema en corriente alterna (figura 4).
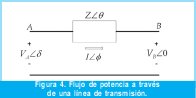
La potencia activa y reactiva del esquema de la figura 4, están dadas por las ecuaciones (2) y (3).
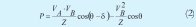
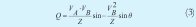
Dependiendo de la característica de la línea se pueden presentar dos casos que determinan relaciones entre la potencia activa y la potencia reactiva, en función de la tensión y/o la frecuencia.
El primer caso es cuando Z es puramente inductiva (Z=jX), con lo cual se tiene θ=90°, y las ecuaciones (2) y (3) se reducen a
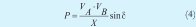
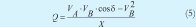
De las anteriores ecuaciones, y considerando pequeñas diferencias de fase entre VA y VB, se puede apreciar la fuerte dependencia de P con respecto al ángulo ä, mientras que 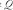 depende de la diferencia de amplitud entre las tensiones VA y VB
depende de la diferencia de amplitud entre las tensiones VA y VB
En el inversor la frecuencia (@) y la amplitud de tensión (E) de la referencia, pueden ser expresadas a través de las ecuaciones (6) y (7), [10].
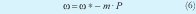
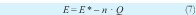
Donde, ω* y E* son la frecuencia y la amplitud de la tensión de referencia del inversor sin carga, y m y n los coeficientes de caída de la frecuencia y la amplitud respectivamente.
En el segundo caso de análisis se tiene que la impedancia de línea es puramente resistiva (Z=R), por lo tanto θ=0°, con lo que las ecuaciones que representan la potencia activa y la potencia reactiva toman la siguiente forma [11].
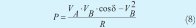
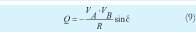
Cuando la impedancia de línea es altamente resistiva, el esquema droop para P 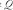 y se invierte.
y se invierte.
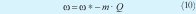

Como se puede apreciar para este caso, P es dependiente de la tensión 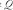 de la frecuencia.
de la frecuencia.
3.1 Análisis de la impedancia de salida del inversor
El inversor debido a la presencia de un inductor de salida usado como filtro, presenta un comportamiento inductivo, haciendo analogía con el sistema de potencia, donde la impedancia de la línea también es de tipo inductivo, por lo tanto el esquema droop a implementar esta dado por las ecuaciones (6) y (7). Sin embargo esto no es del todo cierto ya que la impedancia de salida del inversor depende igualmente de la estrategia de control a utilizar [12]. Existen dos formas de solucionar este inconveniente, la primera radica en utilizar un inductor adicional en serie a la salida del inversor [13], [14], lo que implica un aumento de costos y tamaño de la unidad inversora. Lo segundo es colocar un lazo de control adicional que emule una impedancia virtual [15], [16].
Para implementar el lazo de impedancia virtual es necesario visualizar como la estrategia de control utilizada influye en la impedancia de salida.
La impedancia de salida (ZO_L.A(s)) en lazo abierto del inversor en modo isla puede ser hallada a partir del modelo en pequeña señal de la figura 3 y de los esquemas de lazos de control de la figura 1. Es de aclarar que para este análisis se ha incluido en el modelo de pequeña señal, la resistencia interna (rl) del inductor, con el fin de apreciar su efecto sobre la impedancia de salida del inversor.
La función de transferencia ZO_L.A(s) puede ser calculada haciendo
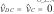 , es decir asumiendo pequeñas variaciones de tensión en la entrada, por ende la impedancia de salida, se define a partir de las ecuaciones (12), (13) y (14).
, es decir asumiendo pequeñas variaciones de tensión en la entrada, por ende la impedancia de salida, se define a partir de las ecuaciones (12), (13) y (14).
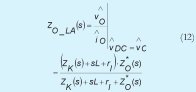
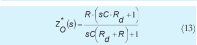
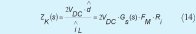
Donde:
Z*O(s) es la impedancia a la derecha del inductor.
ZK(s) representa la impedancia del lado izquierdo vista en los puntos a-b (figura 3), pero teniendo en cuenta los lazos de control actuantes.
Gs(s) es la función de transferencia del controlador de corriente.
FM es la ganancia del modulador PWM bipolar y Ri la ganancia del sensor de corriente.
Para el cálculo de la impedancia en lazo cerrado (ZO_LC(s)) se tiene que,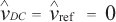 por ende de forma análoga (ZO_LC(s)) se expresa de acuerdo a la ecuación (15).
por ende de forma análoga (ZO_LC(s)) se expresa de acuerdo a la ecuación (15).
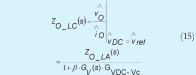
Donde:
GV(s) es la función de transferencia del controlador de tensión.
GVDC_Vc(s) es la función de transferencia de la tensión de entrada a la tensión de control y â es la ganancia del sensor de tensión.
En la figura 5 se muestra el diagrama respuesta en frecuencia de la impedancia de salida del inversor en lazo cerrado para diferentes valores de rl y Rd.
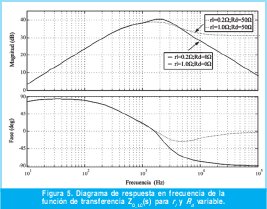
En la figura 5 se aprecia, que debido a la acción de los controladores implementados en el lazo de corriente (P+Resonante) y en el lazo de tensión (PI), el comportamiento es inductivo a bajas frecuencias, lo que permite la conexión en paralelo de los inversores. En altas frecuencias se puede observar como con el aumento de Rd, la impedancia de salida en lazo cerrado toma un carácter resistivo, mientras que la variación de rl es insignificante en todo el rango de frecuencias.
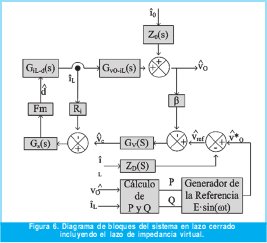
El agregar un lazo que emule una impedancia virtual en el sistema, permite hacer que la impedancia de salida en lazo cerrado del inversor se comporte de forma resistiva, inductiva o una combinación de ambas, con el fin de ajustar las funciones que describen la potencia activa y la potencia reactiva en términos de la frecuencia y la tensión de salida del inversor. En la Figura 6 se muestra un diagrama de bloques que presenta los lazos de control del inversor, incluyendo el lazo de impedancia virtual.
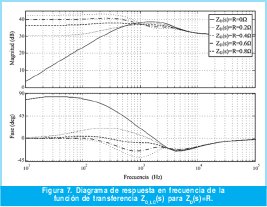
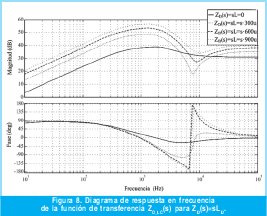
En las figuras 7 y 8 se muestran, los diagramas de respuesta en frecuencia de la impedancia de salida en lazo cerrado para una ZD(s)=R, puramente resistiva, y una ZD(s)=sLD , puramente inductiva respectivamente.
En el diagrama de respuesta en frecuencia (figura 7), se aprecia como la impedancia de salida en lazo cerrado es forzada a través de los lazos de control a comportarse resistivamente; mientras que en el diagrama de respuesta en frecuencia (figura 8) se mantiene el comportamiento inductivo, similar al presentado sin el lazo de impedancia virtual.
Al no tener una resistencia en serie con el condensador de salida o que el valor de la resistencia sea pequeño del orden de unos cuantos ohmios, el comportamiento en alta frecuencia no sería de tipo resistivo, presentándose un THD de tensión considerablemente alto, al manejar cargas no lineales. Esto se debe a que el valor de la reactancia de salida es dependiente de la frecuencia [17]. La solución es incluir en el lazo de la impedancia virtual, una impedancia inductiva junto a un filtro pasa alto de la corriente del inductor [18].
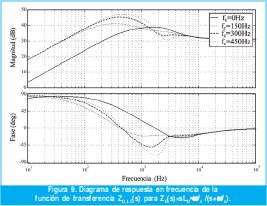
La figura 9 muestra el diagrama de respuesta en frecuencia para la impedancia de lazo cerrado, teniendo en cuenta el filtro pasa alto presentado en la ecuación (16).
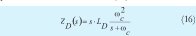
Donde:
ωc es la frecuencia de corte del filtro en radianes/seg.
Con el fin de analizar el comportamiento de ZO_LC(s) cuando la frecuencia de corte del filtro aumenta, se tomaron las frecuencias de corte de 150Hz, 300Hz y 450Hz (figura 9).
Aunque el efecto no es muy notorio se puede apreciar como con una frecuencia de corte del filtro cercana a la fundamental, la impedancia de salida cambia su comportamiento inductivo por uno resistivo en el rango de 200Hz a 2kHz aproximadamente. Dibujando nuevamente el esquema droop de la figura 1, se pueden visualizar mejor sus bloques en la figura 10.
3.2 Implementación de los esquemas droop
Debido a las características de control utilizadas en el inversor y al comportamiento de la impedancia de salida del inversor en lazo cerrado, así como al uso de la resistencia de amortiguación Rd , finalmente se ha optado por no utilizar el lazo de impedancia virtual empleado por diferentes autores [8], [17]. Lo anterior en razón a que se obtienen resultados similares en cuanto a la posibilidad de los convertidores para trabajar en paralelo, así como al comportamiento resistivo que presenta la impedancia de salida a alta frecuencia, ideal para disminuir el THD de la tensión cuando se manejan cargas no lineales.
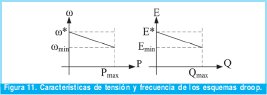
Como la impedancia de salida del inversor a bajas frecuencias presenta un comportamiento inductivo se hace uso de las relaciones establecidas en (6) y (7). Realizando una representación grafica de dichas ecuaciones, la figura 11 muestra las características de tensión y frecuencia de los esquemas droop para el caso en que la impedancia de salida del inversor sea inductiva.
Con base en las características de la figura 11 se determinan las constantes m y n (figura 10), estableciéndose una variación del 0.2% en torno a la frecuencia nominal, lo que implica que ω*=2•π50.5, ωmin=2• π •49.5 y Pmax=440W, con lo que se obtiene una pendiente negativa m=0.001. Mientras que para una variación de aproximadamente el 0.05% de la tensión pico de la tensión de salida se tiene que E*=325V, Emin=324.85V y 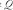 max=150VAr, lo que establece una pendiente negativa n=0.001.
max=150VAr, lo que establece una pendiente negativa n=0.001.
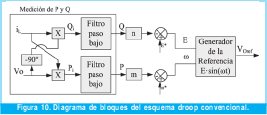
La potencia activa (P) puede ser calculada como producto de la multiplicación de la tensión de salida por la corriente de salida y el filtrado de dicho producto a través de un filtro paso bajo. De manera similar se calcula la potencia reactiva (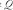 ), pero aquí hay que tener en cuenta que la corriente se salida se encuentra desfasada 90°. Dicho desfase se consigue utilizando un filtro paso bajo, de la misma forma en que se empleó para obtener la componente en cuadratura en el diseño del PLL.
), pero aquí hay que tener en cuenta que la corriente se salida se encuentra desfasada 90°. Dicho desfase se consigue utilizando un filtro paso bajo, de la misma forma en que se empleó para obtener la componente en cuadratura en el diseño del PLL.
Se debe tener en cuenta que las desviaciones en frecuencia y tensión son inherentes a la operación de los esquemas droop. Estas desviaciones pueden limitar el intercambio de potencia y la estabilidad del sistema [19]. Con el fin de evitar desviaciones en frecuencia en estado estable, se ha propuesto en [12] el siguiente esquema:
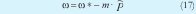
Donde:
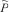 es la señal de potencia activa sin la componente DC.
es la señal de potencia activa sin la componente DC.
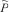 se determina a través de la ecuación (18).
se determina a través de la ecuación (18).
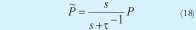
Donde;
τ es la constante de tiempo de la acción transitoria del esquema droop.
El filtro paso bajo, esquematizado en el diagrama de bloques de la figura 10, deja de ser un filtro paso bajo al agregar en cascada el término de la ecuación (18), que corresponde a un filtro paso alto, y el bloque se rediseña como un filtro paso banda.
4. RESULTADOS DE SIMULACIÓN
Las simulaciones del inversor fueron realizadas en PSIM 7.05.
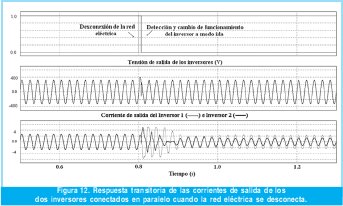
En la figura 12 se muestran las principales formas de onda de dos inversores operando en paralelo tras la desconexión de la red eléctrica.
En la figura 12 también se observa cómo los dos inversores antes de la desconexión de la red en 0.8 segundos, entregan la potencia para la que fueron programados (440W cada uno), en este caso se encuentran entregando la misma cantidad de potencia a la red. Al producirse la desconexión los dos inversores se ajustan para manejar la carga, es decir se reparten la cantidad de potencia que entregan en función de las pendientes m y n programadas para el esquema droop. Para este caso, el segundo inversor posee una m=0.002 y una n=0.0015, con lo que el inversor 1, maneja 420W y el inversor 2 maneja 245W, para un carga total de 665W. Adicionalmente se observa que los valores de tensión y frecuencia permanecen dentro de los rangos establecidos por los diferentes estándares y normas.
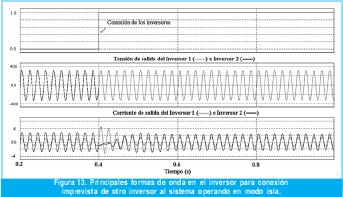
La figura 13 muestra cómo al conectar de improviso en modo isla otro inversor, el sistema en general se acondiciona y se produce un reparto de carga entre los mismos. El hecho de que dichos inversores, funcionando como fuente de tensión se puedan conectar en paralelo, se debe a la característica inductiva de la impedancia de salida en lazo cerrado a la frecuencia fundamental.
La figura 13 muestra como los dos inversores (programados ambos, con los mismos valores de pendientes m y n) en un principio se encuentran manejando cargas locales que demandan la misma potencia (430W), pero por separado. En 0.4 segundos se colocan en paralelo y se aprecia como las tensiones y las corrientes convergen hasta colocarse en fase, mediante el ajuste que han realizado los controladores.
Con el fin de evitar respuestas transitorias como las presentadas en las figuras 12 y 13, primero se deben igualar las condiciones finales de los controladores que funcionan cuando el inversor se encuentra en modo red, a las condiciones iniciales de los controladores en modo isla. Posteriormente, al interconectar un sistema a otro se debe plantear la necesidad de diseñar un lazo que permita hacer cero la diferencia de fase entre los inversores con el fin de interconectarlos.
5. CONCLUSIONES
En el presente artículo se analizó el efecto que posee la impedancia de salida de los inversores en la conexión en paralelo de los mismos, para operar en modo isla. Se demostró como considerando la característica de impedancia de salida en el diseño del controlador, así como la inserción de una resistencia en serie con el condensador de salida, la cual obedece la resistencia de amortiguación, insertada en el modo red, presenta resultados similares a los expuestos cuando se utilizan lazos de realimentación de impedancia (comportamiento inductivo del inversor a bajas frecuencias y comportamiento resistivo a altas frecuencias), pero con la ventaja de aprovechar las características propias de diseño del inversor, sin necesidad de lazos de realimentación adicionales. Finalmente, se validaron mediante simulaciones los esquemas droop junto a la utilización de un controlador PI y la resistencia de amortiguación como alternativa para funcionamiento de inversores en modo isla con posibilidad de interconectarlos en paralelo. En trabajos futuros se pretende validar experimentalmente lo expuesto en este artículo.
REFERENCIAS BIBLIOGRÁFICAS
[1] REN21 Steering Committee. "Renewable 2009, Global Status Report". Worldwatch Institute Washington, DC. 2009.
[2] R.H. Lasseter, et al. "White paper on integration of distributed energy resources. The CERTS microgrid concept". Consortium for Electric Reliability Technology Solutions. 2002, pp. 1-27.
[3] PSIM 7.0 User´s Guide (2006), Powersim Inc.
[4] N. Mohan, T.M. Underland, W.P. Robbins, "Power electronics: converters, applications, and design". 3th ed. International. John Wiley & Sons. 2003.
[5] Y. S. Jung, et. al. "A new small signal modeling of average current mode control". Power Electronics Specialists Conference, 1998. PESC 98 Record. 29th Annual IEEE, vol. 2. 1998, pp.1118-1124.
[6]D. M. Sable, R.B. Ridley, "Comparison of performance of single-loop and current-injection control for PWM converters that operate in both continuous and discontinuous modes of operation". Power Electronics, IEEE Transactions on, vol. 7, No.1, Jan 1992, pp.136-142.
[7] D. N. Zmood, D.G. Holmes, "Stationary frame current regulation of PWM inverters with zero steady-state error". Power Electronics, IEEE Transactions on, vol.18, No.3, May 2003, pp. 814-822.
[8] R. W. Erickson, "Fundamental of power electronics". Norwell, MA: Kluwer. 1997.
[9] J. Grainger, W. Stevenson, "Power System Analysis". McGraw-Hill. 1994.
[10] M. C. Chandorkar, et. al. "Control of parallel connected inverters in standalone AC supply systems". Industry Applications, IEEE Transactions on, vol. 29, No.1, 1993, pp.136-143.
[11] J. M. Guerrero, et. al. "Decentralized Control for Parallel Operation of Distributed Generation Inverters Using Resistive Output Impedance". Industrial Electronics, IEEE Transactions on, vol. 54, No.2, April 2007, pp.994-1004.
[12] J.M. Guerrero, et. al. "Output Impedance Design of Parallel-Connected UPS Inverters With Wireless Load-Sharing Control". Industrial Electronics, IEEE Transactions on, vol. 52, No.4, Aug. 2005, pp. 1126-1135.
[13] J. F. Chen, C.L. Chu, C.L. Huang, "The parallel operation of two UPS by the coupled-inductor method". Industrial Electronics. Proceedings of the IEEE International Symposium on, May 1992, pp.733-736.
[14] C. C. Hua, et. al., "Parallel operation of inverters for distributed photovoltaic power supply system". Power Electronics Specialists Conference, 2002. pesc 02. 2002 IEEE 33rd Annual, vol. 4, 2002, pp. 1979-1983.
[15] K. De Brabandere, et. al. "A Voltage and Frequency Droop Control Method for Parallel Inverters". Power Electronics, IEEE Transactions on, vol. 22, No.4, July 2007, pp.1107-1115.
[16] J. M. Guerrero, et. al. "A wireless controller for parallel inverters in distributed online UPS systems". Industrial Electronics Society, 2003. IECON '03. The 29th Annual Conference of the IEEE, vol. 2, 2003, pp. 1637-1642.
[17] S. J. Chiang, et. al. "A multimodule parallelable series-connected PWM voltage regulator". Industrial Electronics, IEEE Transactions on, vol. 48, No.3, Jun. 2001, pp.506-516.
[18] J. M. Guerrero, "A wireless controller to enhance dynamic performance of parallel inverters in distributed generation systems". Power Electronics, IEEE Transactions on, vol. 19, No.5, Sept. 2004, pp. 1205-1213.
[19] E. A. A. Coelho, P.C. Cortizo, P.F.D. Garcia, "Small-signal stability for parallel-connected inverters in stand-alone AC supply systems". Industry Applications, IEEE Transactions on, vol.38, no.2, Mar/Apr 2002, pp.533-542.
César Leonardo Trujillo Rodríguez
Ingeniero Electrónico, Universidad Distrital. Mágister en Ingeniería Eléctrica, Universidad Nacional de Colombia. Candidato a Doctor en Ingeniería Electrónica, Universidad Politécnica de Valencia, España. Profesor en Electrónica de Potencia en la Universidad Distrital Francisco José de Caldas y pertenece como investigador al grupo LIFAE y al grupo GSEI en donde realiza estudios sobre calidad de potencia eléctrica, microrredes eléctricas y fuentes renovables de energía. cltrujillo@udistrital.edu.co
David Velasco de la Fuente
Ingeniero Industrial, Universidad de Valladolid. Mágister en Ingenierías de Sistemas Electrónicos, Universidad Politécnica de Valencia. Candidato a Doctor en Ingeniería Electrónica de la Universidad Politécnica de Valencia, España. Actualmente se desempeña investigador en Electrónica de Potencia en la Universidad Politécnica de Valencia y pertenece al grupo GSEI en donde realiza estudios sobre microrredes eléctricas y fuentes renovables de energía. davede@posgrado.upv.es
Emilio Figueres Amorós
Ingeniero Técnico Industrial, Universidad Politécnica de Valencia. Mágister en la École Nationale Supérieure d'Electronique, d'Electrotechnique, d'Informatique et Hydraulique de Toulouse, Francia. Doctor en Ingeniería Industrial de la Universidad Politécnica de Valencia. Actualmente se desempeña como profesor y director del Departamento de Ingeniería Electrónica de la Universidad Politécnica de Valencia. Pertenece como investigador al grupo GSEI, en donde realiza estudios sobre modelamiento y control de convertidores de potencia, procesamiento de potencia de fuentes de energía renovables y convertidores conectados a red para generación de potencia distribuida y mejoramiento de la calidad de potencia. efiguere@eln.upv.es
Gabriel Garcerá Sanfeliú
Ingeniero, Magíster y Doctor de Telecomunicación de la Universidad Politécnica de Valencia, España. Actualmente se desempeña como profesor y director del Grupo de Investigación en Sistemas Electrónicos Industriales-GSEI, de la Universidad Politécnica de Valencia, en donde realiza estudios sobre modelamiento y control de convertidores de potencia, control robusto de convertidores conmutados, circuitos de corrección de factor de potencia, sistemas de alimentación ininterrumpida, inversores conectados a red, y convertidores para fuentes de energía renovables. ggarcera@eln.upv.es
Rubén Ortega González
Ingeniero Electricista, Escuela Superior de Ingeniería Mecánica y Eléctrica ESIME, del Instituto Politécnico Nacional IPN-México. Mágister en Ingeniería de Sistemas en la Sección de Estudios de Posgrado e Investigación de la ESIME-IPN. Actualmente se desempeña como profesor en la Escuela Superior de Cómputo del IPN, en el departamento de Sistema Electrónicos y pertenece al Grupo de Sistemas Electrónicos, así como al grupo GSEI en donde realiza estudios sobre, microrredes eléctricas y fuentes renovables de energía. rortegag@ipn.mx
Creation date:
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.





2.jpg)










