DOI:
https://doi.org/10.14483/23448393.21253Published:
2024-09-19Issue:
Vol. 29 No. 3 (2024): September-DecemberSection:
Education in EngineeringBolstering the Spatial Rotation Ability to Understand the Topics of Point and Line in Descriptive Geometry
Potencialización de la habilidad espacial de rotación para comprender las temáticas del punto y línea en geometría descriptiva
Keywords:
descriptive geometry, spatial ability, previous ideas, pre-test, post-test (en).Keywords:
habilidad espacial, ideas previas, pre-test, post-test, geometría descriptiva (es).Downloads
References
M. C. Linn and A. C. Petersen. "Emergence and characterization of sex differences in spatial ability: A meta-analysis," Child Dev., vol. 56, no. 6, pp. 1479-1498, 1985. https://doi.org/10.2307/1130467
D. F. Lohman, "Spatial ability: Individual differences in speed and level. Technical Report No. 9. Aptitude Research Project," Stanford Univ., CA, School of Education, 1979.
G. McGee, "Human spatial abilities: Psychometric studies and environmental, genetic, hormonal and neurological influences," Psychol. Bulletin, vol. 86, no. 5, pp. 889-918, 1979. https://doi.org/10.1037/0033-2909.86.5.889
S. A. Sorby and B. J. Baartmans, "The development and assessment of a course for enhancing the 3-D spatial visualization skills of first year engineering students," J. Eng. Edu., vol. 89, 2000. https://doi.org/10.1002/j.2168-9830.2000.tb00529.x
D. Jaison, M. B. Weaver, and S. Ray, “WIP teaching engineers to sketch: Impacts of feedback from an intelligent tutoring software on engineers’ sketching skill development," in 2022 IEEE Front. Edu. Conf. (FIE), 2022. [Online]. Available: https://doi.org/10.1109/FIE56618.2022.9962419
A. A. Kahharov, "Intensive methods of developing students' spatial imagination in the teaching of graphic sciences," Annals Romanian Soc. Cell Biology, vol. 25, no. 4, art. 11885, 2021. [Online]. Available: http://annalsofrscb.ro/index.php/journal/article/view/4042
N. A. Aguilera-González, "How to include augmented reality in descriptive geometry teaching," Procedia Comp. Sci., vol. 75, pp. 250-256, 2015. https://doi.org/10.1016/j.procs.2015.12.245
K. Dent and M. M. Smyth, "Capacity limitations and representational shifts in spatial short-term memory," Visual Cog., vol. 13, no. 5, pp. 529-572, 2006. https://doi.org/10.1080/13506280444000760
K. Cotton and T. J. Ricker, "Examining the relationship between working memory consolidation and long consolidation," Psychonomic Bulletin Rev., 2022. https://doi.org/10.3758/s13423-022-02084-2
O. Ha and N. Fang, "Spatial ability in learning engineering mechanics: Critical review," J. Prof. Issues Eng. Edu. Prac., vol. 142, no. 2, art. 0000266, 2016. https//doi.org/10.1061/(ASCE)EI.1943-5541.0000266
J. Buckley, D. Canty, and N. Seery, "Spatial working memory in mental rotations: A case for exploring neural efficiency and cognitive strategies," 2018. [Online]. Available: https://sites.asee.org/edgd/wp-content/uploads/sites/22/2018/07/43-J-Buck.pdf
B. N. Verdine, R. M. Golinkoff, K. Hirsh-Pasek, and N. S. Newcombe, "Spatial skills, their development, and their links to mathematics," Links Spatial Math. Skills Preschool Years, vol. 82, no. 1, pp. 7-30, 2017. https://doi.org/10.1111/mono.12280
L. M. Weckbacher and Y. Okamoto, "Mental rotation ability in relation to self-perceptions of high school geometry," Learn. Indiv. Diff., vol. 30, pp. 58-63, Feb. 2014. https://doi.org/10.1016/j.lindif.2013.10.007
C. Carbonell Carrera, J. L. Saorín, and S. Hess-Medler, "Spatial orientation skill for landscape architecture education and professional practice," Land, vol. 9, no. 5, art. 161, 2020. https://doi.org/10.3390/land9050161
M. Giner, "Problemas en el desarrollo de la lateralidad," 2007. [Online]. Available: http://psicopedagogias.blogspot.com.es/2007/11problemas-en-el-desarrollo-de-la.html
C. Ramos, I. C. Angel, U. G. López, M. Y. M. Cano, and R. Core, "Core elements of STEM approach educational experiences," Rev. Científica, vol. 45, no. 3, art. 19298, 2022. https://doi.org/10.14483/23448350.19298
F. N. Jiménez, L. Beleño, J. Agudelo, and J. L. Muñiz, "Didactic units in physics as learning enhancers for engineering students," Form. Univ., vol. 13, no. 6, pp. 143-154, Dec. 2020. https://doi.org/10.4067/S0718-50062020000600143
M. Prosser, K. Trigwell, E. Hazel, and F. Waterhouse, "Students’ experiences of studying physics concepts: The effects of disintegrated perceptions and approaches," Eur. J. Psychol. Edu., vol. 15, pp. 61-74, 2000. https://doi.org/10.1007/BF03173167
L. S. Nadelson, B. C. Heddy, S. Jones, G. Taasoobshirazi, and M. Johnson, "Conceptual change in science teaching and learning: Introducing the dynamic model of conceptual change," Int. J. Edu. Psychol., vol. 7, no. 2, pp. 151-195, Jun. 2018. https://doi.org/10.17583/ijep.2018.3349
M. J. Kirker and I. Stonebraker, "Architects, renovators, builders, and fragmenters: A model for first year students' self-perceptions and perceptions of information literacy," J. Acad. Librarianship, vol. 45, no. 1, pp. 1-8, Jan. 2019. https://doi.org/10.1016/j.acalib.2018.10.009
S. A. Sorby, "Educational research in developing 3-D spatial skills for engineering students," Int. J. Sci. Edu., vol. 31, no. 3, pp. 459-480, Feb. 17, 2009. https://doi.org/10.1080/09500690802595839
T. J. van Weert and A. Pilot, "Task-based team learning with ICT: Design and development of new learning," Edu. Info. Tech., vol. 8, pp. 95-214, Jun. 1, 2003. https://doi.org/10.1023/A:1024562515675
S. A. Sorby, T. Drummer, and R. Molzon, "Experiences in using spatial skills testing instruments with younger audiences," J. Geom. Graph., vol. 10, no. 2, pp. 227-235, 2006. [Online]. https://www.heldermann-verlag.de/jgg/jgg10/j10h2sorb.pdf
J. Houser and C. Kloesel, Obra filosófica reunida de Charles Sanders Peirce, vol. I (1867-1893). Mexico: Fondo de Cultura Económica, 2012.
J. Dewey, Cómo pensamos. Barcelona, Spain: Ediciones Paidós Ibérica S.A., 1989.
Z. C. G. Escobar, "De la ruptura a la sutura de la secuencia tecnológica desde las posibilidades divergentes del pragmatismo: a partir del pensar, el aprender y el creer," PhD dissertation, Universidad Tecnológica de Pereira, Pereira, Colombia, 2017.
R. Guay, Purdue Spatial Visualization Test: Rotations, 1977.
B. M. del R. Ordaz, "Diseño de un producto multimedia como recurso que coadyuve al proceso de enseñanza-aprendizaje de la geometría descriptiva en las licenciaturas de diseño," MS thesis, Universidad Autónoma Metropolitana, 2010.
S. A. Sorby, "Using adaptive comparative judgment to holistically assess creativity of design solutions: A comparison of first-year students and educators’ judgments," in Annual Conf. Expo. Harbor Eng. Edu. 30 Years, 2023.
J. M. Gentil, "Papel de la geometría descriptiva en la enseñanza de la arquitectura," 1986. [Online]. Available: https://idus.us.es/bitstream/handle/11441/51269/papel%20de%20la%20geometria.pdf;jsessionid=B9AD368CA06EF768B8F5351F88CCDCFA?sequence=1
R. Hernández, S. Fernández, C. Baptista, P, Metodología de la investigación, 6th ed. Mexico, D.F., Mexico: McGraw-Hill Education, 2014.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Recibido: 14 de octubre de 2023; Aceptado: 25 de abril de 2024
Abstract
Objective:
The main objective is to determine how the spatial rotation ability (HER) is enhanced in first-year engineering students of Universidad Tecnológica de Pereira (UTP).
Methodology:
A qualitative study is proposed which is aimed at understanding the role of students’ prior ideas in the development of the HER. Initially, a test (PSVT: R) is administered to a group of students as a pre-test. Four of these students are selected using a Student’s t-test. Then, an instrument that measures the notions regarding the concepts of point and line that students have developed since childhood is applied.
Results:
After conducting the post-test, progress in the students’ HER is evident. This difference was statistically significant (p<0.05). The tests of the four selected students were analyzed using the Atlas ti software.
Conclusions:
The development of the HER was evidenced in the results of the normalized PSVT: R post-test, implying the evolution of students’ (previous, vague, and imprecise) ideas regarding 3D notions of point and line.
Keywords:
spatial ability, previous ideas, pre-test, post-test, descriptive geometry.Resumen
Objetivo:
El objetivo principal es determinar cómo se potencializa la habilidad espacial de rotación (HER) en estudiantes de primer año de ingeniería de la Universidad Tecnológica de Pereira (UTP).
Métodología:
Se propone un estudio cualitativo orientado a comprender el rol de las ideas previas de los estudiantes en el desarrollo de la HER. Para ello, inicialmente se aplica una prueba (PSVT: R) a un grupo de estudiantes a manera de pre-test. Se seleccionan cuatro de estos estudiantes mediante una prueba t de Student. Luego, se aplica un instrumento que mide las nociones sobre los conceptos de punto y línea que los estudiantes han desarrollado desde su infancia.
Resultados:
Una vez realizado el post-test, se evidencia el progreso en la HER de los estudiantes. Esta diferencia fue estadísticamente significativa (p<0.05). Las pruebas de los cuatro estudiantes seleccionados fueron analizadas mediante el software Atlas ti.
Conclusiones:
Se evidenció el desarrollo de la HER en los resultados del post-test normalizado PSVT: R, lo que implica la evolución de las ideas (previas, vagas e imprecisas) de los estudiantes respecto a nociones en 3D sobre el punto y la línea.
Palabras clave:
habilidad espacial, ideas previas, pre-test, post-test, geometría descriptiva.Introduction
Through the testing of previous ideas regarding point and line, students sharpen their understanding of grounding and palpation, as through a duct or a pipe in 3D. They can visualize and imagine the relationship of a point seen from a plan view with the same line, albeit represented in an elevation view. This allows them to improve their ability to retain information, which is essential when performing or re-performing post-tests (PSVT:R).
Through the development of the spatial ability of rotation (HER), first-year students acquire the method for and faculty of learning the aforementioned subject in the field of descriptive geometry and in all STEM areas (science, technology, engineering, and mathematics).
Testing previous ideas regarding point and line enables the utilization of tools, such as software, that allow students to dynamize their HER.
As for spatial abilities, various studies have been conducted, mainly in the field of psychology 1, in the form of meta-analysis of the characterization of said ability in relation to gender differences, as well as regarding the classification of the spatial relations associated with the ability to quickly rotate and visualize figures in two or three dimensions (mental rotation) and with the ability to mentally manipulate visual information through staged or sequential analysis, imagining the rotations of objects in space. This is especially useful in engineering graphics.
When referring to spatial skills, special emphasis must be placed on mental rotation, which facilitates the accurate and quick rotation of 2D and 3D figures. This is supported by spatial orientation, allowing students to physically or mentally orient themselves in space. In a meta-analysis of the difficulties of 2D and 3D rotation 1, three spatial skills were identified: 1) spatial orientation, which requires students to locate horizontal or vertical positions on a stationary screen while ignoring distracting information and any difficulties in locating themselves in space (preconceptions); 2) mental rotation, i.e., the ability to imagine how objects appear when rotated in two- or three-dimensional space; and 3) spatial visualization, or the ability to manipulate complex spatial information when one requires multiple steps to produce a correct solution.
Spatial ability 2 refers to the ability to generate, maintain, and manipulate abstract visual images. It has been divided into two hierarchies: spatial visualization, known as spatial vision and described as the ability to manipulate, rotate, and mentally invert objects from graphic representations; and spatial orientation, which depends on laterality and psychomotor development, allowing students to orient themselves physically or mentally in space 3.
For the development of spatial skills, the following tools have been used: manual sketching to perform spatial maneuvers with bodies, perspectives, views, sections, rotations, and symmetries, and the development of surfaces or folds, etc.4; and tools such as Texas A&M University’s SketchTivity, which uses advanced technology to provide timely information and feedback to enhance instruction and motivation in learning to draw 5.
The use of information and communication technologies (ICTs), combined with AutoCAD’s 2D and 3D capabilities in explaining topics of descriptive geometry 6, as well as the use of augmented reality (AR) for teaching in this area 7, aims to stimulate students’ interest in the use of technology and develop perception and spatial analysis skills.
Other works on spatial skills have focused on spatial memory. First-year college students appear to have spatial working memory (SWM), which refers to the system of psychological processes and representations underlying the ability to remember the location of objects in the world for short periods of time 8. Some of the information initially held in the working memory can be retained for longer periods of time and eventually stored in the long-term memory 9.
These works show that spatial information regarding the position of a stimulus should be stored briefly before subsequent rotations, especially in processes requiring multiple rotations or steps. Moreover, it has been claimed that additional storage is necessary to retrieve target rotation sequences with the aim of comparing the target and the potential stimuli after obtaining a multi-step solution.
SWM is considered to be of great importance for students’ space and as a psychological mechanism inherent to mental rotations 10,11.
Other research works have focused on mental rotation and mental folding 12 and their similarities and differences from various perspectives (definitions, cognitive processes, components, neurological bases, developmental trajectories, malleability, predictive validity, and psychometric properties), in addition to studying the marked gender differences in mental rotation.
Another study examined the relationship between mental rotation, performance in mathematics, and mathematical self-perception in 113 high school students 13.
Interpreting a landscape requires understanding the relationships between the map, the represented space, and the observer, for which it is necessary to use spatial thinking when solving spatial problems. This is done through the spatial orientation test (perspective taking/spatial orientation test), which is aimed at measuring the spatial orientation component. The results show that map-based tasks are more efficient than route-based ones. Strategies using 2D and a 2D/3D combination are more efficient than those using only 3D 14. Using the same measurement tool and the same population cohort allowed for comparisons based on quantitative data. Data from all these workshops were collected in a single study. By using statistical inference methods and comparisons between different factors, the most effective combinations of variables in the development of spatial orientation could be identified.
Spatial orientation depends on memory capacity and, to a large extent, on the process of lateralization and psychomotor development. In addition, it is governed by the categories of space and time that we use to understand our environment, to remember it, and to react accordingly, with the purpose of processing all the external information received 15. Today, it is emphasized that spatial skills are essential for many applications, especially for STEM education 16. The current goal is to use active learning strategies to develop experiences with the STEM approach, for which it is necessary to integrate innovative and creative teaching practices that allow developing spatial skills. Here, the teacher should be an instigator of doubts and a shaper of intentions, allowing students to propose solutions to problems of their community.
Prior ideas
The state of the art on prior ideas in engineering freshmen (first-year students) focuses on the elaboration of didactic units for subjects in areas such as mathematics, physics, and chemistry, among others. This design is based on the knowledge of prior ideas and the identification of students’ learning styles 17.
Students, when faced with formal instruction, bring their own ideas about the natural phenomena to be taught in the classroom, i.e., they have prior mental schemas 18. These schemas allow subjects to interpret the information imparted and significantly influence the understanding of scientific concepts. Knowledge of students’ prior ideas should lead the teacher in planning a didactic unit while aiming to achieve conceptual change 19.
Students are not blank slates when they arrive at the university, nor do they remain frozen in time. From the moment they acquire the skills to question prior knowledge, the university campus becomes a space for transformative growth, as they strive to understand themselves in the face of academic changes and their vision of themselves as researchers 20.
The factors that influence the development of spatial skills are related to students’ previous experiences. According to 21, the factors that seem to be significant in students with well-developed spatial skills, whose absence can hinder development, are as follows: having played with construction games during childhood (Lego, blocks, and puzzles); having participated in workshops or product development or mechanics classes in high school (having studied at a university with a vocational technical modality); having used 3D computer games or video games (the spatial attention capacity improves when players train in a persistent way, perfecting their working memory capacity); having participated in some types of sports; and having well-developed mathematical skills.
This includes students who were born in geographic locations where they had to develop their spatial skills for survival and work from an early age, as well as those who were fortunate enough to be born into a household of professionals in the arts, engineering, architecture, crafts, general manufacturing, and areas dedicated to industrial and automotive mechanics.
How students think from the perspective of what they bring to their minds is essential in research. This is a complex and meticulous construct, influenced by beliefs, innate characteristics, and learning histories. The mere fact of tapping into this potential inherent in their human condition allows this work to empower students to become the best they can be, as well as to acquire the skills and motivation to learn when testing prior ideas in 3D. This involves the concepts of point and line when, within the area of descriptive geometry, they decipher or reveal the solution to real 3D problems in a 2D surface.
Regarding the preconceptions of first-year engineering students, our initiative is structured to transform what they know, how they know, why they know, and their captivation, fascination, or interest 22 into learning dynamics that allow them to automatically relate their prior knowledge of point and line to the 3D and 2D reality of the preconceptions test. This, in order to spark their interest and curiosity in this subject of descriptive geometry.
Currently, at the university, students can enroll in technical programs (engineering and technology) without having taken any technical drawing subject. This allows for the coexistence of young people with no previous knowledge of geometry and those who, although they studied drawing in high school, have not developed their spatial vision skills 23.
Theoretical framework
The school that supports this research work is pragmatism; objective knowledge may be impossible, so truth can be redefined as that which functions within our limited way of experiencing reality. As indicated by Pierce, ”consider the effects of the objects of your conception. Then, your conception of these effects is the totality of your conception of the object" (24, p. 33).
The real first lesson we are entitled to when learning logic is how to clarify our ideas. However, it is unquestionable that, for an individual, it is much more valuable to have a few clear ideas than to have many confusing ones:
It is terrible to see how a single confused idea, a single formula without significance, hidden in the head of a young person acts, sometimes, as the obstruction of an artery by inert matter, preventing cerebral irrigation and condemning its victim to perish in the fullness of his intellectual vigor and amidst intellectual abundance. (24, p. 173)
For (25, p. 35), to be thoughtful means to be logical; such a person ties the dots, recognizes, calculates, risks an explanation: ”the real potential of intellectual education is the transformation of natural potentialities into proven and experienced abilities". Reflective learning is contextualized knowledge; it means contemplating knowledge with regard to its relations with other things. Reflective learning opens the door to a new logic of thought: that of understanding the third dimension 26.
The prior ideas that students bring with them regarding the concepts of point and line are linked to their personality, upbringing, informative experiences (in primary and middle school), and social context. These ideas are part of each student’s particular history.
As a first contribution to the urgent need to identify students who can rotate figures in 2D and 3D and implicitly execute the conversion from 2D to 3D, it is necessary to identify, by means of standardized tests (PSVT:R), the population to be intervened. This testing process was developed and implemented by 27. It has 30 items, and it provides a model in its original state, which is then rotated in any of the three Cartesian axes. This rotation model is called matrix rotation. This test also provides an exercise proposal consisting of a solid in its original state. Five possible answers are given on how that solid should be rotated with regard to the rotation shown in the matrix. This first perspective, called diagnostic, will allow determining, through a qualitative approach, the percentage of students in each of the aforementioned categories.
The current importance of point and line study for an engineering student lies in its contribution to the maturation of spatial reasoning (i.e., the student’s ability to imagine a body in different positions). This is something that every engineering student must cultivate from the first semesters, in order to build a solid foundation that allows them to address the difficulties and demands of the subjects in the curriculum, which necessitate a HER.
Spatial reasoning involves a student’s ability to create drawings, elaborate 3D structures, and visualize the shape and surface of a completely finished object before it is built 28.
The study of point and line is currently important for graduating engineers because it is related to the competence of communication, which allows them to decipher, interpret, explain, convince, know, perceive, and grasp projects with words and not with equations.
The concepts of point and line, understood and assimilated by engineering students at the beginning of their studies, are transversal to the curriculum and are fundamental in the contents of engineering programs. Students must apply these concepts while making themselves understood to all audience levels.
Capitalizing on how points and line move within a parallelepiped in the three main planes of projection, the auxiliary planes of elevation, and the auxiliary planes is enriching for engineers when it comes to using the appropriate language and linking explanations with understanding, especially regarding a topic related to some area of engineering or a tool for everyday life.
The line the trajectory of a moving point that moves constantly and in the same direction will always represent, for instance, the route of an airplane, the trajectory of a missile, the path of a tunnel, the course of a road, the layout of a viaduct, or the design of a hot air extraction duct, among others. This is also included in the calculation of slope, bearing, true length, and position coordinates. It is an invaluable tool to generate mental resources that aid in solving any problem in professional life. Design is a key element in contemporary engineering education, with design projects now playing a fundamental role in several first-year engineering courses 29.
Descriptive geometry is not an old-fashioned tool for engineers. This field is a part of the graphic expression of architecture 30 and has to do with graphic language, or the set of rules that enable the graphic communication of space through drawing and the methodology of geometry. In addition, when the mathematician Gaspar Monge, its creator, dubbed it as a language necessary to the engineer when conceiving a project, he immortalized it as a science that allows solving problems related to the geometry of space, where representations are built from 3D into 2D, and vice versa, through the construction of ideas. The mathematician Theodore Olivier distinguished two distinct fields: the geometrical one, with its abstract and theoretical character of spatial problems; and the graphic one, given its value as an execution of drawing, i.e., as a simple material construction on a sheet of paper. These fields are still valid today, with the support of derived digital tools.
In Latin America, which harbors countries with a broken and irregular topography, with incalculable water resources in the rivers and seas, civil engineers, architects, topographers, mining engineers, electrical engineers, and mechanical engineers are required. The region’s development is supported by the exploitation of its mineral and energy resources, in addition to agricultural exports. This range of needs ratifies descriptive geometry as an essential subject in the construction of the curriculum of knowledge, which determines the spatial development of engineering students.
In Latin America, descriptive geometry will never fall into disuse due to its contribution to the rigor and accuracy in science and engineering applications and its role in achieving a capacity for the rational perception of space, essential for operating in 2D on a sheet of paper. The ability to see in space, to rotate figures around one or more axes, and to interpret and provide real solutions to engineering problems in the transition from 3D to 2D only add to the importance of the subject.
Methodology
Considering that this research seeks to understand the development of the HER in favoring the learning of point and line within the Descriptive Geometry course in first-year students at Universidad Tecnológica de Pereira (UTP), a qualitative approach seemed to be the most appropriate choice, given the nature of the problem. However, given the use of the PSVT:R test before and after the didactic unit, we considered that it had nested quantitative aspects, given the nature of the data obtained in the test. Likewise, the scope of this research was comprehensive since it sought to specify properties, characteristics, and group profiles; some variables were discovered, and it was possible to add others to be measured 31.
Application of the PSVT test: R
Initially, we applied the test remotely to a group of 15 students, who signed an informed consent. The test took 20 minutes, and, after it was applied, Student’s t-test was conducted based on the response template and two hypotheses:
-
H 0. The HER test does not indicate that the students have spatial abilities.
-
H A . The test indicates that the students have spatial abilities.
Note that a statistical analysis was performed to identify trends and frequencies.
At this point in this document, we will look at the instruments used as tools to measure the students’ prior ideas regarding point and line.
A. Instrument 1 - Intervention: measuring preconceptions
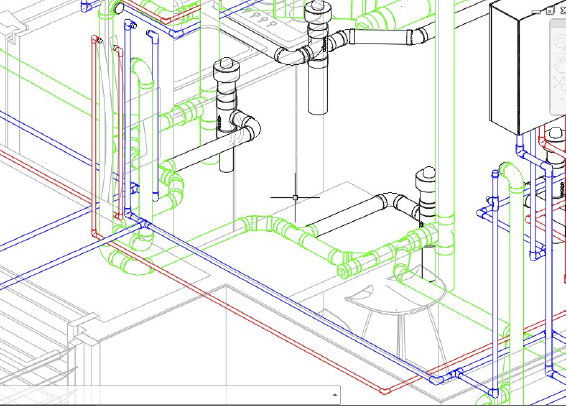
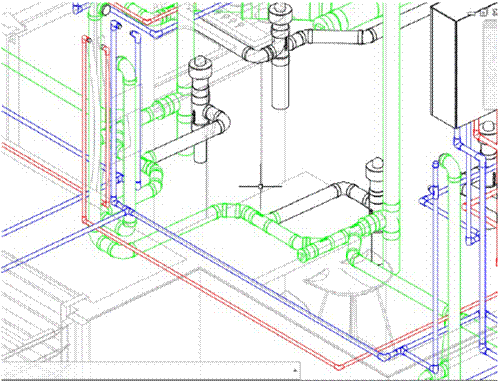
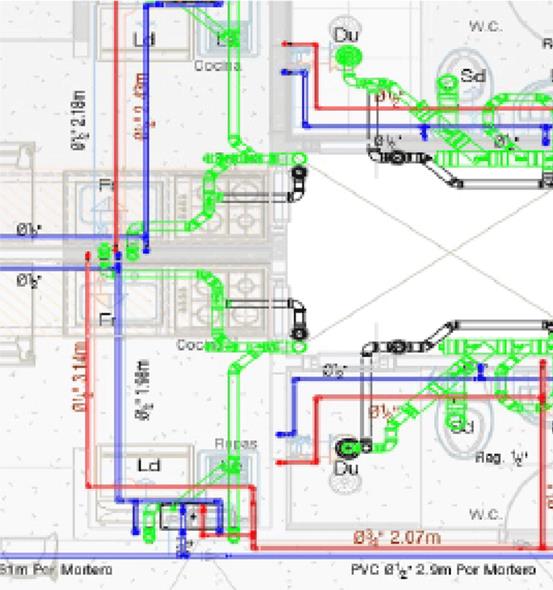
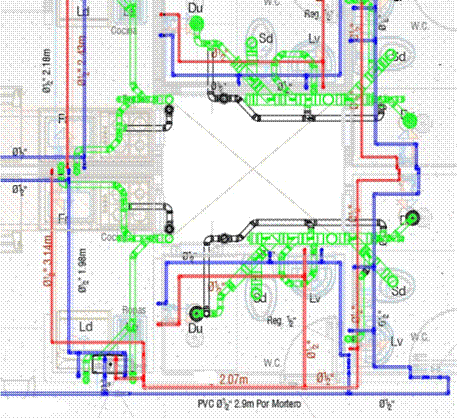
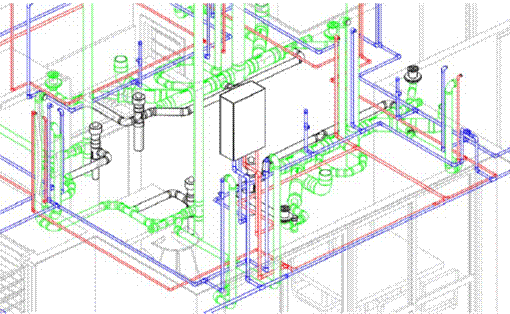
In the hydraulic circuit, shown in 3D (Fig. 1) and in 2D (Fig. 2), determine, based on the criteria of crossing or cutting lines, AND observing from the front view, whether or not:
-
the horizontal cold water pipe (blue, 1.98 m span) is below the hot water pipe (red, 3.14 m span)
-
the horizontal cold water pipe (blue, 1.98 m section) and the hot water pipe (red, 3.14 m section)represent two perpendicular lines
From the top view, based on the observation and analysis of the 2D (Fig. 3) and 3D (Fig. 4) representations, determine whether or not:
-
the 2.9 m cold water (PVC) lines and the 2.07 m diameter 1/2 hot water line are parallel
From the top 2D plan view and the right 3D side view (Fig. 4), determine whether or not:
-
the 1/2 diameter cold water line (PVC) and the 1/2 diameter hot water line cross or intersect with the 3/4 diameter (black) sanitary sewer pipe
Figure 1: 3D plan of partial distribution, hydraulic circuit
Figure 2: Partial hydraulic circuit, from plan view (top)
From the plan top view (Fig. 3), determine:
-
whether the main drain line (green), located on the right side of the plan, intersects the 3/4diameter drainpipe (black)
-
whether the 1/2 diameter hot and cold-water lines are perpendicular, intersecting, or parallel tothe black and green drain pipes in the layout (for this analysis, please refer to the 3D drawing provided in Fig. 4)
Figure 3: Partial hydraulic circuit, from plan view (top)
Figure 4: 3D plan of partial distribution, hydraulic circuit
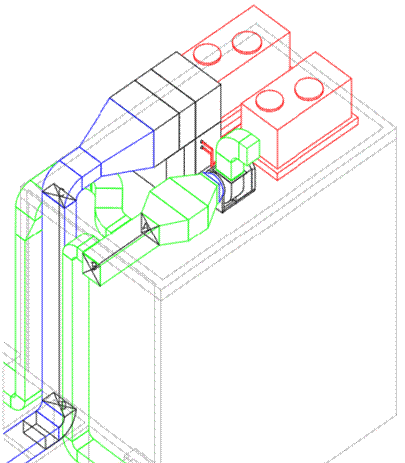
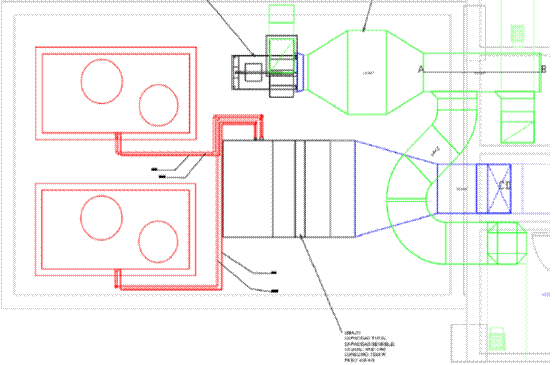
In the HVAC system shown in 3D (Fig. 5) and 2D (Fig. 6), determine whether the medical air injection (blue) and the contaminated air extraction (green) ducts, represented by lines AB and CD, can be considered to be:
-
parallel lines
-
perpendicular lines
-
intersecting lines
-
don’t know
In this plant representation, it is necessary to determine whether the air injection duct, which comes from the handling unit
-
is represented by a line as a point
-
is perpendicular or parallel to the contaminated air duct
Figure 5: HVAC installation, 3D partial view
Figure 6: Partial view of the HVAC installation, 2D drawing
Results
The analysis of PSVT:R, both the pre-test and the post-test, by means of a Student’s t-test (tendency and frequency) allowed determining the extent to which the students improved their HER with respect to both of the above-presented hypotheses (H 0 and H A ).
Tables I and II show the group of students along with their number of correct answers and their score.
Table I: Pre-test group results
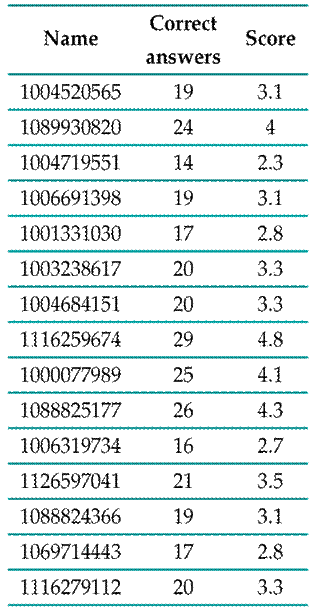
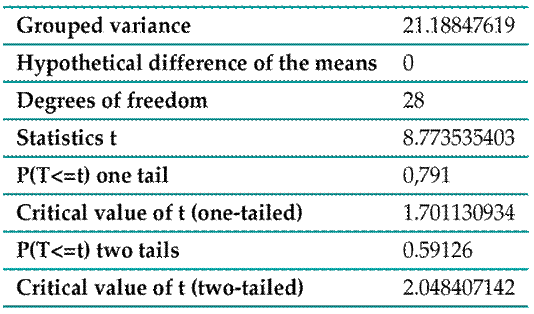
Table II: Pre-test student’s T-test analysis
Hypothesis
95 % confidence level with 14 degrees of freedom.
As the p-value (Excel output) for one tail is 0.791, it falls in the region of acceptance. Therefore, the null hypothesis is accepted: not all students have spatial thinking.
Hypothesis
95 % confidence level with 14 degrees of freedom.
Figure 7: Student’s t distribution
Table III: Post-test group results
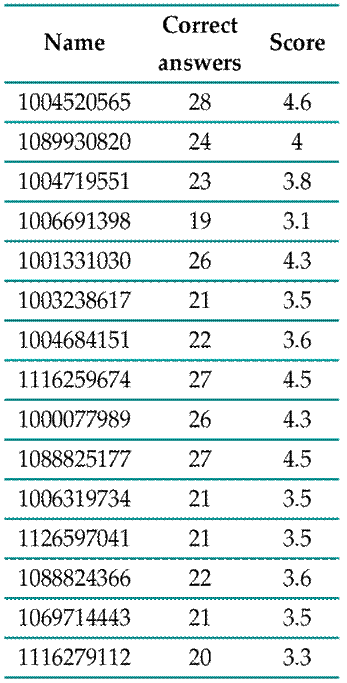
If the alternative hypothesis is accepted, then all students are able to think spatially.
It can be observed that the p-value for one tail is 0.0088. Since this value is lower than α = 0,05, it can be said, with 95 % confidence, that the alternative hypothesis is accepted, which means that the students obtained a better average in the post-test.
Pre-test and post-test analysis
This subsection presents the analyses carried out in the SPSS software with regard H 0 and H A . These hypotheses are presented below.
Figure 8: Student’s t distribution
Table IV: Student’s T-test post-test analysis
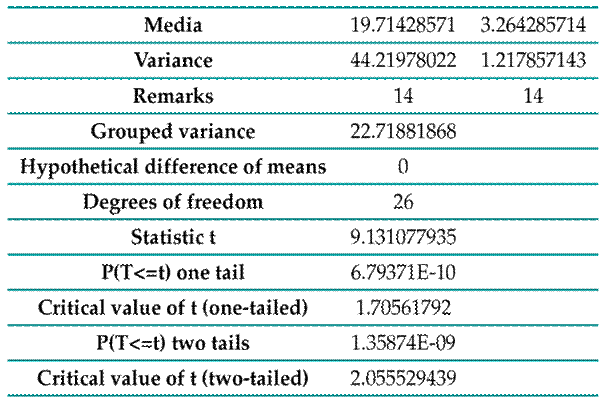
Table V: Continued student’s T-test post-test

-
H 0. The post-test is equal to the pre-test in grade point average.
-
H A . The post-test is higher than the pre-test in grade point average.
The alternative hypothesis is accepted, indicating that the students scored higher in the post-test.
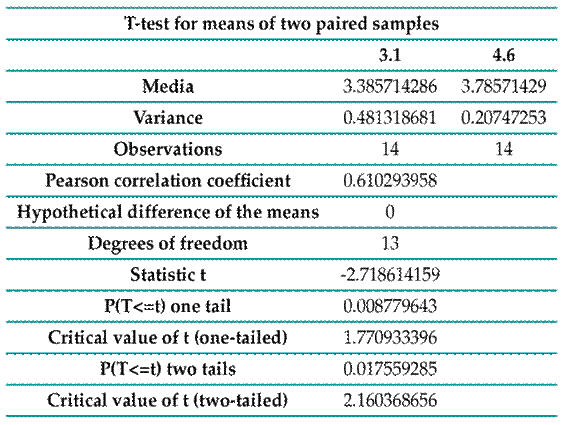
Figure 9: Analysis in EXCEL
Table VI: Pre-test and post-test student’s T-test analysis
Analyzing the test on the notion of point and line using Atlas ti 2023
After applying the test that measures the notion of point and line, some units of analysis were identified for each of the students. From them, some categories were established, with their corresponding codes. This was done using the Atlas ti 2023 software.
Initially, with the results of the PSVT:R, a quantitative analysis was performed. Regarding the qualitative analysis, we considered a work unit of four students for an in-depth case study. These students were selected because they had the lowest HER test scores.
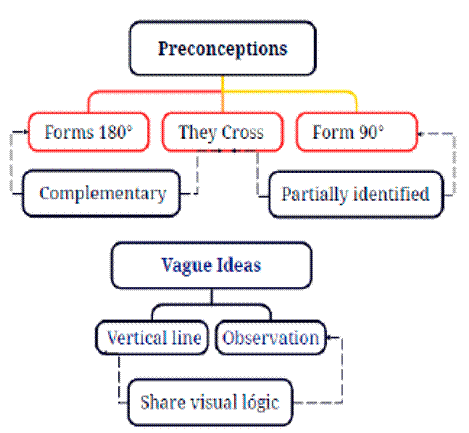
Analysis 1006319734. It can be seen how, throughout this test, the student responds with her own criteria, rooted in her simple notion of point and the line, based on her preconceptions and life experiences (from their childhood, adolescence, and high school years).
-
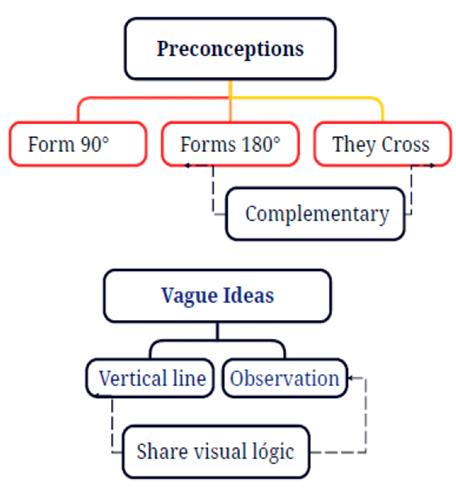
From the analysis units (90.-b. the blue and red pipes FORM A 180° ANGLE), (49.-f. they do not cut because they are parallel), (98.-a. yes, they are parallel because they never cross), (58.-9. yes, they are parallel; these ducts never cross or cut), (73.-f. yes, they are parallel because they never cross), (60.-c. yes, ducts B and C are parallel, because they FORM A 180° ANGLE), ( 30.-f. parallel lines), (61.-d. yes, ducts D and E are parallel lines because they never touch each other), (29. they FORM A 180° ANGLE), (50. g. they do not cross, they FORM A 180° ANGLE), (48.-e. parallel because they never touch each other), and (31.-g. no, the lines never cross each other because they are parallel), the subcategory FORM A 180° ANGLE emerges, corresponding to the first preconceptions: the notion that everything on the planet is flat.
-
In the units of analysis (72.-e. yes they FORM A 90°ANGLE perpendicular ducts), (76.i. if the ducts (E, I) are perpendicular, they form a 90° angle), (59.b. if they are perpendicular, they FORM A 90° ANGLE), (127.b. yes, they are on different axes. They FORM A 90° angle), (126.a. no, because they are not on the same axis; they FORM A 90° ANGLE), and (75.h. no, they are parallel. They FORM A 90° ANGLE. They are perpendicular), the subcategory FORM A 90° ANGLE is identified as a category of an individual’s first notions of knowledge regarding basic displacements in space.
-
In the units of analysis (46.c.2. vertical because it is the line CD), (28. d.2. VERTICAL LINE observed as a point from top view), (27. c.2. the line CD is observed from the front view, VERTICAL LINE), (47. d.2. vertical, because it is the line AB), the subcategory VERTICAL LINE is identified, which is associated with observing a line as a point from a plan view if this line is in its true length.
-
From the units of analysis (26.b. represented by the AB blue duct, clean air), (44.a. CD is green colored and ascending), (25.a. CD is green colored), (45.b. AB blue colored, carries medicinal air), the subcategory OBSERVATION arises.
Figure 10: Axial coding: preconceptions and vague ideas
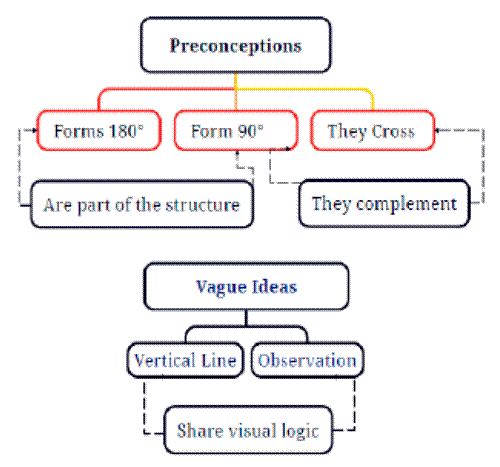
Analysis 1001331030. It is observed how the student answers this test with his own criteria, rooted in his simple notion of point and line, due to the ingrained prejudices from his childhood, adolescence, and high school years.
-
In the units of analysis (27.c. it is a VERTICAL LINE; in 3D, it is CD), (28.d. it is a VERTICAL LINE; according to 3D, it is AB), (46.c. the extraction duct represented by the VERTICAL LINE, green), and (10.a. it is a vertical duct), in interrelation with the unit (47.a. injection duct represented by a VERTICAL LINE, blue), the subcategory VERTICAL LINE is observed, which is related to the basic notion of the first graphs analyzed by the students.
-
From the units of analysis (44.a. the discharge duct represented by CD), (26.b. AB, because the air discharge duct is CD), (134.b. no, because they do not touch according to the 3D plan), (133.a. no, because one is vertical and the other is horizontal), (46.c. the extraction duct represented by the green vertical line), (47.d. injection duct represented by a blue vertical line), and (45.b. the injection duct represented by AB), the subcategory OBSERVATION arises.
-
For the subcategories VERTICAL LINE and OBSERVATION, there are two common units of analysis: (46.c. the extraction duct represented by the green vertical line) and (47.d. extraction duct represented by a vertical line, blue). This is evidence of the visual logic and geometric affinity of the two sub-categories.
-
In the units of analysis (75.i. yes because, according to the 2D plane, they intersect at a point), (74.h. no because, according to the 2D plane, they intersect at a point), (73.g. yes because, according to the 2D plane, they intersect at a point), (58.b. ducts A and F are perpendicular according to the 2D plane), (105. b. no, in no part of the plane do they intersect), (120.b. according to the 3D plane, the pipes intersect), (86.b. no, because at no point in the 2D plane do they touch), (135.c. they do not intersect according to the 2D and 3D planes), and (134.b. no, because they do not touch according to the 3D plane), the subcategory FORM A 90° ANGLE arises, which is closely related to the OBSERVATION subcategory, as they have two coded units in common (134.b. and 133.a.) and are in coincidence or synchrony. This convergence demonstrates a geometric connection, which is visually perceived by the student during their exploration and inspection of the test.
-
From the units of analysis (105.b. no, in no part of the plane do they CROSS), (93.a. no because, in the 3D plane, there is a blue pipe above), (120.b. according to the 3D plane, the pipes CROSS), (86.b. no, because at no point in the 2D plane do they touch), and (85.a. no, because according to the 2D view, they do not CROSS), the subcategory CROSS emerges, defining lines that neither intersect nor are parallel and have different directions.
-
From the units (60.d. ducts D and E are parallel accordingFrom the units (60.d. ducts D and E are parallel according to 2D plan), (59.c. ducts B and C are parallel according from the 2D view), (72. yes, they are parallel according to the 2D plan), (49. they do not intersect or cut each other; AB and CD are parallel), (48.e. lines AB and CD are parallel), (57.a. ducts A and B are parallel according to the 2D plan), (30.f. they do not intersect; they do not cut), (71.e. yes, they form a 90° angle; lines G, H, and I are parallel), (29.e. the lines are parallel to each other), (94.b. no because, from the 2D view, the lines are parallel), (31.g. they do not intersect anywhere), (104.a. yes because from the 3D view, the pipes are parallel), (50.g. they do not intersect), and (93.a. no because, in the 3D plane, the blue pipe appears to be above), the subcategory FORM A 180° ANGLE emerges, which is related to the fact that using 3D images is the best way to validate and recall student’s prior ideas. to 2D plan), (59.c. ducts B and C are parallel according from the 2D view), (72. yes, they are parallel according to the 2D plan), (49. they do not intersect or cut each other; AB and CD are parallel), (48.e. lines AB and CD are parallel), (57.a. ducts A and B are parallel according to the 2D plan), (30.f. they do not intersect; they do not cut), (71.e. yes, they form a 90° angle; lines G, H, and I are parallel), (29.e. the lines are parallel to each other), (94.b. no because, from the 2D view, the lines are parallel), (31.g. they do not intersect anywhere), (104.a. yes because from the 3D view, the pipes are parallel), (50.g. they do not intersect), and (93.a. no because, in the 3D plane, the blue pipe appears to be above), the subcategory FORM A 180° ANGLE emerges, which is related to the fact that using 3D images is the best way to validate and recall student’s prior ideas.
Figure 11: Axial coding: preconceptions and vague ideas
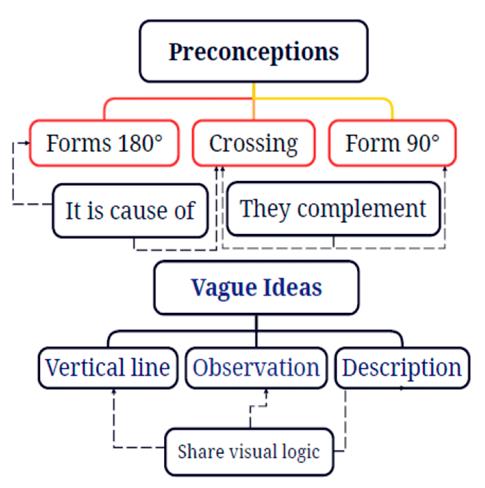
Analysis 1004719551. It is observed how, throughout this test, the student responds with defined criteria, reinforced by her primitive knowledge of point and line, by her prejudices and experiences from her childhood, adolescence, and secondary education years.
-
From the units of analysis (55. they are parallel lines), (94. they never intersect), (111. they are parallel lines (AB and CD); they never intersect), (29. they do not intersect), (69. parallel lines (D and E)), and (27. parallel lines (AB and CD)), the subcategory FORM A 180° ANGLE emerges. This subcategory reveals the logical coherence of the student’s prior knowledge about the notion of 180° in space.
-
In the units (79. they do not cut because they CROSS), (85. in 3D, the cold water pipe CROSSES over the hot water pipe), (95. the cold and hot water pipes CROSS over the drain pipe), and (78. the hot and cold water pipes CROSS over the green and black drain pipes), the subcategory CROSS is observed, which, from a 3D view, allows the student to assume a logical position, based on the experience collected during her upbringing, adolescence, and puberty.
-
From the units of analysis (121.b. ducts AB and CD are perpendicular), (71.h. the ducts E and I form perpendicular lines), (56.b. A and F FORM A 90° ANGLE), (68.e. between ducts B and G, H and I FORM A 90° ANGLE), (72.i. ducts E and I are perpendicular), and (70.9. ducts C and G form perpendicular lines), the subcategory FORM A 90° ANGLE arises, which is related to the prior ideas of students, as these are the most common shapes in their context.
-
In the units (26. the AB line is vertical), (25.c. the CD line is vertical), (45.d. the AB line is vertical), (44.c. the CD line is vertical), the subcategory VERTICAL LINE is observed, which is associated, in a basic and primary way, with the first images that young students drew in their childhood.
-
From the units of analysis (43.b. AB carries medicinal air), (23. CD is green), (42.a. CD is green), and (24.b. AB is the blue duct and carries clean air), the subcategory OBSERVATION arises.
Figure 12: Axial coding: preconceptions and vague ideas
Analysis 1069714443. In this test, the student responds with the judgment or methods stemming from his basic notion of point and line, from the preconceptions and habits built throughout his childhood, adolescence, and passage high school years. taken from the network, 1069714443 Network Source: Atlas. Ti 23
-
Based on the units of analysis (58.c. the extraction pipeline is represented by a VERTICAL LINE), (30.c. the extraction pipeline is represented by the VERTICAL LINE CD), (10. because this line AB is represented as a VERTICAL LINE), (32.d. the injection pipeline is represented by the VERTICAL LINE AB), and (60.d. the injection pipeline is represented by a VERTICAL LINE), the subcategory VERTICAL LINE is defined, which is related to the first graphs studied by students in their first stage of school life.
-
In the units (30.c. the extraction duct is represented by the vertical line CD), (75.a. the ducts represented by the letters A and B are parallel lines), (36.f. the ducts represented by the lines AB and CD do not intersect), (109.b. the horizontal cold water pipes (blue) and the hot water pipe), (34.e. the ducts represented by the lines AB and CD are parallel), (92.f. the ducts denoted by the letters D and E are parallel lines), (118.a. yes, they are parallel lines because they never intersect and form a 180° angle), (62.e. the ducts represented by the lines AB and CD are parallel), (66.g. the ducts represented by the lines AB and CD do not intersect), (64.f. the ducts represented by the lines AB and CD do not intersect), (28.b. the clean air injection duct is represented by the letters AB), (79. c. the ducts arranged between B and C are represented by two parallel lines), (38.g. the ducts represented by the lines AB and CD do not intersect), (54.a. the air discharge duct is represented by the letters CD), (81.d. they do not intersect because they are parallel lines, and, according to the 3D plan, they form a 180° angle), (56.b. the clean air injection duct is represented by the letters AB), (136.b. the hot and cold water lines are parallel and intersect the green and black drainage pipes), (95.i. the duct lines formed between E and I are perpendicular), (146.a. the ducts represented by AB and CD are not parallel lines; they intersect), the subcategory OBSERVATION is observed. This is related to the main characteristics of the student, and it allows him to react to the stimuli generated by any kind of action.
-
From the units (34.e. the ducts represented by lines AB and CD are parallel), (75.a. the ducts represented by letters A and B form parallel lines), (109.b. the horizontal cold water (blue) and hot water (red) pipes), (64.f. the ducts represented by the lines AB and CD do not intersect), (79.c. the ducts arranged between B and C represent two parallel lines), (38.g. the ducts represented by the lines AB and CD do not intersect), (92.f. the ducts represented by the letters D and E form parallel lines), (79.c. the ducts arranged between B and C represent two parallel lines), (81.d. they do not intersect because they are parallel lines, and, according to the 3D plan, they form A 180° ANGLE), (66.g. the ducts represented by the lines AB and CD do not intersect because they form parallel lines), (62.e. the ducts represented by lines AB and CD are parallel), (118.a. yes, they are parallel lines because they never intersect and FORM A 180° ANGLE), and (135.a. the 1/2 diameter green drainage line intersects the black 3/4 diameter drainage pipe; both pipes intersect), the subcategory FORM A 180° ANGLE arises. This implies that the student can see the difference between a line that crosses and one that intersects.
-
In the units (28.b. the clean air injection duct is represented by the letters AB, blue), (26.a. the air discharge duct is represented by the letters CD), (56. the clean air injection duct is represented by the letters AB), and (108.a. the cold water pipe is passing over the hot water pipe), the subcategory DESCRIPTION appears. Students can recognize the vague idea of confusing intersecting lines with a simple description.
-
Based on the units of analysis (108.a. the chilled water pipe is passing over hot water pipe), (119.b. the 1/2 diameter chilled water (PVC) lines and the hot water line intersect the sewer pipe), (100. 101.a. the 5/8 and 1 1/8 diameter cooling pipes and injection duct CROSS each other), (146.a. the AB and CD ducts do not form parallel lines; they CROSS), (148.c. the AB and CD ducts CROSS each other, because they form a 90° angle), and (101. they CROSS each other because it can be seen in the 3D plan which clean air duct is above the other), the subcategory CROSS is defined. This is the reason why the ducts form 180° angles and lines that do not intersect and are not parallel. They have different directions and no common points. They have different directions and no common points.
-
In the units of analysis (93.g. the lines of ducts C and G are perpendicular), (147.b. the ducts AB and CD correspond to perpendicular lines), (91.e. between duct B and the line of variable section of ducts G, H, and I, there are perpendicular lines), (77.b. between duct A and F, there are two perpendicular lines), (94.h. the lines of ducts D and H are not parallel), (136.b. the hot and cold water lines are parallel and intersect at 90° with the green and black drainage pipes), (95.i. the lines formed between ducts E and I are perpendicular), (148.c. the ducts of AB and CD intersect because they FORM 90° ANGLES), and (119.b. the 1/2 diameter cold water lines (PVC) and the hot water line intersect the drainage pipe), the subcategory FORM A 90° ANGLE is observed. Two lines are perpendicular if one of them is in true length and forms an angle of 90° with respect to the other.
Figure 13: Axial Coding: preconceptions and vague ideas
Conclusions
In the studied group of students, the development of the HER was demonstrated, as a result of testing prior ideas in 3D regarding point and line. As a consequence, the results of the standardized test, called post-test (PSVT:R), were obtained. Since the p-value (Excel output) for one tail is 0.0000000679, it falls in the rejection region. Therefore, the alternative hypothesis is accepted: all students have spatial thinking.
In the analysis of the pretest and posttest, it can be observed that the p-value for one tail is 0.0088. Since this value is less than α=0.05, it can be said, with a confidence level of 95 %, that the alternative hypothesis is accepted, which means that the students obtained a better average in the post-test.
Through the analysis conducted via the Atlas ti tool, it was possible to observe that the students answered the test with their own criteria, rooted in their traditions and customs, which allow them to express and respond from their primitive and simple notion of point and line, a notion that is influenced by their experiences, prejudices, and habits and molded since their childhood, adolescence, and high school stages
References
License
Copyright (c) 2024 Hernando Parra Lara, Carlos Alberto Ospina Parra

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.




2.jpg)










