DOI:
https://doi.org/10.14483/23448393.2160Published:
2006-11-30Issue:
Vol. 12 No. 2 (2007): July - DecemberSection:
Science, research, academia and developmentFundamentos Económicos y Matemáticos para un Modelo de Equilibrio general Computable
Keywords:
Matriz insumo producto, metodología, modelo de equilibrio, general computable, RAS (es).Downloads
References
Lya Sierra, Karina Manrique, «Análisis del Impacto de Acuerdo CAN MERCOSUR en el Valle del Cauca», Tesis para optar por el titulo de Maestría., Pontificia Universidad Javeriana, Bogotá, Cundinamarca, Colombia, 2007.
O´ryan, P, De Miguel J y Millar S., Ensayo sobre Equilibrio General Computable: Teoría y Aplicaciones. Centro de Análisis de Políticas Públicas, Universidad de Chile. Santiago de Chile 2003.
López, E, Ripio M y F. Cepeda., Crónica de los Modelos de Equilibrio General en Colombia, Borradores Semanales de Economía- Banco de la República, 13. Bogotá 1994.
Cárdenas, M. Chaparro J, Gamboa M, Reina M y Zapata J., Tratado de Libre Comercio Colombia-Estados Unidos: Análisis del Impacto Económico sobre la Región BogotáCundinamarca. Fundación para la Educación Superior y el Desarrollo (FEDESARROLLO), 2004.
Ferrari, C., Análisis Económico en Equilibrio General, Pontificia Universidad Javeriana, Facultad de Ciencias Económicas y Administrativas. Bogotá, D.C.2005.
Ferrari, C., Política Económica y Mercados, Pontificia Universidad Javeriana, Facultad de Ciencias Económicas y Administrativas. Bogotá, D.C.2005.
Rivas, G., Patrones de Demanda de los Hogares en las Cuatro Principales Ciudades de Colombia, Universidad Nacional de Colombia, Trabajo de Grado para optar el titulo de Magíster en Economía, Bogota 2000.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Ingeniería, 2007-00-00 vol:12 nro:2 pág:20-29
Fundamentos económicos y matemáticos para un modelo de equilibrio general computable
Karina Manrique López
Docente, Universidad Distrital. Investigadora del grupo de investigación GIO, Universidad Distrital.
Lya Paola Sierra
Docente, Pontificia Universidad Javeriana. Investigadora del grupo de investigación IDEAS, Pontificia Universidad Javeriana Cali.
Resumen
Este artículo describe la forma y la importancia de los Modelos de Equilibrio General Computable (MEGC) para predecir impactos económicos en una economía. En este sentido, se realiza una explicación detallada de las etapas que se deben seguir para la construcción de un MEGC, empezando por la modelación económica y matemática, hasta la realización del ejercicio de política. Para lo anterior, se toma como base el MEGC para el Valle del Cauca construido por Sierra y Manrique (2007), el cual mide los impactos de una mayor apertura comercial del valle del Cauca debido al acuerdo CAN-MERCOSUR.
Palabras clave:
Matriz insumo producto, metodología, modelo de equilibrio, general computable, RAS.
Abstract
This article describes the for m and relevancy of the Computable General Equilibrium Models (CGEM), used to predicts economic impact in one economy. Includes detailed explanation of the process and phases to develop the GCEM, beginning with the economic and mathematic model, and including the policy statements. All the study is based on the Valle del Cauca´s CGEM model developed by Sierra and Manrique [1], quantifying the impact of the big ger commercial opening in the Valle del Cauca due to CAN-MERCOSUR agreement.
Key words:
Input output matriz, methodology, equilibrium model,general computable, RAS.
1. Introducción
En muchos de los casos, el estudio de la economía se basa en la construcción de modelos basados en diagramas y ecuaciones que simplifican la realidad con el fin de comprenderla mejor. Los modelos de Equilibrio General Computable (MEGC) explican en términos generales como está organizada la economía, describen el comportamiento de los agentes y su relación con los diferentes mercados. En este sentido, el modelo plantea matemáticamente los supuestos económicos que representan la conducta de los agentes en cada mercado, la interacción de estos forma un sistema de ecuaciones cuya solución determina las condiciones de equilibrio entre la oferta y la demanda.
La importancia de los MEGC radica, en la caracterización detallada de los agentes y su comportamiento en los mercados. Adicionalmente, representan una importante herramienta para predecir los efectos de un evento económico en la totalidad del sistema.
El objetivo de este artículo es detallar el proceso de construcción de un modelo de equilibrio general computable, partiendo de los supuestos económicos hasta crear un sistema de ecuaciones que den for ma al MEGC. Este modelo servirá como instrumento para entender el funcionamiento de los mercados y generar proyecciones que midan impactos de política económica como los acuerdos comerciales.
Se sigue para esto, la elaboración del MEGC realizado y aplicado al Valle del Cauca que mide el impacto que tiene en la economía del departamento el acuerdo de libre comercio entre la Comunidad Andina de Naciones (CAN) y el Mercado Común del Sur (MERCOSUR)1 Sierra y Manrique (2007). Por lo tanto, el artículo se centra en la metodología de construcción del Modelo de Equilibrio General Computable, más no en los resultados que arroja el ejercicio de política.
La fabricación de modelos económicos de este tipo, facilitará la comprensión del mundo, de las relaciones entre los mercados y sectores, servirá para entender el grado de integración de una economía y los efectos que en ella tiene los diferentes choques de política.
La organización del documento es la siguiente: la primera sección presenta la revisión de la literatura asociada a los Modelos de Equilibrio General Computable MEGC, partiendo de su definición hasta los últimos trabajos realizados en Colombia sobre el tema. En la segunda sección, se desarrolla el modelo propuesto aplicado al Valle del Cauca, partiendo de un diagrama que explica las etapas de modelación. En la tercera sección, se presentan las conclusiones del documento.
2. Revisión de la literatura
Los modelos MEGC hacen una caracterización de los agentes económicos y de su comportamiento en la economía bajo los principios de racionalidad. Además representa las relaciones entre ellos y los mercados, generando así equilibrios competitivos.
Una de las formas de entender en que consiste un modelo de equilibrio general computable es definir cada una de las palabras que lo componen. En este sentido un MEGC debe cumplir con las siguientes condiciones:
1.Debe ser un Modelo. Los economistas utilizan los modelos para describir las relaciones económicas mediante la abstracción de la realidad. En este sentido los modelos, son una herramienta para entender el comportamiento económico, que da la posibilidad de simular y evaluar el impacto de las políticas económicas.
2.Debe ser general. Incorpora el comportamiento económico de la mayoría de los agentes en la economía y de su relación con los otros mercados. En este sentido los MEGC integran en un sistema las decisiones de las empresas, de los consumidores, del gobierno, del sector externo entre otros; con los mercados de bienes, de factores, de capitales etc.
3. Debe ser de equilibrio. Se asume que cada mercado se encuentra en equilibrio después de que los agentes han maximizado su utilidad o beneficio bajo los principios de optimalidad. Por lo tanto, cuando los mercados están en equilibrio la oferta y la demanda se igualan arrojando, así un conjunto de precios que asigna los recursos de una manera eficiente.
4. Debe ser computable. Genera resultados numéricos.
Por lo anterior se puede decir que la ide básica detrás de un Modelo de Equilibrio General Computables es: representar en un programa la economía, descrita a través de la relaciones de los agentes económicos en lo mercados, que se comportan de acuerdo con los principios de la optimización microeconómica.
Los MEGC, en cuanto a la modelación, pueden ser de corte neoclásico, o, de corte estructuralista. De igual modo, los MEGC se subdividen de acuerdo con su estructura en Estáticos y Dinámicos (O´Ryan, 2000). (Ver Figura 1).
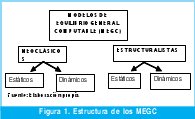
[1] Los modelos de corte neoclásico siguen todos los supuestos del modelo ArrowDebreu (1954), en el cual los mercados funcionan perfectamente, existe competencia perfecta; los agentes maximizan el beneficio por lo que el mercado asigna eficientemente los recursos; existe pleno empleo, y el ahorro determina la inversión de la economía. De acuerdo con los anteriores supuestos, los precios y cantidades varían de forma endógena para determinar el conjunto de precios que vacía los mercados. De igual forma, estos modelos neoclásicos cumplen con el primer y el segundo teorema del bienestar.
La corriente estructuralista tiene sus comien zos en los años 70 cuando se promulgaban supuestos y especificaciones más realistas para los modelos neoclásicos. Estos modelos se definie ron como micro estructuralistas y macro estructuralistas (Robinsón, 1989). Los primeros se enfocaron en relajar algunos supuestos neoclásicos muy restrictivos (modelaron rendimientos decrecientes a escala y salarios y tipos de cambio normal fijos). Los macro estructuralistas se enfocaron en hacer consistente el modelo neoclásico a nivel macro (se involucra la identidad ahorro igual a la inversión y e cierre del sector externo y balanza de pagos) Los MEGC estructuralistas incorporan modelación con oligopolio, desempleo complementariedad de las importaciones, etc.
En la práctica, los MEGC combinan aspectos de las dos corrientes anteriores y modelan de acuerdo con el mejor contexto económico existente en la realidad de la región. En la actualidad se utilizan, en mayor medida, aspectos de corte neoclásico a los que se les incorporan los siguientes aspectos de tipo estructural:
- Coeficientes de capital sectorial fijos que determinan tasas de beneficios distintos entre sectores.
- Diferencias salariales entre sectores diferentes.
- Imperfecta sustitución entre factores e insumos.
- Imperfecta sustitución entre bienes y servicios nacionales con importaciones o exportaciones. Esto implica que se tomen los bienes domésticos y los extranjeros como diferenciados y no exista un único precio. [2]
Como se puede observar en la Figura 1. Los MEGC se subdividen, a su vez, en Estáticos y Dinámicos. Los primeros representan una radiografía de toda la estructura económica en un solo momento del tiempo. Para conocer el impacto de una política específica en el modelo, se realiza un ejercicio de estática comparativa. Los segundos están dirigidos a periodos de tiempo mayores y determinan el equilibrio en una secuencia de años. El modelo se dinamiza cuando se diferencian las ecuaciones de los sistemas, permitiendo así establecer canales de transmisión de la conducta de los agentes de un periodo a otro.
La introducción de los MEGC a los países en desarrollo lo realizaron Adelman y Robinson (1978) con trabajos referentes a Corea, y Taylor (1980) con aplicaciones a Brasil. A partir de estos trabajos, los MEGC se hicieron bastante comunes para los países en desarrollo, sobre todo en aplicaciones al comercio internacional y a la tributación. Los economistas que realizaron revisiones bibliográficas al respecto son Shantayanan, Devarajan y Robinson (1986); Shoven y Whalley (1984), y De Melo (1988). [3]
Algunos de los modelos que contienen vín culos con comercio exterior y miden los im pactos de acuerdos comerciales en el bienes tar, el empleo, la producción y el retorno d factores para Colombia son realizados po DNP (2003), López y Botero (2004) y Martín y Ramirez (2005). Todos estos artículos hacen referencia a los impactos para nación deriva dos del Tratado de Libre Comercio entr Colombia y Estados Unidos.
Los MEGC para un departamento en particular son escasos en la literatura colombiana, debido a que aún no se ha implementado un sistema de cuentas departamentales bien estructuradas. Fedesarrollo, junto con un grupo de investigadores encabezados por Mauricio Cárdenas (2004), construyeron un MEGC para la región de Bogotá-Cundinamarca con el objetivo de medir el impacto del Tratado de Libre Comercio con Estados Unidos en la región. [4]
Otra investigación regional es la desarrollada por Ferrari (2004) en la que se realiza un MEGC para la región del Putumayo, involucrando en su modelo características específicas en la región, como el cultivo de coca. El modelo permite analizar diversas alternativas de política económica sobre el comportamiento económico del departamento a fin de paliar las consecuencias derivadas de la erradicación de la coca en el mismo. Sierra y Manrique (2007) [1]
3. Modelo de equilibrio general computable para el valle del cauca
En esta sección se describe la construcción de un modelo MEGC para el Valle del Cauca, partiendo de las etapas de modelación detalladas en la Figura 2. En ella, se pueden observar los pasos a seguir en el momento de empezar a plantear un Modelo de Equilibrio General Computable.
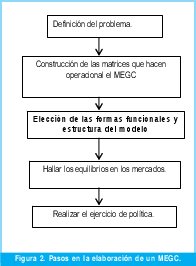
3.1 Definición del problema
Los MEGC sirven para realizar análisis del impacto de políticas económicas. Son un instrumento para entender los mercados y generar proyecciones sobre dichos impactos. En nuestro caso particular, se construyo un MEGC para evaluar el impacto del acuerdo de complementación económica CAN MERCOSUR en el Valle del Cauca. Específicamente se quiere evaluar como cambia el volumen del comercio y la producción de los sectores industriales.
3.2. Construcción de las matrices que hacen operacional el MEGC
Para que el Modelo de Equilibrio General Computable sea operacional es necesario contar con un caso base. En el MEGC del Valle la presentación de los datos del equilibrio inicial se realiza mediante una matriz insumo producto. Dentro de la matriz están representados los sectores económicos considerados y las relaciones de compra y venta que realizan entre ellos. Por lo tanto, la matriz permite conocer los consumos que realiza cada uno de los sectores de los otros con el objetivo de producir un determinado bien. Leontief (1951) describe de una forma más clara los fundamentos de esta matriz:
«Las cantidades que figuran en las filas indican la manera como la producción de cada uno de los sectores de la economía se distribuye entre los demás. Recíprocamente, las cantidades que figuran en las columnas indican los insumo de bienes y servicios que cada sector recibe de los demás» (Pág. 70, Leontief 1951)
En esta matriz están incluidas entonces las compras y ventas de insumos que hacen todos los sectores industriales en los mercados de bienes ya sea transables o no transables. Plasma, entonces la estructura económica del Valle del Cauca.
Adicionalmente, son necesarias dos matrices. La matriz de flujos intersectoriales la cual consigna los salarios, impuestos indirectos, ingresos mixtos y excedentes brutos de explotación de cada sector. Y la matriz de demanda y oferta agregadas que incluye el consumo de los hogares, el consumo del gobierno, la inversión privada y la inversión publica. Estas dos matrices fueron creadas a partir de datos departamentales.
Por el contrario, al no existir matrices insumoproducto para el Valle del Cauca fue necesario construir una matriz regional con base en la Matriz Insumo Producto (MIP) nacional. Para este efecto se siguieron los siguientes pasos:
a. Se agregó los 59 sectores de la Matriz Nacional a 25 sectores de acuerdo con la caracterización propia de la economía del Valle y a la información disponible en el departamento. Se incluyeron dos sectores que no se encuentran clasificadas en la matriz insumo producto nacional, pero son característicos de la región. Estos son los sectores de Caña de Azúcar y Otros Productos Agrícolas sin Caña, los cuales fueron construidos en base a la información de Planeación Departamental del Valle del Cauca (ver Anexo 1).
b. Una vez agregados los sectores de la matriz nacional, se procedió a ajustar la matriz nacional a la departamental utilizando la metodología de ajuste para las filas y columnas conocida como RAS. (Anexo 2) La idea fundamental de este enfoque radica en suponer que la matriz regional se encuentra inscrita en la nacional. Para utilizar esta metodología es necesario conocer la Producción Bruta, el Valor Agregado total y la Demanda Final en cada sector económico del departamento. A partir de estos datos es posible obtener la demanda intermedia de insumos tomados como vectores límites que generan las ventas y compras intersectoriales regionales a partir de la MIP nacional.
Una vez se tiene la estructura matricial para un año específico, se seleccionan las formas funcionales que tendrán las funciones de utilidad, producción, etc. Es decir, se genera la estructura del modelo definiendo los supuestos económicos y matemáticos, así como las elasticidades de las funciones. En el siguiente apartado se analiza paso a paso la estructura y supuestos del modelo.
Definido el año base (en el caso del MEGC del Valle es el 2004) y las formas funcionales de los mercados, el modelo se dinamiza cuando se diferencian las ecuaciones de los sistemas en las matrices, lo que permite establecer canales de transmisión de la conducta de los agentes de un periodo a otro.
3.3. Elección de formas funcionales y estructura del modelo.
La modelación económica se logra a través de funciones matemáticas que implican formas de comportamiento de los agentes dentro de la economía. El supuesto más importante que se sigue es la racionalidad económica, en donde cada uno de los agentes persigue un objetivo coherente y toma decisiones óptimas para alcanzarlos. Por ejemplo, los consumidores buscan maximizar su utilidad, las firmas sus beneficios y el gobierno el bien público. En este sentido los agentes optimizan estas decisiones sujetas a restricciones de ingreso, o, tecnología. A continuación se describe la forma como se modela cada uno de los mercados en el MEGC del Valle con sus respectivos agentes y los demás supuestos económicos que se requirieron.
Los mercados que definen la economía modelada son: [5], [6]
3.3.1. Mercado de bienes
Se encuentran en este mercado compradores y vendedores de bienes finales e intermedios. Se determinó dos tipos de sub-mercados: el de bienes transables y el bienes no transables. En el primero están incluidos los sectores que intercambian bienes de carácter internacional, ya sea porque los exportan o porque los importan. En este caso, el precio de los bienes está determinado exógenamente, ó a nivel internacional. Los sectores que comercian bienes no transables lo hacen solo a nivel nacional, no venden ni compran al mundo y el precio es determinado internamente o dentro del modelo.
3.3.1.1. El Mercado de ajuste exógeno o debienes Transables
En la figura 3 se puede observar la oferta, la demanda y el precio internacional del mercado de bienes transables. Se supone que existen diferentes niveles de productividad para los distintos productores en cada sector, es por eso que la oferta tiene forma escalonada. Cada tramo expresa la cantidad producida al correspondiente nivel de productividad.
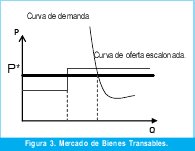
El mercado es exógeno porque el equilibrio de mercado es decir el precio y/o la cantidad de equilibrio es determinado por fuera de dicho mercado, es decir el precio corresponde al internacional nacionalizado, ó, puede tratarse de un mercado administrado.
Las ecuaciones que representan este mercado son las siguientes:
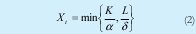
Xi: Representa una función de producción tipo Leontieff el supuesto implícito es que la tecnología no cambia en un periodo de tiempo determinados ya que la estructura de la matriz es de coeficientes fijos, con complementariedad perfecta entre los insumos productivos. El producto siempre emplea la misma proporción de factores para cada nivel de producción y no puede cambiar de un momento a otro la tecnología.
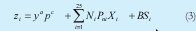
La demanda total es la demanda de las familias, las empresas y el gobierno.
La demanda de las familias es de tipo Cobb Douglas. En donde zi representa la cantidad demandada, y el ingreso monetario, que proviene de los salarios y las utilidades menos los impuestos directos, p el precio del bien, a y c son las elasticidades ingreso y precio. No hay bienes sustitutos. Matemáticamente es una función homogénea de grado cero. Esta estructura implica que el consumidor responde ante los cambios en los precios a menor precio mayor consumo.
Demanda de bienes intermedios: las empresas en cada sector demandan insumos, éstos se representa como una proporción de la producción total del sector.
Demanda del gobierno en bienes y servicios: Es el consumo que proviene de los gastos corrientes.
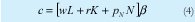
Los costos están determinados por la cantidad y precio de los insumos: capital rK, Trabajo wL, más los insumos nacionales Npn.
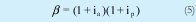
β: El beta incorpora la tasa activa como el costo del capital y la tasa pasiva como la representación de la mínima utilidad que se debería tener, si se supone que el dinero permanezca en un banco.
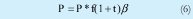
P representa el precio internacional nacionalizado, ya que f es la tasa de cambio y t los impuestos aduaneros.
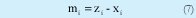
mi: Las importaciones son la demanda menos la producción.

exi: Las exportaciones son la producción menos la demanda.
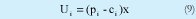
Las utilidades son la diferencia entre el precio y el costo, por la cantidad.
3.3.1.2. El Mercado de ajuste endógeno, ó, de bienes No Transables:
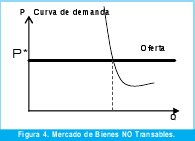
En la figura 4. se puede observar la oferta y la demanda en el mercado de bienes no transables. Como se anotó, el mercado es de ajuste endógeno porque su equilibrio representado ya sea por el precio y/o la cantidad-son determinados dentro de este. En este caso, la demanda determina tanto el nivel de precios como la cantidad del bien (tal como se muestra en la figura).
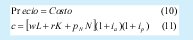
2.3.2. Mercado de Trabajo:
El mercado laboral esta compuesto por los trabajadores que ofrecen sus horas de trabajo y las empresas que los demandan. Para el MEGC del Valle del Cauca suponemos que existen dos tipos de trabajadores, los calificados y los no calificados. En el primer grupo, se encuentran las personas que están dentro de la Población Económicamente Activa (PEA) con algún tipo de estudio superior. En el segundo, se encuentran las personas dentro de la (PEA) que solo estudiaron hasta la secundaria o que no poseen ningún tipo de estudio.
Cada tipo de «oferta» de trabajo tiene un mercado. Se supone en este modelo que el mercado de mano de obra calificada arroja un salario competitivo. Es decir que la oferta y la demanda determinan el salario. Por su parte la demanda laboral de calificados depende del nivel de actividad de las empresas. Esta está dada por el coeficiente laboral producto multiplicado por el nivel de producción.
(ver ecuación 13). La oferta laboral surge del problema de maximización de los agentes, que deben decidir entre consumo (C) y ocio (H) (ver ecuación 12). El consumo es función de los ingresos totales (wc Lc), más sus ingresos no laborales ( s ). El ocio es la diferencia entre su tiempo disponible y las horas dedicadas al trabajo (1-Lc ). A continuación se describen las ecuaciones del mercado de mano de obra calificada.
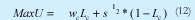
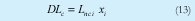
De la solución se deriva la siguiente función de oferta laboral calificada
Donde es decir, se asume que la renta de los depósitos es el único ingreso no laboral de las familias.
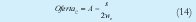
En el caso del mercado de mano de obra no calificada los salarios son los correspondientes al salario mínimo ajustado cada año de pendiendo de la inflación del periodo anterior. La ecuación (15) representa esa formulación. La demanda de mano de obra no calificada, ecuación (16), tal como en el caso de los trabajadores calificados, depende de la actividad de las empresas.
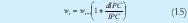

3.3.3 Mercado de crédito:
No existe un mercado de crédito propiamente dicho. Las tasas de interés son determinadas a nivel nacional, así como la oferta. Sin embargo si se modela una demanda de crédito que depende de la utilidad neta del sector, su rentabilidad y la tasa de interés activa de acuerdo con la siguiente ecuación.

Esta función es de tipo Cobb Douglass, sus exponentes expresan directamente las elasticidades de la variable dependiente en relación a la respectiva variable independiente. En este caso existe una relación entre la utilidad neta, la rentabilidad re y la tasa de interés activa la ia, α β y y son las elasticidades utilidad, precio cruzado y precio propio. La forma en que se determinan las elasticidades debe provenir de una estimación econometrita basada en datos históricos.
3.3.4. La inversión:
Es la variable que dinamiza la economía, hace crecer el stock de capital de manera que genera crecimiento en los periodos siguientes. Los recursos para la inversión se obtienen de la siguiente forma:
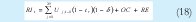
En donde Uj representa las utilidades sectoriales de las empresas descontando los impuestos, OC la oferta de crédito nacional y departamental y RE los recursos externos
3.4. Hallar los datos
La construcción de un modelo de equilibrio general requiere el uso de información proveniente de fuentes oficiales como es el caso del Departamento Administrativo Nacional de Estadísticas DANE y el Banco de la Republica principalmente. Es necesario aclarar, que una parte de la información se construye a través de estimaciones consistentes con los datos y metodologías oficiales.
Para la obtención de otros datos, como por ejemplo, la información de las elasticidades ingreso y precios (a,c) de la ecuación del consumo de los hogares ( zi = ya pc ) se tomó de RIVAS [7]. Así mismo, Los cambios en el ingreso ( y ) son estimados por el modelo a partir de la variación de utilidades y los salarios consignados en la cuentas de las matrices descritas anteriormente.
Por otro lado, la inversión privada es el elemento que dinamiza la economía departamental debido a que hace posible el aumento de la capacidad instalada de producción y como consecuencia genera expansión en la producción luego de su maduración. Las relaciones Capital- Producto establecen la relación entre inversión y expansión de la capacidad de producción sectorial. El indicador correspondiente es la Relación Marginal Capital Producto (ICOR) y la Relación Media Capital Producto (COR). El ICOR está definido en la ecuación (19)
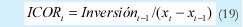
Donde,
Inversiónt-2= Inversión neta en el periodo t( xt - xt-1 )= Crecimiento del producto para un periodo determinado
El COR se supone equivalente a la tasa marginal capital producto promedio para los años (2000-2003), estimada a partir de la formación bruta de capital y la variación del PIB en dicho periodo.
Los datos correspondientes a la inversión neta fueron tomados del sistema de Cuentas Nacionales del DANE. Otras estadísticas que fueron necesarias para completar la estructura de la inversión fueron el Stock de Capital y la rentabilidad sectorial. El primero se tomó del Informe de Coyuntura Económica Regional ICER y de la Cámara de Comercio de Cali para 2003 y el segundo se tomó del estudio Observatorio Económico para el Valle del Cauca 2003.
3.5. Hallar los equilibrios del mercado
Mediante un proceso iterativo se solucionan los equilibrios en cada mercado. El encuentro de la demanda con la oferta genera un conjunto de precios eficientes, ya sea de bienes transables, o, no transables, o, de factores como los salarios y las tasas de interés. Una vez resuelto cada mercado y el sistema en el año base, se generan los mismo equilibrios en cada año de la proyección.
3.6. Experimento de política
Para analizar los efectos económicos de políticas comerciales en los MEGC, se realizan experimentos controlados que sólo modifican algunas de las variables exógenas del modelo manteniendo constante todo lo demás. En este sentido, se pregunta al modelo qué habría pasado si hubiese sido implementada una política dada (como desgravación arancelaria) en el año base y el resto de condiciones domésticas y externas hubieran permanecido sin modificaciones. Este análisis, entonces, hace énfasis en los efectos de la política impuesta aislándola de otros factores.
En el caso del MEGC del Valle del Cauca se realizan dos experimentos de política económica. En este tipo de experimentos no solo se quiere probar si una desgravación arancelaria derivada del acuerdo con el MERCOSUR tiene efectos positivos en la economía de departamento, sino también, se quiere examinar si políticas favorables a las exportaciones (tipos de cambio competitivos y bajas tasas de interés) o negativas como (reevaluación del tipo de cambio y altas tasas de interés) afectan los resultados.
En el primer experimento, se aplica una política de desgravación arancelaria correspondiente al calendario establecido por el acuerdo CAN-MERCOSUR y adicionalmente se considera una política monetaria acorde con tipos de interés bajos y devaluación de la moneda. En el segundo experimento, se emplea la misma política de desgravación arancelaria, pero en cambio, se considera una política monetaria acorde con tipos de interés altos y reevaluación de la moneda.
4. Conclusiones
La importancia de los modelos de equilibrio general, radica en que la modelación de la economía a través de su interrelación en los mercados, permite capturar los efectos directos e indirectos de las políticas económicas, en el corto y mediano plazo. Para el cumplimiento de este objetivo es necesario identificar la estructura productiva de la región, consignada en la matriz regional Insumo Producto, lo que da un punto de partida para futuras investigaciones.
De otro lado, la elaboración del modelo responde al estudio, selección y clasificación de datos, teorías y metodologías que desarrollan el objetivo planteado en un MEGC, de esta forma el artículo se constituye en una herramienta metodológica para la elaboración de este tipo de modelos.
Referencias bibliográficas
[1] Lya Sierra, Karina Manrique, «Análisis del Impacto de Acuerdo CAN MERCOSUR en el Valle del Cauca», Tesis para optar por el titulo de Maestría., Pontificia Universidad Javeriana, Bogotá, Cundinamarca, Colombia, 2007.
[2] O´ryan, P, De Miguel J y Millar S., Ensayo sobre Equilibrio General Computable: Teoría y Aplicaciones. Centro de Análisis de Políticas Públicas, Universidad de Chile. Santiago de Chile 2003.
[3] López, E, Ripio M y F. Cepeda., Crónica de los Modelos de Equilibrio General en Colombia, Borradores Semanales de Economía- Banco de la República, 13. Bogotá 1994.
[4] Cárdenas, M. Chaparro J, Gamboa M, Reina M y Zapata J., Tratado de Libre Comercio Colombia-Estados Unidos: Análisis del Impacto Económico sobre la Región Bogotá- Cundinamarca. Fundación para la Educación Superior y el Desarrollo (FEDESARROLLO), 2004.
[5] Ferrari, C., Análisis Económico en Equilibrio General, Pontificia Universidad Javeriana, Facultad de Ciencias Económicas y Administrativas. Bogotá, D.C.2005.
[6] Ferrari, C., Política Económica y Mercados, Pontificia Universidad Javeriana, Facultad de Ciencias Económicas y Administrativas. Bogotá, D.C.2005.
[7] Rivas, G., Patrones de Demanda de los Hogares en las Cuatro Principales Ciudades de Colombia, Universidad Nacional de Colombia, Trabajo de Grado para optar el titulo de Magíster en Economía, Bogota 2000.
Karina Manrique
Obtuvo el título como magíster en Economía de la Pontificia Universidad Javeriana, Bogotá. Licenciada en Matemáticas de la Universidad Distrital Francisco José de Caldas. Actualmente se desempeña como docente de la Universidad Distrital. Investigadora del Grupo GIO.
Lya Paola Sierra
Obtuvo el título en Economía de la Pontificia Universidad Javeriana, Cali. Obtuvo su título de maestría en Economía de la Pontificia Universidad Javeriana, Bogotá. Investigadora del Grupo IDEAS.

Anexo II. Metodología RAS para regionalización de la matriz nacional a la departamental2
Para trabajar el RAS partimos de una matriz distribuida de la siguiente forma:

ui es el vector de suma de las filas de los consumos intermedios recientes.
vi es el vector de suma de las columnas de los consumos intermedios recientes.
Creation date:
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.





2.jpg)










