Ingeniería, 2004-00-00 vol:9 nro:1 pág:37-51

FA Tool, herramienta de asignación de frecuencia en redes celulares por medio de algoritmos genéticos

Juan Carlos Gómez Paredes
Miembro del Grupo de Comunicaciones, U. Distrital Francisco José de Caldas.
Jorge Andrés Acero Hernández
Ingeniero Electrónico, U. Distrital Francisco José de Caldas.
Aldo Camilo García Suárez
Ingeniero Electrónico, U. Distrital Francisco José de Caldas.

Resumen

Este artículo presenta un software, como solución al problema de asignación de frecuencia en redes celulares, denominado FA Tool, capaz de realizar una estimación del número de canales necesarios por estación base y determinar un plan de frecuencias mediante un proceso basado en algoritmos genéticos (GA) modificados, que permite establecer las bases y un primer acercamiento al estudio de la optimización automática de frecuencias.

Palabras clave:
Asignación de frecuencia, Algoritmos genéticos, Redes celulares, Optimización.

Abstract

This paper presents a software, as solution to the problem of assignment of frequency in cellular nets, denominated FA Tool, able to carry out an estimate of the number of necessary channels for station bases and to determine a plan of frequencies by means of a process based on genetic algorithms (GA) modified, that it allows to establish the bases and a first approach to the study of the automatic optimization of frequencies.

Key words:
Frecuency Assignment, Genetic Algorithms, Cellular nets, optimization.

I. INTRODUCCIÓN

FA Tool es una herramienta de optimización para resolver un problema de asignación de frecuencia (FAP) dado en GSM. La herramienta opera en un mapa específico que consta de 40 celdas simulando una red celular. Estas celdas pueden manejar tráfico no uniforme (diferente número de canales por celda) y todas utilizan la misma potencia de transmisión y antenas omnidireccionales. Las frecuencias son asignadas (de acuerdo a condiciones previamente establecidas por el usuario) a cada una de las celdas por un algoritmo de optimización que es una implementación mejorada de Algoritmos Genéticos (GA), que es una técnica de búsqueda con conducta probabilística incorporada. Aquí, esta técnica combina las ventajas de búsqueda al azar con (una optimización matemática) el modelo de selección natural. Empieza básicamente con una solución factible inicial e intenta encontrar mejores soluciones. Durante el proceso de búsqueda en el algoritmo se aceptan malos individuos con una probabilidad que disminuye con el tiempo, que permite al algoritmo investigar más allá de los mínimos locales. La asignación de frecuencia resulta, en frecuencias asignadas, y relaciones señal-a-interferencia.

II. EL PROBLEMA DE ASIGNACIÓN DE FRECUENCIA

Cuando dos transmisores usan (casi) la misma frecuencia de portadora, ellos pueden interferir. El nivel de interferencia depende de muchos factores, como la distancia entre transmisores / receptores, la posición geográfica de los transmisores, la potencia de la señal, la dirección en que la señal se transmite, y las condiciones del tiempo. Causas más complejas de interferencia pueden ser los productos de intermodulación, emisiones espurias y respuestas espurias. En caso de que el nivel de interferencia sea alto, la relación señal-a-inteferencia (SIR) puede causar una inaceptable calidad. Sin embargo, la disponibilidad limitada de frecuencias ocasiona su reuso por los múltiples transmisores dentro de la misma red [1].

Como consecuencia, un operador debe escoger cuidadosamente las frecuencias en que cada estación transmite para evitar altos niveles de interferencia. La selección de las frecuencias de tal manera que la interferencia se evite, o mejor, se minimice, se llama Problema de Asignación de Frecuencias (FAP - en inglés, Frequency Assignment Problem). Otros autores [2] lo definen como un problema de optimización cuyo blanco es planear la red lo mejor posible. La planificación esta basada en el reuso de frecuencias dentro de la misma red y apunta a lograr un uso más eficiente del espectro, manteniendo el nivel de calidad de la red en un estándar alto. Como el espectro de radio disponible es un recurso limitado y el crecimiento de su demanda en las recientes décadas ha incrementado su precio, se aumenta la importancia de una buena planificación de la red, por consiguiente, los planificadores de las redes celulares se enfrentan a tareas cada vez más complicadas y se espera de ellos mejores resultados. Por ello, es habitual el uso de herramientas software, bien sean propias o comerciales, que faciliten la planificación y optimización.

Definición de asignación de frecuencia

Una asignación de frecuencia es una función [3] que asigna a cada miembro de un conjunto de transmisores una frecuencia operando de un conjunto de frecuencias disponibles. Por consiguiente, si A es una asignación para el conjunto de transmisores V y si v es un transmisor que pertenece a V, entonces A(v) denota la frecuencia asignada a v por A. En un problema típico de asignación de frecuencia, se intenta hallar una asignación de frecuencia (es decir, un función de un conjunto dado de transmisores en un conjunto dado de frecuencias) que satisfaga ciertas condiciones (por ejemplo, una colección de reglas limitantes de interferencia) y que minimice la cantidad de espectro utilizado por la asignación.

III. MODELO DE PROPAGACIÓN

El modelo empleado calcula la señal y la interferencia en cualquier punto. No toma en cuenta el terreno o cualquier otro factor que de una pérdida de trayectoria aparte de la distancia y la separación de frecuencia.

La asignación de frecuencia se considera exitosa si se logra la cobertura total en los puntos de prueba de recepción y con un mínimo SIR requerido. Para la evaluación de la asignación, una ley de potencia inversa es suficiente y expresa como una señal interferente se atenúa rápidamente con la distancia y con la separación de canal. Este modelo puede ser usado porque nuestro interés no es un estudio directo de propagación, aunque el modelo no puede ser totalmente exacto, es suficientemente representativo para el patrón de atenuación.

Si el punto de recepción es r_i, dónde i = 1, ...,N_r, se sintoniza al transmisor T_k, dónde k = 1,... ,N_t, entonces la señal s_i, en r_i se da por:

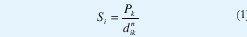
donde P_k es la potencia de la señal transmitida, y d_ik es la distancia entre el transmisor T_k y el receptor r_i, n es el exponente por pérdida de trayectoria. La interferencia total Ii en el punto de recepción r_i se da por:

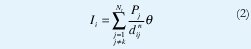
donde N_t es el número de transmisores y, para cada j, θ es tomado como

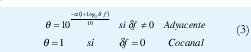
donde δf es la separación de canal entre el transmisor deseado Tk y el transmisor interferente T_j. Alfa es un factor de atenuación para interferencia de canal adyacente y es medido en dB/octava. Este modelo fue propuesto por Leese y Gower [4] para este tipo de evaluación.

Para cada punto de recepción, la estrategia es asegurar que las señales interferentes que son co-canal con el transmisor deseado sean distribuidas para que ellos no lleven un SIR inadecuado. Esto puede lograrse introduciendo condiciones no binarias [5] que da una penalización conforme a la gravedad de la interferencia, como forma de calificación en el algoritmo genético, tal que no todos los transmisores puedan tener el mismo canal. Esta idea es razonable porque las violaciones más altas generarán lógicamente interferencia más alta y consecuentemente las penalizaciones más altas en el modelo matemático. Esta extensión al modelo de condición binaria (interferencia simple) da buenos resultados de SIR y span [5].

IV. FUNCIÓN OBJETIVO

De acuerdo a la sección anterior, la relación Señala-Interferencia (SIR) se define como:

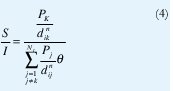
de esta forma, la función objetivo genérica seria:

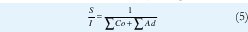
Como las distancias no son equidistantes, pero las potencias se asumen iguales, la función objetivo FA Tool-Obj [5] queda de la forma

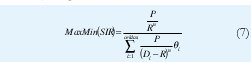
Donde R es el radio de la celda y D la distancia euclidiana entre transmisores (se asume que estos se encuentran en el centro de la celda), n es el exponente por pérdida de trayectoria. La distancia puede expresarse en términos de R.

El objetivo en FA Tool es la maximización del mínimo SIR [5]. El SIR para una frecuencia en una celda específica se calcula por la ecuación 6. Pero antes de realizar esto hay que efectuar los siguientes pasos:

i. Elegir un conjunto de condiciones

El conjunto de condiciones (figura 1) contiene las distancias espaciales mínimas entre celdas (medido desde sus centros) para asignar una separación mínima en frecuencia.

ii. Realizar la matriz de separación

La matriz de separación es una matriz cuyos elementos dan la separación que debe existir entre las frecuencias que corresponden a una celda (fila) con respecto a otra (columna). Esta separación se representa por un número con valores de 0, 1, 2, etc. Un 0 significa que las dos celdas apenas interfieren y por consiguiente la misma frecuencia puede reusarse. Un 1 implica que los transmisores localizados en estas celdas deben usar frecuencias que mantienen una separación mínima de una unidad. Un 2 o un número más alto significa que estas celdas deben usar frecuencias de por lo menos dos unidades de separación. Esto normalmente se requiere para frecuencias en la misma celda, dependiendo del equipo de la estación base (factor alfa). La matriz de separación debe construirse con una precisión extrema para que refleje la red lo más cercano a la realidad.

iii. Hacer matrices de penalización

La matriz de penalización indica el grado de violación que puede haber cometido cada elemento de una asignación y al igual que la matriz de separación, son generadas de acuerdo a las características de cada problema en particular y son el instrumento que permite de forma indirecta la optimización de nuestra función objetivo (ecuación 6), pues cada posible asignación es evaluada en aptitud de acuerdo a la cantidad de penalizaciones que esta posea.

V. IMPLEMENTACIÓN DEL ALGORITMO GENÉTICO PIRAMIDAL MODIFICADO EN FA TOOL

El algoritmo genético piramidal modificado es nuestra propia versión de los algoritmos genéticos, para tener mejores resultados principalmente en el aspecto de los mínimos locales y el tiempo computacional. El concepto original de los algoritmos genéticos es tener una población final, bastante superior en aptitud con respecto a las anteriores, es la noción de la selección natural: conservar las características de una especie como población no como individuo. Pero resulta que el objetivo no es obtener un conjunto de buenas soluciones, sino un solo individuo excelente. Esto puede resultar un tanto pretencioso, pero si se ve a cada individuo como una especie diferente la idea puede empezar a tener sentido.

De esta manera había que ingeniar la forma de conservar a los mejores individuos de alguna forma, y de ahí surge el algoritmo genético piramidal modificado [5]. Es decir, a la primera población que es generada al azar, se le califica y se ordena de acuerdo a su aptitud, esta es la idea propuesta por los algoritmos genéticos piramidales [6], y nosotros agregamos que los mejores individuos siempre se conservarán hasta que algún hijo lo supere. De esta forma, las características de los mejores individuos siempre se conservan, hasta que uno de sus hijos en una operación de cruce o una de sus mutaciones produzca mejores características. Esto desde el punto de vista de la naturaleza, seria como si los mejores individuos son los que se reproducen y no van a morir hasta que nazca un individuo con mejor aptitud y lo reemplace.

Representación cromosómica

Por las características del problema presentado, definimos que un individuo es una matriz de M*N que representa una asignación completa, donde las columnas indican el número de celdas y las filas indican el número de canales por celda.

Por lo tanto, precisamos como gen de un cromosoma, el conjunto de frecuencias que asigna un canal a todas las celdas y que cumple con los requisitos de la matriz de separación, (es decir, no tiene violaciones), en otras palabras, son las filas de la matriz asignación. Y se define como

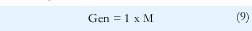
Donde M es el número de celdas. El gen también es presentado en la Figura 3.

Cromosoma o individuo para nuestro caso es lo mismo, y corresponde a una posible asignación completa. Se define como

Donde N es el número de canales por celda. Note que cuando hay igual número de canales por celda el tráfico es uniforme, y el individuo es una matriz cuadrada o rectangular. Cuando el tráfico no es uniforme, la matriz es irregular y hay que llenar con ceros los espacios libres, siendo esto un individuo computacionalmente ineficiente. Una solución original encontrada para tráfico no uniforme [5] se expondrá en la próxima sección.

Población inicial

La población inicial comienza con la creación de genes aleatoriamente, formados por números al azar, que están limitados por una cota de span dada por la formula FA Span. La colección de genes forma un individuo de acuerdo al requisito de canales por celda. Recuerde que el número de genes por celda lo determina su número de canales.

De esta manera son creados todos los individuos para formar la población que puede ser de mínimo 2 y no superior a los 20 individuos.

En la Figura 4 se presenta un individuo (Cromosoma) de 2 celdas y tráfico uniforme de 4 canales.

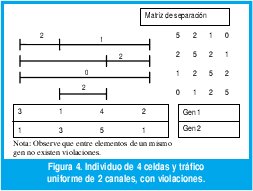
Calificación - fitness

La aptitud del individuo puede ser establecida observando la compatibilidad entre genes, de acuerdo a la matriz de separación. Esto se hace evaluando elemento por elemento si existe la separación apropiada, de lo contrario se asigna una penalización de acuerdo a la gravedad de la falta. De esta manera se va llenando una matriz de error por elemento.

Por ejemplo, para el elemento 1 de la Figura 4, se tiene.

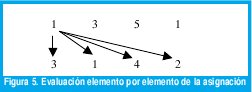
Se hace la siguiente evaluación

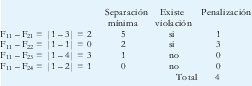
Así sucesivamente, se evalúa elemento por elemento hasta que se llene la matriz (denominada, matriz de error del individuo [5]) que se observa a continuación;

Crossover y mutación

La operación de cruce se realiza entre los dos individuos con mejor calificación, es decir, los que tienen el menor número de violaciones, escogiendo del segundo mejor individuo los 4 mejores genes y del mejor individuo los 4 peores genes, de esta forma se cruzan generando 16 hijos, creando la nueva generación conservándose solamente los dos padres. Esta nueva generación se vuelve a calificar y se ordena.

Después de la generación inicial, se hace mutación en los dos padres (es decir, en las dos mejores calificaciones) en un porcentaje preestablecido de los genes, creando dos nuevos hijos en la población. Estos nuevos genes mutados son generados al azar y su posición que ocupan en el cromosoma es aleatoria.

VI. GENERALIZACIÓN DEL ALGORITMO PARA TRÁFICO NO UNIFORME

El algoritmo esta diseñado para que el tráfico uniforme (es decir, igual número de canales por cada celda) sea un caso particular de tráfico no uniforme. Esto se puede demostrar si nos remitimos a la teoría de conjuntos, y se ve el problema como una unión de subconjuntos.

Sea V las condiciones del problema impuesto, entonces definase v(i) como subconjuntos de soluciones parciales en el que

V = {v₁, v₂, v₃,, v_n}

Y para cada v(i) existe un span tal que, V(i) sp (número de celdas, canales por celda, Factor-P ).

De esta manera, existe un conjunto solución A que es igual a A = {v₁ v₂ v_n}, la unión de sus subconjuntos solución. Y el rango de frecuencias de cada asignación es igual a,

Vi = {1, maxsp₁} si i = 1 Si es una matriz cuadrada

Vi = {max spi_{+ 2}, max spi + max sp_i+1} en otros casos

Siendo i un entero positivo Z+.

En lugar de resolver un gran problema, que consume bastante tiempo (por que cada elemento de la asignación tiene que ser evaluado con respecto a todos), se resuelven muchos problemas pequeños, trayendo consigo una mejora en el tiempo de ejecución. Todo esto gracias a que la fórmula FA span puede ser aplicada a todo tipo de casos y esta ajustada para cumplir con los requisitos de calidad de voz subjetiva.

De esta manera, el algoritmo solución lo conforman subrutinas que son resueltas por algoritmos genéticos.

VII. FÓRMULA EMPÍRICA PARA CALCULAR EL SPAN

Como el objetivo es maximizar el mínimo SIR, sin desperdiciar demasiado espectro (span) y este varía de acuerdo al número de canales y celdas utilizadas, se hace necesario tener una fórmula para dimensionar el espectro que se va a ocupar, y que cumpla con el compromiso SIR Vs Span.

La formula que se ha denominado FA span [5], depende del número de celdas, del número de canales y de un factor de proximidad denotado como factor-P.

La subrutina que reconoce el factor-P determina cual es el posible núcleo de la red, es decir la celda que esta más rodeada por otras celdas. Dependiendo del factor-P y una vez identificado, de acuerdo a la red se analizan dos casos por separado:

Caso uno: canales por celda igual a 1

Este corresponde a una particularidad en el que todas las celdas tienen solo un canal. En este caso el span depende únicamente de la cantidad de celdas y un valor empírico (denotado por VA) determinado por el factor-P.

En la tabla No. 1 se observa el comportamiento del valor con respecto al factor-P.

Caso dos: canales por celda > 1

En este caso se toma como variable independiente el número de canales. A partir del factor de proximidad y sabiendo que 2 es la mínima separación adyacente en frecuencia y que el número de canales puede justificar un límite superior de span entonces se tiene que:

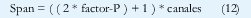
En ambos casos el factor-P se introduce como variable independiente. Es evidente que la regla encontrada no pertenece a valores óptimos que si pueden ser obtenidos por otros constructos matemáticos [1], por que el espacio de búsqueda no puede ser el óptimo debido a la naturaleza aleatoria que poseen los algoritmos genéticos.

VIII. RESULTADOS

FA Tool fue desarrollado en Microsoft Visual Studio versión empresarial, usando Visual Basic, versión 6.0., así que puede correr sobre cualquier computador que soporte un ambiente Windows.

Para realizar las diferentes simulaciones, se tomó como referencia el siguiente problema base con los siguientes parámetros:

7 celdas, en forma de cluster, con 5 canales cada una. Conjunto de condiciones D1 = { 7 , 3, 1, 1, 1, 0 }

Red General
Mutaciones = 25% de la población
Generaciones = 300
Tamaño de la población = 20 individuos
Exponente por pérdida de trayectoria, n = 4
Factor de los filtros,α= -24 dB/oct

Y se obtuvieron los siguientes resultados mostrados en la tabla No. 2.

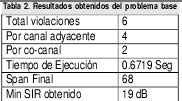
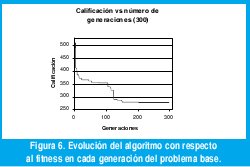
En la figura 6, se observa el rendimiento del algoritmo genético con respecto a la calificación del mejor individuo en cada generación. Por las características del problema el mejor individuo es el que tiene la menor calificación, idealmente puede llegar a tener calificación cero.

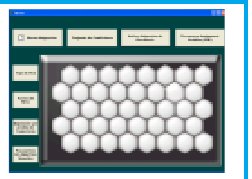
IX. FA Tool Versión 1.0

En la figura 7 se enseña la presentación del software.

Opciones del software

Las opciones del software están distribuidas por la pantalla principal por medio de botones, ellos son:

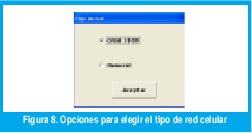
Botón Tipo de red:

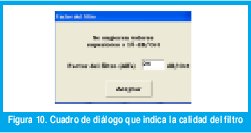
Este botón da acceso a dos posibles opciones (ver figura 10);

- Red GSM1800
- Red general celular

Opción Red GSM1800

Da la posibilidad de trabajar con redes GSM con un espectro fijo de 1805 a 1880 MHz. Cuando se da aceptar a esta opción surge el siguiente cuadro de diálogo;

1. Probabilidad de bloqueo: Indica el grado de calidad servicio de la red, 0.5%, 1%, 2%, 5%
2. Lambda promedio del sistema: Indica el número de llamadas por hora que realiza un abonado en promedio.
3. Tiempo promedio del sistema: Indica el tiempo promedio de duración de una llamada.

Con estos datos, el número de canales es calculado por la Formula de Erlang B, por medio de tablas incorporadas en el software.

Opción Red celular general: Maneja un número de canales ilimitado, teniendo por consiguiente un espectro ilimitado. Esta opción es utilizada para realizar diversas pruebas (para casos de referencia, como por ejemplo el Philadelfia Dataset [1]).

Botón Exponente por pérdida de trayectoria.

Se incluye en la ecuación que calcula el SIR.

Botón. Opciones GA.

1. Mutaciones
2. Número de generaciones
3. Cantidad de individuos de la población inicial.

Botón Conjunto de condiciones

Se da la posibilidad al usuario escoger entre dos conjuntos.

Donde

D1 = {√7,{√3 ,{1,{1, {1, {0 } indica un patrón de reuso de N=7. D2 = { 2 √3 , √3 , 1, 1, 1, 0 } indica un patrón de reuso de N=19.

Botón Nueva asignación:

Resetea el programa para iniciar la solución a un nuevo problema.

Botón Iniciar asignación:

Una vez establecidas las condiciones, con este botón se pone en marcha el algoritmo.

Hoja de resultados

Después de que el usuario da la opción de "Iniciar asignación de frecuencia", FA Tool comienza a desarrollar el algoritmo. El tiempo de ejecución del software dependerá del número de celdas y canales del problema. Al cumplir con el número de generaciones previamente establecido, FA Tool muestra un cuadro de diálogo que se puede ver en la figura 14.

FA Tool da diferentes resultados, para que el usuario pueda elegir de entre varias opciones, ellas son:

Botón Matriz asignación:

Muestra en una matriz tres elementos en cada una de sus posiciones, el primero es la asignación de frecuencias para mínima interferencia en enteros si es una red general o en MHz si es una red GSM. El segundo es la relación señal-a-interferencia, y el tercero la cantidad de violaciones que ha tenido la asignación.

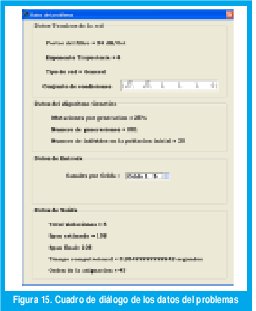
Botón. Datos del problema y Tiempo computacional.

Este indica al usuario en un cuadro de diálogo, cuatro diferentes tipos de datos: los datos técnicos de la red, datos del algoritmo genético, Datos de entrada y Datos de salida.

Botón Mapa de interferencia.

Se da visualización a un mapa de colores como se observa en la figura 16.

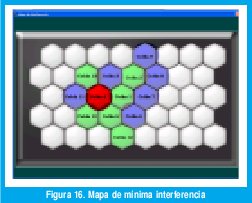
La intensidad del color identifica la relación señala-interferencia mínima de la celda. Además, cada celda contiene información específica de ella. En forma de cuadro de diálogo como se observa a continuación (figura 17), en este caso especifico, el cuadro corresponde a la celda 4 que es la más interferida. Como se observa en esta celda la portadora con peor SIR de todo el sistema tiene 15 dB y es la frecuencia 10, que esta interfiriendo con la celda 11 y 3 por canal adyacente. Observe además que de los 4 canales asignados a esta celda 3 tienen un SIR superior a 23 dB.

Finalmente, los siguientes botones contienen las matrices que indican los parámetros que condicionan la solución del problema, ellos son: Botón Matriz distancia euclidiana, Matriz de separación en frecuencia, Matriz de penalización co-canal, Matriz de penalización adyacente

IX. CONCLUSIONES

Fa Tool es una herramienta pedagógica capaz de explorar y evaluar el efecto de parámetros variantes, que se puede mejorar para realizar nuevos perfeccionamientos a los algoritmos y la posibilidad de construir híbridos entre ellos. FA Tool puede ser una herramienta de investigación inestimable como punto de partida para el desarrollo de soluciones a problemas de asignación de frecuencia particulares más complejos. Además, se distingue por:

• Ser fácil de usar y tener una interfaz amigable.
• Utilizar varios formatos de entrada para realizar la matriz de condiciones.
• Ser dúctil con respecto a los dominios de frecuencia (las frecuencias disponibles).
• Hallar las asignaciones de una manera flexible con respecto a las condiciones.
• Finalmente, FA Tool produce buenos resultados de asignación de frecuencia.

El algoritmo genético piramidal modificado tiene como ventaja sobre el AG tradicional que siempre va ser creciente la aptitud de los individuos, y tiene más probabilidad de encontrar mejores soluciones en tiempos mucho más cortos. Claro que de esta forma la aptitud promedio de la población en general permanecerá constante y no mejorara con respecto a la del mejor individuo.

Los algoritmos genéticos permitieron explorar espacios de soluciones muy amplios, evitando caer en mínimos locales mediante estrategias mejoradas hechas al algoritmo.

Es importante que se encuentren métodos para evaluar la actuación de estas técnicas heurísticas. Comparando simplemente un heurístico con otro no da la información sobre la calidad real de las asignaciones obtenidas. Además, la calidad de una asignación de frecuencia puede depender más del modelo de predicción de cubrimiento usado para el pronóstico de la interferencia que de los modelos heurísticos de optimización utilizados.

REFERENCIAS BIBLIOGRÁFICAS

[1] Koster A.M.C.A. Frequency Assignment. Models and Algorithms. PhD thesis, Maastricht University, Noviembre de 1999.

[2] Montemanni Roberto. Upper and lower bounds for the fixed spectrum frequency assignment problem. PhD thesis, University of Glamorgan, Noviembre 2001.

[3] HALE W. K. Frequency assignment: theory and applications. Proceedings of the IEEE, 1980, Vol. 68, pp. 1497-1514.

[4] W.J.Watkins, S. Hurley, and D.H. Smith. Evaluation of models for area coverage. Technical Report No. 98003, Cardiff University, December 1998.

[5] Acero Jorge y García Aldo, Algoritmos Genéticos (GA) aplicados a la solución del problema de asignación de frecuencia (FAP) en la banda de comunicaciones móviles GSM, Trabajo de grado, Ingeniería Electrónica, Universidad Distrital. Bogotá, 2004.

[6] S. Hurley, D.H. Smith, and S.U. Thiel. FASoft: A system for discrete channel frequency assignment. Radio Science, pp. 1921-1939, 1997.

Juan Carlos Gómez Paredes
Ingeniero en Telecomunicaciones, Msc. en Comunicaciones, profesor Facultad de Ingeniería Universidad Distrital Francisco José de Caldas.

Jorge Andrés Acero
Hernández Ingeniero Electrónico, Universidad Distrital Francisco José de Caldas. jorgeacero@terra.com.co

Aldo Camilo García Suárez
Ingeniero Electrónico, Universidad Distrital Francisco José de Caldas. aldokmilo@hotmail.co