DOI:
https://doi.org/10.14483/23448393.22292Published:
2025-03-31Issue:
Vol. 30 No. 1 (2025): January-AprilSection:
Education in EngineeringBibliometric Analysis and Overview of Matrix Product States in the Bose-Hubbard Model
Estudio bibliométrico y revisión del uso de estados producto de matrices en el modelo de Bose-Hubbard
Keywords:
matrix product states, density matrix renormalization group, strongly correlated systems, Bose-Hubbard model, tensor networks (en).Keywords:
estados producto de matrices, grupo de renormalización de matriz de densidad, sistemas fuertemente correlacionados, modelo de Bose-Hubbard, redes de tensor (es).Downloads
References
W. Wang, “Linear limit continuation: Theory and an application to two-dimensional bose–einstein condensates,” Chaos Sol. Frac., vol. 182, p. 114735, 2024. https://doi.org/10. 1016/j.chaos.2024.114735
A. Jahn and J. Eisert, “Holographic tensor network models and quantum error correction: A topical review,” Quantum Sci. Technol., vol. 6, no. 3, p. 033002, 2021. https://doi.org/10.1088/2058-9565/ac0293
A. J. Ferris and D. Poulin, “Tensor networks and quantum error correction,” Phys. Rev. Lett., vol. 113, p. 030501, 2014. https://doi.org/10.1103/PhysRevLett.113.030501
A. S. Darmawan and D. Poulin, “Tensor-network simulations of the surface code under realistic noise,” Phys. Rev. Lett., vol. 119, p. 040502, 2017. https://doi.org/10.1103/PhysRevLett.119.040502
S. F. Caballero-Benítez, “Materia cuántica en cavidades de alta reflectancia (many-body CQED),” 2022. [Online]. Available: https://doi.org/10.48550/arXiv.2201.06641
H. A. Gersch and G. C. Knollman, “Quantum cell model for bosons,” Phys. Rev., vol. 129, pp. 959–967, Jan 1963. https://doi.org/10.1103/PhysRev.129.959
Y. Nakamura, Y. Takasu, J. Kobayashi, H. Asaka, Y. Fukushima, K. Inaba, M. Yamashita, and Y. Takahashi, “Experimental determination of bose-hubbard energies,” Phys. Rev. A, vol. 99, no. 3, p. 033609, Mar 2019. http://dx.doi.org/10.1103/PhysRevA.99.033609
G. Sangiovanni, A. Toschi, E. Koch, K. Held, M. Capone, C. Castellani, O. Gunnarsson, S.-K. Mo, J. W. Allen, H.-D. Kim, A. Sekiyama, A. Yamasaki, S. Suga, and P. Metcalf, “Static versus dynamical mean-field theory of mott antiferromagnets,” Phys. Rev. B, vol. 73, no. 20, May 2006. http://dx.doi.org/10.1103/PhysRevB.73.205121
G. Co’, “Introducing the random phase approximation theory,” Universe, vol. 9, no. 3, p. 141, 2023. https://doi.org/10.3390/universe9030141
R. T. Scalettar, “An introduction to the Hubbard Hamiltonian,” in Quantum materials: Experiments and theory, E. Pavarini, E. Koch, J. van den Brink, and G. Sawatzky, Eds. Jülich, Germany: Forschungszentrum Jülich, 2016, pp. 4.1–4.27. [Online]. Available: http://www.cond-mat.de/events/correl16
U. Schollwöck, “The density-matrix renormalization group,” Rev. Mod. Phys., vol. 77, pp. 259–315, Apr 2005. https://doi.org/10.1103/RevModPhys.77.259
M. Iskin, “Mean-field theory for the mott-insulator-paired-superfluid phase transition in the two-species bose-hubbard model,” Phys. Rev. A, vol. 82, p. 055601, 2010. https://doi.org/10.1103/PhysRevA.82.055601
G. Evenbly and G. Vidal, “Tensor network states and geometry,” J. Stat. Phys., vol. 145, no. 4, p. 891–918, Jun 2011. http://dx.doi.org/10.1007/s10955-011-0237-4
H. Tang, J. L. Simancas-García, J. Mai, M. Cheng, I. Iqbal, and L. Y. Por, “Overview of digital quantum simulator: Applications and comparison with latest methods,” SPIN, p. 2440004, 2024. https://doi.org/10.1142/S2010324724400046
M. Brenes, J. J. Mendoza-Arenas, A. Purkayastha, M. T. Mitchison, S. R. Clark, and J. Goold, “Tensor-network method to simulate strongly interacting quantum thermal machines,” Phys. Rev. X, vol. 10, p. 031040, 2020. https://doi.org/10.1103/PhysRevX.10.031040
J. J. Mendoza-Arenas, “Dynamical quantum phase transitions in the one-dimensional extended fermi–hubbard model,” J. Stat. Mech., vol. 2022, p. 043101, 2022. [Online]. Available: https://doi.org/10.1088/1742-5468/ac6031
J. Reslen, “Entanglement at the interplay between single- and many-bodyness,” J. Phys. A, vol. 56, p. 155302, 2023. https://doi.org/10.1088/1751-8121/acc291
D. Jaschke, M. L. Wall, and L. D. Carr, “Open source matrix product states: Opening ways to simulate entangled many-body quantum systems in one dimension,” Comput. Phys. Commun., vol. 225, pp. 59–91, 2018. https://doi.org/10.1016/j.cpc.2017.12.015
V. M. F. Verstraete and J. Cirac, “Matrix product states, projected entangled pair states, and variational renormalization group methods for quantum spin systems,” Adv. Phys., vol. 57, no. 2, pp. 143–224, 2008. https://doi.org/10.1080/14789940801912366
M. Zheng, Y. Qiao, Y. Wang, J. Cao, and S. Chen, “Exact solution of the bose-hubbard model with unidirectional hopping,” Phys. Rev. Lett., vol. 132, p. 086502, Feb 2024. http://dx.doi.org/10.1103/PhysRevLett.132.086502
V. Colussi, F. Caleffi, C. Menotti, and A. Recati, “Quantum gutzwiller approach for the two-component bose-hubbard model,” SciPost Phys., vol. 12, no. 3, p. 111, Mar 2022. http://dx.doi.org/10.21468/SciPostPhys.12.3.111
G. Catarina and B. Murta, “Density-matrix renormalization group: a pedagogical introduction,” Eur. Phys. J. B, vol. 96, p. 111, Aug 2023. http://dx.doi.org/10.1140/epjb/s10051-023-00575-2
I. Georgescu, S. Ashhab, and F. Nori, “Quantum simulation,” Rev. Mod. Phys., vol. 86, no. 1, p. 153–185, Mar 2014. http://dx.doi.org/10.1103/RevModPhys.86.153
S. R. White, “Density matrix formulation for quantum renormalization groups,” Phys. Rev. Lett., vol. 69, pp. 2863–2866, Nov 1992. https://doi.org/10.1103/PhysRevLett.69. 2863
A. Haller, “Matrix product states: A variational approach to strongly correlated systems,” Bachelor’s thesis, Johannes Gutenberg University Mainz, 2014. [Online]. Available: https: //www.tmqs.lu/images/haller_bsc.pdf
S. Keller, M. Dolfi, M. Troyer, and M. Reiher, “An efficient matrix product operator representation of the quantum chemical hamiltonian,” J. Chem. Phys., vol. 143, p. 244118, 2015. https://doi.org/10.1063/1.4939000
J. Cui, J. I. Cirac, and M. C. Bañuls, “Variational matrix product operators for the steady state of dissipative quantum systems,” Phys. Rev. Lett., vol. 114, p. 220601, 2015. https://doi.org/10.1103/PhysRevLett.114.220601
A. Strathearn, P. Kirton, D. Kilda, J. Keeling, and B. Lovett, “Efficient non-markovian quantum dynamics using time-evolving matrix product operators,” Nat. Commun., vol. 9, p. 3322, 2018. https://doi.org/10.1038/s41467-018-05617-3
S. Moudgalya, N. Regnault, and B. A. Bernevig, “Entanglement of exact excited states of affleck-kennedy-lieb-tasaki models: Exact results, many-body scars, and violation of the strong eigenstate thermalization hypothesis,” Phys. Rev. B, vol. 98, p. 235156, 2018. [Online]. Available: https://doi.org/10.1103/PhysRevB.98.235156
B. Pirvu, V. Murg, J. Cirac, and F. Verstraete, “Matrix product operator representations,” New J. Phys., vol. 12, p. 025012, 2010. https://doi.org/10.1088/1367-2630/12/2/ 025012
N. Nakatani and G. K.-L. Chan, “Efficient tree tensor network states (ttns) for quantum chemistry: Generalizations of the density matrix renormalization group algorithm,” J. Chem. Phys., vol. 138, p. 134113, 2013. https://doi.org/10.1063/1.4798639
S. Szalay, M. Pfeffer, V. Murg, G. Barcza, F. Verstraete, R. Schneider, and O. Legeza, “Tensor product methods and entanglement optimization for ab initio quantum chemistry,” Int. J. Quantum Chem., vol. 115, no. 19, p. 1342 – 1391, 2015. https://doi.org/10.1002/qua.24898
D. Liu, S.-J. Ran, P. Wittek, C. Peng, R. B. Garcia, G. Su, and M. Lewenstein, “Machine learning by unitary tensor network of hierarchical tree structure,” New J. Phys., vol. 21, p. 073059, 2019. https://doi.org/10.1088/1367-2630/ab31ef
M. Niedermeier, M. Nairn, C. Flindt, and J. L. Lado, “Quantum computing topological invariants of two-dimensional quantum matter,” Phys. Rev. Res., vol. 6, p. 043288, 2024. https://doi.org/10.1103/PhysRevResearch.6.043288
A. Wulff, B. Chen, M. Steinberg, Y. Tang, M. Möller, and S. Feld, “Quantum computing and tensor networks for laminate design: A novel approach to stacking sequence retrieval,” Comput. Methods Appl. Mech. Eng., vol. 432, part A, p. 117380, 2024. https://doi.org/10.1016/j.cma.2024.117380
A. Termanova, A. Melnikov, E. Mamenchikov, N. Belokonev, S. Dolgov, A. Berezutskii, R. Ellerbrock, C. Mansell, and M. Perelshtein, “Tensor quantum programming,” New J. Phys., vol. 26, p. 123019, 2024. https://doi.org/10.1088/1367-2630/ad985b
A. Singh Bhatia and D. E. Bernal Neira, “Federated learning with tensor networks: a quantum ai framework for healthcare,” Mach. Learn. Sci. Technol., vol. 5, p. 045035, 2024. https://doi.org/10.1088/2632-2153/ad8c11
G. Evenbly, “Hyperinvariant tensor networks and holography,” Phys. Rev. Lett., vol. 119, p. 141602, 2017. https://doi.org/10.1103/PhysRevLett.119.141602
A. Peach and S. F. Ross, “Tensor network models of multiboundary wormholes,” Class. Quantum Gravity, vol. 34, no. 10, p. 105011, 2017. https://doi.org/10.1088/1361-6382/aa6b0f
A. Jahn, M. Gluza, F. Pastawski, and J. Eisert, “Holography and criticality in matchgate tensor networks,” Sci. Adv., vol. 5, no. 8, p. eaaw0092, 2019. https://doi.org/10.1126/sciadv.aaw0092
F. Verstraete, V. Murg, and J. Cirac, “Matrix product states, projected entangled pair states, and variational renormalization group methods for quantum spin systems,” Adv. Phys., vol. 57, no. 2, p. 143 – 224, 2008. https://doi.org/10.1080/14789940801912366
J. I. Cirac, D. Pérez-García, N. Schuch, and F. Verstraete, “Matrix product states and projected entangled pair states: Concepts, symmetries, theorems,” Rev. Mod. Phys., vol. 93, p. 045003, 2021. https://doi.org/10.1103/RevModPhys.93.045003
N. Schuch, D. Pérez-García, and I. Cirac, “Classifying quantum phases using matrix product states and projected entangled pair states,” Phys. Rev. B Cond. Mat. Mater. Phys., vol. 84, p. 165139, 2011. https://doi.org/10.1103/PhysRevB.84.165139
R. Orús, “A practical introduction to tensor networks: Matrix product states and projected entangled pair states,” Ann. Phys., vol. 349, pp. 117–158, 2014. https://doi.org/10.1016/j.aop.2014.06.013
J. Jordan, R. Orús, G. Vidal, F. Verstraete, and J. Cirac, “Classical simulation of infinite-size quantum lattice systems in two spatial dimensions,” Phys. Rev. Lett., vol. 101, p. 250602, 2008. https://doi.org/10.1103/PhysRevLett.101.250602
G. Vidal, “Class of quantum many-body states that can be efficiently simulated,” Phys. Rev. Lett., vol. 101, no. 11, 2008. https://doi.org/10.1103/PhysRevLett.101.110501
Y.-Y. Shi, L.-M. Duan, and G. Vidal, “Classical simulation of quantum many-body systems with a tree tensor network,” Phys. Rev. A, vol. 74, p. 022320, 2006. https://doi.org/10.1103/PhysRevA.74.022320
S. Holtz, T. Rohwedder, and R. Schneider, “The alternating linear scheme for tensor optimization in the tensor train format,” SIAM J. Sci. Comput., vol. 34, no. 2, pp. A683–A713, 2012. https://doi.org/10.1137/100818893
V. Murg, F. Verstraete, O. Legeza, and R. Noack, “Simulating strongly correlated quantum systems with tree tensor networks,” Phys. Rev. B, vol. 82, p. 205105, 2010. https://doi.org/10.1103/PhysRevB.82.205105
L. Tagliacozzo, G. Evenbly, and G. Vidal, “Simulation of two-dimensional quantum systems using a tree tensor network that exploits the entropic area law,” Phys. Rev. B, vol. 80, p. 235127, 2009. https://doi.org/10.1103/PhysRevB.80.235127
M. L. Wall, A. Reilly, J. S. Van Dyke, C. Broholm, and P. Titum, “Quantum tensor network algorithms for evaluation of spectral functions on quantum computers,” Phys. Rev. B, vol. 110, p. 214402, 2024. https://doi.org/10.1103/PhysRevB.110.214402
R. Huang, H. Yi, and P. H. Li, “Variational quantum recurrent neural networks for multi-feature forecasting,” Int. J. Quantum Inf., vol. 22, no. 7, p. 2450029, 2024. https://doi.org/10.1142/S0219749924500291
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Recibido: 11 de junio de 2024; Revisión recibida: 30 de marzo de 2025; Aceptado: 4 de abril de 2025
Abstract
Context:
Quantum many-body systems have been a prominent topic over the past two decades, underpinning advancements in superconductors, ultracold atoms, and quantum computing, among other fields. This bibliometric analysis explores key concepts, influential authors, and the current significance of a powerful family of algorithms in computational physics, i.e., density matrix renormalization group (DMRG) algorithms. Special emphasis is placed on the use of tensor product states in developing classical simulations of quantum systems.
Method:
This paper presents a literature review sourced from the SCOPUS database. It analyzes trends and approaches related to uncertainty in numerical developments for quantum many-body systems, with a focus on the Bose-Hubbard Model, in order to better understand the imposition of additional constraints to ensure the validity of the results.
Results:
The increasing number of publications on this topic over the last decade indicates a growing interest in solutions for many-body quantum systems, driven by promising advances in superconductive materials, quantum computing, and other impactful areas.
Conclusions:
This work explored essential foundational works to help beginners understand a well-established technique that aims to overcome the limitations of classical computing. The use of matrix product states in DMRG algorithms is gaining significant traction in various fields, including quantum computing, machine learning, and statistical mechanics, with the purpose of addressing the challenges related to quantum many-body systems.
Acknowledgments:
This work was supported by Universidad del Valle under internal project CI. 71344.
Keywords:
matrix product states, density matrix renormalization group, strongly correlated systems, Bose-Hubbard model, tensor networks.Resumen
Contexto:
Los sistemas cuánticos de muchos cuerpos han sido un tema prominente durante las últimas dos décadas, sustentando avances en superconductores, átomos ultrafríos y computación cuántica. Este análisis bibliométrico explora conceptos clave, autores influyentes y la significancia actual de una poderosa familia de algoritmos en física computacional, i.e., los algoritmos del grupo de renormalización de matriz de densidad (DMRG). Se pone un énfasis especial en el uso de estados producto de tensor en el desarrollo de simulaciones clásicas de sistemas cuánticos.
Métodos:
Este artículo presenta una revisión de la literatura obtenida de la base de datos de SCOPUS. Analiza tendencias y enfoques relacionados con el concepto de incertidumbre dentro del marco de desarrollos numéricos para sistemas cuánticos de muchos cuerpos, con énfasis en el modelo de Bose-Hubbard. Esto, con el objetivo de entender mejor la imposición de restricciones adicionales para asegurar la validez de los resultados.
Resultados:
El número creciente de publicaciones sobre este tema en la última década indica un mayor interés en soluciones para sistemas cuánticos de muchos cuerpos, impulsadas por avances promisorios en materiales superconductores, computación cuántica y otras áreas de impacto.
Conclusiones:
Este trabajo exploró los trabajos fundamentales para ayudar a los principiantes a comprender una técnica bien establecida que promete sobrepasar las limitaciones de la computación clásica. El uso de los estados de producto de matrices en los algoritmos DMRG está ganando una tracción significativa en numerosos campos, incluyendo la computación cuántica, el aprendizaje automático y la mecánica estadística, con el fin de abordar los desafíos asociados con los sistemas cuánticos de muchos cuerpos.
Acknowledgments:
Este trabajo fue apoyado por la Universidad del Valle bajo el proyecto interno Cl. 71344.
Palabras clave:
estados producto de matrices, grupo de renormalización de matriz de densidad, sistemas fuertemente correlacionados, modelo de Bose-Hubbard, redes de tensor.1. Introduction
Since the theoretical statistical-mechanical development by Bose and Einstein 1 and its experimental corroboration, ultracold quantum gases have been a topic of high interest for the scientific community.
Given their emergent physical properties, these types of systems attract great interest, bringing many fields together, such as condensed matter, quantum simulators, quantum information, and quantum error correction 2-4. Additionally, thanks to the development of tools for controlling cold atoms in atomic physics and quantum optics, it is possible to obtain highly controllable systems by leveraging phenomena such as radiation pressure and dipole force, which allow cooling and trapping low-energy atoms in periodic structures generated by laser light called optical lattices5.
Among the many models that include interactions between atoms in optical lattices, this document focuses on the Bose-Hubbard (BH) model introduced in 1963 by Gersch and Knollman 6. This model describes bosons that can hop between the sites of a discrete lattice and interact when they coincide at the same site. It has undergone extensive theoretical and experimental scrutiny 7, and it has been studied using a wide range of techniques developed within the condensed matter community, from static mean-field approaches to the more complex dynamic mean-field theory 8, in addition to various diagrammatic approaches such as random phase approximation 9 and expansions based on spin and orbital angular momentum degeneracy 10. It has also been widely addressed using numerical methods like exact diagonalization (ED) and quantum Monte Carlo (QMC) 10.
However, describing a quantum system through the eigenstates of its Hamiltonian implies problems with the exponential growth of its Hilbert space. Therefore, in 1992, White developed an algorithm that extracted information from the system based on the eigenstates of the density matrix operator. This is known as the density matrix renormalization group (DMRG) algorithm11 and enables the study of interacting many-body systems of low and high dimensionality with internal degrees of freedom.
The scope of traditional quantum mechanics is limited when investigating behavioral regimes different from the approximations made during theoretical calculations. Therefore, a few numerical methods have been developed to determine physical properties of high interest, such as observables and system correlations. The development of the DMRG has led to two decades of significant advances in addressing these problems; it became possible to relate the low-dimensional long-range phenomena of the BH model, which constitute the desired superfluidity and Mott insulator properties 12.
The success of the DMRG lies in its matrix product states (MPS), a type of tensor network (TN) that only deals with one spatial dimension 13. These are capable of handling the problem regarding the exponential growth of Hilbert spaces through truncations without losing system information or being limited to approximate systems. This paper seeks to explore how extensively MPS algorithms have been studied and assess their continued relevance based on recent research trends and output quality.
2. Methodology
The methodology followed in this work consists of several steps, ranging from defining the scope of the analysis to interpreting the results. A bibliometric approach was employed to examine the application of MPS in the BH model using data from SCOPUS. The process involved data collection, cleaning, visualization, and interpretation to identify key trends and contributions in the field. A summary of the methodology is presented in Table I.
Table I: Summary of the bibliometric analysis methodology
Step
Description
Definition of scope
This study focused on the application of MPS in the BH model and other TN methods in physics and engineering. The bibliometric analysis considered publications from 2013 to 2023.
Data collection
A SCOPUS query was formulated using relevant keywords. Search filters were applied to refine the results to articles discussing MPS and the BH model. Metadata, including titles, authors, publication years, journal/conference details, and citation counts, were extracted.
Data cleaning and processing
Duplicate entries and irrelevant publications were removed. Author names and affiliations were standardized where necessary, and consistency across bibliographic records was ensured.
Visualization and interpretation
Publication trends over the selected period were analyzed using VOSviewer. Co-authorship networks, journal impact, and keyword co-occurrence patterns were examined. Plots, charts, and network graphs were generated to illustrate trends.
Discussion of findings
The results were compared against those of prior studies to identify trends and research gaps. Key contributors and emerging themes in the field were highlighted.
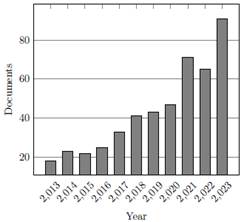
The keywords used during the data collection stage were "tensor networks", "matrix product state", "many-body systems", "strongly correlated systems", "ultra cold atoms", "Bose-Hubbard Hamiltonian", "spin-1", and "bosons"for the decade between 2013 and 2023. Fig. 1 presents the research dynamics as evolving with the 479 scientific publications identified, where a pronounced increase in interest is observed from 2020 onward. The exact query entry used was as follows: TITLE-ABS-KEY ( "Tensor Networks" AND "Matrix Product State" OR "Many-body systems" OR "Strongly correlated systems" OR "Ultra Cold atoms" OR "Bose-Hubbard Hamiltonian" OR "Spin-1" OR "Bosons" ) AND PUBYEAR > 2012 AND PUBYEAR < 2024.
Figure 1: Publishing intensity regarding TNs in many-body systems over the last 10 years.
Figure 2: Documents per year by country.
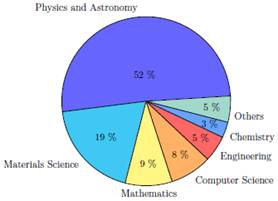
Furthermore, Fig. 3 illustrates the distribution of the research fields involved, highlighting "physics and astronomy"with 421 publications, followed by "materials science"with 155 documents and "mathematics"with 72.
Figure 3: Distribution of fields of study with regard to scientific publications.
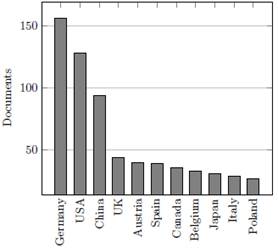
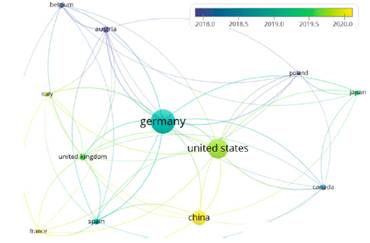
As a result of this bibliometric analysis, an important aspect emerges: Fig. 4 shows that many countries are actively engaged in TN research in the context of many-body systems and ultra cold atoms. The top three contributors are Germany (156 publications), United States (128), and China (94). Out of these publications, 12 papers have an author from Latin American countries, and four of them have a Colombian author 14-17. The topics addressed were quantum thermal machines and entanglement between single- and many-bodyness. The institutes responsible for most of the publications are consistent with Fig. 4: the first four of them are the Max Planck Institute, Universiteit Gent, Universität Wien, and the Munich Center for Quantum Sciences.
Figure 4: Countries, their collaborators, and highest average of documents published by year
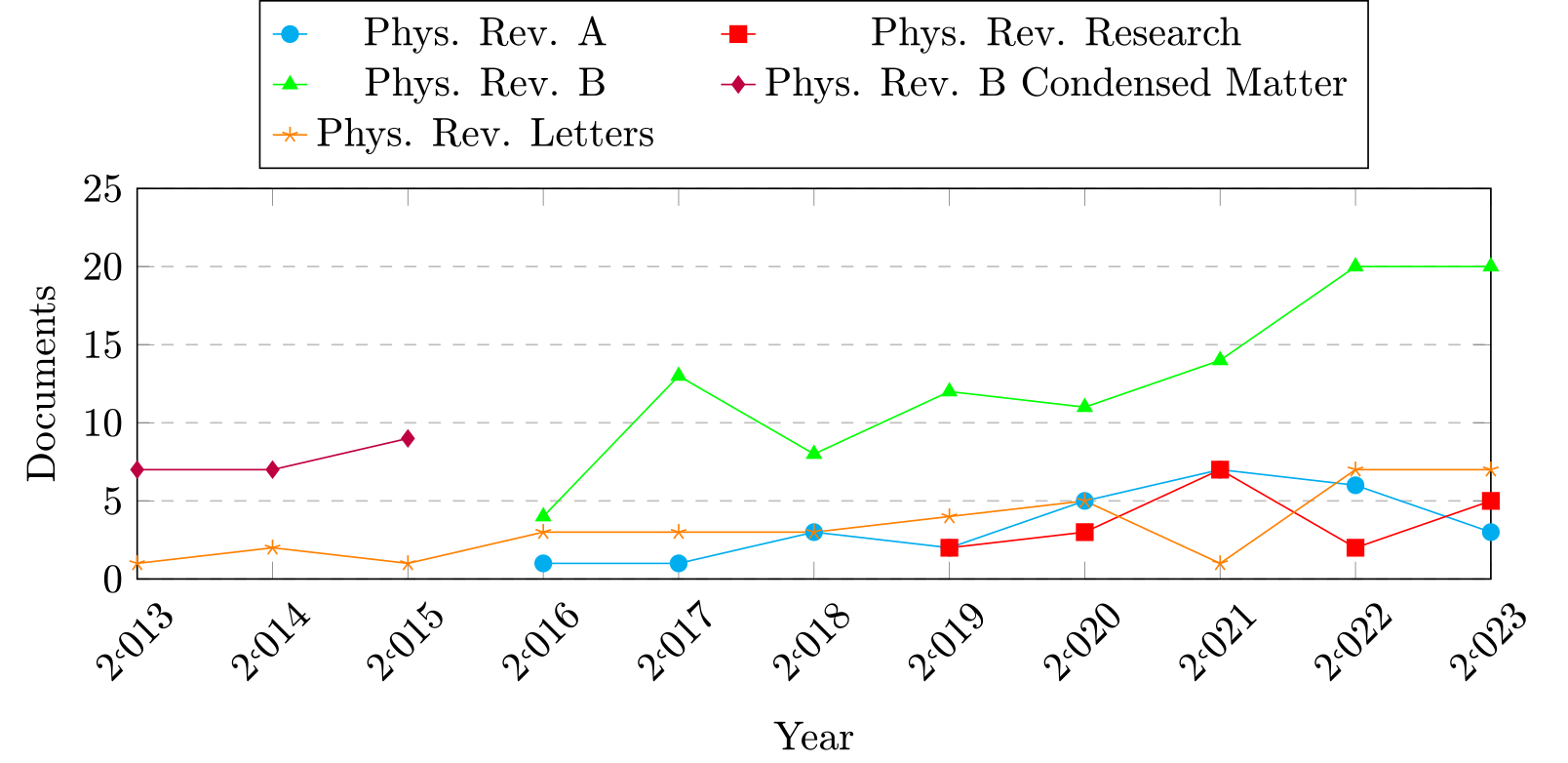
The five journals that published the most articles on the topics over the past decade all belong to the Physical Review family, as illustrated in Fig.5.
Figure 5: Documents per year by source.
Finally, Fig. 6 shows the 26 most frequent keywords, each appearing more than 20 times in the selected articles. These reflect the main elements around which this topic revolves, including the determination of a ground state in quantum many-body systems, their phase diagrams, and certain fields of interest, e.g., quantum optics, statistical mechanics, and machine learning.
Figure 6: Most relevant keyword appearance by year
3. Results and discussion
Different logical operators were used in the query string to filter the initial 479 publications, focusing only on the topics most relevant to this research. By replacing the operator OR with AND before "spin- 1ïn the query, we obtained 34 publications more directly related to our research topic.
The use of MPS and TNs to address many-body quantum systems has recently attracted substantial attention. With the growth of quantum computing and machine learning, MPS provide powerful solutions to problems where perturbative methods or exact diagonalization fail to accurately describe the complex dynamics of entangled quantum systems 18.
Fig. 4 indicates that research in this field is particularly prominent in Germany, where Frank Verstraete, JI Cirac, and MM Wolf developed foundational approaches in 2007 19 and remain as the leading researchers. Institutions such as the Max Planck Institute of Quantum Optics, Universiteit Gent, Universität Wien, and the Munich Center for Quantum Science and Technology (MCQST) are among Europe's leading research centers in this area. Additionally, China and the United States have also contributed significantly to the field, even surpassing Germany in average annual publications. Three institutes that are ranked among the top 10 in these countries are the Chinese Academy of Sciences, the University of the Chinese Academy of Sciences, and the California Institute of Technology.
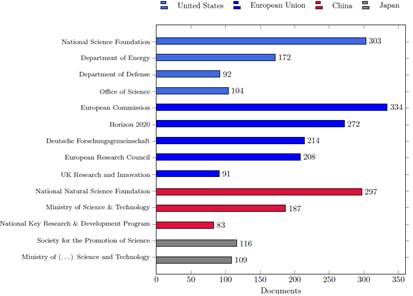
The dominance of certain institutions in the field of TN research is not merely a result of geographical biases, but rather a reflection of strategic investments in science and technology by both the public and private sectors (Fig.7). Governments in these regions prioritize funding for quantum technologies, artificial intelligence, and condensed matter physics, leading to well-financed research programs and cutting-edge facilities. Additionally, strong collaboration between academia and the industry foster innovation and accelerate publication rates. As shown in Fig. 7, the top 14 funding agencies supporting TN research highlight the crucial role of sustained financial backing in maintaining institutional leadership within this rapidly growing field.
Figure 7: Top 14 funding sponsors by number of published documents on TNs from 2013 to 2023. The data highlight the leading institutions investing in TN research, with significant contributions from the United States, the European Union, China, and Japan
3.1. Bose-Hubbard model
Numerical developments flourish only when applied to complex systems, which is why quantum many-body models - such as the Fermi-Hubbard, Lieb-Liniger, and Bose-Hubbard models, among others - serve as essential benchmarks to evaluate their efficiency and precision 20. However, physics frequently involves complexities requiring the study of models with non-Hermitian Hamiltonians or quartic interaction terms, as is the case with the BH model, which describes a system of bosons in a 1D chain that interact and hop in a unidirectional fashion. The Hamiltonian that describes this model 20
corresponds to Eq. (1):
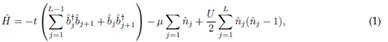
where
and
=
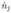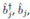are bosonic creation, annihilation, and particle number operators applied to the j-th site; L refers to the total sites; U quantifies the on-site interaction strength; Є is set depending on boundary conditions; and t characterizes hopping between first neighbors. The model is indeed integrable from the perspective of the quantum inverse scattering method 20. Many exact solution approaches can be adopted using ansätze such as Bethe 20 or Gutzwiller 21.
3.2. Density matrix renormalization group
Investigating quantum many-body systems is crucial in condensed matter physics. Two main challenges include modeling complex interactions and solving these models computationally. In the latter, many computational issues also emerge, mainly due to the fact that the dimension of the Hilbert space of the whole system grows exponentially (d n ) with the amount of particles (n) involved and the internal degrees of freedom (d) which do not happen in classical mechanics, where the computational memory required is proportional to one times the other (dn) 22. To avoid this issue, based on the variational principle, Steven R. White developed the DMRG in 1992 23 after realizing that the eigenstates of the density matrix provide a more suitable description for quantum systems than those of the Hamiltonian 24.
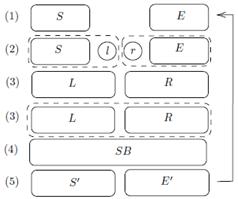
Figure 8: Schematic description of the infinite-system DMRG algorithm, as adapted from 22
The procedure is as follows. First, we examine two blocks: system (S) and environment (E) (Fig. 8). These blocks are part of the overall system under analysis, so their labels are chosen arbitrarily. Next, we expand the system by adding a physical site to each block, resulting in the formation of blocks left (l) and right (r). We then create block SB (superblock) by combining blocks L and R. SB represents the entire system that we aim to describe at each iteration. It is important to note that aggregating these blocks requires consideration of both their individual Hamiltonians and their mutual interactions.
Finally, if we were to truncate blocks L and R using their corresponding low-energy states (5), we would create the new blocks S' and E' to be employed in the initial step of the subsequent iteration 22.
An alternative in the algorithm comes in step (5), where diagonalizing becomes viable using a well behaved eigenstate |ψ⟩ (usually the ground state or among the lowest-energy eigenstates) to construct the density matrix. Considering multiple target states is not out of the picture, as long as the sum of the amplitudes of probability equals the identity, as shown in Eq.(2).
3.3. Matrix product states
Tensor network states (TNS) are extensively used within the DMRG community to estimate the ground states of Hamiltonians represented on lattices in d dimensions. The simplest type of TN, which we will briefly explain, consists of MPS where there is only a single spatial dimension (D=1). This is the core of the remarkable success of White's DMRG. Whether it be their dynamics with the time evolution block decimation algorithm (TEBD) or their variations, MPS have been very useful since they can accurately provide the properties of a ground state 13.
Constructing an MPS requires dealing with a system that can be split into two subsystems, e.g, a 1D chain of spins, as shown in Eq. 3. Starting from a physical lattice with L sites, a bipartite system is formed, where the second subsystem is taken as the lattice at site L and the first subsystem is the rest of the lattice. This is then represented as an entangled state, and singular value decomposition (SVD) is performed on the probability amplitude coefficients. After regrouping, the right site of the lattice is represented on an appropriate basis, with the left side representing the lattice from site 1 to L - 1. This process is iterated until all sites are included (Fig. 9) 25.
where the
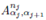correspond to contractions of,
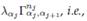the Schmidt coefficient (λ) and the element from the transformation matrix (Г), to the desired base (Fock's in this case).
Figure 9: Pictorial (left) and mathematical (right) representations of the MPS
3.4. Matrix product operators
In the same spirit, a quantum state can be represented in terms of products of matrices, and an analogous representation can be formulated for operators. This becomes really useful when intending to measure the expectation values of global operators that, rather than acting in a single site, act throughout the entire chain, as is the case for most Hamiltonians 26-29. To this effect, the operators must be represented as a product of matrices, as shown in Eq. (5) for a general operator.
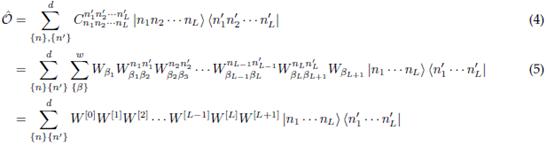
In Eq. (5), the element
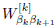denotes a ω x ω matrix, where w is the local dimension of the matrix product operator (MPO) and {|nk⟩} are the local basis vectors. Moreover, the matrices at the free ends of the chain will have a different structure. They are not square matrices; instead, they are column and row vectors of dimensions 1 x ω and ω x 1. Thus, the product between W s yields a scalar, as shown in Eq. (6).
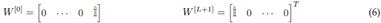
Figure 10: Graphic representation (left) and mathematical expression (right) of the MPO
The graphic representation of Eq. (5) is presented in Fig.10. The true wonders of the MPO representation lie in the fact that it allows expressing exactly any local Hamiltonian with (relatively) small matrices of dimension ω x ω. Moreover, the structure of this representation is almost identical to that of a MPS; both of them are represented by a list of tensors at each site and, therefore, computing expectation values becomes an easier task 30. Taking into account that we are working with a Hamiltonian composed of a sum of finite-range interactions, we can construct the W matrix as entirely lower (or upper) triangular matrices by imposing that the top-left and bottom-right components be identity operators
For example, consider an operator that is the sum of single-site local terms:
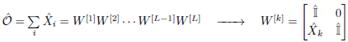
For that specific operator, the internal dimension of the MPO is ω = 2, and each operator (including that top-right о) is d x d matrices. If we carry out the same procedure for a nearest-neighbor operator that also has single-site local terms, the following is obtained:
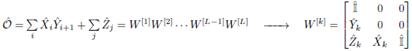
Note that, in both the first and the second operator, the terms which act upon a single site always remain in the bottom-left corner. The BH Hamiltonian in Eq. (1) can also be expressed in this way, as seen in Eq. (7).
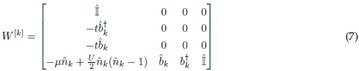
3.5. Other TN representations
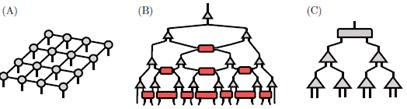
Another interesting result from our SCOPUS analysis is the need for a higher-dimensional representation of states, as MPS are limited to one spatial dimension. When it comes to other physics fields such as quantum chemistry 31,32, machine learning 33, quantum computation 34-37, and holography 2,38-40, systems with higher dimensions (d = 2) are the norm rather than the exception. This is why other generalizations of MPS and MPO exist.
Among the most commonly used representations are projected entangled-pair states (PEPS) 41-45, the multiscale entanglement renormalization ansatz (MERA) 46, and tree tensor networks (TTNs) 47-50 (Fig. 11). The first natural generalization corresponds to PEPS, where the linear MPS is replaced by a lattice that can take many geometries aside from the traditional squared lattice, as shown in Fig. 11a. Translational invariance can once again be exploited for finite and infinite systems by choosing a unitary cell that is repeated over the whole lattice 13.
Figure 11: Depiction of other TN representations: a) projected entangled-pair states, b) multiscale entanglement renormalization, c) tree tensor networks
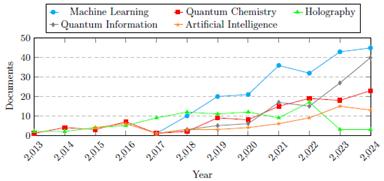
TNs have rapidly emerged as a powerful framework for tackling complex problems in quantum many-body physics, quantum information, and beyond, as showcased in Fig. 12. Their ability to efficiently represent and manipulate high-dimensional data makes them invaluable for studying entanglement structures, simulating quantum systems, and optimizing variational methods. As research continues to uncover new applications, from enhancing quantum algorithms 51 to accelerating neural network training, TN methods 52 have become increasingly relevant for newcomers seeking to work at the forefront of computational and theoretical advancements. Given their expanding role in interdisciplinary research, mastering TNs is not just an asset but a necessity for those aiming to stay ahead in modern physics and computer science.
Figure 12: Number of documents published per year on TNs in the fields of machine learning, quantum chemistry, artificial intelligence, quantum information, and holography.
4. Conclusions
■ This paper reviews key foundational literature to introduce beginners to a well-established technique that aims to overcome the current limitations of classical computing.
■ TNs are now becoming a trending technique for d = 1, 2 in many fields of physics and computer science, such as condensed matter physics, quantum chemistry, machine learning, artificial intelligence, and quantum computing, bridging theoretical insights with practical applications.
■ Newer research directions are exploring physical systems beyond simplified toy models, where richer and more complex physics emerges. Examples include the spin-1 BH model, SU(N) Hubbard models, and topological matter, all of which push the boundaries of TN methods in capturing interesting correlations and exotic quantum phenomena.
■ Future work may explore the integration of MPS with neural network-based quantum states, or the adaptation of MPS-inspired techniques to two-dimensional lattice models through PEPS or MERA frameworks.
References
5. Author contributions
License
Copyright (c) 2025 Juan Sebastián Gómez, Karen Cecilia Rodríguez
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.
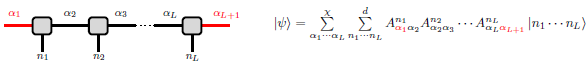
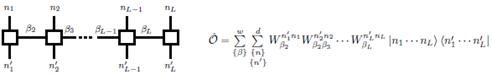
2.jpg)
