DOI:
https://doi.org/10.14483/23448393.2268Published:
2001-11-30Issue:
Vol. 7 No. 1 (2002): January - JuneSection:
Science, research and developmentAnálisis del Patrón Biométrico del Iris para Comprobar la Identidad de Personas
Keywords:
Demodulación de imagen, reconocimiento estadístico de patrones, identificación biométrica, teoría de decisión estadística, filtros bidimensionales de Gabor, Wavelets, análisis de textura. (es).Downloads
References
Daugman J. G., "High Confidence Visual Recognition of Persons by a Test of Statistical Independece", IEEE Trans. Pattern Anal. Machine Intell. Vol. 15 No. 11, Nov. 1993, pp. 1148 1161.
Daugman J. G., "Complete Discrete 2-D Gabor Transforms by Neural Networks for Image Analysis and Compression", IEEE Trans. Acous. Speech & Signal Proc. Vol. 36 No. 7, Jul. 1988, pp. 1169 1179.
Sidney C., Gopinath R. A., y Guo H. Introduction to Wavelets and Wavelet Transforms. 1ª Edición. New Jersey. Prentice Hall 1998.
Sing Lee T., "Image Representation Using 2D Gabor Wavelets" IEEE Trans. Pattern Anal. Machine Intell. Vol. 18 No. 10, Oct. 1996, pp. 959 - 970.
Daugman J. G y Dawning C. J., "Demodulation, Predictive Coding, and Spatial Vision", Journal of de Optical Society of America, Nov. 1994 , pp 641-660
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Ingeniería, 2002-00-00 vol:7 nro:1 pág:44-50
Análisis del patrón biométrico del iris para comprobar la identidad de personas
IRIS BIOMETRIC PATTERN ANALYSIS FOR PERSONAL IDENTITY VERIFICATION.
Pedro E. Castro H. Héctor E. Carranza Q. Edmundo Vega O.
Resumen
Presentamos aquí la implementación práctica de un sistema biométrico para la identificación de personas con base en la demodulación PM de la imagen del iris, mediante la utilización de una familia Wavelet multiescala y auto-similar de filtros en cuadratura bidimensionales, selectivos en frecuencia que utilizan funciones básicas de Gabor. La comprobación de identidad se basa en la ejecución de una prueba de independencia estadística entre los códigos complejos, resultantes de la proyección de la imagen sobre los filtros, por medio de la medida de la distancia de Hamming normalizada y estableciendo un umbral, a partir de una curva de estrategia, para la decisión. La realización de este proyecto está principalmente basada en los resultados que arrojó el trabajo pionero del Dr. John G. Daugman [1] sobre esta técnica biométrica particular en 1993. La aplicación esta enmarcada en la nueva tecnología de la Instrumentación Virtual, utilizando una cámara de video convencional, una tarjeta de adquisición de imagen, un computador personal y usando IMAQVisionTM sobre LabView6iTM como plataforma de trabajo.
Palabras clave:
Demodulación de imagen, reconocimiento estadístico de patrones, identificación biométrica, teoría de decisión estadística, filtros bidimensionales de Gabor, Wavelets, análisis de textura.
Abstract
We present here the practical implementation of a biometric system for recognition of persons based on the PM demodulation of the iris image, through the use of a self-similar, multi-scale Wavelet family of two-dimensional frequency-selective quadrature filters that use Gabor basic functions. The identity verification is based on the execution of a test of statistical independence between the resulting complex codes of the image projection on the filters, by means of the measure of the normalized Hamming distance and establishing a criterion as of a strategy curve for the decision. The accomplishment of this project this mainly based on the results that fearlessness the pioneer work of Dr. John G. Daugman [1] on this particular biometric technique in 1993. The framework of the application is the new technology of the Virtual Instrumentation, using a conventional video camera, an image acquisition board and a personal computer with the use of IMAQVisionTM and LabView6iTM as a development platform.
Key words:
Image demodulation, statistical pattern recognition, biometric identification, statistical decision theory, bidimensional Gabor filters, Wavelets, texture analysis.
I. INTRODUCCION
Con el inicio de la era de la información, se han venido experimentando diversos cambios en el área tecnológica y científica. Las máquinas han representado un papel muy importante en la evolución del hombre en búsqueda de más conocimiento y del mejoramiento de la calidad de vida. La tendencia es clara y conduce hacia la automatización. Todo lo que nos rodea hoy en día son artefactos que proporcionan un servicio en diferentes entidades y que hacen más eficientes y rápidas las operaciones. Dichos dispositivos se basan en las tecnologías de punta, desarrolladas en áreas como la inteligencia artificial, la lógica difusa, las comunicaciones digitales y el procesamiento digital de señales. Todas estas orientadas a continuar el desarrollo de máquinas al servicio del hombre, dándoles cada vez una apariencia más natural y personalizada. De esta manera, el modelamiento de diferentes características sensoriales del cuerpo humano sirve para construir artefactos que realicen funciones repetitivas con un alto grado de precisión, y es así como actualmente podemos hacer que nuestro computador ejecute operaciones con sólo pronunciar las palabras, o a hacer que reconozca y convierta el contenido del mensaje de una gráfica en formato de texto que podemos extraer mediante la utilización de accesorios adicionales como un escáner, un micrófono y todos aquellos elementos sensoriales que nos permiten llevar a cabo una transducción y una posterior conversión de señal análoga a digital.
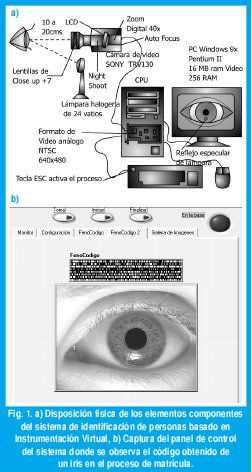
Ahora, con la utilización de una cámara convencional, una tarjeta de adquisición de imagen y una aplicación adecuada de bajo costo, como se muestra en la Figura 1 a) , es posible tener acceso a una a red privada para teletrabajo, a un sistema de control supervisado jerárquico remoto, a una sucursal virtual de un banco o corporación y quizá tener una consulta médica en línea a través de una red telemédica, etc., basándose exclusivamente en patrones biométricos para el reconocimiento del usuario.
En este caso particular, el reconocimiento de la textura de nuestro iris, como patrón para realizar identificación de personas, se ha desarrollado con base en modelos matemáticos concebidos a partir de los estudios realizados en las células simples del córtex visual del cerebro de los mamíferos y fundamentada en la demodulación de imagen [2], el análisis Wavelet multiescala bidimensional complejo en coordenadas polares, la teoría de la información, la teoría de decisión estadística y probabilidad, la codificación predictiva, la visión artificial, complementadas en algunos casos con la utilización de redes neuronales con el propósito de mejorar en velocidad y eficiencia.
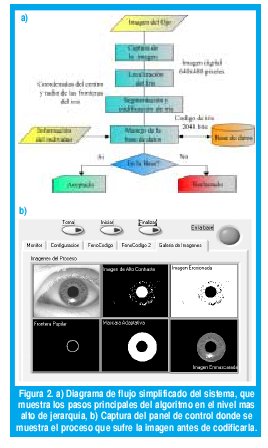
El trabajo expuesto en este artículo describe la implementación de un sistema de identificación de personas por medio del análisis de la textura del iris; que es un rasgo facial único, altamente diverso, inherentemente estocástico y por que no; caótico, mediante la descomposición multiescala de sus fasores característicos en baja resolución, utilizando la Instrumentación Virtual. La figura 2 muestra de forma sencilla el funcionamiento de la aplicación desarrollada en G para el sistema..
II. DESCRIPCIÓN DEL MONTAJE
La presente aplicación fue desarrollada en LabView 6i sobre el sistema operativo Windows 9X, en un PC con procesador Pentium III de 750 MHz, 256MB de RAM y 32MB de Vídeo. La cámara de vídeo utilizada es una SONY TRV-130. (ver figura 1 a)
El proyecto fue desarrollado por etapas hasta ensamblar la versión completa, cada etapa de acuerdo a su funcionalidad se convertía en un SubVI, que de acuerdo a las necesidades de diseño era reformado. Esta versatilidad propia de Labview y el ambiente gráfico nos daba la posibilidad de realizar grandes modificaciones en la estructura del algoritmo principal en muy poco tiempo. Gracias a la modularidad de las funciones era posible plantear diversas soluciones a un mismo problema y escoger la de mejor desempeño.
La cámara de vídeo utilizada tiene cuatro funciones que permiten obtener un estándar de imagen apropiado para el análisis. Con el zoom se puede lograr una toma del iris a una distancia relativamente grande, cerrando el campo visual. Las lentillas de Close Up complementan la función de ajuste del tamaño de la imagen, reduciendo la distancia focal y por tanto realizando una toma restringida al tamaño de la órbita ocular. Night Shoot permite aprovechar la alta sensibilidad de la cámara en el rango IR para realizar un registro con baja intensidad de luz y evitar molestias en la retina. Con el auto enfoque se consigue una toma de alta definición dentro del intervalo de distancias determinadas por la profundidad de campo. La pantalla LCD da retorno visual al usuario para que se ubique adecuadamente antes de almacenar la imagen.
III. PROCESAMIENTO DE LA IMAGEN
A. Método para encontrar el iris
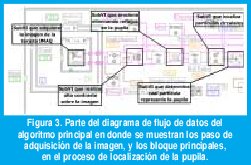
El análisis comienza estableciendo la visibilidad de un iris en la imagen (ver figura 2), localizando sus fronteras externa e interna. Debido a la geometría circular del iris, este proceso debe llevarse a cabo a partir de la imagen en coordenadas rectangulares por medio de un algoritmo detección de bordes de forma circular. Para localizar la pupila hemos utilizado un filtro que a partir de un rango de umbrales de intensidad en escala de grises (determinado por el estándar de imagen definido por nosotros) produce una imagen binaria de alto contraste, que realiza una primera aproximación de la ubicación de la frontera interna del iris. Posteriormente sometemos la imagen resultante a otro filtro que elimina los posibles reflejos especulares de las fuentes de luz en la pupila, y así poder utilizar un detector de partículas circulares que permite localizar exactamente la frontera pupilar (ver figura 3).
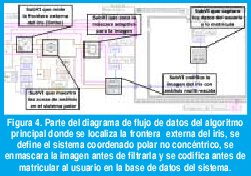
El proceso de localización de la frontera límbica es un poco diferente; se utilizó un detector de bordes a lo largo de trayectorias en línea recta a diferentes orientaciones, desde la esclerótica hacia el centro de la pupila, los puntos de intersección detectados entre las trayectorias mencionadas con el borde externo del iris, son suficientes para encontrar por extrapolación el conjunto de puntos que componen la circunferencia que describe la frontera límbica. Para definir los puntos a partir de los cuales se originan dichas trayectorias, se hace una primera aproximación de la frontera realizando una búsqueda circular aumentando en pasos discretos el radio, teniendo como referencia el centro pupilar, calculando la media del histograma de intensidades correspondiente a esta región de interés. Cuando la media está en un valor que conforme a la toma estándar; representa la esclerótica, el radio acumulado en ese momento se asocia a la longitud de las trayectorias (ver figura 4).
B. Sistema coordenado polar doblemente adimensional.
Los dos procesos anteriores nos proporcionan las coordenadas de los centros y radios de las fronteras que delimitan el iris (frontera pupilar con subíndice p y frontera límbica o esclerótica con subíndice s). Con base en estos datos generamos un sistema coordenado polar no concéntrico definido por las siguientes ecuaciones:
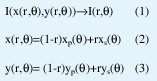
Este sistema permite establecer las zonas de análisis del iris, manteniendo siempre referencia a las mismas regiones del tejido sin importar la contracción pupilar, el tamaño total del iris, la distancia de la cámara al ojo y factor de acercamiento (zoom). La no concentricidad del sistema coordenado es requerida debido a que la pupila es típicamente nasal e inferior al centro del iris. Este modelo, que representa intrínsecamente la deformación de la malla trabecular debido a la dilatación o contracción de la pupila, asigna a cada punto en la imagen del iris un par de coordenadas polares: el radio que abarca el intervalo unitario [0,1] y el ángulo en el intervalo típico [0,2π].
A causa de la oclusión normal de los párpados, las sombras de las pestañas y a que hemos localizado en la toma estándar el reflejo especular de la luz en la parte inferior de la pupila (reflejo producido por la lámpara que ilumina el ojo, localizada abajo de la cámara, formando un ángulo con la horizontal descrita por la trayectoria focal), hemos eliminado dos zonas del análisis: la región donde ocluye normalmente el párpado superior, y una región descrita por un sector angular truncado inferior de 45°.
La invarianza con la rotación para corregir el movimiento de la cabeza y del ojo en su órbita se realiza en una etapa subsecuente de análisis sobre el código obtenido. El esquema total de reconocimiento es de esta manera invariante con la traslación plana, rotación y dilatación de la imagen del iris.
V. CONSTRUCCIÓN Y CAPACIDAD DE INFORMACION DEL CÓDIGO
El código propuesto es de una longitud de 2048 bits sin compresión, para compatibilidad con el estándar de capacidad de las tarjetas magnéticas de crédito (una representación de este código se encuentra en la figura 1 b) . Está longitud de código establece un límite superior en la capacidad de información del código de iris y es importante saber cuál es su capacidad real. Esta capacidad se ve reducida por correlaciones intrínsecas existentes entre los operadores que codifican la señal. Por esto es importante conocer la entropía de la fuente asociada con una señal típica del iris humano, que puede ser mucho menor que el límite superior determinado por la resolución de imagen, a causa de correlaciones radiales inherentes. Estas entropías reducidas influencian directamente los niveles de confidencia asociados con cualquier estrategia de decisión. El método que utilizamos hace que podamos reconocer eficientemente un iris ejecutando la prueba de independencia estadística. Esto es una medida de que tanto un código predice otro y confirma que son originados por procesos aleatorios independientes. Normalmente, la prueba de independencia estadística se pasa si los códigos de iris provienen de ojos diferentes y si los códigos provienen del mismo iris la prueba es fallida.
A. Obtención del Código de iris
Los filtros bidimensionales de Gabor propuestos por Daugman [1] y que utilizamos para el reconocimiento de iris definidos en el sistema coordenado polar doblemente adimensional son:
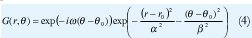
Donde es la frecuencia radial que es inversamente proporcional a los parámetros de escala α, β, a través de una constante K. La selección de un conjunto de valores para ω nos permite establecer una familia Wavelet multiescala autosimilar de filtros en cuadratura bidimensionales selectivos en frecuencia, con ancho de banda logarítmico constante, cuyas localizaciones son especificadas por r y θ abarcan todas las zonas de análisis (ver figura 6).

Las proyecciones de imagen resultantes son complejas por que se utilizan ambas componentes; las partes reales de estos filtros deben ajustarse de manera que tengan volumen cero y por consiguiente respuesta DC nula; las partes imaginarias inherentemente carecen de respuesta DC por simetría impar. Todo esto para hacer que el código de iris sea independiente de la intensidad de luz.
Cada bit en un código de iris representa una coordenada de uno de cuatro vértices del cuadrado unitario lógico en el plano complejo. Este es calculado por evaluación, a una escala de análisis, del signo tanto de la parte real como de la imaginaria de las proyecciones de imagen en cuadratura de una región local en la imagen del iris I(ρ,Φ) sobre un filtró Gabor bidimensional complejo particular:
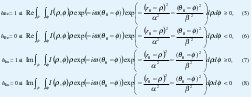
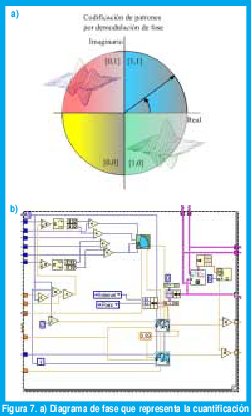
De esta manera, un filtro bidimensional de Gabor complejo, con un conjunto particular de parámetros de posición y tamaño en el dominio adimensional del iris, realiza una cuantificación de fase en baja resolución de la señal de textura local aproximándola a un vértice del cuadrado unitario lógico asociado con este filtro mediante las ecuaciones anteriores (ver figura 7).
B. Longitud de los códigos
Lograr la conmensurabilidad entre los códigos de iris es un objetivo primordial de este método de codificación y se consigue obteniendo una representación en formato universal con longitud constante de todos los iris, sin importar la cantidad de detalle en el iris. Si no hay conmensurabilidad entre los códigos, surge el problema de comparar códigos de diferentes longitudes, produciendo acuerdo y desacuerdo parcial en su lista de características. Esta dificultad ha hecho que el reconocimiento de huellas dactilares automático no sea tan práctico. La conmensurabilidad facilita y hace objetivo el proceso de comparación de códigos, así como el cálculo de los niveles de confidencia para cada decisión, incrementando la velocidad y la confiabilidad de las decisiones.
C.Número de grados de libertad independientes en un código de iris
Aunque hay 2048 bits en cualquier código de iris generado por nuestro sistema, dicho código posee mucho menos de 2048 grados de libertad binarios independientes (Daugman comprobó que son 173 grados de libertad independientes [1]). Esto se produce por la existencia de correlaciones radiales sustanciales en el iris. Por ejemplo, un proceso ciliar dado tiende a propagarse a través de una distancia radial en el iris, ejerciendo su influencia en muchas partes remotas del código, reduciendo de esta manera su independencia. Similarmente, una característica como un pliegue influencia diferentes partes del código asociados con varias escalas de análisis, puesto que el espectro de Fourier de una característica puntual como está puede abarcar muchas octavas. Finalmente, correlaciones inherentes son introducidas por la propiedad pasabanda de los filtros Gabor bidimensionales, específicamente por el ancho de banda finito determinado por los parámetros α,β y ω en la ecuación (4).
El número de grados de Libertad independientes puede ser estimado por un examen de la distribución de las distancias de Hamming calculadas a lo largo de una población de códigos de iris no relacionados. Comparando cada par de códigos de iris A y B bit por bit, la distancia de Hamming normalizada HD se define como la fracción de bits que no concuerdan entre ellos:
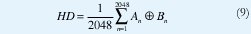
Donde el operador XOR es igual a1, sí y solo sí los dos bits An y Bn son diferentes (ver figura 5).
Puesto que los estados (1,0) de cada bit de cualquier código de iris son equiprobables a priori, existe una probabilidad p=0.5 de que cualquier par de bits de diferentes códigos de iris no coincidan (cada uno de los cuatro estados 00,01,10,11 tiene una probabilidad de 0.25); los bits coinciden en dos de los casos y no coinciden en los otros dos). Si cada uno de los 2048 bits en un código de iris dado fuese completamente independiente de cualquier otro, entonces la distribución esperada para las distancias de Hamming observadas entre dos códigos de iris independientes podría ser una distribución binomial con p=0,5 y N=2048.
La distribución binomial para N intentos de Bernoulli con probabilidades p y q predice que la probabilidad de observar una fracción x=m/N de eventos entre los N intentos es:
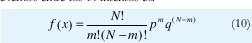
D. Decisión estadística en el reconocimiento
El problema de reconocimiento del patrón de un iris que pertenece a un individuo, después de buscarlo en una base de datos considerablemente grande, esta relacionado con la teoría de decisión estadística, la cual resuelve el problema de asignar un nivel de confidencia a una decisión de reconocimiento. Convirtiendo de esta manera el problema de reconocimiento de patrones en una prueba simple de independencia estadística.
Las decisiones si/no pertenece tienen cuatro posibles resultados: aceptación de auténtico (AA), aceptación de impostor (AI), rechazó de auténtico (RA) y rechazo de impostor (RI). El primero y el cuarto de los resultados son deseados y los restantes son errores. El algoritmo debe maximizar las probabilidades condicionales de AA y RI, mientras minimiza las probabilidades condicionales de AI y RA.
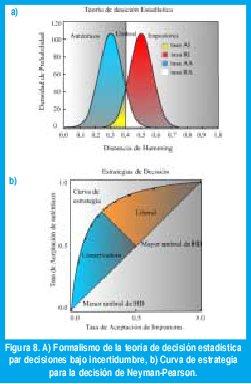
El formalismo de Neyman-Pearson para problemas de decisión en los que la probabilidad a priori es desconocida y el costo del error no es fijo, pero las distribuciones finales son conocidas, está resumida en la figura 8 a. Una medida de la distancia de Hamming entre los códigos de iris constituye un punto en la abscisa. Esta medida es considerada como una muestra de uno de dos procesos aleatorios (auténticos o impostores), cuya distribuciones de probabilidad han sido arbitrariamente mostradas aquí como gaussianas con grandes traslapes con propósitos de ilustración. Las dos distribuciones Pa(x) y Pi(x), especifican respectivamente la densidad de probabi- lidad de una distancia de Hamming particular, x, que surge de dos comparaciones del mismo iris, o de dos comparaciones de iris diferentes. Cualquier distancia de Hamming menor que un umbral de decisión elegido, como se indica por la línea punteada en la figura anterior, es juzgada como perteneciente a la distribución de auténticos, mientras que cualquier distancia de Hamming mayor que este umbral es juzgada como perteneciente a la distribución de impostores. Las probabilidades de los cuatro posibles resultados AA, AI, RA y RI son iguales a las áreas bajo las dos funciones de densidad de probabilidad, Pa(x) y Pi(x), en cada lado del umbral de decisión U:
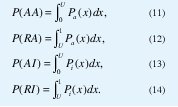
Estas cuatro probabilidades son representadas por las cuatro áreas sombreadas en la figura 8 a).
Es claro que las cuatro probabilidades están separadas en dos pares que deben sumar la unidad, y dos pares que son gobernados por la inecuaciones:
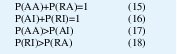
Las tasas de error, P(RA) y P(AI), se minimizan si las dos distribuciones de distancias de Hamming Pa(x) y Pi(x), tienen mínimo traslape. Su traslape puede ser reducido si las dos medias están bien separadas entre sí, o si sus varianzas fueran más pequeñas.
La manipulación del umbral de decisión U, con el propósito de implementar diferentes estrategias de decisión apropiadas para los costos de cada tipo de error en una aplicación, es ilustrada esquemáticamente la figura 8 b siguiente. Dicho diagrama de estrategia y decisión de Neyman-Pearson, gráfica P(AA) contra P(AI) como un lugar geométrico de puntos. Cada punto en dicha gráfica representa una estrategia de decisión especificada por una diferente elección del umbral U.
La inecuación (17) establece que la curva de estrategia de Neyman-Pearson mostrada en la figura aparece siempre por encima de la línea diagonal. Las estrategias que son excesivamente conservadoras o excesivamente liberales corresponden a deslizarse a lo largo de la curva hacia los extremos de la diagonal. Independientemente de donde el umbral de decisión se ha ubicado a lo largo de esta curva, la capacidad total del método de reconocimiento de patrones puede ser medido por la longitud del segmento de recta en la figura 8 b uniendo la línea diagonal y el punto de pendiente 1 en la curva de estrategia. Esta distancia es denominada detectabilidad d, definida como la diferencia entre las medidas de las dos distribuciones que son mostradas esquemáticamente en la figura 8 a, divididas por una medida conjunta de sus desviaciones estándar.
RESULTADOS
El método morfológico de detección de partículas, para la localización de la pupila como la mejor referencia en la ubicación del iris, ha demostrado ser efectivo, al utilizar un filtro de alto contraste que define un umbral de intensidad en la escala de grises, bajo el cual se encuentran los valores propios de una zona oscura como la pupila. A partir de la obtención de sus coordenadas y radio se facilitó el análisis geométrico para la ubicación de la circunferencia que representa la frontera límbica; éste ha garantizado una buena aproximación al borde real ya que las trayectorias parten de zonas claras correspondientes a esclerótica de manera que el primer cambio brusco de intensidad es un punto de frontera.
El número de segmentos elegido (28) no sólo garantiza la compatibilidad con la longitud de los códigos utilizados en las tarjetas magnéticas, sino que permite establecer un número suficiente de zonas de análisis donde el tamaño del filtro sea el apropiado para que los tiempos de procesamiento de la imagen sean relativamente pequeños (nuestra aplicación tarda en este proceso aproximadamente 20 segundos, debido a que la aplicación depende de la plataforma de desarrollo y a que no esta compilada). El tamaño de cada segmento establece el rango de frecuencia utilizadas, porque restringe el número de pixeles que definen los rasgos de una zona. Los segmentos se distribuyeron de forma que se eliminaron del análisis las zonas de oclusión normal de los párpados y una zona inferior angular donde cae el reflejo de la luz, lo cual no influye en la capacidad de información del código obtenido ya que se hace de igual forma para todas la imágenes.
El muestreo angular de la imagen para la aplicación del filtro, se define a partir del perímetro del limbo con lo cual se garantiza el análisis del detalle, aunque se produce un sobre muestreo en la zona cercana a la frontera pupilar produciendo un efecto de amplificación de los detalles. Esto no representa problema alguno en el código resultante; sin embargo el tiempo de procesamiento es igual para un segmento cercano a la pupila (pocos pixeles) que para uno lejano (mayor numero de pixeles).
Los tiempos de comparación con la base y de localización son mucho menores que el empleado en la codificación. Este es uno de los problemas que estamos tratando de corregir en la actualidad. El desempeño total aun no ha sido evaluado; pero hemos hecho algunas pruebas de cómo se comporta el sistema en la toma de decisiones con una base de datos pequeña y un umbral empírico. El resultado de dichas pruebas se observa en la figura 9, en la que se observa una clara separación entre la distribución de impostores con la distancia calculada del código auténtico.
CONCLUSIONES
Nuevamente se ratifica el poder de las transformaciones matemáticas wavelet en el área de la neurofisiología permitiendo el modelamiento de funciones biológicas que pueden ser aprovechadas en procesos de identificación de patrones en la textura de la malla trabecular.
Los tiempos de procesamiento en el sistema pueden ser mejorados complementándolo con técnicas de implementación en hardware con dispositivos lógicos programables que realicen un gran numero de multiplicaciones en punto flotante en modo dedicado en el caso del proceso de filtrado de la imagen. La utilización de métodos de análisis de basados en regiones de interés facilita el manejo de las características geométricas de una imagen en particular.
Esta ventaja en el desarrollo del sistema presente nos permite concentrarnos en etapas subsecuentes relacionadas con el reconocimiento de texturas, donde la elaboración de un código fenotípico conmensurable con base en la demodulación de la fase de la imagen, ha demostrado ser muy útil en el reconocimiento de patrones y en la implementación de sistemas automáticos en los cuales se requiere un alto grado de confiabilidad en las decisiones tomadas. De esto depende la seguridad de muchas de las operaciones y transacciones realizadas en diferentes entidades que ofrecen un diverso número de servicios en los cuales la identidad de una persona es un factor crítico.
REFERENCIAS
[1] Daugman J. G., "High Confidence Visual Recognition of Persons by a Test of Statistical Independece", IEEE Trans. Pattern Anal. Machine Intell. Vol. 15 No. 11, Nov. 1993, pp. 1148 -1161.
[2] Daugman J. G., "Complete Discrete 2-D Gabor Transforms by Neural Networks for Image Analysis and Compression", IEEE Trans. Acous. Speech & Signal Proc. Vol. 36 No. 7, Jul. 1988,pp. 1169 - 1179.
[3] Sidney C., Gopinath R. A., y Guo H. Introduction to Wavelets and Wavelet Transforms. 1ª Edición. New Jersey. Prentice Hall 1998.
[4] Sing Lee T., "Image Representation Using 2D Gabor Wavelets" IEEE Trans. Pattern Anal. Machine Intell. Vol. 18 No. 10, Oct. 1996, pp. 959 - 970.
[5] Daugman J. G y Dawning C. J., "Demodulation, Predictive Coding, and Spatial Vision", Journal of de Optical Society of America, Nov. 1994 , pp 641-660
Pedro Enrique Castro Hernández
Ingeniero Electrónico Universidad Distrital Francisco José de Caldas. Miembro del Grupo de Investigación LIV. peterhenrycasher@hotmail.com
Héctor Emerson Carranza Quiroga
Ingeniero Electrónico Universidad Distrital Francisco José de Caldas. Miembro del Grupo de Investigación LIV. emersonud@yahoo.com
Edmundo Vega
Director del proyecto de grado y del laboratorio de Electrónica. Universidad Distrital Francisco José de Caldas Laboratorio de Instrumentación Virtual - Sala "Leonardo Davinci" (LIV)
Creation date:
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.





2.jpg)










