DOI:
https://doi.org/10.14483/23448393.1884Published:
2003-11-30Issue:
Vol. 9 No. 2 (2004): July - DecemberSection:
Science, research, academia and developmentCálculo de las coordenadas espaciales de una escena 3-D por medio del análisis de imágenes estereoscópicas
Keywords:
Correspondencia basada en los rasgos, detección de bordes, extracción de líneas, clique máximo, reconstrucción 3-D (es).Downloads
References
R.Horaud and T.Skordas, "Stereo correspondence through feature grouping and maximal cliques," IEEE Transactions on Pattern Analysis and Machine intelligence, vol. 11, no. 11, Nov. 1989.
M. Adjouadi, F. Candocia, and J. Riley, "Exploiting Walsh-based attributes to stereo vision," IEEE Transactions on Signal Processing, vol. 44, no. 2, Feb. 1996.
M. Lew, T. Huang, and K.Wong, " Learning and feature selection in stereo matching," IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 16, no. 9, Sep. 1994.
M. Brown, D. Burschka, and G. Hager, "Advances in computational stereo," IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 25, no. 08, Aug. 2003.
C. Sun, "Fast stereo Matching using rectangular subregioning and 3-D maximum-surface techniques," International Journal of Computer Vision, vol. 47, no. 1/2/3, May. 2002.
Z. Zhang, R. Deriche, O. Faugeras, Q.T. Luong, "A robust technique for matching two uncalibrated images through the recovery of the unknown epipolar geometry," Institut National De Recherche En Informatique Et En Automatique. No 2273, May. 1994.
T. Kanade, and M. Okutomi, "A stereo matching algorithm with an adaptive window: theory and experiment," IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 16, no. 9, Aug. 1994.
N. Ahuja, and L.Abbott, "Active stereo: integrating disparity, vergence, focus, aperture and calibration for surface estimation," IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 15, no. 10, Oct. 1993.
Z. Zhang, "Estimating motion and structure from correspondences of line segments between two perspective images," IEEE Transactions on Pattern Analysis and Machine Intelligence., vol. 17, no. 12, Aug. 1995.
C. Schmid, and A. Zisserman, "Automatic line matching across views," Proceedings of the IEEE conference on Computer vision and Pattern Recognition, 1997.
S. Feo, et al, "Sistema de visión estereoscópica para la detección y localización de objetos," Tesis de grado (Ingeniero de Sistemas), Universidad Nacional, Bogotá 2003.
M. Bernal, y A. Garcia, "Análisis de escenas 3D: una aproximación a partir de la estereoscopia," Tesis de grado (Ingeniero Electrónico), Universidad Javeriana, Bogotá 1998.
J. Canny, "A computational approach to edge detection," IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. PAMI-8, no. 6, Nov. 1986.
R. Beveridge, and E. Riseman, "How easy is matching 2D line models using local search," IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 19, no. 6, Jun. 1997.
Ze-Nian LI, "Stereo correspondence based on line matching in Hough space using dynamic programming," IEEE Transactions on Systems, Man and Cybernetics, vol. 24, no. 1, Jan. 1994.
J.C. Regin, "Solving the maximum clique problem with constraint programming," Proceedings CPAIOR, 2003.
C. Bron, and J. Kerbosch, "Finding all cliques of an undirected graph," Communications of the ACM, vol. 16, no. 9, 1973.
D. Scharstein and R. Szeliski, "A Taxonomy and Evaluation of Dense Two-Frame Stereo Correspondence Algorithms," Int'l J. Computer Vision, vol. 47, no. 1, pp. 7-42, 2002.
S. Blostein, and T. Huang, "Error analysis in stereo determination of 3-D point positions," IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. PAMI-9, no. 6, Nov. 1987.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Ingeniería, 2004-00-00 vol:9 nro:2 pág:35-43
Cálculo de las coordenadas espaciales de una escena 3-D por medio del análisis de imágenes estereoscópicas
Gerardo Muñoz
Miembro Grupo de Investigación LAMIC, Universidad Distrital Francisco José de Caldas.
Alejandro Rubiano Miembro Grupo de Investigación LAMIC, Universidad Distrital Francisco José de Caldas.
Resumen
En este trabajo se aborda la reconstrucción tridimensional de una escena 3-D por medio de análisis de imágenes estereoscópicas compuestas por líneas rectas. Para la detección de bordes se utiliza el método propuesto por Canny y un método heurístico para el seguimiento del borde. Los píxeles detectados como bordes se interpolan a un modelo lineal y se mide la varianza que indica que tan bien se ajustan los datos al modelo. Una etapa de detección de colinealidad se encarga de identificar los segmentos que se fragmentaron en el proceso anterior. Para cada línea en la imagen derecha se buscan las parejas de correspondencias posibles en la imagen izquierda. Las asignaciones correctas se hallan aplicando la teoría de grafos, en donde una pareja equivale a un nodo del grafo. La matriz de adyacencia es construida determinando la compatibilidad entre nodos y el clique máximo es rastreado. Los extremos de una línea se calculan en tres dimensiones utilizando triangulación y el mapa de profundidad denso se obtiene interpolando los puntos que se encuentran entre las líneas.
Palabras Clave:
Correspondencia basada en los rasgos, detección de bordes, extracción de líneas, clique máximo, reconstrucción 3-D.
Abstract
This paper addresses the reconstruction of a 3-D scene from stereoscopic images containing straight line segments. First the edges of the images are detected based on both Canny's approach and a heuristic method to track the edge points. Each line is extracted by fitting the pixels to a linear model and measuring the variance which gives an estimate of how well the data adjust to the model. Due to fragmentation of segments a collinearity detection stage is implemented and the corresponding pairs are searched. A Graph theory method is applied to find the right matches. Each node of the graph represents a corresponding pair and the adjacency matrix is built establishing the compatibility between nodes. Then the maximum clique is found and 3-D line coordinates are calculated by means of triangulation. Finally an interpolation stage takes place and a dense depth map is recovered.
Key Words:
Feature-based matching, edge detection, line extraction, maximum clique, 3-D reconstruction.
I. INTRODUCCIÓN
La reconstrucción de un entorno tridimensional utilizando imágenes estereoscópicas es una tarea de gran complejidad debido a la enorme cantidad de información que se maneja [1], [2], [3]. Si solo se tratara de un punto en el espacio, el desplazamiento horizontal de las proyecciones en los planos de las imágenes izquierda y derecha sería suficiente para determinar las coordenadas de tal punto, es decir todo se reduciría a un problema de triangulación. Sin embargo, si se considera la multitud de puntos que conforman una imagen con variedad de objetos, tonalidades y formas, surge inmediatamente un problema; antes de aplicar la operación de triangulación es necesario hallar el par de píxeles de las imágenes que corresponden al mismo punto en el espacio tridimensional.
Pero la complejidad es aún mayor ya que en la mayoría de los casos técnicamente no existe un par de píxeles que correspondan a un punto específico en el espacio. Por ejemplo, al imaginarse una superficie cuadrada perfectamente paralela y equidistante de los planos de las imágenes, el área de las proyecciones respectivas sería igual en la imagen derecha e izquierda. En este caso cada píxel en una imagen tendría su par correspondiente en la otra. Sin embargo, si la superficie deja de ser paralela y sufre una rotación sobre su eje central en cualquier dirección, es claro que el área visible estaría en función del punto de vista. Es decir que el área proyectada en una imagen sería más grande que en la otra. Esto implica que la correspondencia píxel a píxel ya no sería uno a uno, como en el caso anterior, sino que a un mismo píxel de una imagen corresponderían varios píxeles en la otra.
Para solucionar el problema de la correspondencia se han desarrollado una gran cantidad de algoritmos en las ultimas dos décadas [4]. En general estas técnicas se pueden dividir en dos: aquellas que se basan en el área y aquellas basadas en los rasgos o la combinación de ambas [5]. La primera recurre a la intensidad absoluta de los píxeles y mide la similitud entre dos regiones de las imágenes con una función de correlación cruzada [6], [7]. Estos métodos generan mapas de profundidad densos ya que indagan en todos los puntos de la imagen. La segunda utiliza bordes, vértices, líneas, contornos cerrados, etc como primitivas para efectuar la correspondencia. Esto permite la recuperación parcial de los puntos en la escena por lo que es necesaria la implementación de técnicas de interpolación para generar mapas de profundidad densos [8].
Otro problema es la falta de textura en los objetos. Por ejemplo, al registrar con una cámara digital una pared bien iluminada se puede encontrar que los píxeles tienen aproximadamente el mismo valor de intensidad. La utilización de un método basado exclusivamente en la intensidad de los píxeles fallaría en este tipo de superficie homogénea, ya que no existen regiones que se puedan hacer corresponder de manera única entre las dos imágenes.
En este trabajo se implementa el análisis de imágenes estereoscópicas basado en la extracción y correspondencia de líneas rectas y las relaciones entre ellas, ideas tomadas del artículo de Horaud y Skordas [1]. Aunque este método es computacionalmente más costoso que aquel basado en la intensidad de los píxeles y está limitado a escenas con presencia de líneas rectas, tiene también grandes ventajas. No depende, para su éxito, en la textura de los objetos, sino en los rasgos de la imagen, es decir, los bordes y las esquinas de las superficies. El método de correspondencia es línea a línea, y no, píxel a píxel, lo cual disminuye el espacio de búsqueda. Además, una etapa de interpolación entre líneas rectas genera un mapa de profundidad denso, por lo que es posible equiparar los resultados obtenidos con otros métodos que utilicen técnicas completamente diferentes.
Entre los artículos escritos por Zhang, en [9] textualmente se reconstruyen las líneas rectas utilizando imágenes estereoscópicas. En ese trabajo se muestran varias pruebas sobre imágenes reales de escenas complejas, sin embargo no se efectúa una evaluación cuantitativa de la calidad de la reconstrucción de los segmentos. Schmid y Zisserman [10] plantean un método de correspondencia de líneas rectas pero tampoco se muestra con qué precisión se reconstruyen las líneas en 3-D.
A nivel local (Bogotá, Colombia) la recuperación de la profundidad de los objetos de una escena 3-D se ha enfocado a métodos basados en el área, los cuales utilizan la correlación cruzada como herramienta principal a la hora de efectuar la correspondencia [11], [12]. Sin embargo la diferencia más importante con esos trabajos es que aquí se utilizan principalmente imágenes sintéticas para determinar la calidad de la reconstrucción efectuada por el algoritmo, lo que permite tener una idea precisa de la aplicabilidad y las limitaciones del método desarrollado. Además se encontró que la resolución de la imagen es la principal limitante a la hora de elegir las escenas con la que se puede trabajar, cosa que no se suele tener en cuenta en otros trabajos.
II. MODELO ESTEREOSCÓPICO
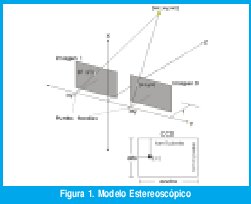
El modelo que describe la forma como un punto en tres dimensiones, dado por las coordenadas [wx,wy,wz], se proyecta sobre un par de imágenes, se conoce como modelo estereoscópico. Este modelo está basado en una cámara de cajón con un orificio minúsculo en vez de la lente, que permite obtener la transformación de perspectiva inversa necesaria para efectuar los cálculos de triangulación. En este trabajo se consideran solamente cámaras con planos de imagen paralelos como la muestra la figura 1, esto con el objetivo de simplificar la tarea de la reconstrucción.
Como se observa el punto focal de cada cámara está ubicado detrás del plano de la imagen, lo cual permite obtener imágenes no invertidas. Por su parte cada imagen es considerada como un dispositivo CCD (charge-coupled device) de dimensiones ancho x alto en centímetros como en la figura 1. Cada uno de los parámetros asociados al modelo se explica en la tabla 1.
A. Restricción Epipolar

Un punto en tres dimensiones se proyectará en la imagen 0 en un píxel [r0,c0] y en la imagen 1 en un píxel [r1,c1]. Las coordenadas r0 y r1 son exactamente iguales y la variación en la coordenada c esta dada por Tal variación recibe el nombre de disparidad y solamente se produce a lo largo del eje horizontal más conocido como línea epipolar. Esta característica da lugar a la importante restricción epipolar que dice: "El espacio de búsqueda de la posible pareja de un punto de coordenadas [ro,co] está restringido a la línea epipolar".

Es conveniente resaltar el hecho de que la línea epipolar es completamente horizontal solamente en el caso en que los planos de las imágenes son paralelos. Esto reduce la complejidad en la búsqueda de las parejas y en la reconstrucción de la escena tridimensional, razón por la cual se adoptó el modelo de la figura 1.
B.Restricción de Posición
Sea [r0,c0] la proyección en la imagen 0 de un punto en tres dimensiones, entonces la pareja de este píxel en la imagen 1 se encontrará en cualquier posición [r0,c1] donde c1≥c0. Esto significa que tomando como referencia la imagen 0 (imagen derecha), cualquier punto en la otra imagen sufre un desplazamiento hacia la derecha en función de la profundidad. Si la referencia es la imagen 1 (imagen izquierda) entonces los puntos en la imagen 0 se desplazan hacia la izquierda. De aquí en adelante la imagen referencia para todos las pruebas será la imagen 0 o imagen derecha, que es aquella cuyo punto focal yace en la coordenada [0 -Hy 0].
C. Oclusión y su Restricción
Las restricciones anteriores son límites geométricos del espacio de búsqueda que se cumplen para cualquier tipo de imagen estereoscópica basada en el modelo de la figura 1. Sin embargo el tratamiento de tales imágenes se hace muy complejo si no se incurre en más restricciones.
La primera tiene que ver con el tipo de superficies permitidas en las escenas tridimensionales y establece que: "todas las superficies analizadas serán opacas, es decir no transparentes". Esto implica que los píxeles entre dos líneas cualesquiera pertenecen a una sola superficie y que cualquier línea detectada nunca estará detrás de alguna superficie.
Si las superficies que se manejan son opacas entonces se presenta el fenómeno de la oclusión que significa la obstrucción visual de una superficie sobre otra. En estereoscopia la oclusión tiene sus consecuencias en que la información espacial de una región tridimensional aparece solamente en una de las imágenes. En ausencia de tal información no es posible realizar la reconstrucción de aquellas regiones utilizando los métodos convencionales de triangulación. Como este trabajo de grado utiliza líneas rectas para realizar la reconstrucción, la falta de información se ve reflejada en ambigüedades para las cuales no se llegó a una solución. Ésta es pues la segunda restricción: "los extremos de las líneas rectas que aparezcan en la imagen 0 tendrán que aparecer en la imagen 1".
III. DETECCIÓN DE BORDES
Los bordes en las imágenes son áreas con un fuerte contraste de intensidad. Su detección es un problema fundamental ya que reduce significativamente la cantidad de información en las imágenes.
El problema de la detección fue formulado por Canny [13] de la siguiente forma: Se tiene una señal borde G(x) de sección transversal conocida bañada en ruido Blanco Gaussiano, n o ; esta señal se convoluciona con un filtro con respuesta al impulso dada por f(x) y con ancho de banda -W≤f≤W. El diseño de tal filtro, según Canny, debe maximizar los siguientes criterios:
Buena detección: consiste en la capacidad del filtro para discriminar entre un borde y el ruido. En términos más precisos este criterio corresponde a la maximización de la relación señal a ruido.
Buena localización: los puntos que sean marcados como bordes deben estar tan cerca como sea posible del centro del borde verdadero.
Baja multiplicidad de la respuesta: dependiendo del ancho de banda del filtro se presentan varios máximos cerca al centro del borde por efecto del ruido y que pueden ser detectados como bordes pero no lo son. Es entonces necesario que la función f (respuesta del filtro) no presente muchos picos en la vecindad del borde.
Canny transforma la maximización del producto de los criterios de buena detección y buena localización en una minimización que utiliza funcionales integrales. Después de un complejo análisis y manipulación matemática llega a la conclusión de que el filtro óptimo hallado puede ser aproximado a la primera derivada del Gaussiano G(x) dada por:
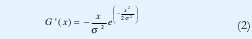
En dos dimensiones el borde presenta también una determinada orientación. Canny expande sus resultados creando una máscara en dos dimensiones. Ésta máscara se forma convolucionando el filtro de detección en una dimensión alineado perpendicular a la tangente del borde, con un filtro de proyección alineado paralelo al borde. La máscara de proyección que utiliza Canny es la función Gaussiana con la misma varianza que aquella de la derivada del Gaussiano del filtro de detección.
Dado que la derivada y la convolución son asociativas, la imagen se puede convolucionar con la función Gaussiana primero y luego tomar la derivada en la dirección n normal al borde, así:
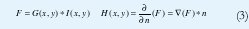
La dirección n normal a la tangente del borde se puede estimar de la dirección del gradiente dado por
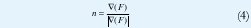
Remplazando y despejando se llega a que la magnitud del gradiente, H, se expresa como:
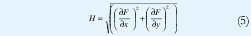
Para determinar donde está localizado un borde se deben buscar los máximos de H, más exactamente, un borde se detecta en aquellas regiones en donde la derivada de H, en la dirección de n, se hace cero, es decir:
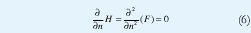
Remplazando y despejando se llega a que la matriz de cruces por cero, J, esta dada por:

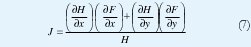
Para generar una matriz binaria Edge que contenga los bordes de la imagen original se cuenta con dos arreglos matriciales: la magnitud del gradiente de la imagen filtrada dada por H y la matriz de cruces por cero dada por J. El primero corresponde a la magnitud de los bordes y el segundo a la ubicación de estos dentro de la imagen. Un "1" dentro de la matriz de bordes Edge corresponde a un punto dode se presenta cruce por cero y además tiene una magnitud mayor que un umbral Tr. Un "0" cuando no se cumplen tales condiciones.
En este trabajo se implementó un método que demostró ser efectivo para realizar el seguimiento de un borde basado en los arreglos matriciales H y J. El algoritmo utiliza dos estilos de plantillas direccionales, la tipo T y la tipo Esquina, cuya orientación depende de los dos píxeles inmediatamente detectados a los cuales se les llama píxeles semilla, tal como lo muestra la figura 2. La plantilla tipo T es usada en los bordes horizontales o los bordes verticales y se aplica cuando los píxeles semilla están alineados vertical u horizontalmente. La plantilla tipo Esquina se utiliza en bordes oblicuos cuando los píxeles semilla forman un ángulo de 45º. Para efectos de visualización el píxel actual aparece en negro y en gris los píxeles que fueron detectados anteriormente, mientras que las casillas con círculos grises numerados representan aquellos píxeles que pueden servir de extensión del borde actual.
Como las plantillas están destinadas a detectar el píxel por donde hay cruce por cero entonces utilizan la información del arreglo matricial J que se dedujo anteriormente. Cada vez que se detecta un cambio de signo, ya sea de más a menos o de menos a más, es porque un cruce por cero tuvo lugar. Es aquí cuando se comprueba que tal píxel tiene suficiente umbral como para ser etiquetado como borde. Solo el primer par de píxeles semilla debe cumplir con un nivel de umbral igual o mayor que el nivel máximo Tr2, de ahí en adelante, una vez que se empieza a hacer el seguimiento del borde, lo único que pregunta es si los píxeles están por encima de umbral mínimo Tr1. El seguimiento del borde, que genera un vector Puntos donde se almacenan las coordenadas de los píxeles, termina cuando una plantilla encuentra que ninguna de las posibles casillas cumple con el nivel de umbral o con la condición de cruce por cero. Esto quiere decir que el algoritmo de seguimiento puede recorrer un tramo formado por varios bordes de diferentes orientaciones, siempre y cuando se cumplan los requisitos anteriores.
IV. EXTRACCIÓN DE LÍNEAS
El método utilizado es la interpolación por mínimos cuadrados el cual establece que: la recta que mejor se ajusta a un conjunto de puntos es aquella cuya suma de los cuadrados de las distancias de los puntos a la recta sea mínima.
La ecuación de una línea recta esta dada por y = mx+b. Por lo tanto, la suma de los cuadrados de las distancias de los n puntos a la recta es Los valores de m y b que minimizan esta ecuación se encuentran igualando a cero las derivadas con respecto a m y con respecto a b.
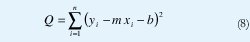
Sin embargo cualquier conjunto de puntos puede ser interpolado a una recta, así que es necesario establecer una medida que indique qué tan bien se ajustan los puntos a una línea recta. Para esto se utiliza la varianza de los datos dada por
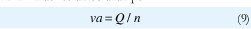
En la implementación práctica el algoritmo toma el primer dato del vector Puntos y comienza una línea. Cada vez que avanza por el vector Puntos, calcula los valores de m y b, y con estos calcula el valor de va. Es entonces cuando pregunta si la varianza es mayor que un umbral u. Si esto ocurre termina la línea que había comenzando y empieza una nueva.
V. DETECCIÓN DE LÍNEAS COLINEALES
La etapa de extracción de líneas agrupa píxeles que se ajustan a una recta pero está influenciada por el efecto del ruido. Es por eso que una línea recta, que debería detectarse como un solo trazo en ausencia del ruido, puede llegar a formar varios tramos individuales y por lo tanto generar varias piezas de información en lugar de una. Este efecto es perjudicial ya que aumenta el número de líneas rectas y, como se verá más adelante, el error en la reconstrucción tridimensional. Esto se debe al hecho de que entre más pequeña sea una línea más susceptible será al error. Una etapa de detección de líneas colineales (o líneas alineadas) busca darle un poco de robustez al algoritmo anterior. Sin embargo no está destinada a corregir el fenómeno del fraccionamiento de líneas, es decir que su trabajo no es unir las líneas colineales, ya que no es una regla que las líneas colineales correspondan a una sola recta. Esta etapa simplemente se encarga de la detección de la alineación, información que utilizará en su debido momento.
Para determinar si una línea L0 es colineal con otra L1 se efectúa una medición basada en la suma del cuadrado de la distancia perpendicular (SPD squared perpendicular distance), la cual se utiliza en [14], con un objetivo similar. Como lo muestra la figura 3 los límites de la operación, C1 y C2, son establecidos por los extremos de uno de los segmentos. La distancia vertical entre las líneas L0 y L1 en el punto Ck esta dada por
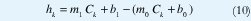
mientras que la distancia perpendicular a L0 se expresa como:
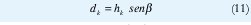
De esta manera la SPD desde el punto C1 al punto C2 tiene la forma:
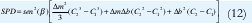
Tal como aparece en la ecuación anterior, la SPD es directamente proporcional a la longitud de la proyección de la línea L1 sobre la línea L0, o p como aparece en la figura 3. Para hacer esta medición independiente de la longitud de las líneas, entonces se toma la SPD ponderada por la longitud del segmento, es decir SDPp=SDP/p. De aquí en adelante cuando se hable de la SPD se hace referencia a la SPDp.
VI. CORRESPONDENCIA ESTEREOSCÓPICA
Una de las tareas más difíciles en estereoscopia es la correspondencia. En general la correspondencia elige un rasgo de una imagen e implementa algún método para encontrar el rasgo correspondiente en la otra imagen. La razón por la cual las líneas rectas representan un buen rasgo para aparear es que reducen la ambigüedad de las posibles correspondencias gracias a que son un elemento discreto que codifica bastante información; una línea recta tiene una inclinación, una longitud y un par de extremos que la limitan.
El modelo de correspondencia utilizado en este trabajo es uno a uno, es decir, a cada línea de la imagen derecha le corresponde una línea diferente y solamente una en la imagen izquierda. Los extremos de una línea L0 en la imagen derecha establecen una región de búsqueda en la imagen izquierda como lo muestra la figura 4. Todas las líneas en la imagen izquierda, o sus equivalentes colineales, que intercepten esta región son posibles parejas de L0. Las líneas se truncan cuando exceden los límites, como en el caso de a, y las líneas colineales, como el caso de b y c, se unen para forman un solo segmento.


La gran limitación de este procedimiento, y que también se presenta en otros trabajos como en [9] y [15],es la ineficacia para emparejar líneas con región epipolar igual a cero, es decir líneas completamente horizontales. En ausencia de los defectos por fragmentación no existe ambigüedad para efectuar la búsqueda de parejas, pero si se presentan fragmentaciones aleatorias en este tipo de líneas no se puede llegar a emparejar con métodos convencionales.
A. Aplicación de los Grafos a la Estereoscopia
Las siguientes definiciones se basan en la notación utilizada en [16]. Un grafo G=(V,E) consiste en un conjunto de nodos o vértices V y un conjunto de arcos E, donde cada arco une un par de nodos distintos (i,j). La matriz simétrica de n x n, tiene aij= 1 si (i,j)∈ E, y aij = 0 si (i,j) E. Esta matriz es conocida como la matriz de adyacencia de G. El clique de un grafo G=(V,E) es un subconjunto C, de V, completo. Un conjunto es completo si todos sus nodos están unidos entre sí. El problema del clique máximo consiste en hallar cliques de máxima cardinalidad o máximo número de elementos. El algoritmo presentado en [17] se utilizó para el rastreo del clique máximo.
La figura 5 muestra el par estereoscópico de un modelo de 4 líneas que servirá para explicar la técnica de correspondencia. Los números se utilizan para identificar las rectas de la imagen 0 y las letras para las líneas de la imagen 1. La tabla II muestra el resultado de la búsqueda de parejas, es decir para cada línea de la imagen derecha se hallan las posibles parejas en la imagen izquierda de acuerdo con los parámetros establecidos en la sección anterior.
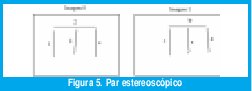

El vector parejas define el tamaño de la matriz de adyacencia Ag que para este ejemplo es de 6 x 6. Los nodos de Ag corresponden a una pareja de líneas mi = (Li0, Li1) donde Li0 pertenece a la imagen derecha y Li1 a la imagen izquierda.
Para llenar las casillas de Ag, cada uno de los nodos se compara con todos los demás. Como Ag es simétrica, el número de comparaciones, O, necesarias para completar toda la matriz de n x n es:
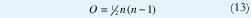
Ag(i,j) = 1 si dos nodos mi = (Li0 ,Li1) y mj = (Lj0 ,Lj1) son compatibles, es decir, si se cumple que: Relación(Li0,Lj0) =Relación(Li1,Lj1). Las relaciones que Horaud y Skordas definen, son: igualdad, colinealidad, misma unión y derecha e izquierda junto con la relación T, que se adoptó en este trabajo. Aplicando estas definiciones a los elementos de la tabla 2 se obtiene el procedimiento que implica 15 comparaciones, descrito en la tabla 3.
Con estos valores la matriz de adyacencia tiene la forma de la figura 6. El clique máximo hallado, aplicando el algoritmo de Bron y Kerbosch [17] a la matriz de adyacencia Ag, es: C = [m1, m3, m4, m6]. Como se puede ver sus elementos constituyen las correspondencias perfectas.
En este trabajo se desarrolló un algoritmo al que se le llamó operador de relación. Él tiene la tarea de construir la matriz de adyacencia con base en la comparación entre las mediciones que logra establecer entre una par de líneas de la misma imagen y sus correspondientes parejas en la otra.
VII. RECONSTRUCCIÓN DE LAS SUPERFICIES
Una vez se conocen las parejas respectivas de las líneas de la imagen derecha, entonces es posible determinar las coordenadas espaciales de cada segmento, pero ahora en tres dimensiones. Para esto se utilizan las ecuaciones de proyección inversas del modelo estereoscópico.
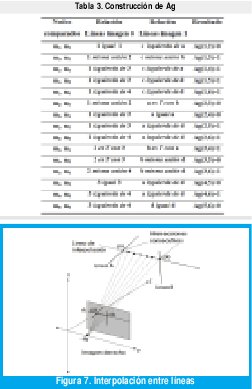
Para obtener superficies continuas es necesario utilizar un método que estime las coordenadas de los puntos que se encuentran entre las líneas. Ya que las caras de las superficies con que se trabaja son planas, el método más inmediato consiste en trazar líneas entre los puntos de las rectas que ya se tienen, hasta llenar todos los espacios vacíos. Esta interpolación resulta muy compleja si se hace directamente sobre las líneas en 3D, por lo tanto es imprescindible usar la información de la imagen de líneas detectadas para realizar esta tarea.
La interpolación que se llevó a cabo en este trabajo consiste en trazar líneas horizontales por cada píxel vertical de la imagen; cada línea se intercepta con una recta en un píxel dado, y dos intersecciones horizontales consecutivas determinan una línea. Esta recta se conoce en dos dimensiones y se tienen todos los datos para obtener sus coordenadas en 3D. Por lo tanto aquellos píxeles entre dos intersecciones consecutivas se pueden calcular fácilmente. En la figura 7 se visualiza el método de interpolación de superficies.
A. Evaluación del Error
El algoritmo general entrega dos tipos de resulta dos que pueden ser evaluados con precisión respecto a los datos originales del modelo sintético, estos son:las coordenadas de las líneas en tres dimensiones y el mapa de profundidad de la escena. Para el primer caso se procede así: se calcula la distancia euclidiana en tres dimensiones entre un extremo de la línea del modelo original y el extremo de la línea hallada por el algorit mo; después se promedian las distancias encontradas para los dos extremos de cada línea. Esto se hace para todas las líneas de la imagen y los resultados se muestran por medio de un histograma.
La precisión del mapa de profundidad hallado se evalúa por medio de dos mediciones, una de las cuales se utiliza en [18]:
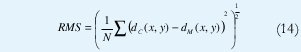
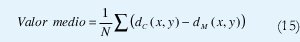
Donde dC es el mapa de profundidad computado, dM es el mapa de profundidad del modelo original y N es el número total de píxeles examinados.
VIII. RESULTADOS DEL ALGORITMO GENERAL
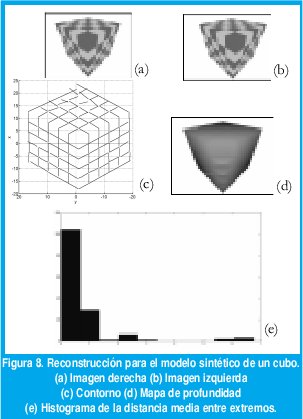
Las estructuras repetitivas son utilizadas con frecuencia en estereoscopia por la gran cantidad de parejas que generan. La imagen sintética del cubo que se muestra en la figura 8 tiene una resolución de 1280 x 960 píxeles.
Al comparar las figuras 8a y 8b se observa un desplazamiento horizontal de la imagen derecha a la imagen izquierda. Como ya se sabe, este desplazamiento no es igual para todos los puntos sino que depende de la profundidad de una forma inversa: a mayor profundidad menor disparidad y viceversa.
Las primeras etapas del algoritmo tienen la función de extraer las líneas de las dos imágenes. La máscara Gaussiana tiene dimensiones 4 x 4 y σ=1 para detectar los bordes con la mayor precisión con respecto al borde real. La varianza del error utilizada es de 0.28 y la longitud mínima de cada línea se fijó en 10 píxeles. En la imagen derecha, que es la de referencia, se encontraron 148 líneas mientras que en su homóloga, 154, lo que indica que hubo unión y fragmentación de segmentos.
Debido a la alineación de todos los segmentos, el algoritmo de colinealidad detecta cada hilera de líneas como colineales. Esto con un umbral de la SPD igual a 10.
El algoritmo de búsqueda de parejas encontró 285 asignaciones. Ya que el número de parejas es igual al número de nodos, la matriz de adyacencia tiene un tamaño de 285 x 285. El clique máximo hallado, que corresponde al resultado de la correspondencia, es de 146 nodos. Esto muestra que tan solo dos líneas de la imagen de referencia se quedaron sin su respectiva pareja.
En la figura 8c se presenta una vista frontal de la reconstrucción en 3D de cada una de las líneas. A simple vista se observa que la mayoría de las líneas está acorde con el modelo original. Esto se reitera con el histograma de la figura 8e que se realizó para las parejas de líneas que no se unieron ni fragmentaron con respecto al modelo ideal y que, como se puede deducir, fueron 131 de un total de 146. Tal como se observa solamente un pequeño grupo de líneas presenta un error de 6 cm, no obstante la mayoría está por debajo de 3cm.
Finalmente y luego de 7 minutos de procesamiento en una torre de 1.8GHz, la interpolación de superficies entrega el modelo de la figura 8d. Los puntos más claros son los que están más cerca de la cámara y los puntos más oscuros tienes más profundidad. Las líneas blancas sobre la superficie del cubo se producen porque los segmentos no están unidos en los extremos y dejan pequeños espacios sin intersecciones consecutivas necesarias para la interpolación. El valor RMS calculado es de 1.1cm y el error promedio es de 0.58 cm. Estos datos sirven para mostrar la precisión de los resultados y el criterio para determinar si son buenos o malos depende de la aplicación en la que se trabaje. Sin embargo son útiles para realizar comparaciones con otros resultados.
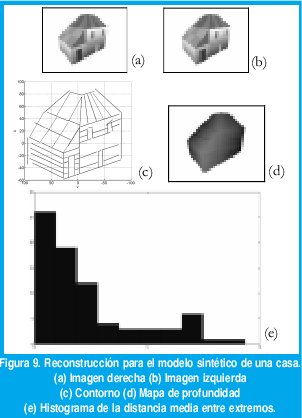
La última imagen sintética que se muestra en la figura 9a y 9b tiene una resolución de 1280 x 960 píxeles. En la imagen derecha se hallaron 81 líneas y 76 en la otra imagen. El algoritmo encontró 139 parejas posibles y un clique máximo de 78 nodos. La reconstrucción y el error medio entre los extremos se muestran en la figura 9c y 9e respectivamente. Como se ve todos las distancias están por debajo de 10 cm, pero como siempre la mayoría presenta errores por debajo de 5 cm. El valor RMS para el mapa de profundidad que se muestra en la figura 9d es de 1.3 cm con un promedio de 0.96 cm. Este ha sido el modelo que presenta el mayor error en todas las mediciones. Con esta resolución el tiempo de procesamiento fue de aproximadamente 6 minutos en la misma torre.
IX. CONCLUSIONES
El algoritmo del cálculo de las coordenadas espaciales de una escena 3-D a partir del análisis de imágenes estereoscópicas descrito en el presente articulo, es aplicable a imágenes compuestas por objetos con líneas rectas. La información que proveen las rectas tal como la inclinación, la longitud y la ubicación de sus dos extremos, las convierte en un elemento apropiado para realizar el apareamiento de rasgos ya que reduce la ambigüedad en la correspondencia estereoscópica. Sin embargo la estereoscopia no es solo un problema de hallar las correspondencias correctas sino que además requiere modelos matemáticos e instrumentación de gran precisión para poder aprovechar sus beneficios en aplicaciones prácticas.
La resolución de la cámara es una de las responsables de la precisión de los resultados. Esto es porque la digitalización de las imágenes hace que la máxima precisión en la localización de un punto en 3D esté dentro de un margen espacial conocido como ROU (region of uncertainty), que se explica ampliamente en [19]. Sin embargo, esto tiene solución ya que para una misma profundidad, una cámara con más resolución utiliza mas píxeles para registrar el valor de la disparidad, por lo tanto la precisión de los resultados aumenta.
Por otro lado el problema de la precisión del algoritmo de extracción de líneas no tiene una solución tan obvia. La estrategia que se utilizó en este proyecto se basa en el criterio del umbral de la varianza. Cuando un grupo de píxeles excede este valor es porque se ha llegado al final de una línea, sin embargo este método tiene sus desventajas. Las rectas ideales tienen una varianza que se mantiene muy baja en todo su trayecto y entonces al llegar a las esquinas se incluyen píxeles que no pertenecen a la línea para llegar al umbral necesario para detenerse. Este defecto se atenúa con la resolución pero no se resuelve. Un futuro estudio podría contemplar la exploración de nuevas técnicas y modelos matemáticos que permitan determinar con la mayor precisión en qué punto comienza y en qué punto termina una línea recta, cuando los bordes, conformados por valores discretos, se curvan en las esquinas.
La eficacia de la teoría de grafos en estereoscopia y específicamente el concepto de clique, que implica la conexión completa entre elementos, depende enteramente de los criterios de compatibilidad o incompatibilidad entre nodos que se utilicen para construir la matriz de adyacencia, criterios que deben permanecer invariantes frente al cambio de perspectiva.
La aplicación de las técnicas desarrolladas en este trabajo a imágenes reales requiere la previa caracterización de las superficies de los objetos involucrados, con el objetivo de entregar al algoritmo un par de imágenes con suficiente contraste de las líneas de interés.
REFERENCIAS BIBLIOGRÁFICAS
[1] R.Horaud and T.Skordas, "Stereo correspondence through feature grouping and maximal cliques," IEEE Transactions on Pattern Analysis and Machine intelligence, vol. 11, no. 11, Nov. 1989.
[2] M. Adjouadi, F. Candocia, and J. Riley, "Exploiting Walsh-based attributes to stereo vision," IEEE Transactions on Signal Processing, vol. 44, no. 2, Feb. 1996.
[3] M. Lew, T. Huang, and K.Wong, " Learning and feature selection in stereo matching," IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 16, no. 9, Sep. 1994.
[4] M. Brown, D. Burschka, and G. Hager, "Advances in computational stereo," IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 25, no. 08, Aug. 2003.
[5] C. Sun, "Fast stereo Matching using rectangular subregioning and 3-D maximum-surface techniques," International Journal of Computer Vision, vol. 47, no. 1/2/3, May. 2002.
[6] Z. Zhang, R. Deriche, O. Faugeras, Q.T. Luong, "A robust technique for matching two uncalibrated images through the recovery of the unknown epipolar geometry," Institut National De Recherche En Informatique Et En Automatique. No 2273, May. 1994.
[7] T. Kanade, and M. Okutomi, "A stereo matching algorithm with an adaptive window: theory and experiment," IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 16, no. 9, Aug. 1994.
[8] N. Ahuja, and L.Abbott, "Active stereo: integrating disparity, vergence, focus, aperture and calibration for surface estimation," IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 15, no. 10, Oct. 1993.
[9] Z. Zhang, "Estimating motion and structure from correspondences of line segments between two perspective images," IEEE Transactions on Pattern Analysis and Machine Intelligence., vol. 17, no. 12, Aug. 1995.
[10] C. Schmid, and A. Zisserman, "Automatic line matching across views," Proceedings of the IEEE conference on Computer vision and Pattern Recognition, 1997.
[11] S. Feo, et al, "Sistema de visión estereoscópica para la detección y localización de objetos," Tesis de grado (Ingeniero de Sistemas), Universidad Nacional, Bogotá 2003.
[12] M. Bernal, y A. Garcia, "Análisis de escenas 3D: una aproximación a partir de la estereoscopia," Tesis de grado (Ingeniero Electrónico), Universidad Javeriana, Bogotá 1998.
[13] J. Canny, "A computational approach to edge detection," IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. PAMI-8, no. 6, Nov. 1986.
[14] R. Beveridge, and E. Riseman, "How easy is matching 2D line models using local search," IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 19, no. 6, Jun. 1997.
[15] Ze-Nian LI, "Stereo correspondence based on line matching in Hough space using dynamic programming," IEEE Transactions on Systems, Man and Cybernetics, vol. 24, no. 1, Jan. 1994.
[16] J.C. Regin, "Solving the maximum clique problem with constraint programming," Proceedings CPAIOR, 2003.
[17] C. Bron, and J. Kerbosch, "Finding all cliques of an undirected graph," Communications of the ACM, vol. 16, no. 9, 1973.
[18] D. Scharstein and R. Szeliski, "A Taxonomy and Evaluation of Dense Two-Frame Stereo Correspondence Algorithms," Int'l J. Computer Vision, vol. 47, no. 1, pp. 7-42, 2002.
[19] S. Blostein, and T. Huang, "Error analysis in stereo determination of 3-D point positions," IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. PAMI-9, no. 6, Nov. 1987.
Gerardo Muñoz
Universidad Distrital FJC. Facultad de Ingeniería. Grupo LAMIC. gmunoz@udistrital.edu.co
Alejandro Rubiano
Ingeniero Electrónico. Universidad Distrital FJC. Grupo LAMIC. rubsem@yahoo.com
Creation date:
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.





2.jpg)










