DOI:
https://doi.org/10.14483/23448393.2283Publicado:
1998-11-30Número:
No 1 (1999)Sección:
Ciencia, investigación, academia y desarrolloSobre Aprovechamiento de los clasificadores generados con el algoritmo clásico: C4.5
About reusing clasifiers generated by classical algorithm: C4.5
Palabras clave:
Aprendizaje automático, Aprendizaje a partir de ejemplos, Mejora de l precisión. (es).Descargas
Referencias
Ranilla, J.: ABANICO: Aprendizaje Basado en Agrupación Numérica en Intervalos COntinuos. Memoria de Investigación del Tercer Ciclo en Ciencias de la Computación e Inteligencia Artificial, Universidad de Oviedo, 1995.
Quinlan, J. R.: C4.5: Programs for Machine Learning, pp. x+302, Morgan K aufmann Publishers, San Mateo (California), 1993.
Quinlan, J. R.: Discovering rules from large collections of examples: a case study. En D. MICHIE, (Eds.), Expert Systems in the Micro-Electronic Age, Edinburgh University Press, pp. 168-201, 1979.
Breiman, L., Friedman, J. H., Olshen, R. A., & Stones, C. J: Classification and Regression Trees. Belmont, Wadsworth International Group, 1984.
Fiol Roig, G.: Contribución a la adquisición inductiva de conocimiento. Tesis doctoral, Universidad de las Islas Baleares, 1991. Dirigida por José Miró Nicolau.
Murthy, S. K., Kasif, S., & Salzberg, S.: A system for induction of oblique decision trees. Journal of Artificial Intelligence Research, 2, pp. 1-32, 1994.
Michalski, R. S., & Larson, J. B.: Selection of the Most Representative Training Examples and Incremental Generation of VL1 Hypotheses: the Underlying Methodology and the Description of Programs ESEL and AQ11. Report of Intelligent Systems Group, Report No. 867, Dept. of Computer Science, University of Illinois, Urbana, 1978.
Clark, P., Niblett, T.: The CN2 Induction Algorithm. Machine Learning, 3, pp. 261-284, 1988.
Cendrowska, J.: PRISM: An Algorithm for inducing modular rules. International Journal of Machine Studies, 27, pp. 349-370, 1988.
Salzberg, S.: Learning with nested generalized exemplars, pp. xviii+159. Kluwer Academic Publishers, Boston, 1990.
Botana, F.: SHAPE: Sistema Heurístico de Aprendizaje a partir de Ejemplos. Tesis doctoral, Departamento de Computación, Universidade da Coruña, 1992. Dirigida por A. Bahamonde y A. Blanco Ferro.
Montes Gracia, C.: MITO: Método de Inducción TOtal. Tesis doctoral, Universidad Politécnica de Madrid, 1994. Dirigida por Juan Pazos Sierra.
Michie, D., Spiegelhalter, D. J., & Taylor, C. C. (Ed.), Machine Learning, Neural and Statistical Classification, p. xiv+289, Ellis Horwood, Hertfordshire, Gran Bretaña, 1994.
Rumelhart, D., & McClelland, J., Parallel Distributed Processing, MIT Press, Cambridge, MA, 1986.
Cover, T. M., & Hart, P. E.: Nearest Neighbor pattern classification, IEEE Transactions on Information Theory, 13:1, pp. 21-27, 1967.
Aha, D. W.: A Study of Instance-based Algorithms for Supervised Learning Tasks: Mathematical, Empirical and Psychological Evaluations. Ph. D. Dissertation, University of California at Irvine, 1990.
Cost, S., Salzberg, S.: A Weighted Nearest Neighbor Algorithm for Learning with Symbolic Features. Machine Learning, 10, pp. 57-78, 1993.
Kohonen, T.: Self-Organizing Maps, p. xv+362. Springer Series in Information Sciences, Springer Verlag, Berlin, 1995.
Shapire, R, The Design and Analysis of Efficient Learning Algorithms. An ACM Doctoral Dissertation Award, 1991.
Ranilla, J., Mones, R., & Bahamonde, A.: El Nivel de Impureza de una regla de clasificación aprendida a partir de ejemplos. Actas de la VII Conferencia de la Asociación Española para la Inteligencia Artificial, CAEPIA-97, pp. 479-488, Málaga 1997.
Ranilla, J., Mones, R., & Bahamonde, A.: El Nivel de Impureza de una regla de clasificación aprendida a partir de ejemplos. Revista Iberoamericana de Inteligencia Artificial, 4, pp. 4-11, 1998.
Ranilla, J., Mones, R., & Bahamonde, A.: El Nivel de Impureza de una regla de clasificación aprendida a partir de ejemplos. Revista de la Asociación de Técnicos de Informática, NOVATICA, 131, pp. 37-43, 1998.
Michalski, R. S., Carbonell, J. G., & Mitchell, T. M.: Machine Learning. An Artificial Intelligence Approach, Vol. I, Tioga Pub., Palo Alto, California, 1983.
Quinlan, J. R.: Improved Use of Continuous Attributes in C4.5. Journal of Artificial Intelligence Research, 4, pp.7790, Morgan Kaufmann Publishers, 1996.
Murphy, P., & Aha, D. W.: UCI repository of machine learning databases -a machine-readable data repository. Maintained at the Department of Infor mation and Computer Science, University of California, Irvine. Anonymous ftp from ics.uci.edu in the directory pub/ machine-learning-databases, 1998.
Kohavi, R., John, G., Long, R., Manley, D., & Pfleger, K.: MLC++: A machine learning library in C++. In Tools with Artificial Intelligence, IEEE Computer Society Press, pp. 740-743, 1994.
Thrun, S. B., Bala, J., Bloedorn, E., et al: The MONK's Problems - A Performance Comparison of Different Learning algorithms. Technical Report CS-CMU-91-197, Carnegie Mellon University, 1991.
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Investigación y Ciencia
Ingeniería, 1999-00-00 vol: nro:1 pág:19-28
Sobre Aprovechamiento de los clasificadores generados con el algoritmo clásico: C4.5
ABOUT REUSING CLASIFIERS GENERATED BY CLASSICAL ALGORITHM: C4.5
Ana María Peña Reyes
Resumen
Uno de los requisitos más importantes a la hora de evaluar un sistema de aprendizaje automático es su capacidad para sintetizar el conocimiento presente en los datos de entrada. También lo es tener procedimientos de medida y comparación de los niveles en que el conocimiento ha sido absorbido por el sistema. Otro punto a considerar es el formato en el que presenta ese conocimiento para ser utilizado por nosotros. Sin embargo la capacidad de sintetización de un sistema se ve a menudo disminuida por la presentación de los datos de entrada al algoritmo. Aquí se verá un método para tratar de reducir este hecho mediante la reutilización de clasificadores menos exitosos generados previamente. Este método, como se verá en las pruebas experimentales, es eficaz en la mayoría de los casos probados. También analizaremos las ventajas y los posibles problemas que pueden aparecer al utilizar este tipo de métodos.
Palabras clave:
Aprendizaje automático / Aprendizaje a partir de ejemplos / Mejora de la precisión.
Abstract
One of the most important aspects when we are evaluating a machine learning system is its capability for synthesizing knowledge available in input data. Also it is to have the right procedures for measuring and comparing the levels of absorption of such knowledge. Another point to take in consideration is the format this knowledge is showed to us for being applied. However, synthesizing capabilities of a system are often reduced by the way input data is presented to the algorithm. Here is shown a method that tries to decrease this factor through reusing less-successful previously generated classifiers. This method, as seen in experimental tests, is efficient in most of the examples tested. We also analyze advantages and problems encountered when using this type of methods.
Key words:
Accuracy improvement / Learning from examples / Machine learning
1. INTRODUCCIÓN
Dado el algoritmo clásico de aprendizaje automático, C4.5, queremos aprovechar los clasificadores dados por este sistema. Si tenemos un conjunto de ejemplos EX y se somete al sistema de aprendizaje automático (Machine learning) C4.5, el clasificador que se obtiene presentará, en general, un cierto error incluso sobre el mismo conjunto de ejemplos de entrenamiento: el llamado error de reescritura. En este artículo presentaremos un dispositivo de disminución de este error aplicando sucesivamente el sistema de aprendizaje C4.5 a distintos conjuntos de entrenamiento construidos a partir del original y teniendo en cuenta los errores de reescritura que se cometan, de manera que el sistema de aprendizaje C4.5 se centre sobre los errores cometidos de clasificación, es decir, estudie las partes más difíciles de aprender del conjunto de entrenamiento. El riesgo que se corre al utilizar este dispositivo es el llamado sobre ajuste del clasificador a los ejemplos de entrenamiento (overfitting), lo que, en general, no garantiza que el error estimado sobre los casos no vistos sea menor. Por tanto, se necesitará ponderar experimentalmente estos riesgos sobre los problemas de uso frecuente en la comunidad científica en este campo.
Veremos que el dispositivo antes aludido disminuye el error, pero presenta algunos problemas que serán analizados y daremos posibles soluciones, mostraremos gráficamente las comprobaciones experimentales que se hicieron con los conjuntos de entrenamiento conocidos en la comunidad científica de esta área, para apreciar la disminución del error que mencionamos.
2. DESARROLLO
2.1 Algunos conceptos
En esta sección presentaremos algunos conceptos que serán básicos para el desarrollo de este artículo, que nos ayudaran a enfocar el tema.
El sentido que le damos al aprendizaje, tal como aparece en [1], será el de un proceso llevado a cabo por una computadora que es capaz de resolver un problema: sintetizar procedimientos capaces de realizar tareas de las que sólo tenemos algunas descripciones parciales sobre el modo en que nos gustaría que se llevasen a cabo. Lo aprendido, la solución de un algoritmo de aprendizaje automático, será pues el solucionador de problemas (utilizaremos la palabra solucionador cada vez que nos refiramos al encargado de resolver). En términos generales el esquema de este planteamiento lo podemos observar en la figura 1.
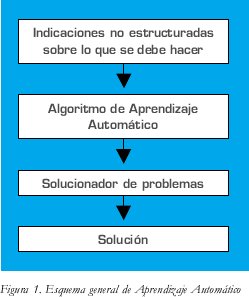
Los diferentes sistemas de aprendizaje pueden agruparse en familias teniendo en cuenta cómo son cada una de las componentes del esquema anterior. En primer lugar cabe establecer esta clasificación dependiendo del tipo de dato o indicaciones no estructuradas que el algoritmo de aprendizaje es capaz de asimilar.
Los problemas a resolver tienen en el aprendizaje a partir de ejemplos, implícita o explícitamente, una fuerte carga de previsión. Es decir, queremos anticipar el comportamiento de algún fenómeno y para ello nos servimos de una muestra representativa de sus actuaciones. Para ser precisos, usaremos colecciones de ejemplos descritos por tablas atributo-valor donde habrá un atributo con un carácter especial: la conducta observada. El ejemplo i de esta colección tendría el siguiente aspecto:
Ejemploi: Atributo1, Atributo2,..., Atributon,Clase. Por supuesto, el interés está en que la previsión de la conducta que haga en cada caso el solucionador de problemas sea la verdadera. Pero este término es demasiado ambiguo; de hecho, para los problemas que se tratarán, resultará desconocida la verdadera conducta, ya que necesitamos sintetizar un dispositivo para tratar de anticiparla. Lo relevante en la práctica es que la solución que proponga el cálculo de lo aprendido sea útil en un sentido amplio que dependerá del contexto.
Otra manera de interpretar los ejemplos de entrenamiento es como pares formados por descripciones de entradas (problemas) y salidas (soluciones) del solucionador de problemas que se quiere construir. Entonces, un algoritmo de aprendizaje automático no pretenderá entrar en el conocimiento profundo (semántica) de los fenómenos con los que se trabaja sino que trata de inducir las reglas generales, sintácticamente plausibles, que se siguen.
2.2 Agrupación de los Sistemas de Aprendizaje
Con miras a que el lector logre ubicar adecuadamente el sistema de aprendizaje C4.5 que estamos utilizando presentamos la siguiente clasificación de Sistemas de Aprendizaje reconocida por la comunidad científica.
Los diferentes sistemas de aprendizaje pueden agruparse en familias teniendo en cuenta cómo son cada una de las componentes de la gráfica del esquema anterior. En primer lugar cabe establecer esta clasificación dependiendo del tipo de dato o indicaciones no estructuradas que el algoritmo de aprendizaje es capaz de asimilar. Por esta razón se habla de aprendizaje a partir de ejemplos y aprendizaje por analogía.
Dependiendo del tipo de solucionador de problemas que se construya pueden hacerse clasificaciones en, al menos, dos tipos. El solucionador de problemas puede ser un clasificador en categorías discretas, una función de rango numérico o un procedimiento para realizar alguna tarea más compleja que las anteriores.
El segundo tipo en la clasificación de los sistemas de aprendizaje está dado por el carácter de legibilidad humana o no, es decir, producen un resultado simbólico humanamente inteligible o un resultado computacionalmente efectivo pero no asimilable por humanos (p.ej.: redes neuronales).
Por supuesto, luego están los algoritmos concretos que, en cada categoría y subcategoría de estas esbozadas anteriormente pueden, a su vez, organizarse en clases o familias o grupos. En este artículo nos centramos en sistemas de aprendizaje a partir de ejemplos que produzcan clasificadores inteligibles desde el punto de vista humano. Estos pueden ser clasificados a su vez en función de diversos aspectos. Si nos fijamos en el mecanismo de aplicación del conocimiento sintetizado tenemos aplicación por distancias mínimas o por ajuste exacto. Dependiendo de la geometría de las regiones de decisión en el espacio de atributos podemos tener clasificadores paralelos u oblicuos.
Siguiendo en los principios que guían el diseño de los sistemas de aprendizaje, podemos, en parte, usar la clasificación que hace Quinlan en [2]. Entonces tendremos:
Generalizaciones simbólicas. Habitualmente llamados, en inglés, Machine Learning, aunque este término es mucho más amplio y seguramente podría aplicarse a cualquier sistema de aprendizaje automático. Son los tipos de sistemas que producen solucionadores de problemas inteligibles humanamente y que explícitamente tratan de generalizar los datos que aparecen en los ejemplos para darles un carácter universal. Por un mecanismo de equiparación los problemas que se vayan planteando se resolverán como la generalización más próxima a ellos en algún sentido.
La subclasificación aquí se establece por el tipo de dato que codifica el solucionador de problemas. Hay dos tipos, los que codifican árboles de decisión (ID3 [3], CART [4],[5], C4.5 [2], OC1 [6],) y los que emplean reglas de clasificación (AQxx [7], CN2 [8], PRISM [9], NGE [10], SHAPE [11], C4.5, MITO [12], ABANICO [1]).
Estadísticos. Hay varias técnicas de clasificación construidas desde puntos de vista estadístico. Generalmente tratan con valores numéricos y suelen hacer conjeturas sobre las distribuciones de los valores de los atributos. En [13] pueden verse un buen número de estas técnicas.
Basados en Redes de Neuronas Artificiales. El tipo de solucionador no es humanamente inteligible pero es computacionalmente ejecutable. Como ejemplo y siguiendo el enfoque de Rumelhart [14] podemos citar Backpropagation, donde la red de funciones se concibe como una interconexión de unidades de computación.
Basados en el Recuerdo de Instancias. Sería discutible si el tipo de solucionador es o no humanamente inteligible. Recuerdan prototipos de casos que se le suministran como entrenamiento y, al igual que con las reglas o los árboles de decisión, al planteársele nuevos problemas los equiparan con los casos que recuerdan. Los más parecidos van a marcar el modo de resolver el problema.
Como eventualmente el conjunto de casos que se recuerdan pueden ser todos los de entrenamiento o bien ser un número muy elevado, es difícil decidir si es o no humanamente inteligible el solucionador de problemas. Pertenecen a este grupo los sistemas k-NN (Nearest k Neighbors) [15], IBx [16], PEBLS [17], LVQx [18].
2.3 Validación experimental de un sistema de aprendizaje a partir de ejemplos
En esta parte exponemos las diferentes formas de validar experimentalmente los sistemas de aprendizaje a partir de ejemplos, en este artículo validamos el dispositivo con Aciertos y fallos sobre el conjunto de prueba y con Validación cruzada (Cross Validation).
Todo algoritmo de aprendizaje automático está sujeto a la posibilidad de errores en la clasificación que hagan sus resultados (reglas, árboles, etc.). Por supuesto este no es el caso cuando se aplican los algoritmos de aprendizaje a problemas donde las poblaciones son finitas, pequeñas y conocidas; en este supuesto entonces el aprendizaje automático tiene una componente de condensador de información más que de inducción aplicable a casos no vistos, pero, en general, se trabaja con muestras finitas de poblaciones eventualmente infinitas. El problema, tras sintetizar el clasificador, es ser capaces de estimar el error que cometerá este sistema sobre casos cualesquiera de esa población eventualmente infinita.
Una primera aproximación consiste en aplicar el clasificador a los propios ejemplos de entrenamiento. Pero esta estimación, llamada error de reescritura, es muy sesgada. Si la generalización es nula, las reglas o las ramas de los árboles pueden repetir la información de los ejemplos de entrenamiento y así se tendría un error nulo de reescritura. Pero esto no es deseable por varias razones: la estructura del clasificador es demasiado compleja aún así puede haber error de reescritura (puede haber ruido y entonces datos contradictorios) debe haber mecanismos de aprendizaje previstos para aplicar el clasificador a casos no vistos a este fenómeno (aquí citado en grado extremo, se le llama sobre - ajuste o, en inglés, overfitting). Para estimar el error de clasificación se emplean los siguiente métodos:
Reescritura. Mide el porcentaje de aciertos, o de errores, en la predicción de las reglas sobre los ejemplos de entrenamiento.
Aciertos y fallos sobre el conjunto de prueba. Se utiliza en aquellos problemas donde se dispone de una batería específica de ejemplos para validar el comportamiento de los sistemas. La diferencia con el método anterior radica en que los errores o aciertos de las reglas sintetizadas por el conjunto de entrenamiento se miden sobre dichas instancias, no vistas durante el aprendizaje y que normalmente se llaman ejemplos de prueba o conjunto de test.
Partición (Hold out). Similar al anterior pero usado cuando se carece de batería de prueba. Este método divide aleatoriamente el conjunto total de ejemplos en dos conjuntos cuyos tamaños respectivos están habitualmente en las proporciones: 2/3 1/3 ó 7/10 3/10. El conjunto de mayor tamaño, el de entrenamiento, se somete al algoritmo de aprendizaje y, con las reglas obtenidas, se realiza una predicción sobre el conjunto de prueba.
Validación cruzada (Cross Validation). El problema del hold out reside en que el número de ejemplos eliminados en cada caso es una proporción demasiado alta (1/3 ó 3/10) como para asumir que no va a tener repercusiones notables en el conjunto de clasificadores inducidos. Como caso particular de submuestreo y con la idea de subsanar la deficiencia comentada, surge el método validación cruzada. Aquí, los ejemplos disponibles se dividen aleatoriamente en N bloques de igual tamaño y se realizan N clasificaciones diferentes. En cada una de ellas, se omite un bloque de los datos de entrenamiento y las reglas resultantes se aplican sobre los ejemplos del bloque omitido. La operación se repite cierto número de veces y la media del porcentaje de aciertos o errores es la estimación que proporciona este método.
En ciertas condiciones y para garantizar que las proporciones de las clases se mantienen, se usa la variante conocida como validación cruzada estratificada, que únicamente difiere del método normal en que respeta, en la medida de lo posible, la distribución original de las clases en el conjunto total de ejemplos en cada bloque.
En los experimentos que se describen a continuación se ha repetido 5 veces la validación usando en cada una de ellas 10 bloques (N =10), que denotamos por validación cruzada (5, 10),con lo cual el sistema de inducción se habrá aplicado 50 veces sobre distintos conjuntos de entrenamiento y prueba.
Dejando uno fuera (Leaving one out). Este método equivale al anterior cuando el número de bloques coincide con el total de ejemplos disponibles. Para cada ejemplo se obtienen las reglas con los restantes como conjunto de entrenamiento y, con las reglas así obtenidas, se estudia si la predicción sobre el ejemplo es acertada o no. El resultado final es el porcentaje de aciertos o errores. Esta técnica, computacionalmente costosa, produce un estimador casi insesgado de la tasa de error verdadera.
2.4 Descripción del dispositivo base
Por ideas sugeridas en la tesis de Shapire [19], hemos construido un dispositivo que empuja o fuerza a disminuir el error de reescritura que se ha cometido al someter un conjunto de ejemplos a un cierto algoritmo de aprendizaje. Este dispositivo de empuje parte de un conjunto de entrenamiento y un sistema de aprendizaje dados. Sea EX el conjunto de entrenamiento, C4.5 el sistema de aprendizaje a utilizar y sea M el dispositivo que vamos a construir. M procede aplicando sucesivamente en tres fases el sistema de aprendizaje C4.5 a distintos conjuntos de entrenamiento construidos a partir del original y tiene en cuenta los errores de reescritura que se cometen, con la idea de centrar el sistema en los ejemplos o partes del conjunto de ejemplos inicial más difíciles de aprender.
El dispositivo M comienza, en una primera fase, por someter un conjunto de ejemplos de partida EX1=EX al sistema de aprendizaje C4.5, siendo h1 el clasificador que se obtiene. Este clasificador presenta un cierto error incluso sobre el mismo conjunto de ejemplos de entrenamiento, como se dijo anteriormente, el llamado error de reescritura. Se pretende forzar a que disminuya dicho error, para esto, un nuevo conjunto EX2 es construido a partir del original de la siguiente manera:
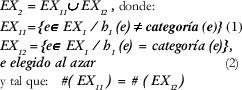
donde # representa el cardinal de un conjunto, por lo tanto el # (EX2) = 2 # (EX11)
Así, al concluir la fase II, EX2 contiene el conjunto de ejemplos fallados (1) y un subconjunto de ejemplos acertados elegidos al azar (2). Se somete ahora el nuevo conjunto de ejemplos EX2 al sistema de aprendizaje automático C4.5 obteniendo el clasificador h2.
Un nuevo conjunto de ejemplos EX3 es construido de la siguiente forma:
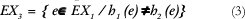
De nuevo se realiza otro aprendizaje con el sistema C4.5 sobre el conjunto de ejemplos creado, EX3, produciendo el clasificador h3, con lo cual finaliza la fase III.
Por último, M genera el clasificador h que será el "voto por mayoría" de {h1, h2, h3} que expresamos de la siguiente forma:
Dadas dos clases y un ejemplo e de E, definimos h(e) así:
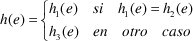
Obsérvese que cuando se tiene más de dos clases, y se producen tres resultados distintos dos a dos, se toma la clasificación ofrecida por h1 porque es el clasificador obtenido inicialmente y así se puede garantizar, como mínimo, un comportamiento igual de bueno al que ofreció el sistema de aprendizaje original, C4.5.
Desde un punto de vista teórico, se sabe que el clasificador obtenido siguiendo este dispositivo tendrá un error acotado por 3x 2 - 2 x 3 siendo x el error (en tanto por 1) de reescritura original. De esta forma el error se verá sensiblemente disminuido.
2.5 Problemas que se presentan y posibles soluciones
A la hora de probar el dispositivo, capaz de realizar su labor sobre una computadora, aparecen una serie de problemas a los que hay que dar alguna solución para hacer efectivo el algoritmo. Entre ellas podemos destacar las siguientes:
•Que el conjunto EX2 sea muy pequeño, con lo que se puede llegar a que el clasificador h2 sea vacío. Esto puede producirse por varios motivos:
(a1) Cuando hay un porcentaje de acierto inicial muy elevado, con lo que el número de ejemplos fallados es bajo. De esta manera se dispone de pocos ejemplos para construir el conjunto EX2.
(a2) El sistema base no ofrece reglas por defecto, que podrían paliar la ausencia de reglas inducidas.
(a3) Los parámetros para el aprendizaje en el sistema base son demasiado exigentes.
•Que el conjunto EX2 sea vacío. En este caso el porcentaje de acierto inicial sería ya del 100%, con lo que no nos interesa intentar mejorarlo.
•Que no podamos obtener EX3. Si ∀e, e∈ EX1, h1(e) = h2(e), entonces los dos clasificadores h1 y h2 clasifican de igual manera al conjunto de ejemplos inicial EX1, con lo que EX3, que se construiría con los ejemplos clasificados de distinta forma es vacío.
Sería conveniente disponer de instrumentos que eviten caer en estos problemas, sobre todo el (a1), ya que un alto porcentaje de acierto inicial puede deberse a que se está produciendo un sobre - ajuste (overfitting) en los ejemplos originales.
El eje central de la solución a estos problemas es un mecanismo de substracción de un cierto número de reglas, obligando a un aumento en el porcentaje de error del clasificador obtenido, de manera que con un número mayor de fallos se pueda construir un conjunto de entrenamiento más grande y así poder centrar mejor el sistema base sobre los fallos cometidos inicialmente. De este modo se espera obtener al final clasificadores concretos para estos ejemplos inicialmente erróneos.
Este dispositivo debe construirse teniendo en cuenta una serie de restricciones entre las cuales están las siguientes:
•Que el número de reglas eliminado haga au mentar el porcentaje de error más allá del 50%, con lo que se vería imposibilitado para seguir el proceso en condiciones normales. Se obligaría a construir los conjuntos de ejemplos de la fase II de manera diferente, pues no se tendrían suficientes ejemplos buenos para hacerlo y en el caso de duplicarlos habría que plantearse qué ejemplos se duplicarían de manera que no se introdujesen más factores de distorsión en el proceso (lo que se quiere es centrar el sistema base en los fallos y así lo que se estaría haciendo es abrir el foco, puesto que acabaríamos con un conjunto de entrenamiento mayor que el inicial).
•Que las reglas eliminadas no sean reglas buenas. Es evidente que en un proceso de poda de reglas como el que se propone, no parece lógico ni deseable quedarse con reglas poco representativas para ejercer la tarea de clasificación. Se impone pues una labor de selección de reglas en función de su bondad, lo cual implica a su vez la necesidad de emplear algún tipo de medida para evaluar las reglas, de tal manera que se pueda establecer una ordenación en las mismas en base a tal medida y así la tarea de poda se limitará a establecer el nivel de corte en la ordenación. Existen diversas medidas que pueden ser empleadas para imponer una ordenación en un conjunto de reglas: el número de aciertos de la regla (A) o el número de fallos (F) (en orden inverso al anterior), el número total de ejemplos cubiertos o sobre los que es aplicable la regla (daría una idea de la extensión de la regla), la probabilidad de acierto de la regla (A/A+F) o, análogamente, la probabilidad de fallo de la regla (F/A+F) (en orden inverso), la especificidad o generalidad de la regla (se querrían reglas generales, que no reflejasen detalles puntuales del conjunto de entrada), otras medidas más complejas (p. ej. El nivel de impureza [20], [21] y [22]), también podría ser alguna combinación de las anteriores o incluso según los criterios del propio sistema base empleado.
Para aprovechar mejor las particularidades del sistema de aprendizaje de base, en el prototipo inicial se ha optado por usar la ordenación de las reglas según los criterios de los sistemas utilizados.
•También ha de tenerse en cuenta que puede haber ocasiones en que no sea recomendable la substracción de reglas. La idea perseguida con la substracción es la de posibilitar conjuntos de entrenamiento mayores a las fases siguientes, simultáneamente, eliminar reglas que reflejen casos no generales del conjunto de entrenamiento (posible overfitting del propio sistema base). Cuando el número de ejemplos fallados (o mejor el porcentaje de fallo) sea suficiente para continuar el proceso se continuará sin efectuar la poda de reglas. Tampoco es recomendable eliminar reglas de manera que se dejen clases sin reglas. Esto podría hacerse realizando la poda en cada conjunto de reglas de cada clase, en vez de en el conjunto total de las reglas del clasificador o realizarla de manera que la proporción de reglas se mantuviera para cada clase, es decir una poda estratificada.
Asimismo, en contra de lo que se podría pensar a priori el proceso de substracción no pierde reglas por el hecho de eliminarlas. Los ejemplos fallados pasan a la siguiente fase y son susceptibles de volver a generar reglas iguales o similares que los clasifiquen correctamente.
Para la cantidad de reglas a eliminar por defecto y por exceso surgen problemas con los números impares, por ejemplo si suponemos un conjunto de 3+3+1 reglas para 3 clases, la última regla por defecto, podríamos optar por considerar 2+2+1 (por exceso) o bien 1+1+1 (por defecto) ya que, manteniendo las proporciones y sin dejar clases sin reglas, tendríamos que quedarnos con 1,5 reglas de las 2 primeras clases y media de la tercera.
Todo esto lleva a la conclusión de que el dispositivo de substracción puede ser, y de hecho lo es, un heurístico complejo teniendo en cuenta todas estas situaciones.
Para el prototipo utilizado en las pruebas se decidió utilizar un dispositivo de poda bastante agresivo, consistente en la eliminación del 50% de las reglas en orden inverso de bondad; es decir, se queda solo con la mitad formada por las mejores reglas. La eliminación tiene en cuenta el número de reglas de cada clase, de manera que no se eliminen todas las reglas de una clase, y tampoco se elimina la regla por defecto, en el caso de que la hubiere. Los casos de empate discutidos en el último apartado se han resuelto por defecto.
2.6 Resultados
Los ejemplos escogidos tratan de constituir una muestra representativa de todo tipo de conjunto, de diversas y variadas características, para no introducir sesgos causados por la utilización de un tipo concreto de conjunto.
Las pruebas se han realizado sobre conjuntos de ejemplos del almacén de la Universidad de California en Irvine (UCI repository) [25], que constituye un referente en el aprendizaje automático.
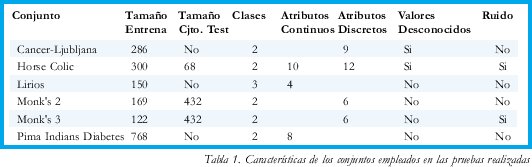
Se ha experimentado con los siguientes conjuntos y las características se resumen en la tabla 1.
Como se puede observar, en los problemas elegidos hay: conjuntos de varios tamaños, problemas con y sin conjuntos de prueba específicos, dominios con dos clases y tres clases (Lirios), problemas donde el tipo de los atributos es continuo, simbólico o mezcla de ambos y también están presentes conjuntos con valores desconocidos (missing values) y con ruido en los valores de los atributos como es el caso de Monk´s 3 y Horse Colic.
En el prototipo desarrollado para la evaluación experimental del dispositivo se tomó el sistema implementado en la librería MLC++ [26], C4.5 [2] en su vertiente basada en reglas (C4.5-rules). Las reglas de clasificación constituyen la estructura más popular para la presentación del conocimiento extraído o aprendido por un algoritmo de aprendizaje automático, es por esto que hemos escogido estos sistemas mundialmente conocidos.
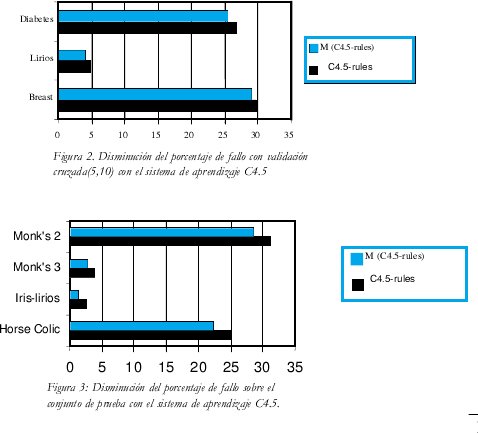
No presentamos aquí todas y cada una de la pruebas individuales que se hicieron para validar el dispositivo (100 pruebas por cada método para estimar el error), solo graficamos en las figuras 2 y 3 el promedio de los resultados de cada prueba con cada ejemplo. Observamos que el comportamiento del prototipo fue bueno, máxime si tenemos en cuenta la agresividad antes comentada del mecanismo de substracción empleado en el mismo.
Una parte de las pruebas se hicieron con validación cruzada y los conjuntos denominados "Pima Indians Diabetes", "Iris" (también denominado Lirios en castellano) y el "Breast Ljubljana" (Cáncer Ljubljana) que son conjuntos de entrenamiento que no tienen conjunto de test, (ver tabla 1), se hicieron 100 veces validación cruzada (5, 10) (ver numeral 2.3). Otra parte de las pruebas se realizaron con Aciertos y fallos sobre el conjunto de prueba (ver numeral 2.3) y los conjuntos "Monk's 2", "Monk's 3", "Iris" y "Horse Colic" que tienen conjunto de prueba, salvo el caso de Iris que se toma el mismo conjunto como conjunto de prueba (ver tabla 1).
Observando las dos gráficas, podemos ver la disminución de la que hablamos, en términos generales podemos también ver que es diferente esa disminución en cada ejemplo, esto es claro debido al tipo de problema, con ruido, por ejemplo (ver tabla 1) y al tipo de validación utilizada; por ejemplo en Iris se ve que la disminución fue significativa utilizando aciertos y fallos sobre el conjunto de prueba como método para estimar el error de clasificación (ver numeral 2.3).
3. CONCLUSIONES
En este artículo hemos presentado un dispositivo que aprovechando los clasificadores generados con el algoritmo C4.5 de aprendizaje automático a partir de ejemplos disminuye el error de reescritura, aplicando el sistema de aprendizaje C4.5 a diferentes conjuntos de entrenamientos construidos a partir del original.
Se ha presentado también un mecanismo de poda llamado de substracción, introducido en el dispositivo para permitirle flexibilidad, siendo este un campo de estudio para buscar heurísticos que mejoren el comportamiento del dispositivo en cada una de las etapas.
comportamiento del mecanismo con problemas de todo tipo en la mayoría de las situaciones que se pueden presentar a un sistema de aprendizaje automático (problemas con ruido, missing-values, atributos simbólicos, numéricos y mezclados), así como la estabilidad de los resultados. Pero existen algunos casos en que la complejidad del conjunto de entrenamiento es tal que no disminuye acentuadamente el error, lo cual no justificaría la aplicación del dispositivo.
Con este resultado se ha abierto una puerta para continuar el estudio de disminución del error con este dispositivo para su generalización a todos los sistemas de aprendizaje automático a partir de ejemplos existentes, se muestra por sus pruebas y aplicaciones muy prometedor en sus bondades.
BIBLIOGRAFÍA
[1] Ranilla, J.: ABANICO: Aprendizaje Basado en Agrupación Numérica en Intervalos COntinuos. Memoria de Investigación del Tercer Ciclo en Ciencias de la Computación e Inteligencia Artificial, Universidad de Oviedo, 1995.
[2] Quinlan, J. R.: C4.5: Programs for Machine Learning, pp. x+302, Morgan K aufmann Publishers, San Mateo (California), 1993.
[3] Quinlan, J. R.: Discovering rules from large collections of examples: a case study. En D. MICHIE, (Eds.), Expert Systems in the Micro-Electronic Age, Edinburgh University Press, pp. 168-201, 1979.
[4] Breiman, L., Friedman, J. H., Olshen, R. A., & Stones, C. J: Classification and Regression Trees. Belmont, Wadsworth International Group, 1984.
[5] Fiol Roig, G.: Contribución a la adquisición inductiva de conocimiento. Tesis doctoral, Universidad de las Islas Baleares, 1991. Dirigida por José Miró Nicolau.
[6] Murthy, S. K., Kasif, S., & Salzberg, S.: A system for induction of oblique decision trees. Journal of Artificial Intelligence Research, 2, pp. 1-32, 1994.
[7] Michalski, R. S., & Larson, J. B.: Selection of the Most Representative Training Examples and Incremental Generation of VL1 Hypotheses: the Underlying Methodology and the Description of Programs ESEL and AQ11. Report of Intelligent Systems Group, Report No. 867, Dept. of Computer Science, University of Illinois, Urbana, 1978.
[8] Clark, P., Niblett, T.: The CN2 Induction Algorithm. Machine Learning, 3, pp. 261-284, 1988.
[9] Cendrowska, J.: PRISM: An Algorithm for inducing modular rules. International Journal of Machine Studies, 27, pp. 349-370, 1988.
[10] Salzberg, S.: Learning with nested generalized exemplars, pp. xviii+159. Kluwer Academic Publishers, Boston, 1990.
[11] Botana, F.: SHAPE: Sistema Heurístico de Aprendizaje a partir de Ejemplos. Tesis doctoral, Departamento de Computación, Universidade da Coruña, 1992. Dirigida por A. Bahamonde y A. Blanco Ferro.
[12] Montes Gracia, C.: MITO: Método de Inducción TOtal. Tesis doctoral, Universidad Politécnica de Madrid, 1994. Dirigida por Juan Pazos Sierra.
[13] Michie, D., Spiegelhalter, D. J., & Taylor, C. C. (Ed.), Machine Learning, Neural and Statistical Classification, p. xiv+289, Ellis Horwood, Hertfordshire, Gran Bretaña, 1994.
[14] Rumelhart, D., & McClelland, J., Parallel Distributed Processing, MIT Press, Cambridge, MA, 1986.
[15] Cover, T. M., & Hart, P. E.: Nearest Neighbor pattern classification, IEEE Transactions on Information Theory, 13:1, pp. 21-27, 1967.
[16] Aha, D. W.: A Study of Instance-based Algorithms for Supervised Learning Tasks: Mathematical, Empirical and Psychological Evaluations. Ph. D. Dissertation, University of California at Irvine, 1990.
[17] Cost, S., Salzberg, S.: A Weighted Nearest Neighbor Algorithm for Learning with Symbolic Features. Machine Learning, 10, pp. 57-78, 1993.
[18] Kohonen, T.: Self-Organizing Maps, p. xv+362. Springer Series in Information Sciences, Springer Verlag, Berlin, 1995.
[19] Shapire, R, The Design and Analysis of Efficient Learning Algorithms. An ACM Doctoral Dissertation Award, 1991.
[20] Ranilla, J., Mones, R., & Bahamonde, A.: El Nivel de Impureza de una regla de clasificación aprendida a partir de ejemplos. Actas de la VII Conferencia de la Asociación Española para la Inteligencia Artificial, CAEPIA-97, pp. 479-488, Málaga 1997.
[21] Ranilla, J., Mones, R., & Bahamonde, A.: El Nivel de Impureza de una regla de clasificación aprendida a partir de ejemplos. Revista Iberoamericana de Inteligencia Artificial, 4, pp.4-11, 1998.
[22] Ranilla, J., Mones, R., & Bahamonde, A.: El Nivel de Impureza de una regla de clasificación aprendida a partir de ejemplos. Revista de la Asociación de Técnicos de Informática, NOVATICA, 131, pp. 37-43, 1998.
[23] Michalski, R. S., Carbonell, J. G., & Mitchell, T. M.: Machine Learning. An Artificial Intelligence Approach, Vol. I, Tioga Pub., Palo Alto, California, 1983.
[24] Quinlan, J. R.: Improved Use of Continuous Attributes in C4.5. Journal of Artificial Intelligence Research, 4, pp.77- 90, Morgan Kaufmann Publishers, 1996.
[25] Murphy, P., & Aha, D. W.: UCI repository of machine learning databases -a machine-readable data repository. Maintained at the Department of Infor mation and Computer Science, University of California, Irvine. Anonymous ftp from ics.uci.edu in the directory pub/ machine-learning-databases, 1998.
[26] Kohavi, R., John, G., Long, R., Manley, D., & Pfleger, K.: MLC++: A machine learning library in C++. In Tools with Artificial Intelligence, IEEE Computer Society Press, pp. 740-743, 1994.
[27] Thrun, S. B., Bala, J., Bloedorn, E., et al: The MONK's Problems - A Performance Comparison of Different Learning algorithms. Technical Report CS-CMU-91-197, Carnegie Mellon University, 1991.
Ana María Peña Reyes
ofesora Facultad de Ingeniería de la Universidad Distrital Magister en Matemáticas de la Universidad Nacional de Colombia. Estudios de Maestría en Ingeniería de Sistemas en la Universidad Nacional de Colombia. Candidata a Doctor en Inteligencia Artificial y Ciencias de la Computación de la Universidad de Oviedo, España. Email: anamaria@aic.uniovi.es
Creation date:
Licencia
A partir de la edición del V23N3 del año 2018 hacia adelante, se cambia la Licencia Creative Commons “Atribución—No Comercial – Sin Obra Derivada” a la siguiente:
Atribución - No Comercial – Compartir igual: esta licencia permite a otros distribuir, remezclar, retocar, y crear a partir de tu obra de modo no comercial, siempre y cuando te den crédito y licencien sus nuevas creaciones bajo las mismas condiciones.





2.jpg)