DOI:
https://doi.org/10.14483/23448393.18453Published:
2022-08-19Issue:
Vol. 27 No. 3 (2022): September-DecemberSection:
Mechanical EngineeringSobre la determinación del umbral del rango del factor de intensidad de tensiones y los factores que lo afectan
On Determining the Stress Intensity Factor Range Threshold and the Factors that Affect It
Keywords:
crack closure, load ratio, microstructure (en).Keywords:
cierre de grieta, relación de carga, microestructura (es).Downloads
References
ASME, “Article KD-4, Fracture Mechanics Evaluation”, Boiler and Pressure Vessel Code, Section VIII, Rules for Construction of Pressure Vessels, Division 3, New York, American Society of Mechanical Engineers, 2019.
British Standard, Guide to Methods for Assessing the Acceptability of Flaw in Metallic Structures, BS 7910, London, The British Standard Institution, 2019.
C. A. Cabrera Arias, F. S. Garay Rairan, I. Arango Calderón y Ó. E. Gómez Vargas, “Design of a troubleshooting digital test bench for the beechcraft king C-90, 200, B200, 300 and 350 aircraft GCU”, Ingeniería, vol. 25, no. 3, pp. 393-409, 2020. https://doi.org/10.14483/23448393.16903 DOI: https://doi.org/10.14483/23448393.16903
S. Rodríguez Pulecio, J. J. Coronado Marín y N. Arzola de la Peña, “Mecánica de la fractura aplicada a ejes de molinos de caña de azúcar”, Ingeniería, vol. 10, no. 2, pp. 23-29, 2005. https://doi.org/10.14483/23448393.2713
U. Zerbst et al., “Fatigue and fracture of weldments”, in Fatigue and Fracture of Weldments. Springer, 2018. https://doi.org/10.1007/978-3-030-04073-4_1 DOI: https://doi.org/10.1007/978-3-030-04073-4
K. J. Miller, “The behaviour of short fatigue cracks and their initiation part I - A review of two recent books”, Fat. Frac. Eng. Mater. Struct., vol. 10, no. 1, pp. 75-91, 1987. https://doi.org/10.1111/j.1460-2695.1987.tb01150.x DOI: https://doi.org/10.1111/j.1460-2695.1987.tb01150.x
M. Su, L. Xu, C. Peng, Y. Han, and L. Zhao, “Fatigue short crack growth, model and EBSD characterization of marine steel welding joint”, Int. J. Fatigue, vol. 156, 2022. https://doi.org/10.1016/j.ijfatigue.2021.106689 DOI: https://doi.org/10.1016/j.ijfatigue.2021.106689
K. Hasegawa, D. Dvořák, V. Mareš, B. Strnadel, and S. Usami, “Suitability of fatigue crack growth thresholds at negative stress ratios for ferritic steels and aluminum alloys in flaw evaluation procedures”, Eng. Fract. Mech., vol. 248, 2021. https://doi.org/10.1016/j.engfracmech.2021.107670 DOI: https://doi.org/10.1016/j.engfracmech.2021.107670
D. Taylor, A Compendium of Fatigue Thresholds and Growth Rates, London, Engineering Materials Advisory Services, 1985.
U. Zerbst, M. Vormwald, R. Pippan, H.-P. Gänser, C. Sarrazin-Baudoux, and M. Madia, “About the fatigue crack propagation threshold of metals as a design criterion - A review”, Eng. Fract. Mech., vol. 153, pp. 190-243, 2016. https://doi.org/10.1016/j.engfracmech.2015.12.002 DOI: https://doi.org/10.1016/j.engfracmech.2015.12.002
ASTM, Standard Test Method for Measurement of Fatigue Crack Growth Rates, ASTM E647-15e1, West Conshohocken, PA, ASTM International, 2015.
L. P. Pook, “Mixed-mode fatigue crack growth thresholds: a personal historical review of work at the National Engineering Laboratory, 1975-1989”, Eng. Fract. Mech., vol. 187, pp. 115-141, 2018. https://doi.org/10.1016/j.engfracmech.2017.10.028 DOI: https://doi.org/10.1016/j.engfracmech.2017.10.028
J. M. Barsom, “Fatigue behavior of pressure-vessel steels”, WRC Bulletin, 194, New York, The Welding Research Council, 1974.
A. Hobbacher, Recommendations for Fatigue Design of Welded Joints and Components, document XIII-2151-07 / XV 1254-07, Paris, International Institute of Welding, 2007.
G. Marci, “Determination of the partitioning point dividing ΔK into ΔKeff”, Eng. Fract. Mech., vol. 53, no. 1, pp. 23-36, 1996. https://doi.org/10.1016/0013-7944(95)00082-7 DOI: https://doi.org/10.1016/0013-7944(95)00082-7
S. C. Forth, J. C. Newman, and R. G. Forman, “Generating fatigue crack growth thresholds with constant amplitude loads”, Fatigue 2002, pp. 2337-2344 , 2002.
D. J. Bang, and A. Ince, “A short and long crack growth model based on 2-parameter driving force and crack growth thresholds”, Int. J. of Fatigue, vol. 141, 2020. https://doi.org/10.1016/j.ijfatigue.2020.105870 DOI: https://doi.org/10.1016/j.ijfatigue.2020.105870
J. C. Newman, “A review of modelling small-crack behavior and fatigue-life predictions for aluminum alloys”, Fat. Fract. Eng. Mater. Struct., vol. 17, no. 4, pp. 429-439, 1994. https://doi.org/10.1111/j.1460-2695.1994.tb00242.x DOI: https://doi.org/10.1111/j.1460-2695.1994.tb00242.x
D. Leonetti, J. Maljaars, and H. H. Snijder, “Fracture mechanics based fatigue life prediction for a weld toe crack under constant and variable amplitude random block loading—Modeling and uncertainty estimation”, Eng. Fract. Mech., vol. 242, 2021. https://doi.org/10.1016/j.engfracmech.2020.107487 DOI: https://doi.org/10.1016/j.engfracmech.2020.107487
K. Sadananda, A. Arcari, and A. K. Vasudevan, “Does a nucleated crack propagate?”, Eng. Fract. Mech., vol. 176, pp. 144-160, 2017. https://doi.org/10.1016/j.engfracmech.2017.02.003 DOI: https://doi.org/10.1016/j.engfracmech.2017.02.003
A. K. Vasudevan, K. Sadanada, and N. Louat, “A review of crack closure, fatigue crack threshold and related phenomena”, Mater. Sci. Eng. A, vol. 188, no. 1-2, pp. 1-22, 1994. https://doi.org/10.1016/0921-5093(94)90351-4 DOI: https://doi.org/10.1016/0921-5093(94)90351-4
A. H. Noroozi, G. Glinka, and S. Lambert, “A two parameter driving force for fatigue crack growth analysis”, Int. J. Fatigue, vol. 27, no. 10-12, pp. 1277-1296, 2005. https://doi.org/10.1016/j.ijfatigue.2005.07.002 DOI: https://doi.org/10.1016/j.ijfatigue.2005.07.002
A. H. Noroozi, G. Glinka, and S. Lambert, “A study of the stress ratio effects on fatigue crack growth using the unified two-parameter fatigue crack growth driving force”, Int. J. Fatigue, vol. 29, no. 9-11, pp.1616-1633, 2007. https://doi.org/10.1016/j.ijfatigue.2006.12.008 DOI: https://doi.org/10.1016/j.ijfatigue.2006.12.008
D. J. Bang, A. Ince, and L. Q. Tang, “A modification of UniGrow 2-parameter driving force model for short fatigue crack growth”, Fat. Fract. Eng. Mater. Struct., vol. 42, no.1, pp. 45-60, 2019. https://doi.org/10.1111/ffe.12865 DOI: https://doi.org/10.1111/ffe.12865
D. J. Bang, A. Ince, and M. Noban, “Modeling approach for a unified crack growth model in short and long fatigue crack regimes”, Int. J. Fatigue, vol. 128, 2019. https://doi.org/10.1016/j.ijfatigue.2019.06.042 DOI: https://doi.org/10.1016/j.ijfatigue.2019.06.042
H. Kitagawa, and S. Takahashi, “Applicability of fracture mechanics to very small cracks or the cracks in the early stages”, Proceedings of 2nd International Conference on Mechanical Behavior of Materials, pp. 627-631, 1976.
B. Atzori, and P. Lazzarin, “Notch sensitivity and defect sensitivity under fatigue loading: Two sides of the same medal”, Int. J. Fract., vol. 107, pp. 1-8, 2001. https://doi.org/10.1023/A:1007686727207 DOI: https://doi.org/10.1023/A:1007686727207
B. Atzori, and P. Lazzarin, “A three-dimensional graphical aid to analyze fatigue crack nucleation and propagation phases under fatigue limit conditions”, Int. J. Fract., vol. 118, no. 3, pp. 271-284, 2002. https://doi.org/10.1023/A:1022965909483 DOI: https://doi.org/10.1023/A:1022965909483
M. N. James, C. J. Christopher, Y. Lu, and E. A. Patterson, “Local crack plasticity and its influences on the global elastic stress field”, Int. J. Fatigue, vol. 46, pp. 4-15, 2013. https://doi.org/10.1016/j.ijfatigue.2012.04.015 DOI: https://doi.org/10.1016/j.ijfatigue.2012.04.015
R. O. Ritchie, “Mechanisms of fatigue crack propagation in metals, ceramics and composites: Role of crack tip shielding”, Mater. Sci. Eng.: A, vol. 103, no. 1, pp. 15-28, 1988. https://doi.org/10.1016/0025-5416(88)90547-2 DOI: https://doi.org/10.1016/0025-5416(88)90547-2
R. Pippan, and A. Hohenwarter, “Fatigue crack closure: A review of the physical phenomena”, Fat. Fract. Eng. Mater. Struct., vol. 40, no. 4, pp. 471-495, 2017. https://doi.org/10.1111/ffe.12578 DOI: https://doi.org/10.1111/ffe.12578
H. J. Schindler, “On the significance of crack tip shielding in fatigue threshold— Theoretical relations and experimental implications”, in J. C. Newman, and R. S. Piascik (Eds.), Fatigue Crack Growth Thresholds, Endurance Limits, and Design, ASTM International, 2000. https://doi.org/10.1520/stp13425s DOI: https://doi.org/10.1520/STP13425S
R. Pippan, “The effective threshold of fatigue crack propagation in aluminium alloys. I. The influence of yield stress and chemical composition”, Phil. Magazine A, vol. 77, no. 4, pp. 861-873, 1998. https://doi.org/10.1080/01418619808221216 DOI: https://doi.org/10.1080/01418619808221216
K. J. Miller, “Materials science perspective of metal fatigue resistance”, Mater. Sci. Tech., vol. 9, no. 6, pp. 453-462, 1993. https://doi.org/10.1179/mst.1993.9.6.453 DOI: https://doi.org/10.1179/mst.1993.9.6.453
C. Santus, and D. Taylor, “Physically short crack propagation in metals during high cycle fatigue”, Int. J. Fatigue, vol. 31, no. 8-9, pp. 1356-1365, 2009. https://doi.org/10.1016/j.ijfatigue.2009.03.002 DOI: https://doi.org/10.1016/j.ijfatigue.2009.03.002
U. Zerbst, and M. Madia, “Fracture mechanics based assessment of the fatigue strength: Approach for the determination of the initial crack size”, Fat. Fract. Eng. Mater. Struct., vol. 38, no. 9, pp. 1066-1075, 2015. https://doi.org/10.1111/ffe.12288 DOI: https://doi.org/10.1111/ffe.12288
X. Cai, R. Xia, M. Huo, and J. Xu, “A threshold formula for fatigue crack growth with mean stress intensity factors”, Int. J. Mech. Sci., vol. 135, pp. 639-645, 2018. https://doi.org/10.1016/j.ijmecsci.2017.12.014 DOI: https://doi.org/10.1016/j.ijmecsci.2017.12.014
D. Kujawski, and F. Ellyin, “A unified approach to mean stress effect on fatigue threshold conditions”, Int. J. Fatigue, vol. 17, no. 2, pp. 101-106, 1995. https://doi.org/10.1016/0142-1123(95)95888-n DOI: https://doi.org/10.1016/0142-1123(95)95888-N
D. N. Lal, and T. K. G. Namboodhiri, “A model for the effect of mean stress on the threshold condition for fatigue crack propagation”, Mater. Sci. Eng.: A, vol. 130, no. 1, pp.37-49, 1990. https://doi.org/10.1016/0921-5093(90)90079-i DOI: https://doi.org/10.1016/0921-5093(90)90079-I
V. Kloster, H. A. Richard, and G. Kullmer, “Experimental characterization of the threshold and fatigue crack growth behaviour regarding negative stress ratios”, Ann. Nuclear Energy, vol. 40, no. 1, pp. 14-24, 2013.
K. Walker, “The effect of stress ratio during crack propagation and fatigue for 2024-T3 and 7075-T6 aluminum”, in M. S. Rosenfeld (Ed.), Effect of Environment and Complex Load History on Fatigue Life, ASTM International, 1970. https://doi.org/10.1520/stp32032s DOI: https://doi.org/10.1520/STP32032S
T. Mann, “The influence of mean stress on fatigue crack propagation in aluminum alloys”, Int. J. Fatigue, vol. 29, no. 8, pp. 1393-1401, 2007. https://doi.org/10.1016/j.ijfatigue.2006.11.010 DOI: https://doi.org/10.1016/j.ijfatigue.2006.11.010
V. M. Radhakrishan, “Endurance diagram”, Int. J. Fatigue, vol. 12, no. 6, pp. 513-517, 1990. https://doi.org/10.1016/0142-1123(90)90224-3 DOI: https://doi.org/10.1016/0142-1123(90)90224-3
H. Döker, “Fatigue crack growth threshold: Implications, determination and data evaluation”, Int. J. Fatigue, vol. 19, no. 93, pp. 145-149, 1997. https://doi.org/10.1016/s0142-1123(97)00058-3 DOI: https://doi.org/10.1016/S0142-1123(97)00058-3
R. Schmidt, and P. Paris, “Threshold for fatigue crack propagation and the effects of load ratio and frequency”, in J. Kaufman, J. Swedlow, H. Corten, J. Srawley, R. Heyer, E. Wessel, and G. Irwin (Eds.), Progress in Flaw Growth and Fracture Toughness Testing, ASTM International, 1973. https://doi.org/10.1520/stp49638s DOI: https://doi.org/10.1520/STP49638S
Z. Chen, The Effect of R Ratio and Temperature on Fatigue Crack Growth Threshold of Power Plant Steels, Doctoral Thesis, ETH, Zurich, 2018. https://doi.org/10.3929/ethz-b-000274863
Y. Yamada, and J. C. Newman Jr, “Crack closure under high load-ratio conditions for Inconel-718 near threshold behavior”, Eng. Fract. Mech., vol. 76, no. 2, pp. 209-220, 2009. https://doi.org/10.1016/j.engfracmech.2008.09.009 DOI: https://doi.org/10.1016/j.engfracmech.2008.09.009
J. A. Newman, W. T. Riddell, and R S. Piascik, “Effects of Kmax on fatigue crack growth threshold in aluminum alloys”, in J. C. Newman, and R. S. Piascik (Eds.), Fatigue Crack Growth Thresholds, Endurance Limits, and Design, ASTM International, 2000. https://doi.org/10.1520/stp13426s DOI: https://doi.org/10.1520/STP1372-EB
J. A. Newman, The Effects of Load Ratio on Threshold Fatigue Crack Growth of Aluminum Alloys, Ph.D. Dissertation, Virginia Tech., 2000. https://vtechworks.lib.vt.edu/handle/10919/29418
B. L. Boyce, and R. O. Ritchie, “Effect of load ratio and maximum stress intensity on the fatigue threshold in Ti-6Al-4V”, Eng. Fract. Mech., vol. 68, no. 2, pp. 129-147, 2001. https://doi.org/10.1016/s0013-7944(00)00099-0 DOI: https://doi.org/10.1016/S0013-7944(00)00099-0
M.-L. Zhu, F.-Z. Xuan, and S.-T. Tu., “Effect of load ratio on fatigue crack growth in the nearthreshold regime: A literature review, and a combined crack closure and driving force approach”, Eng. Fract. Mech., vol. 141, pp. 57-77, 2015. https://doi.org/10.1016/j.engfracmech.2015.05.005 DOI: https://doi.org/10.1016/j.engfracmech.2015.05.005
R. Sunder, “Why and how residual stress affects metal fatigue”, Advanced Materials Springer Proceedings in Physics, vol. 175, 2016. https://doi.org/10.1007/978-3-319-26324-3_34 DOI: https://doi.org/10.1007/978-3-319-26324-3_34
J. W. Sheldon, K. R. Bain, and J. K. Donald, “Investigation of the effects of shed-rate, initial Kmax, and geometric constraint on ΔKth in Ti-6Al-4V at room temperature”, Int. J. Fatigue, vol. 21, no. 7, pp. 733-741, 1999. https://doi.org/10.1016/s0142-1123(99)00037-7 DOI: https://doi.org/10.1016/S0142-1123(99)00037-7
I. Verpoest, E. Aernoudt, A. Deruyttere, and M. De Bondt, “The fatigue threshold, surface condition and fatigue limit of steel wire”, Int. J. Fatigue, vol. 7, no. 4, pp. 199-214, 1985. https://doi.org/10.1016/0142-1123(85)90051-9 DOI: https://doi.org/10.1016/0142-1123(85)90051-9
R. C. McClung, “Analysis of fatigue crack closure during simulated threshold testing”, in J. C. Newman, and R. S. Piascik (Eds.), Fatigue Crack Growth Thresholds, Endurance Limits, and Design, ASTM International, 2000. https://doi.org/10.1520/stp13435s DOI: https://doi.org/10.1520/STP13435S
T. H. Topper, and M. T. Yu, “The effect of overloads on threshold and crack closure”, Int. J. of Fatigue, vol. 7, no. 3, pp. 159-164, 1985. https://doi.org/10.1016/0142-1123(85)90027-1 DOI: https://doi.org/10.1016/0142-1123(85)90027-1
H. A. Richard, and M. Sander, Fatigue Crack Growth, Berlin, Springer, 2016. DOI: https://doi.org/10.1007/978-3-319-32534-7
R. W. Hertzberg, “On the calculation of closure-free fatigue crack propagation data in monolithic metal alloys”, Mat. Sc. Eng.: A, vol. 190, no. 1-2, pp. 25-32, 1995. https://doi.org/10.1016/0921-5093(94)09610-9 DOI: https://doi.org/10.1016/0921-5093(94)09610-9
J. Petit, G. Hénaff, and C. Sarrazin-Baudoux, “Environmentally assisted fatigue in the gaseous atmosphere”, Compr. Struct. Integr., vol. 6, pp. 211-280, 2003. https://doi.org/10.1016/b0-08-043749-4/06130-9 DOI: https://doi.org/10.1016/B0-08-043749-4/06130-9
O. N. Romaniv, A. N. Tkach, and N. Lenets, “Effect of fatigue crack closure on near‐threshold crack resistance of structural steels”, Fat. Fract. Eng. Mat. Struct., vol. 10, no. 3, pp. 203-212, 1987. https://doi.org/10.1111/j.1460-2695.1987.tb00478.x DOI: https://doi.org/10.1111/j.1460-2695.1987.tb00478.x
D. A. Lados, D. Apelian, and J. K. Donald, “Fatigue crack growth mechanisms at the microstructure scale in Al-Si-Mg cast alloys: Mechanisms in the near-threshold regime”, Acta Materialia, vol. 54, no. 6, pp. 1475-1486, 2006. https://doi.org/10.1016/j.actamat.2005.11.019 DOI: https://doi.org/10.1016/j.actamat.2005.11.019
P. Hutař, S. Seitl, and T. Kruml, “Effect of specimen geometry on fatigue crack propagation in threshold region”, Int. Conf. on Fracture (ICF 12), vol. 4, pp. 2914-2922, 2009.
P. C. Paris, H. Tada, and J K. Donald, “Service load fatigue damage —A historical perspective”, Int. J. Fatigue, vol. 21, Supplement I, pp. S35-S46, 1999. https://doi.org/10.1016/S0142-1123(99)00054-7 DOI: https://doi.org/10.1016/S0142-1123(99)00054-7
D. Kujawski, “Enhanced model of partial crack closure for correlation of R-ratio effects in aluminum alloys”, Int. J. Fatigue, vol. 23, no. 2, pp. 95-102, 2001. https://doi.org/10.1016/s0142-1123(00)00085-2 DOI: https://doi.org/10.1016/S0142-1123(00)00085-2
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Recibido: 13 de agosto de 2021; Aceptado: 24 de abril de 2022
Resumen
Contexto:
El umbral del rango del factor de intensidad de tensiones ΔKth es un valor por debajo del cual la propagación de grietas de fatiga es insignificante. Este suele usarse para establecer la vida a fatiga de un elemento ingenieril. Sin embargo, su determinación, la forma en que diferentes factores influyen en su valor y su aplicación aún son temas de discusión.
Método:
Este trabajo discute sobre los métodos y criterios existentes para la determinación de ΔKth y los factores que lo afectan.
Resultados:
Los métodos experimentales estándar ASTM son los ensayos más usados. Sin embargo estos pueden resultar inexactos, pues los ensayos de pre agrietamiento a compresión pueden producir resultados conservativos. Recientemente se han propuesto muchos métodos analíticos y numéricos para determinar el umbral. Muchos factores y variables afectan el valor de ΔKth. tales como el cierre de grieta, la geometría, el tamaño de la grieta. las características de la carga, la microestructura, las propiedades del material, el ambiente, las tensiones residuales y las cargas de modo mixto.
Conclusiones:
El umbral puede determinarse mediante ensayos estándar ASTM o métodos teóricos o numéricos. Se ha avanzado mucho en este campo, pero se requiere más investigación para mejorar los métodos experimentales y obtener métodos analíticos o numéricos que capturen más integralmente las diferentes complejidades, factores y variables que afectan el umbral.
Palabras clave:
cierre de grieta, relación de carga, microestructura.Abstract
Context:
The stress intensity factor range threshold ΔKth is a value below which fatigue crack propagation is insignificant. This factor is usually employed to establish the fatigue life of an engineering element. However, its determination, the way in which the different factors influence its value, and its application are still subjects of discussion.
Method:
This paper discusses the methods and criteria for determining ΔKth and the factors that affect it.
Results:
Standard ASTM experimental methods are the most used tests. However, they may prove to be inaccurate, since compression pre-cracking tests can yield conservative results. In recent years, many sound analytical and numerical methods for the determination of the threshold have been proposed. Many factors and variables can affect the value of ΔKth, such as crack closure, geometry, crack size, load characteristics, microstructure, material properties, environment, residual stresses, and mixed-mode loads.
Conclusions:
The threshold can be determined via standard ASTM tests or theoretical or numerical methods. Much progress has been made in this field, but more research is required to improve experimental methods and obtain analytical or numerical methods that more comprehensively capture the different complexities, factors, and variables that affect the threshold.
Keywords:
crack closure, load ratio, microstructure.Introducción
La mecánica de fractura es una ciencia relativamente nueva que estudia elementos agrietados. Es una ciencia importante, ya que muchas estructuras y máquinas son propensas a desarrollar grietas y fallar por fatiga o a tener defectos tipo grieta producidos durante la fabricación. Algunas de las aplicaciones de la mecánica de fractura son recipientes a presión 1, estructuras metálicas 2, industria aeronáutica 3 y ejes de transmisión 4.
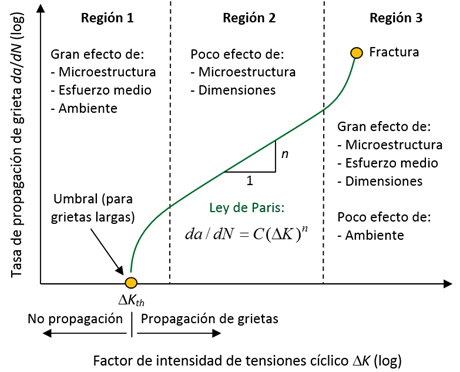
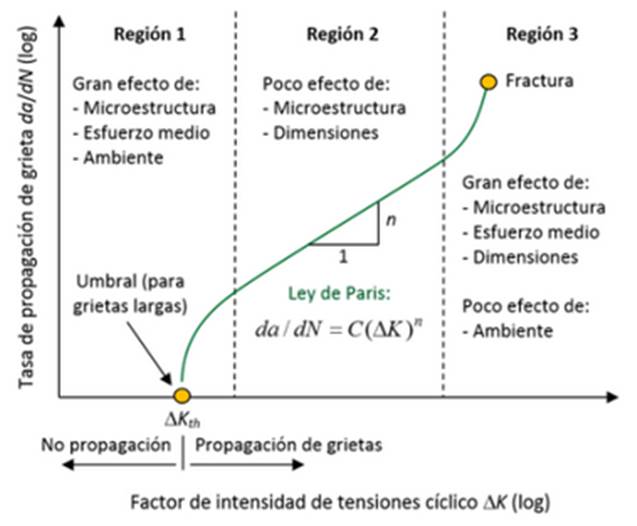
Por su parte, el factor de intensidad de tensiones K, de la mecánica de fractura elástica lineal (LEFM), es un parámetro que representa la intensidad del campo de tensiones en las vecindades de una grieta de un componente. Este parámetro aplica cuando la zona de deformación plástica en las vecindades de la grieta es muy pequeña comparada con el campo de tensiones elásticas. El comportamiento típico de la propagación de grietas por fatiga en la mecánica de fractura puede describirse a través de la curva sigmoidal 5 en escala logarítmica (figura 1) de la velocidad de propagación de la grieta da/dN (siendo a la extensión de la grieta y N número de ciclos) contra el rango del factor de intensidad de tensiones ΔK = Kmax - Kmin, mas Kmin para determinada relación de carga R= Kmin/ Kmax (K mínimo sobre K máximo).
Figura 1: Diagrama de crecimiento de grietas largas da/dN - ΔK. Basado en 5
En esta curva se pueden distinguir tres regiones, cada una de las cuales obedece a sus propias características. En la región 2 se observa un crecimiento estable con una relación casi lineal en escala logarítmica entre da/dN y ΔK, que es conocida como la Ley de Paris, da/dN = C(ΔK)n, donde C y n son parámetros empíricos. Esta ley permite cuantificar la propagación de grietas en esta zona. En la región 3 la velocidad de propagación de la grieta es grande, correspondiente a una aceleración en la propagación de la grieta, hasta que se presenta colapso plástico o una fractura inestable cuando Kmax alcanza un valor crítico conocido como la tenacidad a la fractura Kc. Este comportamiento inestable es atribuido a la interacción entre mecanismos dinámicos y estáticos de crecimiento de grietas. La región l se caracteriza por una rápida reducción de da/dN cuando ΔK se aproxima de forma asintótica hacia un valor característico, denominado umbral del rango del factor de intensidad de tensiones ΔKth.
Usualmente, la mayor parte de la vida de fatiga de un componente (alrededor del 80% 6) transcurre en la región umbral de propagación; lo cual está generalmente asociado a pequeños tamaños de grieta. De acuerdo con Su et al.7, el crecimiento de grietas cortas ocupa del 50 al 90% de la vida útil a la fatiga de diversos metales. Por lo tanto, describir el comportamiento de las grietas en la zona umbral es de gran importancia, y comprender el significado del umbral ΔKth, es crucial para el entendimiento de dicho comportamiento. Es más, establecer con exactitud el valor de ΔKth es importante, con el fin de determinar si algún defecto crecerá o no 8. Taylor 9 publicó valores de ΔKth de muchos materiales, para aplicaciones prácticas de ingeniería.
En el análisis por fatiga, el umbral del rango del factor de intensidad de tensiones ΔKth es utilizado dentro de la filosofía de diseño basado en la tolerancia de daño 10. Esta filosofía ha adoptado el concepto de ΔKth, en diseños de ingeniería con vida infinita o una extensa vida a fatiga. Una grieta será tolerada si ΔK es menor a ΔKth ldealmente, ΔKth, es el valor para el cual la velocidad de propagación de grietas es cero. El concepto más generalizado para describir el umbral de propagación es el basado en la LEFM. Se define como el valor del rango del factor de intensidad de tensiones por debajo del cual no se aprecia el crecimiento de grietas (válido para grietas largas; véase la sección Tamaño de la grieta) bajo condiciones de servicio de carga cíclica, teniendo en cuenta los métodos y la tecnología disponible para el monitoreo de la grieta. El estándar ASTM E647-15e1 11 lo define como el valor asintótico de ΔK de la curva da/dN vs. ΔK, donde da/dN toma un valor próximo a cero; para efectos prácticos, se toma un valor (arbitrario) de 10-10m/ciclo para la mayoría de materiales 11. El umbral existe porque no son posibles tasas de crecimiento de grietas por fatiga da/dN menores a aproximadamente un espaciado de la red cristalina. Los valores experimentales de dicho umbral, en modo I, son consistentes con esta observación. aunque a veces se ha observado crecimiento de grietas de menos de aproximadamente un espaciado de la red 12.
En la literatura se pueden encontrar curvas y ecuaciones para determinar ΔKth. Por ejemplo, Hasegawa et al. 8 presentan curvas y ecuaciones para aceros ferríticos y aleaciones de aluminio, suministradas en el boletín de la WRC (Welding Research Council) 13, en la Sección VIII de la ASME (American Society of Mechanical Engineers) 1. por el IIW (International Institute of Welding)14 y por el BS (British Standards) 79102.
En el presente artículo se discute sobre los métodos y criterios existentes para la determinación de ΔKth y sobre los factores que lo afectan. La segunda sección presenta los métodos para determinarlo. La tercera sección discute los factores que inciden en su valor. Finalmente, la cuarta sección presenta las conclusiones.
Métodos para determinar ΔKth
Debido a su importancia en el diseño por fatiga, se han hecho innumerables esfuerzos por calcular ΔKth. bien sea a través de métodos experimentales, estimaciones numéricas o modelos teóricos o semiteóricos.
Métodos experimentales
Es difícil determinar ΔKth experimentalmente, ya que toma mucho tiempo establecer si la grieta está creciendo o no 8. Usualmente, se halla por extrapolación o directamente de la curva de propagación de la grieta.
Métodos estándar ASTM
Este método permite observar la evolución de la extensión de la grieta en función del número de ciclos. Los ensayos se realizan en muestras preagrietadas estandarizadas para ensayos de mecánica de fractura, para una mejor comparación de datos, sometidas por lo general a carga de tracción pura (modo I), con control de carga ya una frecuencia constante. El preagrietamiento se realiza con el fin de iniciar una grieta desde una entalla que permita a la grieta salir de la zona afectada por la plasticidad generada alrededor de esta entalla.
El estándar ASTM E647-15e18 propone tres modos de control de carga para conducir los ensayos de propagación de grietas: el método de amplitud de fuerza constante para da/dN ?γτ; 10-8m/ciclo, el método de disminución de K para da/dN ?γτ; 10-8m/ciclo y el método de control de K alternativo.
El método de amplitud de fuerza constante se vuelve cada vez más difícil de usar a medida que las tasas de crecimiento disminuyen por debajo de 108 m/ciclo, debido a consideraciones previas al agrietamiento. Por lo tanto, el método de disminución de K es más aconsejable para las tasas mayores a 108 m/ciclo y no es adecuado para determinar el umbral. Por su parte, el método de reducción de K no se recomienda para tasas de crecimiento de grietas superiores a 108 m/ciclo, ya que el historial de carga anterior a los asociados niveles de ΔK puede influir en el comportamiento de la tasa de crecimiento de grietas por fatiga cercana al umbral. Finalmente, el método de control de K alternativo puede hacerse con Kmax o Kmedio constante; se puede obtener una estimación más conservadora del umbral mediante este método 11.
Método de disminución de K
La disminución de la fuerza durante la prueba de disminución de K puede hacerse en pasos de fuerza decrecientes (figura 2(a)) o de manera continua por una técnica automatizada 11. En este método, la relación entre K y el tamaño de la grieta a para una prueba con C constante está dada por la ecuación (1) 11:

Figura 2: Métodos de la norma ASTM E 647-15e1
donde ΔKi y ai son el rango del factor de intensidad de tensiones y la extensión de la grieta al inicio del ensayo. C es la rapidez de reducción de carga (gradiente de K normalizado), el cual debe cumplir con la relación de la ecuación (2) 11:
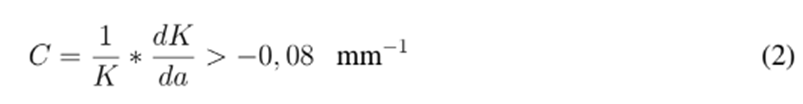
Se recomienda que la relación de fuerzas (fuerza mínima sobre fuerza máxima) y C sean mantenidos constantes durante la prueba. Para determinar el umbral, ΔK se reduce hasta alcanzar ΔKth este será el ΔK correspondiente a la velocidad de propagación mínima definida en el ensayo, que para la mayoría de materiales es de 10-10m/ciclo 11.
Método de control de K alternativo
Este puede hacerse con Kmax o Kmedio constante, y la estimación del umbral es más conservadora. Para hallar el umbral, se reduce progresivamente ΔK, aumentando gradualmente Kmin (figura 2c), si el ensayo se hace con Kmax constante, o disminuyendo Kmax y aumentando Kmin(figura 2(b)), si el ensayo se hace con Kedio Constante, hasta alcanzar ΔKth (por ejemplo, 10-10m/ciclo. Generar datos con un gradiente de K adecuado, utilizando un valor constante y positivo de C, reduce el tiempo de prueba, entre otras ventajas. 11.
Método de preagrietamiento a compresión
Los métodos anteriores son adecuados para estudiar el crecimiento de grietas largas 16. Este método puede ser empleado para cualquier tamaño de grieta y garantiza la obtención de un ΔKth libre de efectos de cierre de grieta. Además, este procedimiento se usa con frecuencia para generar preagrietamiento de materiales frágiles. En este método, al igual que a tracción cíclica, se crea una grieta que surge desde la raíz de una entalla sometida a elevadas cargas cíclicas de amplitud constante a compresión (la carga máxima y la carga mínima están a compresión). El método de preagrietamiento a compresión se realiza a una amplitud de carga ΔK definida y una relación de carga R definida. Posteriormente, la grieta se propaga aplicando una pequeña carga de tracción, con una reducción progresiva de la velocidad de propagación, hasta que crezca fuera del campo de tensiones residuales a tracción creadas por las cargas compresivas. Por último, se aplica una carga de amplitud constante, para un R determinado, para terminar de definir la curva de propagación 16. El número de ciclos es relativamente amplio, con el fin de reducir las tensiones residuales al mínimo.
Métodos analíticos y numéricos
Los métodos experimentales pueden llegar a ser costosos y demandar mucho tiempo 8, en especial cuando se requieren bajas frecuencias cíclicas. Esto, debido al gran número de ciclos requerido. Además, son incapaces de considerar todos los factores que influyen en la medida. Lo ideal sería tener modelos teóricos o semi teóricos y numéricos que incluyan al menos algunos de los factores que intervienen en el crecimiento de grietas. Los modelos semi teóricos son modelos mecánicos que se usan en conjunto con parámetros determinados de manera experimental.
Se han desarrollado muchos métodos de predicción de crecimiento de grietas, tanto para grietas cortas como largas, teniendo en cuenta la plasticidad alrededor del frente de la grieta, la carga y el concepto de cierre de grietas. Las grietas cortas exhiben características de propagación bastante diferentes a las de las largas; por ejemplo, las tasas de crecimiento de grietas cortas presentan una variabilidad significativa, las cuales se ven afectadas por tensiones locales, microestructura del material, límites de grano, dislocaciones, tamaño de grano y resistencia de fluencia 17. Por ejemplo, Su et al. 7 indican que cuando la longitud de una grieta superficial en aceros austeníticos es menor a 3 granos, la tasa de crecimiento es obstaculizada por la microestructura. y dicho efecto se reduce con el crecimiento de la grieta.
Newman 18 propuso un modelo numérico para predecir el crecimiento de grietas. postulando que el cierre de grieta afecta significativamente dicho crecimiento. El modelo incorpora varios parámetros de ajuste que dependen de datos experimentales. Sin embargo, según Bang e Ince 17, El modelo no tiene en cuenta que las evidencias experimentales indican que no se desarrolla un cierre de grieta significativo para grietas cortas, y esos modelos basados en el cierre de grieta no pueden proporcionar resultados precisos para grietas cortas 19. Otros autores también han usado el enfoque de cierre de grieta para estimar la propagación de grietas cortas y largas (por ejemplo. 6).
En contraste, Vasudevan et al. 20, 21 sugirieron un modelo de doble parámetro de propagación de grietas (enfoque unificado) basado en ΔK y Kmax, sin tener en cuenta el cierre de grieta. Esto debido al cuestionamiento de los métodos basados en el cierre de grieta, los cuales sobreestiman de manera sustancial el crecimiento de grietas cortas 17. Al trabajar con este par de parámetros, se tienen en cuenta los efectos de la relación de carga (R). En el enfoque unificado se supone que las fuerzas impulsoras (ΔK) y Kmax deben ser lo suficientemente grandes para inducir el daño por fatiga y, por lo tanto, propagar las grietas, tanto cortas como largas. Entonces, las grietas cortas también deben tener umbrales de crecimiento de grietas correspondientes, para tener en cuenta la resistencia de los materiales a la propagación de grietas cortas. 17
Más tarde, se propuso la teoría UniGrow. Noroozi y Glinka 22, 23 introdujeron la teoría UniGrow basada en dos parámetros de fuerza conductora. En esta teoría, los efectos de la tensión residual sobre el comportamiento de crecimiento de las grietas bajo cargas de fatiga se consideran corrigiendo los dos parámetros de fuerza impulsora, ΔK y Kmax. con el factor de intensidad de tensiones residuales, Kr17.
Recientemente, en 24, 25) sugirieron un modelo UniGrow modificado, el cual considera las tasas de propagación de grietas, tanto cortas como largas. Se informa que dicho modelo modificado tiene una correlación adecuada con datos de crecimiento de grietas largas, pero el modelo no se correlacionó con datos de grietas cortas 17.
Por otro lado, la integral J cíclica de la mecánica de fractura elastoplástica puede ser, en teoría, aplicada a grietas cortas, debido al tamaño considerable de la zona plástica en comparación con la longitud de la grieta; sin embargo, no está comprobado todavía que funcione para grietas cortas. Otro método propuesto para evaluar el crecimiento de grietas cortas es el diagrama Kitagawa-Takashi 26, el cual fue modificado por Atzori y Lazzarin 27, 28 para determinar el límite de fatiga de grietas largas y cortas.17
Recientemente, Christopher et al. 29 propusieron un modelo de crecimiento de grietas, conocido como modelo CJP, para tener en cuenta el impacto de la zona plástica en la punta de la grieta y su interacción con el campo de tensiones elásticas. El modelo CJP incluye una serie de parámetros para describir los efectos de aumento y retardo del crecimiento de grietas.
Finalmente, en 17 proponen un modelo que combina el enfoque unificado y el modelo UniGrow para predecir el comportamiento de grietas tanto cortas como largas. El modelo tiene en cuenta los parámetros de las fuerzas impulsoras y los umbrales correspondientes. Las variables que considera son ΔK , Kmax., Kr y los correspondientes umbrales de crecimiento de grietas, Kth y Kmax,th. De esta manera, se unifica el comportamiento de las grietas por fatiga en los dos regímenes: grietas cortas y largas.
Realmente, hay muchos métodos de propagación de grietas cortas; una revisión detallada puede encontrarse en 17. Muchos de los métodos propuestos tienen una validez razonable bajo condiciones específicas. A pesar de que es difícil que los diferentes modelos capturen todos los factores y complejidades presentes en diferentes casos, recientemente se ha avanzado para conseguir aproximaciones cada vez más satisfactorias, acordes con los datos experimentales. Así, hay que seguir avanzando para que los modelos, tanto analíticos como numéricos, sean cada vez más universales. Por ahora, los métodos experimentales continúan siendo la mejor forma de determinar el umbral de propagación.
Factores que afectan a ΔK th
Estudios intrínsecos y mecanismos extrínsecos
Estudios en la zona umbral han determinado que existen dos tipos de procesos que pueden intervenir en el valor de ΔKth: procesos intrínsecos y procesos extrínsecos 30. Los primeros producen nueva superficie de fractura en el frente de grieta 31; se refieren a mecanismos de fatiga que reflejan los cambios en la resistencia propia del material a la propagación de grietas, en los que actúan mecanismos en el frente de la grieta o delante de este. Los segundos son mecanismos de fatiga que están relacionados con la reducción en la fuerza conductora de la grieta, y que actúan en el ancho de la grieta.
Los efectos de los mecanismos intrínsecos sobre ΔKth pueden reflejarse en un factor intrínseco del umbral de propagación ΔKthint: asimismo, los mecanismos extrínsecos se reflejan en un ΔKthext.La suma de estos dos factores da como resultado el umbral de propagación de grietas total, tal como se indica en la ecuación (3):

ΔKthint representa la resistencia propia del material a la propagación de grietas por fatiga, para una grieta considerada ideal, y ha sido propuesto como el límite de emisión de dislocaciones para una punta de grieta ideal. Este factor es el resultado de mecanismos que previenen que efectos microplásticos ocurran cerca de la punta de grieta, como dislocaciones atrapadas en los límites de grano, sistemas de deslizamiento interrumpidos por inclusiones, relaciones de carga microscópicamente finitas, entre otros 32.
ΔKthext está compuesto de diferentes contribuciones que pueden ser clasificadas dentro de tres grandes grupos:
-
Protección geométrica (desviación y ramificación de la grieta) (figura 3). Usualmente, no se establece cuantitativamente, ya que para hacerlo es necesario conocer la geometría microscópica y un criterio para la propagación en modo mixto, que generalmente es supuesto 33.
-
Protección de zona (figura 3). Como microgrietas o efectos producidos por discordancias de diferentes fases. En materiales metálicos homogéneos no suele ser importante.
-
Protección por contacto (figura 3). Comprende los mecanismos de cierre de grieta y el "puenteo" o acoplamiento de la grieta.
Figura 3: Representación de las diferentes contribuciones a ∆Kth. Basada en 30
Dado que la contribución de la protección geométrica y la protección de zona representan solo un pequeño aumento en ΔKth y que la mayor contribución viene de la protección por contacto. una predicción imprecisa de la protección geométrica y de zona no acarreará un gran error en la aproximación total. En muchos de los experimentos que se han llevado a cabo, se miden solamente el ΔKth y el efecto del cierre de grieta. Por lo tanto, se suele emplear el factor ΔKtheff, el cual es la resta del umbral total y la contribución del cierre de grieta. Entonces, ΔKth puede expresarse de acuerdo con la ecuación (4) (figura 3):

Donde ΔKclth representa el aporte únicamente de los efectos de los diferentes mecanismos de cierre de grieta. Entonces ΔKtheff representa el límite físico de carga más bajo, el cual garantiza que la grieta no se propagará incluso sin la presencia de algún mecanismo de cierre de grieta. ΔKclth presenta una alta dispersión y sensibilidad a las condiciones de ensayo y del material (a diferencia de ΔKtheff, el cual suele estar dentro de un estrecho rango para un tipo de material). Por consiguiente, es conveniente realizar una descripción del comportamiento del fenómeno del cierre de grieta y sus diferentes mecanismos en la zona umbral de propagación.
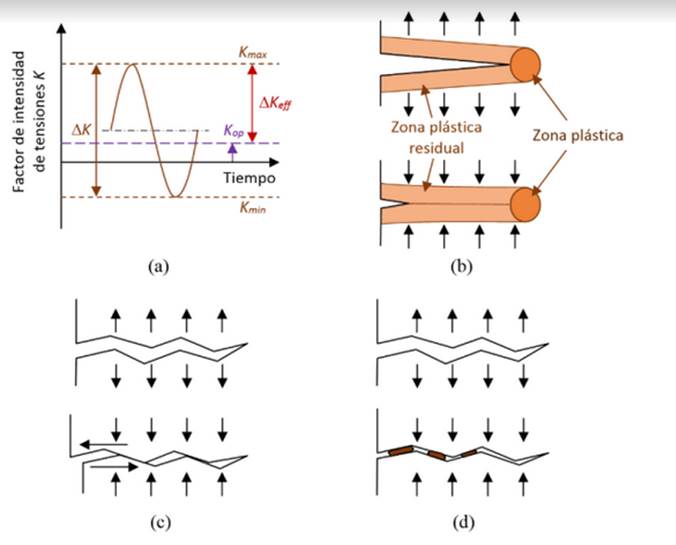
Cierre de grieta
En un elemento agrietado sometido a una carga cíclica tracción-tracción (es decir, Kmin y Kmax son ambos positivos) las superficies de fractura pueden aún estar en contacto entre sí, por lo que la grieta estaría completamente abierta solo en una parte del ciclo de carga. Lo anterior se conoce como cierre de grieta. Se supone que no existe daño en la punta de la grieta cuando sus caras están en contacto, por lo que esta parte del ciclo de carga no tiene efecto en el crecimiento de la grieta; es decir, la grieta sólo se propaga cuando está abierta. Una parte de la fuerza aplicada es usada para reabrir las caras de la grieta interferida, por lo que la magnitud efectiva del rango del factor de intensidad de tensiones es menor, lo cual conlleva a un menor daño por ciclo. De esta forma, la ecuación (5) define un rango del factor de intensidad de tensiones efectivo ΔKtheff:

Donde Kcl representa el factor de intensidad de tensiones en el momento en que entran en contacto las caras de la grieta. Una vez Kmin supera el valor de Kcl. el efecto del cierre de grieta es nulo.
Para la mayoría de los materiales metálicos existen diferentes mecanismos físicos por los que puede manifestarse el cierre de grieta. Los más importantes se discuten brevemente a continuación (figura 4).
Figura 4: Mecanismos del cierre de grieta. a) nomenclatura; b) cierre de grieta inducido por plasticidad (PICC); c) cierre de grieta inducido por rugosidad (RICC); d) cierre de grieta inducido por óxido (OICC). Basada en 6
Cierre de grieta inducido por plasticidad PICC (plasticity-induced crack closure): es causado por las zonas plásticas formadas, bajo carga, delante del frente de la grieta. Cuando la grieta se propaga bajo carga cíclica, quedan deformaciones residuales en el material estirado plásticamente, entre las superficies de la grieta. Esto causa un desajuste geométrico, en especial en las zonas en las que prevalecen condiciones de tensión plana, donde la zona plástica es más grande.
Cierre de grieta inducido por partículas de óxido OICC (oxide-induced crack closure): es causado por la formación de productos corrosivos, como partículas de óxido, que cubren el ancho de la grieta, con grosores del orden del desplazamiento de apertura de la punta de la grieta CTOD (crack tip opening displacement); estas partículas aparecen como resultado del contacto reiterado entre las superficies de fractura de la grieta o también de partículas presentes en el ambiente.
Cierre de grieta inducido por rugosidad de superficie RICC (roughness-induced crack closure): surge del desplazamiento mutuo de las dos caras de la grieta a causa de la deformación plástica en la punta de la grieta, el cual genera asperezas en la cara de esta. En este tipo de cierre ocurre contacto discreto de puntos a lo largo del ancho de la grieta.
El cierre de grieta está presente en todas las regiones de la curva de propagación de grietas; sin embargo, su influencia se concentra principalmente en la zona umbral. El cierre de grieta es el principal mecanismo para explicar el comportamiento del crecimiento de grietas en la zona umbral. Bajo este concepto se ha podido explicar la relación que guardan diferentes factores como la carga aplicada, el ambiente, la microestructura, entre otros, con el umbral de propagación ΔKth.
De acuerdo con Pippan y Hohenwarter 31, el cierre de grieta inducido por plasticidad puede predecirse para tensión plana, deformación plana y en la región de transición entre estas dos. También, para todo tipo de condiciones de carga, incluida la carga de amplitud constante y variable. para grietas cotas y para la transición de deformación en pequeña escala a la de gran escala. Por el contrario, la predicción de cierre inducido por rugosidad inducido por óxido no es tan sencilla. Información detallada sobre la contribución de los efectos del cierre de grieta sobre el umbral de propagación de grietas se suministra en 31.
Tamaño de la grieta
En la región umbral, la LEFM suele usarse como herramienta para describir el comportamiento de la propagación de grietas a través del concepto de ΔKth, por debajo del cual las grietas no deberían propagarse. Esto es cierto para grietas largas, por lo que su aplicación a grietas cortas es bastante discutida, ya que el principio de similitud en la mecánica de fractura no se cumple. Este principio establece que todas las grietas, sin importar su tamaño en un mismo material, tendrán la misma velocidad de propagación, es decir, se comportan igual (como grietas largas) si el historial de la fuerza conductora de la grieta Δk es el mismo.
El comportamiento de propagación de grietas largas y de grietas cortas presenta varias diferencias, principalmente en la región umbral de propagación. Las grietas cortas crecen con una velocidad de propagación mayor que las grietas largas, para un Δk determinado, además de continuar propagándose por debajo del umbral ΔKth determinado con ensayos de propagación de grietas estándar (para grietas largas) 31, 34. Así, la estimación del tiempo de vida de un elemento que contiene pequeñas grietas o defectos con información para grietas largas será poco segura.
Con el fin de comprender la relación entre tamaño de grieta y crecimiento de grietas y el umbral de propagación ΔKth es importante distinguir los diferentes tamaños de grieta existentes. Esto permite clasificar las observaciones e identificar los conceptos específicos aplicables para cada tipo de grieta. Si bien no existen límites claros, en la literatura se encuentran frecuentemente los siguientes. De acuerdo con Su et al. 7, las grietas pueden clasificarse como microestructuralmente cortas, grietas en la zona de transición, físicamente cortas y largas.
Grietas microestructuralmente cortas su tamaño es comparable con el de las dimensiones microestructurales características del material, como el tamaño de grano o la distancia entre fases; por esta razón, la mecánica de fractura basada en la mecánica del medio continuo no puede aplicarse 10. De acuerdo con el estándar ASTM E647-15e1 11, una grieta microestructuralmente corta tiene una longitud correspondiente a 5 a 10 granos; sin embargo, la longitud varía bajo diferentes condiciones 7. Zona de transición las grietas en la zona de transición tienen un tamaño de entre 5 y 10 granos y 0,5 mm 7.
Grietas físicamente cortas para las cuales la extensión de la grieta supera considerablemente la escala de la zona plástica. por lo general con extensiones entre 0,5 y 1,5 mm 7 o 0,5 y 1 mm 17.
Grietas largas la definición de una grieta larga no es posible en términos absolutos 19; su tamaño típicamente comprende muchos granos. Por ejemplo, Santus y Taylor 35 indican que una grieta es larga si su tamaño es 10 veces el promedio del tamaño de grano o de otra barrera microestructural. Para muchos materiales, una grieta es larga usualmente si es mayor que 1 a 2 mm 7 o 0,5 a 1 mm 17. pero el valor exacto depende del material y puede salirse de estos rangos.
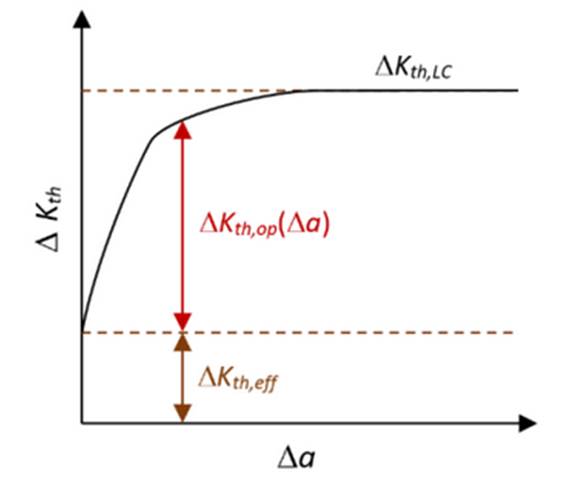
Se cree que el umbral de propagación para grietas microestructuralmente cortas está limitado por ΔKtheff o por ΔKthint, el cual no muestra ninguna dependencia con respecto a la extensión de la grieta. El comportamiento por debajo del umbral intrínseco del material está caracterizado por un comportamiento discontinuo, de aceleración y desaceleración, producto de la aleatoriedad en la dirección y la oposición de las barreras microestructurales presentes en el material y por la alta irregularidad en la forma de la grieta. El umbral para grietas físicamente cortas sí depende de la extensión de la grieta: aumenta de manera acelerada y uniforme en la medida en que aumenta la extensión de la grieta para luego crecer lentamente hasta alcanzar un valor constante, el cual es considerado como el umbral para grietas largas ΔKth,LC en una determinada relación de carga R.
Este comportamiento es trazado en una curva denominada curva de resistencia o curva R, como la de la figura 5.
Figura 5: Curva de resistencia o curva R. Basada en 36
La dependencia de la longitud de la grieta con respecto a ΔKth puede explicarse a través de los efectos del cierre de grieta 36. En la figura 6 se aprecia como U = ΔKeff /ΔK, el cual es un parámetro adimensional que representa el efecto del cierre de grieta, es función de la extensión de la grieta. Para una grieta considerablemente corta (microestructuralmente) U = 1, es decir, no presenta efecto de cierre, ya que la grieta no tiene un recorrido suficiente que permita la acumulación de material detrás de la punta de la grieta, ni rugosidad de superficie de la grieta que pemita que el fenómeno se manifieste. La grieta crece con la aplicación de un historial de carga (grietas físicamente cortas), manifestándose el efecto de cierre de grieta y aumentando a medida que la zona plástica deformada o partículas corrosivas se acumulan en el ancho de la grieta, U< 1, hasta que el cierre de grieta se satura y se alcanza un valor independiente del tamaño de grieta U LC (grietas largas). A partir de allí, el crecimiento de la grieta puede ser descrito por la curva da/Dn - ΔK pero corregido por el efecto del cierre de grieta. Así pues, puede deducirse que el aumento de ΔKth con el aumento de la extensión de la grieta es causado por el correspondiente aumento del cierre de grieta.
Figura 6: Esquema de la dependencia del parámetro adimensional de cierre U con el tamaño de la grieta Basada en 36
Condiciones de carga
Diferentes condiciones de carga suelen implicar diferentes comportamientos en la zona umbral y en ΔKth. A continuación, se tratan algunas de las condiciones de carga más relevantes.
Relación de carga (R)
El umbral ΔKth, depende fuertemente de la relación de carga (R) o del factor de intensidad de tensiones medio 37. Por esto, en la literatura se han propuesto varias relaciones empíricas 38)-(44. Estas muestran que hay varios patrones de variación del umbral con la relación Ry que se deben usar diferentes fórmulas empíricas para diferentes materiales 37.
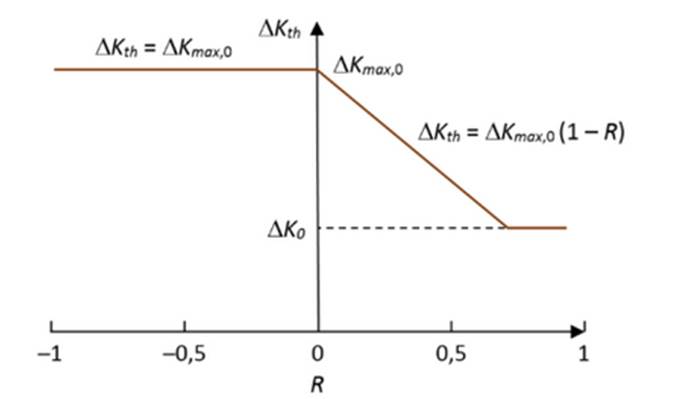
Además, se han propuesto varios conceptos para la explicación física de los efectos de R sobre ΔKth. como las tensiones residuales a compresión o tracción, o efectos del ambiente provocados por reacciones químicas en la vecindad de la punta de la grieta. Sin embargo, ha sido el cierre de grieta el mecanismo tradicionalmente aceptado y el de resultados más consistentes. Para que haya propagación de grietas, la grieta debe estar abierta. Esto se logra con la aplicación de una carga de tracción. Las caras de la grieta se separan cada vez más en la medida en que se aumenta la relación de carga, estando más abierta, haciendo que el CTOD sea más grande que las partículas de óxido, las rugosidades de las superficies de fractura de la grieta y los desplazamientos de deformación plástica, lo que reduce los efectos del cierre de grieta hasta que prácticamente desaparecen. Partiendo del concepto de cierre de grieta, es posible distinguir dos tipos de comportamiento, descritos por la ecuación (6) 45:

Donde Re representa el R crítico en que se presenta el cambio en el comportamiento. Sin embargo, en la literatura es fácil encontrar estudios cuyos resultados experimentales han demostrado desviarse considerablemente del comportamiento basado en el cierre de grieta, como el mostrado en la figura 7 y en 8, en el que se presentan curvas similares a la de la figura 7 (y las ecuaciones correspondientes), para aceros ferríticos y aleaciones de aluminio, suministradas en el boletín del WRC (Welding Research Council) 13, en la Sección VIII de la ASME (American Society of Mechanical Engineers) 1, por el IIW (International Institute of Welding) 14) y por el BS (British Standards) 7910 2.
Figura 7: Esquema de los efectos de R sobre ΔKth segun el efecto teórico del cierre de grieta. Basada en
(46)
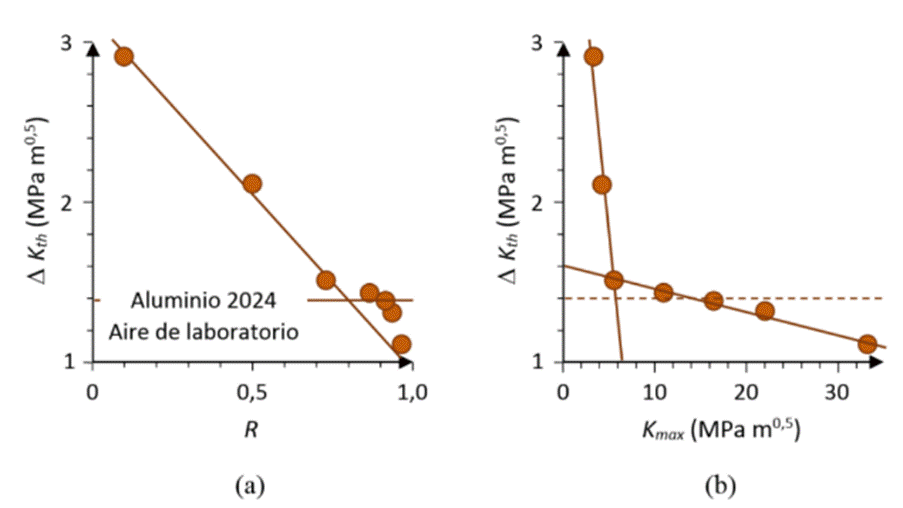
Según la ecuación (6). para R ?γτ; RC se espera que Kmin sea mayor a Kcl , de manera que el efecto del cierre de grieta desaparece y de esta manera ΔKth pasa a ser independiente de R, adoptando un valor constante igual a ΔKtheff Sin embargo, este no siempre es el caso: varios estudios han mostrado que luego de superar Rc, ΔKth continúa decreciendo con el aumento de R, desviándose del comportamiento que venía trayendo, como en la figura 8. Similarmente, Cai et al. 37 presentan seis tipos de curvas R vs. ΔKth en las que se aprecia la diversidad de las relaciones entre R y ΔKth, de acuerdo con diferentes experimentadores y diferentes materiales. Por lo tanto, se ha considerado que en este rango (R ?γτ; RC) el efecto del cierre de grieta aún puede estar presente o que otros mecanismos se manifiestan, como se explica a continuación.
Figura 8: a) ΔKth - R; (b) ΔKth - Kmax: con presencia de cierre de grieta u otros mecanismos para R elevados. Basada en 49
Presencia de cierre de grieta a nivel microestructural con grandes valores de R. Como se ha mencionado, a grandes valores de R la presencia de cierre de grieta se cree que es nula. Es probable que las técnicas o los métodos empleados para determinar el nivel de los efectos del cierre de grieta en estos niveles de carga, seguramente muy bajos, no sean lo suficientemente sensibles o desarrollados para detectarlos, siendo imperceptibles y por lo tanto considerados como inexistentes. Los métodos generalmente usados evalúan el nivel de cierre de forma global, pero estudios como el de Yamada y Newman 47, que lo miden de forma local, para una escala microestructural cerca y delante de la punta de la grieta, han mostrado que pequeños niveles de RICC y de OICC pueden seguir estando presentes a R elevados.
Efectos de Kmax Es probable que el cierre de grieta no sea el único mecanismo que afecta el crecimiento de la grieta, por lo que se han propuesto otros mecanismos como el efecto de Kmax. Este efecto se ha atribuido a cambios en los mecanismos de daño: de un crecimiento de grieta normal a la aparición de mecanismos de modo estático (de fractura a tracción) en la punta de la grieta, como división o desgarro dúctil, cuando Kmax alcanza valores cercanos a la tenacidad a la fractura
KIC (0,3 KIC ?λτ; Κmax ?λτ; 0,6ΚIC ) 48. Una posible explicación es que el incremento de Kmax fomenta un mayor movimiento de dislocaciones, llevando a que más dislocaciones se acumulen en barreras microestructurales y, así, ocurra un mayor daño en la punta de la grieta causado por el aumento en la formación de micro vacíos y microgrietas. Cuanto mayor es el aumento de Kmax. acercándose a KIC, mayor es la reducción de ΔKmax.
Otra hipótesis para grandes valores de Kmax es la de los mecanismos de agrietamiento por carga sostenida SLC (sustained load cracking), como fluencia o agrietamiento asistido por hidratos, que dependen del tiempo de exposición y de las condiciones ambientales. Estos pueden mostrar un crecimiento de grieta estable bajo cargas monotónicas cuando K supera un umbral que es menor a KIC (como en aleaciones de titanio). Los efectos sobre ΔKth podrían aparecer cuando Kmax supere un umbral de SLC. El comportamiento estaría dominado por cargas estáticas más que por cargas cíclicas 10, 50.
Para el lector interesado, Zhu et al. 51 presentan una revisión histórica de la investigación sobre la relación entre el cierre de grieta y el factor R
Tensiones residuales macroscópicas
Las tensiones residuales macroscópicas pueden ser consideradas como una carga estática interna adicional actuando de forma superpuesta a la carga cíclica que afecta el valor de R y de Kmax de forma local, llevándolos a un mayor o menor nivel, dependiendo del tipo de tensión residual. Por lo tanto, de forma indirecta, afectan el valor de ΔKth, bien sea a través de efectos del cierre de grieta o por los efectos de Kmax.
La presencia de un pico de tensión residual de tracción en la punta de la grieta, de magnitud suficientemente grande, debería suprimir cualquier efecto del cierre de grieta, manteniendo la grieta abierta. Este comportamiento es equivalente a tener un R local más alto. De manera que ΔKth será menor al esperado en un material sin tensiones residuales. El efecto contrario se espera con la presencia de tensiones residuales compresivas, es decir, la grieta se mantendrá cerrada aun para valores pequeños de R.
Sin embargo, determinar la influencia de tensiones residuales sobre ΔKth suele tornarse problemático, ya que por lo general la presencia de las tensiones residuales en un componente no es homogénea, sino que muestra importantes variaciones a través del grosor del componente, así como en otras direcciones, pasando por tensiones residuales a tracción y compresión 52. Así pues, la relación de carga total no será constante, sino que dependerá de la sección del componente a analizar. Además, los métodos para su medición resultan complejos.
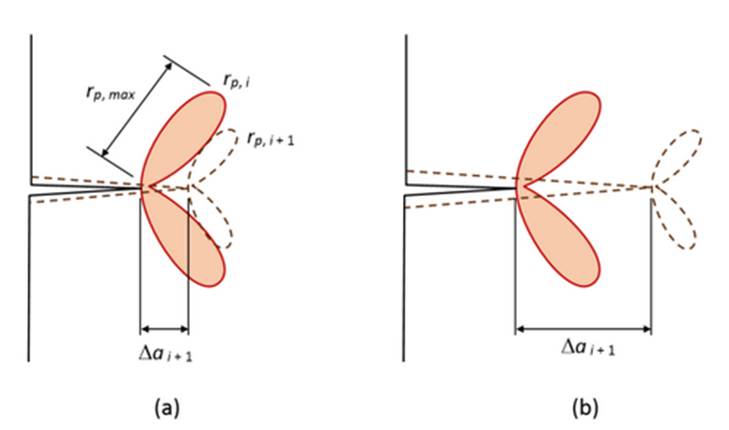
Historial de carga (reducción de carga)
Los procedimientos de reducción de carga manteniendo R constante han mostrado valores poco conservativos de ΔKth La tendencia es que con grandes valores iniciales del ensayo de ΔK y una alta velocidad de reducción de carga se obtienen ΔKth más altos. Gradientes de reducción de carga más cortos, es decir, una velocidad de reducción de carga más alta hará que la deformación plástica en un paso de reducción de carga se encuentre más cerca del anterior (figura 9(a)). Además, cuanto mayor sea el valor del ΔK inicial., mayor será el tamaño de la zona plástica generada. Así pues, el material deformado plásticamente se acumulará en el ancho de la grieta, estando muy próximo a la punta de la grieta, alterando así el estado de tensiones en dicha punta, y aumentando los efectos de PICC 53.
Figura 9: Formas de aplicar la reducción de carga: (a) demasiado rápido; (b) forma correcta . Basada en 54
Por lo tanto, lo que se busca para eliminar los efectos del historial de carga es la aplicación de un ΔKy una velocidad de reducción de carga C más baja (figura 9b). Mientras más grande sea el ΔK inicial menores serán los valores de C requeridos para evitar valores de ΔKth, demasiado altos 55. La velocidad de la reducción de carga debe ser la adecuada, de tal forma que la zona plástica del ciclo de carga anterior no interfiera sobre la zona plástica actual. Sin embargo, el PICC no es el único mecanismo de cierre que debe ser evitado: si la reducción es muy lenta, puede llegar a propiciar la formación de partículas corrosivas que aumentan el OICC. El OICC es promovido por gradientes de carga muy bajos, lo que se traduce en un mayor lapso de tiempo disponible para que partículas corrosivas se consoliden en capas.
Amplitud de carga variable
La amplitud de carga en aplicaciones reales no es totalmente constante. Son frecuentes los cambios en la tensión media y en la relación de carga, por cambios de servicio o condiciones accidentales,. creando patrones de carga complejos en los que es difícil determinar el comportamiento de la propagación de grietas. Una de las secuencias de amplitud de carga variable más documentadas, relativamente sencilla y común en áreas como la aeronáutica, es la de sobrecargas o descargas periódicas contenidas en una base de amplitud constante. Dependiendo de diversos factores, secuencias de amplitud de carga variable pueden generar una reducción o una aceleración en el crecimiento de la grieta.
El comportamiento de ΔKth para secuencias de carga con sobrecargas o descargas es diferente a los valores esperados para ensayos con una carga de amplitud constante. Cuando se aplican sobrecargas, son introducidas también tensiones residuales. Una sobrecarga a tracción produce tensiones residuales compresivas cerca de la punta de la grieta, mientras que sobrecargas a compresión generan tensiones residuales a tracción. También, cuando se aplican sobrecargas pueden originarse el PICC y desviaciones de la grieta. Para considerar el efecto de las sobrecargas sobre el umbral de propagación, son fundamentales dos factores: la relación de carga o magnitud de la sobrecarga y la frecuencia de carga a la que se realiza (la cantidad de ciclos por cada sobrecarga). Por ejemplo, un aumento en la relación de la sobrecarga a tensión muestra una mejora en ΔKth ; y el aumento en la frecuencia de una sobrecarga compresiva, es decir, el número de ciclos entre picos o sobrecargas es menor y la reducción del umbral de propagación es mayor 56.
Modo mixto de carga
En ingeniería es común encontrar aplicaciones con carga mixta, es decir, una combinación de cargas torsionales (modo III), de corte (modo II) y a tracción (modo I), estáticas y cíclicas. Conocer el umbral de propagación bajo el efecto de una carga mixta tendría enormes beneficios prácticos. El problema es que este es un fenómeno que resulta bastante complejo, ya que diferentes combinaciones de cargas superpuestas llegan a presentar comportamientos completamente diversos. Además, la medición del cierre de grieta para grietas en modo de corte es aún una tarea bastante compleja 5. Simplificando el comportamiento del modo mixto de carga. puede hacerse una estimación sencilla de la no propagación de grietas (válida para efectos prácticos de diseño, aunque no siempre con resultados satisfactorios) partiendo de la descripción del crecimiento de grieta bajo condiciones de carga mixta con un rango del factor de intensidad de tensiones equivalente ΔKeq. Así pues, Richard y Sander 57. por ejemplo, proponen que una grieta sujeta a una carga mixta bidimensional (I+II) se propagará si ΔKeq supera el umbral de propagación ΔKIth , de acuerdo con la ecuación (7):

Igualmente, una grieta sujeta a una carga mixta tridimensional (I + II + III) se propagara si ΔKeq supera el umbral de propagación ΔKIth, de acuerdo con la ecuación (8):

Se toma ΔKIth como límite en las anteriores ecuaciones, ya que generalmente ΔKIth es menor que ΔKIIth y ΔKIIIth siendo de esta manera la estimación más conservadora.
ΔKtheff módulo de Young y vector de Burger
Los mecanismos intrínsecos que gobiernan el comportamiento de ΔKthint (o de ΔKtheff aún no son totalmente entendidos. La estimación de este factor a través de diferentes modelos suele involucrar una gran cantidad de variables microestructurales y mecánicas que permiten buenas aproximaciones; cuantas más variables se utilicen, mayor precisión se obtiene. Sin embargo, varios de estos parámetros utilizados son difíciles de determinar, ya sea empírica o analíticamente, por lo que la aplicación de la mayoría de estos modelos es limitada. Lo que suelen tener en común los diferentes modelos es que muestran una relación proporcional al módulo de Young E, que ha permitido estimaciones más sencillas, involucrando sólo dos variables: E y el vector de Burger b, con los que se obtienen resultados razonables. Entonces, puede decirse que ΔKtheff depende principalmente de las propiedades elásticas, representadas por E, como una medición indirecta de la resistencia de las uniones metálicas; y de la red cristalina, caracterizada por b, que cuantifica la distorsión de esta. Hertzberg 58 observó que el vector de Burger era equivalente a la relación ΔKtheff /E)2, en varios sistemas de aleaciones metálicas, con lo que de una regresión lineal obtuvo la ecuación (9):

Relación válida para la mayoría de metales aleados. Para metales puros, introducir el factor 3/4 en la ecuación (9) permite que los resultados obtenidos concuerden satisfactoriamente con los experimentales.
El módulo de elasticidad E se encuentra relacionado con la fuerza de las uniones interatómicas del material y el crecimiento de grietas en sistemas metálicos implica la ruptura de estas uniones, convirtiéndose entonces en una posible explicación de la relación encontrada.
El crecimiento de grietas en materiales dúctiles es causado por el movimiento de dislocaciones (deformación plástica) en la punta de la grieta. El vector de Burger permite cuantificar la distorsión de la red cristalina, siendo este la magnitud de la distorsión mínima en la red debido a dislocaciones y. por tanto, el avance de grieta más pequeño posible.
Propiedades microestructurales
La microestructura influye en el componente extrínseco del umbral de propagación asociado a mecanismos de protección, principalmente los niveles del efecto del cierre de grieta. Existe una gran cantidad de parámetros microestructurales que pueden afectar al ΔKth, pero la mayoría puede asociarse con cambios en el grado de rugosidad de la superficie de fractura, y por lo tanto con el RICC. y en menor medida con la deflexión de la grieta. Tamaños de grano, límites y orientación de grano, inclusiones, proporción, distribución y morfología de una segunda fase, límites de fase y precipitados, entre otros, pueden causar la desviación y la ramificación de la grieta, que mejoran el modo de desplazamiento de corte (II), y de esta forma el RICC.
El efecto de la microestructura sobre el valor de AKthefy es por lo general mínimo. Se pueden considerar efectos como tortuosidad, desviación, acoplamiento o ramificación de las grietas.
Actualmente es un desafío encontrar la forma ideal de llevar a cabo cambios en las características microestructurales del material. y que estos resulten en un efecto positivo en la resistencia a la propagación de grietas. Esto debido a que estos cambios pueden resultar en efectos negativos sobre las propiedades mecánicas del material, o en cambios en otras características microestructurales que no permitan el efecto esperado. Encontrar el equilibrio o el punto óptimo es el objetivo de tratamientos térmicos o mecánicos llevados a cabo.
Ambiente
El efecto del ambiente es muy difícil de cuantificar debido a la gran variedad de mecanismos inducidos por el ambiente que pueden llegar a afectar a la fuerza conductora de la grieta. Se han propuesto numerosos mecanismos intentando explicar la influencia del ambiente en la propagación de grietas de fatiga. Sin embargo, en la zona umbral de propagación es posible considerar las contribuciones del ambiente sobre ΔKth a partir de la competición entre dos tipos de mecanismos de oxidación frecuentes, con efectos opuestos 59. El primer tipo es el de los mecanismos de cierre de la grieta ya conocidos, predominantemente el inducido por óxido en atmósferas gaseosas (en ambientes líquidos probablemente dominará el cierre inducido por fluido viscoso), que causan la desaceleración de la grieta y el aumento de ΔKth. El segundo tipo se refiere a procesos de corrosión por fatiga (la fragilización por hidrógeno como el más destacado), los cuales aceleran el crecimiento de las grietas y reducen el valor de ΔKth. Continúa siendo un gran reto establecer exactamente el efecto del ambiente sobre ΔKth ya que determinar la contribución o la presencia de los mecanismos mencionados depende de numerosos factores del ambiente como el tipo de ambiente, la humedad, la presión, la temperatura y la frecuencia, entre otros, aparte de otros no relacionados con el ambiente. Además, la influencia de un mecanismo puede contrarrestar la influencia de otro o incluso compensarlo.
Geometría y ancho de la muestra
Los efectos de la geometría y las dimensiones de la muestra aún no son completamente entendidos. Algunos han intentado explicar su influencia por medio de la relación entre el grosor de la muestra y el cierre de grieta. Romaniv et al. 60 explicaron el efecto del grosor de la muestra sobre el umbral de propagación a partir del efecto del estado tensión -deformación sobre el cierre de grieta. EI OICC aumenta con el incremento del grosor debido al aumento de las restricciones plásticas en la punta de la grieta, que proporcionan el comienzo de la formación de partículas corrosivas. En cambio, el PICC se reduce con el aumento del grosor debido a que un menor grosor promueve condiciones de tensión plana, condiciones ideales para que ocurra el PICC. De esta manera, en condiciones donde el PICC predomine, ΔKth decrece con el aumento del grosor de la grieta; mientras que con un OICC mayor el efecto será el inverso (figura 10).
Figura 10: Dependencia del grosor de la muestra sobre ΔKth. Basada en 61
En cuanto a la geometría de la muestra, se tiende a asumir que el valor de ΔKth es independiente de esta, aunque varios ensayos realizados con diferentes tipos de geometrías han mostrado resultados que presentan una gran dispersión. por lo que la tendencia no ha sido aún definida. Sin embargo, en estudios como 62. la relación de la geometría de la muestra con ΔKth se vincula con el nivel de restricción geométrica, cuantificado con la "tensión T" (parámetro que no suele ser con- siderado dentro de LEFM, pero que en la zona umbral su magnitud y signo pueden llegar a afectar el tamaño y la forma de la zona plástica). El nivel de restricción puede influir en la intensidad del cierre de grieta. Un bajo nivel de restricción está asociado a una menor triaxialidad de tensiones en la punta de la grieta, lo que produce tamaños de la zona plástica cerca a la punta de la grieta más grandes, y puede llevar a una mejor estabilización de la grieta en modo I durante su propagación. Esto puede conducir a que una geometría con un bajo nivel de restricción (T <0) alcance una menor rugosidad en la superficie de fractura, un menor RICC. y por lo tanto exhiba un ΔKth más bajo que una geometría con un alto nivel de restricción (T> 0).
Conclusiones
El umbral del rango del factor de intensidad de tensiones ΔKth es un parámetro importante, ya que está relacionado con el tiempo de vida de un componente mecánico, y muchos de estos están sometidos a valores de ΔK cercanos a dicho umbral.
En este trabajo se discutió acerca de los métodos existentes para la determinación de ΔKth. Se describieron los métodos experimentales (estándar ASTM E647-15e1 11), los cuales son los más aplicados, aunque pueden arrojar resultados inexactos. Por ejemplo, de acuerdo con Zerbst et al. 10, los métodos estándar para la determinación experimental de ΔKth arrojan resultados no conservativos en ciertos casos. También, se presentó el método de preagrietamiento a compresión, el cual puede producir resultados conservativos. Con respecto a los ensayos experimentales, debería ser un objetivo mejorar los métodos, las técnicas de ensayos y la tecnología para determinar ΔKth. Si bien se ha avanzado, aún existen dificultades en la aplicación de este parámetro en situaciones prácticas de ingeniería. Se describieron también modelos semi teóricos o numéricos. Se ha avanzado significativamente en los últimos años, obteniéndose resultados acordes con datos experimentales; sin embargo, se debe seguir avanzando en la investigación. para que estos modelos sean más universales.
En este artículo también se discutió sobre los factores que afectan a ΔKth. Es posible distinguir dos factores de ΔKth: un factor intrínseco ΔKthint ( ο ΔKtheff ). correspondiente a mecanismos que actúan en la punta de la grieta, y un factor extrínseco, en el que intervienen mecanismos en el ancho de la grieta. A partir de estos, y haciendo particular énfasis en los mecanismos de cierre de grieta, se analizó la forma en que los parámetros más influyentes como el tamaño de la grieta a, la relación de carga R, la microestructura y el ambiente afectan al valor de ΔK. Otros factores que inciden en el umbral son la geometría de la probeta o componente, las propiedades del material en escalas microscópicas y fenomenológicas, el historial de la carga (por ejemplo, carga de amplitud variable), las tensiones residuales y las cargas de modo mixto (10.
Los valores de ΔKth encontrados en la literatura presentan una dispersión significativa, atribuida principalmente al factor extrínseco. Esto trae problemas en el análisis de fatiga. ya que la estimación de vida de un componente responde de forma sensible a pequeñas variaciones de ΔKth. Una solución a la dispersión en los resultados es la de considerar la situación como libre de efectos extrínsecos como el cierre de grieta, tomando como umbral de propagación a ΔKtheff, cuyos valores pueden limitarse a un estrecho rango para una aleación determinada. Sin embargo, esto traería como consecuencia una estimación demasiado conservativa. Es de vital importancia lograr un entendimiento más profundo de los mecanismos que actúan en la etapa de propagación de grietas a fatiga en la región umbral, principalmente los extrínsecos, para la comprensión de ΔKth. También es importante encontrar una manera de reducir la dispersión en los resultados.
Por un lado, el cierre de grieta es el concepto más importante para comprender y racionalizar de manera uniforme el efecto de la mayoría de los parámetros que intervienen en el valor del umbral de propagación. Sin embargo, estudiar los efectos de cierre de grieta presenta muchas complejidades. Por ejemplo, separar cuantitativamente la contribución de cada uno de los mecanismos de cierre es una tarea difícil. Por lo tanto, modelar el umbral de propagación con base en el cierre de grieta es discutible. Por lo anterior, seguramente sea necesario, al menos, desarrollar una reinterpretación del fenómeno del cierre de grieta. A pesar de esto, la apuesta en los últimos años y en un futuro cercano para lograr una mayor comprensión del crecimiento de grietas en la región del umbral y una estimación más precisa del umbral de propagación parece seguir siendo el entender mejor el fenómeno del cierre de grieta y el lograr un método más exacto de medición, principalmente en la zona umbral, en donde se presentan mayores dificultades. Si bien el efecto de cierre de grieta es el mecanismo más importante, otros mecanismos como protección de zona, protección geométrica o fenómenos causados por el ambiente, como la fragilización por hidrógeno, también requieren una mejor comprensión.
Por otro lado, en algunas investigaciones (por ejemplo, 63,64) se ha cuestionado sobre los métodos basados en el cierre de grieta, ya que sobreestiman de manera sustancial el crecimiento de grietas cortas y afectan al umbral 17. Por esto, se ha formulado otro tipo de conceptos alternativos al cierre de grieta. Por ejemplo, Vasudevan et al. 21 sugirieron un modelo de propagación de grietas basado en ΔK y en ΔKmax, sin tener en cuenta el cierre de grieta. También, se han propuesto teorías como las aproximaciones multifractales y la de tensiones residuales en la punta de la grieta.
Recientemente, se han propuesto muchos métodos y teorías alternativas, fundamentadas tanto teórica como experimentalmente. Se resaltan la teoría UniGrow (parámetro Kapa) 22. 23 y la teoría de doble parámetro 21 (basada en ΔK y en ΔKmax). Muchos de los métodos desarrollados tienen una validez razonable bajo condiciones particulares. Sin embargo, hay que seguir avanzando para que los modelos, tanto analíticos como numéricos, sean cada vez más universales. También, se debe avanzar en el desarrollo de modelos de problemas con carga mixta (modo I, II y III), cargas estáticas y cíclicas, ya que hay aplicaciones reales con carga mixta. Sin embargo, este es un fenómeno complejo que representa mayores complejidades y retos.
Finalmente, se debe avanzar para que las estimaciones de ΔKth a partir de principios básicos consideren los diferentes factores, variables y complejidades del comportamiento en la zona umbral de propagación. Por ejemplo, se debe establecer con mayor exactitud el efecto del ambiente sobre ΔKth. ya que hay muchos mecanismos y variables asociados, tales como tipo de ambiente, humedad, presión y temperatura, entre otros, los cuales interactúan de manera compleja. Como opinan algunos, el umbral basado en LEFM puede no ser suficiente para predecir la no propagación de grietas en situaciones reales, en escenarios tan complejos como condiciones de amplitud de carga variable con patrones de carga impredecible, o en condiciones de carga mixta con combinaciones difíciles de precisar. Esto dificulta la generalización de la información obtenida en ensayos y la posibilidad de aplicarlos en problemas específicos reales de ingeniería. En una aplicación práctica, el valor de ΔKth dependerá de diferentes parámetros que se combinan de una manera compleja. siendo muy difícil distinguir el efecto de cada uno por separado. Así pues, los resultados obtenidos experimentalmente difícilmente pueden ser transferibles a aplicaciones reales.
References
License
Copyright (c) 2022 Kebin Alberto Medina Bernal, Libardo Vicente Vanegas Useche

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.








2.jpg)










