Ingeniería, 2004-00-00 vol:9 nro:1 pág:8-12

Métodos combinados para la estimación de parámetros en señales de espectroscopía de resonancia magnética

Héctor F. Cancino De Greiff
Miembro del Grupo de Investigación en DSP, U. Distrital Francisco José de Caldas
Víctor A. Nieto Ramírez
Ingeniero Electrónico, U. Distrital Francisco José de Caldas.

Resumen

En el presente trabajo se desarrollan algunos méto- dos de estimación de parámetros y de estimación espectral en señales de Espectroscopía de Resonancia Magnética (EMR) para un doble propósito: por una parte, posibilitar el procesamiento completo de la estimación de los parámetros constitutivos de la señal en el dominio del tiempo: amplitud, frecuencia, constante de decaimiento y fase, y en segundo lugar, generar la descripción de las propiedades de los métodos de estimación de parámetros en el dominio de la frecuencia, para valorar el efecto de la aplicación de los métodos de estimación en el dominio del tiempo. [2]

Se evalúan en consecuencia los diferentes métodos de predicción lineal tales como el de predicción hacia adelante, predicción lineal hacia atrás mediante la descomposición en valores singulares a través de la matriz de Vandermonde para el análisis de los parámetros amplitud y fase y luego a través de la matriz Toeplitz para obtener los factores de amortiguación y la frecuencia de cada una de las funciones que constituyen el FID (Free Induction Decay) de las señales de ERM. Estos valores comparados con los datos de partida, avalan los métodos empleados. Se analizan otros métodos tales como el de espacios de estado y diferentes métodos combinados mediante el desempeño en la estimación con el cálculo del error y la varianza empleando los métodos de Monte Carlo.

Palabras Claves:
Predicción lineal, métodos no iterativos, estimación espectral, señales de ERM, descomposición en Valores Singulares, métodos de Monte Carlo.

Abstract

In this work we develop some parameter and spectral estimation methods in Magnetic Resonance Spectroscopy Signals (MRS). We do this with a dual purpose: first, to enable the full estimation process for the constituent parameters of the time-domain signal: Amplitude, frequency, damping constant and phase. Second, to generate the parameter estimation in the frequency domain in order to evaluate the effect of the application of time domain estimation methods [2].

We evaluate different linear prediction methods such a forward prediction, backward prediction through singular values decomposition employing the Vandermonde matrix for the analysis of amplitude and phase parameters and trough Toeplitz matrix to obtain the damping factors and frequency of each function that constitute the FID (Free Induction Decay) of MRS. This values are compared to the initial data in order to validate our methods. Other methods such as state space and combined methods are also analyzed by means of their estimation performance and the computation of the error and variance using Monte Carlo methods.

I.INTRODUCCIÓN

El problema fundamental para la cuantificación de las señales de FID de ERM consiste en la solución de la matriz de datos formada a partir del vector de la señal. De la manera como se conforme esta matriz está determinado el sentido de la predicción y la estructura de la misma. Así, se pueden tener predicción lineal hacia adelante y hacia atrás con matrices de estructura Toeplitz o Hankel.[1, 2, 3, 5].

Para solucionar esta matriz de una manera no iterativa y eficiente se utiliza la descomposición en valores singulares SVD [12]. La SVD permite la adecuada inversión de la matriz de datos y posee características especiales para poder diferenciar entre los valores singulares de la señal y los que el ruido adiciona [12,13]

Al descomponer la matriz de datos obtenida a partir de los datos de una señal FID libre de ruido y con grado de predicción mayor al número de componentes de la señal en valores singulares, se obtienen un total de Np número de valores singulares, donde p es el grado de la predicción lineal con el que se conforma la matriz de datos y N el número de muestras, sin embargo sólo son diferentes de cero un número igual al de componentes exponenciales de la señal [6,7].

Al adicionar ruido a la señal todos los valores singulares en la SVD son diferentes de cero, no obstante, para relaciones señal a ruido no muy bajas es posible observar una discontinuidad en estos valores y determinar el número de componentes de la señal.Cuando la relación señal a ruido SNR de la señal FID es muy baja, esta discontinuidad no es nada clara, sin embargo por medio de un estudio del rango de la matriz de datos es posible determinar el número de exponenciales o componentes espectrales presentes.

II. MATERIALES Y MÉTODOS

Los métodos de predicción lineal empleados en este trabajo fueron:

1. Predicción Lineal hacia delante: Este programa tiene como parámetros de entrada un vector que contiene los valores del FID que se pretende cuantificar, un vector concerniente a la informa ción del muestreo de la señal, además, el número de componentes de la señal que han sido estimados y la relación señal a ruido con la que se desea trabajar [8,9].

2. Predicción lineal hacia atrás. Se utilizan las mismas variables y parámetros de entrada que para el programa anterior.

3. Predicción lineal hacia atrás con promediación de los valores singulares que consiste en comparar los valores singulares que pertenecen al ruido y que se encuentran en las últimas posiciones de la diagonal principal de la matriz S (de datos) y restarlos de los valores singulares de la señal.

4. Método de Espacios de estado. Este método aplica predicción lineal hacia atrás con estructura Hankel y no permite un grado de predicción lineal mayor al número de componentes exponenciales. Se utiliza el espacio de estado para realizar la cuantificación de la señal. El programa que realiza este procedimiento recibe como parámetros de entrada los datos de los métodos anteriores. Este procedimiento involucra el cálculo de los vectores singulares de la señal por SVD del FID en estructura Hankel y predicción lineal hacia atrás.

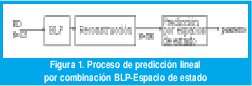
5. Método Combinado BLP - Espacio de estado. Utiliza la predicción lineal hacia atrás para efectuar una primera cuantificación de la señal y a partir de estos parámetros se reconstruye la señal con mayor número de muestras (en este caso 500). A la señal reconstruida se le aplica predicción lineal por espacio de estado, logrando cuantificar la señal estimada a partir de la reconstruida, ver figura 1.

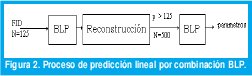
6. Método Combinado BLP: Este método, al igual que el anterior, utiliza la predicción lineal hacia atrás para efectuar una primera cuantificación de la señal y a partir de estos parámetros reconstruir el FID con mayor número de muestras (en este caso 500 muestras) con un grado de predicción p=63. A la señal reconstruida se le aplica otro proceso BLP con un grado mayor (p=252) logrando cuantificar la señal estimada a partir de la reconstruida. El proceso es ilustrado en la figura 2.

III. RESULTADOS Y DISCUSIÓN

Los experimentos consistieron en obtener mediante métodos de Monte Carlo para 100 repeticiones el valor medio y la varianza de los parámetros estimados. Estos experimentos se desarrollaron por los 6 métodos de predicción ya mencionados para SNR desde 5dB hasta 35dB en forma continuada. De igual forma, se realizó el gráfico del inverso de la varianza del error en logaritmo versus la SNR (dB) así como el error absoluto en porcentaje del valor promedio del parámetro estimado. Este procedimiento se llevó a cabo con el fin de observar el lugar donde ocurren los limites inferiores de Cramér Rao.

a.Análisis de desempeño en la estimación del parámetro frecuencia:

Se desarrolló un programa para la estimación del desempeño de los métodos de predicción lineal para el parámetro de frecuencia. En la figura 3 se muestran el error y la varianza máximos en el cálculo de dicho parámetro.

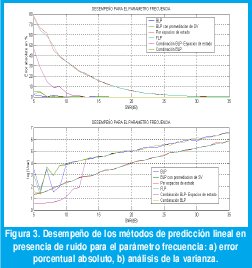
Un resumen del desempeño de los métodos de la estimación del parámetro frecuencia es mostrado en la Tabla 1. Todos los métodos presentan una desviación mayor a 0.01 Khz, en la SNR umbral (error > 10%).

Se puede establecer en consecuencia que el método más apropiado para el cálculo de este parámetro es el método combinado BLP con una SNR umbral de 8.5 dB presentando un error porcentual absoluto máximo de 4.65 %. El método BLP con promediación de valores singulares presenta una SNR umbral similar, con errores porcentuales un poco mayores.

b.Análisis del desempeño en la estimación del parámetro amortiguación α

Se desarrolló un programa para la estimación del desempeño de los métodos de predicción lineal para el parámetro amortiguación , a partir del cual se obtuvieron los resultados que aparecen en la figura 4, donde se muestran el error y varianza máximos para el cálculo de dicho parámetro del FID analizado.

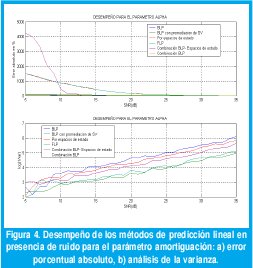
Un resumen del desempeño de los métodos de predicción lineal en la cuantificación del parámetro amortiguación es mostrado en la Tabla 2. Todos los métodos presentan una varianza mayor a 0.001 para sus respectivas SNR umbral o error menor al 10%.

En consecuencia se establece, que el método más apropiado para el cálculo de este parámetro es el método combinado BLP o combinado BLP- espacios de estado y que es recomendable que la SNR sea mayor a 15.82 dB. Todos los métodos presentan errores porcentuales absolutos grandes para SNR pequeñas y su desempeño en todos los métodos es menor que para el parámetro frecuencia. Los valores de a pequeños introducen los más grandes errores en la cuantificación.

c.Análisis de errores en la estimación del parámetro amplitud.

La estimación del desempeño de los métodos de predicción lineal para determinar el parámetro de amplitud se evaluó mediante un programa de computación, cuyos resultados se muestran en la figura 5, donde aparecen el error y la varianza máximos.

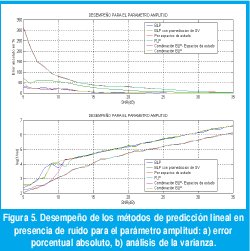
Un resumen del desempeño de los métodos de predicción lineal para amplitud se muestra en la tabla 3.

En este caso, los errores en todos los métodos, son inversamente proporcionales al valor del parámetro. En consecuencia se puede establecer que el método más apropiado para el cálculo de este parámetro es el combinado BLP y que la SNR del FID sea mayor a 12.65 dB. El desempeño de todos los métodos es mejor con respecto al del parámetro constante de decaimiento pero no mejor al de frecuencia. Los valores de amplitud pequeños introducen los errores más grandes en la cuantificación.

d.Análisis del desempeño en la estimación del parámetro fase

En la figura 6 se muestran el error y varianza máximos en el cálculo del parámetro fase del FID analizado, obtenidos a través de un programa de computación.

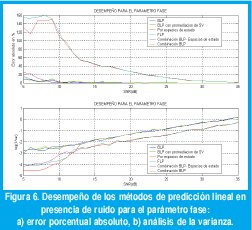
Un resumen del desempeño de los métodos de predicción para la estimación del parámetro fase es mostrado en la tabla 4.

e.Consideraciones finales sobre el efecto de la reducción de ruido en la extracción de parámetros.

De acuerdo con los resultados obtenidos, se deduce que no hay un solo método óptimo para la estimación de todos los parámetros de señales exponencialmente amortiguadas FID en medio de ruido. Sin embargo se aprecia que el método como predicción lineal hacia adelante prácticamente queda descartado frente al desempeño de los métodos basados en BLP.

IV. CONCLUSIONES

Los métodos de predicción lineal que permiten diferenciar entre los polos de la señal y los polos debidos al ruido presentan un mejor desempeño en la estimación de todos los parámetros del FID. El método de predicción lineal hacia delante queda descartado por presentar errores con índices de desviación elevados, su desempeño es muy similar al de predicción lineal por espacios de estado, por lo que estos métodos no son viables para su aplicación en señales de ERM.

Las técnicas basadas en BLP presentan un mejor desempeño frente a los demás procesos por permitir aumentar el grado de la predicción lineal a un número mayor al de componentes exponenciales de la señal FID. Para los métodos de predicción lineal basados en BLP el umbral de decisión, que permite diferenciar los polos de la señal de los demás polos producidos por el ruido, funciona adecuadamente para cualquier SNR siempre que el grado de la predicción sea mayor a N/3. El valor mínimo del grado de la predicción lineal que se debe aplicar para lograr un error mínimo debe estar entre N/3 y N/2, con tendencia más marcada hacia N/2.

El parámetro que menos es afectado por el ruido es la frecuencia y el más afectado es la constante de decaimiento, pues tiene que ver directamente con la envolvente de la señal. La amplitud aunque debería presentar la mayor afectación por el ruido, presenta una adecuada respuesta para los métodos basados en BLP con una SNR mayor a 12 dB.

El método de predicción lineal hacia adelante y el de espacios de estado presentan el menor tiempo computacional. Los métodos basados en BLP sin combinación presentan un tiempo mayor pero bajo con respecto a los combinados que requieren un tiempo elevado de procesamiento, especialmente el de combinación de BLP. La principal característica que incrementa el tiempo computacional del método de combinación de BLP es el aumento del grado de la predicción, pues este proceso trae implícitamente otro para encontrar los ceros de un polinomio de orden elevado.

Los parámetros que tienen un valor pequeño tienen más influencia del ruido y el éxito del método depende de la manera como se estimen estos valores. Los valores próximos presentan mayores errores al ser elucidados e inciden fuertemente en el éxito del método de predicción.

No existe un solo método óptimo para la estimación de parámetros de señales exponencialmente amortiguadas FID en medio de ruido. Considerando que los SNR umbrales permiten establecer un criterio apropiado para la escogencia del método se puede establecer que para señales FID inmersas en ruido el método óptimo para la predicción del parámetro frecuencia es el método de combinación de BLP; para la constante de decaimiento el método de combinación BLP Espacios de estado o combinación BLP; para la amplitud el método combinado BLP y finalmente para el parámetro fase el método de combinación BLP o BLP con promediación de valores singulares.

Si el análisis se realiza de manera global, sin tener en cuenta los parámetros individualmente el mejor método de predicción lineal es el de combinación de BLP para un FID con una SNR mayor a 22 dB.

REFERENCIAS BIBLIOGRÁFICAS

[1] Kumaresan & Tufts. "Estimating the Parameters of Exponentially Damped Sinusoids and Pole-Zero Modeling in Noise". IEEE. Transactions on acoustic, speech, and signal processing, vol. Assp-30. Nº 6, December 1982. pp 833-840.

[2] De Beer R. "c59 Quantitative In Vivo NMR." University of Technology Delft Department of Applied Physics, August 3, 1994. Lecture Notes, Available in Internet, http://dutnsic.tn.tudelft.nl:8080/pif_beer.html.

[3] Department of Structural Biology, Fairchild Building, Stanford, CA 94305, USA "Linear Prediction spectral analysis of NMR data," Progress In Nuclear Magnetic Resonance Spectroscopy. Nov. 1998.

[4] John G. Proakis y Dimitris G. Manolakis "Tratamiento digital de señales" Prentice Hall 1998. pp 939-941.

[5] Y. Hua y T. K. Sarkar. "Matrix pencil method for estimating parameters of exponentially damped undamped sinusoids in noise," IEEE Transactions on Acoustic, Speech, And Signal Processing mayo de 1990.

[6] D. W. Tufts. "Improved spectral resolution III: efficient," Proceeding of IEEE. October 1980.

[7] Caspary O., Tomczak M., Staiquily P. "DSP-Based AR spectral estimation with zoom effect for NMR spectroscopy" Centre de Recherche en Automatique de Nancy -CNRS URA 821. Université de Nancy I, 54506 Vandooeuvre Cedex IEEE 1993.

[8] Diop A., Briguet A. and Graveron-Demilly D., «Automatic In Vivo NMR Data Processing Based on an Enhancement Procedure and Linear Prediction Method», Magn. Reson. in Medicine, 27 (1992) pp. 318-328.

[9] Koeh P., "Linear Prediction Spectral Analysis of NMR data Elsevier Science" B.V Received 10 de November de 1998 pp 1-43.

[10] Li Y., Ray Liu K.J., Razavilar J., "A Parameter Estimation Scheme for Damped Sinusoidal Signals Based on Low-Rank Hankel Approximation", Electrical Engineering Department and Institute for Systems Research, University of Maryland at College Park .September 26, 1998.

[11] Li Y., Ray Liu K.J., Razavilar J., "Improved Parameter Estimation Schemes for Damped Sinusoidal Signals", Electrical Engineering Department and Institute for Systems Research, University of Maryland at College Park .1999.

[12] Naugler D., Cushley R. "Spectral Estimation of NMR Relaxation" Journal of Magnetic Resonance". Vol 145, N° 2, August 2000. pp 209-215.

[13] Vanhamme Leentje, "Improved Method for Accurate and Efficient Quantification of MRS Data With Use Prior Knowledge", Journal of Magnetic Resonance, vol 129 Article No NM971244 January 1997 a Julio 1997 pp 35-43.

[14] Vanhamme Leentje, "Time Domain Quantification of Series of Biomedical Magnetic Resonance Spectroscopy Signals", Journal of Magnetic Resonance, vol 140, No 1 September 1999 pp 120-130.

Héctor F. Cancino De Greiff
Ingeniero Electrónico de la Universidad Distrital "Francisco José de Caldas" , UDFJC, Bogotá, Colombia. MSc. de la Universidad Central de Venezuela UCV, Caracas. PhD en Ciencias Técnicas con la Universidad Central de las Villas UCLV, Cuba. Profesor asociado de la UDFJC. Participante en varios proyectos de investigación en el campo de DSP.

Víctor A. Nieto Ramírez
Ingeniero Electrónico de la Universidad Distrital "Francisco José de Caldas" , UDFJC, Bogotá, Colombia. Presidente de la Rama estudiantil del IEEE de la Universidad Distrital en el 2002. Nombrado Presidente distinguido de Colombia por la sección del IEEE en el mismo año.