Ingeniería, 2004-00-00 vol:9 nro:1 pág:17-25

Desarrollo Hardware de un Procesador Difuso Tipo Dos

Miguel A. Melgarejo Rey
Investigador Adjunto Laboratorio de Automática, Microelectrónica e Inteligencia Computacional, Universidad Distrital.
Carlos A. Peña Reyes
Senior Reseacher, Laboratoire de Systemes Logiques, EPFL.

Resumen

Este artículo presente una propuesta arquitectural para un sistema difuso tipo dos de intervalo basado en hardware. En primer lugar, se describe un modelo computacional, el cual considera una organización paralela del proceso de inferencia difusa. A partir de este modelo, se concibe una arquitectura hardware con varias etapas pipeline para la ejecución paralela de las inferencias. difusas tipo dos. La arquitectura se emplea para especificar un procesador difuso tipo dos, el cual se implementa sobre tecnología FPGA. Los resultados muestran que este procesador puede ejecutar más de 30 millones de inferencias difusas tipo dos por segundo. Como contexto de aplicación, el procesador se emplea para la realización hardware de dos filtros difusos adaptativos.

Abstract

This paper presents an architectural proposal for a hardware-based interval type-2 fuzzy inference system. First, it presents a computational model which considers parallel inference processing. Taking into account this model, we conceived a hardware architecture with several pipeline stages for full parallel execution of type-2 fuzzy inference. The architectural proposal is used for specifying a type-2 fuzzy processor, which is implemented over FPGA technology. Implementation results show this processor performs more than 30 millions of type-2 fuzzy inferences per second. As target application, it is used to implement two fuzzy adaptive filters.

I. INTRODUCCIÓN

La lógica difusa tipo dos es un campo de investigación emergente. Se ha mostrado que los sistemas difusos tipo dos son capaces de tratar con fuentes de incertidumbre tales como: múltiple significado de las etiquetas lingüísticas, información de entrenamiento ruidosa y medidas contaminadas por ruido [10, 23, 24]. De hecho, la lógica difusa tipo dos es una mejor opción que la lógica difusa tradicional (tipo uno) para tratar fenómenos cuya naturaleza es no lineal y estocástica al mismo tiempo [10, 13].

Varias aplicaciones que utilizan sistemas difusos tipo dos han sido presentadas recientemente [1316,30,21,22]. Algunas de ellas necesitan de altas velocidades de procesamiento para operar en tiempo real. Además, estas mismas aplicaciones son prometedoras en el contexto de los sistemas móviles. Lo anterior hace que la implementación en hardware dedicado de sistemas difusos tipo dos sea conveniente.

Según la revisión de estado de arte del presente trabajo, a la fecha no hay realizaciones hardware de sistemas difusos tipo dos. Un modelo computacional y una arquitectura hardware básica para un sistema difuso tipo dos de intervalo (IT2FLS) se han propuesto en un trabajo anterior de los autores[20]. Dicha arquitectura incluye las secciones típicas de un IT2-FLS: fusificación, motor de inferencia, reducción de tipo y defusificación. Las dos ultimas etapas se basan en el cálculo de conjuntos frontera, o las llamadas formas cerradas de Wu y Mendel [31].

En este artículo se presenta la generalización de esta arquitectura, se describe su realización sobre tecnología FPGA (Field Programmable Gate Array). Varios aspectos metodológicos de la implementación hardware de sistemas difusos tipo uno se revisaron al momento de concebir las etapas de fusificación y motor de inferencia. Para la reducción de tipo, se propone emplear Aritmética.

Distribuida (AD). Con el fin de garantizar un buen desempeño en velocidad de la implementación final y dada la naturaleza paralela de los sistemas difusos tipo dos, se consideró una organización hardware paralela con pipeline para la arquitectura.

Teniendo en cuenta la propuesta arquitectural y una revisión de aplicaciones, se diseño un procesador difuso tipo dos. Este se limitó a dos entradas, una salida, un máximo de ocho conjuntos difusos tipo dos por entrada y nueve conjuntos singleton tipo dos a la salida. El procesador se implementó sobre una FPGA de ultima generación. Algunas características de esta tecnología se explotaron con el fin de garantizar un bueno desempeño en área y velocidad. Esta implementación se confrontó con una solución software en términos de velocidad de procesamiento versus complejidad computacional.

El artículo se organiza de la siguiente forma: La sección dos introduce los conjuntos difusos tipo dos de intervalo. En la sección tres, se describe el proceso de inferencia en un IT2FLS y se considera un modelo computacional de este proceso. Luego, en la sección cuatro, teniendo en cuenta el modelo computacional, se propone una arquitectura hardware general. Los resultados de implementación del procesador difuso tipo dos se exponen en la sección cinco. Finalmente, se concluye y se comenta el trabajo a futuro en la sección seis.

II. CONJUNTOS DIFUSOS TIPO DOS DE INTERVALO

La lógica difusa tipo dos se considera en este momento como una extensión de la lógica difusa tradicional. La transición de lógica difusa tipo uno a tipo dos se documenta en [10,13,31].

2.1 Conjuntos difusos tipo dos

Un conjunto difuso tipo uno es el conjunto difuso tradicional que se describe en la literatura [33,27,23], el cual se representa por medio de una función de pertenencia tipo uno. Un ejemplo se muestra en la Figura 1(a), donde la función de pertenencia es Gaussiana.

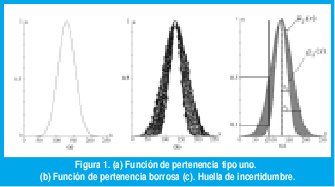
Considere hacer borrosa la función de pertenencia tipo uno de la Figura 1(a). Por ejemplo, mueva los puntos de la curva tanto a la derecha como a la izquierda, pero no necesariamente en la misma proporción, tal como se muestra en la Figura 1(b). Esta situación se puede presentar cuando varios expertos definen la misma etiqueta lingüística, o cuando un solo experto trata de definir una función de pertenencia tipo uno bajo condiciones ruidosas.

Note que la función de pertenencia borrosa podría capturarse y limitarse por dos fronteras, tal como se presenta en la Figura 1(c). Obsérvese también, que en cada valor puntual x' de x, no hay un solo valor de pertenencia, en lugar de ello, hay toda una colección de valores, tantos como la línea vertical toca entre las dos fronteras. Es posible asignar una distribución de amplitud para toda esa colección de puntos. El propósito de la distribución es medir el grado de confianza que se tiene para cada posible valor de pertenencia en x'. Haciendo esta asignación para todo x, se obtiene una figura tridimensional, a la cual se le denomina función de pertenencia tipo dos y representa un conjunto difuso tipo dos A [23].

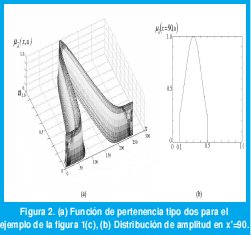
Una posible función de pertenencia tipo dos para el ejemplo de la figura 1(c), y una muestra de su distribución de amplitud en x=90 se presentan en la Figura 2. A la distribución de amplitud para cada punto x=x' se le llama un corte vertical o función de pertenencia secundaria [10,23]. El dominio de una función de pertenencia secundaria se denomina pertenencia primaria. En la Figura 2(b), la pertenencia primaria en x'=90 es el intervalo [0.1,0.5].

2.2 Conjuntos difusos tipo dos de intervalo y su representación

Note que cada función de pertenencia secundaria es un conjunto difuso tipo uno, en ese sentido, un conjunto difuso tipo dos puede verse como una colección de conjuntos difusos tipo uno. Cuando to- das las funciones de pertenencia secundarias son conjuntos difusos tipo uno de intervalo (i.e., todos sus valores en el dominio tienen grado de pertenencia igual a uno), el conjunto difuso tipo dos correspondiente se denomina conjunto difuso tipo dos de intervalo. Las funciones de pertenencia secundarias de intervalo reflejan que la incertidumbre asociada a las pertenencias primarias es uniforme, es decir, que se tiene el mismo grado de confianza para todos los posibles valores de pertenencia.

Como todos los grados de pertenencia secundarios son iguales a uno para los conjuntos difusos tipo dos de intervalo, su incertidumbre puede reflejarse fácilmente por medio de una Huella (FOU) [5]. Un ejemplo de una FOU Gaussiana se muestra en la Figura 1 (c).En este caso la FOU se construye dejando fijo el valor medio de una función de pertenencia tipo uno Gaussiana y variando su desviación estándar entre [σ₁,σ₂].

Note que una FOU es la unión de todas las pertenencias primarias, además que está limitada por dos funciones de pertenencia tipo uno: una función de pertenencia superior (UMF), la cual se nota como µ_i (x), y otra inferior (LMF) con notación µ_i (x).

III. PROCESO DE INFERENCIA Y MODELO COMPUTACIONAL

Un sistema difuso es tipo dos cuando al menos uno de los conjuntos del antecedente o del consecuente es un conjunto difuso tipo dos [13]. Un sistema difuso tipo dos de intervalo es un sistema basado en reglas, en el cual, se usan conjuntos tipo dos de intervalo para describir las variables lingüísticas.

El diagrama de bloques de un IT2FLS se muestra en la Figura 3. Dos grandes secciones se identifican: La sección lógica que está conformada por el fusificador y el motor de inferencia, y la sección de procesamiento de salida que contiene al reductor de tipo y al defusificador.

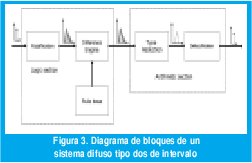
El desempeño de una implementación hardware de un algoritmo depende en gran medida del modelo computacional que se escoja [1]. Teniendo en cuenta la estructura mostrada en la Figura 3, se considera un modelo de ejecución que consta de las siguientes tareas: (1) Adquisición de las entradas puntuales y fusisicación sigleton tipo dos, (2) Cálculo de las operaciones en los antecedentes y consecuentes, (3) Reducción de tipo y (4) Defusificación.

A continuación se hará una breve revisión del proceso de inferencia en un IT2FLS, la cual será de utilidad en la definición del modelo computacional. El modelo se describirá paralelamente a la exposición del proceso de inferencia.

3.1 Fusificación singleton en sistemas difusos tipo dos de intervalo.

La primera operación que se lleva a cabo en la sección lógica es la fusificación, la cual se encarga de mapear un valor puntual en un conjunto difuso tipo dos [13,23,5].

La fusificación singleton es el método computacionalmente más sencillo. Esta fusificación asigna dos valores de pertenencia a cada punto del universo discurso. Un valor se obtiene de µ_i (x) , y se denomina valor de pertenencia superior. El otro se obtiene de µ_i(x), y se le llama valor de pertenencia inferior.

En cuanto al modelo computacional se refiere, tanto la adquisición de varias entradas así como su fusiciación singleton tipo dos se llevan a cabo en paralelo. Nótese que la adquisición de una entrada es independiente de las otras, por lo tanto todas se pueden adquirir y fusificar simultáneamente.

3.2 Motor de inferencia (operaciones en el antecedente y el consecuente)

Esta etapa opera según una base de reglas. Tanto esta base como la estructura de las reglas no depende de la naturaleza de los conjuntos difusos. Luego, la representación de las reglas en un sistema difuso tipo dos es igual que en un sistema tipo uno [23]. El motor de inferencia se encarga de combinar y calcular las reglas para obtener un mapeo de los conjuntos difusos del antecedente en los conjuntos del consecuente.

Al igual que en sistemas tipo uno, existen diversas opciones para ejecutar las operaciones del antecedente y del consecuente de un sistema tipo dos [27,10,23]. Con el fin de ilustrar nuestra elección, se presenta el siguiente ejemplo. Considere la regla que se muestra en la Figura 4, la cual corresponde a un IT2FLS con dos entradas y una salida. El proceso de inferencia se ejecuta como sigue:

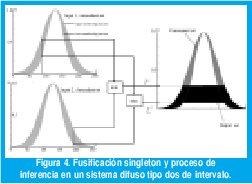
1. Se obtienen los valores de pertenencia inferiores y superiores de los conjuntos del antecedente.

2. Se calcula un AND lógico entre los valores de pertenencia superiores con el fin de obtener el valor de activación superior fⁱ. En este ejemplo, se usa una t-norma mínimo.

3. Se calcula un AND lógico entre los valores de pertenencia inferiores para obtener el valor de activación inferior fⁱ. Aquí se emplea la misma t-norma del numeral dos.

4. Se calcula una t-norma entre la función de pertenencia superior del conjunto consecuente respectivo y el valor de activación superior. En este caso la t-norma empleada es de tipo mínimo.

5. La operación del numeral cuatro se ejecuta para la función de pertenencia inferior del conjunto consecuente y el valor de activación inferior.

Note que en una inferencia tipo dos, la incertidumbre se propaga desde la entrada hacia la salida como el intervalo de activación [fⁱ, fⁱ].

En el modelo computacional que se está definiendo, las operaciones del antecedente y del consecuente se calculan separadamente por cada regla de la base. De nuevo, un calculo basado en hardware puede explotar paralelismo. Varias reglas activas se pueden procesar simultáneamente y sus intervalos de activación obtenerse a través del computo paralelo de las t-normas respectivas.

3.3 Reducción de tipo y defusificación

La reducción de tipo se obtiene al aplicar el principio de extensión de Zadeh[33] a la defusificación. En términos generales, la reducción de tipo representa un mapeo de un conjunto difuso tipo dos en un conjunto difuso tipo uno [10,23,31]. En este sentido, si la defusificación trata de ubicar el mejor punto que representa a todo un conjunto difuso tipo uno, la reducción de tipo trata de establecer el mejor conjunto difuso tipo uno que representa a un conjunto tipo dos. Es posible proponer un reductor de tipo equivalente por cada método de defusifcación [10].

El resultado de la reducción de tipo de un conjunto difuso tipo dos de intervalo es un conjunto difuso tipo uno de intervalo [13,30], por tanto, la reducción de tipo como procedimiento computacional, conSiste en calcular un intervalo. Con el fin de revisar este concepto, se presenta en la figura 5, un ejemplo tanto de defusificación como reducción de tipo altura. Note que en la misma for ma como la defusificación altura aproxima el centroide de un conjunto difuso tipo uno, la reducción de tipo altura de un conjunto difuso tipo dos de intervalo, trata de encontrar un centroide generalizado, el cual consiste en un intervalo limitado por los puntos [y_l,y_r] [23].

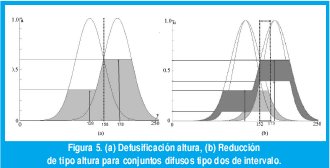
La reducción de tipo de un conjunto difuso tipo dos general es computacionalmente costosa. Dos procedimientos se han propuesto para calcular la reducción de tipo de conjuntos difusos tipo dos de intervalo: el procedimiento iterativo de Karnick y Mendel [10] y las formas cerradas de Wu y Mendel [30,31].

A través del primer método, se calcula exactamente la reducción de tipo, pero dada su naturaleza iterativa es computacionalmente costo. Razón por la cual, no es apropiado para una implementación hardware. El segundo método hace una estimación de la reducción de tipo. Para ello, obtiene dos conjuntos frontera que limitan al conjunto difuso tipo uno que se obtendría de calcular exactamente la reducción de tipo. Este procedimiento hace uso de expresiones cerradas, motivo por el cual se incluyó en el modelo computacional.

Los conjuntos frontera se usan para estimar la incertidumbre en la salida de un IT2FLS. Igualmente, estos conjuntos son una alternativa para calcular directamente la defusificación.

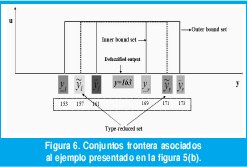
La Figura 6 muestra los conjuntos frontera interior y exterior del ejemplo de reducción de tipo considerado en la Figura 5(b). El centroide generalizado es un intervalo cuyos limites son y_l e y_r. Debido a la incertidumbre, y_r e y_l pueden caer en los intervalos [y_r, y_r] e [y_l, y_l] respectivamente. En ese orden de ideas, dos conjuntos difusos tipo uno de intervalo podrían definirse: El conjunto frontera interior [y_r, y_r] y el conjunto frontera exterior [y_l , y_r]. Tanto y_l como y_r se estiman de los conjuntos frontera de la siguiente manera:

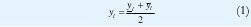
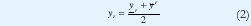
El valor puntual de salida se obtiene del promedio de y_l e y_r, lo cual es simplemente la defusificación de un conjunto difuso tipo uno de intervalo.

Teniendo en cuenta el hecho que un IT2FLS es una colección de sistemas difusos tipo uno interiores [23,31], es posible obtener y_l e y_r calculando cuatro de tales sistemas, los cuales reciben el nombre de sistemas difusos tipo uno frontera:

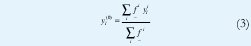
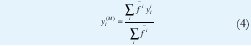
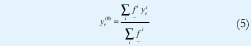
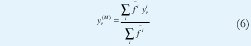
donde yⁱ_l e y r son los puntos que definen el i centroide generalizado del i-esimo conjunto difuso tipo dos de intervalo del consecuente e i=1...M. Estos sistemas difusos son fronteras, en el sentido que tan solo usan las LMFs (o UMFs) de los conjuntos del antecedente junto con los puntos extremos de los centroides generalizados de los conjuntos del consecuente.

El conjunto frontera interior se obtiene de (3)-(6) como:

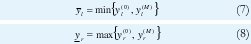
mientras que el conjunto frontera exterior se calcula como sigue:

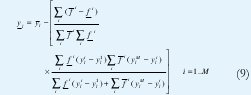
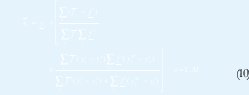
En el modelo computacional se considera la reducción de tipo altura dado que el calculo de los conjuntos frontera se simplifica. En la reducción de tipo altura, yⁱ_l e yⁱ_r son el mismo punto yⁱ en el dominio del i-esimo conjunto del consecuente [31]. Usualmente yi es el punto con el máximo valor de pertenencia en la UMF del conjunto. Note que cuando se calcula la reducción de tipo altura por medio de (3)- (10), y_l⁽⁰⁾ es igual a y_r⁽⁰⁾ e y_l^(M) a y_r^(M) , luego, el numero de sistemas frontera se reduce de cuatro a dos.

Si se tiene presente en la reducción de tipo altura que yⁱ_l= y^l_r= yi, y si se considera. que los coeficientes de las combinaciones lineales en (3)-(6) son los términos yⁱ, y en (9)-(10), son los términos y^M-yⁱ e yⁱ-y¹, algunas de estas combinaciones comparten coeficientes. Esta observación debe tenerse en cuenta con el fin de reducir la cantidad de recursos físicos que demandaría una implementación hardware.

Aunque dos estructuras dedicadas serían necesarias para calcular y_l and y_r, estas podrían compartir recursos hardware teniendo en cuenta la similitud de las expresiones (3)-(10) en el caso de la reducción de tipo altura.

IV. ARQUITECTURA HARDWARE

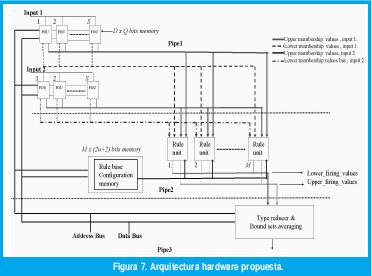
En la Figura 7 se presenta la arquitectura propuesta para implementación sobre hardware digital de un IT2FLS. Según la revisión de aplicaciones, en particular, ecualización de canales no lineales y variantes en el tiempo [15], Control de calidad de sistemas de sonido [21] y control adaptativo de plantas no lineales [22], arquitectura se especificó para tener dos entradas y una salida. Teniendo presente el modelo computacional definido en la sección anterior, la arquitectura se organizó como una secuencia de tres etapas pipeline.

La primera etapa está conformada por 2S unidades de fusisicación (S conjuntos difusos tipo dos por entrada). En la segunda etapa se encuentra un arreglo de M unidades de inferencia, las cuales se encargan de evaluar paralelamente la base de reglas del sistema. La ultima etapa calcula la reducción de tipo altura por medio de una reorganización de las formas cerradas de Wu y Mendel. Se considera un máximo de M conjuntos difusos tipo dos singleton a la salida, por lo tanto la arquitectura se limita a sistemas difusos tipo dos de base completa.

A continuación se presentan los aspectos metodológicos tenidos en cuenta en la concepción de cada una de las etapas de la arquitectura.

4.1 Unidades de fusificación.

La fusificación basada en memoria es el método más usado en procesadores difusos tipo uno [12,1,2]. Este método permite implementar cualquier función de pertenencia y ofrece tiempos de computo bajos, siendo entonces, apropiado para procesamiento difuso de alta velocidad. Sin embargo, el tamaño de las memorias crece exponencialmente con la resolución.

Otra estrategia es el uso de generadores aritméticos. Estos circuitos son estructuralmente simples, pero se limitan generalmente al computo de funciones de pertenencia trapezoidales [2,7]. Este aspecto puede reducir el campo de aplicación de la implementación final.

Otras aproximaciones aritméticas menos usadas implementan funciones de pertenencia Gaussianas [4]. Teniendo en mente una arquitectura de propósito gneral, sería necesario combinar tanto generadores aritméticos trapezoidales como Gaussianos. Sin embargo, esta estrategia demandaría una considerable cantidad de recursos hardware en un procesador difuso tipo dos paralelo.

Se escogió un esquema de búsqueda por tabla basado en memoria para llevar a cabo la fusificación, dado que se puede lograr un balance apropiado entre precisión y complejidad [12]. Igualmente hay algunas razones de orden tecnológico que motivaron esta escogencia, tal como se verá en la sección cinco. Se propone aquí emplear una sola memoria (marcada como FOU en la figura 7) para llevar a cabo todo el proceso de fusificación singleton en un conjunto tipo dos. Cada conjunto se representa por medio de sus funciones de pertenencia superior e inferior.

La Figura 8 muestra la propuesta de unidad de fusificación. Suponga que el ancho de la memoria es Q bits, por facilidad Q debería ser un múltiplo de dos. La función de pertenencia inferior se almacena en los Q/2 bits menos significativos, mientras que la función de pertenencia superior se almacena en los Q/2 bits más significativos.

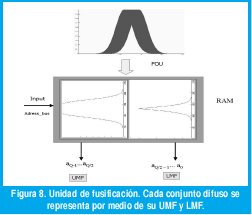
Las entradas se almacenan en dos registros. El ancho W de estos registros depende del tamaño de memoria D que se elija, donde W=log₂(D). Cada entrada se fusifica al momento de direccionar las memorias de sus unidades de fusificación asociadas. El direccionamiento se lleva a cabo con el valor de salida del registro correspondiente. Note que la fusificación para ambas entradas se ejecuta en paralelo sobre todos los conjuntos del antecedente.

4.2 Unidades de inferencia (rule units)

Las unidades de inferencia se encargan de calcular cada una de las reglas del sistema. Para este efecto, ellas emplean t-normas mínimo. La t-norma mínimo es la más empleada en la realización de procesadores difusos tipo uno, dado que es una mejor opción que la t-norma producto para efectos de una implementación hardware [4,1,2,8]. De hecho, el operador mínimo es estructuralmente más simple que un multiplicador (t-norma producto), lo cual se ve reflejado en que demanda menor cantidad de recursos físicos para su implementación. Otra ventaja del operador mínimo, es el hecho de introducir un menor retardo en la ruta critica de la implementación final, lo cual se traduce como un mejor desempeño en velocidad de procesamiento.

Una unidad de inferencia, como la mostrada en la Figura 9(a), calcula un intervalo de activación. Esta unidad consiste en dos estructuras idénticas: Si1 para calcular fⁱ y Si₂ para fⁱ. Cada estructura tiene dos multiplexores MQⁱ11 y MQⁱ₂₁ un operador mínimo. Los multiplexores y seleccionan respectivamente la función de pertenencia inferior y superior del conjunto antecedente asociado a la entrada uno y la iesima regla del sistema, mientras que los multiplexores MQⁱ₁₂ y MQⁱ₂₂ hacen lo mismo para la entrada numero dos El operador mínimo MU₁ⁱ calcula el mínimo entre las salidas de los multiplexores MQⁱ_u y MQⁱ₁₂, valor que corresponde a fⁱ. El operador mínimo MUⁱ₂ calcula f_i de las salidas de los multiplexores MQⁱ21 y MQⁱ22 .

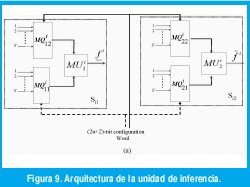
4.3 Memoria para la configuración de la base de reglas

La configuración de cada una de las unidades de inferencia se almacena en esta memoria. (Figura 7, rule base configuration memory). La configuración de cada regla consiste en establecer los valores de selección de los multiplexores MQⁱ. En cada unidad de inferencia, aquellos multiplexores que se encuentran asociados a la misma entrada, tienen el mismo valor de configuración.

Cada valor de configuración tiene un tamaño de u bits, el cual depende del máximo numero de conjuntos por entrada S, siendo u=Log₂(S). Luego, una palabra de 2u bits bastaría para configurar una regla. Dos bits adicionales se agregan para habilitar los multiplexores, definiéndose de esta forma la activación de la unidad de inferencia. Note que el mecanismo de bits de activación permite configurar bases que contengan desde una hasta M reglas.

Según las consideraciones anteriores, el tamaño de memoria para almacenar la base de reglas sería de M × (2u + 2) bits, donde M es el máximo numero de reglas que se va a manejar. Además, en cuanto a organización hardware se refiere, esta memoria debe tener una salida por cada valor de configuración.

4.4 Reducción de tipo y promedio de los conjuntos frontera

La concepción hardware de la reducción de tipo altura es quizás el punto más importante de la propuesta arquitectural que se está presentando.

El computo de la reducción de tipo se encuentra dividido en siete secciones pipeline, tal como se muestra en la Figura 10. La primera sección consta de cinco bloques, tres de los cuales calculan las combinaciones lineales de las formas cerradas WuMendel y los dos restantes calculan las sumatorias de los valores de activación superiores e inferiores. La forma con se organizan las combinaciones lineales se presenta en la Tabla I.

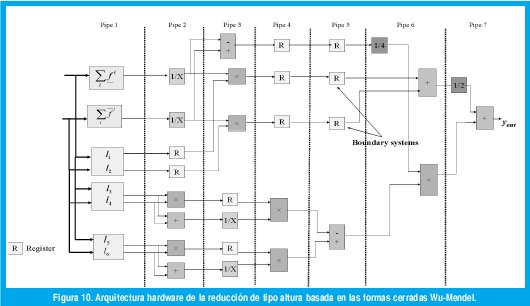
Las siguientes secciones completan el calculo de las formas cerradas. Los sistemas frontera al igual que parte de los términos a la derecha de (9) y (10) se obtienen entre las secciones Pipe 2 y Pipe 5 (ver Figura 10). Todos los componentes involucrados tienen una latencia de un ciclo de reloj y las operaciones se llevan a cabo usando aritmética de punto fijo. Usar este tipo de aritmética hace necesario introducir escalamiento entero tanto para las divisiones como para las multiplicaciones [3].

De la Figura 10 se puede observar que las formas cerradas se han reorganizado. Esto se hizo con el fin de ahorrar recursos hardware en la implementación final. Por ejemplo, en lugar de calcular rt= ∑(fⁱ-fⁱ)/∑fⁱ ∑ fⁱ, se propone iobtener independientemente los términos ri=1 f y rs= 1 f i (Pipe 2) para luego restarlos (Pipe 3). Note que ri-rs es equivalente a rt, Además que rs y ri también se emplean para calcular los sistemas frontera, por lo tanto, su computo independiente ahorra un multiplicador y un divisor.

El promedio de los conjuntos frontera, que se necesita para calcular el valor de salida (defusificación), se lleva a cabo en las etapas Pipe 6 y Pipe 7. Note que un calculo explicito de (1) y (2) no se realiza. De las expresiones (9) y (10) se observa que y_l e y_r dependen respectivamente de y_l e y_r . Por lo tanto, si se reemplaza (9) en (1) y (10) en (2), se promedia y_lⁱ e y_r y se hace yⁱ_l = y_rⁱ= yⁱ (Reducción de tipo altura), la salida defusificada puede obtenerse como sigue:

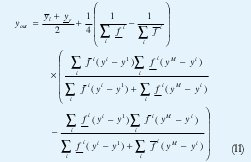
Una implementación hardware explicita de las formas cerradas para calcular la salida del sistema, demandaría cinco sumadores y dos multiplicadores (aparte de los que se usarían en las combinaciones lineales). Con la reorganización propuesta en (11), se emplea tan solo un multiplicador (Pipe 6) y tres sumadores (Pipe 3,6,7) para el mismo propósito.

Note que los puntos extremos del conjunto frontera interior ( y_l e y_r). se suman en (11), por lo tanto identificar la magnitud relativa entre ellos (ecuaciones (7) y (8) ), no tiene ninguna incidencia en el calculo de la salida del sistema.

V. IMPLEMENTACIÓN

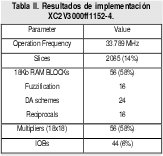
En esta sección se describe la implementación FPGA de un procesador difuso tipo dos basado en nuestra propuesta arquitectural. Las características de este procesador se resumen en la tabla II.

5.1 Materiales y herramientas de implementación

El procesador se especificó usando el lenguaje de descripción de hardware VHDL (Very high speed integrated circuit Hardware Description Language). La especificación se sintetizó, simulo e implementó respectivamente por medio de las herramientas Leonardo Spectrum®, Modelsim® de Mentor, Graphics© y Foundation ISE 5.1® de Xilinx©. Tanto los multiplicadores como bloques de RAM de doble puerto se obtuvieron de la herramienta Xilinx Core Generator.

5.2 Resultados de implementación

Algunas figuras de desempeño de la implementación final, refereidas a la FPGA Xilinx Virtex II XC2V3000ff1152-4 [32], se muestran en la tabla II. Se pueden hacer las siguientes observaciones a partir de los datos condensados en esta tabla:

1. Debido a la organización paralela considerada en la propuesta arquitectural, la velocidad de procesamiento medida en millones de inferencias difusas tipo dos por segundo, coincide con la frecuencia de operación obtenida.

2. Este procesador puede implementarse en una FPGA de menor tamaño,siempre y cuando esta tenga los recursos de memoria suficientes.

5.3 Medida del costo computacional

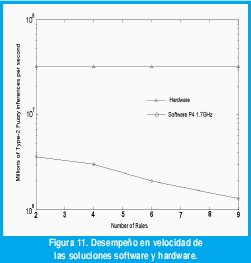
Varios sistemas difusos tipo dos de intervalo se implementaron a manera de solución software. Estos sistemas se verificaron sobre una maquina Intel pentium IV de 1.7 GHz. Mientras que la solución hardware se verificó sobre el sistema de desarrollo ADMXRC2-PCI de Alpha Data a una velocidad de 32MHz.

En la Figura 11 se presenta el desempeño en velocidad de las soluciones software y hardware. Aquí tan solo se pretende mostrar el costo que puede llegar a tener un sistema difuso tipo dos en términos computacionales. Seleccionar entre una solución hardware o software dependerá del dominio de aplicación.

VI. CONCLUSIONES Y TRABAJO FUTURO

Se ha presentado una propuesta arquitectural para un sistema difuso tipo dos de intervalo y la implementación FPGA de un procesador difuso tipo dos basado en esta propuesta. Según nuestro conocimiento, esta es la primera realización microelectrónica de un sistema difuso tipo dos.

Lo anterior es un logro original, sin embargo no deja de ser el único. También se presentó una extensión de la aritmética distribuida para calcular paralelamente dos combinaciones lineales que comparten coeficientes.

En cuanto a los resultados de implementación se refiere, se observó que el desempeño en velocidad del procesador difuso tipo dos, para un nivel de complejidad de nueve reglas, es un orden de magnitud mayor que el desempeño de una solución software sobre un procesador de propósito general de última generación.

A partir de esta primera realización hardware de un IT2FLS, se visualizan los siguientes contextos para trabajo futuro en esta área:

•Extensión y optimización de la arquitectura propuesta. A partir de esta, desarrollar un procesador que permita implementar sistemas difusos tipo dos de base incompleta y motor de inferencia con agregación.

•Concepción, desarrollo y validación de un procesador difuso tipo dos sobre full custom. Por ejemplo, el procesador podría incluir circuitos analógicos para fusificación y reducción de tipo.

•Implementación hardware dedicada de sistemas difusos tipo dos y sus algoritmos de sintonía. Se podría pensar en sistemas hardware neurodifusos tipo dos o difusos tipo dos evolutivos.

REFERENCIAS BIBLIOGRÁFICAS

[1] Ascia G et al, 1999, VLSI Hardware Architecture for Complex Fuzzy Systems, IEEE Transactions on Fuzzy Systems, Vol. 7 ,No. 5, pp. 553-570.

[2] Baturone I et al.,2000, Microelectronic design of fuzzy logic based systems, CRC Press , March , 2000.

[3] Baundendistel K,1994, An improved method of scaling for real-time signal processing applications, IEEE Transactions on Education, Vol. 3, No. 3, pp.281-288

[4] Blake J. J. et al,1998 , The implementation of fuzzy systems, neural networks and fuzzy neural networks using FPGAs, Information Sciences, Volume 112, pp. 151-168.

[5] Bob R. I & Mendel J. M, 2002, Type-2 fuzzy sets made simple, IEEE Trans. on Fuzzy Systems, Vol. 10, No. 2, pp 117-127

[6] Coffman K., 2000, Real World FPGA Design with Verilog, Pretince Hall PTR , New Jersey.

[7] Djuro G. & Jaime B, 2000, Hardware implementations of fuzzy membership functions, operations, and inference, Computers & Electrical Engineering, Volume 26, Issue 1, pp. 85-105.

[8] Gaona A et al., 2003, Sequential fuzzy inference system based on Distributed Arithmetic, Proc. of 2003 IEEE international symposium on computational intelligence for measurement systems and applications, pp.125-130

[9] ITC & UIT, 2003, ITC Specification of Digital Terrestrial Television Transmissions in the United Kingdom, Technical document independent television commission, London UK.

[10] Karnick, N. N &. Mendel, J. M, 1999, Type-2 fuzzy logic systems, IEEE Trans. on fuzzy systems, Vol. 7, pp 643-658.

[11] K. Coffman, 2000, Real World FPGA Design with Verilog, Pretince Hall PTR , New Jersey.

[12] Lago E. et al, 1998, XFVHDL: A tool for the synthesis of fuzzy logic controllers, proc. of DATE'98 Design Automation and Test in Europe, pp. 102-107

[13] Liang Q. & Mendel J.M, 2000, Interval type-2 fuzzy logic systems: theory and design, IEEE Trans. On Fuzzy Systems, Vol 8. pp 535-550.

[14] Liang Q. et al, 2000a, Conection admission control in ATM networks using survey based type-2 fuzzy logic systems, IEEE Trans. Syst., Man., Cybern., Vol 30,pp 329-339.

[15] Liang, Q. et al, 2000b, "Equalization of nonlinear time-varying channels using type-2 fuzzy adaptive filters", IEEE. Trans. On Fuzzy Systems, Vol. 8, No. 5, pp 551-563.

[16] Liang Q. et al, 2001, MPEG VBR video traffic modeling and classification using fuzzy techniques, IEEE trans. On Fuzzy systems , Vol 9 , no 1, pp. 183 - 193.

[17] Lopez S. et al, Frequency domain singleton fuzzification in the design of hardware based fuzzy logic controllers, Proc. of the 18th IEEE international symposium on Intelligent Control, 2003.

[18] McEachern J. F. & Miyamoto R. T, 2003, Emerging tecnologies: ONR's need for intelligent computation in underwater sensors, Computational Intelligence The experts speak , IEEE Press - Wiley Interscience, , Chap. 5, pp 60-61.

[19] Melgarejo M. & Olea D, 2003, Distributed Arithmetic in the Design of High Speed Hardware Fuzzy Inference Systems, 22nd International Conference of the North American Fuzzy Information Processing Society, pp. 116-120.

[20] Melgarejo M et al, 2004, Computational model and architectural proposal for a hardware type-2 fuzzy system, 2nd IASTED Conference on Neural Network and Computational Intelligence, Switzerland, (To appear)

[21] Mellin P. & Castillo O, 2002, A New Approach for Quality Control of Sound Speakers Combining Type-2 Fuzzy Logic and Fractal Theory, Proc. of the 2002 IEEE international conference on Fuzzy systems, pp. 825 -828.

[22] Mellin P. & Castillo O, 2003, Intelligent control of non linear plants using Type-2 Fuzzy Logic and Neural Networks, Proc. of the 2003 IEEE international conference on Fuzzy Systems, pp. 1558 -1562.

[23] Mendel J. M, 2001a., Uncertain Rule-Based Fuzzy Logic Systems , introduction and new directions, Prentice Hall PTR, Upper Saddle River, NJ.

[24] Mendel J. M., 2001b, "The perceptual computer: an architecture for computing with words, Proc. of the 2001 IEEE International Conference on Fuzzy Systems", pp. 35-38.

[25] Patra S., Mulgrew B, 1998, Efficient Architecture for bayesian equalization using fuzzy filters, IEEE Transacations on circuits and systems II: Analog and digital signal processing , Vol. 45 , No. 7, pp.812-820.

[26] Obermann S. & Flynn M, 1997, Division algorithms and implementations, IEEE Transactions on Computers, Vol. 46, Issue: 8, pp 833-854.

[27] Wang L. X., 1997, A course on Fuzzy Systems and Control, New Jersey, Prentice Hall,

[28] Wang W et al, 2001, Low power FIR filter FPGA implementation based on distributed arithmetic and residue number system, Proc. of the 44th IEEE 2001 Midwest Symposium on Circuits and Systems, Vol: 1, pp. 102 -105

[29] White S. A., Applications of Distributed Arithmetic to Digital Signal Processing: A tutorial Review, IEEE ASSP Magazine, Vol. 6 No 3, 1989.

[30] Wu H. & Mendel J.M, 2001, Introduction to Uncertainty bounds and their use in the design of interval type-2 fuzzy logic systems, pro. of the 2001 IEEE International Conference on Fuzzy Systems, pp. 662-665.

[31] Wu H., Mendel J.M, 2002, Uncertainty Bounds and their use in the design of interval type 2 fuzzy logic systems, IEEE transactions on Fuzzy systems, Vol 10, No 5, pp. 622-639.

[32] Xilinx, 2002, Virtex-II 1.8V Field Programmable Gate Arrays, Xilinx product specification V 2.3.

[33] Zadeh, L. A, 1975, "The Concept of a Linguistic Variable and its Application to Approximate Reasoning", Information Sciences, 8, pp. 43-80.

Miguel A. Melgarejo Rey
Ingeniero Electrónico Universidad Distrital, Grado de Honor Francisco José de Caldas. Magíster en Ingeniería Electrónica y computadores, Universidad de los Andes, Graduado con Honores y tesis de maestría laureada. Profesor Asistente Facultad de Ingeniería, Universidad Distrital. Investigador Adjunto Laboratorio de Automática, Microelectrónica e Inteligencia Computacional, Universidad Distrital. mmelgarejo@ieee.org

Carlos A. Peña Reyes
Ingeniero Electrónico Universidad Distrital Francisco José de Caldas. Especialista en control automático, Universidad del Valle. Doctor en Informática y ciencias de la computación, École Polytechnique Fédérale de Lausanne (EPFL), Suiza. Senior Reseacher, Laboratoire de Systemes Logiques, EPFL. c.penha@ieee.org