Ingeniería, 2000-00-00 vol:5 nro:2 pág:71-77

Desarrollo de un filtro digital promedio en fpga.

DEVELOPMENT OF A FPGA BASED AVERAGE DIGITAL FILTER.

Miguel Alberto Melgarejo Rey

Resumen

En este artículo se presenta el proceso de modelado , diseño y prueba para una estructura de filtrado digital promedio basado en FPGA. Se hace énfasis en la metodología de desarrollo sobre hardware, debido a que las operaciones de computo requeridas por esta clase de filtros se adaptan fácilmente a la arquitectura de las PLDs. Los resultados de este trabajo se aplicaron en la supresión de AWGN en un sistema de control discreto.

Palabras claves:
Filtros digitales ,ADF , FPGA.

Abstract

This paper presents the modeling, design and probe of a FPGA-based digital average filter. PLD-based hardware implementation is recommended due to average filters use simple computational operations. The filter was used into a discrete time control system in order to reduce AWGN.

Keywords :
Digital filters , ADF , FPGA.

INTRODUCCION

El filtrado digital se ha convertido en uno de los tópicos de mayor desarrollo en los últimos años, ya que cuenta con un amplio soporte teórico unido a las facilidades de experimentación sobre plataformas convencionales como los DSPs . En la actualidad, las aplicaciones demandan elevadas tasas de computo para el manejo de información asociada a grandes anchos de banda , haciéndose necesario el uso de estructuras dedicadas en hardware para el tratamiento efectivo de tales procesos. En cuanto al filtrado promedio se refiere, se sabe que éste puede ser utilizado como un método eficaz para eliminar ruido aditivo o en otro caso como par te de procesos para la compresión de señales aleatorias. Este documento presenta en primer lugar un estudio teórico soportado por simulación en Matlab de las características espectrales del filtrado promedio simple y en cascada, Como base para el desarrollo de una arquitectura en VHDL y su posterior prueba sobre un PLD, evaluándose los resultados de compilación. Finalmente, se presenta el concepto de pre-procesador ADF para la eliminación de ruido en un sistema de control discreto.

I. FILTRADO DIGITAL PROMEDIO.

Un ADF ( Average Digital Filter ) puede ser considerado como un filtro FIR ( Finite Impulse Response ) donde todo los coeficientes presentan el mismo valor equivalente al inverso multiplicativo del número de elementos de retención que conforman el filtro. Su representación matemática está dada por la ecuación (1), donde y[n] es la salida, x[n] representa los elementos de retención y N la longitud del filtro, indicando el número de muestras que se requieren promediar.

La etapa inicial de análisis consiste en suministrar un impulso unitario, la energía de

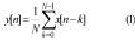
esta señal se encuentra distribuida uniformemente sobre todo el espectro; esto implica que dentro de un mismo paquete temporal se accede a todas las señales armónicas, siendo posible evaluar el comportamiento del filtro ante cada una de estas señales. En la ecuación (1) , puede observarse que la respuesta al impulso del filtro promedio es una señal tipo cajón, cuyo espectro es una función SINC simétrica sobre cero. Para efectos prácticos solo se considera el comportamiento sobre el espectro positivo , el cual es de naturaleza pasa-bajo. [1]. La figura (1) presenta diferentes respuestas espectrales ( en potencia ) para varios ADFs, cuya longitud es una potencia de dos. En la medida que N crece, la pendiente de transición entre la banda de paso y la banda de corte aumenta así como el numero de lóbulos presentes en esta última.

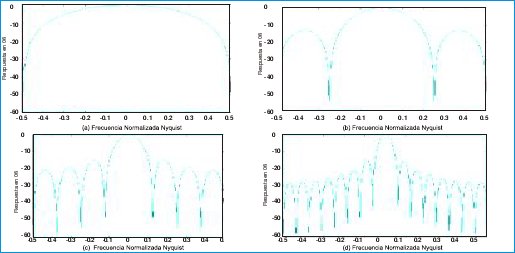
Figura 1.Respuesta espectral para N=2(a) ,4 (b),8 (c),16 (d) , en la medida que N aumenta la pendiente de transición se pronuncia , luego para una misma frecuencia de muestreo se puede cambiar la frecuencia de corte con tan solo modificar la longitud del filtro.

La frecuencia de corte estándar (-3dB) , presenta un decrecimiento inversamente proporcional a la longitud del filtro, esto puede observarse en la ecuación (2) siendo esta una relación adecuada para determinar la frecuencia de corte (fc) del ADF en función de la frecuencia de muestreo (fs), considerando que la longitud del filtro es una potencia de dos.

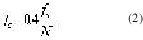
El comportamiento pasa-bajo del ADF hace de este una herramienta interesante para eliminar ruido aditivo gaussiano. Esta clase de ruido presenta dependencia armónica, siendo sus componentes múltiplos aleatorios superiores de la señal sobre la cual se presenta; luego, pueden ser eliminadas aplicando una estrategia que tan solo tome la envolvente principal o promedio. Este proceso se observa en la figura (2).

El AWGN puede ser eliminado eficientemente en la medida que la longitud del filtro aumente , pero esto puede llevar a la supresión de algunas componentes de alta frecuencia de la señal principal, por tal razón es necesario realizar un estudio espectral previo, para establecer la longitud del filtro y la frecuencia de muestreo que garantice un filtrado adecuado.[2]

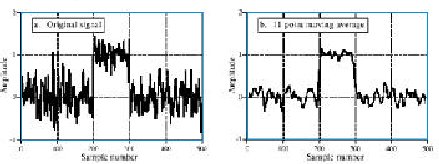
Figura 2. Reducción de AWGN empleando un ADF . Esta clase de filtro trata de extraer la señal de mayor amplitud , descartando las perturbaciones aleatorias que se dan sobre esta.

II.BANCOS ADF

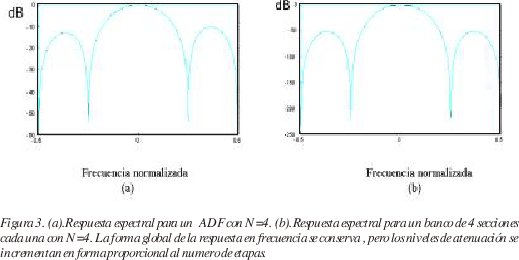
Un ADF de longitud N presenta una respuesta espectral del tipo SINC con un número particular de lóbulos con niveles de atenuación proporcionales a la frecuencia.

Si dos o mas de estos filtros son dispuestos en cascada, la forma de la respuesta espectral se conserva ( número de lóbulos ) , pero los niveles de atenuación se ven incrementados en un factor equivalente al numero de etapas que se coloquen. Por lo tanto , este método puede ser empleado para controlar la pendiente de transición por medio de una estructura fija (en software o hardware), considerando una frecuencia de muestreo constante y una corta longitud por etapa.

El hecho de colocar una serie de sistemas discretos en cascada equivale a realizar una multiplicación de sus funciones de transferencia. El análisis espectral de la función resultante en Z (circulo unitario), indica que es el resultado de la multiplicación de todas las respuestas en frecuencia; si la estructura LTI es la misma en todas las etapas, entonces lo obtenido es una potencia k de la respuesta básica [1]. Para efecto de análisis, es común recurrir a estudios logarítmicos, luego la potencia k, se convierte en factor multiplicativo de la respuesta en magnitud del filtro empleado.

III. DESARROLLO EN HARDWARE.

Se presenta un modelo digital desarrollado en VHDL (Very high Speed integrated circuit Hardware Description Language), el cual implementa la ecuación en diferencia del ADF haciendo uso de un proceso secuencial sincronizado. Es necesario destacar que dicho modelo se restringe a longitudes de filtro que son potencias de dos, considerando que la división para este caso equivale únicamente a desarrollar un desplazamiento hacia la derecha de la magnitud obtenida de los diferentes valores acumulados. Por lo tanto una estructura aparentemente compleja como un divisor, se transforma en un "shifter".[3]

Es necesario destacar dos particularidades importantes de un ADF desarrollado en hardware : en primer lugar, no es necesario el uso de aritmética de punto flotante, los valores provenientes del cuantificador generan sumas completas , las cuales al ser sometidas sobre el concatenador tendrán un valor de aproximación o redondeo máximo de 0.5 que solo se hace apreciable para valores bajos de señal y se ubican dentro la zona normal de ruido inherente. En segundo lugar, no presenta modificación en la resolución de salida con respecto a la de entrada, la acumulación implica un desplazamiento hacia izquierda equivalente al introducido por el divisor pero en sentido contrario.[4]

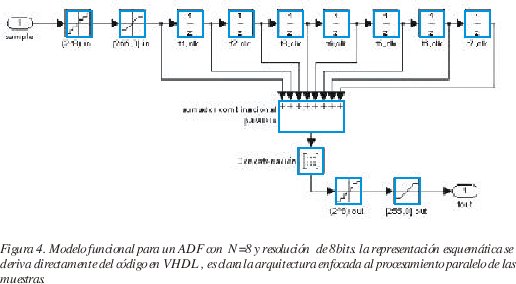
La figura (4) presenta una estructura para un ADF con N= 8 y resolución de 8 bits, el modelo funcional en VHDL se especifica a continuación:

library IEEE;
use IEEE.std_logic_1164.all;

Entity filtro is
port (
sample: in integer range 0 to 255;
clk: in STD_LOGIC;
fout: out INTEGER range 0 to 255
);
end filtro;
Architecture filtro_arch of filtro is
Begin
Process ( clk )
Variable t0,t1,t2,t3 : integer range 0 to 255;
Variable t4,t5,t6,t7 : integer range 0 to 255;
Begin
Wait until ( clk'event and clk' = '1' );
t7:=t6;
t6:=t5;
t4:=t3;
t3:=t2;
t2:=t1;
t1:=t0;
t0:=sample; fout <= (t0+t1+t2+t3+t4+t5+t6+t7)/8;
end process;
end filtro_arch;

El encabezado define las librerías y recursos de descripción que se van a emplear , se recurre a la norma IEEE 1164 , donde se especifican las interacciones booleanas y aritméticas que se pueden desarrollar sobre un valor tipo entero.

La entidad define tanto el puerto de entrada (sample) como de salida ( fout ), representado como enteros en el rango de cero a 255 (8 bits), también es posible definirlos directamente como vectores de bits del tipo standard logic, igualmente se incluye una línea de sincronismo (clk ).

La arquitectura se maneja por medio de un solo proceso secuencial que se sincroniza con los flancos de subida presentes en la línea clk. Se hace uso de variables internas de proceso, las cuales representan los ocho retenedores de la estructura. La salida se calcula como la suma dividida por ocho de las variables internas empleadas. Es necesario especificar, que la acumulación de t0..t7 se hace sobre un solo ciclo de reloj al igual que el desplazamiento , esto indica que el modelo desarrollado es una representación natural de la ecuación en diferencias.[5]

El modelo incluye estructuras combinacionales cuya velocidad de procesamiento tan solo depende del RDT ( Route Delay Time ) de la FPGA, dicho modelo solo es viable para longitudes de filtro menores a N=16, para longitudes mayores la descripción en VHDL del filtro debe ser modular, con el fin de tener una especificación interpretable fácilmente.

El proceso de edición y simulación funcional se llevó a cabo sobre MODELSIM, con el fin de garantizar la integridad lógica del diseño así como su comportamiento temporal.

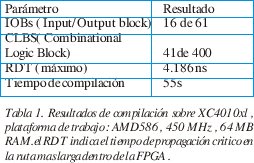
Posteriormente, el modelo fue llevado a la herramienta XILINX FOUNDATON SERIES 1.5 para efectos de compilación sobre una FPGA XC4010XL. los resultados de este proceso se presentan en la tabla (1).

La figura 5, Presenta los resultados de la simulación real sobre la FPGA en donde se evalúan el mínimo tiempo de muestreo para el filtro y el comportamiento del mismo ante oscilaciones de la señal de sincronismo.

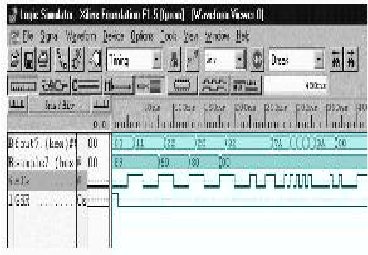Figura 5. Resultados de la simulación sobre XC4010XL, mínimo tiempo de muestreo de 5ns , las oscilaciones (glitch) dentro de la señal de sincronismo pueden ser criticas a esta escala.

Como resultado de la síntesis y compilación se obtuvo un archivo de 35KB de longitud , el cual contiene la cadena de bits para arrancar la FPGA. La configuración de la misma se llevo a cabo por medio del sistema de desarrollo XS40V1.4 de Xess Corp.[6] Paralelamente se desarrollo una aplicación en software para generar señales senoidales, contaminarlas con AWGN y llevarlas al sistema de desarrollo empleando el puerto de comunicaciones de 14 bits incluido en éste , con el fin de establecer un sistema integral aplicable a la adecuación de señal en un sistema de adquisición de datos.

IV. COMPENSADOR DISCRETO CON PRE-PROCESADOR ADF.

La arquitectura desarrollada para ADFs de longitud 2k , fue integrada como modulo de pre-procesamiento en un regulador discreto de velocidad para un conjunto de motor DC- generador trifásico de 200W ; considerando que la FPGA en primera instancia se encontraba administrando los procesos de conversión AD y DA , así como el acceso al microprocesador.

Además, se hizo necesario incluirlo como solución a dos problemas: degradación de la señal del sensor debido a las fuertes perturbaciones mecánicas de la planta, las cuales se veían reflejadas como oscilaciones aleatorias en la señal de retroalimentación haciendo inestable el sistema.

En segundo lugar,la presencia del filtro dentro del lazo de control dio la posibilidad de obtener una identificación adecuada de la planta para el diseño automático del compensador discreto, liberando al microprocesador de obtener la tendencia del sistema.

El modelo completo del sistema de control se presenta en la figura 6.; el pre-procesador se encuentra conformado por cuatro ADFs en cascada de longitud N=8 y resolución de 8 bits.

Todas las operaciones se sincronizan con una señal de reloj de 10MHz , siendo esta limitada en esencia por el acceso del microprocesador al puerto y las respectivas multiplexaciones en el sistema de adquisición.

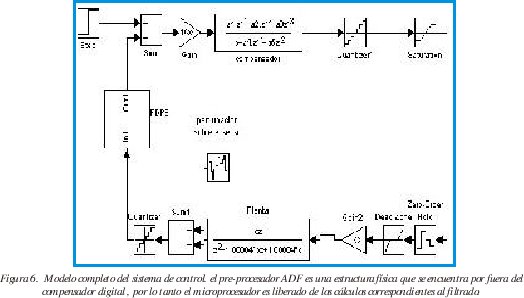
En la figura 7 se puede observar el efecto de supresión de AWGN en el lazo de control; la estructura de cuatro etapas de longitud N=8, no elimina completamente las perturbaciones, es claro que las componentes de baja frecuencia sobreviven quedando dentro de los limites tolerables, de manera que no afecten la dinámica del sistema de control.

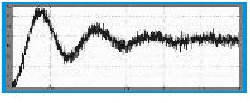
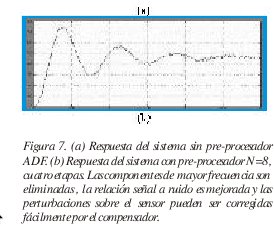
Dentro del proceso de optimización de la señal, se llevaron a cabo varias pruebas con pre-procesadores ADF con igual numero de etapas y N= 16, aunque la supresión de AWGN mejoraba, se hacía evidente una pérdida de componentes armónicas de la señal de control (alta frecuencia), lo cual se traducía como un aumento del tiempo de respuesta del sistema, caso similar para N=8 y mayor número de etapas. Por lo tanto, se hace necesario desarrollar una metodología, la cual debe tener en cuenta las características dinámicas requeridas y la relación señal a ruido, con el fin de diseñar el compensador digital adecuado y su respectivo pre-procesador ADF.

El modelo final se presenta en la figura 8, los recursos necesarios para su implementación equivalen aproximadamente a la cuarta parte del tamaño lógico de la FPGA empleada.[7]

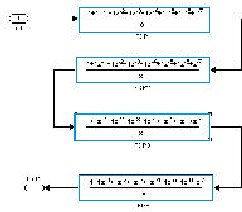
Figura 8. Estructura final del pre-procesador empleado . El tamaño lógico del banco crece linealmente con el número de etapas , en este caso 170 CLBS para cuatro etapas de 41 CLBS cada una.

CONCLUSIONES

•Se ha desarrollado un modelo en VHDL para un filtro digital promedio de longitud N=8; dicho modelo fue implementado en una FPGA de baja capacidad empleando un 10% de los recursos lógicos de este dispositivo.

•El modelo desarrollado puede encadenarse para conformar bancos de filtros promedio;los recursos lógicos de la FPGA utilizados por un banco ADF (basado en este modelo) se incrementan linealmente con el número de etapas que lo conforman.

•Se introdujo un banco ADF ( cuatro etapas con N=8 ) dentro del sistema de adquisición de datos basado en FPGA de un sistema de control discreto, mejorando de esta forma la figura de ruido del sistema sin emplear componentes adicionales de hardware y liberando de cálculos adicionales al microprocesador de control.

REFERENCIAS

[1] Proakis J. et al , "Tratamiento digital de señales", tercera edición, Madrid, PRENTICE HALL , 1998 , pag 509-520.

[2] Chi-jui C. et al," FPGA implementation of Digital Filters", Proceedings of the international conference on signal processing applications and technology , 1993.

[3] Smith D. ," HDL chip design" , fourth edition, Madison AL. , Doone Publications, 1996, pag 130-200.

[4] Evans J.," Efficient FIR Filter Architectures Suitable for FPGA Implementation ", IEEE transactions. On circuits and systems , july 1994.

[5] González G. et al ," Diseño e implementación de un filtro FIR con coeficientes programables y fase lineal en FPGA ", trabajo de grado,Universidad Distrital Francisco José de Caldas, Santafé de Bogotá , Junio de 1998.

[6] Melgarejo M. et al , " Filtro FIR adaptativo sobre celdas lógicas programables FPGA ", memorias del Primer congreso internacional de ingenierias eléctrica y electrónica, Universidad Industrial de Santander , Bucaramanga , Marzo de 2000.

[7] XILINX Corp. , 1999 Xilinx DATA BOOK, octubre de 1999.

Miguel Alberto Melgarejo Rey
Estudiante de ingeniería electrónica, décimo semestre. Universidad Distrital Francisco José de Caldas. Miembro del grupo de investigación en dispositivos lógicos programables y técnicas digitales. Realiza su proyecto de grado sobre sistemas de inferencia difusa basados en FPGA aplicados a sistemas de control no lineal. Correo electrónico : gilp@udistrital.edu.co