DOI:
https://doi.org/10.14483/23448393.2378Published:
2008-11-30Issue:
Vol. 14 No. 2 (2009): July - DecemberSection:
Science, research, academia and developmentDiseño de circuitos analógicos basados en amplificadores operacionales usando algoritmos genéticos con función de aptitud difusa
Operational Amplifier Analog Circuit Design Using Genetic Algorithms With Fuzzy Fitness Function
Keywords:
algoritmo genético, amplificador operacional, circuito analógico, sistema de inferencia difusa, función de aptitud, función de transferencia. (es).Downloads
References
El B. Grimbledy. "Automatic Analogue Circuit Synthesis using Genetic Algorithms". The University of Reading, Reading. 2000.
V. Aggarwal. "Evolving Sinusoidal Oscillators Using Genetic Algorithms". Netaji Subhas Institute of Technology, New Delhi. 2002.
D. H. Horrocks, Y.M.A. Khalifa. "Genetic Algorithm Design of Electronic Analogue Circuits Including Parasitic Effects". School of Engineering, University of Wales, College of Cardiff, Cardiff. 1996.
C. A. Peña. "Coevolutionary Fuzzy Modeling". Lecture Notes in Computer Science. Springer-Verlag, Alemania. 2004.
R. L. Haupt, D. H. Werner. "Genetic Algorithms in Electromagnetics". John Wiley & Sons, Inc, New Jersey. 2007.
M. D. Vose. "The Simple Genetic Algorithm". MIT Press, Cambridge, MA, August. 1999.
M. C. Cirillo and A. A. Poli. "On the use of the normalized mean square error in evaluating dispersion model performance". Atmospheric environment. Part A, general topics, Vol 27, No. 15, pp. 2427-2434. 1993.
S. Sumathi, T. Hamsapriya, P. Surekha. "Evolutionary Intelligence". Springer-Verlag, Berlin. 2008.
M. Affenzeller, S. Winkler, S. Wagner y A. Beham. "Genetic algorithms and genetic programming - Modern concepts and practical applications". Numerical Insights. CRC Press. 2009.
Z. Michalewicz. "Genetic Algorithms + Data Structures = Evolution Programs". Springer-Verlag, Heidelberg, 3ra Edición. 1996.
L. X. Wang. "A course in Fuzzy Systems and Control". 1st ed., New Jersey: Prentice Hall International. 1997.
J. Karki."Analysis of the Sallen-Key architecture". Texas instruments application report SLOA024B, Sep. 2002.
D. Goldberg. "Genetic Algorithms in Search, Optimization and Machine Learning". Addison-Wesley.1989.
J. H. Holland. "Adaptation in Natural and Artificial Systems". Cambridge, MA: The MIT Press. 1992.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Ciencia, Investigación, Academia y Desarrollo
Ingeniería, 2009-00-00 vol:14 nro:2 pág:42-50
Diseño de circuitos analógicos basados en amplificadores operacionales usando algoritmos genéticos con función de aptitud difusa
OPERATIONAL AMPLIFIER ANALOG CIRCUIT DESIGN USING GENETIC ALGORITHMS WITH FUZZY FITNESS FUNCTION
Héctor Hostos
Estudiante de la Facultad de Ingeniería, Universidad Distrital.
Federico Sanabria
Estudiante de la Facultad de Ingeniería, Universidad Distrital.
Miguel Melgarejo
Profesor de la Facultad de Ingeniería, Universidad Distrital.
Resumen
Este artículo presenta una propuesta para el diseño de circuitos analógicos basados en amplificadores operacionales usando un algoritmo genético simple. La entrada al algoritmo es la función de transferencia requerida por el diseñador expresada como la respuesta al escalón unitario que el circuito debería exhibir. Adicionalmente, una característica especial del algoritmo radica en que la función de aptitud se implementa como un sistema de inferencia difusa. Se incluye en el artículo un resumen de la metodología utilizada para el diseño del algoritmo y resultados con múltiples funciones de transferencia para un circuito de topología específica.
Palabras clave:
algoritmo genético, amplificador operacional, circuito analógico, sistema de inferencia difusa, función de aptitud, función de transferencia.
Abstract
This paper presents a genetic algorithm approach to the design of analog circuits consisting of operational amplifiers. The input of the algorithm is the transfer function of the required system. The fitness function of the genetic algorithm is implemented by means of a fuzzy inference system. A summary of the methodology used in the design is included and results with a specific circuit topology for multiple transfer functions are reported.
Key words:
genetic algorithm, operational amplifier, analog circuit, fuzzy inference system, fitness function, transfer function.
1. INTRODUCCIÓN
En el proceso de diseño de circuitos analógicos es muy común que a la hora de requerir respuestas que implican circuitos complejos se tenga que hacer uso de herramientas de optimización numérica [3]. La razón de esto es que el modelamiento matemático de este tipo de topologías que genera mejores resultados es la mayoría de las veces complejo. Estas herramientas se basan en topologías clásicas y en aproximaciones del comportamiento de los circuitos que solo alcanzan soluciones en mínimos locales [1].
Es por esta razón que buscando soluciones a este tipo de problemas surgen diferentes paradigmas como por ejemplo, la computación evolutiva [1]. Esta ciencia aborda el estudio de los fundamentos y las aplicaciones de técnicas computacionales basadas en los principios de la evolución natural [4]. Son técnicas que pueden ser vistas como métodos de búsqueda y optimización; dentro de las reportadas se pueden citar: estrategias de evolución [8], programación evolutiva [9] y los algoritmos genéticos [10].
Tomando como referencia los resultados obtenidos en [1],[2] y [3], se propone en este trabajo emplear un algoritmo de este tipo, el cual a partir de una función de transferencia específica, encuentre un circuito basado en un amplificador operacional, resistencias y capacitancias. La estructura de la red en ésta aproximación es estática lo que quiere decir que el algoritmo solo determina los valores de los elementos pasivos, no cuales de esos elementos deben formar el circuito. El propósito del algoritmo es generar una buena solución teniendo en cuenta el error con respecto a la respuesta al paso que genera la función de transferencia objetivo.
El parámetro más importante en la definición del algoritmo evolutivo es la función encargada de evaluar a las posibles soluciones del problema. Este parámetro recibe el nombre de función de aptitud [6] y en esta propuesta se realiza mediante un sistema de inferencia difusa. Se busca de esta forma integrar una perspectiva cualitativa de evaluación que podría ser derivada de un experto humano [1].
El artículo se estructura así: primero se muestran ciertos fundamentos que cubren aspectos generales de los algoritmos genéticos y los sistemas difusos. Luego se presenta un resumen de la propuesta de diseño. En tercer lugar, se describen los resultados para distintas funciones de transferencia con un circuito de topología Sallen-Key, que en la práctica es comúnmente usado debido a su simplicidad [12]. Por último, se presentan algunas conclusiones.
2. FUNDAMENTOS
Esta sección presenta una revisión de las técnicas de inteligencia computacional consideradas en este trabajo. El lector que esté interesado en profundizar sobre estos temas puede consultar [1], [6], [8], [9], [10], [13], [14] para algoritmos genéticos y [4] y [11] para sistemas difusos.
2.1 Algoritmos genéticos
Los algoritmos genéticos son un proceso iterativo de búsqueda de soluciones cuasi óptimas, regido por una serie de principios que se inspiran en las leyes de la evolución de las especies (la sobrevivencia del más apto). Una de las características más importantes de estos algoritmos es que no requieren de un conocimiento profundo del problema, pues bajo ciertas restricciones no tienen limitantes respecto a la forma de las soluciones que se planteen. Así, es posible explorar respuestas que tal vez con los métodos de diseño convencionales no se considerarían.
El algoritmo genético se inicia estableciendo una población inicial de posibles soluciones al problema, las cuales son seleccionadas aleatoriamente. A partir de estas, se evalúa una función de aptitud que cuantifica el desempeño de las soluciones respecto a cuán bien se aproximan a la solución que requiere el problema.
Luego de evaluar la función de aptitud, se realiza un proceso de selección donde se eliminan todas las posibles soluciones que no estén dentro del rango de idoneidad necesario. Con las soluciones que quedan se inicia un proceso para crear nuevos pobladores o una nueva generación. Para ello se hacen acciones como el cruce entre dos elementos para generar uno nuevo con las características de los originales, la copia o el paso de los elementos de la generación actual a la siguiente y la mutación o cambio aleatorio de las características de los individuos. En esta nueva generación se realiza un proceso similar al de la primera, buscando generar soluciones cada vez mejores.
Idealmente el algoritmo continúa así hasta converger a la solución óptima o hasta que se cumpla algún parámetro que el diseñador determina para detener el algoritmo. Es responsabilidad del diseñador determinar cuándo se debe detener el algoritmo. El estado al que converge el algoritmo y la calidad de la solución hallada dependen fundamentalmente de sus parámetros, tales como la función de aptitud, la cantidad de generaciones que se corre el algoritmo, los métodos de cruce, copia y mutación, entre otros.
2.1.1 Cromosomas y genes
Los cromosomas son cada una de las posibles soluciones que se consideran en la población. Conceptualmente son unidades que contienen toda la información necesaria para determinar la posible solución al problema. Generalmente, para facilitar el trato de los datos se representan en forma de vector o de matriz. Así como en genética, el gen es una parte integrante del cromosoma, en los algoritmos genéticos cada gen posee una unidad de información de la posible solución que forma el cromosoma.
2.1.2 Cruce de cromosomas
Esta es una de las acciones que se realizan sobre los cromosomas seleccionados de la generación presente para crear los elementos una nueva generación. El operador de cruce mezcla los genes de dos cromosomas priorizando de alguna forma aquellos que generen mejores respuestas. El nuevo elemento es un cromosoma completamente diferente a los originales con un desempeño que puede ser mejor o peor que los cromosomas padre, esto depende de la forma como se lleve a cabo la mezcla.
2.1.3 Copia de cromosomas
Esta es la acción mediante la cual se pasan los mejores cromosomas de la generación anterior hacia la nueva. Esto se lleva a cabo para comparar estos individuos con las nuevas soluciones creadas por la acción de cruce y para preservar el acervo genético que introducen estas soluciones.
2.1.4 Mutación de cromosomas
Este es el proceso con el que se realizan cambios aleatorios en las posibles soluciones de las nuevas generaciones. Su propósito es aumentar el rango de estudio hacia horizontes más grandes y no restringirse a rangos pequeños que pudiesen tener solo mínimos locales.
2.1.5 Función de aptitud
Esta función sirve para medir la adaptación de un cromosoma a su entorno, o en términos más prácticos, para evaluar el desempeño de una posible solución en el problema que se está resolviendo.
2.2 Sistemas difusos
El término de sistema difuso puede ser interpretado de muchas formas. Un determinado sistema que procese una variable lingüística o un número difuso, ya puede ser considerado como sistema difuso. Sin embargo, en la literatura se asocia este concepto a aquel sistema que procesa variables puntuales mediante una base de reglas con los conceptos de lógica difusa. Un nombre generalmente asignado es el de "sistema de inferencia difusa".
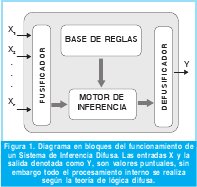
La arquitectura típica de un sistema de este tipo se ilustra en la Figura 1. Este se puede apreciar como un sistema de múltiples entradas y una salida, en el caso de requerirse más de una salida lo apropiado sería generar otro sistema.
La base de reglas representa el conocimiento que el sistema modela y relaciona las variables de entrada con la de salida de una forma lingüística e interpretable por el ser humano. La fusificación transforma valores puntuales de entrada en valores difusos. El motor de inferencia simula el proceso de toma de decisiones realizado por un ser humano empleando la implicación difusa. La defusificación proporciona salidas puntuales según la variable difusa inferida por el motor.
3. METODOLOGÍA
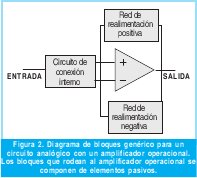
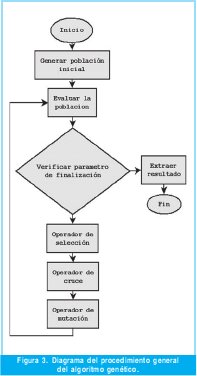
Lo primero que se define es la red generalizada que va a ser optimizada mediante el algoritmo genético. El problema se limita a una red de un amplificador operacional como la que se muestra en la Figura 2. La metodología para el desarrollo del algoritmo genético se muestra en la Figura 3.
Cada subproceso del algoritmo genético se describe a continuación. Dado que se trata de un algoritmo genético canónico, se hace énfasis en la forma como se definieron los operadores requeridos para esta aplicación en particular.
3.1 Población del algoritmo genético
La respuesta del circuito generalizado depende fundamentalmente de los valores de los elementos pasivos que lo conforman. Por tanto se puede decir que el cromosoma se debe conformar con estos valores. Este se construye como un vector donde cada celda (gen) contiene el valor real limitado de uno de los elementos del circuito, originándose así un vector de tamaño igual al número de elementos pasivos.
La población se construye como una matriz conformada por los vectores que representan los cromosomas de la población. El objetivo de esta construcción matricial es facilitar la manipulación de los datos en los procesos del algoritmo. Para la representación de los parámetros en el cromosoma se utilizan valores dentro del rango de la Tabla I. Estos rangos obedecen a valores de elementos que comúnmente se utilizan en estos circuitos y que se pueden encontrar en el mercado de componentes electrónicos.

La población inicial es la primera matriz de cromosomas. Esta es una matriz con valores aleatorios distribuidos uniformemente. Se pretende con esta inicialización permitir que la búsqueda se realice sobre rangos amplios del espacio solución.
3.2 Función de aptitud
Las recomendaciones para el diseño de esta función son múltiples [5]. En este trabajo se ha tenido en cuenta que el principal propósito de esta función es evaluar lo que realmente se pretende optimizar. Por tanto, se considera emplear un sistema de inferencia difusa (FIS por sus siglas en inglés), el cual a partir de cierto conocimiento del problema calcula la aptitud de los individuos. Se propone un sistema de una entrada y una salida con fusificación síngleton, motor de inferencia Mamdani producto y defusificador por centroide discreto [11].
3.2.1 Entrada al sistema de inferencia difusa
La entrada al sistema es una métrica de error que pondera la diferencia entre la respuesta temporal del circuito requerido ante una entrada paso con la respuesta temporal del candidato en evaluación ante esta misma entrada. Es necesario aclarar que aunque se trata de la evaluación de circuitos analógicos, las respuestas temporales se tratan como señales discretas dado que se obtienen de simulaciones computacionales de estos circuitos. Por tanto, solo es de interés garantizar que exista una similitud entre las respuestas en los instantes de muestreo.
Una de las formas más usadas para comparar señales en el tiempo es la métrica del error cuadrático medio normalizado [7] (NMSE por sus siglas en inglés):
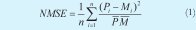
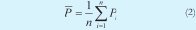
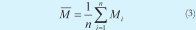
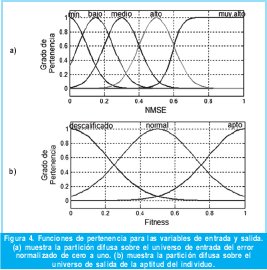
Donde Pi representa cada valor de la señal obtenida del circuito solución en evaluación y Mi concierne a cada valor de la señal de referencia.
3.2.2 Conjuntos difusos y base de reglas
Las funciones de pertenencia del sistema de inferencia difusa se eligen gaussianas y sigmoidales dado que este tipo de funciones tienen una mayor capacidad de generalización en comparación con funciones triangulares o trapezoidales [11]. Esta característica permite obtener sistemas difusos con comportamientos globales no lineales más ricos, con una base de reglas relativamente pequeña. El conjunto de funciones propuestas en este caso se presenta en la Figura 4. Estas funciones representan la apreciación lingüística que tiene un experto con respecto a los posibles valores de NMSE calculados a partir de (1).
Para el universo de discurso de entrada se elige un número de etiquetas lingüísticas razonable que caracterice cada candidato en relación a su NMSE y que además sea interpretable. Para el caso de la variable de salida, se aprecia una distribución uniforme de solo tres etiquetas lingüísticas, ya que para el problema en cuestión no hacen falta más descripciones. La base de reglas la componen las relaciones (4-8).

3.2.3 Función no lineal equivalente
La función no lineal equivalente al sistema difuso se presenta en la Figura 5. Notese que la partición lingüística genera cuatro regiones de interés en relación al valor de aptitud de los individuos. La primera región corresponde a los individuos cuyo NMSE está por debajo de 0.3, los cuales obtendrán calificaciones superiores al 50% de la escala, siendo aquellos que tendrían mayores oportunidades de ser seleccionados. La segunda es una región de poca variabilidad entre 0.3 y 0.6, donde los individuos tienen oportunidades similares de ser seleccionados sin ser las mejores. En tercer lugar, se encuentra una región nuevamente de descenso entre 0.6 y 0.8 donde los individuos tienen calificaciones por debajo del 50% de la escala. Finalmente aparece una zona de poca variabilidad donde los individuos tienen las oportunidades más bajas de ser seleccionados.
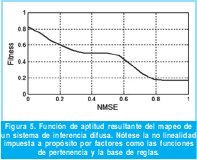
Esta función resultante puede ejercer presión selectiva para diferentes clases de individuos. La primera región garantiza que ninguno de los mejores individuos obtendrá máxima probabilidad de ser seleccionado, lo cual evitaría convergencia prematura hacia determinadas soluciones. Mientras que la cuarta región garantiza que los individuos con el peor desempeño tengan una probabilidad pequeña de ser seleccionados, lo que permitiría conservar la diversidad genética.
3.3 Proceso de selección y cruce
El operador de selección consiste en una implementación hibrida entre selección elitista y selección por ruleta, esto con razón de explotar al máximo los beneficios que brinda cada uno de estos métodos [5].
La selección inicia con la aplicación del operador elitista, este elige un porcentaje de los mejores individuos en dependencia del resultado del proceso de evaluación. Estos quedan habilitados para ser padres y son además ordenados de acuerdo con la calificación resultante de la simulación. Seguidamente se ejecuta el operador de ruleta, el cual trabaja con los individuos resultantes de la selección elitista. Este elige los individuos que harán parte del proceso de cruce. En este operador, a cada individuo se le asigna una probabilidad de ser elegido en dependencia del puesto que obtuvieron en el proceso de evaluación.
El proceso empieza asignándole a cada uno de los individuos un rango de una nueva variable, que va de cero a uno, en función del puesto que obtuvieron en el proceso de evaluación. El mejor individuo obtiene el rango más grande y el peor el más pequeño. Seguidamente se genera un número aleatorio entre cero y uno, si el valor del número generado cae dentro del rango asignado a algún cromosoma, ese cromosoma es seleccionado para el cruce.
El procedimiento se realiza dos veces para generar los cromosomas padres. En vista de que el cromosoma representa valores reales de los parámetros de la posible solución, el cruce se realiza promediando todos los valores de ambos cromosomas, se genera así por cada operación de cruce un solo hijo. Este proceso se repite las veces necesarias para generar un número constante de individuos.
Adicionalmente, por la forma en que se asignan los rangos, es consecuente que los mejores individuos de la población tengan siempre más probabilidad de ser elegidos que los peores. La decisión de incluir los peores individuos dentro del proceso evolutivo se debe a que estos individuos pueden tener características genéticas que enriquecerían el desarrollo del mismo.
A continuación se forma un nuevo conjunto de individuos concatenando los individuos resultantes del proceso de cruce con los individuos resultantes del proceso de selección elitista. Este conjunto tiene siempre un número constante de individuos. La nueva población se genera aplicando el operador que se describe a continuación.
3.4 Proceso de mutación
En este paso se altera el valor de una resistencia y una capacitancia por cromosoma de forma aleatoria, el operador cambia el valor del elemento respetando el rango previamente establecido. De los individuos disponibles en la población se decide mutar a sólo un 10% por generación. Lo anterior se define de esta manera teniendo en cuenta que esta tasa proporcionó buenos resultados experimentales en el algoritmo implementado en [5].
4. RESULTADOS
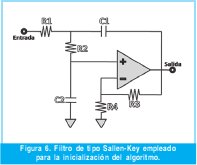
La topología del circuito se elige como un filtro tipo Sallen-Key, el cual muestra en la Figura 6. De este circuito se deduce la siguiente función de transferencia [12]:
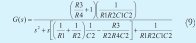
Se hacen tres pruebas que consisten en considerar como referencia al algoritmo tres funciones de transferencia distintas. La primera de segundo orden de tipo sobreamortiguado, cuya respuesta se asemeja a la de un sistema de primer orden. En segundo lugar se considera un sistema de tipo subamortiguado con una alta componente oscilatoria y finalmente un sistema de tercer orden. El parámetro de parada en todas las pruebas es el número de generaciones necesario para que el algoritmo converja. La entrada del sistema en todas las pruebas es la función paso.
Es importante resaltar que debido al carácter estocástico del algoritmo genético [10] y con el fin de atenuar varianzas estadísticas, los resultados presentados a continuación recopilan la información de múltiples experimentos para cada una de las pruebas mencionadas.
4.1. Sistema de referencia de segundo orden sobreamortiguado
La función de transferencia en cuestión es:
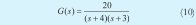
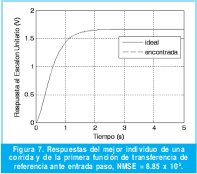
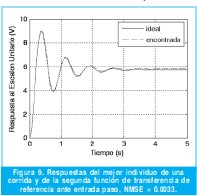
De esta primera prueba se realizaron 30 experimentos, en cada uno de ellos el algoritmo genético se ejecutó durante 30 generaciones. A manera de ilustración se exhibe en la Figura 7 la respuesta del mejor individuo obtenido en el último experimento. Se puede ver que las respuestas se solapan dado que el NMSE obtenido es de 8.85x10-5.
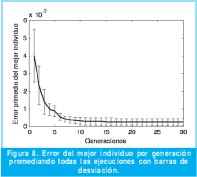
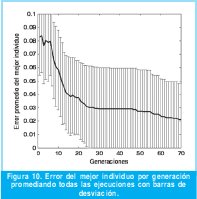
El promedio de las curvas de error de los mejores individuos por generación en todos los experimentos se muestra en la Figura 8, incluyendo también barras de desviación. De esta se aprecia que el algoritmo converge rápidamente dado que la función de transferencia es del mismo orden que la del circuito, además porque la respuesta de referencia tiene una dinámica simple.
4.2. Sistema de referencia de segundo orden subamortiguado
La función de transferencia corresponde esta vez a:
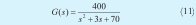
La anterior fue escogida intencionalmente con un alto grado de oscilación para observar el comportamiento del algoritmo. De nuevo se realizan treinta experimentos en igualdad de condiciones. El algoritmo se ejecuta con setenta generaciones, debido a que en esta ocasión la convergencia requiere de más tiempo. La mejor respuesta obtenida en el último experimento se muestra en la Figura 9, donde el NMSE es igual a 0.0033.
El desempeño del algoritmo empeora en comparación al caso anterior, sin embargo la respuesta es aceptable para el número de generaciones adoptado. La curva del error promedio de los mejores individuos por generación se presenta en la Figura 10. La escala vertical es diez veces más grande que la empleada en la Figura 8, aún así las barras de desviación se observan más amplias, lo que da a entender que el algoritmo convergió a varias soluciones no similares durante los experimentos.
4.3 Sistema de referencia de tercer orden
La función de transferencia en este caso es:
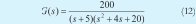
Se aprecia que el denominador se compone de dos factores que deben generar una respuesta muy parecida a la de un sistema de segundo orden sub-amortiguado.
Esta vez la intención no es causar un comportamiento muy oscilatorio, tan sólo se quiere apreciar el comportamiento del circuito para sistemas de mayor orden. El algoritmo se detiene en doscientas generaciones. Al igual que los anteriores casos, se realizan 30 experimentos.
La respuesta del mejor individuo en el último experimento se muestra en la Figura 11, en este caso el NMSE obtenido es igual a 0.0030. El resultado es aceptable considerando que el circuito es por naturaleza de segundo orden y se le está forzando a seguir una respuesta de tercer orden. El gráfico del error promedio de los mejores individuos por generación se presenta en la Figura 12. Con respecto a la misma escala vertical que la Figura 8, las barras de desviación son más pequeñas que en las pruebas anteriores dado que la respuesta de referencia es más suave y así le resulta más fácil al algoritmo llegar al óptimo.

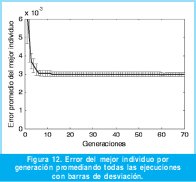
Para las tres anteriores pruebas se apreciaron comportamientos característicos. En el primer caso según la Figura 7 y 8, el algoritmo converge mucho antes de las 30 generaciones estipuladas y genera una respuesta tan acertada, que al graficarla junto con la de referencia, estas se superponen. En el segundo caso se aprecia que el algoritmo se enfrenta a una referencia más particular por lo que ya no se solapan del todo las gráficas en la Figura 9 y las barras de desviación en la Figura 10 son más considerables que el caso anterior. Por último, el tercer caso es una muestra de convergencia temprana pero no de una respuesta necesariamente óptima.
5. CONCLUSIONES
Se ha presentado una propuesta para el diseño evolutivo de circuitos analógicos basados en amplificadores operacionales. La propuesta hace uso de un algoritmo genético simple cuya función de aptitud está dada por un sistema de inferencia difusa, lo cual ha permitido incluir una valoración lingüística de los individuos solución. En particular, la función de aptitud difusa presenta una serie de regiones interesantes que favorecen tanto a la convergencia del algoritmo como a la diversidad genética de las poblaciones.
La propuesta se ha validado sobre tres casos de aplicación. En cada uno de ellos se logró emular satisfactoriamente la respuesta al escalón de un sistema de determinado orden por medio de un circuito relativamente simple como es el filtro de Sallen-Key. Por tanto el método propuesto adquiere un valor interesante para el diseño de computadores analógicos, los cuales se aplican en la simulación de algunos procesos físicos en el área de control.
Como trabajo futuro se propone llevar esta propuesta de diseño hacia circuitos analógicos más complejos cuyo análisis matemático directo sea complicado. Igualmente valdría la pena explorar algoritmos evolutivos más interesantes que permitieran realizar optimización de múltiples objetivos, lo que permitiría incluir variables de interés adicionales al NMSE.
REFERENCIAS BILIOGRÁFICAS
[1] El B. Grimbledy. "Automatic Analogue Circuit Synthesis using Genetic Algorithms". The University of Reading, Reading. 2000.
[2] V. Aggarwal. "Evolving Sinusoidal Oscillators Using Genetic Algorithms". Netaji Subhas Institute of Technology, New Delhi. 2002.
[3] D. H. Horrocks, Y.M.A. Khalifa. "Genetic Algorithm Design of Electronic Analogue Circuits Including Parasitic Effects". School of Engineering, University of Wales, College of Cardiff, Cardiff. 1996.
[4] C. A. Peña. "Coevolutionary Fuzzy Modeling". Lecture Notes in Computer Science. Springer-Verlag, Alemania. 2004.
[5] R. L. Haupt, D. H. Werner. "Genetic Algorithms in Electromagnetics". John Wiley & Sons, Inc, New Jersey. 2007.
[6] M. D. Vose. "The Simple Genetic Algorithm". MIT Press, Cambridge, MA, August. 1999.
[7] M. C. Cirillo and A. A. Poli. "On the use of the normalized mean square error in evaluating dispersion model performance". Atmospheric environment. Part A, general topics, Vol 27, No. 15, pp. 2427-2434. 1993.
[8] S. Sumathi, T. Hamsapriya, P. Surekha. "Evolutionary Intelligence". Springer-Verlag, Berlin. 2008.
[9] M. Affenzeller, S. Winkler, S. Wagner y A. Beham. "Genetic algorithms and genetic programming - Modern concepts and practical applications". Numerical Insights. CRC Press. 2009.
[10] Z. Michalewicz. "Genetic Algorithms + Data Structures = Evolution Programs". Springer-Verlag, Heidelberg, 3ra Edición. 1996.
[11] L. X. Wang. "A course in Fuzzy Systems and Control". 1st ed., New Jersey: Prentice Hall International. 1997.
[12] J. Karki."Analysis of the Sallen-Key architecture". Texas instruments application report SLOA024B, Sep. 2002.
[13] D. Goldberg. "Genetic Algorithms in Search, Optimization and Machine Learning". Addison-Wesley.1989.
[14] J. H. Holland. "Adaptation in Natural and Artificial Systems". Cambridge, MA: The MIT Press. 1992.
Federico Andrés Sanabria Muñoz
Estudiante de Ingeniería Electrónica de la Universidad Distrital Francisco José de Caldas. Actualmente está adscrito al grupo de investigación del Laboratorio de Automática, Microelectrónica e Inteligencia Computacional (LAMIC) de la Universidad Distrital Francisco José de Caldas donde realiza estudios en el campo de Inteligencia Computacional. fasanabriam@correo.udistrital.edu.co
Héctor Leonardo Hostos Orjuela
Estudiante de Ingeniería Electrónica de la Universidad Distrital Francisco José de Caldas. Actualmente está adscrito al grupo de investigación del Laboratorio de Automática, Microelectrónica e Inteligencia Computacional (LAMIC) de la Universidad Distrital Francisco José de Caldas donde realiza estudios en el campo de Inteligencia Computacional. hlhostoso@correo.udistrital.edu.co
Miguel Melgarejo
Ingeniero Electrónico de la Univerisdad Distrital Francisco José de Caldas. Magister en Ingeniería Electrónica y Computadores de la Universidad de los Andes. Ha sido investigador del Centro de Microelectrónica de la Universidad de los Andes e investigador invitado del Logic Systems Laboratory de la Ecolé Polytechnique Federale de Lausanne, Suiza. Actualmente es profesor asistente de la facultad de ingeniería de la Universidad Distrital Francisco José de Caldas e investigador del Laboratorio de Automática, Microelectrónica e Inteligencia Computacional (LAMIC) en la misma universidad.
Ha publicado 45 artículos técnicos y dos capítulos de libro. Ha servido como miembro del comité de programa del IEEE World Congress on Computational Intelligence (2008) y de la International Conference on Intelligente Computing (2008 y 2010). Igualmente ha servido como miembro del comité técnico del IEEE Latin American Symposium on Circuits and Systems (2010) y de la IEEE International Conference on Fuzzy Systems (2008-2010). Sus areas de interés son: Sistemas difusos tipo dos, computación evolutiva, sistemas empotrados y procesamiento digital de señales. mmelgarejo@udistrital.edu.co
Creation date:
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.





2.jpg)










