DOI:
https://doi.org/10.14483/23448393.1879Published:
2003-11-30Issue:
Vol. 9 No. 2 (2004): July - DecemberSection:
Science, research, academia and developmentAplicación de un procesador difuso tipo II en la ecualización de canales no lineales y variantes en el tiempo
Keywords:
Ecualización de canal, Lógica di-fusa tipo dos, procesadores difusos, sistemas difusos (es).Downloads
References
M. Melgarejo, C. Peña-Reyes, "Desarrollo hardware de un procesador difuso tipo dos", revista Ingeniería , Universidad Distrital Francisco José de Caldas, Vol. 9 No. 1, 2004. pp 17-25
M. Melgarejo, C. Peña-Reyes, "Pro Two: a hardware based platform for real time Type-2 Fuzzy inference", Proceedings of the 2004 IEEE International Conference on Fuzzy Systems, Budapest HU, Jul. 2004
X.L. Wang , J. M. Mendel , " Fuzzy Adaptive filters, with application to non linear channel equalization", IEEE Transactions on Fuzzy Systems, Vol 1 No 3, August 1993.
P sarwal,. D.N. Srinath, " A Fuzzy Logic System For Channel Equalization", IEEE Transactions on Fuzzy Systems , Vol. 3 No. 2, May 1995
S. K. Patra , B. Mulgrew , " Efficient Architecture for bayesian equalization using fuzzy filters" , IEEE Transacations on circuits and systems II: Analog and digital signal processing , Vol. 45 , No. 7, July 1998.
Q. Liang and J. Mendel, " Equalization of nonlinear time-varying channels using type-2 fuzzy adaptive filters", IEEE. Trans. On Fuzzy Systems, Vol. 8, No. 5, pp 551-563, Oct 2000.
Q. Liang and J. Mendel, " Overcoming time-varying co-channel interference using type-2 fuzzy adaptive filters ", IEEE. Trans. On Circuits and systems II , Vol. 47 pp 1419-1429, Dec. 2000.
J. F. McEachern , R. T. Miyamoto, " Emerging technologies: ONR's need for intelligent computation in underwater sensors", Computational Intelligence The experts speak , IEEE Press - Wiley Interscience, 2003, Chap. 5, pp 60-61.
UIT, "ITC Specification of Digital Terrestrial Television Transmissions in the United Kingdom", July 2003.
Alpha Data Parallel systems, "ADM-XRC-II PCI Mezzanine card User Manual", http://www.alpha-data.com , 2002, Version 1.5.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Ingeniería, 2004-00-00 vol:9 nro:2 pág:4-9
Aplicación de un procesador difuso tipo II en la ecualización de canales no lineales y variantes en el tiempo
Miguel A.Melgarejo Rey
Miembro del Grupo de Investigación LAMIC.
Carlos A. Peña Reyes
Novartis Institutes for Biomedical research, Bassel, Suiza.
Resumen
En este artículo se da continuación al trabajo Desarrollo Hardware de un procesador difuso tipo dos. Aquí se presenta y justifica el contexto de aplicación dado a nuestro procesador, el cual se emplea a manera de filtro difuso adaptativo para la ecualización en tiempo real de un canal de comunicación no lineal y variante en el tiempo. El ecualizador se caracteriza en términos de su tasa de bit erroneos (Bit Error Rate) y se confronta con un ecualizador de canal basado en lógica difusa tipo uno. Igualmente, se observa experimentalmente como la resolución de las operaciones internas del procesador afecta el desempeño del ecualizador. En ese sentido se muestra que un ecualizador difuso tipo dos es más robusto que un tipo uno cuando la resolución de sus operaciones internas disminuye.
Palabras clave:
Ecualización de canal, Lógica difusa tipo dos, procesadores difusos, sistemas difusos.
Abstract
This article describes an application context for a Type-2 fuzzy processor which has been implemented as a hardware solution. The processor is used to implement a fuzzy adaptive filter intended to perform a real-time equalization of a non-linear, time-variant communications channel. The fuzzy equalizer is characterized in terms of its Bit Error Rate and it is compared with a Type-1 fuzzy channel equalizer. Besides, it is observed experimentally how the resolution of the internal operations disturbs the performance of the equalizer. In this sense it is shown that a Type-2 fuzzy equalizer is more robust than a Type-1 when the resolution of their internal operations decreases.
Key Words:
Channel equalization, Type-2 fuzzy logic, fuzzy processors, fuzzy systems.
I. INTRODUCCIÓN
En este artículo se presenta el contexto de aplicación para el procesador difuso tipo dos reportado en [1] y [2]. El contexto se limita a la implementación de filtros difusos adaptativos (Fuzzy Adaptive Filters FAF) para la ecualización de canales de comunicación no lineales y variantes en el tiempo. Wang et al [3] proponen usar un sistema difuso tipo uno a manera de ecualizador para un canal de comunicación. Sarwal et al [4] exponen un algoritmo de agrupamiento para diseñar el ecualizador a partir de la observación de la salida del canal. Patra et al [5] derivan una estructura basada en sistemas difusos tipo uno aplicada a la ecualización bayesiana de canales digitales. Liang et al [6,7] extienden la idea de Patra a sistemas difusos tipo dos. En este último trabajo se muestra que esta clase de sistemas tienen un mejor desempeño, con respecto a las soluciones típicamente usadas, cuando los canales de comunicación son variantes en el tiempo.
En la actualidad, varias aplicaciones demandan tasas de transmisión elevadas, las cuales se ven limitadas por los algoritmos de ecualización que se usan. Los sistemas difusos tipo dos se perfilan como una solución apropiada para esta problemática. Sin embargo, la realización software de estos sistemas puede llegar a no satisfacer los requisitos de procesamiento que exigen algunas de las aplicaciones. Tal es el caso de ciertos sistemas de comunicación naval, donde el número de señales a transmitir al igual que las tasas de muestreo hacen que las velocidades de transmisión estén por encima de 10Mb/s [8]. Otra aplicación representativa es la transmisión terrestre de televisión digital donde las tasas de transmisión estándar según norma europea se encuentran entre 18.1 y 24.3 Mb/s [9]. Estas dos aplicaciones además de demandar elevadas tasas de procesamiento en los sistemas receptores, también exigen que las solucio nes aplicadas estén empotradas, con el fin de optimizar espacio y consumo de potencia. En este orden de ideas, la realización hardware de ecualizadores de canal ba sados en lógica difusa tipo dos se hace necesaria, razón por la cual se escogió esta aplicación para efectos de prueba de nuestro procesador.
El artículo se organiza de la siguiente manera: la sección II presenta una introducción a la ecualización de canales no lineales por medio de filtros difusos adaptativos. En la sección III se explica el proceso de sintonía típico de un ecualizador difuso. Los resultados experimentales obtenidos con nuestro procesador se muestran en la sección IV. Finalmente, se concluye en la sección V.
II. ECUALIZACIÓN DE CANALES NO LINEALES POR MEDIO DE FILTROS DIFUSOS ADAPTATIVOS
2.1 Modelo del canal
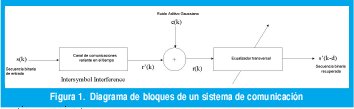
El diagrama de bloques de un sistema de comunicación, el cual se encuentra sometido a interferencia entre símbolos y ruido aditivo Gaussiano se muestra en Fig.1. Donde s (k) es el símbolo que se va a transmitir, e (k) es el ruido y r (k) la salida del canal. Esta última se expresa de la siguiente forma [3,5,6]:
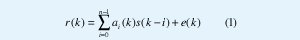
donde αi (k) son los coeficientes del canal. En (1) se asume que s (k-i ) es binaria y toma los valores +1 y -1 , los cuales se presentan con igual probabilidad.
La estructura típica de un ecualizador de canal se muestra en Fig. 2. Las entradas del ecualizador son la salida presente y anteriores del canal r(k), r (k1),...., r (k-p+1) donde p es el orden del ecualizador. Es conveniente notar este conjunto de muestras en forma vectorial tal como sigue:
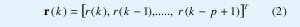
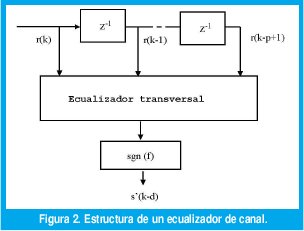
de (1) se observa que r(k) depende del vector de entrada s(k), el cual se define como:
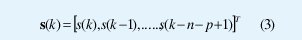
Teniendo en cuenta que s(k) es una señal binaria d( +1 ó -1 ), hay ns=2 n + p posibles combinaciones a la entrada del canal [4]. En la Fig. 1 la señal sin ruido r'(k) se expresa como:
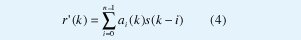
Haciendo
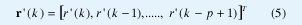
donde r'(k) se denomina un estado de canal. Obsérvese de (4) y (5) que cada una de las combinaciones de entrada s(k) genera un estado de canal, luego la probabilidad de ocurrencia de r'(k) es 1/ns [3,4,5].
Una decisión correcta del ecualizador mostrado en Fig. 2 se da cuando:
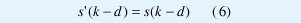
donde s'(k-d) es el valor de salida decidido por el ecualizador y d se conoce como el retardo de decisión. Teniendo en cuenta las posibles categorías para s(k-d) ( +1 ó -1), los estados de canal pueden ser clasificados en dos grupos:
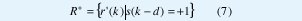
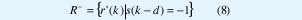
dado que cada s(k-d) tiene igual probabilidad de ocurrencia, el número de elementos en R+ y R- es igual [3,4].
2.2 Ecualización Bayesiana
En [3,5] se muestra que la decisión de salida de un ecualizador Bayesiano con normalización se puede expresar como sigue:
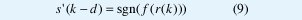
donde f(r(k)) tiene la siguiente forma:
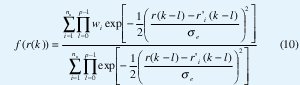
Donde σ es la desviación estándar del ruido de canal e(k). Este modelo de ecualizador tiene un buen desempeño cuando los canales son invariantes en el tiempo [3,4,6].
2.3 Sistemas difusos como ecualizadores de canal
La salida de un sistema difuso tipo uno con fusificación singleton, funciones de pertenencia gaussianas, motor de inferencia producto y defusificación altura se expresa como sigue [3,4]:
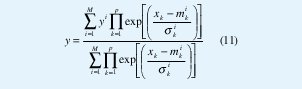
Note que (10) puede implementarse a través de (11), en otras palabras, un ecualizador bayesiano es equivalente al sistema difuso tipo uno descrito por (11) [5].
De (10) y (11) se observa que los ecualizadores Bayesianos, implementados a manera de sistemas difusos tipo uno, tan solo consideran la magnitud de los estados de canal y la desviación estándar del ruido de e(k). Cuando un sistema difuso tipo uno se emplea como ecualizador de canal , se le denomina filtro difuso. Si el sistema difuso se sintoniza a partir de las señales r (k) o r'(k), se le denomina filtro difuso adaptativo [6,7].
III. ECUALIZACIÓN DE CANALES VARIANTES EN EL TIEMPO POR MEDIO DE SISTEMAS DIFUSOS TIPO DOS. (Ejemplo de diseño)
El ecualizador descrito por (10) se obtiene cuando el canal es invariante en el tiempo, es decir que los coeficientes ai son constantes. Cuando el canal es variante en el tiempo, es necesario incluir la información relativa a la variación de los coeficientes del canal dentro del algoritmo de ecualización. Como se mencionó en la sección anterior, para un ecualizador basado en (11) tan solo es posible tener en cuenta el valor de los estados de canal (valor medio de las funciones de pertenencia Gaussiana) y la desviación estándar del ruido e(k). En este orden de ideas, Liang et al [6,7] han considerado usar un sistema difuso tipo dos TSK sin normalización a manera de ecualizador para canales no lineales y variantes en el tiempo.
En este caso, la sintonía del ecualizador se lleva a cabo a partir de un proceso de agrupamiento (clustering) de la salida del canal ( sin ruido ). En ese sentido se habla de un filtro difuso adaptativo tipo dos (T2-FAF). El proceso sintonización se ilustrará sobre el canal considerado en [6].
3.1 Sintonía
La sintonía de un sistema difuso hace referencia a establecer los parámetros de los conjuntos difusos de la entrada y la salida. En el caso de un sistema difuso tipo uno y funciones de pertenencia Gaussiana, los parámetros que se deben establecer son la media y la desviación estándar de las funciones de pertenencia. En el caso de un sistema difuso tipo dos con huellas de incertidumbre Gaussianas es necesario tener en cuenta la naturaleza de la incertidumbre a tratar. En este orden de ideas, se tendría dos posibilidades, en la primera, se debe establecer el valor medio de las funciones de pertenencia gaussianas mMF y el intervalo de variación de su desviación estándar [σ1,σ2], el cual se puede expresar en términos de un valor medio k=(σ1) +σ2 y una desviación estándar d=(σ1 -σ2)/2. En la + 2 segunda, es necesario determinar la desviación estándar de las funciones de pertenencia σMF y el intervalo de variación del valor medio [m1,m2], el cual al igual que en el caso anterior podría darse en términos de un valor medio y una desviación estándar.
La confrontación presentada anteriormente, tiene como propósito ilustrar que el diseño de un sistema difuso tipo dos involucra un grado de libertad más que en el caso de un sistema difuso tipo uno.
A continuación se ilustrará conceptualmente el proceso de sintonía (diseño) de un filtro difuso adaptativo tipo dos para el canal propuesto en [6]. La ecuación en diferencias que describe a este canal es la siguiente:
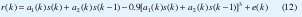
Antes de iniciar la exposición del proceso de sintonía es necesario definir algunas cosas. Los coeficientes son variantes en el tiempo y su variación obedece a un proceso estocástico gaussiano coloreado (Colored Gaussian Sequence), el cual se obtiene al pasar ruido blanco gaussiano por un filtro pasa-bajos. Para los dos coeficientes, el ruido empleado tiene desviación estándar qr y media cero.
El ruido de canal e(k) tiene valor medio cero y su desviación estándar σe depende del hecho que:
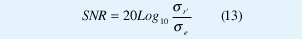
Donde SNR es la relación señal a ruido en el canal, σr' es la desviación estándar de la salida del canal, dado que los coeficientes del canal varían con el tiempo.
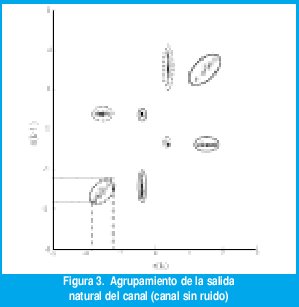
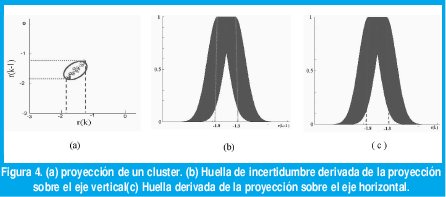
El primer paso en el proceso de diseño es llevar a cabo un agrupamiento de la salida natural del canal o salida sin ruido r'(k). Fig. 3 presenta una muestra de agrupamiento obtenida a partir de una secuencia binaria de entrada de cien mil símbolos. Obsérvese que para este canal se presentan ocho estados (cada cluster define un estado). Los estados resaltados en óvalos punteados se dan cuando la entrada s(k) es el símbolo +1, mientras que los resaltados en óvalos continuos se dan cuando s(k) es 1.
En este caso la estimación de s(k) se llevará a cabo por medio de la observación de r (k) y r (k-1), luego estas dos variables serán las entradas del T2-FAF. El número de reglas del sistema difuso es igual al número de estados del canal, en este caso es de ocho. Esta equivalencia se debe al hecho que el ecualizador debe estimar s(k) a partir de una de las ocho posibles situaciones (clusters) que se presentan en su entrada.
Por lo tanto, el segundo paso es definir la base de reglas del sistema difuso. Cada regla tiene la siguiente forma:
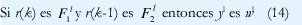
Donde F1l y F2l son huellas de incertidumbre construidas a partir de funciones gaussianas con valor medio incierto. En cuanto al consecuente se refiere wl es +1 cuando el cluster rojo (s (k) = +1) y -1 cuando el cluster es verde (s (k) = -1).
La variación del canal puede observarse como la presencia de incertidumbre en el valor medio de sus coeficientes [6]. Razón por la cual se eligieron huellas de incertidumbre con desviación estándar única y valor medio incierto. Tal como se muestra en Fig. 4, el intervalo de variación del valor medio de cada F1l se obtiene a partir de la proyección del l-esimo cluster sobre el eje horizontal, mientras que los intervalos de las funciones F2l se determinan de las proyecciones sobre el eje vertical. La desviación estándar de las funciones de pertenencia gaussianas interiores se obtiene de la relación señal a ruido del canal según (13).
IV. RESULTADOS EXPERIMENTALES
El procesador difuso tipo dos que se implementó, se utilizó para la realización hardware de dos Filtros difusos adaptativos. Estos filtros se aplicaron en la ecualización del canal descrito por (12). Nótese que es posible emplear nuestra arquitectura hardware para la realización de un sistema difuso tipo uno. Para ello, basta con hacer iguales las funciones de pertenencia superior e inferior de cada huella de incertidumbre.
Una diferencia importante entre los resultados reportados en [6] y los que aquí se presentarán, es el hecho que en ese trabajo los experimentos se ejecutaron por medio de sistema difusos (tipo uno y tipo dos) TSK sin normalización, mientras que aquí, los resultados se derivan de sistemas difusos Mamdani tipo uno con normalización y tipo dos basados en las formas cerradas Wu-Mendel.
4.1 Metodología
En Fig. 5 se presenta un diagrama conceptual de la metodología empleada en la aplicación del procesador difuso tipo dos. El primer paso consiste en programar la FPGA con la cadena de configuración obtenida del proceso de ubicación e interconexión. La programación se lleva a cabo a través del sistema de desarrollo ADMXRC2 de la empresa alpha data [10].
La siguiente tarea es diseñar el filtro difuso adaptativo, lo cual consiste en determinar los parámetros de las huellas de incertidumbre. Para este efecto se generaron algunas rutinas en el ambiente de trabajo MATLAB® 5.1 de la empresa Mathworks©.
Una vez estimadas las huellas de incertidumbre, es necesario llevarlas al formato que se maneja en la arquitectura hardware. Para ello se debe obtener las funciones de pertenencia superior e inferior de cada huella, discretizarlas, cuantificarlas y transformarlas en esquemas de búsqueda por tabla. En [1] se explicó que el consecuente del procesador se configura a través de los esquemas de aritmética distribuida. Por tanto, se debe generar el contenido de las memorias de estos esquemas según la base de reglas que se haya definido en el diseño del FAF.
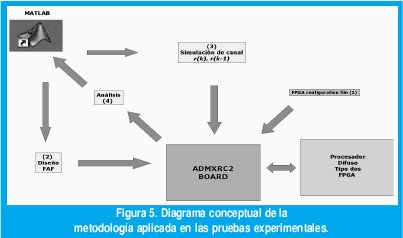
La simulación del canal se lleva a cabo por medio de MATLAB. Antes de ejecutarla, es necesario definir tanto la relación señal a ruido del canal como la desviación estándar de la variación de sus coeficientes. El resultado de esta simulación es el par de secuencias r (k) y r (k-1). Con estas dos secuencias se construye un tabla , la cual se almacena en memoria. Luego a través de una sencilla rutina, el procesador central lee esta tabla y la envía al procesador difuso. La salida del FAF se lee y almacena en memoria en la medida que se envía la secuencia de entrada. El resultado de este proceso es una secuencia binaria, la cual se lleva a MATLAB para efectos de análisis.

4.2 Resultados Cualitativos.
En Fig. 6 se presentan algunos resultados cualitativos para diversas condiciones de canal. La señal de entrada elegida fue una imagen en tonos de gris de 128x128 píxeles. Cada píxel tiene una representación entera de 8 bits, por lo tanto el número total de símbolos ecualizados es de 131072 ( 128x128x8).
La relación señal a ruido es de 20dB en todos los casos. La condición de canal hace referencia al valor de qr, el cual se definió como la desviación estándar del ruido blanco que da origen al proceso gaussiano coloreado. Recuérdese que este proceso es el que introduce incertidumbre en el valor medio de los coeficientes del canal.
En términos cualitativos se nota que el FAF tipo dos tiene un mejor desempeño que el tipo uno, y es más robusto cuando qr tiende a incrementarse. Esta observación es original de Liang et al en [6] para sistemas TSK tipo uno y tipo dos, los cuales fueron implementados a modo de rutinas software sobre procesadores de propósito general y alta resolución. Aquí, el mismo resultado se está validando para otra clase de sistemas difusos, con la diferencia que nuestros filtros están soportados por una estructura hardware dedicada de baja resolución.
4.3 Resultados cuantitativos
La medida cuantitativa del desempeño de los filtros se da en términos de su tasa de bits erróneos (Bit Error Rate BER). Este parámetro hace referencia a la razón entre el número de símbolos estimados de forma errónea Be y el número total de símbolos recibidos Bt:
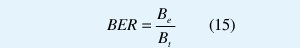
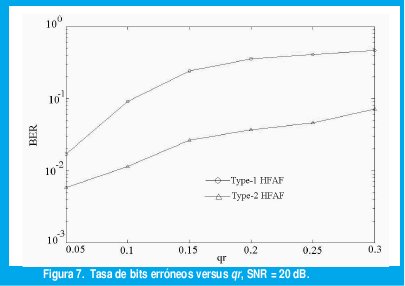
En Fig. 7 se presenta una comparación entre el desempeño del FAF tipo uno y tipo Dos. Por cada condición de canal se considera la tasa promedio, la cual se estimó de una secuencia de 10 realizaciones (pruebas). En cada realización se empleó como señal de entrada al canal s(k) una cadena binaria aleatoria de 10000 símbolos.
Es claro que el desempeño del FAF tipo dos es mejor con respecto al tipo uno, igualmente nótese que su BER aumenta menos rápido cuando qr se incrementa. Se podría decir en este caso particular, que el FAF tipo dos es más robusto que el tipo uno cuando la incertidumbre en los coeficientes es mayor.
Los resultados presentados en Fig. 7 motivaron el estudio del comportamiento de los filtros cuando la resolución de los sistemas difusos disminuye. Tanto el FAF tipo uno como tipo dos se implementaron a manera de rutinas en software. La resolución de salida efectiva de los sistemas difusos se fijó en 32 bits y se corrieron las mismas pruebas que se realizaron para las versiones hardware. Posteriormente, se comparó el desempeño de los filtros software (los cuales se denominaran de aquí en adelante como filtros de alta resolución) y las filtros hardware ya probados (las cuales se denominaran filtros de baja resolución) a través de la siguiente figura de robustez:
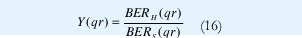
Donde BERH((qr) es la tasa de bits erróneos de la versión de baja resolución dada una condición de canal qr, y BERS(qr) es la tasa de bits erróneos de la versión de alta resolución. El propósito de la figura de robustez Y(qr) medir que tanto cambia el desempeño del FAF cuando la resolución efectiva de salida disminuye.
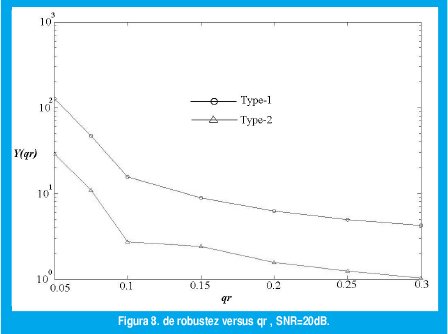
En Fig. 8 se presenta Y(qr) dado un SNR de 20 dB. Note que para el FAF tipo dos, la diferencia entre los desempeños de su versión de alta y baja resolución es menor que para el FAF tipo uno. Este es el resultado experimental más importante que se obtuvo de estas pruebas. A partir de este se deja abierta la siguiente pregunta: "Son siempre los filtros difusos adaptativos tipo dos más robustos que los tipo uno ante la disminución de la resolución efectiva de sus operaciones internas?".
V. CONCLUSIONES
Se ha presentado el contexto de validación de un procesador difuso tipo dos implementado en hardware. Este procesador se empleó para tratar el problema de ecualización de canales no lineales y variantes en el tiempo por medio de lógica difusa tipo dos.
Los resultados muestran que es posible implementar filtros difusos adaptativos tipo dos que operen en tiempo real sobre esta plataforma hardware. Se validaron algunos resultados ya reportados en relación al desempeño de los sistemas difusos tipo dos versus los tipo uno en el problema de ecualización de canales. Como aporte original de este trabajo se observó que un FAF tipo dos es más robusto que un tipo uno frente a un decremento en la resolución efectiva de sus operaciones internas. Esto sugiere que los FAFs tipo dos pueden ser candidatos interesantes a la hora de implementar ecualizadores de canal con área de implementación reducida.
REFERENCIAS BIBLIOGRÁFICAS
[1] M. Melgarejo, C. Peña-Reyes, "Desarrollo hardware de un procesador difuso tipo dos", revista Ingeniería , Universidad Distrital Francisco José de Caldas, Vol. 9 No. 1, 2004. pp 17-25
[2] M. Melgarejo, C. Peña-Reyes, "Pro Two: a hardware based platform for real time Type-2 Fuzzy inference", Proceedings of the 2004 IEEE International Conference on Fuzzy Systems, Budapest HU, Jul. 2004
[3] X.L. Wang , J. M. Mendel , " Fuzzy Adaptive filters, with application to non linear channel equalization", IEEE Transactions on Fuzzy Systems, Vol 1 No 3, August 1993.
[4] P sarwal,. D.N. Srinath, " A Fuzzy Logic System For Channel Equalization", IEEE Transactions on Fuzzy Systems , Vol. 3 No. 2, May 1995
[5] S. K. Patra , B. Mulgrew , " Efficient Architecture for bayesian equalization using fuzzy filters" , IEEE Transacations on circuits and systems II: Analog and digital signal processing , Vol. 45 , No. 7, July 1998.
[6] Q. Liang and J. Mendel, " Equalization of nonlinear time-varying channels using type-2 fuzzy adaptive filters", IEEE. Trans. On Fuzzy Systems, Vol. 8, No. 5, pp 551-563, Oct 2000.
[7] Q. Liang and J. Mendel, " Overcoming time-varying co-channel interference using type-2 fuzzy adaptive filters ", IEEE. Trans. On Circuits and systems II , Vol. 47 pp 1419-1429, Dec. 2000.
[8] J. F. McEachern , R. T. Miyamoto, " Emerging technologies: ONR's need for intelligent computation in underwater sensors", Computational Intelligence The experts speak , IEEE Press - Wiley Interscience, 2003, Chap. 5, pp 60-61.
[9] UIT, "ITC Specification of Digital Terrestrial Television Transmissions in the United Kingdom", July 2003.
[10] Alpha Data Parallel systems, "ADM-XRC-II PCI Mezzanine card User Manual", http://www.alpha-data.com , 2002, Version 1.5.
Miguel A. Melgarejo Rey
Ingeniero Electrónico Universidad Distrital, Grado de Honor Francisco José de Caldas. Magíster en Ingeniería Electrónica y computadores, Universidad de los Andes, Graduado con Honores y tesis de maestría laureada. Profesor Asistente Facultad de Ingeniería, Universidad Distrital. Investigador Adjunto Laboratorio de Automática, Microelectrónica e Inteligencia Computacional, Universidad Distrital. mmelgarejo@ieee.org
Carlos A. Peña Reyes
Ingeniero Electrónico Universidad Distrital Francisco José de Caldas. Especialista en control automático, Universidad del Valle. Doctor en Informática y ciencias de la computación, École Polytechnique Fédérale de Lausanne (EPFL), Suiza. Consultor, Novartis Institutes for Biomedical research, Bassel , Suiza. c.penha@ieee.org
Creation date:
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.





2.jpg)










