DOI:
https://doi.org/10.14483/23448393.2855Published:
2008-11-30Issue:
Vol. 8 No. 1 (2003): January - JuneSection:
Science, research, academia and developmentSistema de inferencia difusa secuencial basado en aritmética distribuida
Distributed Arithmetic Based Sequential Fuzzy Processor
Keywords:
Lógica Difusa, Hardware Difuso, Diseño FPGA, Aritmética Distribuida. (es).Downloads
References
Darwin, C. R. (1859). The origin of species. Londres: John Murrap.
Goldberg, D.E. (1986). Genetic Algorithms in Search, Optimization, and Machine Learning. Cambridge: MIT Press.
Kinnear, K.E.(1994). Advances in Genetic Programing. MIT Press.
Koza, J.R. (1992) Genetic programming: on the programing of coputers by mean of natural selection. MIT Press.
Lemone, K.A.(1999). Fundamentos de compiladores. Mexico: CECSA.Autores
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Ciencia, Investigación, Academia y Desarrollo
Ingeniería, 2003-00-00 vol:8 nro:1 pág:71-75
Sistema de inferencia difusa secuencial basado en aritmética distribuida
DISTRIBUTED ARITHMETIC BASED SEQUENTIAL FUZZY PROCESSOR
David Camilo Olea Salgado
Miembro del Grupo de investigación: Laboratorio de Automática, Microelectrónica e Inteligencia Computacional LAMIC.
Andrés Eduardo Gaona Barrera
Miembro del Grupo de investigación: Laboratorio de Automática, Microelectrónica e Inteligencia Computacional LAMIC.
Miguel Alberto Melgarejo Rey
Miembro del Grupo de investigación: Laboratorio de Automática, Microelectrónica e Inteligencia Computacional LAMIC.
Resumen
Este artículo presenta el diseño y validación de un sistema de inferencia difusa tipo Mamdani de dos entradas, 16 reglas y una salida, orientado a implementación en celdas lógicas programables. El motor de inferencia del sistema opera secuencialmente con el fin de optimizar recursos lógicos de la arquitectura. La etapa de defusificación del sistema es de tipo novel dado que se emplea el esquema de Aritmética Distribuida Paralela. La arquitectura puede ser modificada por medio de una herramienta software de alto nivel.
Palabras Clave: Lógica Difusa, Hardware Difuso, Diseño FPGA, Aritmética Distribuida.
Abstract
This article presents the design and validation of a Mamdani type hardware fuzzy inference system with two inputs, 16 rules and one output. Fuzzy inference engine of this system works sequentially in order to optimize hardware resources. Defuzzification stage is novel due to it is based on a distribute arithmetic approach. Systemss architecture can be modified by means of a high level software tool.
Key words: Fuzzy logic, Fuzzy Hardware, FPGA Design, Distributed Arithmetic.
I. INTRODUCCIÓN
Diversos problemas de procesamiento de información en tiempo real podrían ser tratados con Sistemas de Inferencia Difusa (FIS) [1-3]. Para este efecto es necesario que tales sistemas tengan algún grado de flexibilidad y al mismo tiempo una tasa de computo apropiada [4-7]. En este sentido podría pensarse en soluciones software, las cuales, siendo flexibles presentan limitaciones en velocidad. Por otro lado, las soluciones hardware a medida (circuitos integrados de aplicación específica) ofrecen altas velocidades de procesamiento, pero en general sus prestaciones para reconfiguración son mínimas.
Como solución al problema existente entre velocidad y flexibilidad en los FIS hardware, se proponen los dispositivos de lógica programable FPGAs (Field Programmable Gate Array)[8-12], los cuales, al ser dispositivos reconfigurables, son flexibles y exhiben altas velocidades de procesamiento.
El FIS que se presenta en este artículo, se basa en una arquitectura modular secuencial, pretendiendo de este modo minimizar la utilización de área en la implementación hardware. Dentro de este mismo enfoque, y buscando mejorar la resolución en la salida del bloque de defusificación, sin afectar la velocidad, se utilizó la Aritmética Distribuida (DA) [1516], metodología que no ha sido explorada en desarrollos anteriores en materia de fuzzy hardware.
El sistema de inferencia difusa propuesto tiene un máximo de: dos entradas, cada una con cuatro conjuntos difusos, una base de 16 reglas, y una salida con cuatro conjuntos difusos (singletons) [14]. El sistema puede tener menor cantidad de reglas o conjuntos de entrada o salida dependiendo de las especificaciones del usuario. Estas especificaciones son tomadas por una herramienta software encargada de generar automáticamente archivos VHDL (Very high speed integrated circuit Hardware Description Language) que describen en su totalidad al sistema.
La razón de usar una descripción en módulos, en donde se identifiquen claramente las partes principales de un FIS (fusificador, motor de inferencia y defusificador), radica en que el sistema pueda ser fácilmente adaptado a diferentes aplicaciones, o trabajar en sistemas autónomos o interdependientes (Ej. neuro-difuso) [1,5].
El documento se organiza de la siguiente forma: la sección II presenta una descripción detallada de la arquitectura. Se hace énfasis en la etapa de defusificación, resaltándose los elementos conceptuales más importantes de la aritmética distribuida y como estos fueron empleados en el diseño de ésta etapa. En la sección III se describe el diseño de la herramienta software usada para generar los bloques funcionales en VHDL descritos en la sección II. La sección IV muestra los resultados de la implementación sobre la FPGA V600ehq240 de Xilinx. La sección V resume las pruebas experimentales realizadas para validar funcionalmente la arquitectura propuesta.
II. ARQUITECTURA PROPUESTA
La arquitectura propuesta para la implementación hardware, se presenta en la Fig. 1; esta ya ha sido validada por medio de simulación numérica en trabajo anterior realizado por los autores [14].
A continuación se describen tres grandes bloques funcionales de la arquitectura: fusificación, matriz de relación-agregación y defusificación, en los cuales se resaltan algunos aspectos de diseño tenidos en cuenta al momento de su concepción.
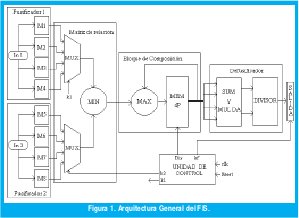
A. BLOQUES DE FUSIFICACIÓN
Cada bloque de fusificación genera cuatro salidas a partir de la misma entrada, estas salidas proporcionan un valor que representa la relación entre el dato actual de la entrada con respecto a las funciones de pertenencia definidas por el usuario.
El esquema para esta operación se presenta en la Fig. 2. Note que se usa una memoria (M1, M2,..,M8) por cada uno de los conjuntos difusos del sistema difuso, donde es mapeado el valor de pertenencia correspondiente al valor de entrada. Cada memoria tiene un tamaño de 256 posiciones por 8 bits.
B. GENERACIÓN DE LA MATRIZ DE RELACIÓN Y COMPOSICIÓN
Este bloque compara cada uno de los valores arrojados por el fusificador de la entrada 1 con cada uno de los valores del fusificador de la entrada 2, generando así un vector de 16 posiciones (con 16 reglas sería una matriz de 4x4) con los mínimos de estas comparaciones, de acuerdo a la implicación tipo Mamdani (1). El bloque también se encarga de verificar cuales valores le pertenecen a una misma salida, tomando el máximo entre ellos (conjunción clásica) [1-2].
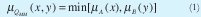
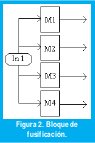
Funcionalmente esto se realiza mediante dos multiplexores conectados a cada una de las salidas de las memorias y a una unidad de mínimo, su esquema es mostrado en la Fig.3. Asociado a este bloque existe una unidad de control que se encarga de colocar los valores apropiados de cada función de pertenencia a la entrada del mínimo, mediante los buses k1 y k2, dependiendo de la base de reglas que el usuario haya definido.
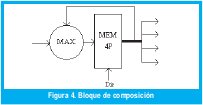
A continuación el valor de cada mínimo, como se muestra en Fig. 4, entra a ser comparado con el existente en una de las cuatro posiciones de una tabla o banco de registros (MEM 4P); los valores de la tabla son colocados en cero al iniciar cada inferencia difusa. Cada posición de la tabla representa una de las salidas difusas. Mediante el bus Dir que proviene de la unidad de control, se establece el índice de la tabla de acuerdo con la regla que se este procesando en el momento.
Para que el sistema sea un poco más eficiente en cuanto a velocidad se refiere, a medida que se calcula un mínimo se inicia el cálculo del máximo, de acuerdo a las reglas definidas. Esto con lleva a que en este proceso se requiere un ciclo de reloj más que la cantidad de reglas definidas, es decir, en el caso que se definan las 16 reglas, son empleados máximo 17 ciclos de reloj. Dicho proceso esta a cargo del bloque llamado UNIDAD, el cual secuencia estos procesos de acuerdo a la entrada de reloj.
C. DEFUSIFICADOR
Este bloque utiliza la defusificación denominada Centro de Área (COA) [1], usando singletons (2), para obtener un único valor de salida, b.
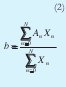
En la ecuación (2), X es el resultado de la agregación (entradas a este bloque), A es la altura de las funciones de pertenencia de salida, b la salida del sistema y N el número total de conjuntos difusos de salida.
A nivel hardware este bloque esta dividido en dos partes, la primera se encarga de la realizar las dos sumatorias, y la segunda es la que ejecuta la división. Para la primera parte, se empleó el esquema de Aritmética Distribuida (DA) [15] para la efectuar la multiplicación, este esquema ofrece enormes ventajas, en cuanto a velocidad y ahorro de recursos hardware, así como una fácil implementación.
Teniendo en cuenta que los coeficientes A son constantes, es decir, los valores de los singletons. Esta sumatoria de productos se puede convertir en una serie de sumas sucesivas, como se muestra en Fig. 5, empleando algunas memorias (N1,N2,...,N8.) para almacenar estos coeficientes.
Según el planteamiento de la DA [15] y de la representación binaria de cualquier número X escalizada a n bits mostrada en (3), una serie como la del dividendo de (2), se puede expresar como en la ecuación (4).

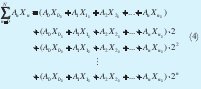
de este modo se pueden mapear en una memoria, los valores los coeficientes A y sus respectivas sumas como se muestra en la Fig. 6.
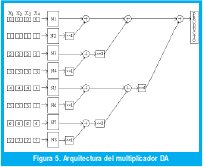

Cada uno de los Xn es descompuesto en sus respectivos bits, formando ocho nuevas palabras de máximo 4 bits (depende de la cantidad de salidas), que direccionan cada una de las ocho memorias, que tienen el mismo contenido. Esta arquitectura se puede emplear de modo serial, usando una sola memoria, un acumulador y un desplazador, el inconveniente es que emplea más ciclos de reloj.
El bloque que realiza la división, lo hace mediante una multiplicación entre el dividendo y el inverso del divisor, que se encuentra almacenado en una tabla, generada en código VHDL. La tabla es direccionada por el divisor y luego se toman solamente los bits más significativos de la multiplicación, es decir, la parte que corresponde al valor entero, como salida total del sistema. Al ser netamente combinacional, es lo suficientemente veloz, pero utiliza una mayor cantidad de recursos hardware.
III. GENERACIÓN AUTOMÁTICA DE LA DESCRIPCIÓN VHDL DEL SISTEMA
Para que el sistema sea de fácil implementación y entendimiento para el usuario final, se diseñó una aplicación en Matlab© para generar el código VHDL de la arquitectura, dadas las especificaciones del sistema de inferencia difusa.
En la herramienta software se pueden definir: las funciones de pertenencia correspondientes a cada entrada, las cuales pueden tener diversas formas (triangulares, gaussianas, tipo S, tipo Z, tipo p, entre otras), las reglas (con implicación and), y los singletons de salida. Cada uno de estos parámetros es almacenado en un archivo que genera la herramienta automáticamente, para después ser leído e interpretado.
De esta forma son generados archivos VHDL, correspondientes a cada módulo; estos se adaptan de acuerdo a lo descrito por el usuario, minimizando la utilización de recursos hardware, y de ciclos de reloj. La arquitectura de la forma creada es modular, flexible y/o exclusiva para un sistema especifico, que en campo puede operar independientemente de un sistema de computo, elevando de este modo su velocidad.
IV. IMPLEMENTACIÓN EN FPGA
Se ha seguido una metodología topdown tradicional para desarrollo y prueba. En primer lugar se ha realizado una validación lógica de cada una de las secciones descritas, con el fin de corregir errores de diseño. Asegurándose de esta forma que cada módulo cumpliera con las especificaciones propias requeridas por el sistema. Posteriormente la arquitectura fue llevada a la FPGA VirtexE® V600ehq240 por medio del software Xilinx Foundation® 4.1.
Las rutas más largas pueden ser optimizadas por el diseñador trabajando directamente sobre la matriz de CLBs de la FPGA. Aunque se logran rutas óptimas, los tiempos de diseño crecen considerablemente. Los resultados de distribución de rutas y congestión en la FPGA se presenta en Fig. 7. Los sectores oscuros representan las secciones donde hay mayor congestión combinacional.
Luego se procedió a hacer la simulación sobre la FPGA escogida, en el software Xilinx Foundation 4, obteniéndose los resultados que se enuncian en la tabla 1. En esta se puede observar en su orden, la frecuencia máxima de operación, el consumo de potencia estimado, la cantidad de bloques funcionales, Mega Inferencias difusas por segundo (MFLIPS) y porcentaje de área usada del dispositivo.


V. VERIFICACIÓN
La verificación del sistema se hizo mediante un código en Matlab©; que permite comparar la salida y señales intermedias entregadas por el sistema en simulación, ante diversos valores de entrada.
Los resultados de estas pruebas permiten evaluar la precisión del sistema con diferentes valores de entrada y su error aproximado en la respuesta final de la inferencia. Este error fue menor del 2%, y la contribución a su incremento se debe en gran medida al bloque de división; este no es tan preciso en el rango donde la función 1/X es altamente no lineal.
También fueron hechas pruebas físicas sobre el dispositivo FPGA mediante la creación de una tabla con distintos valores para las entradas del sistema, esquema denominado self in test. Esto fue hecho para corroborar la velocidad de operación del sistema dado en simulación. Los resultados fueron satisfactorios debido a que el sistema efectivamente opera a la frecuencia y velocidad dada en simulación, además que la respuesta del sistema ante diversas entradas es igual a lo arrojado por las simulaciones.
VI. CONCLUSIONES
Se ha presentado una arquitectura de un sistema de inferencia difusa secuencial con la cual fueron obtenidos buenos resultados de velocidad de procesamiento y de área de silicio en un dispositivo FPGA.
Defusificar empleando el esquema de Aritmética Distribuida, resultó apropiado, ya que este método, permite un ahorro significativo de recursos hardware, a la vez que permite una operación más veloz del sistema. Sin perjuicio de las características de flexibilidad ofrecidas. Además la respuesta del sistema posee un error bajo debido a que la DA maneja una resolución de 8 bits, lo cual es bueno para un sistema como este.
La velocidad de procesamiento del sistema es relativamente alta para un sistema secuencial, pero se buscan mejores tasas de procesamiento, sin variar el esquema de fusificación y defusicación empleadas debido a sus buenos resultados.
Como elemento complementario se creó una herramienta software que genera automáticamente la descripción VHDL del sistema de inferencia difusa, en este sentido, nuestro trabajo se encuentra a la vanguardia en materia de sistemas de desarrollo para fuzzy hardware.
Este tipo de sistemas, donde se puede observar y cambiar fácilmente los parámetros de un sistema difuso, pueden trabajar con sistemas autónomos e interdependientes, que de acuerdo a determinadas condiciones modifique dichos parámetros; con lo cual el sistema llegue a ser adaptable.
VII. TRABAJO FUTURO
Buscar un método para lograr hacer una división mas eficiente en cuanto a recursos se refiere, sin perder las ventajas logradas a nivel de velocidad de funcionamiento.
Probar el sistema en una aplicación real, preferiblemente un sistema de control de una planta altamente no lineal, con el fin de evaluar su desempeño y prestaciones en las condiciones donde son más usados y necesarios los sistemas difusos.
Aprovechando el espacio disponible del dispositivo usado, plantear un mayor paralelismo en la arquitectura, especialmente en la parte de la implicación y la agregación, con el objeto de mantener la misma frecuencia de operación, pero aumentando la cantidad de inferencias difusas, ya que allí esta el mayor retardo del sistema.
REFERENCIAS BIBLIOGRÁFICAS
[1]. L. X. Wang, A course on Fuzzy Systems and Control, New Jersey, Prentice Hall, 1997.
[2]. C.C. Lee, "Fuzzy Logic in Control Systems: Fuzzy Logic Controller, Part I and II", IEEE Transactions on Systems, Man and Cybernetics, vol. 20 no.20, 1990.
[3]. Takeshi Yamakawa, "A Fuzzy Inference Engine in Nonlinear Analog and Its Application to a Fuzzy Logic Control ", IEEE Transactions on Neural Networks, vol. 4 no. 3, 1993.
[4]. I. Baturone, S. Sanchez, A. Barriga, L. Huertas, " Optimization of Adptive fuzzy processor design", XIII conference on Design of circuits and integrated Systems ( DCIS'98), pp. 316-321, Madrid, 1998.
[5]. J. E. Cardona, E. Caicedo, E. Owen, "Una aproximación a los instrumentos virtuales para el control con redes neuronales y lógica difusa", memorias del primer congreso internacional en inteligencia computacional, vol 1, pp 98-102, Medellín, Colombia, 2001.
[6]. Liliane Peters, Shuwei Guo, "Three Generations of Fuzzy Hardware", in Fuzzy Hardware: Architectures and Applications, A.Kandel G. Langholz (Eds), Kluwer Academic Pub, ISBN: 0792380290, 1998.
[7]. A. Barriga, R. Senhadji, C. J. Jiménez, I. Baturone, S. SánchezSolano, "A design methodology for application specific fuzzy integrated circuits", IEEE International Conference on Electronics, Circuits and Systems (ICECS'98), Vol. 1, pp. 431434, Lisboa, 1998.
[8]. E. Lago, C. J. Jiménez, D. R. López, S. Sánchez-Solano, A. Barriga, "Xfvhdl: a tool for the synthesis of fuzzy logic controllers", Design Automation and Test in Europe (DATE'98), pp. 102-107, Paris - France, 1998.
[9]. E. Lago, M. A. Hinojosa, C. J. Jiménez, A. Barriga, S. SánchezSolano, "FPGA implementation of fuzzy controllers", XII Conference on Design of Circuits and Integrated Systems (DCIS' pp. 715-720, Sevilla, 1997.
[10]. Donald Hung and William Zajac, "Implementing a Fuzzy Inference Engine using FPGA ", Proceedings of the 6th IEEE International ASIC Conference, NY, 1993, pp 349-352.
[11]. Donald Hung, "Custom Design of a Hardware Fuzzy Logic Controller", Proceedings of the 3d IEEE Internetional Conference on Fuzzy Systems, Orlando, FL, 1994, pp. 1781 1785.
[12]. Michael McKenna and Bogdan Wilamowski, "Implementing a Fuzzy Systems on a Field Programmable Gate Array", Proceedings of the INNS-IEEE International Joint Conference on Neural, 2001.
[13]. Justin G. R. Delva, Ali M. Reza, and Robert D. Turney, "FPGA Implementation of a Nonlinear Two Dimensional Fuzzy Filter", CORE Solutions Group, Xilinx San Jose, March 15, 1999.
[14]. David Olea, Andrés Gaona, Miguel Melgarejo "Descripción modular con orientación a implementación hardware de un Sistema de Inferencia Difusa", IEEE Latin America CAS Tour 2002, Universidad de los Andes, Bogotá, Colombia, Octubre 2002.
[15]. Stanley A. White "Applications of Distributed Arithmetic to Digital Signal Processing: A tutorial Review", IEEE ASSP Magazine Vol 6 No 3, 1989.
[16]. Amit Sinha and Anantha Chandrakasan, "Energy Efficient Filtering Using Adaptive Precision and Variable Voltage", Proc. of IEEE Application Specific Integrated Circuits Conference, Washington, Sept. 1999.
David Camilo Olea Salgado
Estudiante Universidad Distrital. dacamol@hotmail.com
Andrés Eduardo Gaona Barrera
Estudiante Universidad Distrital. angaona@hotmail.com
Miguel Alberto Melgarejo Rey Profesor Universidad Distrital. mmelgarejo@ieee.org
Creation date:
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.





2.jpg)










