DOI:
https://doi.org/10.14483/23448393.2815Published:
2001-11-30Issue:
Vol. 7 No. 2 (2002): July - DecemberSection:
Science, research, academia and developmentGeoestadística aplicada a estudios de contaminación ambiental
Keywords:
Interpolación, Geoestadística, Distancia Inversa, Autocorrelación Espacial, Estación, Material Particulado, Predicción. (es).Downloads
References
BURROUGH, Peter and MCDONNELL Rachael. Principles of Geographical Information Systems: spatial information systems and geostatistics. Great Britain: Oxford University Press, 1998. 333 p. ISBN 0-19-823366-3.
COLLINS JR, Fred. A Comparison of Spatial Interpolation Techniques in Temperature Estimation. Colorado, U.S.A. Universidad de Minesota. Citado en Mayo 4 de 2002. http://www.sbg.ac.at/geo/ idrisi/gis_environmental_modeling/sf_papers/collins_fred/ collins.htm
CUADOR GIL, José Quintín. La Geoestadística, su surgimiento y evolución.. 2da versión. Cuba. Universidad de Pinar del Río, Departamento de Computación. Junio de 2000. Disponible en Internet. ISSN 1562-3297
DUBRULE, Olivier. Geostatistics in Petroleum Geology. Tulsa, Oklahoma, U.S.A: AAPG (The American Association of Petroleum Geologists), 1998. 52 p. (Serie; no.38). ISBN: 0-89181197-7.
GIRALDO HENAO, Ramón. INTRODUCCION A LA GEOESTADISTICA. Teoría y aplicación. Bogotá: Departamento de estadística. Universidad Nacional de Colombia, 2002. 94 p.
GORDON S. Thomas. Interactive Analysis and Modelling of SemiVariograms. Snowden Associates Pty. Disponible en Internet: http://www.ai-geostats.org/online_papers/_papers/0000001e.htm
GUPTILL, Stephen and MORRISON Joel. Elements of spatial data quality. s.l. The International Cartographic Association, 1997. 202 p. ISBN 0-08-042432-5.
ISAAKS, Edward H. and SRIVASTAVA, R. Mohan. Applied Geostatistics. Oxford University Press. 561 páginas. Disponible en Internet: http://www.oup-usa.org/isbn/0195050134.html
JOHNSTON, Kevin. et al. Using ArcGISTM Geostatistical Analyst, GIS by ESRITM, Disponible en Internet: http://www.zo. ntu. edu. tw/Courses/GIS/2001-12-05/Using_ArcGIS_Geostatistical_Analyst.pdf
MAJURE, James J. et al. GIS, spatial statistical graphics, and forest health Iowa State University. Disponible en Internet: http://www.public.iastate.edu
MYERS, Donald E. Elements of Geostatistics.. Arizona. Disponible en Internet: http://www.ento.vt.edu/~sharov/PopEcol/lec2/ geostat.html
SANCHEZ IPIA, Albert Hamersson y SIABATO VACA, Willington Libardo. Análisis de gases contaminantes en zonas urbanas, Bogotá. Universidad Distrital Francisco José de Caldas. 2002, 83 p. (Serie; Ciencia y Medio Ambiente -Jóvenes Talentos-). ISBN: 958-8175-06-2.
SANCHEZ IPIA, Albert Hamersson y SIABATO VACA, Willington Libardo. Modelo para el análisis del comportamiento de gases contaminantes y material particulado en la zona urbana del altiplano de Bogotá Fase I. Bogotá, 2001, 246 p. Proyecto de investigación (Ingeniero Catastral y Geodesta). Universidad Distrital Francisco José de Caldas. Facultad de Ingeniería.
SANCHEZ IPIA, Albert Hamersson y SIABATO VACA, Willington Libardo. Modelo de calidad del aire para Bogotá, Bogotá D.C. Universidad Distrital Francisco José de Caldas. 2002, p.65-71 ISSN: 0121-750X.
SHARMA, Tara. Spatial Interpolation Techniques in GIS Disponible en Internet: http://www.geog.ubc.ca/courses/klink/gis.notes/ ncgia/u40.html
TODA LA TEORIA SOBRE KRIGING. Disponible en Internet: www.ems-i.com/gmshelp/Interpolation/Interpolation_Schemes/ Kriging/Kriging.htm
ULRICH Leopold. Application of Geostatistics for Spatial Analysis of Heavy Metals in Soil. Germany. Soil Science Department, Faculty of Geography and Geo sciences, University of Trier. Disponible en Internet: http://www.geocities.com/leop6101/abstract.htm
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Ingeniería, 2002-00-00 vol:7 nro:2 pág:31-38
Geoestadística aplicada a estudios de contaminación ambiental
Jhon William Cely Pulido
Director Grupo de Investigación NIDE. Universidad Distrital Francisco José de Caldas.
Willington Libardo Siabato Vaca
Investigador Grupo NIDE.
Alber Hamersson Sánchez Ipia
Investigador Grupo NIDE.
Adriana Patricia Rangel Sotter
Investigadora Grupo NIDE.
Resumen
En este artículo se presenta una primera aproximación a partir de la geoestadística al modelamiento de polutantes en espacios urbanos, dentro del desarrollo de la segunda fase del proyecto de investigación titulado "Modelo para el análisis del comportamiento y distribución de gases contaminantes y material particulado en la zona urbana del altiplano de Bogotá".
Complementa la primera fase del proyecto en la cual se desarrolló una aproximación al problema desde la perspectiva del modelo de pluma de gauss1.
La geoestadística como técnica de predicción hace parte de la interpolación espacial, por eso es importante el entendimiento de esta para poder comprender la esencia del modelo geoestadístico, que en su desarrollo ha planteado una fundamentación teórica, una primera aproximación al esquema metodológico para la implementación de cualquier modelo geoestadístico a geociencias y la incorporación del modelo geoestadístico al proyecto de investigación.
Palabras clave:
Interpolación, Geoestadística, Distancia Inversa, Autocorrelación Espacial, Estación, Material Particulado, Predicción.
Abstract
Some people say that Geostatistics is the art of modeling spatial data. A more specific definition is: "Geostatistics is a statistical methodology used to estimate, forecast, and simulate correlated spatial data, which uses in its analysis exploratory and interpolative methods2"
Geostatistics is a useful tool for improving estimations of a variable for non-measured locations if it is compared with other estimation techniques, for example, IDW (Inverse Distance Weighted interpolation).
Using Geostatistics for modeling air pollutants behavior in Bogotá has two immediate advantages: It is not necessary to collect as much information as it is with the Gaussian Plume Model. The exploratory analysis used the Bogotá's air quality network data (14 stations taking 24 air pollutant measures a day) for a first approach. It is not mandatory to collect information about each air pollutant source. For this reason, it is possible to draw some conclusions faster than with other approaches.
A preliminary analysis conclusion was obtained through the use of cross validation to compare IDW against Geostatistics (Ordinary Kriging) RMSE (Root Mean Square Error). This conclusion applies for Bogotá case and says that it is better to use IDW instead of Geostatistics for estimating air pollution based on the available sample points (air quality stations). The research team thinks that this conclusion is the direct result of the lack of sample points. Based on this Geostatistical analysis, the research team realized that DAMA must to extend and crowd the station network for better future estimations.
Key Words:
Interpolation, Geostatistics, Inverse Distance Weight, Spatial Autocorrelation, Station, Pollutant Distribution, Prediction.
I. INTRODUCCIÓN
La geoestadística es una técnica estadística usada para la estimación, predicción y simulación de datos correlacionados espacialmente, que se ha conocido como el arte de modelar datos espaciales.
Su importancia radica en que permite describir la continuidad espacial de las variables y estimar valores muy cercanos a los reales en puntos desconocidos.
El objetivo principal para esta etapa de la investigación es crear un modelo Geoestadístico sustentado en técnicas de interpolación espacial y compararlo con los resultados obtenidos en el Modelo de Pluma de Gauss.
La Geoestadística tuvo su origen en procesos de búsqueda y exploración de minerales, es por esto la asignación del prefijo "GEO" para referirse a ciencias de la tierra. A lo largo de su evolución se han identificado cuatro generaciones:
- Geoestadística Lineal: Dedicada a la teoría de las funciones aleatorias.
- Geoestadística no Lineal: Dedicada a la aplicación minera y a la gran difusión de esta ciencia.
- Geoestadística de tercera generación: Dedicada a desarrollo de los diferentes tipos de Kriging.
- Geoestadística de cuarta generación: La cual utiliza algoritmos Geoestadísticos a través de herra mientas computacionales.
II. INTERPOLACIÓN ESPACIAL
La interpolación es un proceso que permite modelar variables espaciales, predecir su comportamiento, determinar radios de influencia y tiempos de duración de un fenómeno. También resuelve problemas de decisión frente a procesos que se ven afectados por el comportamiento de ciertas variables, y en general, para proveer información ya sea sobre el presente o un futuro probable.
La estimación de valores desconocidos a partir de una muestra mediante técnicas de interpolación se practica constantemente en muchas áreas de la ciencia, y de hecho con frecuencia son inseparables de los procesos realizados en el arte de la investigación, en especial los relacionados con las ciencias de la tierra. El proceso normal es obtener a partir de una muestra el comportamiento general de un fenómeno.
La interpolación espacial es el procedimiento que se utiliza para estimar valores de una o más variables en lugares donde no existe o no se conoce información a partir de mediciones en puntos ubicados en la misma área o región. Cuando la estimación de los valores de las variables se hace en lugares por fuera del área que cubren las mediciones tomadas, el proceso se llama extrapolación.
La interpolación espacial proporciona diferentes metodologías para realizar el análisis de datos espaciales: la Interpolación Geoestadística y la Interpolación Simple. Ambas metodologías pueden hacer estimaciones globales o locales, y tienen tanto interpoladores exactos3 como aproximados. La diferencia entre estas radica en los supuestos que se hacen en cada una, en el número de parámetros de decisión que intervienen y en la predicción del error de estimación.
La interpolación simple se basa en un principio de las ciencias naturales del cual se deriva la continuidad de los datos, donde en un proceso dado, la razón de cambio es constante y como mínimo se deben conocer dos valores, de lo contrario se hace imposible conocer el error de la estimación.
La Geoestadística por su parte, en su análisis utiliza métodos exploratorios y de interpolación, estos métodos requieren un conocimiento básico estadístico, pues cuando hay variación irregular en los datos, la muestra es representativa y/o la interpolación simple arroja resultados incoherentes con la realidad, los métodos geoestadísticos proporcionan estimaciones probabilísticas de la calidad de la interpolación. Paralelamente, proporcionan una herramienta (semivariogramas) que permiten explorar y obtener una mejor comprensión de los datos, además se tiene el control para crear las mejores estimaciones basadas en la información disponible, permitiendo la toma de decisiones óptimas.
El método Geoestadístico se basa en los supuestos de estacionariedad en la variable, hipótesis intrínseca y distribución de probabilidad en los datos. En caso que la variable modelada se comporte como una distribución normal, el método será más exacto. La eficacia de este método depende de la uniformidad del área de estudio.
En general, se puede decir que los métodos geoestadísticos son superiores a la interpolación simple cuando hay una muestra representativa y depende también de la calidad de estimación que se requiera. Debido a que en algunas ocasiones se necesita hacer predicción por fuera de los lugares donde se posee información o del tiempo de toma de datos, se hace necesario completar el análisis espacial con la extrapolación, donde se supone que el fenómeno se comporta de la misma manera que los datos más cercanos al punto a estimar.
III. KRIGING Y EL SEMIVARIOGRAMA
El estimador por excelencia de la Geoestadística es Kriging, conocido como BLUE (Best Linnear Unbiased Estimator). Con la aplicación de Kriging se consigue minimizar la varianza del error de predicción, puesto que este utiliza en su estimación las características de variabilidad y correlación espacial del fenómeno estudiado. Ante esto es necesario hacer una depuración inicial de los datos utilizados en las estimaciones.
En Geoestadística es indispensable mencionar la correlación espacial, la cual consiste en la estimación de la dependencia espacial entre los datos medidos de una variable, este proceso se hace a través de un análisis estructural utilizando variogramas.
Los variogramas son estimadores de la varianza poblacional relacionados con la dirección y la distancia, e indican como varían las dependencias espaciales que existen entre un punto de origen y otro punto a una determinada distancia, independientemente de su posición.
Para facilidad de aplicación del sistema de ecuaciones de Kriging, se utiliza la función de semivarianza que da como resultado el semivariograma. En un conjunto de datos, para que el semivariograma pueda estimar la varianza poblacional es fundamental que los datos tengan cierta regularidad en su distribución, es decir que tengan algún grado de estacionariedad.
En el modelamiento de un semivariograma existen dos etapas, una es la construcción del semivariograma experimental y la segunda es realizar el modelo del semivariograma.
El semivariograma experimental se construye gráficamente con la nube de puntos de las distancias entre los diferentes pares de puntos muestreados, mientras que el modelo del semivariograma se realiza a través del ajuste de las funciones teóricas que soportan la construcción de este modelo. Entre las más conocidas están el Modelo Exponencial, Modelo Esférico, Modelo Gaussiano y el Modelo Potencial, cuyas diferencias radican en la forma de crecimiento de la función a lo largo del rango.
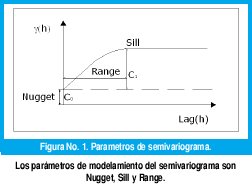
El semivariograma esta descrito por tres parámetros, "Nugget", "Sill" y "Range".
El Nugget, conocido también como pepita, es el valor en que el modelo del semivariograma intercepta al eje coordenado "y", es decir al eje de la semivarianza. Este valor puede ser atribuido a errores de medida o fuentes espaciales de variación en la distancia de las muestras.
El Sill ó meseta, es el limite superior de cualquier modelo de semivariograma, valor donde se alcanza el rango.
El Range ó rango, es la distancia en la cual la función de semivarianza deja de crecer y a partir de donde los pares de puntos muestreados no se consideran autocorrelacionados. Estos tres parámetros se describen gráficamente en la figura 1.
Una vez construido el Modelo del semivariograma se aplica un método de interpolación Geoestadística, el utilizado para este proyecto fue Kriging debido a que utiliza los pesos de los valores estimados provenientes de las combinaciones lineales, porque la esperanza del estimador coincide con la de la variable y porque minimiza la varianza de los errores.
El objetivo de Kriging es estimar el valor de la variable "Z" en un punto Xo no medido con anterioridad, para ello se realiza una suma ponderada de los pesos de la variable por el valor mismo de dicha variable, de tal manera que la ecuación básica que representa Kriging es:
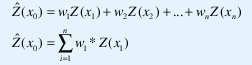
La estimación por Kriging puede ser puntual o zonal dependiendo del espacio que se vaya a tomar para estimar el valor de la variable.
Aunque Kriging reúne un conjunto de métodos de predicción espacial que se basan en la minimización del error medio cuadrático, en realidad todos tienen la misma fundamentación y se diferencian en el tipo de estimador (Lineal / No lineal), media utilizada, tendencia y forma de evitar el sesgo.
Después de haber aplicado el tipo de Kriging seleccionado de acuerdo al fenómeno que se este tratando se evalúa la bondad del ajuste de la estimación a través de un método llamado Validación Cruzada que se fundamenta en excluir la observación de uno de los "n" puntos muestreados y con los valores restantes y el modelo de semivariograma escogido, predecir a través de Kriging el valor de la variable en estudio en la ubicación del punto que se excluyó. Si el modelo escogido describe una buena estructura de auto-correlación espacial, la diferencia entre el valor estimado y el valor observado debe ser mínima, de lo contrario se rechaza el modelo y se replantea el proceso.
IV. ESQUEMA METODOLÓGICO PARA EL ANÁLISIS GEOESTADÍSTICO
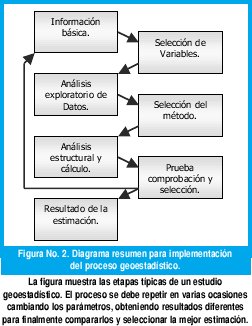
En general, para realizar un buen análisis Geoestadístico se debe realizar un proceso iterativo para poder obtener resultados óptimos, en la Figura No. 2 se muestra el ciclo metodológico para realizar este tipo de análisis, el cual está basado en modelos estadísticos que incluyen auto-correlación y permiten realizar estimaciones de fenómenos. Se asume que antes de hacer el Análisis Geoestadístico o cualquier otro tipo de análisis se ha definido el problema o el fenómeno que se espera investigar; se debe tener claro cuáles son los puntos muestreados con los que se cuenta, puesto que son la base para realizar la estimación.
En general el esquema metodológico para un análisis geoestadístico se describe en siete pasos:
1. Información básica. Para realizar un buen análisis Geoestadístico, se necesita utilizar una muestra representativa de la variable que se desea investigar y adicionalmente para observar el resultado obtenido, se recomienda tener una espacialización de la zona o lugar donde ocurre el fenómeno a examinar.
2. Selección de las variables a utilizar. Al seleccionar las variables, se debe escoger aquellas que tengan mayor influencia sobre el fenómeno, con un tamaño de muestra representativo.
3. Análisis Exploratorio de los datos. Antes de aplicar Geoestadística como tal, se debe hacer una depuración inicial de los datos para evitar errores en el análisis. Por ejemplo, se debe observar que tipo de distribución tienen los datos, buscar si la muestra tiene alguna tendencia, si existen valores atípicos y decidir si deben incluirse o retirarse de la muestra, analizar la distribución espacial y los estadígrafos de los valores de la variable.
4. Selección del método. Se escoge el método que se va a utilizar para hacer la interpolación, bien sea determinístico (Interpolación por Distancia Inversa, Interpolación por Distancia Inversa Cuadrada, Interpolación por Shepard, Interpolación Polinomial, etc.) o estocástico (Kriging Ordinario,Simple, Universal, Residual, Indicador,Probabilístico, Lognormal, Disyuntivo, Bloques) y la variable a utilizar; es de resaltar que se puede hacer el análisis individual o en conjunto para las variables dependiendo del método de análisis que se utilice, Kriging o Co-Kriging.
5. Análisis estructural y cálculo. Se calcula el variograma experimental utilizando una función de correlación espacial, bien sea la semivarianza o covarianza, de acuerdo a la nube de puntos generada en el semivariograma experimental se busca el modelo teórico (Esférico, Exponencial, Gaussiano y Potencial) que mejor se ajuste y se obtiene el modelamiento del semivariograma, se define el número y tamaño de los Lag que se van a utilizar en el modelo (Se recomienda que el tama- ño del Lag sea similar a la distancia promedio que existe entre la ubicación espacial de los datos). Se define si hay isotropía o anisotropía mediante el análisis del Semivariograma desde diferentes ángulos de referencia; con base en la existencia o no de la autocorrelación direccional se debe definir la vecindad de análisis para cada uno de los datos y posteriormente se hace la verificación del error de predicción, lo cual se puede realizar mediante Validación Cruzada que usa todos los datos para predecir la autocorrelación del modelo, cuyo procedimiento es omitir un valor de la variable y predecir dicho valor con los demás datos, luego se compara la predicción y el valor medido de la variable, este proceso se repite para cada uno de los valores muestreados.
6. Prueba, Comprobación y Selección. Se hacen diferentes ensayos para escoger el mejor método, ya sea determinístico o estocástico, y el mejor modelo dentro de ellos; en la práctica es realizar los pasos 4 y 5 tantas veces como sea necesario para encontrar el mejor modelo Geoestadístico. Escoger el método más apropiado depende del tamaño de la muestra y la precisión que se desee obtener en la predicción. Similarmente escoger el mejor modelo se fundamenta en seleccionar aquel cuyos errores de predicción sean mínimos. Si los resultados obtenidos en esta etapa no están dentro de parámetros especificados en el planteamiento del problema, se debe regresar al paso 1, es decir, mejorar la muestra y volver a realizar el ciclo de análisis.
7. Salida Final. Los resultados se pueden observar en tablas como las de la Validación Cruzada, Histogramas, QQPLOT (muestra los quantiles de las diferencias entre los errores estandarizados y los quantiles correspondientes de una distribución normal), Análisis de Tendencia, Nubes de puntos del Semivariograma o del covariograma, etc. y/o en mapas como los de Predicción, Probabilidad, Predicción del error estándar y de quantiles para cada uno de los anteriores pasos.
Este proceso se debe repetir para cada una de las variables que se deseen estimar dentro del análisis a realizar. Este esquema metodológico es uno de los aportes generados por este proyecto, el cual permite realizar el análisis Geoestadístico en forma general para cualquier solución planteada ante un fenómeno de ubicación espacial.
MODELO GEOESTADÍSTICO PARA BOGOTÁ
Aplicando el modelo geoestadístico para el caso particular de Bogotá y teniendo en cuenta las consideraciones locales se realizaron los siguientes procesos y obtuvieron los siguientes resultados.
INFORMACIÓN UTILIZADA
La información utilizada para esta etapa de la investigación es coincidente con la base de datos implementada en la fase inicial que contiene las mediciones del DAMA en el periodo 1997-2000, esta base de datos incluye tal y como ya se mencionó anteriormente información de las variables humedad, presión, radiación, temperatura, lluvia, velocidad del viento, dirección del viento, azimut, elevación, metano, monóxido de carbono, óxidos de nitrógeno, dióxidos de nitrógeno, ozono, material particulado y dióxido de azufre. Es de destacar que en general las mediciones de las variables están en registros horarios diarios para cada mes, sin embargo, por diversas razones no hay mediciones para algunos periodos de tiempo.
DEFINICIÓN Y MEDICIÓN DE VARIABLES
Aunque se tomen valores de múltiples variables, se utilizó únicamente PM10, que son materiales sólidos que se producen por la acción del viento sobre las áreas desprovistas de vegetación, en los procesos de combustión de las fábricas, en la fracturación de rocas y materiales de construcción, en los humos de los gases de los vehículos y también por efecto de la resuspensión del material de las vías no pavimentadas cuando sobre ellas circulan vehículos; la unidad en que se expresa el nivel de concentración de esta variable en la atmósfera es Microgramo/m3.
Se selecciona esta variable porque es uno de los tipos de sustancias conocidas como contaminantes primarios que influye en la calidad del aire de la ciudad, además desde el punto de vista de la salud humana son de mayor interés las partículas cuyo tamaño no excede las 10 micras (PM10) debido a que pueden ingresar al tracto respiratorio y producir daños en los tejidos y órganos que lo conforman, y adicionalmente existen valores de esta variable en la mayoría de las estaciones metereológicas medidas a diario.
MARCO Y ANÁLISIS
El análisis se realiza para los días 24 de Abril de 2000, 13 de Febrero y 26 de Abril de 2001 a las 14 horas, además se incluye el día del 15 de Febrero de 2002, este periodo se tiene en cuenta por ser la fecha actualizada que más mediciones tiene sobre la variable a analizar.
El análisis consiste en escoger entre los métodos de interpolación existentes dos o más para hacer estimaciones y comparar los resultados que arrojan cada uno de los métodos seleccionados. Se utilizó entonces para hacer el análisis un método determinístico y uno estocástico, el método determinístico seleccionado fue Interpolación por Distancia Inversa mientras el estocástico fue Kriging Ordinario, se selecciona Distancia Inversa porque es el método de interpolación más sencillo, utiliza pocos parámetros de decisión, las estadísticas simples son aceptables y es un buen parámetro de comparación; paralelamente se escoge Kriging Ordinario dentro de los otros tipos de Kriging porque en principio éste utiliza la media de la muestra, la variable medida se asume que es estacionaria porque al hacer las pruebas de predicción con tendencia y sin esta, los errores de predicción son menores cuando se hacen los cálculos sin tendencia, además aunque gráficamente se podría notar alguna tendencia esta no se podría comprobar con la muestra con que se cuenta, el método permite usar modelos de los errores de medición y por experiencia es el más usado para fenómenos ambientales. Se hace un análisis individual de la variable PM10 y no en conjunto con otras variables porque el número de datos existentes no son suficientes para mejorar la estimación lograda con una sola variable.
La gráfica de Caja y Bigote esta formada por cuatro elementos: Bigote, Caja, Puntos y Línea. El bigote indica el rango de distribución de los datos, es decir el valor máximo y mínimo de la muestra; la varianza está representada por la caja, la amplitud de está es directamente proporcional al valor de la varianza; la Línea índica la mediana de la muestra, la ubicación relativa de la línea y la caja con respecto al bigote representan el sesgo de la muestra, si la línea se encuentra en la mitad de la caja indica que la media y la mediana son muy cercanas, siendo esto típico en las distribuciones normales; los puntos en la gráfica son valores atípicos y pueden o no estar presentes en ella.
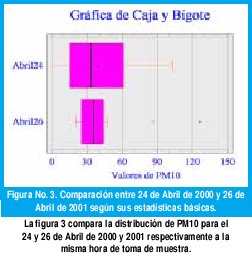
Es evidente, que la distribución para el 26 de Abril era mas homogénea y menos sesgada, además se observa como la mediana se encuentra en la mitad del intervalo de varianza, significando esto que la distribución tiende a ser normal. En términos ambientales, esto significa que la distribución del Material Particulado para el 26 de Abril de 2001 en Bogota D.C. era uniforme en el área urbana.
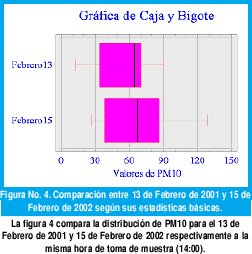
Siguiendo el mismo análisis se infiere de la Figura No. 4 que las distribuciones son mucho menos homogéneas que las observadas anteriormente.
RESULTADOS DE LA ESTIMACIÓN
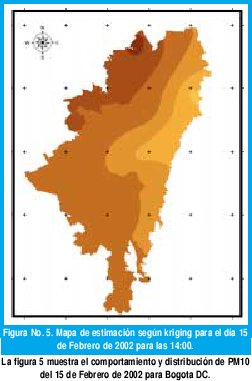
Dentro de los resultados que se obtuvieron en el análisis Geoestadístico, uno de los más importantes es el mapa de estimaciones. Se ilustran distribuciones espaciales estimadas por los dos métodos nombrados.
De acuerdo a los resultados obtenidos aplicando Kriging Ordinario para la muestra del 15 de febrero de 2002 a las 14:00, la mayor concentración de PM10 se encuentra en la parte noroccidental de la ciudad (en la figura se representa por el tono oscuro) y la menor se encuentra en la parte oriental (en la figura se representa por el tono claro). El rango hasta donde se consideró auto-correlación es 2 km.
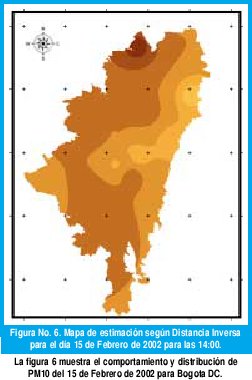
Realizando el mismo análisis por el método de Distancia Inversa se observa que la mayor concentración de PM10 es coincidente con el anterior resultado en la parte noroccidental de la ciudad, de igual forma para la menor concentración. Se muestra entonces un comportamiento uniforme.
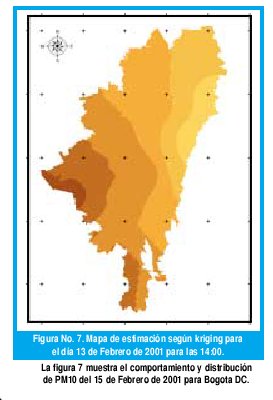
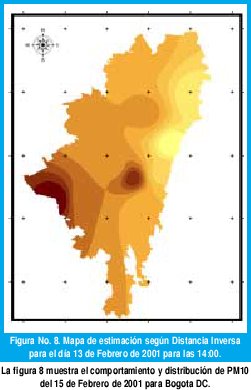
Para las 14:00 del 13 de Febrero de 2001, la mayor contaminación según Kriging Ordinario se concentra en la parte sur y occidental de la ciudad y la menor concentración de contaminación se encuentra en la parte nororiental. Se muestra un comportamiento decreciente en sentido Oeste - Este en la contaminación en forma de bandas, lo que representa un comportamiento estable de los niveles de concentración de PM10.
En este caso, resalta una mancha de gran concentración en la parte central de la ciudad que no se hizo evidente en los anteriores resultados, en especial si se compara con la figura número 7.
COMPARACIÓN DE LOS MODELOS
El modelo Geoestadístico toma en cuenta las mediciones que representan el comportamiento de la variable medida en cada una de las zonas en donde se encuentran ubicadas las estaciones de muestreo, por otro lado, el modelo de Pluma de Gauss involucra las fuentes de emisión in situ una por una, siempre y cuando se involucren en el análisis; esto implica que el modelo de Pluma de Gauss sea más preciso a la hora de clasificar los contaminantes según su origen, permita involucrar una muestra más representativa a la hora de un análisis debido a que es más sencillo y económico tomar los datos de una fuente directa como las chimeneas, que construir una estación de monitoreo, pero tiene restricciones, pues no tiene en cuenta la correlación espacial entre las diversas variables que intervienen en el fenómeno de contaminación atmosférica que si es tenido en cuenta en el modelo Geoestadístico.
De lo anterior se deduce que el modelo Gaussiano puede llegar a diferenciar el comportamiento y/o distribución de gases contaminantes y material particulado por diferentes tipos de origen como el antropogénico y el natural, mientras que el Geoestadístico no.
A través del modelo Geoestadístico se tiene un mejor manejo de los datos que se desean analizar, pues permite el control del error de las predicciones desde la misma formulación del algoritmo de interpolación, permite conocer el grado de auto-correlación entre los puntos muestreados para poder modelarla y dar como resultado la estimación. El algoritmo de estimación usado dentro de la Geoestadística tiene la característica de ser BLUE (Best Linear Unbiased Estimator) en la medida en que se cumplan los supuestos del modelo.
Dentro del modelo Geoestadístico se manejan los conceptos de remoción de tendencias y anisotropía, lo que conlleva a un mayor y más detallado análisis, permite obtener resultados del mismo conjunto de datos que conforman la muestra, brinda la posibilidad de utilizar diferentes algoritmos, hacer análisis multitemporal y extrapolación de datos.
El modelo Geoestadístico inicialmente solo involucra el contaminante en análisis sin verificar su comportamiento influenciado por variables físicas a las cuales siempre estará sujeto; se debe tener presente que aunque un análisis con el modelo Geoestadístico utilizando Co-Kriging se puede tener más de una variable dentro del análisis, estas variables deben estar altamente correlacionadas y se utilizan exclusivamente para mejorar la predicción de la variable en estudio
CONCLUSIONES
De acuerdo a la muestra tomada para hacer el análisis de Material Particulado (PM10) en la zona urbana de Bogotá para los días analizados se concluye que el mejor método de interpolación entre los utilizados es Distancia Inversa, para ello la herramienta de decisión utilizada fue la Validación Cruzada. Aunque Kriging es considerado BLUE sus estimaciones obtienen un intervalo de error mayor al de Distancia Inversa posiblemente debido al tamaño de muestra con el que se cuenta.
Para los días que se tomaron como muestra, la contaminación producida por Material Particulado en la zona Urbana de Bogotá no es uniforme, presenta una mayor concentración en el costado occidental y sur de la ciudad, esta situación es el reflejo de la ubicación de fuentes fijas de contaminantes tales como zona industrial, canteras, relleno sanitario y plantas asfálticas. La menor concentración de Material Particulado se encuentra en el costado oriental de la ciudad lo cual con seguridad es producido por el gran pulmón ambiental que generan los cerros orientales y la alta precipitación en este lugar que hace un lavado de los contaminantes, llevando la contaminación a la superficie urbana y a los suelos.
Al comparar el modelo Geoestadístico para los días analizados con el Modelo de Pluma de Gauss se corrobora el comportamiento de la contaminación decreciente en sentido Oeste-Este, pero no se puede precisar si existe anisotropía en el contaminante PM10 por el tamaño de la muestra.
Los productos desarrollados (correlación espacial y el modelado del Semivariograma) en este proyecto son una base para el análisis de la concentración y comportamiento de contaminantes en la ciudad de Bogotá Distrito Capital y en otras zonas urbanas del país.
Si no es aumentado el número de estaciones que midan los contaminantes de la ciudad de Bogotá, se sugiere utilizar Interpolación por Distancia Inversa en lugar de usar Geoestadística para hacer la predicción de la contaminación provocada por material particulado en el Distrito Capital.
RECOMENDACIONES
Se espera continuar con el proyecto de investigación desarrollando un tercer modelo (Matemático, Estadístico o Físico) para hacer un prototipo de la predicción de la contaminación provocada por material particulado en el Distrito Capital y extender los análisis a otros contaminantes.
Finalmente, no hay que perder de vista que la atmósfera y los fenómenos que en ella se producen, en muchos aspectos, permanecen inexplorados o aun fuera del alcance de nuestro conocimiento y por tanto no son modelables (al menos por ahora), por lo cual se decidió cerrar este articulo con esta frase de Henri Poincaré, matemático y físico francés de finales del siglo XIX y comienzos del siglo XX, que ha acompañado al grupo de investigadores en el recorrido de este proyecto:
"Puede pasar que pequeñas diferencias en las condiciones iniciales produzcan unas muy grandes en el fenómeno final. Un pequeño error en lo anterior producirá un enorme error en lo posterior. La predicción se torna imposible..." Henri Poincaré. (1854-1912)
BIBLIOGRAFÍA
- BURROUGH, Peter and MCDONNELL Rachael. Principles of Geographical Information Systems: spatial information systems and geostatistics. Great Britain: Oxford University Press, 1998. 333 p. ISBN 0-19-823366-3.
- COLLINS JR, Fred. A Comparison of Spatial Interpolation Techniques in Temperature Estimation. Colorado, U.S.A. Universidad de Minesota. Citado en Mayo 4 de 2002. http://www.sbg.ac.at/geo/idrisi/gis_environmental_modeling/sf_papers/collins_fred/collins.htm
- CUADOR GIL, José Quintín. La Geoestadística, su surgimiento y evolución.. 2da versión. Cuba. Universidad de Pinar del Río, Departamento de Computación. Junio de 2000. Disponible en Internet. ISSN 1562-3297
- DUBRULE, Olivier. Geostatistics in Petroleum Geology. Tulsa, Oklahoma, U.S.A: AAPG (The American Association of Petroleum Geologists), 1998. 52 p. (Serie; no.38). ISBN: 0-89181-197-7.
- GIRALDO HENAO, Ramón. INTRODUCCION A LA GEOESTADISTICA. Teoría y aplicación. Bogotá: Departamento de estadística. Universidad Nacional de Colombia, 2002. 94 p.
- GORDON S. Thomas. Interactive Analysis and Modelling of Semi-Variograms. Snowden Associates Pty. Disponible en Internet:http://www.ai-geostats.org/online_papers/_papers/0000001e.htm
- GUPTILL, Stephen and MORRISON Joel. Elements of spatial data quality. s.l. The International Cartographic Association, 1997. 202 p. ISBN 0-08-042432-5.
- ISAAKS, Edward H. and SRIVASTAVA, R. Mohan. Applied Geostatistics. Oxford University Press. 561 páginas. Disponible en Internet: http://www.oup-usa.org/isbn/0195050134.html
- JOHNSTON, Kevin. et al. Using ArcGISTM Geostatistical Analyst, GIS by ESRITM, Disponible en Internet:h t t p : / / w w w. z o . n t u . e d u . t w / C o u r s e s / G I S / 2 0 0 1 - 1 2 - 0 5 /Using_ArcGIS_Geostatistical_Analyst.pdf
- MAJURE, James J. et al. GIS, spatial statistical graphics, and forest health Iowa State University. Disponible en Internet: http://www.public.iastate.edu
- MYERS, Donald E. Elements of Geostatistics.. Arizona. Disponible en Internet: http://www.ento.vt.edu/~sharov/PopEcol/lec2/geostat.html
- SANCHEZ IPIA, Albert Hamersson y SIABATO VACA, Willington Libardo. Análisis de gases contaminantes en zonas urbanas, Bogotá. Universidad Distrital Francisco José de Caldas. 2002,83 p. (Serie; Ciencia y Medio Ambiente -Jóvenes Talentos-).ISBN: 958-8175-06-2.
- SANCHEZ IPIA, Albert Hamersson y SIABATO VACA, Willington Libardo. Modelo para el análisis del comportamiento de gases contaminantes y material particulado en la zona urbana del altiplano de Bogotá Fase I. Bogotá, 2001, 246 p. Proyecto de investigación (Ingeniero Catastral y Geodesta). Universidad Distrital Francisco José de Caldas. Facultad de Ingeniería.
- SANCHEZ IPIA, Albert Hamersson y SIABATO VACA, Willington Libardo. Modelo de calidad del aire para Bogotá, Bogotá D.C. Universidad Distrital Francisco José de Caldas. 2002, p.65-71 ISSN: 0121-750X.
- SHARMA, Tara. Spatial Interpolation Techniques in GIS Disponible en Internet: http://www.geog.ubc.ca/courses/klink/gis.notes/ncgia/u40.html
- TODA LA TEORIA SOBRE KRIGING. Disponible en Internet: www.ems-i.com/gmshelp/Interpolation/Interpolation_Schemes/Kriging/Kriging.htm
- ULRICH Leopold. Application of Geostatistics for Spatial Analysis of Heavy Metals in Soil. Germany. Soil Science Department, Faculty of Geography and Geo sciences, University of Trier. Disponible en Internet: http://www.geocities.com/leop6101/abstract.htm
NOTAS
- SÁNCHEZ, Alber; SIABATO, Willington. Et al. Revista INGENIERIA, Modelo de calidad de aire para Bogotá. Colombia, Bogotá DC, Grupo Editorial GAIA,2002, p 65.
- JOHNSTON Kevin. Et al. Using ArcGISTM Geostatistical Analyst, GIS by ESRITM, Interpolador exacto, es aquel que da un valor de predicción igual a la muestra en el mismo punto de toma de la medición.
Adriana Patricia Rangel Sotter
Ingeniera Catastral y Geodesta. Universidad Distrital Francisco José de Caldas. Investigadora Grupo NIDE. asotter@msn.com
Alber Hamersson Sánchez Ipia
Ingeniero Catastral y Geodesta. Universidad Distrital Francisco José de Caldas. Investigador Grupo NIDE. hamersson@hotmail.com
Willington Libardo Siabato Vaca
Ingeniero Catastral y Geodesta. Universidad Distrital Francisco José de Caldas. Investigador Grupo NIDE. wsiabato@eudoramail.com
Jhon William Cely Pulido
Ingeniero Catastral y Geodesta. Msc. Teleinformática. Esp. SIG. Director Grupo de Investigación NIDE. Universidad Distrital Francisco José de Caldas. jwcely@express.net.co
Creation date:
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.





2.jpg)










