DOI:
https://doi.org/10.14483/23448393.15271Publicado:
2020-07-03Número:
Vol. 25 Núm. 2 (2020): Mayo - AgostoSección:
Ingeniería IndustrialUn Problema de Enrutamiento del Vehículo con Enfoque de Ventanas de Tiempo para Mejorar el Proceso de Entregas
A Vehicle Routing Problem with a Time Windows Approach to Improve the Delivery Process
Palabras clave:
Problema de Enrutamiento del Vehículo, Proceso de Entregas, Logística, Optimización, Nivel de Servicio, Ventanas de tiempo (es).Palabras clave:
Vehicle Routing Problem, Delivery Process, Logistics, Optimization, Service Level, Time Windows (en).Descargas
Referencias
Ma, Wei-min, Dan-dan Dong, and Ke Wang, "Competitive analysis for the on-line vehicle routing problem", in 4th International Conference on New Trends in Information Science and Service Science, IEEE, 2010, pp. 430-435.
I. Stefan, P. Toth, and D.Vigo. "Chapter 1: The family of vehicle routing problems.", in Vehicle Routing: Problems, Methods, and Applications, Second Edition. Society for Industrial and Applied Mathematics, 2014, pp. 1-33. https://doi.org/10.1137/1.9781611973594.ch1
L E Giraldo Paez, J L Torijano Moreno, " Desarrollo de una propuesta de mejoramiento para un proceso de ruteo en una empresa comercializadora de materias primas", tesis de maestría, Universidad Icesi, Cali, Colombia, 2014.
R Ballou, "Logística: Administración de la cadena de suministro", Quinta edición, Pearson educación, Ciudad de México, 2004.
H. Stadtler, "Supply chain management-an overview.", in Supply chain management and advanced planning, Springer, Berlin, Heidelberg, 2008, pp. 9-36. http://dx.doi.org/10.1007/978-3-540-74512-9_2
J Bao , T Cai , Z Jiang, "Research on vehicle routing problem with soft time windows and distribution time constraints of vehicles", in International Conference on Future Information Technology and Management Engineering, Vol. 1, IEEE, 2010, pp. 205-208
N.A. El-Sherbeny, "Vehicle routing with time windows: An overview of exact, heuristic and metaheuristic methods", Journal of King Saud University-Science, Vol. 22(3), pp.123-131, 2010. http://dx.doi.org/10.1016/j.jksus.2010.03.002
L. Rocha Medina, J. Orjuela Castro, E. González La Rota, "Una revisión al estado del arte del problema de ruteo de vehículos: Evolución histórica y métodos de solución". Ingeniería, Vol. 16(2), pp.35-55, 2011.
R. Pino , J. Lozano, C Martínez, & V Villanueva, "Estado del arte para la resolución de enrutamiento de vehículos con restricciones de capacidad", en 5th International Conference on Industrial Engineering and Industrial Ma-nagement, Cartagena, Colombia, 2011.
G. Laporte, "Fifty years of vehicle routing", Transportation Science, Vol. 43(4), pp. 408-416, 2009. https://doi.org/10.1287/trsc.1090.0301
D Innis & B La Londe, «Customer Service: The Key to Customer Satisfaction, Customer Loyalty, and Market Share", Journal of Business Logistics, Vol. 15(1), pp.1-27, 1994.
E.M. Frazzon, A. Albrecht, P. A. Hurtado, "Simulation-based optimization for the integrated scheduling of production and logistic systems", IFAC papers on line, 49(12), pp.1050-1055, 2016. http://dx.doi.org/10.1016/j.ifacol.2016.07.581
L K de Oliveira, B R Pinto e Oliveira, V de Assis Correia, "Simulation of an urban logistic space for the distribution of goods in Belo Horizonte, Brazil”, Procedia-Social and Behavioral Sciences, Vol.125(20), pp. 496-505,
http://dx.doi.org/10.1016/j.sbspro.2014.01.1491
G. Erdoğan "An open source spreadsheet solver for vehicle routing problems.", Computers & operations research, Vol. 84, pp. 62-72, 2017. http://dx.doi.org/10.1016/j.cor.2017.02.022
J. Oyola, H. Arntzen, D.L. Woodruff, "The stochastic vehicle routing problem, a literature review, part II: solution methods", EURO Journal on Transportation and Logistics, Vol. 6(4), pp. 349-388, 2017. http://dx.doi.org/10.1007/s13676-016-0099-7
P.C. Pop, L. Fuksz., A.H. Marc, "A variable neighborhood search approach for solving the generalized vehicle routing problem", In International Conference on Hybrid Artificial Intelligence Systems, Springer, Cham, june, 2014. http://dx.doi.org/10.1007/978-3-319-07617-1_2
E. Majercakova, P. Majercak, "Application of Clarke-Wright method for solving routing problem in distribution logistics", Logi-Scientific Journal on Transport and Logistics, Vol. 6(1), pp. 90-99, 2015.
D. Anghinolfi, M. Paolucci, F.Tonelli, "A Vehicle Routing Problem with Time Windows Approach for Planning
Service Operations in Gas Distribution Network of a Metropolitan Area", IFAC-Papers On Line, Vol. 49(12), pp. 1365-1370, 2016. http://dx.doi.org/10.1016/j.ifacol.2016.07.754
C. Cañedo Iglesias, M. Curbelo Hernández , K. Núñez Chaviano, R. Zamora Fonseca, " Los procedimientos de un Sistema de Gestión de Información: Un estudio de caso de la Universidad de Cienfuegos", Biblios, ed. Lima, Perú, 2012. http://dx.doi.org/10.5195/BIBLIOS.2012.40
A. Hoff, H. Andersson, M. Christiansen, G. Hasle, A. Løkketangen, "Industrial aspects and literature survey: Fleet composition and routing", Computers & Operations Research, Vol. 37(12), pp. 2041-2061, 2010. http://dx.doi.org/10.1016/j.cor.2010.03.015
G.K. Rand, "The life and times of the Savings Method for Vehicle Routing Problems". ORION, Vol. 25(2), 2009. http://dx.doi.org/10.5784/25-2-78
M. Desrochers, J.K. Lenstra, F. Soumis, "Vehicle routing with time windows: Optimization and approximation", in Vehicle routing: Methods and studies, Ed. Golden BL & Assad AA, Amsterdam, pp. 65-84, 1988.
J.F. Cordeau, et al, «VRP with time windows", Montréal: Groupe d'études et de recherche en analyse des décisions, 2000. http://dx.doi.org/10.1137/1.9780898718515.ch7
M. Solomon "Algorithms for the vehicle routing and scheduling problem with time window constraints", Operations Research, Vol. 35(2), pp. 254-265, 1987. http://dx.doi.org/10.1287/opre.35.2.254
G. Kim, et al, "City vehicle routing problem (city VRP): A review." IEEE Transactions on Intelligent Transportation Systems 16.4 (2015): 1654-1666.http://dx.doi.org/10.1109/TITS.2015.2395536
M. Islam, S. Ghosh, M. Rahman, "Solving Capacitated Vehicle Routing Problem by Using Heuristic Approaches: A Case Study", Journal of Modern Science and Technology, Vol. 3(1), pp. 135-146, 2015.
J. Munuzuri, R. Grosso, P. Cortes, and J. Guadix, "Estimating the extracosts imposed on delivery vehicles using access time windows in a city" Comput., Environ. Urban Syst., vol. 41, pp. 262-275, 2013. https://doi.org/10.1016/j.compenvurbsys.2012.05.005
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Recibido: 27 de agosto de 2019; Revisión recibida: 18 de febrero de 2020; Aceptado: 18 de mayo de 2020
Resumen
Contexto:
Este artículo plantea resolver el problema de represamiento de entregas identificado en 2018 en una empresa dedicada al servicio de entregas de paquetes y mercancías, localizada en el Valle del Cauca, Colombia, a partir de la optimización del proceso logístico que permita reducir los tiempos del proceso de entregas a los clientes y evitar pérdidas para la empresa. Esto significa generar rutas adecuadas, según el problema clásico denominado problema de enrutamiento del vehículo (VRP, por sus siglas en inglés).
Método:
Se analiza la información de más de 200 clientes para su realización. Se combinaron herramientas de calidad tales como el análisis de Pareto y el enfoque de procesos con técnicas de optimización basadas en el método Clarke-Wright y el uso de ventanas de tiempo por medio del programa VRP Solver 3.0.
Resultados:
Con el diseño de las rutas propuesto para atender las entregas de una de las zonas de mayor demanda en la empresa (zona centro), los resultados de la simulación arrojaron un aumento en el nivel de servicio del 60 %, dado el uso del vehículo para la distribución en una jornada laboral completa y no solo en media jornada. Se evidencia que el aumento en los clientes atendidos genera ingresos adicionales suficientes para cubrir los costos de usar el vehículo una jornada más, con utilidades para la empresa. Asimismo, la capacidad de entrega en Tm se aumenta en un 39 %. De este modo, se elimina la mercancía represada.
Conclusiones:
Con el uso de ventanas de tiempo, se propone un método para la programación de rutas mediante la aplicación de la herramienta VRP Solver 3.0, consecuente con la operación del día a día en operadores logísticos como el caso estudiado. Igualmente, este artículo constituye una manera de acercar los conocimientos teóricos de la academia a la gestión eficiente del servicio en las Pymes. Así, empresas, como la del caso presentado pueden mejorar aún más su nivel de servicio con tecnologías apropiadas para el tratamiento y control de la información de los clientes, con miras a la planificación de las entregas.
Palabras clave:
Logística, nivel de servicio, optimización, problema de enrutamiento del vehículo, proceso de entregas, ventanas de tiempo..Abstract
Context:
This paper proposes to solve the problem of accumulated deliveries, identified in 2018, in a company dedicated to the service of deliveries of packages and merchandise, located in Valle del Cauca,Colombia, based on the optimization of the logistics process that allows reducing delivery times to customers and avoiding wastages for the company. This means generating appropriate routes, according to the classic problem called Vehicle Routing Problem (VRP).
Method:
The information of more than 200 clients is analyzed for its realization. Quality tools, such as Pareto analysis and process approach, were combined with optimization techniques based on the Clarke-Wright method and the use of time windows through the VRP Solver 3.0 program.
Results:
With the design of the routes proposed to meet the deliveries of one of the areas with the highest demand in the company (Central Zone), the results of the simulation showed an increase in the service level of 60 %, given the use of the vehicle to the distribution in a complete working day and not only in half day of work. It is evident that the increase in customers served generates additional income, sufficient to cover the costs of using the vehicle half working day more, with profits for the company. Likewise, the delivery capacity, in Tm, is increased by 39 %. So the accumulated merchandise by delivery is eliminated.
Conclusions:
With the use of time windows, a method for route programming is proposed by applying the VRP Solver 3.0 tool, more consistent with the daily operation of logistics operators as the case studied. Likewise, this article constitutes a way of bringing the theoretical knowledge of the academy to the efficient management of the service in SMEs. Thus, companies like the case presented, can further improve their service level with appropriate technologies for the processing and control of customer information, with the purpose to planning the deliveries.
Keywords:
Delivery process, logistics, optimization, service level, time windows, vehicle routing problem..Introducción
Existen ciertos factores que en los últimos años están influyendo en el transporte de mercancía, tales como: la globalización, la apertura de mercados, el aumento del acceso a las tecnologías por parte de las personas, el consumo mundial, entre otros. Es así como el transporte de mercancías ha tomado mayor importancia en los últimos años, teniendo en consideración que este es el canal que comunica a los productores con los consumidores finales.
El transporte, a su vez, ha sido ampliamente estudiado a través del ruteo de vehículos, considerando restricciones asociadas a capacidad, tiempos de entrega que deben ser reducidos para atender los requerimientos de los clientes y demás criterios implementados por las organizaciones con el objetivo de brindar satisfacción a sus clientes [1].
La mayoría de la literatura que aborda este problema se centra en encontrar diferentes rutas para los vehículos asumiendo que estos serán conducidos por un mismo conductor, este es el clásico problema reconocido del VRP (por sus siglas en inglés de vehicule routing problem). A esto se suman las restricciones colaterales que en muchos de los casos son ventanas de tiempo para recolecciones y entregas [2].
El ruteo tiene como objetivo final dar solución a problemas de transporte (rutas) para vehículos con restricciones en capacidad. Actualmente es uno de los problemas más estudiados debido al auge en la demanda en el transporte de mercancía [3].
Las empresas gastan mucho tiempo y dinero en mejorar sus sistemas logísticos con el fin de mejorar su relación con los clientes y tener mayores beneficios [4]. Con la planeación de rutas está la posibilidad de seleccionar cuál modo de transporte utilizar, la cantidad a enviar y la programación de estas.
Por su parte, [5] afirma que el establecimiento de las rutas para la distribución o recogida de bienes constituyen la parte central de la toma de decisiones operativas de la gestión logística de muchas empresas. En los problemas de planificación de rutas se puede tener en cuenta el objetivo de minimizar los costos asociados a la menor duración de la ruta, al deterioro o pérdida de calidad de los bienes producido por el tiempo acumulado durante la ruta y al cumplimiento de ventanas de tiempo de servicio estrictas en las entregas que cubren las demandas de los clientes [6], [7].
Entre los objetivos que busca el modelo VRP destaca la obtención de un menor costo asociado al transporte, recorriendo la menor distancia y utilizando un menor tiempo de distribución, entre otras diferentes variables sujetas a los requerimientos de las organizaciones o los casos objeto de estudio [8]. También se tienen en cuenta para definir las rutas a los clientes, los vehículos, los depósitos, las restricciones y los objetivos, donde el cliente cuenta con una demanda establecida que necesita ser satisfecha por la flota de vehículos, la cual parte y debe regresar al depósito [9].
Es importante mencionar que el VRP clásico plantea obtener el mejor conjunto de rutas que comiencen y terminen en un depósito o nodos para una flota de vehículos con características idénticas y en la cual los clientes sean visitados solo una vez. Los arcos de estos nodos pueden estar representados en distancias o costos de transporte como resultado de llevar la mercancía del depósito a los diferentes clientes [10].
Otro estudio menciona que para abordar el despacho en una empresa se tiene que hablar primero de distribución física de mercancía [11]. Además, afirma que, con respecto al servicio al cliente, existen factores importantes que dificultan directamente a la función de distribución física en las empresas. Estos aspectos son, por ejemplo, la frecuencia de despachos, la información sobre disponibilidad de inventarios, las fechas de despachos programadas, entre otros aspectos señalados en dicho estudio.
No obstante, debido a la complejidad de las diferentes variaciones del VRP, este ha sido ampliamente estudiado ya desde la parte computacional, más exactamente la simulación, en razón de la cada vez más alta complejidad de los problemas logísticos que se presentan en la actualidad. La programación adecuada e integrada de las operaciones de producción, transporte de inventarios y distribución, puede apoyar el surgimiento de cadenas de suministros adaptables, ágiles y resistentes, esto conlleva a enfoques de optimización, simulación o híbridos que llegan a ser objetivos estratégicos fundamentales de las organizaciones para garantizar costos competitivos y un nivel de servicio adecuado en la cadena de suministro [12].
La simulación en la logística considera aspectos importantes que pueden llevar a ventajas competitivas de las organizaciones como lo son reducción de viajes de vehículos, reducción de tiempos y, por ende, reducción de costos totales. Estos aspectos no solo pueden ser considerados por las organizaciones, sino también en las grandes metrópolis en los cuales la simulación juega un papel fundamental debido a su complejidad, esto puede ayudar al mejoramiento de la movilidad [13].
El VRP Spreadsheet Solver ha sido utilizado en la práctica en múltiples organizaciones de distintos sectores a nivel mundial, algunas de estas organizaciones que presentaron retroalimentación incluyen dos empresas de Estados Unidos en la industria petrolera, una empresa de Argentina en la industria agrícola, una empresa finlandesa en el sector del turismo y dos cadenas de entrega de alimentos refrigerados en Taiwán y Turquía. Todas estas aplicaciones representaron ahorros significativos por concepto de utilidad, ahorro de viajes, entre otros.
Estos estudios y el gran reconocimiento que tiene esta hoja de Excel se deben a que puede resolver más de 64 variantes del VRP, incluyendo características esenciales para resolver, tales como: las visitas selectivas a los clientes, las recolecciones y entregas simultáneas, ventanas de tiempo, composición de flota, restricción de distancias y el destino final de los vehículos [14].
La estructura de la consola del VRP Solver consta de las siguientes entradas, en su orden: locaciones (I), distancias (II), vehículos (III), solución (IV) y visualización (V). Cada una de estas dimensiones se relaciona con alguna o varias de las demás. Por ejemplo, la solución está directamente asociada a los parámetros de las tres primeras dimensiones. La visualización permite establecer la localización de los clientes y a las rutas provenientes de una solución en particular.
Las cinco dimensiones de la consola indican: la lista de paradas para cada vehículo especificado en vehículos (III), la información en localizaciones (I) sobre los tiempos de servicio y los montos de recolección-entrega, así como la distancia y duración en (II). Distancias para calcular los tiempos de salida-llegada del costo de viajar entre clientes. En la opción solución (IV), la hoja de trabajo calcula el beneficio neto (net profit) en lugar del costo para acomodar variantes del VRP que acumulan beneficios cuando los clientes son visitados selectivamente. Finalmente, una serie de características de formato condicional llevan a identificar visualmente soluciones inviables y facilitan la construcción manual de soluciones. Así, un vehículo que excede su capacidad o límite de distancia o un cliente que se visita fuera de su ventana de tiempo, aparece resaltado en rojo.
De este modo, es posible copiar y pegar listas de clientes entre rutas de vehículos con el fin de modificar manualmente las rutas. En la sección 4.3 se presenta la matriz de solución inicial con las condiciones actuales: un solo vehículo y una sola jornada de trabajo de 8:00 a. m. a 12:00 p. m., entre otras.
El programa VRP Solver 3.0 utiliza, entre otros, el algoritmo conocido como heurística estocástica de ClarkeWright, el cual comienza con una solución de viajes ida y vuelta a cada cliente y combina las rutas que tendrán un mejor impacto en el costo total esperado [15]. Aquí el ahorro es una medida de la reducción de costos obtenida al combinar dos rutas pequeñas en una ruta más grande [16]. La utilidad de esta heurística puede evidenciarse en [17], donde se exponen diversas aplicaciones en la optimización del proceso de distribución. Adicionalmente, con miras a optimizar el uso de los recursos en la distribución, se apunta a minimizar el tiempo total de servicio y a balancear la carga de trabajo tripulación-vehículo, tal como se plantea en [18].
En este problema se abordó el diseño de rutas para atender las entregas del sector “centro” en la ciudad de Cali de una empresa transportadora de mercancía, zona que está presentando problemas de despacho tales como el represamiento de la mercancía. Esta acumulación alcanza en promedio el 20 %, esto es, de las 107,825 Tm que en promedio demanda la zona mensualmente, se está quedando sin entregar 21,565 Tm aproximadamente. Esto conlleva a un bajo servicio al cliente, altos costos de almacenamiento de la mercancía y pérdidas que afectan las utilidades.
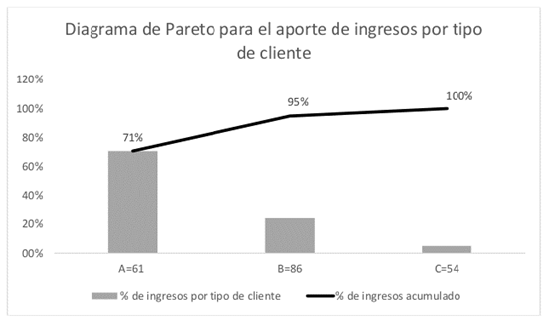
Para la solución del problema se partió de una serie de objetivos: analizar el proceso de entregas seguido actualmente por la compañía, aplicar mediante un programa de simulación las mejoras que permitan establecer soluciones a este problema, analizar los resultados obtenidos y proponer las rutas necesarias para la distribución de mercancía en esta zona. Inicialmente, se analizó el comportamiento comercial de los clientes; utilizando el diagrama de Pareto se clasificaron los clientes por el peso en las ventas. Este fue un insumo importante en la simulación de las rutas para atender 52 clientes.
Métodos y materiales
Para el análisis del caso se observaron los hechos que ocurrían al interior de la compañía, se entrevistó el personal del proceso de distribución y se consultó literatura especializada acerca del problema de ruteo vehicular con el uso ventanas de tiempo.
Técnicas de recolección de datos. Las fuentes de información utilizadas para el análisis de este caso se pueden dividir en dos partes:
-
Fuentes primarias. Se utilizó entrevista estructurada con el personal a cargo de la planeación de las rutas y observación directa del proceso de entrega de la mercancía. Se entrevistó a 20 personas durante dos semanas. Se indagó sobre cuatro aspectos: eficiencia de la planeación de la ruta para la zona “volumen centro”, posibilidad de ampliar la jornada del vehículo de esta ruta, frecuencia de las quejas de los clientes de esta zona y la posibilidad de apoyar la zona con recursos (vehículos) de otras rutas. Con las entrevistas se determinó la capacidad del vehículo y los horarios de todo el proceso.
-
Fuentes secundarias. Revisión de literatura especializada con respecto al VRP y datos del proceso de planeación de rutas.
Análisis de la información. Con herramientas de gestión de procesos como el diagrama SIPOC y el diagrama de Pareto, se analizaron aquellos aspectos que influían en el represamiento de la mercancía.
La información de entrada que se utiliza en la simulación desarrollada a través de la herramienta VRP Solver se identifica desde el ruteo de las guías, documento que contiene: nombre de cliente, dirección, método de pago, costos de entrega para el cliente, vehículo asignado y el valor declarado de la mercancía. Así pues, mediante estas guías se analizaron las frecuencias de los clientes en el mes de estudio y vehículo asignado.
Finalmente, se diseñaron las rutas a través del programa VRP Solver 3.0, el cual implementa una variante de la búsqueda adaptativa de vecindarios dentro de la herramienta de solución de hojas de cálculo VRP debido a su flexibilidad para adaptarse a muchas variantes del VRP como las que se describen en [17]. El algoritmo diversifica la búsqueda mediante la eliminación aleatoria de clientes de la solución en cuestión y se intensifica mediante la reinserción de los clientes y la búsqueda local [14].
La función objetivo para el VRP Solver 3.0 planteada en [14] maximiza el beneficio total recaudado a través de los ingresos provenientes de los clientes atendidos (1) menos los costos de viaje de los vehículos (2), el costo fijo de usar los vehículos (3) y la penalización por violar los plazos o las ventanas de tiempo establecidas (4).
Las restricciones, 26 en total, establecen las reglas de visita para los clientes de los vehículos [14]. La idea con el tercer término (3) de esta función es reducir el número de veces que el vehículo tenga que regresar a la bodega desde donde es despachado.
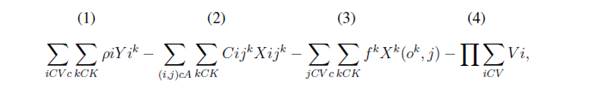
K: cantidad de vehículos.
Pi: beneficio del cliente i.
Y ik: variable de decisión acerca del beneficio que representa el cliente i con el uso del vehículo k.
El valor de Y es 1 si se le entregó al cliente, 0 si no se hizo.
Cijk: es el costo de visitar un cliente localizado sobre el arco (i; j) con el vehículo k.
Xijk: el valor de X es 1 si el vehículo atraviesa el arco (i; j), 0 si no lo hizo, para cada vehículo k.
fk: costo de contratar o usar un vehículo k.
V i : ventana de tiempo i.
V c : serie de vértices que contiene a los clientes de la zona.
A: conjunto de distancias (i; j).
Ok: origen del depósito para un vehículo k.
π: costo de la penalidad por unidad de tiempo.
Descripción del caso
La compañía objeto de estudio lleva cerca de 64 años en el sector de transporte de mercancía y de pasajeros. Por muchos años estuvo a la par de las grandes compañías del sector. En el último año, el nivel de servicio del sistema de distribución ha decrecido debido a una débil planeación de las rutas asignadas a los vehículos. Esta situación entorpece el flujo de mercancías proveniente de las diferentes partes del país, haciendo que el sistema de entrega no sea eficiente y generando represamiento.
Para corroborar esta problemática, se realizó una entrevista estructurada al personal del proceso de distribución, la cual refleja los siguientes resultados: el 75% de los encuestados consideraban que no era eficiente la planeación de la ruta volumen centro; todos veían necesaria la implementación de la jornada continua para reducir los tiempos de entrega; el 90% de los entrevistados era consciente de la inconformidad de los clientes en la ruta “volumen centro” por el nivel de servicio percibido; finalmente, el 70% del personal consideraba pertinente el apoyo, en recursos, por otras rutas de entrega (centro 1 y centro 2) a la ruta “volumen centro” (ruta crítica).
En estas condiciones, el vehículo asignado solo medio día para la distribución de la mercancía en la ruta “volumen centro” no era suficiente. Esto se debe a que en las condiciones actuales de entrega solo se alcanza a entregar un 80% de la carga, la cual a 2018 tenía un peso promedio de 107,825 Tm por atender. De esta manera, se quedaba 21,560 Tm represadas. Se destaca que a la zona centro de la ciudad de Cali se envía el 40% de toda la mercancía de la bodega, de la cual la ruta “volumen centro” representa el 25% del movimiento de la carga. El otro 60% es entregado a través de otras rutas.
Para el caso de estudio, la empresa suministró una base de datos de 201 clientes de la zona “volumen centro”. Aplicando la herramienta diagrama de Pareto (Figura 1) y considerando los ingresos por venta (COP) que representa para la empresa cada cliente, se eligieron 61 clientes de mayor peso (A) que representa el 70,8% de ingresos de la zona. Teniendo en cuenta que de los 61 clientes aparecían dieciséis que se les había despachado una sola vez durante el mes de estudio, se solicitó a la compañía un histórico de estos clientes para establecer cuáles no continuaban con la compañía, resultando nueve de los dieciséis clientes. Tomando como base esta información se decidió realizar el estudio con 52 clientes (Tabla I y Tabla II).
Figura 1: Peso de los clientes en el mes de estudio.
Tabla I: Datos clientes C0001
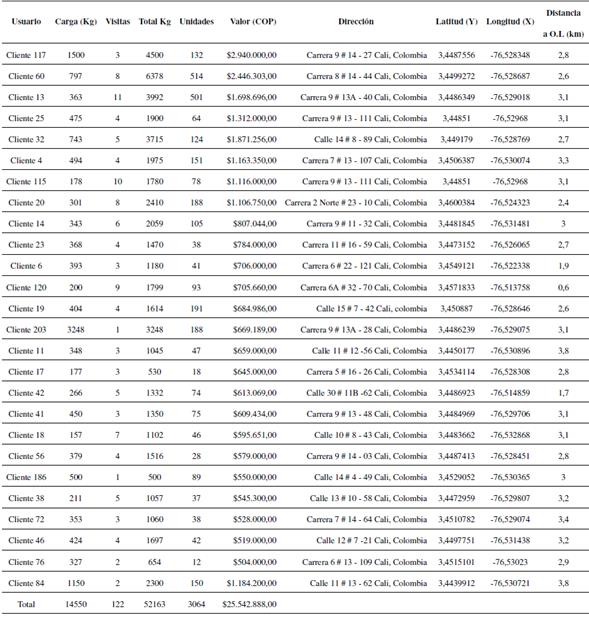
Tabla II: Datos clientes C0002
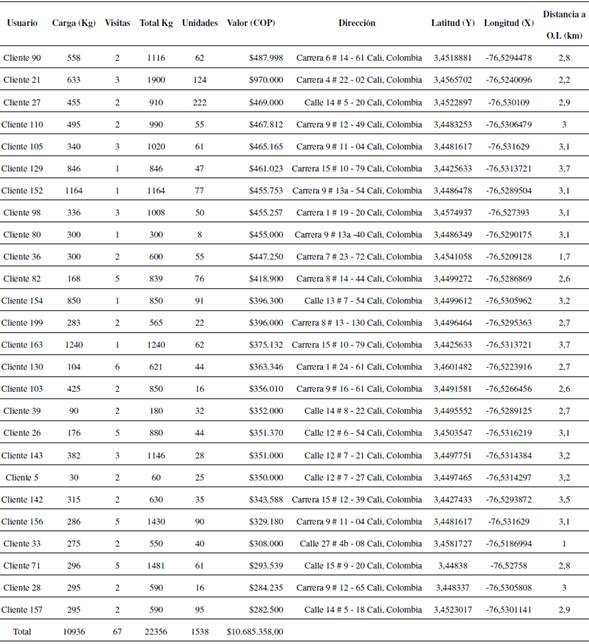
Para un mejor análisis de la información se clasificó a los clientes en dos zonas: C0001 que corresponde a los clientes que representan mayores ingresos para la compañía y C0002 que corresponde a los clientes que representan ingresos menores.
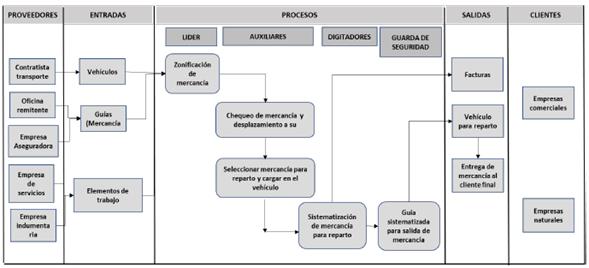
En el análisis del proceso de entrega actual de la compañía, se empleó el diagrama SIPOC (proveedores-insumosp-rocesos-salidas-clientes, por sus siglas en inglés) según se muestra en la Figura 2. El diagrama permitió comprender la operación general de la compañía de una manera sistémica y evidenciar oportunidades de mejora en las áreas de digitación y embarque de la mercancía. El diagrama SIPOC [19], al tener un enfoque de sistemas, permite a los responsables de cada proceso entender cómo se relacionan con los demás procesos, clientes y proveedores. También clarifica cuáles son los requerimientos de entrada para que el sistema opere de acuerdo con las salidas esperadas por los distintos actores, facilitando los procesos de comunicación.
Figura 2: Diagrama SIPOC.
Por ejemplo, el líder del proceso de entregas requiere de los insumos enviados por la oficina remitente de las guías y mercancía, de la empresa aseguradora y del contratista de transporte. El líder es el cliente interno de estas entidades. Igualmente, en la operación de sistematización de la mercancía para el reparto, se evidencia la oportunidad de agregar valor al proceso a través de la creación de una base de datos de los clientes en el área de digitación que mejore la productividad de este proceso y, con ayuda del software, permita el diseño de la ruta automática mente. Por otro lado, al contar con el software y el diseño de la ruta automática, se reducen los tiempos de programación, lo que redundará en un mejor nivel de servicio y mayor agilidad de respuesta, en particular hacia aquellos clientes de mayor frecuencia en la prestación del servicio.
Parámetros de la simulación VRP Solver
Para depurar la información requerida en la simulación se realizaron las siguientes actividades:
-
Identificación de destinatarios (frecuencia de visita).
-
Construcción de lista de clientes por ruta.
-
Cálculo de peso promedio entregado a cada cliente.
-
Ubicación de cada cliente (latitud- longitud) con respecto a un origen de coordenadas.
-
Unificación de clientes de todas las rutas analizadas.
-
Capacidad del vehículo de reparto local.
-
Horario de trabajo.
-
Distancia.
Estos son los parámetros fundamentales observados en el proceso actual de la compañía.
Velocidad
La velocidad máxima en la ciudad de Cali es de 60 km/h, pero debido a que el estudio del caso se ejecutó en la zona centro de la ciudad de Cali y esta zona es de alta complejidad con respecto a la movilidad, se decidió utilizar una velocidad de 40 km/h.
Capacidad
Los parámetros relacionados con la capacidad del vehículo se describen a continuación.
Capacidad de carga: 4,5 Tm.
Volumen de carga: 22,5 _ 0,5 m.
Altura furgón: 2,22 _ 0,05 m.
Ancho furgón: 2,25 _ 0,05 m.
Personal involucrado
Para el reparto de la mercancía de la zona “volumen centro” se cuenta con una tripulación de dos auxiliares de ruta y el conductor del vehículo. El reparto de la mercancía se realiza de 8:00 a. m. a 12:00 p. m. de lunes a viernes, el tiempo estimado de la entrega a cada cliente es de máximo veinte minutos. Debido a que la zona “volumen centro” tiene una restricción horaria a partir de las 10:00 a. m. se decidió trabajar con veinte minutos, ya que antes de la restricción la entrega se podría hacer de forma directa en la ubicación del cliente, ahorrando tiempo que se puede utilizar en repartir a otros clientes.
Además, debido a que por lo general las distancias entre los clientes no son tan amplias, se puede atender a varios de ellos desde una ubicación específica en este tiempo. El rendimiento de un camión de estas dimensiones es de un galón cada 20 kilómetros aproximadamente y tiene un tanque de combustible para 45 galones. Por lo tanto, la distancia máxima del recorrido del camión será de 900 km aproximadamente.
La evacuación de la mercancía objeto de estudio con el procedimiento actual tardaría un total de diecisiete días, esto sale de la división de la cantidad total de mercancía objeto de estudio entre la capacidad del vehículo. Lo anterior quiere decir que para la evacuación de la mercancía el vehículo tiene que salir siempre de bodega con las 4,500 Tm y cumplir con los otros parámetros de horario, algo poco probable debido a la ubicación de los clientes.
Resultados y discusión
A continuación, se presenta la simulación en el programa VRP Solver 3.0 con el procedimiento actual de la compañía.
Parámetros iniciales
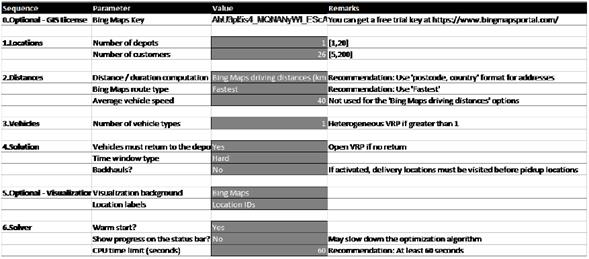
La Figura 3 muestra los parámetros iniciales para la realización de la simulación en el programa VRP Solver 3.0. Se indican: (1) locaciones o clientes (número de clientes a atender, numero de depósitos), (2) distancias, (3) número de vehículos, (4) soluciones (decisión de retorno al depósito, ventanas de tiempo), (5) visualización de la localización de los clientes en la ruta programada. En esencia, son las dimensiones de la consola VRP Solver, presentadas en la introducción de este documento. En (6) de la Figura 3, se plantea iniciar con una solución en caliente con un tiempo mínimo de corte de 60 segundos.
Figura 3: Parámetros iniciales
A continuación, se describen aspectos a destacar entre los parámetros iniciales. En (1) se definen 26 clientes y un depósito o bodega solo para entregas debido a que este es un problema clásico de VRP [20]. En (3) se utiliza un vehículo a 40 km/h y en (4) se define que el vehículo debe regresar a la bodega, además de que se estipulan ventanas de tiempo duras, es decir, aquellas que no permiten que un vehículo llegue fuera de la ventana [21], ni siquiera con sanciones de costos. Según [21], la mayoría de los trabajos publicados han investigado el problema con ventanas de tiempo duras. Destaca los casos presentados por [22]-[24].
Para este caso, las ventanas de tiempo se definen al establecer claramente las horas de entrega, de acuerdo con la jornada laboral y el límite de tiempo de veinte minutos por cliente para el uso de los recursos utilizados en las distintas rutas diseñadas. Esto va en concordancia con [25], quien resalta la importancia de la ventana de tiempo del cliente cuando se aplica VRP en las ciudades.
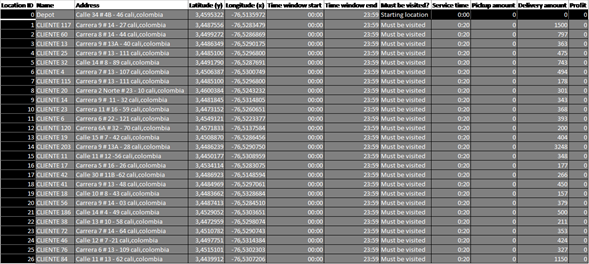
En la Figura 4, se indican los clientes correspondientes a la Tabla I. En esta se exponen las direcciones, coordenadas de cada uno de los clientes, tiempo de servicio y peso de la mercancía entregada a cada uno.
Figura 4: Datos generales clientes
Elaboración matriz de distancias
La matriz de distancias (Tabla III) identifica la distancia entre cada par de ubicaciones que se visitarán. Si se conocen los costos de transporte entre cada par de ubicaciones, el costo se puede utilizar en lugar de la distancia [26].
Tabla III: Matriz de distancia de i a j en la zona C0001 S.A

En la matriz de distancias se definen las distancias entre cada punto que conforma la red logística. La unidad de distancia se representa en kilómetros y la variable (dij) determina la distancia que se debe recorrer para ir del punto i hasta j. Cabe aclarar que en la mayoría de casos la distancia recorrida para ir de i hasta j es diferente a la recorrida para ir de j a i (dij ¹ dji). Uno de los puntos de la ruta corresponde al operador logístico (O.L) que es la bodega donde se almacena la mercancía. Para la obtención de las distancias entre los puntos se utilizó la herramienta Bing Maps, esta se encuentra incluida en la herramienta logística VRP Solver 3.0.
Resultados de las simulaciones
Los parámetros iniciales de capacidad para la simulación en las condiciones actuales (S.A.) se explicitan en la Tabla IV. En esta, C1 indica la carga entregada por el vehículo “volumen centro” en la mañana.
Tabla IV: Parámetros de capacidad S.A.

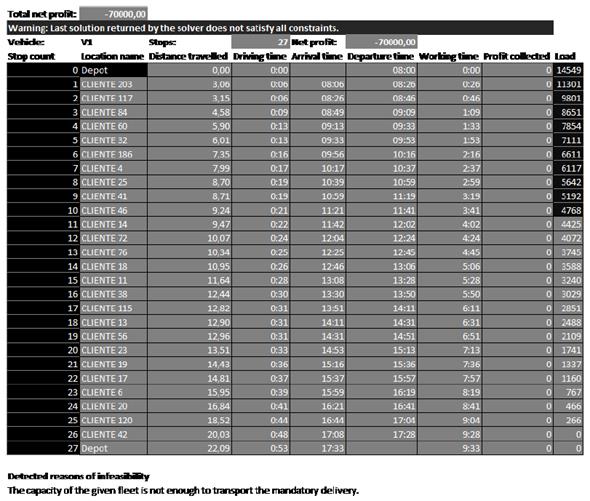
Realizando la incorporación de las variables de la Tabla IV, se procedió a obtener la matriz de solución del software VRP Solver para el vehículo C1. La solución de la Figura 5 evidencia que la capacidad del vehículo y tiempo de entrega no cumplen con los parámetros establecidos en la Tabla IV. Se requieren 27 paradas en total y a lo sumo solo se atenderían diez clientes, terminado a las 11:41 a. m. (departure time) la atención del último (cliente 46). Debido a esto, se hace necesario la reorganización de la zona “volumen centro” de manera que permita el diseño de rutas óptimas.
Figura 5: Matriz de solución inicial.
De acuerdo con los resultados de la simulación actual de la compañía, y analizando los diferentes recursos con los que cuenta la misma, se propone la siguiente alternativa de solución para la distribución de la mercancía:
-
Incorporar las rutas “centro 1” y “centro 2” que operan en el mismo sector de la ciudad y su cantidad de entrega, por lo general es reducida; sin embargo, debido a que estas rutas están comprometidas con los traslados de mercancía de la zona centro al O.L, solo se tomaron como recurso de apoyo en horas de la mañana (media jornada). Esta decisión se justifica debido a que la empresa paga por jornada laborada y no por mercancía entregada, lo que quiere decir que la empresa no incurriría en costos adicionales al utilizar los vehículos de esta zona.
-
Aumentar la jornada del vehículo volumen centro. Esta decisión es necesaria debido a que con el vehículo trabajando solo una jornada es imposible reducir el nivel de represamiento. Representa un costo variable adicional para la compañía que corresponde al pago de la jornada adicional.
Teniendo en cuenta las decisiones tomadas para la simulación, en la Tabla V se presenta la distribución de la mercancía en un día promedio por los tres vehículos. El primer vehículo se ocupa de las cargas C1 y C2 (carga entregada por el vehículo “volumen centro” en la tarde); el segundo vehículo se utiliza en una fracción de su capacidad para la carga C3 (carga entregada por el vehículo “centro 1” en la mañana); el tercer vehículo se utiliza en una fracción de su capacidad para la carga C4 (carga entregada por el vehículo “centro 2” en la mañana). Es decir, el primer y segundo vehículo se utilizaron como recursos de apoyo en el modelo.
Tabla V: Distribución mercancía promedio
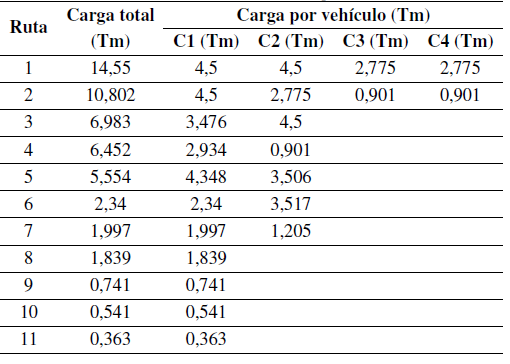
Para la distribución de la mercancía en los vehículos de apoyo que contienen las cargas C3 y C4,en las rutas 1 y 2 se decidió trabajar sobre la mercancía restante para completar el total entregado por la ruta, siendo los vehículos que contienen las cargas C1 y C2 los que repartan la mayor cantidad de mercancía por ser los vehículos de la zona objeto de estudio.
La cantidad simulada en la ruta 1, correspondiente al primer día de entrega (Tabla V), no sería inconveniente en el reparto de la propia mercancía de los vehículos que contiene las cargas C3 y C4 basados en los siguientes datos suministrados por la compañía (Tabla VI).
Tabla VI: Mercancía aproximada transportada por mes y día.

Según la Tabla VI, en promedio las rutas “centro 1” y “centro 2” entregan diariamente en peso 1,500 Tm y 1,250 Tm respectivamente, esto representa, con respecto a la capacidad del vehículo, un 33% y 28 %. Los parámetros de capacidad para la simulación de la ruta 1 se muestran en la Tabla VII.
Incorporando las variables de la Tabla VII, se obtiene la matriz de solución del software VRP Solver para cada vehículo. La Figura 6 indica la distribución de la mercancía para los tres vehículos. Las cargas C1 y C2 corresponden al mismo vehículo, usado en la mañana (V1) y tarde (V2). Los clientes atendidos por V3 (carga C3) y V4 (carga C4) serían por un recurso de apoyo.
Tabla VII: Parámetros de capacidad ruta 1.
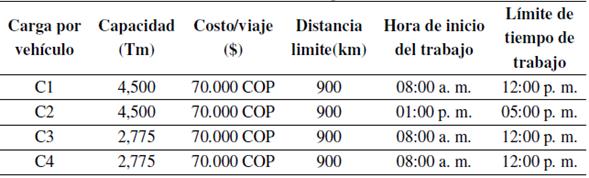
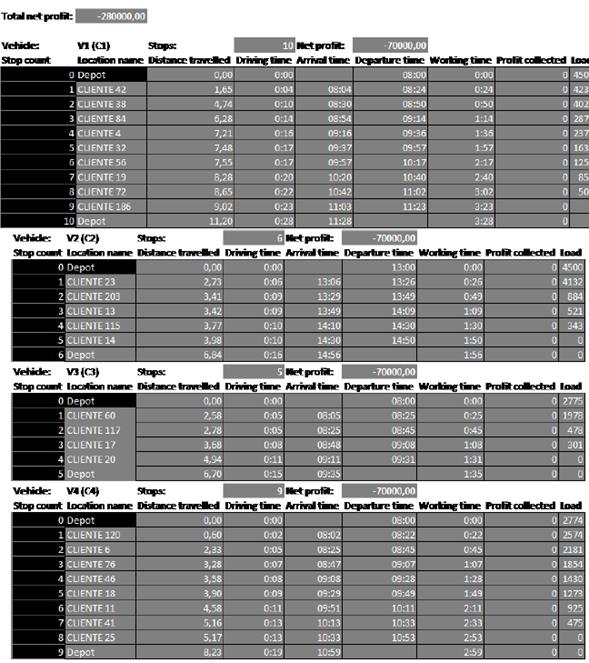
De este modo, se atienden en total 26 clientes. En la Figura 6, vehículo uno (V1), se indica: cada una de las diez paradas (stop count) en la primera columna, luego el nombre de la locación o cliente por donde pasa el vehículo, la distancia recorrida, el tiempo de conducción, el tiempo de arribo, el tiempo de salida, el tiempo de trabajo, el beneficio acumulado y la carga del vehículo. Nótese que después de la novena parada, cliente 186, el vehículo va de regreso al depósito (décima parada) a las 11:23 a. m. sin carga, recorriendo 9,02 km y un tiempo de trabajo acumulado de 3 horas y 28 minutos. Para los demás recursos (V2, V3 y V4), puede notarse, igualmente, que siempre el vehículo inicia en la bodega o depósito y termina allí mismo.
Figura 6: Distribución de la mercancía para los vehículos V1, V2, V3 y V4.
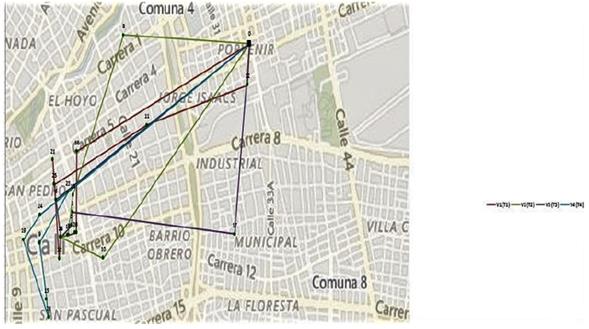
La Figura 7 ilustra la localización geográfica de los 26 clientes principales de la empresa de la zona centro y una posible repartición de la mercancía (simulada) para el primer día de entrega (ruta 1), usando el recurso disponible para esta zona mañana y tarde (V1 y V2) y, además, con recurso de apoyo V3 y V4. Las ubicaciones y las rutas de los vehículos se pueden inspeccionar visualmente generando esta hoja de trabajo opcional. Las opciones en la consola VRP Solver pueden configurarse para mostrar varios detalles sobre las ubicaciones, incluidos los montos de recolección-entrega o los tiempos de servicio. Esta hoja de trabajo simplemente contiene un gráfico de dispersión con el mapa de la región recuperada del servicio web SIG (Sistema de Información Geográfica).
En conclusión, la simulación de la ruta 1, de las once diseñadas, cumple con los parámetros establecidos en la Tabla VII; por lo tanto, la distribución de la mercancía se puede realizar de forma efectiva.
Figura 7: Localización de los clientes.
En la Tabla VIII se ilustran los parámetros de capacidad para la simulación de la ruta 2.
Tabla VIII: Parámetros de capacidad ruta 2.
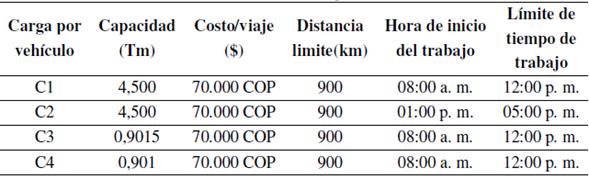
Incorporando las variables mencionadas en la Tabla VIII, se procedió a realizar la simulación en el software, tal como se realizó para la ruta 1.
A continuación, se describen las principales observaciones para la ruta 2.
El vehículo C1 hará un total de nueve paradas, atendiendo un total de ocho clientes. Recorrerá una distancia de 8,97 km entregando un total de 4,500 Tm, iniciando su recorrido a las 8:00 a. m. y finalizando a las 11:01 a. m.
El vehículo C2 hará un total de once paradas, atendiendo un total de diez clientes. Recorrerá una distancia de 9,20 km entregando un total de 4,500 Tm, iniciando su recorrido a la 01:00 p. m. y finalizando a las 04:41 p. m.
El vehículo C3 hará un total de cuatro paradas, atendiendo un total de tres clientes. Recorrerá una distancia de 7,84 km entregando un total de 0,901 Tm, iniciando su recorrido a las 8:00 a. m. y finalizando a las 9:17 a. m.
El vehículo C4 hará un total de cuatro paradas, atendiendo un total de tres clientes. Recorrerá una distancia de 6,29 km entregando un total de 0,901 Tm, iniciando su recorrido a las 8:00 a. m. y finalizando a las 9:12 a. m.
De acuerdo con la simulación realizada para la ruta 2, y teniendo como referencia los resultados obtenidos en la matriz de solución del software, se concluye que la simulación cumple con los parámetros establecidos en la Tabla VIII. Por lo tanto, la distribución de la mercancía en esta ruta es óptima.
Las Tablas IX-Tabla XIV indican los resultados de la simulación para las diferentes rutas.
Tabla IX: Simulación ruta tres

Tabla X: Simulación ruta cuatro

Tabla XI: Simulación ruta cinco

Tabla XII: Simulación ruta seis

Tabla XIII: Simulación ruta siete

Tabla XIV: Simulación ruta ocho

Debido a que las rutas 9, 10 y 11 tienen clientes insuficientes no es posible realizar la simulación por restricciones del VRP Solver 3.0. La solución en este caso sería realizar el diseño de ruta de forma manual, al programar nuevos clientes de la zona que aparezcan durante estos primeros ocho días, esto porque es una de las zonas a donde llegan más encomiendas.
Análisis y discusión
Como se indica en la Tabla XV, el recurso de apoyo sería únicamente necesario para las rutas 1 y 2. A partir de la ruta 3 el vehículo de la zona “volumen centro” puede ser autónomo en la entrega de la mercancía. Dado que la utilización del recurso, a partir de la ruta 3, empieza a disminuir paulatinamente se incorporan los clientes que representan menos ingresos para atender la totalidad de los clientes. Los resultados de la simulación se indican en las Tablas XVI- Tabla XXIII.
Tabla XV: Utilización del recurso clientes C0001
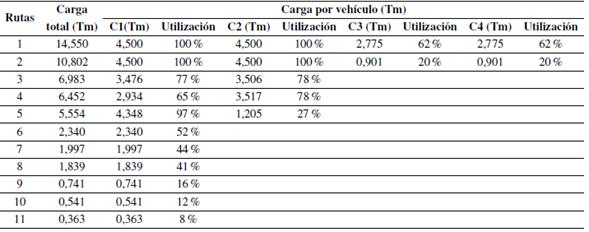
Tabla XVI: Simulación ruta 2 con adición

Tabla XVII: Simulación ruta 3 con adición

Tabla XVIII: Simulación ruta 4 con adición

Tabla XIX: Simulación ruta 5 con adición

Tabla XX: Simulación ruta 6 con adición

Tabla XXI: Simulación ruta 7 con adición

Tabla XXII: Simulación ruta 8 con adición

Tabla XXIII: Simulación ruta 9 con adición

A continuación, se muestra la distribución de la mercancía desde la ruta dos hasta la nueve, incorporando los clientes de la Tabla II. Para la realización de la distribución de las encomiendas se siguieron los parámetros establecidos referentes a capacidad del vehículo y tiempo de laborado, todo esto con la firme intención de utilizar la mayor cantidad del recurso disponible.
Debido a la disponibilidad del recurso de apoyo en la empresa, este se utilizó para una mayor evacuación de la mercancía de la “zona centro”. La selección de los clientes añadidos a cada ruta se realizó validando la cantidad de carga entregada en el tiempo de estudio. Para esto, se utilizó la recolección de datos de las guías y se realizaron cerca de veinte simulaciones, cantidad en la que se cumplieron los parámetros establecidos.
Para una mayor evacuación de la mercancía se decidió atender el máximo de clientes por ruta que corresponde a 26. La Tabla XVI-Tabla XXII presentan los clientes adicionales a cada ruta (tomados de la Tabla II).
La ruta 2 incorpora los clientes 98 y 21, con esto la ruta queda con un total de 26 clientes a atender y una carga total de 11,772 Tm. La ruta 3 incorpora los clientes 129, 80, 154, 163, 152, 130 y 71; con esto, la ruta queda con un total de 26 clientes a atender y una carga total de 11,783 Tm. La ruta 4 incorpora los clientes 130, 105, 143, 90, 27, 199, 36, 21, 71; con esto, la ruta queda con un total de 26 clientes a atender y una carga total de 9,803 Tm.
La ruta 5 incorpora los clientes 82, 26, 156, 105, 98, 143, 90, 27, 110, 28, 142, 5, 36, 103; con esto, la ruta queda con un total de 26 clientes a atender y una carga total de 10,115 Tm. La ruta 6 incorpora los clientes 130, 82, 26, 156, 71, 21, 105, 98, 143, 110, 39, 33, 157, 199, 28, 103, 5, 142; con esto, la ruta queda con un total de 25 clientes a atender y una carga total de 7,563 Tm. La ruta 7 incorpora los clientes 130, 82, 26, 156, 71, 39, 33, 157; con esto, la ruta queda con un total de catorce clientes a atender y una carga total de 3,686 Tm.
La ruta 8 incorpora los clientes 130, 82, 26, 156, 71; con esto, la ruta queda con un total de diez clientes a atender y una carga total de 2,869 Tm. La ruta 9 incorpora los clientes 130, 82, 26,156; con esto, la ruta queda con un total de siete clientes a atender y una carga total de 1,474 Tm.
La simulación de las rutas se realizó bajo un escenario optimista [21] con base en los datos suministrados por la compañía. Se evidencia que en los últimos seis meses la zona “volumen centro” recibió la cantidad de 785,218 Tm de mercancía, aproximadamente, y solo el 3% de esta no fue entregada a tiempo por ausencia del cliente en el sitio.
Por lo tanto, las simulaciones se realizan en un escenario en el cual a todos los clientes se les atiende y se les entrega la mercancía. En la Tabla XXIV se indica el porcentaje de utilización del recurso por vehículo en cada ruta con los clientes añadidos. Con la propuesta dos, según la Tabla XXV, el vehículo se utilizaría mañana y tarde hasta la ruta 7, es decir, siete días de los once. En estos días se alcanzaría a evacuar en la tarde 27,385 Tm (sumando los datos de la columna C2). Con el método actual queda represada esta cantidad de carga.
Tabla XXIV: Porcentaje de utilización del vehículo con clientes adicionales
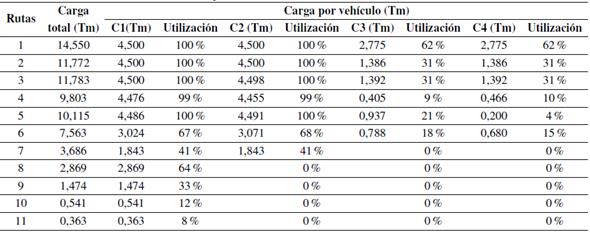
Tabla XXV: Variación de la capacidad del servicio por tipo de propuesta
Con la propuesta de usar un solo vehículo a mañana y tarde, se evacúa en once días 59,934 Tm, es decir, al menos 120 Tm aproximadamente en un mes. Con esta propuesta, se aumenta un 39% la capacidad de entrega, medida en Tm. Lo anterior tomando como referencia las condiciones actuales de la ruta “volumen centro”, donde se entrega un 80% del promedio mensual 107,825 Tm, es decir, no habría mercancía represada. La Tabla XXV muestra la capacidad del servicio para tres propuestas y los ingresos asociados a cada una, teniendo en cuenta el uso del recurso en la jornada laboral solución encontrada.
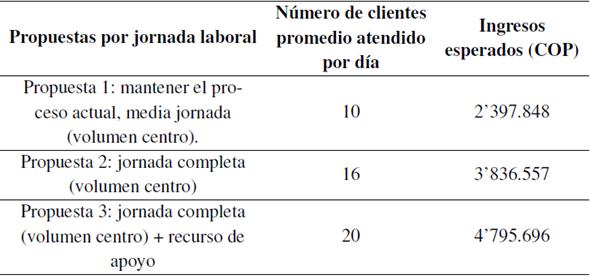
Dada la situación actual de la empresa, que cuenta con un solo vehículo para esta ruta, se elige la segunda propuesta, es decir, el uso del vehículo en jornada completa, como mejor solución para el análisis de la Tabla XXVI y la Tabla XXVII.
Tabla XXVI: Convenciones análisis costo beneficio
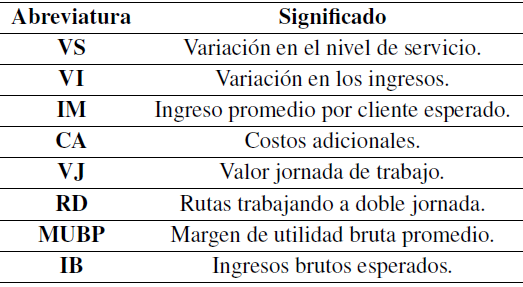
Tabla XXVII: Valores iniciales análisis costo-beneficio
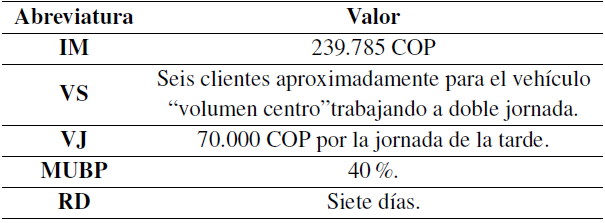
Tabla XXVIII: Análisis costo-beneficio
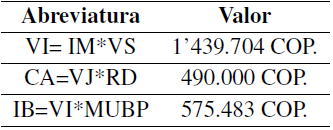
Aumentar la jornada del vehículo en la ruta “volumen centro” permitiría incrementar el nivel de servicio en un 60% (respecto al método actual) para este recurso, trabajando a una jornada y un 100% (de diez a veinte clientes por día) involucrando el recurso de las rutas de “centro 1” y “centro 2”. Esto aumentaría los ingresos y permitirían cubrir los costos adicionales, por lo que disminuiría el nivel de represamiento, ya que a partir de la ruta 6 el vehículo asignado a la zona “volumen centro” podría usarse mañana y tarde (C1 y C2) en entregar nuevas encomiendas, porque la capacidad del vehículo empieza a estar disponible (Tabla XXIV). Además, en la Tabla XXIV se evidencia que en la ruta 8 el vehículo cuenta con una capacidad de uso del 64 %, sin recurso adicional. De este modo, no se requiere de vehículos de otras zonas para completar las entregas y se podría disponer del 36% de su capacidad para programar otros envíos.
Teniendo como referencia la Tabla XXV se realizó el siguiente análisis de costos, de acuerdo con las convenciones de la Tabla XXVI.
Los ingresos brutos (IB) son superiores a los costos adicionales (CA) con una diferencia de 85.483 COP. Por lo tanto, la solución encontrada en esta propuesta es viable. Lo anterior significa que en un mes, tomado como 25 días, la empresa tendría utilidades adicionales promedio de:
GA= 25 X 85.483= 2’137.075 COP.
Actualmente, esta ruta reporta unas ganancias brutas promedio en el mes, con un nivel de servicio de 250 clientes, de:
GB= 250 X 239.785 X 0,4= 23’978.500 COP.
Así, esta solución representaría un incremento de ganancias en la ruta “volumen centro” (GA/GB) del 8,9% y, mejor aún, mejores indicadores de servicio.
Con esta solución se minimizan las distancias del vehículo al evitar que regrese varias veces al depósito y también se imponen ventanas de tiempo duras, acordes con las restricciones de tiempo de permanencia en la ciudad, ya que se definen tiempos máximos de permanencia de atención a los clientes. Así, se contribuye a la sostenibilidad social de la ciudad y algo a la ambiental, asunto que se trata con mayor detalle en [27].
Conclusiones
El desarrollo de este trabajo permitió conocer de manera sistémica la operación logística del negocio, comprender el problema de represamiento de las entregas y su impacto en los clientes.
Se presenta una propuesta para mejorar el nivel de servicio en la distribución de mercancía a partir del diseño de rutas utilizando la herramienta VRP Solver 3.0. Para esto, se tuvieron en cuenta los parámetros encontrados en el proceso actual de la compañía, evidenciando mejoras en el mismo para dar solución a la problemática planteada de retrasos en las entregas, al comparar la solución encontrada con la que actualmente utiliza la compañía.
Se puede evidenciar que el reparto de la mercancía a los clientes objeto de estudio se realizaría en un total de once días, seis días menos que utilizando el procedimiento actual. Se pasaría de atender diez clientes por día en promedio a dieciséis. Esto quiere decir que se aumentaría el nivel de servicio en un 60% con solo usar el vehículo en jornada completa y, por consiguiente, se aumentarían las ganancias brutas en un 8,9% aproximadamente. De esta manera, también se puede concluir que desde la ruta 1 hasta la ruta 8 se logra evacuar el 97% de la mercancía. Con el proceso actual se evidencia que hasta la ruta 8 se habría evacuado un 50 %, un nivel bajo en relación con la propuesta presentada en este artículo. Con esta propuesta también se evidencia un aumento en tansporte de carga aproximadamente en un 39% y, lo más importante, mejoramiento en los indicadores de servicio, pudiendo esto impactar favorablemente en la percepción de valor del cliente.
Una oportunidad de mejora para la distribución de la mercancía en la zona “volumen centro”, y que a futuro podría extenderse a otras rutas de la empresa, sería utilizar la herramienta VRP Solver antes de la digitación de la mercancía. Para esto se debe seleccionar con anterioridad la mercancía que se desea despachar al día siguiente, mejora que podría realizarse cuando los niveles de represamiento estén totalmente estabilizados y se pueda realizar una selección de la mercancía a despachar de acuerdo con algún criterio definido como lo puede ser primero en llegar, primero en salir, etc. Con esto, lo que se busca es tener una ruta definida y poder organizar la mercancía en el vehículo de acuerdo con la ruta que indique el programa, pues se ahorraría tiempo en la organización de la mercancía en el vehículo por parte de los auxiliares.
El artículo combina técnicas de calidad, como el análisis de Pareto y la gestión de procesos, con aquellas propias de la investigación de operaciones como el VRP para mejorar el procedimiento de programación y ejecución de las entregas en una compañía de servicios de envío de paquetes y mercancía, teniendo en cuenta el uso de ventanas de tiempo. Igualmente, constituye una manera de acercar los conocimientos teóricos de la academia a la gestión eficiente de las pymes. Los resultados pueden mejorar con tecnologías apropiadas para el tratamiento y control de la información de los clientes por parte de la empresas pequeñas y medianas, con miras a la planificación de las entregas.
Referencias
Licencia
Derechos de autor 2021 Uriel Pineda Zapata, Hader Carabalí Ararat

Esta obra está bajo una licencia internacional Creative Commons Atribución-NoComercial-CompartirIgual 4.0.
A partir de la edición del V23N3 del año 2018 hacia adelante, se cambia la Licencia Creative Commons “Atribución—No Comercial – Sin Obra Derivada” a la siguiente:
Atribución - No Comercial – Compartir igual: esta licencia permite a otros distribuir, remezclar, retocar, y crear a partir de tu obra de modo no comercial, siempre y cuando te den crédito y licencien sus nuevas creaciones bajo las mismas condiciones.





2.jpg)