DOI:
https://doi.org/10.14483/udistrital.jour.reving.2016.1.a07Published:
2016-01-22Issue:
Vol. 21 No. 1 (2016): January - AprilSection:
Industrial EngineeringImplementación de una Carta de Control para Corridas Cortas en la Industria de Autopartes
Implementation of a Short Run Chart in the Auto Parts Industry
Keywords:
control chart, difference chart, normalized chart, process variability, short run chart (en).Keywords:
Carta de control, Carta para lotes pequeños, variabilidad del proceso, carta normalizada, carta de diferencias. (es).Downloads
References
N. Farnum. Control charts for short runs: nonconstant process and measurement error. Journal of Quality Technology, 24(3):138 – 144, 1992.
L. Haugh and A. Pond. Adjusted individual control charts for short runs. ASQC 49”th Annual Quality congress Proceedings, pages 1117 – 1125, 1995.
D. Holmes and E. Mergen. Process acceptance charts for short runs. Quality Engineering, 1(10):149 – 153,1997.
J. M. Juran and F. M. Gryna. Quality planning and analysis. McGraw Hill International editions, 1993.
Hitoshi Kume. Herramientas estadísticas básicas para el mejoramiento de la calidad. Norma, 1992.
A. Mitra. Fundamentals of quality control and improvement. Prentice Hall, 1998.
P. Sprent. Applied Nonparametric Statistical Methods. Chapman & Hall, 1992.
Wadsworth, Stephens, and Godfrey. Métodos de Control de calidad. Cecsa, 2005.
D. Wheeler. Short Run SPC. SPC press, 1991.
S. Wise and D. Fire. Innovative Control Charting, practical SPC solutions for today’s manufacturing environment. ASQ quality press, 1998.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
DOI: http://dx.doi.org/10.14483/udistrital.jour.reving.2016.1.a07
Implementación de una carta de control para corridas cortas en la industria de autopartes
Implementation of a short run chart in the auto parts industry
Jesús Barrera Cobos,
Escuela Colombiana de Ingeniería. Bogotá, D.C. Colombia.jesus.barrera@escuelaing.edu.co.
Received: 05/08/2015. Modified: 07/10/2015. Accepted: 15/12/2015.
Resumen
Contexto: La industria nacional tiene que adaptarse a las necesidades del mercado, lo que implica en algunos casos el cambio en la realización de sus procesos productivos. Uno de estos cambios tiene que ver con el tamaño de lote de producción, el cual ha pasado de un tamaño de miles de unidades a uno quizás, de algunos cientos. El seguimiento de estos procesos con métodos estadísticos, como las cartas de control, ha llevado al uso de las denominadas cartas de control para lotes pequeños.
Método: En este artículo se presenta la propuesta de implementación de una carta de este tipo en un proceso de fabricación de una empresa del sector automotriz nacional. Inicialmente se plantea el estado actual del proceso, el cual se sigue con una carta de control ¯X-R, usada por la empresa para el seguimiento de la producción; luego se hace mención a algunas de las cartas de control para lotes pequeños, que han sido planteadas por diversos autores.
Resultados: Con base en la información del estado actual del proceso se realiza la elección de la carta para lotes pequeños más adecuada.
Conclusiones: Dadas las características de no homogeneidad de la varianza, determinada mediante una prueba no paramétrica para las referencias analizadas, se decide que la carta a ser usada es la normalizada. De las tres propuestas de carta presentadas la decisión de cuál usar depende de la varianza del proceso al fabricar las distintas referencias.
Palabras clave: carta de control, carta de diferencias, carta normalizada, carta para lotes pequeños, variabilidad del proceso.
Abstract
Context: The national industry has to adapt to market needs, which implies the change in the performance of their production processes. One of these changes has to do with the size of production lot, which has gone from a size of one thousand units of perhaps a few hundred. The monitoring of these processes using statistical methods such as control charts, has led to the use of so-called control charts for short runs.
Method: This article presents the proposed implementation of a chart of this type in a manufacturing process of a company in the national automobile sector. Initially the current state of the process poses with the results shown in the control chart ¯X-R, used by the company to monitor production; then the mention of some of the control charts for short production runs that can be used for this type of variables which have been raised by various authors is made.
Results: Based on the information of the current status process the election of the chart is made more suitable for short production runs.
Conclusions: Given the characteristics of non-homogenity of variance, determined by a nonparametric test for references analyzed, it is decided that the letter to be used is the normalized chart. The decision of which chart to use depends on the variance of the process to manufacture the various references.
Keywords: control chart, difference chart, normalized chart, process variability, short run chart.
1. Contexto
Ante la necesidad de poder satisfacer las necesidades de sus clientes las empresas requieren tener un amplio portafolio de productos, además, dado que hoy en día los diversos clientes de un mismo producto desean ciertas características especiales, las empresas han tenido que empezar a producir lotes cada vez más pequeños de distintas referencias del mismo producto, con el fin de evitar que los clientes busquen otro proveedor.
El control estadísticos de procesos normalmente se hace empleando cartas de control univariadas, llamadas también cartas Shewhart, las cuales fueron propuestas por Walter Shewhart (1924) de los Laboratorios Bell de los EE.UU. [8], [11]. Dichas cartas son apropiadas para tamaños de producción de miles de unidades, situación que se presentaba hasta hace algunas décadas [8].
Ante la necesidad de producir lotes de tamaño pequeño y de controlar el proceso, las cartas Shewhart no son las más adecuadas, debido a que en el establecimiento de sus límites de control se requiere la producción de cierta cantidad de producto, que en ocasiones es comparable al tamaño del lote a ser producido, con lo que el costo y el tiempo de producción se incrementan.
Por estas razones, se han planteado algunas cartas de control a fin de ser utilizadas bajo estas características de proceso [5], [4], [3], [12], [13], [9]. Así, cuando prácticamente se usa el mismo proceso para la producción de diferentes referencias, estas cartas permiten controlar el proceso de fabricación mas allá de controlar la producción de una referencia en particular.
El presente trabajo está orientado hacia la determinación de la carta más adecuada para hacer el seguimiento del proceso de producción, con el muestreo que se sigue actualmente, en cuanto a cantidad de muestras por turno y tamaño de la muestra. Inicialmente se hace una descripción del proceso de fabricación y del tipo de carta de control que la empresa usa para su seguimiento, luego se analiza el estado actual del proceso para las tres referencias seleccionadas. Una vez se ha analizado el estado del proceso se seleccionan las opciones de cartas a usar para después seleccionar la mas adecuada, con base en las propiedades observadas en las referencias seleccionadas realizar la implementación y finalmente se indican algunas conclusiones pertinentes.
1.1. Descripción del proceso
La empresa x manufactura diversos productos para la industria automotriz, para ello cuenta con una planta de última tecnología, lo cual le permite fabricar un producto de acuerdo a las necesidades del mercado. Debido a que la demanda de sus productos en el mercado nacional no requiere la fabricación de grandes volúmenes (por el tamaño de su mercado) de las diferentes referencias, se hace necesaria la fabricación de algunas centenas de unidades por cada lote de producción, el promedio de unidades fabricadas, por lote, es de alrededor de 150.
Actualmente para realizar el seguimiento del proceso la empresa emplea cartas de control ¯x-R [7], [11], [6] en sus diversos productos. A fin de establecer los límites de control de la carta, el personal encargado fabrica una cantidad apreciable (respecto al tamaño del lote) de producto, a la cual se le hace verificación de la característica de interés1 en todos sus elementos, con lo cual el tiempo requerido para ajustar el proceso puede ser tan alto como el requerido para la fabricación del lote completo. Debido a lo anterior la productividad de la empresa no es la adecuada.
Así, la producción se realiza en esquema de isla de trabajo, en la cual cada tipo de producto es hecho en un grupo de máquinas acondicionadas para tal fin; y la empresa ha definido la realización de tres muestreos por turno de ocho horas con un tamaño de muestra de cinco unidades.
En el presente trabajo se considerarán tres referencias (A, B y C) que utilizan un proceso análogo y a las cuales se le hace seguimiento a la misma característica de interés, como es un diámetro, llamado diámetro principal. La medición de esta característica se lleva a cabo con un instrumento adecuado para tal fin, se le realiza procesos de calibración de forma periódica y además se le lleva un registro de calibración. De igual forma el personal encargado del proceso es idóneo y tiene la experiencia y el entrenamiento en el proceso. La maquinaria es sometida a rutinas de mantenimiento de acuerdo a lo recomendado por el fabricante, dicha maquinaria se encuentra diseñada para la clase de trabajo que se realiza en ella y es del tipo de control numérico.
Las especificaciones del cliente para las referencias en cuestión se describen en la tabla I:
L.E.I. hace referencia a límite de especificación inferior y L.E.S. corresponde a límite de especificación superior. Estos límites son dados por los clientes.
2. Método
Se dispone de información de las tres referencias A, B y C, la cual ha sido tomada mediante muestreo (tres muestras de cinco elementos por turno de ocho horas) según lo tiene establecido la empresa. Esta ha establecido límites de control de proceso para cada una de las referencias, con los cuales se lleva a cabo el ajuste del proceso cada vez que se desea realizar la fabricación de una referencia, mediante la fabricación de cierta cantidad de producto en el establecimiento de los límites de control para la carta. En la tabla II se pueden apreciar los límites así como el promedio y el rango para cada una de las referencias.
La tabla III muestra el promedio y el rango para las distintas muestras de cada una de las referencias, durante la fabricación de un lote de cada una de ellas.
Las unidades para los promedios son milímetros así como para los rangos. De igual forma en la tabla III, m indica el número de muestra.
Las cartas de control para la media y para el rango de cada una de las referencias con anterioridad se muestran en las figuras 1, 2 y 3.
2.1. Observaciones a las cartas de control
Con base en las diferentes gráficas realizadas, así como en la información de proceso disponible, se tienen los siguientes comentarios respecto al estado del proceso:
1. Los tres procesos se encuentran bajo control, con la media de las muestras alrededor de la media de la respectiva carta, salvo en el caso de la referencia C, pues se muestra que aunque la variable está dentro del intervalo de aceptación los límites de control para la carta parecen no estar bien determinados.
2. El rango para las diferentes referencias se puede considerar constante, aunque quizás se deba hacer una prueba de igualdad de varianzas, y se halla dentro de los límites de la carta para esta variable.
3. Las referencias A y C tienen un valor medio diferente al valor objetivo, lo que se observa de forma más clara en la carta para la referencia C, figura 3. Lo anterior indica que el proceso para estas referencias no está centrado respecto al valor objetivo, lo que en sí no es un problema siempre y cuando la producción esté cumpliendo las especificaciones del cliente.
2.1.1. Opciones de cartas
En busca de la mejora del proceso se considera la posibilidad de implementar cartas de control para lotes pequeños (short run charts), entre otras cosas. La determinación de qué tipo de carta es la adecuada pasa por el análisis de las diferentes variables y las características que se desea mostrar.
Entre las diferentes cartas a elegir están: 2
Carta de diferencias es tratada en [3], [12] y [13] y también es llamada carta X-nominal o carta X-objetivo; consiste en tomar las diferencias de las mediciones de la variables contra el valor objetivo. Esta diferencia se grafica en una carta ¯X y sus límites son función de la variabilidad del proceso, por lo que si se desea tener varias referencias graficadas en la misma carta su variabilidad debe ser estadísticamente igual y, además, deben tener las mismas unidades de medida.
El propósito de la carta de diferencias es visualizar el estado del proceso aunque este sea utilizado para la fabricación de diferentes productos, es decir, diferente objetivo. Aun cuando los diferentes productos se encuentran bajo control estadístico, interesa observar los cambios que suceden en el proceso al cambiar de producto.
Para un funcionamiento adecuado de la carta se requiere que la variabilidad del proceso sea relativamente constante de producto a producto. Si lo anterior no se cumple se hace necesario utilizar una carta normalizada, también llamada carta Z.
Los límites de control para la carta están dados por:
en donde m¯R es el promedio de los rangos móviles.
El valor nominal que es restado puede ser el promedio histórico para cada producto o el valor objetivo para cada producto. El promedio del rango móvil, m¯R, a partir de la carta control del producto o el rango calculado a partir de los x observados. Se puede utilizar una carta de rango móvil junto con la carta de diferencias, con el propósito de observar la variabilidad del proceso junto con el valor de la variable. Los límites de control de la carta del rango son:
Carta normalizada esta carta es mencionada en [12] y [13] y se utiliza cuando la variabilidad de las referencias no es igual o cuando se desean graficar características diferentes. En su uso se necesita conocer el valor nominal (valor objetivo o el promedio histórico) y desviación estándar (o algún estadístico que permita tener información respecto a la variación intragrupo) para cada uno de los productos.
La expresión para calcular los valores para la carta Z es:
De lo anterior se tiene que los límites de control para la carta están dados por:
donde K es el número de desviaciones estándar de la carta X normal.
Carta porcentaje de valor nominal es mencionada en [3], su idea es que cuando diferentes partes son hechas por un mismo proceso es posible graficar en una misma carta las diferencias entre las partes respecto a su valor nominal (o valor objetivo). En este caso se plantea utilizar la carta en la cual se mire qué tanto la relación x¯i /Ti se desvie de uno (1); x¯i indica el promedio de la muestra y Ti hace referencia al valor objetivo. La interpretación de esta es sugerida como el porcentaje del valor nominal.
2.1.2. Elección del tipo de carta
Debido a las características del proceso de fabricación es posible utilizar la carta de diferencias, la carta normalizada o la carta del porcentaje del valor nominal. La carta de diferencias, así como la carta del porcentaje, se pueden utilizar si la variabilidad del proceso se mantiene constante para las diferentes referencias. Dado que los límites de control de las cartas son función de la desviación estándar de la variable graficada, se hace necesario determinar si la variabilidad del proceso para las distintas referencias se puede considerar igual. Si la variabilidad no se mantiene constante entre referencias es necesario utilizar una carta en la cual sus límites de control no dependan de la desviación estándar, lo cual se logra normalizando los datos, con lo cual se utilizaría la carta normalizada.
Según se menciona en la sección 2, el rango para las tres referencias se puede considerar constante; sin embargo, es posible utilizar una prueba estadística para determinar si la varianza de las medias de las referencias se puede considerar estadísticamente igual. Debido a que la cantidad de datos es pequeña para cada una de las referencias se utiliza una prueba no paramétrica de heterogeneidad de varianzas, rangos cuadrados [10].
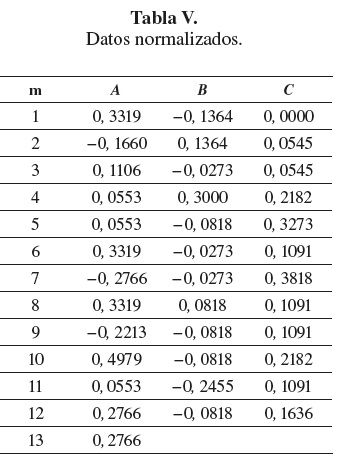
Para la aplicación de la prueba se hallan las desviaciones absolutas de las medias respecto a la media total por referencia, el cual se espera sea el punto medio del intervalo de especificación; es decir, se espera que el proceso tenga como valor objetivo el valor medio de la especificación para cada referencia. Dichas desviaciones se observan en la tabla IV; las diferencias que se aprecian en la tabla IV están dadas en milésimas de milímetro (micrómetros). La prueba no paramétrica para igualdad de varianzas [10] da como resultado un T = 7,37 correspondiente a un p-valor de 0,0089585859, el cual indica que con un nivel de significancia del 5 %, el proceso no tiene la misma variabilidad para las tres referencias.
Dado que interesaba saber si el proceso presenta, para las tres referencias, la misma variabilidad y con base en ello definir el tipo de carta a utilizar, se concluye que se debe usar la carta normalizada.
3. Resultados
La carta normalizada (también llamada carta Zed o Z) para datos normalizados, permite cambios en el valor objetivo así como en la cantidad de dispersión de referencia a referencia. Para su utilización se necesita conocer T, el valor nominal, valor objetivo o el promedio histórico y algún estadístico que permita tener información respecto a la variación intragrupo para cada uno de los productos3.
La expresión para calcular los valores para la carta Z es [12]:
Al usar como estadístico de variación a R¯ se tiene que los límites de control para la carta están dados por:
donde A2 es una constante que depende del tamaño de la muestra para una carta ¯X normal, para un tamaño de muestra de cinco unidades A2 = 0,577.
Normalmente la carta de la variable es acompañada por una carta en la que se muestre la variabilidad de las muestras. En este caso se utiliza una carta de rango normalizado Rij / R¯i, para la cual:
1. La línea central para los rangos es 1.
2. Los límites de control para los rangos son D3 y D4, las cuales son constantes que dependen del tamaño de la muestra y que para el caso son 0 y 2,114 respectivamente [12], [13].
Con base en lo anterior los datos para la carta normalizada se muestran en la tabla V, en milésimas de mm.
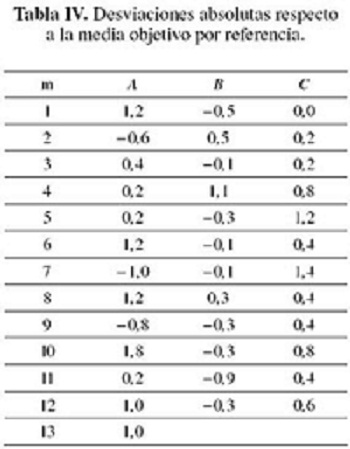
En la figura 4 se muestra la carta normalizada para las tres referencias y también la carta para el rango normalizado. En las cuales los primeros trece valores corresponden a la referencia A, los siguientes doce a la referencia B y los restantes doce a la referencia C.
Con base en la figura 4 se puede comentar lo siguiente:
1.El gráfico de los datos normalizados muestra que los procesos no están centrados respecto a la especificación dada por la empresa, lo cual también se aprecia en cada una de las cartas individuales.
2.En los dos gráficos se aprecia que los procesos se encuentran bajo control.
3.El gráfico del rango se halla alrededor de su valor central.
4. Conclusiones
1.La carta para lotes pequeños implementada presenta el mismo comportamiento que tienen las muestras en las cartas individuales, de manera que el operario tendrá confianza en la información que brinda esta carta.
2.Es muy importante verificar la igualdad de varianzas en el caso de que se pueda utilizar una carta de diferencias, en esta implementación se puede apreciar que aunque la variación entre muestras para las diferentes referencias puede ser muy similar, por el orden de magnitud que se tiene, si no se hubiese realizado dicha prueba se habría realizado una carta de diferencias, con lo cual la carta no mostraría realmente el comportamiento del proceso y llevaría a tomar decisiones erróneas o a no ver a tiempo problemas que podrían estar presentándose.
3.En la implementación práctica de este tipo de cartas, que es muy ventajosa por el hecho de poder observar la evolución del proceso además de la evolución de cada referencia, se tiene que tener en cuenta la necesidad de capacitar a las personas encargadas del registro, de tal forma que la carta muestre el estado del proceso. Se debe observar que para esta implementación la persona encargada de llevar la carta tiene que hacer otras operaciones matemáticas con los resultados obtenidos del muestreo, lo que puede llevar a que sea mejor disponer de un sistema al cual se le entregue los datos medidos y este devuelva la información a registrar en la carta o el mismo sistema realice la carta.
4.Este tipo de cartas permite apreciar si el proceso está o no centrado respecto a las especificaciones para las distintas referencias, sean dadas por el fabricante o por el cliente.
5.Para el caso se muestra que se puede realizar la implementación de cartas de control para lotes pequeños, sin embargo se hace necesario realizar algunas consideraciones respecto a las características a controlar en cuanto a sus unidades y a la variabilidad.
1 La característica de interés es el diámetro del agujero dentro del cual se desplaza un cilindro por efecto de la presión de un fluido.
2 Aquí solo se presentan las cartas más adecuadas según las propiedades de las características que actualmente se siguen, en [1] se mencionan otras cartas para lotes pequeños cuando las características a seguir presentan ciertas particularidades, también en [2] se hace un análisis de las propiedades que tienen los tres estadísticos mencionados en este documento.
3 Entre los estadísticos de la variación intragrupo, se tienen:
y R¯, d2 es una constante que depende del tamaño de la muestra n [12].
Referencias
[1] J. F. Barrera. Cartas de control para lotes pequeños. Revista de la Escuela Colombiana de Ingeniería, (96):87 - 92, 2014.
[2] J. F. Barrera. Estudio de las características de los estadísticos utilizados en algunas cartas de control para lotes pequeños. XXIV Simposio Internacional de Estadística, 2014.
[3] N. Farnum. Control charts for short runs: nonconstant process and measurement error. Journal of Quality Technology, 24(3):138 - 144, 1992.
[4] L. Haugh and A. Pond. Adjusted individual control charts for short runs. ASQC 49"th Annual Quality congress Proceedings, pages 1117 - 1125, 1995.
[5] D. Holmes and E. Mergen. Process acceptance charts for short runs. Quality Engineering, 1(10):149 - 153, 1997.
[6] J. M. Juran and F. M. Gryna. Quality planning and analysis. McGraw Hill International editions, 1993.
[7] Hitoshi Kume. Herramientas estadísticas básicas para el mejoramiento de la calidad. Norma, 1992.
[8] A. Mitra. Fundamentals of quality control and improvement. Prentice Hall, 1998.
[9] D. C. Montgomery. Introduction to statistical quality control. John Wiley & sons, fourth edition, 2001.
[10] P. Sprent. Applied Nonparametric Statistical Methods. Chapman & Hall, 1992.
[11] Wadsworth, Stephens, and Godfrey. Métodos de Control de calidad. Cecsa, 2005.
[12] D. Wheeler. Short Run SPC. SPC press, 1991.
[13] S. Wise and D. Fire. Innovative Control Charting, practical SPC solutions for today's manufacturing environment. ASQ quality press, 1998.
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.




2.jpg)










