DOI:
https://doi.org/10.14483/udistrital.jour.reving.2016.2.a05Published:
2016-05-26Issue:
Vol. 21 No. 2 (2016): May - AugustSection:
Special Section: Best Extended Articles - WEA 2015Local and Global Path Generation for Autonomous Vehicles Using Splines
Generación Local y Global de trayectorias para Vehículos Autónomos Usando Splines
Keywords:
path planning, spline, curve space (en).Keywords:
Planeamento de Trayectorias, splines, arco de la distancia, espacio curvilineo. (es).Downloads
References
Tim D Barfoot and Christopher M Clark. Motion planning for formations of mobile robots. Robotics and Autonomous Systems, 46(2):65–78, 2004.
Ilía Nikolaevich Bronshtein, Konstantin A Semendyayev, Gerhard Musiol, and Heiner Muehlig. Handbook of mathematics. Springer Science & Business Media, 2007.
Keonyup Chu, Minchae Lee, and Myoungho Sunwoo. Local path planning for off-road autonomous driving with avoidance of static obstacles. Intelligent Transportation Systems, IEEE Transactions on, 13(4):1599–1616, 2012.
Randerson Araujo de Lemos, Olmer Garcia, and Janito Vaqueiro Ferreira. Local and global path generation for autonomous vehicles using splines. In Engineering Applications-International Congress on Engineering (WEA), 2015 Workshop on, pages 1–6. IEEE, 2015.
GoogleMaps. Google Company. https://www.google.com.br/maps/@-22.8195851,-47.0631774,15z, 2015.
Thomas M Howard and Alonzo Kelly. Optimal rough terrain trajectory generation for wheeled mobile robots.The International Journal of Robotics Research, 26(2):141–166, 2007.
Unghui Lee, Sangyol Yoon, HyunChul Shim, P. Vasseur, and C. Demonceaux. Local path planning in a complex environment for self-driving car. In Cyber Technology in Automation, Control, and Intelligent Systems (CYBER), 2014 IEEE 4th Annual International Conference on, pages 445–450, June 2014.
Xiaohui Li, Zhenping Sun, Qi Zhu, and Daxue Liu. A unified approach to local trajectory planning and control for autonomous driving along a reference path. In Mechatronics and Automation (ICMA), 2014 IEEE International Conference on, pages 1716–1721, Aug 2014.
OpenStreetMap. The free wiki world map. http://www. openstreetmap. org, 2015.
John W Peterson. Arc length parameterization of spline curves. Journal of Compu ter Aided Design, 2006.
Richard J Sharpe and Richard W Thorne. Numerical method for extracting an arc length parameterization from parametric curves. Computer-aided design, 14(2):79–81, 1982.
Bruno Siciliano, Lorenzo Sciavicco, Luigi Villani, and Giuseppe Oriolo. Robotics: modelling, planning and control. Springer Science & Business Media, 2009.
Roland Siegwart, Illah R Nourbakhsh, and Davide Scaramuzza. Introduction to autonomous mobile robots. The MIT Press, second edition, Febraury 2011.
Jarrod M Snider. Automatic steering methods for autonomous automobile path tracking. Robotics Institute, Pittsburgh, PA, Tech. Rep. CMU-RITR-09-08, 2009.
MarkWSpong, Seth Hutchinson, and Mathukumalli Vidyasagar. Robot modeling and control, volume 3. Wiley New York, 2006.
Hongling Wang, Joseph Kearney, and Kendall Atkinson. Arc-length parameterized spline curves for real-time simulation. In Proceedings of the 5th international conference on Curves and Surfaces, 2002.
Hongling Wang, Joseph Kearney, and Kendall Atkinson. Robust and efficient computation of the closest point on a spline curve. In Proceedings of the 5th International Conference on Curves and Surfaces, pages 397–406, 2002.
Werling, J. Ziegler, S. Kammel, and S. Thrun. Optimal trajectory generation for dynamic street scenarios in a frenét frame. In Robotics and Automation (ICRA), 2010 IEEE International Conference on, pages 987–993, 2010.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
DOI: http://dx.doi.org/10.14483/udistrital.jour.reving.2016.2.a05
Local and Global Path Generation for Autonomous Vehicles Using Splines
Generación Local y Global de trayectorias para Vehículos Autónomos Usando Splines
Randerson Lemos
Autonomous Mobility Laboratoty - LMA, Faculty of Mechanical Engineering UNICAMP, Campinas Brazil. randerson.lemos@gmail.com
Olmer Garcia
School of Engineering, Jorge Tadeo Lozano University, Bogotá, Colombia. olmer.garciab@utadeo.edu.co
Janito V. Ferreira
Autonomous Mobility Laboratoty - LMA, Faculty of Mechanical Engineering UNICAMP, Campinas Brazil janito@fem.unicamp.br
Received: 06-11-2015. Modified: 01-03-2016. Accepted: 05-04-2016
Abstract
Context: Before autonomous vehicles being a reality in daily situations, outstanding issues regarding the techniques of autonomous mobility must be solved. Hence, relevant aspects of a path planning for terrestrial vehicles are shown.
Method: The approached path planning technique uses splines to generate the global route. For this goal, waypoints obtained from online map services are used. With the global route parametrized in the arc-length, candidate local paths are computed and the optimal one is selected by cost functions.
Results: Different routes are used to show that the number and distribution of waypoints are highly correlated to a satisfactory arc-length parameterization of the global route, which is essential to the proper behavior of the path planning technique.
Conclusions: The cubic splines approach to the path planning problem successfully generates the global and local paths. Nevertheless, the use of raw data from the online map services showed to be unfeasible due the consistency of the data. Hence, a preprocessing stage of the raw data is proposed to guarantee the well behavior and robustness of the technique. Keywords: Path planning, Spline, Arc-length, Curvilinear space.
Keywords: Path planning, Spline, Arc-length, Curvilinear space.
Acknowledgements: This work has been cofounded by CNPq and CAPES Brazil.
Language: English.
Resumen
Contexto: Antes que los vehículos autónomos sean una realidad en situaciones cotidianas temas pendientes de las técnicas de movilidad autónoma deben ser resueltos. Por eso, en este artículo es presentado una técnica de planeamiento de trayectorias para vehículos terrestres.
Método: La técnica de planeamiento de trayectorias utiliza splines para generar la ruta global. Para eso, se utilizan puntos obtenidos por servicios en línea de mapas digitales. Sobre esta ruta global, parametrizada por el arco de la distancia, son generadas rutas locales y seleccionada una trayectoria optima por diferentes funciones de costo.
Resultados: Diferentes rutas de pruebas se utilizan para mostrar que el número y la distribución de los puntos de la ruta global están altamente correlacionados con una parametrización exitosa en el arco de la distancia de las splines, lo cual es esencial para un correcto funcionamiento de la técnica de planeamiento de trayectorias.
Conclusiones: El enfoque splines cúbicas al problema de planificación de trayectoria generó correctamente las trayectorias globales y locales. Sin embargo, el uso de los datos en bruto de los servicios de mapas en línea demostró ser inviable debido a inconsistencia de algunos datos. Por lo tanto, se propone una etapa de preprocesamiento de los datos en bruto para garantizar la robustez de la técnica.
Palabras clave: Planeamento de Trayectorias, splines, arco de la distancia, espacio curvilineo.
Agradecimientos: Este trabajo ha sido cofinanciado por las agencias de CAPES y CNPq Brasil.
1. Introduction
Recent technological advances have allowed the implementation of autonomous vehicles and complex driver assistance systems (ADAS) at academy and industry. Although those advances improved the safety and robustness of the autonomous vehicles and systems, there are still several problems, mainly related with safety and liability, far to be completely solved.
The cognition aspects of a mobile vehicle is intrinsic related to its mobility capabilities, which are studied by the robotics navigation field ( [13]). The navigation field organizes its techniques into two groups, which are planning and reacting. The techniques from the planning group are known as global path planing and are concerned with the generation of the global route that guides the vehicle toward a goal position. The techniques from the reacting group are known as local path planning and are concerned with the generation of several local paths that allow the vehicle to avoid obstacles ( [3], [6]-[8], [18]).
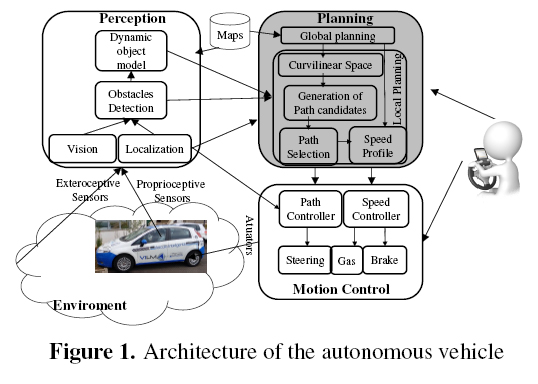
The design of the autonomous vehicles of the Autonomous Mobility Laboratory (LMA) from the Mechanical Engineering Faculty at Unicamp is developed on a FIAT-PUNTO platform called Veículo Inteligˆente do LMA1(VILMA). The architecture of VILMA follows the model described by [13], i. e., it has the blocks of perception, planning and control. The VILMA's architecture is shown in figure 1 and, in gray color, it is stands out the planning block tackle on this paper. We remark that this is an extended version of a short paper recently published in the Workshop on Engineering Applications - WEA2015 - that was held in Bogota, September 2015 ( [4]).
This paper is organized into three sections. The first section exposes the path planning algorithm for terrestrial vehicles adopted by LMA, the second section explains the techniques employed for the generation of the global route from off-the-shelf software and the solutions adopted to solve problems with the arc length parameterization of the curve of the global route, and the third section presents conclusions.
2. Planning algorithm
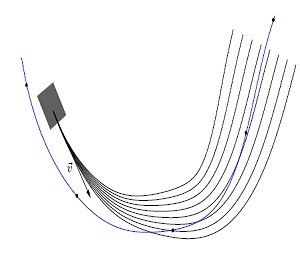
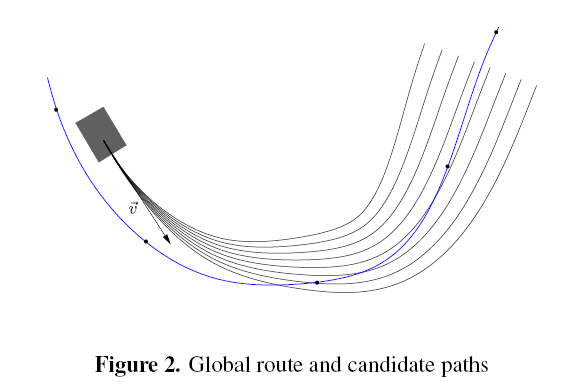
The main goal of the implemented algorithm is to generate smooth paths free of obstacles, that start from an initial position and extend themselves oriented by the global route in direction of a goal position. Figure 2 shows an example of a global route and a set of candidate paths.
The technique presented [3] is didactically divided into four stages, which are: construction, localization, generation and selection.
2.1. Construction
The construction stage, which belongs to the global planning, is responsible to construct the curve of the global route. This curve extends itself over the center of the road from an initial position until a target one. The curve of the global route is parameterized in the arc length distance s and it is constructed by cubic splines from the waypoints of the road. The parameterization process is divided into two stages, which are: the parameterization of the curve of the global route with respect to any parameter; and its reparameterization to the arc length distance s. For convenience, the parameter used in the parameterization of the curve of the global route is the cumulative distance between the waypoints d.
2.1.1. Parametrization of the curve of the global route with respect to the cumulative distance between the waypoints
Since the cumulative arc length distance s is an information not available in the existing databases, parameterized curves with respect to the arc length (x(s), y(s)) can not be obtained by spline interpolation of the waypoints of the road at the first moment. In the literature there are several approaches that propose solutions for this problem ([10], [16], [11]).
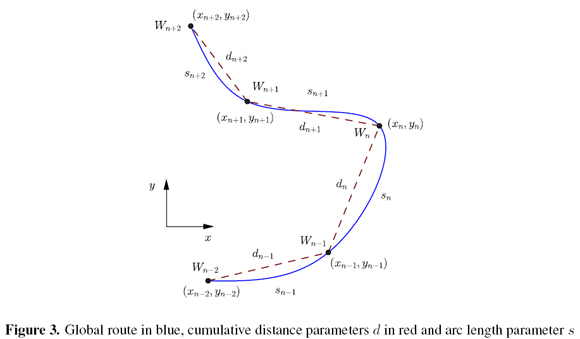
The strategy adopted to handle the arc length parameterization problem was parameterize the curve of the global route with respect to the cumulative distance d between the waypoints and after reparameterize it to the arc length distance s. Figure 3 shows, in red, the cumulative distance parameter d, from which 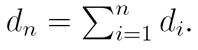
The equations of the curve of the global route parameterized with respect to the cumulative distance between the waypoints d are:
where xi(d) and yi(d) are the Cartesian coordinates of the curve of the global route parameterized with respect to the cumulative distance d, and m, n, o, p are the coefficients of the cubic spline obtained by spline interpolation.
The global route curve parameterized with respect to the cumulative distance d is illustrated by the blue line in figure 3. This curve was constructed by spline interpolation using the Cartesian position (x,y) and cumulative distance d associated to each waypoint.
2.1.2. Global route curve reparameterization with recpect to the arc length distance
Constructed the curve of the global route parameterized with respect to the cumulative distance d, it is performed its reparametrization to the arc length distance s. To perform the reparameterization it is necessary a function that maps from the space of the cumulative distance d to the space of the arc length distance s. This function is obtained by the integration below 2 ([2]).
where ṡ is the derivative of the arc length distance in terms of the parameter t, and dx/dt and dy/dt are the geometric decomposition of ṡ in the x and y directions.
Using the function present above it is possible to obtain for each cumulative distance di the associated arc length distance si. The table I shows an example of the process of the arc length obtainment.
With the waypoints and their associated arc length distance s another cubic spline interpolation is performed to obtain the curve of the global route parameterized in the arc length s. The dataset organization is presented in table II, in which one spline interpolation is performed upon the x dataset to generate x(s) and another is performed upon the y dataset to generate y(s).
In the example presented for the parameterization of the curve of the global route with respect to the arc length s, it was used the original waypoints - the ones used in the construction of the curve of the global route parameterized with respect to d - and their arc lengths s. However, since the equations of the curve of the global route parameterized with respect to d, (x(d), y(d)), are known, it is possible to obtain the arc length of any cumulative distance d and than perform the arc length parameterization for any set of cumulative distances. For example, one global route curve constructed with 100 waypoints can be reparameterized to the arc length with 200 waypoints or with any quantity that is judge adequate. A discussion about the reparameterization resolution is performed in Global Route section. The final equations of the global route arc length parameterized is shown below.
where xi(s) and yi(s) are the Cartesian coordinates of the curve of the global route parameterized with respect to the arc length distance s, and m, n, o, p are the coefficients of the cubic spline obtained by spline interpolation.
2.2. Localization
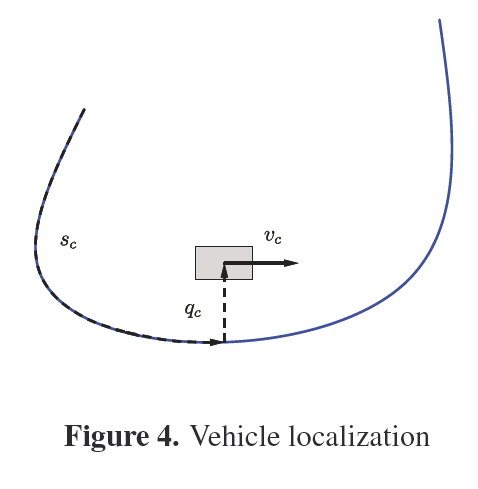
Dedicated to localize the vehicle with respect to the curve of the global route, the localization stage computes the distance traveled sc by the vehicle and its lateral offset qc. The parameters sc and qc are illustrated in Figure 4.
To calculate the values of the parameters sc and qc it is performed the following minimization:
where the parameters xc and yc are the position of the car in Cartesian coordinates, and the parameters x(s) and y(s) are a point on the curve of the global route in Cartesian coordinates. From the minimization it is determined the arc length s of the closest point on the curve of the global route to the vehicle and with it the parameters sc and qc are calculated ( [17]).
2.3. Generation
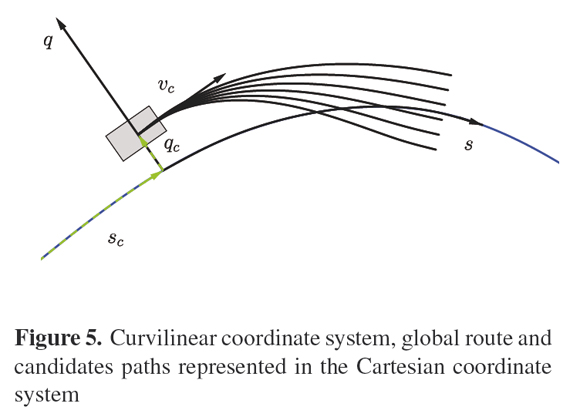
Constructed the curve of the global route parameterized with respect to the arc length s and localized the vehicle, it is performed the generation of the candidate paths. The candidate paths generation is executed in real-time and it is known as local planning. The candidate paths are initially generated in a curvilinear coordinate system defined by the parameters sc and qc and subsequently mapped to the Cartesian coordinate system of the global route. The curvilinear coordinate system s0q and a set of candidates paths represented in the Cartesian coordinate system are shown in Figure 5.
2.3.1. Path candidates generation in the curvilinear coordinate system
The set of equations used to generate the candidates paths in the curvilinear coordinate system are shown bellow:
with 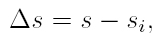
where function q(s) models the lateral offset q of the candidate paths with a cubic polynomial that is function of the arc-length distance s. The parameters a, b, c, and d are the coefficients of the cubic polynomial. This equation is designed to provide smooth candidates paths. The boundary conditions necessary to determine the coefficients a, b, c and d are shown bellow:
The angle θc is defined as the difference between the vehicle orientation and the global route curve orientation at the position specified by the arc length si = sc, ( [12], [15]).
2.3.2. Mapping the candidate paths from the curvilinear coordinate system to the Cartesian coordinate system
The mapping approach is divided into two stages. Firstly, it is determined the curvature k of each candidate path in the Cartesian coordinate system. Subsequently, with the information of the curvature k and the equations of the vehicle model, the position of the candidates paths in the Cartesian system of the curve of the global route is computed. The curvature k of the candidates paths in the Cartesian system of the curve of the global route is determined by the equations below([1], [18]).
where the parameter kb 3 is the curvature of the curve of the global route, and q is the lateral offset of the candidate path. Both parameter are functions of the arc length distance s.
With the curvatures k of the candidate paths and using the differential equations of the bicycle model ( [1], [14]), it is possible to determine the positions of the candidate paths in the Cartesian coordinate system of the curve of the global route. The integration of the differential equations bellow provides the positions of the candidate paths in the Cartesian system of the curve of the global route ( [3]).
2.4. Selection
From the set of candidate paths one is selected to be followed by the autonomous vehicle. The candidate path selected is the one that minimizes the linear combination of the three cost functions show bellow. Theses equations attempt to represent the intrinsic and extrinsic safety of the vehicle when following a candidate path.
The cost function J[i] holds the final cost assigned to the ith candidate path. This cost is result of the linear combination of the three cost functions Cs[i], Ck[i], and Cc[i]. Each of the three cost functions attempt to quantify the safety of the ith candidate path according specific criteria. The parameters ws, wk, and wc are the weights given to the values of the cost functions in the linear combination. These values are design parameters and must me tuned according project necessities.
The cost function Cs[i] is responsible to quantify the safety of the candidate paths. It verifies each candidate path to check each ones are free of obstacle collision and each ones are not. For the candidate paths that are free collision, the safety cost function Cs[i] assigned to each of them a value related to how near or how far theses paths are from the obstacles. To compute the safety cost of the candidate paths it is used a discrete Gaussian convolution shown bellow ([3]):
where Cs[i] is the safety cost of the ith candidate path, N is the number of candidate paths, c[k] is the collision detection of the kth candidate path, g[i] is a Gaussian with mean zero and standard deviation of the risk of collision σ, and Δq is the resolution of the lateral offset of the candidate paths. The collision detection parameter c[k] is one for collision paths and zero otherwise. The standard deviation is a design parameter and it will determine the effective range of the collision detection for each path.
The cost function Ck[i] is responsible to quantify the smoothness of the candidate paths. It assigns high values to paths that suddenly change their direction and low values otherwise. The equation used to compute the cost associated to the smoothness of the paths are shown bellow ([3]):
where sp is arc length along the path, s is the arc length of the base frame, ki is the curvature of a path ith.
The cost function Cc[i] is responsible to quantify the consistency of the candidate paths. It evaluates how different the current generated candidate paths are from the previous candidate path generated/selected and it assigns high values to candidate paths that are significantly different from the previous one. The equation used to compute the cost associate to the consistency of the candidate paths are show bellow ([3]):
where li is the Euclidean distance between a point in the ith candidate path and a point in the selected candidate path of the previous step with the same arc length of the base frame. With the linearly combination of these three cost function one candidate path is selected to be followed by the vehicle.
3. Results
For the proper performance of the technique presented by [3] it is essential to obtain a curve of the global route that is both representative of the real route and properly parameterized with respect to the arc length distance s. The construction of a representative curve of the global route from cubic splines is strongly correlated with the number and the distribution of the waypoints used. Likewise, an appropriate reparameterization to the arc-length distance of the curve of the global route is also strongly related with the number and distribution of the points used in the process, which does not need to be the same number of the waypoints used in the construction stage.
3.1. Construction of the Curve of the Global Route
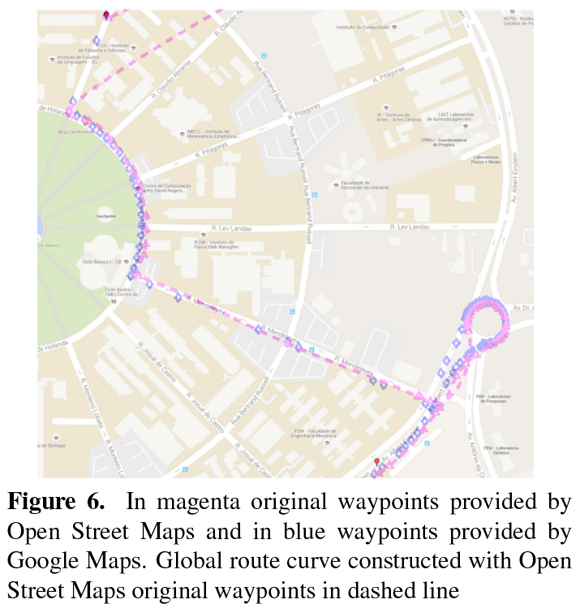
In a market scenario of autonomous vehicles commercialization to the general public, it is coherent to assume that the waypoints utilized in the construction of the curve of the global route will be obtained from off-the-shelf platforms that will integrate maps and route planning systems, as Google Maps ([5]) and Open Street Maps ([9]) do. Unfortunately, the current characteristics of the waypoints provided by those platforms do not allow their direct usage in the construction of the curve of the global route, making necessary a processing stage. The processing stage seeks to eliminate too close waypoints that will contribute to the generation of splines segments with high curvature and to add new waypoints in regions that lack of them, because in these regions the cubics splines will unwanted distance themselves from the real route. The processing stage analyses the euclidean distance between the waypoints, removing or adding waypoints according to the design criterion of maximum and minimum distance. A set of waypoints obtained from the platforms cited are shown in Figure 6.
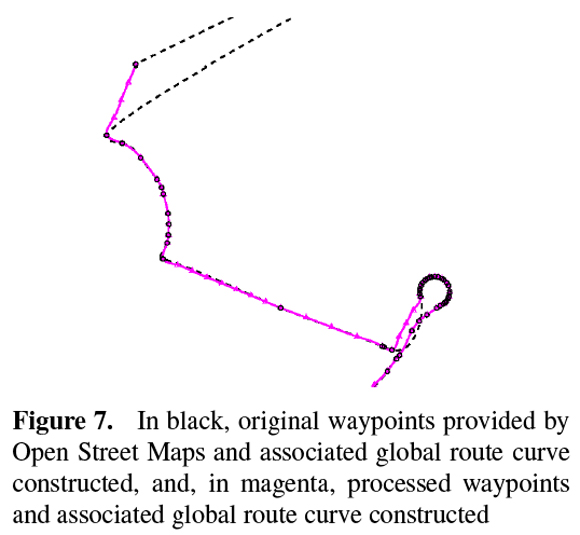
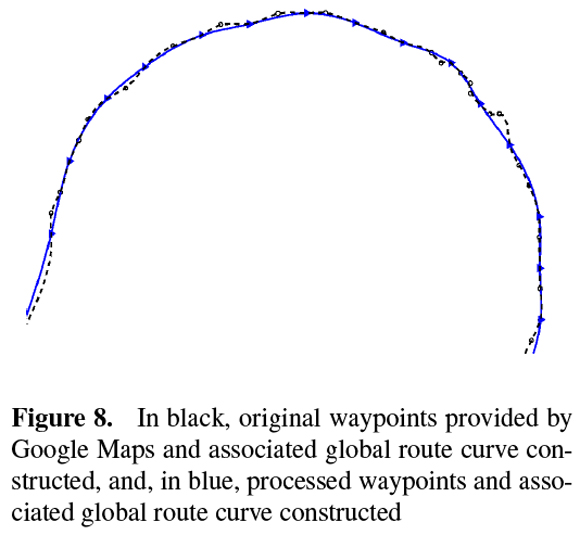
In Figure 6, the blue markers represent the waypoints obtained from Google Maps and the magenta markers represent the one obtained from Open Street Maps. The dashed line represents the curve of the global route constructed from the Open Street Maps waypoints. In Figure 7, in black were represented the original waypoints provided by Open Street Maps and the associated curve of the global route constructed and in magenta were represented the processed waypoints and associated curve. In Figure 8, it is illustrated in details the first roundabout of the real route. In black, the original waypoints provided by Googles Maps and associated curve of the global route constructed and in blue the waypoints processed and associate curve.
From Figures 7 and 8 it is observed a significant improvement in the curve of the global route constructed with the processed waypoints, magenta and blue colors, when compared to the ones constructed with the original set of waypoints provided, black colors. The new waypoints added to the original set of waypoints provided by Open Street Maps allowed the contruction of a representative curve of the global route of the real route, Figure 7. The remotion of some waypoints from the original set provided by Google Maps allowed the construction of a smoother curve in the roundabout, Figure 8.
3.2. Arc length distance reparameterization problem
Once constructed a representative curve of the global route of the real route, the reparameterization to the arc length distance s is performed. An adequate reparaterization, as well as the representative construction discussed above, is essential to the well performance of the technique discussed by [3] because its equating was developed considering a curve of the global route parameterized in the arc length distance s. To analyze the reparameterization quality it will be used the first derivative of the curve of the global route, known as unit velocity or Frnet tangent vector. The equation 13 shows the unit velocity vector.
For a perfect arc length parameterized curve the norm of the vector 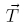 is always unitary, distancing itself from the unit value according to the reparametezitaion quality. The following graphics show the results of the norm of the vector
is always unitary, distancing itself from the unit value according to the reparametezitaion quality. The following graphics show the results of the norm of the vector 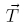 subtracted by one as function of the arc length distance s.
subtracted by one as function of the arc length distance s.
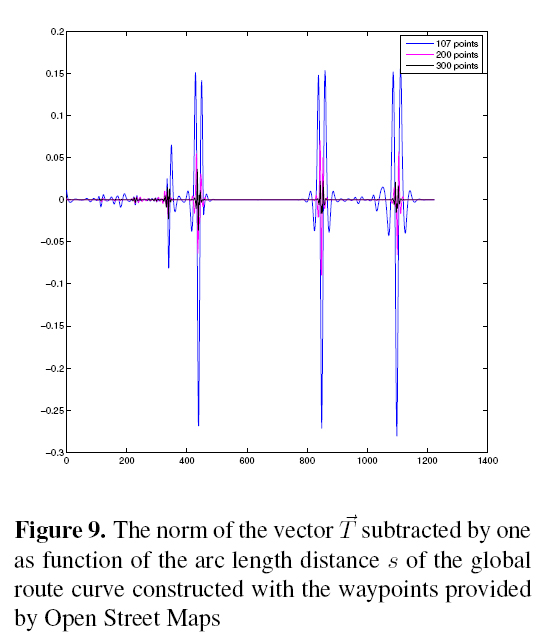
Figure 9 shows the values of the norm of the vector 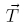 subtracted by one of three different reparemeterizarions performed upon a curve of a global route constructed by the waypoints from Open Street Maps. The blue curve represents the reparameterization quality performed with the 107 processed waypoints. In magenta, the quality of the reparameterizarion performed with 200 points upon the curve of the global route constructed and in blue the quality of the reparameterization
performed with 300 points.
subtracted by one of three different reparemeterizarions performed upon a curve of a global route constructed by the waypoints from Open Street Maps. The blue curve represents the reparameterization quality performed with the 107 processed waypoints. In magenta, the quality of the reparameterizarion performed with 200 points upon the curve of the global route constructed and in blue the quality of the reparameterization
performed with 300 points.
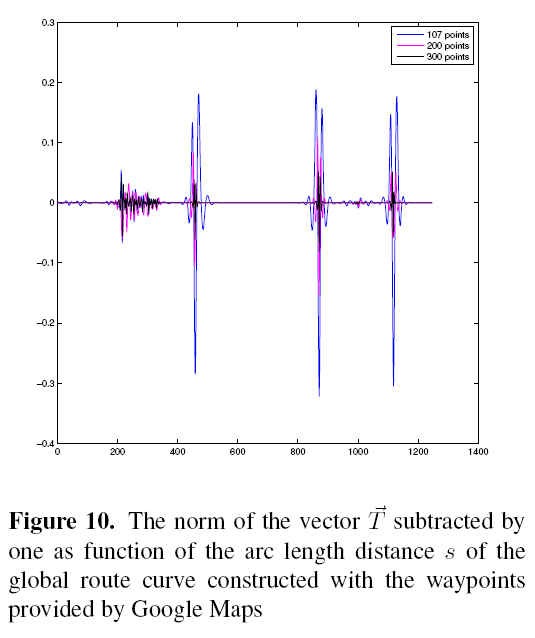
Figure 10 shows the values of the unity velocity vector norm subtracted by one of three different
reparameterization performed upon the curve of the global route constructed by Google Maps waypoints. In blue, the behavior of the norm of the vector 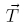 subtracted by one of the performed reparameterization using the google's processed waypoints. In magenta, the quality of the reparameterizarion performed with 200 points on the curve of the global route constructed and in blue
the quality of the reparameterization performed with 300 points.
subtracted by one of the performed reparameterization using the google's processed waypoints. In magenta, the quality of the reparameterizarion performed with 200 points on the curve of the global route constructed and in blue
the quality of the reparameterization performed with 300 points.
From the graphics above, it is possible to note a significant approximation of the values of the norm of the vector 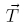 subtracted by one to the number zero, which is the expected result for a perfect
parameterized curve, as the number of points used in the reparameterization increase. These approximation indicates that the reparameterization quality was improved.
subtracted by one to the number zero, which is the expected result for a perfect
parameterized curve, as the number of points used in the reparameterization increase. These approximation indicates that the reparameterization quality was improved.
From the results shown in Figures 9 and 10 it is clear the necessity of find a good trade off between the arc length reparameterizarion quality sought and the number of waypoints used to do it. If, for one side, a curve of the global route badly arc length parameterized is an instability source, decreasing the robustness of the local path planning presented by ([3]), for other side, the use of high waypoints number can overload the communications between planning algorithm and the real time control system process.
4. Conclusions
By the presented in this article, it is possible to conclude that is necessary a prior processing of the original waypoints provided by the on-line maps and route planning Open Street Maps and Google Maps in order to achieve a representative curve of the global route and to perform a satisfactory reparameterization to the arc length s of the constructed curve. The prior processing stage consists in adding, removing and redistributing the original waypoints. In specific to the arc length s reparameterization process, it was shown that perform it with the same waypoints used in the construction stage of the global route curve is likely an inappropriate approach because it generates a curve of the global route badly arc length parameterized. This condition makes necessary an engineering study to reach a good balance between the points utilized in the reparameterization process and the necessary quality of the arc length s parameterized global route curve. It is worth noting that a global route curve badly parameterized in the arc length s will inevitably lead the presented technique or any other based in arc length parameterized curves to a potentially dangerous failure. The arc length s parameterization quality problem can be softened by reducing the size of the paths' lengths, which will lead to smaller integration steps and, consequently, smaller errors.
The presented technique has two main interesting features. First, it works in the arc length space s instead the time space t, which allows the generation of the candidate paths without the profile velocity. Second, it works in the curvilinear coordinate system instead of the Cartesian system, which allows generate the candidates paths with simple cubic polynomials, what would just be possible in the Cartesian system with more complex equation.
Acknowledgment
This work has been cofounded by CNPq and CAPES. Garcia O. was sponsored by a Scholarship PEC/PG CAPES/CNPq-Brazil.
References
[1] Tim D Barfoot and Christopher M Clark. Motion planning for formations of mobile robots. Robotics and Autonomous Systems, 46(2):65-78, 2004.
[2] Ilía Nikolaevich Bronshtein, Konstantin A Semendyayev, Gerhard Musiol, and Heiner Muehlig. Handbook of mathematics. Springer Science & Business Media, 2007.
[3] Keonyup Chu, Minchae Lee, and Myoungho Sunwoo. Local path planning for off-road autonomous driving with avoidance of static obstacles. Intelligent Transportation Systems, IEEE Transactions on, 13(4):1599-1616, 2012.
[4] Randerson Araujo de Lemos, Olmer Garcia, and Janito Vaqueiro Ferreira. Local and global path generation for autonomous vehicles using splines. In Engineering Applications-International Congress on Engineering (WEA), 2015 Workshop on, pages 1-6. IEEE, 2015.
[5] GoogleMaps. Google company. https://www.google.com.br/maps/@-22.8195851,-47.0631774,15z, 2015.
[6] Thomas M Howard and Alonzo Kelly. Optimal rough terrain trajectory generation for wheeled mobile robots. The International Journal of Robotics Research, 26(2):141-166, 2007.
[7] Unghui Lee, Sangyol Yoon, HyunChul Shim, P. Vasseur, and C. Demonceaux. Local path planning in a complex environment for self-driving car. In Cyber Technology in Automation, Control, and Intelligent Systems (CYBER), 2014 IEEE 4th Annual International Conference on, pages 445-450, June 2014.
[8] Xiaohui Li, Zhenping Sun, Qi Zhu, and Daxue Liu. A unified approach to local trajectory planning and control for autonomous driving along a reference path. In Mechatronics and Automation (ICMA), 2014 IEEE International Conference on, pages 1716-1721, Aug 2014.
[9] OpenStreetMap. The free wiki world map. http://www. openstreetmap. org, 2015.
[10] John W Peterson. Arc length parameterization of spline curves. Journal of Compu ter Aided Design, 2006.
[11] Richard J Sharpe and Richard W Thorne. Numerical method for extracting an arc length parameterization from parametric curves. Computer-aided design, 14(2):79-81, 1982.
[12] Bruno Siciliano, Lorenzo Sciavicco, Luigi Villani, and Giuseppe Oriolo. Robotics: modelling, planning and control. Springer Science & Business Media, 2009.
[13] Roland Siegwart, Illah R Nourbakhsh, and Davide Scaramuzza. Introduction to autonomous mobile robots. The MIT Press, second edition, Febraury 2011.
[14] Jarrod M Snider. Automatic steering methods for autonomous automobile path tracking. Robotics Institute, Pittsburgh, PA, Tech. Rep. CMU-RITR-09-08, 2009.
[15] MarkWSpong, Seth Hutchinson, and Mathukumalli Vidyasagar. Robot modeling and control, volume 3. Wiley New York, 2006.
[16] Hongling Wang, Joseph Kearney, and Kendall Atkinson. Arc-length parameterized spline curves for real-time simulation. In Proceedings of the 5th international conference on Curves and Surfaces, 2002.
[17] Hongling Wang, Joseph Kearney, and Kendall Atkinson. Robust and efficient computation of the closest point on a spline curve. In Proceedings of the 5th International Conference on Curves and Surfaces, pages 397-406, 2002.
[18] Werling, J. Ziegler, S. Kammel, and S. Thrun. Optimal trajectory generation for dynamic street scenarios in a frenét frame. In Robotics and Automation (ICRA), 2010 IEEE International Conference on, pages 987-993, 2010.
1 English translation: LMA's Smart Vehicle
2 For clarity and to avoid misunderstood the letter d was replaced by the letter t in the representation of the cumulative distance in equation 2
3 The curvature of the curve of the the global route is easily obtained by 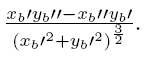
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.

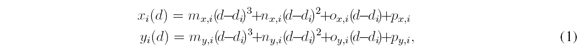
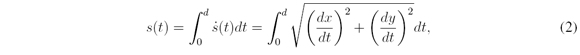


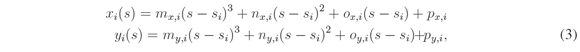
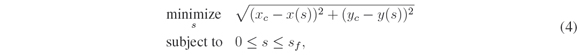
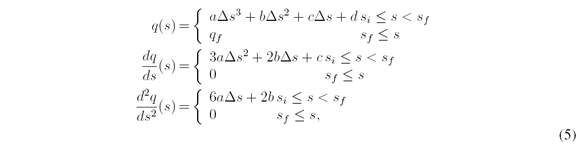
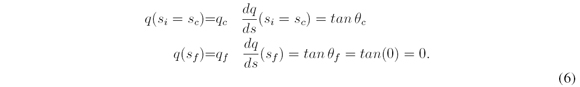
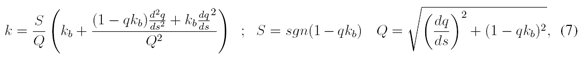
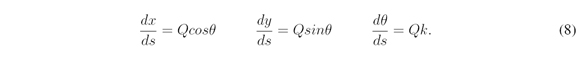
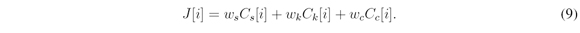
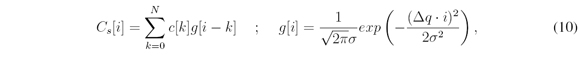
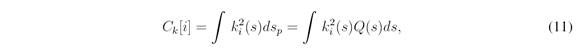
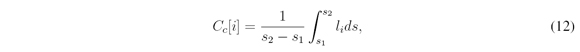
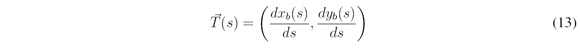



2.jpg)