DOI:
https://doi.org/10.14483/udistrital.jour.reving.2016.2.a08Published:
2016-05-26Issue:
Vol. 21 No. 2 (2016): May - AugustSection:
Special Section: Best Extended Articles - WEA 2015Comparación entre el Índice de Yager y el Centroide para Reducción de tipo de un Número Difuso Tipo-2 de Intervalo
A Comparison Between the Centroid and the Yager Index Rank for Type Reduction of an Interval Type-2 Fuzzy Number
Keywords:
Números Difusos Tipo-2 de Intervalo, Índice de Yager, Ranking (es).Keywords:
Interval Type-2 Fuzzy numbers, Yager Index, Ranking (en).Downloads
References
H. Bustince, E. Barrenechea,M. Pagola, and J. Fernandez. Interval-valued fuzzy sets constructed from matrices: Application to edge detection. Fuzzy Sets and Systems, 60(13):1819–1840, 2009.
Humberto Bustince. Interval-valued fuzzy sets in soft computing. International J. of Computational Intelligence Systems, 3(2):215–222, 2010.
Carlos Celemin and Miguel Melgarejo. A proposal to speed up the computation of the centroid of an interval Type-2 fuzzy set. Advances in Fuzzy Systems, 2013(Article ID 158969):17, 2013.
B.B. Chaudhuri and A. RosenFeld. A modified hausdorff distance between fuzzy sets. Information Sciences, 118:159–171, 1999.
Juan Carlos Figueroa-Garc´ıa,Yurilev Chalco-Cano, and Heriberto Rom´an-Flores. Distancemeasures for interval type-2 fuzzy numbers. Discrete Applied Mathematics, 197(1):93–102, 2015.
Juan Carlos Figueroa-Garc´ıa and Diego Fernando Pach´on-Neira. On ordering words using the centroid and Yager index of an interval type-2 fuzzy number. In IEEE, editor, Proceedings of the Workshop on Engineering Applications (WEA 2015), pages 1–6. IEEE, 2015.
Junhua Hu, Yan Zhang, Xiaohong Chen, and Yongmei Liu. Multi-criteria decision making method based on possibility degree of interval type-2 fuzzy number. Knowledge-Based Systems., 23:21–29, 2013.
Wen-Liang Hung and Miin-Shen Yang. Similarity measures between type-2 fuzzy sets. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, 12(6):827–841, 2004.
Cengiz Kahraman, Basar ¨Oztaysi, ´Irem Uc¸al Sari, and Ebru Turanoˆglu. Fuzzy analytic hierarchy process with interval type-2 fuzzy sets. Knowledge-Based Systems., 59:48–57, 2014.
Nilesh N. Karnik and Jerry M. Mendel. Centroid of a type-2 fuzzy set. Information Sciences, 132(1):195–220, 2001.
Bart Kosko. Fuzziness vs. probability. International Journal of General Systems, 17(1):211–240, 1990.
M. Melgarejo, H. Bernal, and K. Duran. Improved iterative algorithm for computing the generalized centroid of an interval type-2 fuzzy set. In 2008 Annual Meeting of the North American Fuzzy Information Processing Society (NAFIPS), volume 27, pages 1–6. IEEE, 2008.
Miguel A. Melgarejo and Carlos Andrs Pe na. Implementing interval type-2 fuzzy processors. Computational Intelligence Magazine, 2(1):63–71, 2007.
JerryM.Mendel. The perceptual computer: an architecture for computing with words. Proceedings ofModeling With Words Workshop – FUZZ-IEEE 2001, 2001.
Jerry M. Mendel. Uncertain Rule-Based Fuzzy Logic Systems: Introduction and New Directions. Prentice Hall, 2001.
Jerry M. Mendel. An architecture for making judgments using computing with words. Int. J. Appl. Math.
Comput. Sci., 12(3):325–335, 2002.
Jerry M. Mendel. Advances in Type-2 fuzzy sets and systems. Information Sciences, 177:84–110, 2007.
Jerry M.Mendel and Feilong Liu. Super-exponential convergence of the Karnik-Mendel algorithms for computing the centroid of an interval type-2 fuzzy set. IEEE Transactions on Fuzzy Systems, 15(2):309–320, 2007.
Jerry M. Mendel and D. Wu. Perceptual Computing: Aiding People in Making Subjective Judgments. John Wiley & Sons, 2010.
H. T. Nguyen and V. Kreinovich. Computing degrees of subsethood and similarity for interval-valued fuzzy sets: Fast algorithms. In 9th International Conference on Intelligent Technologies InTec08, pages 47–55. IEEE, 2008.
I.B. T¨urksen. Interval-valued fuzzy sets and compensatory AND. Fuzzy Sets and Systems, 51:295–307, 1992.
Dongrui Wu and Jerry M. Mendel. Enhanced Karnik-Mendel algorithms for Interval Type-2 fuzzy sets and systems. In AnnualMeeting of the North American Fuzzy Information Processing Society (NAFIPS), volume 26, pages 184–189. IEEE, 2007.
DongruiWu and JerryM.Mendel. Enhanced Karnik–MendelAlgorithms. IEEE Transactions on Fuzzy Systems, 17(4):923–934, 2009.
R. Yager. A procedure for ordering fuzzy subsets of the unit interval. Information Sciences, 24(1):143–161, 1981.
L. Zadeh. The concept of a linguistic variable and its application to approximate reasoning-I. Information
Sciences, 8:199–249, 1975.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
DOI: http://dx.doi.org/10.14483/udistrital.jour.reving.2016.2.a08
A Comparison Between the Centroid and the Yager Index Rank for Type Reduction of an Interval Type-2 Fuzzy Number
Comparación entre el Índice de Yager y el Centroide para Reducción de tipo de un Número Difuso Tipo-2 de Intervalo
Diego Fernando Pachón-Neira
Universidad Distrital Francisco José de Caldas diego.pachon@outlook.es
Juan Carlos Figueroa-García
Universidad Distrital Francisco José de Caldas, jcfigueroag@udistrital.edu.co
Received: 25-11-2015. Modified: 01-03-2016. Accepted: 13-04-2016.
Abstract
Context: There is a need for ranking and defuzzification of Interval Type-2 fuzzy sets (IT2FS), in particular Interval Type-2 fuzzy numbers (IT2FN). To do so, we use the classical Yager Index Rank (YIR) for fuzzy sets to IT2FNs in order to find an alternative to the centroid of an IT2FN.
Method: We use a simulation strategy to compare the results of the centroid and the YIR of an IT2FN. This way, we simulate 1000 IT2FNs of the following three kinds: gaussian, triangular, and non symmetrical in order to compare their centroids and YIRs.
Results: After performing the simulations, we compute some statistics about its behavior such as the degree of subsethood, equality and the size of the Footprint of Uncertainty (FOU) of an IT2FN. A description of the obtained results shows that the YIR is less wide than centroid of an IT2FN.
Conclusions: In general, YIR is less complex to obtain than the centroid of an IT2FN, which is highly desirable in practical applications such as fuzzy decision making and control. Some other properties regarding its size and location are also discussed.
Keywords: Interval Type-2 Fuzzy numbers, Yager Index, Ranking.
Language: (english).
Resumen
Contexto: Hay una necesidad por defuzzificar y rankear Conjuntos Difusos Tipo-2 de Intervalo(IT2FS), en particular Números Difusos Tipo-2 de Intervalo (IT2FN). Para ello, usamos el Índice de Yager (YIR) para conjuntos difusos aplicado a IT2FNs con el fin de encontrar una alternativa al centroide de un IT2FN.
Método: Usamos una estrategia de simulación para comparar los resultados del centroide y del YIR de un IT2FN. Así pues, simulamos 1000 IT2FNs de cada uno de los siguientes tres tipos: gausianos, triangulares y asimétricos para comparar sus centroides y YIRs.
Resultados: Después de realizar las simulaciones, se calculan algunas estadastísticas de su comportamiento como el grado de cobertura y de igualdad relativas del YIR respecto al centroide así como el tamaño de la Huella de Incertidumbre (FOU) de un IT2FN. La descripción de los resultados obtenidos muestra que el YIR es menos amplio que el centroide.
Conclusiones: En general, el YIR es menos complejo de obtener que el centroide de un IT2FN, lo cual es altamente deseable en aplicaciones prácticas como toma de decisiones y control. Otas propiedades relacionadas con su tamaño y ubicación también son discutidas.
Palabras clave: Números Difusos Tipo-2 de Intervalo, Índice de Yager, Ranking..
1. Introduction
The use of fuzzy sets in last decades have become an important tool to solve problems that involve non probabilistic uncertainty. One of the most important open problems when using fuzzy sets regards to the way to find a crisp measure that represents the behavior of the set. This process is known as Type reduction, and the case of an Interval Type-2 Fuzzy Number (IT2FN) is even more complex than classical fuzzy sets. Also the low availability of efficient Type reduction methods leads to analyze the properties of the most used ones, the IASCO algorithm (see Melgarejo [12]) which comes from the Enhanced Karnik-Mendel algorithm (EKM) (see Karnik & Mendel [22]) and the Yager Index Rank (YIR) for IT2FNs in this case.
Fuzzy sets are specially useful in engineering problems whose statistical information is unreliable or absent, and one of the possible ways to obtain information is via experts opinions and perceptions. Type-2 fuzzy sets cover uncertainty coming from multiple experts perceptions, and the way how they perceive the the problem, so its applicability in engineering is wide, specially in control and decision making problems where multiple experts are involved (see Hu et al [7], Kahraman et al [9], Melgarejo & Peña [13], and Mendel & Wu [19]).
Following the results presented in WEA 2015 (see Figueroa-García & Pachón-Neira [6]), this time we compare the centroid to Yager index for type reduction of IT2FNs in order to see their properties. To do so, we simulate 1000 IT2FNs of three shapes: triangular, gaussian, and non symmetric triangular membership functions and compute their centroids, Yager indexes, and other interesting measures to provide some useful information to readers who want to implement Type-2 fuzzy sets/systems.
The paper is organized into 6 sections; Section 1 introduces the main problem; Section 2 presents some basics about Type-2 fuzzy sets; Section 3 introduces the centroid and Yager index of an IT2FN; Section 4 presents the methodology used for comparing both methods; In section 5, the results of the experiments are presented, and finally Section 6 presents some concluding remarks of the study.
2. Basics on Interval Type-2 fuzzy sets
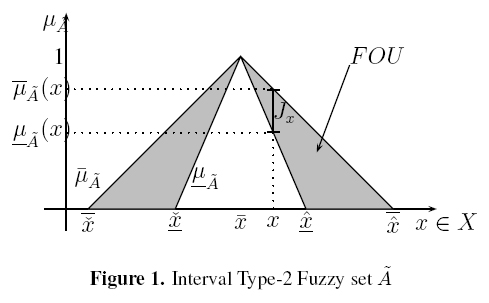
In this paper, we do not make any distinction between definitions of IVFSs and Interval Type-2 fuzzy sets (IT2FSs) given by Mendel [15] since they are equivalent (see Mendel [17], Bustince [2],Bustince et al. [1], and Türksen [21]). A Type-2 fuzzy set is then:
where à represents uncertainty around the word A, Jx is the primary membership of x, u is its domain of uncertainty, and F2(X) is the class of all Type-2 fuzzy sets (see Mendel [15], [19]).
This way, Ã is composed by an infinite amount of embedded Type-1 fuzzy sets namely Ae. Every element x has associated a set of primary memberships Jx weighted by a Secondary fuzzy set fx(u) where u is the domain of uncertainty of x, u ∈ Jx ⊆ [0,1]. Now, an IT2FS is a simplification of a T2FS since its secondary membership function is assumed to be 1, as shown as follows.
where x; u are the primary and secondary variables, and fx(u)/u = 1 is the secondary membership function.
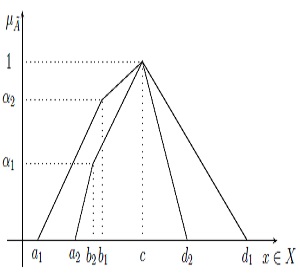
Uncertainty about the word A is conveyed by the union of all of Jx into the Footprint Of Uncertainty of Ã, namely FOU(Ã), which is bounded by two functions: An Upper membership function 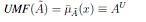 and a Lower membership function
and a Lower membership function 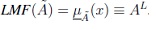 . FOU(Ã) is shown in Figure 1.
. FOU(Ã) is shown in Figure 1.
In Figure 1, à is an IT2FS, the universe of discourse for the primary variable x is the set x ∈X, the support of Ã, supp(Ã) is the interval x ∈ 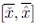 and μà is a triangular membership function with parameters
and μà is a triangular membership function with parameters 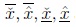 and
and 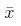 .
.
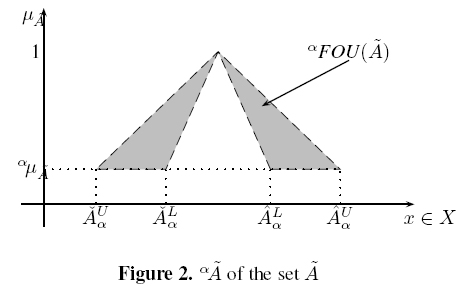
Definition 2.1 (α-cut of an IT2FS) Figueroa-García, Chalco-Cano & Román-Flores [5] have defined the α-cut of an IT2FS as follows:
where 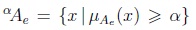 is an α-cut done over an embedded set Ae ∈; Ã. The symbol∫ denotes fuzzy union, so αà is the union of all αAe.
is an α-cut done over an embedded set Ae ∈; Ã. The symbol∫ denotes fuzzy union, so αà is the union of all αAe.
A graphical representation of αà is provided in Figure 2.
2.1. Type-2 fuzzy numbers
In this paper, a Type-2 fuzzy number (T2FN) is considered as the extension of a Type-1 fuzzy number. This means that à is an T2FS whose UMF and LMF are fuzzy numbers (e.g. normal and convex fuzzy subsets of R, Zadeh [25]). α A is closed interval for all α ∈ [0, 1], and its support supp(A) is defined over R. This also means that a fuzzy number is a normal and convex fuzzy set, as shown as follows.
Definition 2.2 (Type-2 Fuzzy Number) Let à 2 F2(R). Then, à is a Type-2 Fuzzy Number(T2FN) iff there exists a closed interval [a,b] ≠ 0 for each UMF 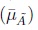 and LMF
and LMF 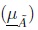 such that
such that
where l : (− ∞; a) → F([0,1]), u ∈; Jx ⊆ [0,1] is monotonic non-decreasing, continuous from the right, and l(x; u) = 0 for x < w1, and r:(b,∞) → F([0,1]); u ∈; Jx ⊆ [0,1] is monotonic non-increasing, continuous from the left, and r(x,u)= 0 for x > w2.
3. Type reduction of an IT2FS
Consider a crisp set SA(x), a classical fuzzy set A(x), and an IT2FS Ã(x), all of them related to the word A. The Type reduction process is simply the process of going from Ã(x) to SA(x) using functions (or methods) namely f. This is:
To do so, we introduce two methods: a centroid based method called the IASCO algorithm, and the YIR method as follows.
3.1. Centroid of an IT2FS
The IASCO algorithm proposed by Melgarejo in [12] is an improvement of the Enhanced Karnik-Mendel algorithm (See Karnik & Mendel in [22]) for Type-reduction of an Interval Type-2 fuzzy set. Given a set Ã, its centroid C(Ã) is composed by an interval set of centroids bounded by two values min{C(Ã)} = Cr(Ã) and max{C(Ã)} = Cr(Ã). Every point enclosed into C(Ã) = [Cl(Ã),Cu(Ã)] is also a possible centroid of Ã, so there is an infinite amount of centroids enclosed into C(Ã) (see Wu and Mendel [22], [23], Mendel and Liu [18], Karnik and Mendel [10], and Melgarejo [3]), as follows:
where à is an interval Type-2 fuzzy set, cl(Ã) and cr(Ã) are the upper and lower centroids. The main equations of the Enhanced Karnik-Mendel (EKM) algorithm for computing C(Ã) (seeWu & Mendel [22]) are provided as follows:
where 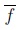 and
and 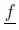 are the UMF and LMF of Ã.
are the UMF and LMF of Ã.
Other authors like Melgarejo [12] proposed the algorithm IASCO (Iterative AlgorithmWith Stop Condition) which improves the computation of C(Ã), as shown as follows:
starting with k = 0, increasing k = k + 1 and computing D0 and P0 for each increment, then we have
if cl(k) ≤ cmin then cmin = cl(k) otherwise stop and do cl = cmin.
In a similar way, to find cr from (9) the recursions are:
starting with k = 0, increasing k = k + 1 and computing D0 and P0 for each increment, then we have
if cr(k) ≥ cmax then cmax = cl(k) otherwise stop and do cr = cmax
If the above condition is satisfied at some point stops the iteration cycle; the latest results are those for cl(Ã) and cr(Ã).
3.2. Yager Index rank for IT2FNs
Ronald Yager [24] has proposed one of the most important ranking methods for fuzzy sets. Based on the works of Figueroa-García & Pachón-Neira [6], Chaudhuri & Rosenfeld [4], and Hung & Yang [8] regarding levels for computing distances, we present the Yager Index for IT2FNs as follows:
in the continuous case, and
in the discrete case, where 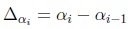 is the size of the partition (also known as the step size of the Riemmann’s integral).
is the size of the partition (also known as the step size of the Riemmann’s integral).
YIR leads to an interval set defined as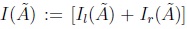 which is easier to obtain than C(Ã) in the sense that any IT2FN is α-convex, so the computation of I(Ã) leads in some cases to closed forms. There is a limitation when using YIR over discrete variables: there is no a guarantee of having convex α-cuts, so we encourage readers to use any interpolation and/or approximation method in cases where α Ã leads to open intervals.
which is easier to obtain than C(Ã) in the sense that any IT2FN is α-convex, so the computation of I(Ã) leads in some cases to closed forms. There is a limitation when using YIR over discrete variables: there is no a guarantee of having convex α-cuts, so we encourage readers to use any interpolation and/or approximation method in cases where α Ã leads to open intervals.
4. Methodology of comparison
The relation between C(Ã) and I(Ã) is measured via subsethood between sets (see Kosko [11], Nguyen & Kreinovich [20], and Figueroa-García, Chalco-Cano & Román-Flores [5]). Consider two sets C(Ã); I(Ã) the set equality and subsethood between C(Ã); I(Ã) are defined as follows:
To do so, we have defined the following measures to compare C(Ãi) to I(Ãi):
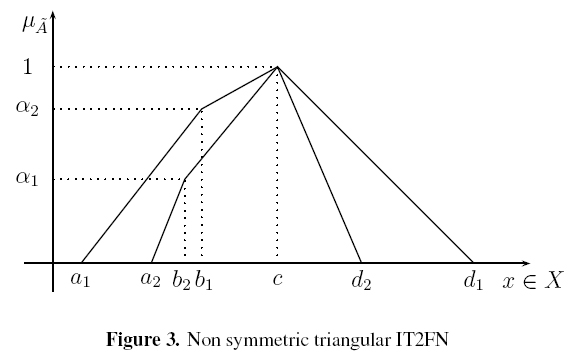
Now, we have performed 1000 simulations of three different different IT2FNs:
Non symmetric triangular (see Figure 3).
We have selected those shapes due to applicability in control and decision making problems and its easiness to implement in real world applications (see Wu & Mendel [19], Mendel [14], [16]).
A description of the procedure is shown in Procedure 1.
5. Results
After computing all measures shown in last section, we collect the results of the simulation procedure in Table I. This way, we present the average values for d=, d⊆ namely 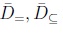 and the average values
and the average values per type of IT2FN.
per type of IT2FN.
In Table I, Center is the average of all central parameters of all simulated IT2FNs. Note that 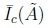 and
and 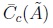 are very close to the central parameter of every set. This indicates that both methods areclose to most possible granule of à which is somehow an expected property. Another interesting finding is that centroid is as wider as the support of à is, while YIR is as wider as the FOU is.
are very close to the central parameter of every set. This indicates that both methods areclose to most possible granule of à which is somehow an expected property. Another interesting finding is that centroid is as wider as the support of à is, while YIR is as wider as the FOU is.
For triangular IT2FNs, a 71% of cases fulfill 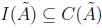 , a 83% of cases fulfill
, a 83% of cases fulfill 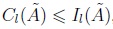 , a 88% of cases fulfill
, a 88% of cases fulfill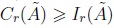 , and a 100% of cases
, and a 100% of cases 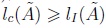 .
.
For gaussian IT2FNs, a 100% of cases fulfill 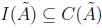 , a 100% of cases fulfill
, a 100% of cases fulfill 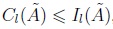 , a 100% of cases fulfill
, a 100% of cases fulfill 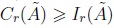 , and a 100% of cases
, and a 100% of cases 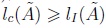 . This happens
due to the inherent symmetry of gaussian distribution which leads to centroid and YIR to converge to the same central value, and again YIR is less wide than centroid.
. This happens
due to the inherent symmetry of gaussian distribution which leads to centroid and YIR to converge to the same central value, and again YIR is less wide than centroid.
For non symmetric IT2FNs, a 57% of cases fulfill 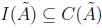 , a 98% of cases fulfill
, a 98% of cases fulfill 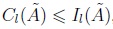 , a 59% of cases fulfill
, a 59% of cases fulfill 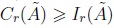 , and a 99% of cases
, and a 99% of cases 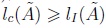 . In this case YIR is still less wide than centroid, but due to the asymmetry of its left shape the YIR is greater than centroid.
. In this case YIR is still less wide than centroid, but due to the asymmetry of its left shape the YIR is greater than centroid.
In Table I, 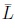 is the average of times that
is the average of times that  which means that even when the centers of YIR and centroid are similar, there are small numerical differences. For instance, only a 7% of all gaussian simulations show this behavior (due to small numerical differences) even when all simulated gaussian IT2FNs were symmetric. It is also clear that this behavior changes in non
symmetric IT2FNs.
which means that even when the centers of YIR and centroid are similar, there are small numerical differences. For instance, only a 7% of all gaussian simulations show this behavior (due to small numerical differences) even when all simulated gaussian IT2FNs were symmetric. It is also clear that this behavior changes in non
symmetric IT2FNs.
In general, both centroid and YIR represent the central value of à in a good way with some numerical differences. While YIR is a function of , the centroid is a function of the support of à which finally leads to different results.
6. Concluding Remarks
From a computational point of view, the IASCO and EKM algorithms use expensive routines whose results are wider measures than the YIR. In most of cases, the centroid is a wider measure than the YIR. For gaussian IT2FNs, a 100% of times the centroid contains the YIR, while for triangular IT2FNs only a 71% the centroid contains YIR. It seems that the FOU of à has a relationship to I(Ã);C(Ã) since as large the FOU is, as large I(Ã);C(Ã) are. Future works will corroborate those results.
In general, the YIR seems to be an easier way to compute the expected value of à than C(Ã) due to its simplicity and good relationship to its FOU. Evidently, the shape of the set infers on the properties of I(Ã);C(Ã), so we recommend to keep in mind that C(Ã) is wider than I(Ã). For gaussian shapes, both I(Ã);C(Ã) obtains the same Ic(Ã);Cc(Ã), for non symmetric triangular shapes most of times Ic(Ã) > Cc(Ã), and for triangular shapes near a half of cases I(Ã) > C(Ã).
For practical applications, we recommend the use of YIR over centroid since YIR has closed equations while IASCO and EKM algorithms are iterative methods. Note that YIR has been designed for IT2FNs while IASCO and EKM algorithms have been designed for all kinds of IT2FSs.
This way, YIR has a great potential in fuzzy optimization, resolution of fuzzy equations, hardware implementation of fuzzy controllers, and other applications where iterative computations are neither allowed nor feasible.
Future work
Other experiments can be performed in the future to see other properties of I(Ã);C(Ã) in other fields such computation of fuzzy functions, fuzzy optimization, fuzzy decision making, etc. Also, some theoretical differences between YIR and centroid could be interesting to be analyzed such as the relationship between I(Ã) and FOU(Ã) and the sizes of I(Ã);C(Ã).
References
[1] H. Bustince, E. Barrenechea, M. Pagola, and J. Fernandez. Interval-valued fuzzy sets constructed from matrices: Application to edge detection. Fuzzy Sets and Systems, 60(13):1819-1840, 2009.
[2] Humberto Bustince. Interval-valued fuzzy sets in soft computing. International J. of Computational Intelligence Systems, 3(2):215-222, 2010.
[3] Carlos Celemin and Miguel Melgarejo. A proposal to speed up the computation of the centroid of an interval Type-2 fuzzy set. Advances in Fuzzy Systems, 2013(Article ID 158969):17, 2013.
[4] B.B. Chaudhuri and A. RosenFeld. A modified hausdorff distance between fuzzy sets. Information Sciences, 118:159-171, 1999.
[5] Juan Carlos Figueroa-García, Yurilev Chalco-Cano, and Heriberto Román-Flores. Distance measures for interval type-2 fuzzy numbers. Discrete Applied Mathematics, 197(1):93-102, 2015.
[6] Juan Carlos Figueroa-García and Diego Fernando Pachón-Neira. On ordering words using the centroid and Yager index of an interval type-2 fuzzy number. In IEEE, editor, Proceedings of the Workshop on Engineering Applications (WEA 2015), pages 1-6. IEEE, 2015.
[7] Junhua Hu, Yan Zhang, Xiaohong Chen, and Yongmei Liu. Multi-criteria decision making method based on possibility degree of interval type-2 fuzzy number. Knowledge-Based Systems., 23:21-29, 2013.
[8] Wen-Liang Hung and Miin-Shen Yang. Similarity measures between type-2 fuzzy sets. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, 12(6):827-841, 2004.
[9] Cengiz Kahraman, Basar Öztaysi, Írem Uçal Sari, and Ebru Turanoglu. Fuzzy analytic hierarchy process with interval type-2 fuzzy sets. Knowledge-Based Systems., 59:48-57, 2014.
[10] Nilesh N. Karnik and Jerry M. Mendel. Centroid of a type-2 fuzzy set. Information Sciences, 132(1):195-220, 2001.
[11] Bart Kosko. Fuzziness vs. probability. International Journal of General Systems, 17(1):211-240, 1990.
[12] M. Melgarejo, H. Bernal, and K. Duran. Improved iterative algorithm for computing the generalized centroid of an interval type-2 fuzzy set. In 2008 Annual Meeting of the North American Fuzzy Information Processing Society (NAFIPS), volume 27, pages 1-6. IEEE, 2008.
[13] Miguel A. Melgarejo and Carlos Andrs Pe na. Implementing interval type-2 fuzzy processors. Computational Intelligence Magazine, 2(1):63-71, 2007.
[14] Jerry M. Mendel. The perceptual computer: an architecture for computing with words. Proceedings of Modeling With Words Workshop - FUZZ-IEEE 2001, 2001.
[15] Jerry M. Mendel. Uncertain Rule-Based Fuzzy Logic Systems: Introduction and New Directions. Prentice Hall, 2001.
[16] Jerry M. Mendel. An architecture for making judgments using computing with words. Int. J. Appl. Math. Comput. Sci., 12(3):325-335, 2002.
[17] Jerry M. Mendel. Advances in Type-2 fuzzy sets and systems. Information Sciences, 177:84-110, 2007.
[18] Jerry M. Mendel and Feilong Liu. Super-exponential convergence of the Karnik-Mendel algorithms for computing the centroid of an interval type-2 fuzzy set. IEEE Transactions on Fuzzy Systems, 15(2):309-320, 2007.
[19] Jerry M. Mendel and D. Wu. Perceptual Computing: Aiding People in Making Subjective Judgments. John Wiley & Sons, 2010.
[20] H. T. Nguyen and V. Kreinovich. Computing degrees of subsethood and similarity for interval-valued fuzzy sets: Fast algorithms. In 9th International Conference on Intelligent Technologies InTec08, pages 47-55. IEEE, 2008.
[21] I.B. Türksen. Interval-valued fuzzy sets and compensatory AND. Fuzzy Sets and Systems, 51:295-307, 1992.
[22] Dongrui Wu and Jerry M. Mendel. Enhanced Karnik-Mendel algorithms for Interval Type-2 fuzzy sets and systems. In Annual Meeting of the North American Fuzzy Information Processing Society (NAFIPS), volume 26, pages 184-189. IEEE, 2007.
[23] DongruiWu and Jerry M. Mendel. Enhanced Karnik-Mendel Algorithms. IEEE Transactions on Fuzzy Systems, 17(4):923-934, 2009.
[24] R. Yager. A procedure for ordering fuzzy subsets of the unit interval. Information Sciences, 24(1):143-161, 1981.
[25] L. Zadeh. The concept of a linguistic variable and its application to approximate reasoning-I. Information Sciences, 8:199-249, 1975.
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.

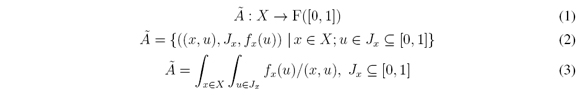
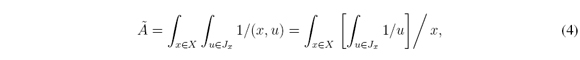
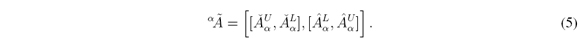
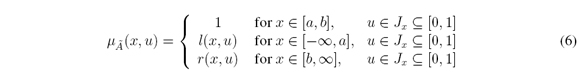
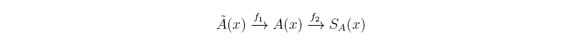
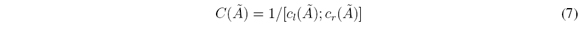
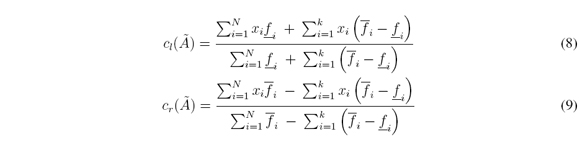
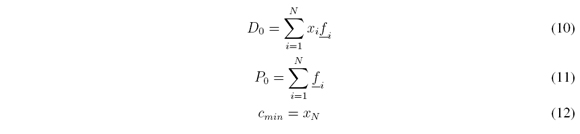
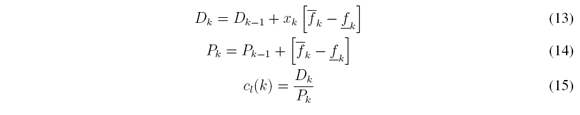
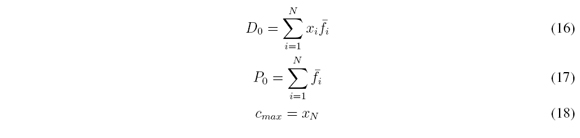
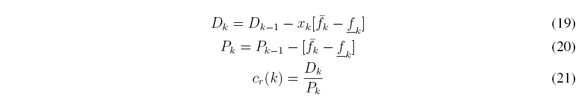
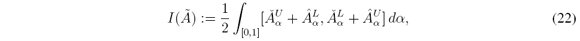
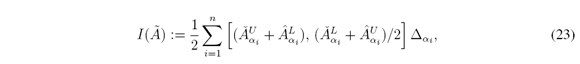
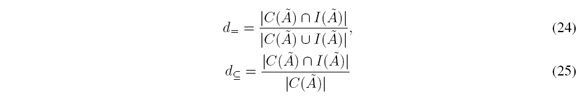
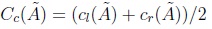
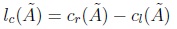
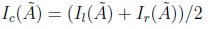
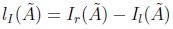
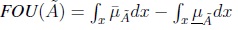
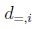 and subsethood
and subsethood 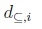
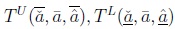
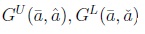





2.jpg)










