Ingeniería, 2008 vol:13 nro:1 pág:27-41

---

Programación y control de piso mediante la modificación del algoritmo de Kaspi-Montreuil y teoría de colas para un ambiente Job Shop

Scheduling and shop floor control by means of the modified algorithm of Kaspi-Montreuil and queues theory for an job shop ambient

Jairo Humberto Torres Acosta

Diana Soraya Ahumada Quito

Víctor Hugo Medina García

Resumen

El funcionamiento eficiente de la cadena de manufactura de una firma, requiere que el sistema de información operacional para el desarrollo de la programación y control de piso (Shop Floor Control), permita la toma de decisiones en escalas mínimas de tiempo. Es por esto que la clave de éxito de cualquier sistema de programación (scheduling system), es que éste le permita a la gerencia tomar decisiones en corto tiempo sobre programación de operaciones, máquinas y tareas. En este contexto, algunas técnicas de secuenciación son una herramienta coherente, que por el tipo de información arrojada como resultado permiten de una manera confiable programar y evaluar el nivel de desempeño del sistema. Sin embargo, se deben incorporar más y mejores técnicas que permitan a la administración contar con una mayor gama de herramientas que mejoren la posibilidad del proceso de toma de decisiones en el escenario del corto tiempo. En este artículo, se tiene como objetivo incorporar el algoritmo de secuenciación Kaspi-Montreuil modificado por los autores del presente artículo, como una técnica para obtener resultados en forma muy rápida, así como la evaluación efectiva de la programación del piso del sistema. De igual manera, la evaluación del desempeño se desarrollará en forma cualitativa y cuantitativa de manera paralela mediante procedimientos de teoría de colas, teniendo en cuenta aspectos fundamentales como los tiempos de espera en cola, tiempos de espera en el sistema, el número de trabajos en cola y los tiempos medios de flujo de proceso. El marco de referencia es el estado del arte sobre el problema de secuenciación de n trabajos en m máquinas en un sistema Job shop.

Palabras clave: Control de piso, Secuenciación, máquinas en paralelo, toma de decisiones, n trabajos en m máquinas, teoría de colas, simulación.

Abstract

The efficient operation of manufacturing system of a factory requires that operational information system for the scheduling and Shop Floor Control, allow the taking of decisions in minimum scales of time. It is for this reason that the key of success of any scheduling system, it is that this allows to the management to make decisions in short time it has more than enough about operations scheduling, machines and tasks. In this context, some techniques of scheduling they are a coherent tool, that for the type of information end the result they allow in a reliable way to schedule and to evaluate the level of performing of the system. However, they should incorporate more and better techniques that allow to the administration to have a bigger range of tools that improve the process of taking of decisions in the short time. In this paper the objective is incorporate the sequence algorithm Kaspi-Montreuil modified by the author of the present article, as a technique that allows to obtain results in very quick form, as well as the effective evaluation of the shop floor control system. In a same way, the evaluation of performing will be developed in a parallel way by means of procedures of queues theory in qualitative and quantitative form, keeping in mind fundamental aspects as the times of wait in line, times of wait in the system, the number of works in queue and the time mean of process flow. The reference mark is the state of the art on the problem of sequence of n works in m machines in a Job shop system.

Key word: Sequence, parallel machines, shop floor control, decisions theory, n works in m machines, queues theory, simulation.

---

1. Introducción

Los enfoques que respecto al proceso de secuenciación de tareas y programación de operaciones han sido tratados por diversos autores son variados pero similares, y en estos se establece en términos generales que deben ser trabajados por métodos tales como el algoritmo de Johnson, reglas de despacho o el diagrama de GANTT, pero ninguno de estos procedimientos ha llegado a reconocerse como óptimo y además, ninguno de ellos evalúa de manera cualitativa el proceso de secuenciación teniendo en cuenta el tiempo que debe esperar cada una de las tareas para su ejecución en el marco de la espera total del sistema de manufactura, ni las colas generadas en el mismo. El problema de la secuenciación de tareas y programación de operaciones es considerado como uno de los problemas más interesantes y complejos en el contexto del análisis de producción [1]. Es por esto que ha sido objeto de una especial atención por parte de los investigadores del tema y aun está lejos de ser resuelto completamente. Para la secuenciación de pocos trabajos en un número pequeño de máquinas la solución puede ser encontrada de manera relativamente sencilla, pero cuando se trata de una gran cantidad de trabajos en un gran número de maquinas en un sistema tipo taller (Job Shop System), la solución óptima no existe [2][3]. Por estas razones, este artículo de investigación presenta de manera diferente, la programación del piso del sistema de manufactura a través del algoritmo de Kaspi-Montreuil modificado, y la evaluación a través del enfoque de teoría de colas.

2. Marco de referencia

La secuenciación de tareas y programación de operaciones hace parte de la programación de producción a corto plazo y tiene como objetivo encontrar el orden de ejecución adecuado de los trabajos, teniendo en cuenta que éstos requieren una serie de procesos en un determinado número de máquinas disponibles para ser realizados. El proceso hace indispensable tener en cuenta algunos supuestos básicos, los cuales permiten definir los parámetros que se ajustan a los modelos específicos [4]. Estos supuestos son:

1. Cada máquina elabora un solo proceso a la vez, por lo tanto la tarea siguiente debe esperar a que el medio de trabajo esté desocupado para poder ejecutarse.

2. Cada uno de los trabajos son independientes, y sus respectivos procesos deben contar con una relación de precedencia.

3. Se debe conocer la descripción de cada uno de los procesos con anticipación, este se obtiene mediante un estudio de métodos y tiempos.

4. Los tiempos de alistamiento de las máquinas son independientes de la secuencia de los procesos y se incluyen en los tiempos de procesamiento.

5. Una vez iniciado el proceso, éste no se interrumpe sino que se espera a que finalice.

2.1. Emulación

El proceso de emulación y perfeccionamiento del sistema de manufactura para el caso concreto de desarrollo del presente artículo, se inicia con la definición de los requerimientos del sistema de información operacional, continuando con el diseño e implementación del programa de procesamiento, el cual permite desarrollar el piso del sistema. Posteriormente, mediante la utilización de información dinámica, se simula la operación y actualización, teniendo en cuenta que para desarrollar cada una de estas etapas se requiere modelar sus características. Sin embargo, es común que las técnicas utilizadas en una fase resulten inapropiadas para la siguiente, y deban ser interpretadas o reflejadas de una manera especial (espejos) para permitir el paso de una fase a la otra [5]. Cuando el proceso de emulación del sistema de manufactura se realiza a través dimplementar. Sin embargo, existen diversas arquitecturas y modelos de referencia que cubren todas las etapas del ciclo de funcionamiento de un sistema de fabricación y contextualmente podría afirmarse que en general pueden servir como referente empírico para soportar el proceso de toma de decisiones en el desarrollo de la actividad de Shop Floor Control de la firma [6].

2.2. Shop floor control system SCFS

De acuerdo con los desarrollos efectuados en el SFCS [2], su función lógica es la adquisición y administración de la información y los datos de planeación, programación, ejecución y control. Sin embargo, a criterio de los autores del presente artículo, otro aspecto que debe ser considerado como parte orgánica del SFCS es el relacionado con el Shop Scheduling [7], pues como se había mencionado anteriormente admite de forma eficiente el funcionamiento (ejecución) del sistema de manufactura, permitiendo verificar las metas y estableciendo medidas de desempeño para el sistema. Una vez determinado el protocolo de adquisición y administración de la información para la planeación, programación, ejecución y control, se define y estructura el denominado Manufacturing Execution Systems MES, el cual establece una secuencia de tareas que deben ser ejecutadas. Algunas actividades del MES se enuncian a continuación:

1. Interfaz del sistema de planeación de producción.

2. Administración y ejecución de las órdenes de trabajo.

3. Administración de las estaciones de trabajo.

4. Administración de equipos y herramientas.

5. Administración y ejecución de la labor y reporte de actividades.

2.3. Simulación

El termino y la técnica de simulación ha sido objeto de un tratamiento minucioso por parte de innumerables autores, por lo cual se tomará el razonamiento siguiente: "Simulación es el desarrollo de un modelo lógico-matemático de un sistema, de tal forma que se obtiene una imitación de la operación de un proceso de la vida real o de un sistema a través del tiempo" [8].

La simulación como técnica requiere la base de información histórica y mediante su análisis se infieren las características de funcionamiento y operación de un sistema y su comportamiento. La planificación y desarrollo de un proceso de simulación requiere el perfeccionamiento de las siguientes etapas:

1. Formulación del problema.

2. Estructura del sistema de información requerido.

3. Formulación del modelo matemático.

4. Evaluación de las características del sistema de información estructurado en relación con su confiabilidad, oportunidad y pertinencia.

5. Formulación y diseño del programa de procesamiento.

6. Validación del programa.

7. Diseño de experimentos para simulación.

8. Análisis de resultados y validación de la simulación.

2.4. Algoritmo de Kaspi-Montreuil

El algoritmo fue desarrollado para la secuenciación de "n" trabajos en "m" máquinas dispuestas en paralelo, teniendo en cuenta las condiciones empíricas del sistema de manufactura como el momento en que llega una orden de producción al sistema (un batche de producción o una corrida de varios lotes), los medios de procesamiento dispuestos en el mismo que pueden estar ocupados en la ejecución de un trabajo o una orden precedente, por lo cual, la secuenciación de los batches y de los trabajos que los componen se hará en la medida en que los medios de trabajo estén disponibles. El objetivo consiste en que la secuenciación de los n trabajos en las m máquinas arroje como resultado el mínimo Makespan.

El algoritmo [9] utiliza el parámetro de los tiempos de disponibilidad actual de las máquinas denotado como A_i para la máquina i y es el tiempo en el cual la máquina estaría disponible para que le sea asignado un trabajo j. El comportamiento óptimo del algoritmo se fundamenta en el teorema que dice que una condición suficiente para que la programación sea óptima, es que los trabajos no programados que tengan el tiempo más corto de procesamiento SPT siempre serán asignados en la máquina que tenga el tiempo de disponibilidad más temprano. Los pasos del Algoritmo son los siguientes:

1. Paso 1. Ordenar los trabajos de acuerdo con los tiempos más cortos de procesamiento SPT tal que t₁≤ t₂≤...≤t_n
2. Paso 2. Realizar la lista de los tiempos de disponibilidad por máquina A_i = a_j ; ∀ j
3. Paso 3. Ordene las máquinas de acuerdo con los tiempos de disponibilidad más tempranos tal que A₁≤ A2₂≤... ≤A_n
4. Paso 4. Programe el trabajo 1 en la máquina 1
5. Paso 5. Haga A₁ = A₁ + t₁. Actualice el orden de los tiempos más tempranos disponibles de la lista de máquinas
6. Paso 6. Remueva el trabajo 1 y actualice la lista de trabajos
7. Paso 7. Si la lista de trabajos no está vacía, retorne al paso 4. Si no, pare.

2.5. Teoría de colas

Una línea de espera o una cola es el efecto que se presenta en un sistema de manufactura cuando la demanda o llegada de órdenes de producción supera la capacidad de los medios de trabajo. Los parámetros generales de un sistema de colas son los siguientes:

S = número de servidores en el sistema.
E(t) = tiempo promedio de servicio.
Lq = número de transacciones en espera
Ce = costo del servicio por unidad de tiempo
Cq = costo de espera por transacción porunidad de tiempo
Ct = costo total por unidad de tiempo

En relación con los parámetros establecidos [10] el modelo matemático se puede representar como:

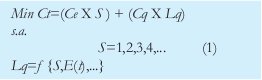
En referencia con el modelo de servidores múltiples en paralelo y población finita de m elementos, se tienen los siguientes parámetros y medidas de desempeño [11].

1. Probabilidad de n elementos en el sistema

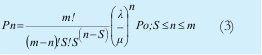
2. Número de elementos en la cola

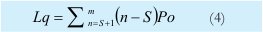
3. Número de elementos en el sistema

4. Tiempo de espera en la cola

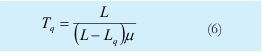
5. Tiempo de espera en el sistema

3. Diseño del modelo para el piso del sistema de manufactura

El modelo para el piso del sistema, se fundamenta en la secuenciación de "n" trabajos en "m" máquinas en paralelo evaluado a través de la modificación del algoritmo de Kaspi-Montreuil y la evaluación mediante teoría de colas. El diseño del modelo en relación con el marco de referencia desarrollado, se estructura teniendo en cuenta los siguientes aspectos:

3.1. Emulación del piso del sistema

En la emulación del piso del sistema se tienen en cuenta los aspectos característicos de su funcionamiento y operación, el sistema de información y los sistemas y procedimientos que permiten desarrollar los aspectos tácticos y operativos de la planeación, programación y control del piso de producción.

3.1.1. Sistema de información

El sistema de información en su aspecto genérico contempla los siguientes parámetros:

1. Tasa de llegada (λ), que determina de acuerdo con la información histórica, la estadística de llegada o liberación de órdenes de producción (batches) en el sistema. La dimensional está dada normalmente en relación con el número de órdenes de producción que se liberan en una unidad de tiempo.

2. Tamaño de los batches , hace referencia a familias de productos o tipos de trabajo i y la cantidad de estos por batch , y sus parámetros se establecen a través de un tamaño mínimo y máximo.

3. Tiempo estándar por unidad de producto (TS/U)_i, hace referencia al tiempo de procesamiento y el tiempo de alistamiento (tiempos de setup) por cada producto dentro de una familia i especifica componente de un batche . Los parámetros responden al criterio de máximos y mínimos.

4. Tamaño de lote (Q_i) por tipo de trabajo i, es la cantidad j de productos que componen una familia de producto o tipo de trabajo en un batche de producción. Igualmente, los parámetros se establecen mediante el criterio de máximo y mínimo.

5. Número de medios de trabajo (m) dispuestos en paralelo.

3.1.2. Comportamiento del piso del sistema

Este comportamiento contempla los parámetros que permiten establecer:

1. Llegada de los batches al sistema, que a su vez contempla los siguientes ítems de información:

a. Número del batche (k = 1, 2, 3,..., K), que determina el orden de prioridad de procesamiento de acuerdo con la regla FIFO.

b. Tiempo entre llegadas t, que establece los espacios de tiempo que transcurren entre una llegada y otra.

c. Tiempo de llegadas de los batches al sistema, que es el comportamiento acumulado de los tiempos entre llegadas ∑t_i para todos los k = 1, ..., K

d. Número de trabajos i por cada batche , define la cantidad de trabajos tipo i que tiene cada batche u orden de producción liberada.

2. Cantidad de trabajos por batche y tamaño por tipo de trabajo, define específicamente los trabajos por batche, por ejemplo, para el batche 1, los trabajos A1, A2 , ..., para el batche 2 los trabajos B1, B2,... y para el tamaño Q_At = 1,2,..,j,...,J, Q_Bt = 1,2,...,j,...,J , etc.

3.1.3. Shop floor control system

En el SFCS se manejan y administran los siguientes parámetros para la planeación, programación, ejecución y control:

1. Niveles de ocupación de los medios de trabajo S (S=1,.., m) del sistema, puesto que cuando las ordenes de producción del período de ejecución comienzan a liberarse, los medios de transformación pueden estar potencialmente ocupados en la ejecución de órdenes de periodos anteriores.

2. El orden ascendente de los niveles de ocupación de los medios de trabajo, lo cual permite determinar el momento en que estos quedan libres y pueden utilizarse en la ejecución de los diferentes batches liberados en las ordenes de producción del período presente.

3. La cantidad de trabajos i por cada batche que son liberados para el período de ejecución presente.

4. Programación y ejecución del piso del sistema, consta de los siguientes elementos de información, ejecución y control:

a. Orden de ejecución, que determina la disposición numérica en que se deben procesar los trabajos de acuerdo con lo establecido en la secuenciación SPT.

b. Reloj de control, que permite establecer en qué momento uno de los medios de trabajo S está disponible para que se ejecute un trabajo de acuerdo con la orden de ejecución pendiente.

c. Los tiempos t_Sj que define el tiempo de ejecución por tipo de trabajo y C_Sj que corresponde al tiempo acumulado que hasta el momento se tiene.

d. La sumatoria ∑t_Sj y ∑C_Sj.

5. Manufacturing execution systems MES, que maneja la siguiente información:

a. El algoritmo de secuenciación que se desarrolla con base en el algoritmo de Kaspi-Montreuil, pero que es ajustado a todo el comportamiento de teoría de colas, el cual va ser explicado más adelante.

b. Interfaz del sistema de planeación de producción y ejecución.

c. Administración de las órdenes de trabajo (ordenes de ejecución).

d. Administración de los medios de trabajo.

e. Administración de la labor y reporte de actividades.

f. Captura y administración automática de la información.

g. Administración del control de producción.

3.1.4. Desempeño del sistema

Hace parte del MES y corresponde a la administración del control de producción. La evaluación del desempeño se efectúa mediante los criterios de la teoría de secuenciación SPT y teoría de colas.

3.2. Simulación de los comportamientos

Para imitar el comportamiento empírico del piso del sistema de manufactura, se recurre a la simulación para verificar su dinámica en relación con los siguientes aspectos:

1. La llegada de los batches de producción al sistema: En donde se simula el comportamiento aleatorio de las llegadas y liberación de las órdenes de producción para el sistema. Para realizar esta representación se utiliza una distribución de probabilidad exponencial.

2. El tamaño de los batches : En donde se simula, la cantidad de trabajos i que componen cada uno de los batches. Para tal fin se utiliza la distribución de probabilidad uniforme.

3. Tiempo estándar por tipo de trabajo (TS/U) _i : Per mite simular el tiempo de procesamiento de una unidad de producto j para un tipo de trabajo i que compone un batche , para lo cual se utiliza la distribución de probabilidad uniforme.

4. Tamaño Q_ki por tipo de trabajo i: Permite simular el tamaño de los lotes de los trabajos tipo i en cada uno de los batches . Se utiliza la distribución de probabilidad uniforme.

3.2.1. Sistema de información

Este comportamiento permite definir el criterio que admite establecer el tiempo entre llegadas TELL con base en la tasa de llegada λ definida en el sistema de información. Para este propósito, se utiliza la distribución de probabilidad exponencial, cuya característica es la medición de los tiempos que transcurren entre la presentación de un evento y otro subsiguiente. Su función de densidad para la generación de variables aleatorias, obtenida a partir del método de la transformada inversa [10] es la siguiente:

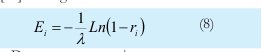
De esta manera se tiene,

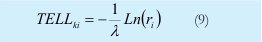
Donde r_i, es el número aleatorio y 1/ es la media. Así mismo, el tiempo de arribo de un batche (TA) es:

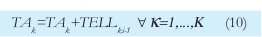
3.2.2. Simulación del tamaóo de los batches

Este comportamiento define la cantidad de trabajos tipo i que componen cada uno de los batches . Se utiliza la distribución de probabilidad uniforme, cuya característica es la probabilidad equivalente de presentación de los eventos. Su función de densidad para la generación de variables aleatorias es:

Donde, a es el límite inferior de la distribución uniforme, b el límite superior y ri el número aleatorio. De esta manera, el tamaño del batche es:

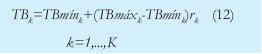
3.2.3. Simulación del tamaño del lote

La simulación de este comportamiento permite establecer la cantidad de productos Q_i que contiene cada tipo de trabajo i del batche . Se utiliza la distribución de probabilidad uniforme. De acuerdo con esto, el tamaño de lote es:

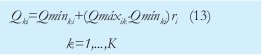
3.2.4. Simulación de los tiempos estándar

Este comportamiento establece los resultados del tiempo estándar por producto en un tipo de trabajo i , perteneciente al batche (TS/ U)_i. La observación del sistema real permite concluir que los tiempos estándar tienen rangos de variación, que podrían definirse entre un mínimo y un máximo permisible. Se utiliza la distribución de probabilidad uniforme. De acuerdo con esto, el tamaño de lote es:

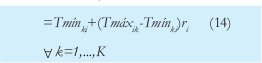
3.2.5. Simulación del escenario

La generación de los números aleatorios r_i para simular la dinámica del sistema en relación con la llegada de los batches, su tamaño, el tamaño de los lotes por tipo de trabajo y el tiempo estándar por producto, para desarrollar el piso del sistema, genera dos escenarios debido a la información dinámica que se trabaja a través de dichos aleatorios. Un escenario relativo a los números aleatorios que cambia constantemente y otro para la evaluación del piso del sistema que siempre corresponde a una información desfasada, razón por la cual no se puede desarrollar de manera coherente el piso y la evaluación del comportamiento.

Debido a esta circunstancia, se debe trabajar un escenario denominado espejo, que permite generar un comportamiento estático temporal, lo cual finalmente admite establecer el comportamiento del sistema, los tiempos y la secuenciación, el piso del sistema, la evaluación de acuerdo con SPT y teoría de colas.

3.3. Shop floor control system SFCS

Una vez establecida la dinámica del sistema mediante la simulación del comportamiento se empieza a definir el piso del sistema desarrollando el comportamiento propiamente dicho, que establece la captura de la información de planeación respecto a los siguientes aspectos:

1. Llegada de los batches al sistema y su tamaño respectivo.

2. Tamaño Q para cada tipo de trabajo por batche.

3. Tiempo por cada tipo de trabajo en relación con su tamaño (TS/Q)_i = Q_i (TS/ U)_i para todos los = 1,...,K e i = 1,...,I

Posteriormente se desarrollan los siguientes aspectos:

3.3.1. Secuenciación SPT

Una vez establecidos los (TS/Q)i , se desarrolla la secuenciación SPT para cada uno de los batches k.

Para = 1; TS/Q₁₁ TS/Q_Q12 ... TS/Q_tm

Para = K; TS/QK1 TS/QK2 d³³... TS/Q_Km

Una vez desarrollada la secuenciación, se establece el orden de ejecución j de los trabajos de acuerdo con la regla FIFO, lo cual significa que los trabajos secuenciados para =1 se ejecutan primero, enseguida los trabajos secuenciados para =2 y finalmente los trabajos secuenciados para =K.

3.3.2. Shop floor control y Secuenciación

En este aspecto fundamental se administra la disponibilidad de los medios de trabajo S y la liberación de las órdenes de producción de acuerdo con el orden de ejecución establecido. Para este propósito se define:

1. Los niveles de ocupación de los medios NO_s, pues se parte del supuesto básico que en el momento en que arriba al sistema el primer batche del presente período de ejecución, los medios S se pueden encontrar potencialmente ocupados con ordenes de trabajo anteriores.

2. Se secuencia el tiempo temprano de arranque, NO₁≤ N_O2≦...≤NO_S

3. Se desarrolla la ejecución del sistema (manufacturing executing systems) mediante la modificación del algoritmo de Kaspi-Montreuil, y los criterios de teoría de colas en lo referente al modelo de servidores múltiples en paralelo población finita (M/M/S) (FCFS/N/N). Este algoritmo se desarrollará en el siguiente epígrafe.

4. Se evalúa el desempeño del sistema con base el criterio SPT, para lo cual se establecen los siguientes comportamientos:

a. Trabajo i del batche asignado al medio de trabajo s en la posición j, TA_isj.

b. Tiempo de espera del trabajo i perteneciente al batche , asignado al medio de trabajo s, en la posición j, W_isj =_isj1. El tiempo de espera de arranque W0 = NO.

c. Tiempo estándar del trabajo i del batche asignado al medio de trabajo s en la posición j, T_isj.

d. Tiempo total en el sistema del trabajo i del batche asignado al medio de trabajo s en la posición j, C_isj

e. El tiempo promedio de flujo de un trabajo i en el medio s, MFT is

f. La espera promedio de un trabajo i en el medio s, MW s is

g. El makespan en el medio , M_isjs

h. Para la evaluación global, se define:

• El tiempo promedio de flujo de un trabajo i en el sistema, MFT

•La espera promedio de un trabajo i en el sistema MW

•El makespan del sistema Misjs = máx {M_s}

3.4. Planteamiento y desarrollo del nuevo algoritmo

Para el desarrollo de los argumentos planteados a lo largo de este artículo se toma como marco de referencia el algoritmo de Kaspi- Montreuil, y el modelo de teoría de colas de servidores múltiples en paralelo para población finita. Como resultado del análisis de estos dos contextos, se observa la necesidad de plantear, estructurar y validar un nuevo algoritmo que se certificará mediante técnicas de simulación, que permitan establecer la secuenciación y programación de operaciones, generando el piso del sistema en el contexto señalado.

3.4.1. Filosofía del algoritmo

Conjugar el trabajo de secuenciación y programación de operaciones con la teoría de colas, de forma tal que se pueda desarrollar la actividad de administración de la información de planeación, programación, ejecución y control del piso del sistema de una manera eficiente y eficaz. Emular el comportamiento de shop floor control system SFCS y el Manufacturing execution systems MES.

3.4.2. Parámetros del nuevo algoritmo

Como se había definido en el epígrafe referente a shop floor control y secuenciación, los parámetros de información que se precisan para la estructuración y desarrollo del nuevo algoritmo se relacionan a continuación:

1. Prioridad FIFO.

2. Nivel de ocupación del medio de trabajo s NO_s, define el tiempo que tiene reservado para trabajar el medio s cuando arriban al sistema las ordenes o batches de producción del período de programación y ejecución actual.

3. Orden de ejecución j, establece el orden en que debe ejecutarse cada trabajo i del batche , de acuerdo con el orden de arribo de cada uno de éstos y la secuenciación efectuada para cada trabajo dentro del batche.

RC_j, define el tiempo en el que un medio de trabajo s, está disponible para procesar el trabajo j que está en turno.

5. Trabajo asignado TACij define el trabajo i del batche , cuya ejecución se efectúa de acuerdo con el orden j {j=1,..., J}. Este trabajo se asigna al medio s disponible, teniendo en cuenta el reloj de control.

6. Tiempo de operación para la tarea tipo i del batche a ejecutar en la posición j , t.

7. Control de tiempo de operación Ctj

8. Tiempo acumulado de trabajo para un medio s en la ejecución del trabajo i ordenado en la posición j, C_sj ; estos parámetros emulan la información que se debe administrar en el Manufacturing Execution System MES.

3.4.3. Estructura del nuevo algoritmo

La aplicación del algoritmo requiere el desarrollo de los siguientes pasos:

Paso 1. Establezca el orden de los batches de acuerdo con el criterio FIFO para = 1,..., K

Paso 2. Secuencie los trabajos i que componen cada batche k de acuerdo con la regla SPT para = 1,..., K e i = 1,..., I

Paso 3. Establezca el orden de ejecución j (j = 1,2,..., J) de acuerdo con los pasos 1 y 2 para = 1,..., K e i = 1,..., I

Paso 4. Establezca los niveles de ocupación de los medios de trabajo s, NOs para s = 1,..., S

Paso 5. Haga; 1. Cs0: Cs0 = NOs para s = 1,..., S 2. Cts0: Cts0 = 0

Paso 6. Haga: j = 1 y determine el valor de J

Paso 7. Haga:

1. RC_j: RC_j = mín. {C_{s j -1}}

2. Seleccionar C_sj = RC_j

3. En s correspondiente a selección, asignar TAkij

4. Haga C_tsj: Sí s = seleccionada C_tsj = t_kij. Si no, C_tj = 0 para s = 1,..., S Si no, C_tj = 0 para s = 1,..., S

5. Haga C_sj: C_sj = C_{sj -1} + C_tj

Paso 8. Haga: j = j + 1

1. Sí j < J, continúe con el paso 7

2. Si no, pare

3.4.4. Prueba del nuevo algoritmo

Suponga el siguiente escenario para el piso del sistema: Llegan dos batches A y B en el orden especificado, y están compuestos A = {a1, a2} y B = {b1, b2}, con tiempos ta1, ta2 y tb1, tb2 en donde ta1 > ta2 y ta1 < ta2. El sistema tiene dos medios de trabajo s1 y s2 con niveles de ocupación NO1 y NO2, en donde NO1 > NO2. De esta forma se tiene:

1. El orden de prioridad FIFO de los batches es A y B.

2. De acuerdo con los tiempos la secuencia

SPT es A = {a₂, a₁} y B = {b₁, b₂}.

3. El orden de ejecución j es j = {1, 2, 3, 4}

correspondiente a {a2, a1, b1, b2} con tiem-

pos ta2, ta1, tb1, tb2.

4. El valor Cs0 es: C10 = NO1 y C20 = NO2

5. J =4 y j = 1

6. Para j = 1 se tiene:

a. RC1 = min { C10, C20} = C20

b. C20 = RC1

c. La selección corresponde a s2, por lo cual se asigna TAA21 = a2

d. Ct11 = 0; Ct21 = ta1

e. C11 = 0 + C10 y C21 = Ct21 + C20 , en donde C11 > C21

7. Para j = 2 se tiene:

a. RC2 = min { C11, C21} = C21

b. C21 = RC2

c. La selección corresponde a s2, por lo cual se asigna TAA22 = a1

d. Ct12 = 0; Ct22 = ta2

e. C12 = 0 + C11 y C22 = Ct22 + C21 , en donde C12 < C22

8. Para j = 3 se tiene:

a. RC3 = min { C12, C22} = C12

b. C12 = RC3

c. La selección corresponde a s1, por lo cual se asigna TAA13 = b1

d. Ct13 = tb1 ; Ct23 = 0

e. C13 = Ct13 + C12 y C23 = 0 + C22 , en donde C13 > C23

9. Para j = 4 se tiene:

a. RC4 = min { C13, C23} = C23

b. C23 = RC4

c. La selección corresponde a s2, por lo cual se asigna TAA24 = b2

d. Ct14 = 0; Ct24 = tb2

e. C14 = 0 + C13 y C23 = Ct24 + C24.

De acuerdo con la prueba de secuenciación efectuada aplicando el nuevo algoritmo, se tiene que el trabajo asignado a s1 es b1, s1 = {b1} y a s2 los trabajos a2, a1, b2, s2 = {a2, a1, b2}.

3.4.5. Desempeño del sistema

Para la evaluación del desempeño del sistema, se toma cada uno de los medios s con los respectivos trabajos asignados y se establecen los siguientes comportamientos:

1. Para cada medio de trabajo s, se genera un nuevo orden de ejecución teniendo en cuenta los trabajos por batche ki asignados a cada medio s, por lo cual, el orden de ejecución por medio de trabajo será j = {1,2,..., Ps} en donde Ps es un tope variable de acuerdo con la cantidad total de trabajos asignados a cada medio s, para s = 1,..., S.

2. Comportamiento de inicio para cada medio s, en donde, de acuerdo con los niveles de ocupación NOs, los trabajos asignados deben esperar para ser procesados. De esta manera, se tiene:

a. Tiempo de espera Ws0 = NOs para s = 1,..., S

b. Tiempo de operación del trabajo asignado Tkiso = 0

c. Tiempo total en el sistema de cada trabajo por batche ki, Ckis0 = 0

3. Para los trabajos asignados a cada medio s se tiene :

a. Wsj = Ckis j-1

b. Ckisj = Wkisj + Tkisj

4. El tiempo promedio de flujo de un trabajo i del batche k en el medio s, es:

5. La espera promedio de un trabajo i en el medio s,

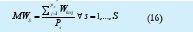
6. El makespan en el medio s, corresponde al tiempo requerido para que sean procesados los trabajos asignados a ese medio de trabajo.

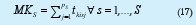
7. Para la evaluación global del sistema, se definen las medidas de desempeño: el flujo promedio del sistema MFT, la espera promedio en el sistema MW y el makespan del sistema Mk. Las formulaciones son:

3.5. Evaluación mediante teoría de colas

Al observar la estructura y funcionamiento del sistema de manufactura en el contexto en que se ha trabajado, se advierte, que todo el comportamiento se puede evaluar a través de la teoría de colas con modelo (M/M/S) (FCFS/N/N), modelo donde existen múltiples servidores (S), atendiendo un orden de primeros en llegar- primeros en ser servidos (FIFO), con población finita (N/N). Esta circunstancia, permite al administrador del sistema tomar decisiones de manera rápida en relación con los recursos que deben utilizarse para la ejecución de los batches de productos que se deben procesar en un determinado período de gestión. Este escenario también per mite administrar el ambiente de información para la planeación, programación ejecución y control del SFCS y MES.

La relación recíproca de la información obtenida mediante la evaluación del sistema a través de los criterios genéricos de SPT y la secuenciación con el nuevo algoritmo de secuenciación es la siguiente:

1. Población total del sistema m: Esta se asimila al valor J del orden de ejecución j = 1,..., J

2. Tiempo promedio de servicio 1/: Este comportamiento se establece tomando la información correspondiente ∑t_kij y la población del sistema m. De esta manera se tiene:

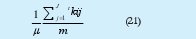
3. Tiempo promedio entre llegadas 1/∑ Esta información se determina al tomar la información del MFT del sistema y el total de batches K que arriban al sistema. La relación que permite establecer el cálculo es:

Con base en esa información se pueden determinar los valores para y , que permiten evaluar el sistema. La evaluación de desempeño del sistema establece el número de trabajos en cola Lq, el número de elementos en el sistema L, el tiempo promedio de espera en la cola Wq, que es análogo a MW de la secuenciación y el tiempo de espera en el sistema W, que es similar al MFT.

3.6. Análisis Estadístico

El objetivo del análisis estadístico es la verificación de la bondad de los resultados obtenidos al efectuar la extrapolación de la información obtenida mediante el algoritmo de secuenciación y posteriormente ser trabajada a través del modelo de teoría de colas correspondiente. La bondad de los resultados se valorará mediante la utilización de tres parámetros de medición que seguidamente serán tratados.

Para el desarrollo del análisis estadístico se considera que el número de experimentos por corrida es 10 (N = 10) y la valoración de los resultados obtenidos se hará tomando como referente los límites obligados o mínimos (Lower bound) así:

1. Límite inferior de porcentaje (LI %), que será el porcentaje mínimo admisible para que se considere que el resultado para W y Wq comparado con MFT y MW sea exitoso o no.

2. Límite inferior de permanencia en el sistema (LI_w) que permite evaluar el comportamiento de W. Este límite inferior es igual al MFT. Los parámetros de medición que se consideran para la evaluación estadística son:

1. Probabilidad de éxito (PE), es el computo entre el número de veces que los resultados objeto de análisis son mayores o iguales al LI % entre el número total de experimentos N.

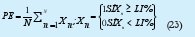
2. Desviación promedio (DP), que corresponde al promedio de las desviaciones que tiene W por encima y por debajo de LI_w.

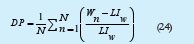
3. Porcentaje de desviación promedio (%DP), es el promedio de las desviaciones entre W y LI_w, dividido entre LI_w.

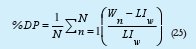
4. Resultados obtenidos

Con el objetivo de validar teóricamente el modelo, se desarrollaron una gran cantidad de replicas a través de simulación con información dinámica. Para la corroboración, se supone un sistema de manufactura al que arriban en promedio 4 batches, y cuenta con 5 medios de trabajo dispuestos en paralelo. Los parámetros de información del sistema se muestran en la tabla siguiente:

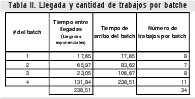
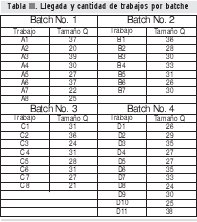
La tasa de llegada λ se transforma a llegadas por minuto, cuyo resultado es 0,004. El proceso de generación de los números aleatorios, así como el espejo no se muestra pues se considera que no es de mayor interés para los lectores. Una vez generada la información dinámica a través de los números aleatorios, la cual es capturada en el espejo, se despliegan las transformaciones pertinentes, creándose el comportamiento del sistema en el cual se establece y administra la información correspondiente a la llegada de los batches al sistema (tabla II) y la cantidad de trabajos que tiene cada uno de ellos, así como el tamaño Q para cada tipo de trabajo (tabla III).

Seguidamente se genera la información el tamaño de los lotes, es decir la cantidad de productos por cada tipo de trabajo i. Los resultados son los siguientes.

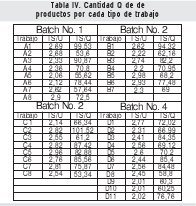
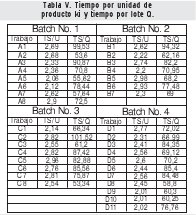
A continuación se genera y administra la información sobre los tiempos por cada unidad de producto ki y el tiempo total para cada lote Q_ki, con lo cual se desarrolla la secuenciación para cada batche k utilizando el criterio SPT. Los resultados son los siguientes.

La secuenciación SPT se efectúa en relación con los tiempos totales para cada tipo de trabajo, lo cual permite determinar y administrar la información sobre el orden de ejecución, que para esta información es j = 1,2,..., 34, en donde el primer lugar corresponde al trabajo A2, el lugar 9 al trabajo B2, el lugar 16 al trabajo C8 y el último lugar (34) al trabajo D₆.

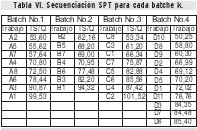
Una vez administrada esta información, se continua con la etapa de ejecución que es concretamente el shop floor control system y el manufacturing execution system en donde se aplica el nuevo algoritmo desarrollado. Esta se considera como la etapa decisiva en el desarrollo del proceso de manufactura. La infor mación específica que se genera y administra es la correspondiente a los niveles de ocupación de los medios de trabajo y el orden en que se pueden ocupar al arrancar la ejecución del período de gestión. Igualmente, se desarrolla la programación y ejecución del sistema. Estos resultados se presentan en las tablas VII y VIII.

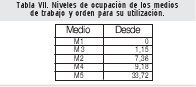
De acuerdo con los resultados de ejecución (tabla VII) se puede observar que efectivamente el trabajo A2 se asigna al medio de trabajo M₁ que se encuentra desocupado en el momento en que comienza el período de gestión.

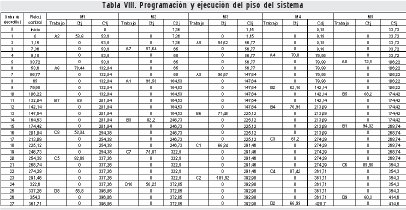
El proceso de programación y ejecución del piso del sistema como se había definido, cumple con el criterio de priorización FIFO ejecutando en primer lugar las tareas del primer batche en arribar al sistema de transformación A = {a2, a5, a7, a4, a8, a6, a3, a1} y en ultimo termino los trabajos del batche D. Igualmente, el reloj de control per mite obser var el momento de tiempo en que un medio de trabajo queda desocupado y empieza la ejecución del siguiente de acuerdo con el turno correspondiente. Por ejemplo, se observa que el ultimo trabajo d6 comienza a ser ejecutado en el tiempo 463,18 y termina en 548,58.

Una vez ejecutada la programación establecida se procede a evaluar el desempeño del sistema utilizando como marco de referencia el criterio SPT con los resultados que se observan en la tabla IX.

El resultado de evaluación se proporciona para cada uno de los medios de trabajo que componen el sistema y a su vez estos permiten la valoración global. Frente a este aspecto se observa que el flujo promedio MFT = 292,36, corresponde al promedio de los cinco medios de trabajo del sistema; la espera promedio en el sistema MW = 218,67 permite establecer, que el tiempo promedio de procesamiento por unidad es 73,69, resultado que se obtiene al establecer la diferencia entre MFT y MW; finalmente, el makespan MK = 547,43 corresponde al máximo de tiempo y se presenta en el medio de trabajo M3.

Una vez obtenidos los resultados generados mediante la utilización del nuevo algoritmo, se procede a desarrollar la evaluación mediante Teoría de colas utilizando el modelo de servidores múltiples, población finita. La determinación de los parámetros del sistema de colas se desarrolla extrapolando la información MFT que permite establecer el valor 1/ y la i j, que dividida entre el número total de productos procesados en todos los batches permite calcular la tasa de servicio . Los resultados obtenidos se presentan a continuación:

1. MFT = 292,36 por lo cual, 1/ = 292,36 y = 0,003420489

2. i j = 2.496,11 y m = 34 por lo cual = 0,014

3. m = 34

4. s = 5

Con esta información y mediante la aplicación de las formulaciones correspondientes se obtuvieron los siguientes resultados:

1. Probabilidad del sistema vacío P0 = 0,000044, equivalente al 0,0044%

2. Número de elementos en la cola Lq = 10

3. Número de elementos en el sistema L = 15

4. Tiempo de espera en la cola Wq = 220,25 minutos

5. Tiempo de espera en el sistema W = 293,66

6. Tiempo promedio de servicio t = 73,42

El resultado W de teoría de colas es equivalente al MFT. MFT = 292,36 y W = 293,66. Considerando el MFT como el lower bound el nivel de confiabilidad para este resultado es 99,56%. El resultado Wq es equivalente a MW. MW = 218,67 y Wq = 220,25 lo cual representa una confiabilidad de 99,29%.

5. Análisis Final

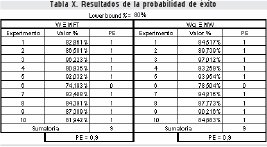
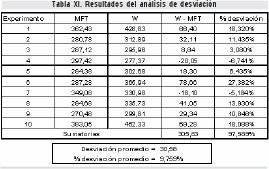
Para el desarrollo del análisis estadístico final, se despliegan 10 experimentos (N = 10) de los cuales se toma la información referente a los porcentajes de confiabilidad para los resultados correspondientes a Wq y W, verificando de esta manera el comportamiento de éxito o de fracaso al compararse con el valor LI %; Los resultados del análisis estadístico se observan en las tablas X y XI.

De los resultados sobre probabilidad de éxito se obtuvo para todos los resultados de número de elementos en el sistema (W a" MFT) que es equivalente al tiempo promedio de flujo, para las 10 replicas todos los resultados estuvieron por encima del lower bound establecido en un 80%, con una probabilidad de éxito del 90%.

De igual manera, los resultados sobre el número de productos en cola (Wqa" MW) equivalente al tiempo promedio de espera, la probabilidad de éxito fue del 90% mientras que en cada experimento se supero el porcentaje del lower bound, con lo que teóricamente se demuestra la bondad del resultado de la investigación.

En relación con el análisis de desviación, el resultado promedio es 30,58 equivalente al 9,75% que teóricamente genera un resultado de efectividad del 90,25%, el cual puede considerarse como bueno.

6. Conclusiones

El énfasis del desarrollo de esta investigación, demuestra la manera sencilla como se puede validar un escenario no convencional para la programación y control de piso de un ambiente de trabajo job shop, mediante algoritmos desarrollados con propósitos específicos y su evaluación mediante teoría de colas, presentando un marco de trabajo que no es común para este tipo de problemas, mostrando un buen desempeño computacional que facilita su implementación como una nueva alternativa de trabajo.

De igual manera, los resultados del análisis estadístico permiten corroborar aunque de forma teórica, la bondad de los métodos utilizados para la evaluación del desempeño del sistema en relación con su coherencia y veracidad.

Finalmente, el resultado cuantitativo muestra un nivel de desempeño que se puede considerar de alta aceptabilidad.

Referencias bibliográficas

[1] A. Elsayed, T. Boucher, Analysis and control of production systems. 3a. edition, Prentice Hall. New Jersey. 1994.

[2] R. Askin, G. Ronald. G. Design and analysis of lean productions system. John Wiley & Sons, Inc. New York. 2002.

[3] D. Montgomery, L. Johnson, Operations research in production planning. Scheduling and inventory control. Wiley & Sons, Inc. New York. 1976.

[4] T. Vollman, T. y W. Berry, Sistemas de planificación y control de la fabricación. Irwin. New York. 1995.

[5] C. Acosta, y F. Sastrón, F. "Implementación orientada a objetos de sistemas de fabricación altamente automatizados mediante la `emulación evolutiva de los recursos de fabricación", XIX Congreso Internacional de Ingeniería Electrónica Electro 97. 1997.

[6] J. H. Torres Acosta, Notas de clase. Planeación y control de la producción II. UDFJC. Bogotá. 2004.

[7] M. Azarang, y E. García, SIMULACIÓN Y ANÁLISIS DE MODELOS ESTOCÁSTICOS. Mc Graw Hill. M éxico.1997.

[8] M. Kaspi, y B. Montreuil, "On the scheduling of identical parallel with arbitrary initial processor available times". Research memorandum No. 88-12. School of industrial engineering. Pardue University. West Lafayette. 1988.

[9] F. Hillier, y G. Lieberman, Introducción a la investigación de operaciones. Mc Graw Hill. México. 1991.

[10] J. Prawda, Métodos y modelos de investigación de operaciones. Volumen 2. Limusa, Noriega editores. México. 1995.

[11] J. Freund, y I. Miller, Estadística matemática con aplicaciones. Prentice Hall. México. 2000.

Jairo Humberto Torres Acosta

Ingeniero Industrial de la Universidad Distrital Francisco José de Caldas, Bogotá, Colombia. Especialista en Ingeniería de Producción en la Universidad Distrital Francisco José de Caldas, Bogotá, Colombia. Magister en Investigación de operaciones en la Universidad Nacional Autónoma de México. Doctor de la Universidad Central Martha Abreu de las Villas, Cuba. Profesor de las áreas de investigación de operaciones, manufactura, ingeniería de calidad e ingeniería de costos a nivel de pregrado y postgrado. Ha publicado cuatro libros en el área de Ingeniería de Manufactura y Costos. Profesor invitado de la Universidad de Oviedo y de la Universidad Pontificia de Salamanca campus de Madrid. Director grupo de investigación "Modelos Matemáticos Aplicados a la Industria MMAI" e investigador grupo "GICOGE". Presidente de la empresa JHTA Inversiones, empresa del sector de transformación de la madera y director Sénior de la empresa SEIP LTDA. (Servicio de Ingeniería y Productividad).E-mail: jatorres@udistrital.edu.co

Diana Soraya Ahumada Quito
Ingeniero Industrial de la Universidad Distrital Francisco José de Caldas, Bogotá, Colombia. Candidato a Magister de la Maestría en Ingeniería Industrial en la Universidad Distrital Francisco José de Caldas, Bogotá, Colombia. Se desempeña como investigadora y asistente del grupo de investigación "Modelos Matemáticos Aplicados a la Industria MMAI" de la Facultad de Ingeniería De la Universidad Distrital Francisco José de Caldas. Coordinadora general del área Fomento Educativo perteneciente a la Dirección de Bienestar Institucional de la Universidad Distrital Francisco José de Caldas. E-mail: dianasaq@hotmail.com

Víctor Hugo Medina García
Doctor en Ingeniería Informática de la Universidad Pontifica de Salamanca campus de Madrid. Magíster en Informática de la Universidad Politécnica de Madrid. Especialista en Marketing de la Universidad del Rosario. Ingeniero de Sistemas de la Universidad Distrital Francisco José de Caldas. Actualmente se desempeña como profesor en el área de Ingeniería de Software y Gestión del Conocimiento en la Universidad Distrital y es investigador del grupo GICOGE reconocido por Colciencias. Es profesor asociado de la Universidad Pontifica de Salamanca campus de Madrid y profesor invitado en la Universidad de Oviedo. e-mail: vmedina@udistrital.edu.co

---

Creation date: