DOI:
https://doi.org/10.14483/udistrital.jour.reving.2015.1.a01Published:
2015-02-18Issue:
Vol. 20 No. 1 (2015): January - JuneSection:
ArticleFuzzy Entropy Relevance Analysis in DWT and EMD for BCI Motor Imagery Applications
Análisis de Relevancia con Entropía Difusa en Aplicaciones BCI con Imaginación Motora mediante Descomposiciones DWT y EMD
Keywords:
fuzzy entropy, wavelet, EMD, BCI (en).Downloads
References
T. M. Vaughan, “ Guest editorial brain-computer interface technology: a review of the second international meeting,” IEEE Transactions on Neural Systems and Rehabilitation Engineering, vol. 11, no. 2, pp. 94– 109, Jun. 2003.
J. Wang, G. Xu, L. Wang, and H. Zhang, “ Feature extraction of brain- computer interface based on improved multivariate adaptive autoregressive models,” 2010 3rd International Conference on Biomedical Engineering and Informatics, pp. 895–898, Oct. 2010.
D. Croz-Baron, J. M. Ramirez, M. Baker, V. Alarcon-Aquino, and O. Carrera, “ A BCI motor imagery experiment based on parametricfeature extraction and Fisher Criterion,” CONIELECOMP 2012, 22nd International Conference on Electrical Communications and Computers, pp. 257–261, Feb. 2012.
C. Chen, W. Song, J. Zhang, Z. Hu, and H. Xu, “ An Adaptive Feature Extraction Method for Motor-Imagery BCI Systems,” 2010 International Conference on Computational Intelligence and Security, pp. 275–279, Dec. 2010.
D. Hu, W. Li, and X. Chen, “ Feature extraction of motor imagery EEG signals based on wavelet packet decomposition,”The 2011 IEEE/ICME International Conference on Complex Medical Engineering, pp. 694–697, May 2011.
L. Zou, X. Wang, G. Shi, and Z. Ma, “ EEG feature extraction and pattern classification based on motor imagery in brain-computer interface,” 9th IEEE International Conference on Cognitive Informatics (ICCI0010), pp.
–541, Jul. 2010.
P. F. Diez, V. Mut, E. Laciar, A. Torres, and E. Avila, “ Application of the empirical mode decomposition to the extraction of features from EEG signals for mental task classification,” Conf. Proc. IEEE Eng. Med. Biol. Soc., vol. 2009, pp. 2579–82, Jan. 2009.
C. Parameswariah, S. Member, M. Cox, and S. Member, “ Frequency Characteristics of Wavelets,” vol. 17, no.3, pp. 800–804, 2002.
N. E. Huang, Z. Shen, S. R. Long, M. L.Wu, H. H. Shih, Q. Zheng, N. C.Yen, C. C. Tung, and H. H. Liu,“ The empirical modedecomposition and Hilbert spectrum for nonlinear and nonstationary time series analysis,” Proc. R. Soc. London A, vol. 454, pp. 903–995, 1998.
HU Guang-shu, “ Digital Signal Process-Theory, Algorithm, and Realization” [M]. Beijing: Tsinghua University Press, 120, 1997, (in Chinese).
R. Gray. Entropy and Information Theory (1st ed.) New York: Springer Verlag, 1990.
A. De Luca and S. Termini, “ A definition of a nonprobabilistic entropy in the setting of fuzzy sets theory,” Inf. Control, vol. 20, no. 4, pp. 301–312, May 1972.
RN. Khushaba, S. Kodagoda, S. Lal, and G. Dissanayake, “ Driver Drowsiness Classification Using Fuzzy Wavelet Packet Based Feature Extraction Algorithm,” IEEE, 2011.
RN. Khushaba, A. Al-Jumaily, A. Al-Ani, “ Novel feature extraction method based on fuzzy entropy and wavelet packet transform for myoelectric Control,” 2007 Int Symp Commun Inf Technol., pp. 352–357, 2007.
B. Blankertz, K. Muller, G. Curio, T. M. Vaughan, G. Schalk, J. R. Wolpaw, A. Schl ¨ ogl, C. Neuper, G. Pfurtsche- ¨ller, T. Hinterberger, M. Schroder, and N. Birbaumer, “ The BCI Competition 2003 : Progress and Perspectives ¨ in Detection and Discrimination of EEG Single Trials,” vol. 51, no. 6, pp. 1044–1051, 2004.
Benjamin Blankertz, Gabriel Curio and Klaus-Robert Muller, Classifying Single Trial EEG: Towards Brain ¨ Computer Interfacing, In: T. G. Diettrich and S. Becker and Z. Ghahramani (eds.), Advances in Neural Inf. Proc. Systems 14 (NIPS 01), 2002
A. Zhang, B. Yang & L. Huang. Feature Extraction of EEG Signals Using Power Spectral Entropy. 2008 International Conference on BioMedical Engineering and Informatics, 435–439, 2008.
X. Qiao, Y. Wang, and D. Li, “ Feature extraction and classifier evaluation of EEG for imaginary hand movements,” 2010 Sixth Int. Conf. Nat. Comput., no. Icnc, pp. 2112–2116, Aug. 2010.
Y. Fang, M. Chen, X. Zheng, and R. F. Harrison, “ Feature Extraction of Motor Imagery in BCI with Approximate Entropy,” vol. 6, no. March, pp. 2485–2491, 2012.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Fuzzy entropy relevance analysis in DWT and EMD for BCI motor imagery applications
Análisis de relevancia con entropía difusa en aplicaciones BCI con imaginación motora mediante descomposiciones DWT y EMD
Boris Medina Salgado, Docente UNAD. boris.medina@unad.edu.co
Leonardo Duque Muñoz, Docente ITM. leonardoduque@itm.edu.co
Recibido: 19-09-2014. Modificado: 12-11-2014. Aceptado: 26-11-2014
Abstract
Rhythm analysis in advanced signal processing methods has long of interest in application areas such as diagnosis of brain disorders, epilepsy, sleep or anesthesia analysis, and more recently in brain computer interfaces. In this paper the Discrete Wavelet Transform (DWT) and Empirical Mode Decomposition (EMD) techniques are applied to extract the brain rhythms from electroencephalographic (EEG) signals in motor imagination tasks, of left-and right hand, using public dataset BCI Competition 2003. Then the brain rhythms are characterized by statistical features. Additionally, fuzzy entropy algorithm was used to perform the relevance analysis to determine the most important features in the training set. Classification stage was performed using K-NN classifiers and SVM, obtaining classification accuracy up to 100% with EMD. Classification results allow us to infer that the techniques used are appropriate to generate solutions in BCI applications for recognizing motor imagination in people with motor disabilities.
Keywords: fuzzy entropy, wavelet, EMD, BCI
Resumen
El análisis de ritmos en métodos avanzados de procesamiento deseñales de interés en áreas de aplicación, tales como diagnóstico de trastornos cerebrales, epilepsia, análisis del sueño o anestesia,y más recientemente en las interfaces cerebro-computador. En este trabajo se aplican la transformada wavelet discreta (DWT) y descomposición por modos empíricos (EMD) para extraer los ritmos cerebrales de señales electroencefalográficas (EEG) en tareas de imaginación de motora, de mano izquierda y derecha, utilizando la bases de datos pública BCI Competition 2003. Los ritmos cerebrales se caracterizan mediante funciones estadísticas; además, se utilizó el algoritmo de entropía difusa para realizar el análisis de relevancia y determinar las características más importantes en el conjunto de entrenamiento. La etapa de clasificación se realizó utilizando clasificadores K-NN y SVM, de la que se obtuvieron porcentajes de precisión de hasta el 100% de clasificación.Los resultados de la clasificación permiten inferir que las técnicas utilizadas son adecuadas para generar soluciones en aplicaciones BCI para el reconocimiento de la imaginación motora en las personas con discapacidad motora.
Palabras claves: entropía difusa, transformada wavelet, EMD, BCI.
1. Introduction
The left-right hand motor imagination can alter neuronal activity in major sensorimotor areas, leading to changes in mu rhythm (noted µ,with frequencies 8−12Hz) and beta rhythm (noted β, with frequencies > 13Hz). The BCI systems require efficient online processing methods to classify these EEG signals in order to build a system that allows communication with its environment to patients with physical disabilities [1].
Several feature extraction techniques have been used for this purpose, including auto regressive models [2],[3], Common Spatial Patterns [4] and Wavelet Transform [5],[6]. Two methods for characterizing EEG signals in motor imagination task are used in this work. First, the Discrete Wavelet Transform (DWT), and second, the Empirical Mode Decomposition (EMD), which have shown promise in the treatment of EEG signal [6],[7] are used to decompose the EEG signal in its brain rhythms. Then, the brain rhythms are characterized with statistical functions as relative energy and standard deviation. Additionally, fuzzy entropy algorithm is used to perform a relevance analysis and determinate the most important features in the trainingset.Finally,different classifiers are used to recognize patterns of motor imagination.The application of this method was used to analyze the data set provided by Graz BCI Competition 2003.
2. Methods
2.1. DiscreteWaveletTransform(DWT)
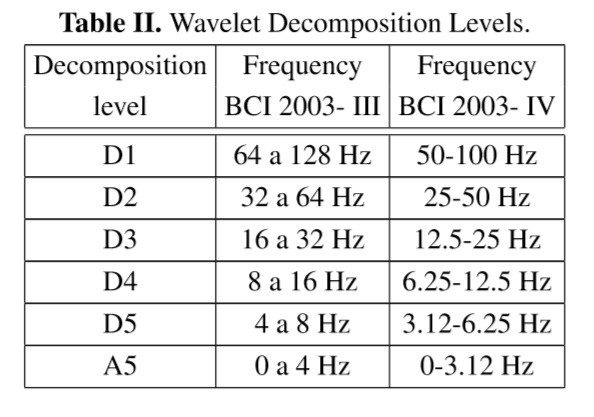
Specifically, DWT analyzes the signal in different scale bands (frequency bands) ∆Fn, with different resolutions by decomposing the signal into approach and detail components. DWT employs two sets of functions called scaling functions and wavelet functions, which are associated with low-pass filters and high-pass filters, respectively. The decomposition of the signal into different frequency bands ∆Fn, is performed iteratively, producing a set of approximation and detail coefficients at different levels or scales [8]. For x(t) signal, DWT decomposition equation is given by (1):
Where x(t) represents a time-domain signal, Cn, k represents the approximation coefficients to the level n and traslation factor k,while dj,k (j = 1ton) represents the detail coefficients at level j,ψ(t) is the wavelet function and φ(t) is a scale function.The mother wavelet selection, determines the signal representation. Daubechies, Coiflet and Symlet are generally used as mother wavelet families.The coefficients derived from wavelet decomposition are too long to be used as features for classification; in this paper, two features were used to characterize the wavelet coefficients in each sub-levels of decomposition.
2.2. Empiricalmodedecomposition(EMD)
Through EMD, used for the analysis of nonstationary and nonlinear signals, the different functions are obtained by intrinsic modes (IMF) that compose it. The general procedure used to decompose the EEG signals into IMF is proposed in [9], described in Table I, where i represents the total number of IMF produced.
The original data are the sum of the IMF cj(t) components plus the final residue rn(t), expressed as in (2).
In EMD analysis, the first IMF has the highest frequency content, this frequency content decreases with increasing in the IMF component, until n-IMF component, which is almost a linear function of time. Compared with wavelet decomposition, the components of the IMF have lowerfrequency content, are useful for analyzing low-frequency oscillations, and canbe used in the Hilbert spectral analysis to obtain instantaneous frequency [10]. Hilbert transform is mainly used to construct the analytical signal z(t) = x(t)+iy(t).The analytical signal can be separated into its component signal amplitude α(t) and instantaneous phase θ(t), whose real part is equal to the original signal, as shown in (3), where ωj is instantaneous frequency.
2.3. Fuzzyentropy
Information theory founded by Shannon, has been formally engaged with communication systems in its infancy, but has also been applied to other areas such as clustering, fuzzy systems and decision making. The theory of information relates to the quantification of the information. The quantity of information is defined as the amount of information conveyed in an event and depends on the probability of the event [11]. The definition of the amount of information means the logarithm of the probability of an event x, P(x). The average amount of information on all events, based on the classical information theory, called entropy, and is given by (4).
In the probabilistic approach, Shannon entropy is a well-known measure of uncertainty and is extensively covered in the literature. An extension of the Shannon entropy is the fuzzy entropy concept, in which the fuzzy sets used to assist estimation of entropy. Fuzzy entropy differs from Shannon classical entropy from the point at which fuzzy entropy contains fuzzy uncertainties (possibilistic) while Shannon entropy contains randomness uncertainties (probabilistic).
Fuzzy entropy,as Shannon entropy satisfies the four axioms of De Luca-Termini [12]. Shannon entropy is defined from a discrete random variable x with probability function p(xi),given by (4),where i denotes the number of elements and p(xi) denotes the occurring probability of the element xi .
From Shannon entropy, in [13] Khushaba defines fuzzy entropy of the elements of the class i along each specific feature function f (fuzzyset), as in (5) ,where P(f,ci ) can be interpreted as the degree to which the sample is pre-defined to belong to class i really contributes to that specific class.
Complete entropy diffuse along the C-class is given by (6):
Fuzzy equivalent for the joint probability of the training patterns belonging to class i, is given by (7).
Where Ai is the set of indices of the training patterns belonging to class i, NP is the total number of patterns, and µik represents the k−th fuzzy membership value belonging to class i, given by (8), with fuzziness parameter m, for the k −th measurement vector xk and the i−th centroid vector vi .
The fuzzy entropy measure was used to evaluate the significance of the different characteristics of the signal, so a high value represents fuzzy entropy function which does not contribute greatly to the deviation between classes, and an entropy value under presents more informative features. The most informative features translate into groups with minimum overlap and maximum class separability [14].
3. Experimental Set-up
In this paper, we used data collected from online BCI experiments, and analyzed as described in this section.
3.1. DataBases
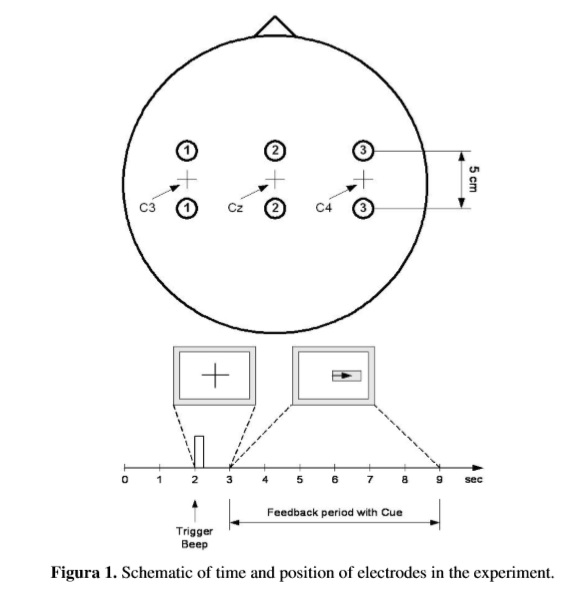
Database Graz BCI Competition 2003 – III was provided by the Department of Medical Informatics, Institute of Biomedical Engineering, Graz University of Technology [15].This dataset was recorded from a normal subject (female, 25y) during a feedback session. The subject sat in a relaxing chair with armrests. The task was to control a feedback bar by means of imagery left or right hand movements. The order of left and right cues was random. The positions of the electrodes and the distribution system are shown in Figure 1.
The experiment consists of 7 runs of 40 trials each. All of them were carried out the same day. In total there were 280 trials 9s length. During the first two seconds , t = 2s an acoustic stimulus indicates the beginning of the test, trigger channel (# 4) was located in a low to high and a cross “+” is displayed for 1 second, then t = 3s, an arrow ( left or right) is shown for reference. At the same time, the subject was asked to move one bar in the direction of the signal. The recording was performed using an amplifier g.tec and Ag/AgCl.
Three bipolar channels (anterior EEG “+” , later “-”) were measured at C3, Cz and C4 .EEG samples were taken with 128 Hz, filtered between 0.5 and 30Hz.
Database Graz BCI Competition 2003–IV was provided by Fraunhofer-FIRST, Intelligent Data Analysis Group (Klaus- Robert Müller), and Department of Neurology at Freie Universität Berlin [16]. This data set was recorded from a normal subject during a session without feedback. The subject was seated in a normal chair, relaxed arms resting on the table, fingers in the standard position to write on the computer keyboard. The task was to press with the index and little fingers the corresponding keys on your order when your own pace. The experiment consisted of 3 sessions of 6 minutes each. All sessions were held on the same day with few breaks in between. Pressing was performed at an average rate of 1 key per second.
3.2. Experiments
Because the channel Cz is independent in motor imagination [6], only C3 and C4 channels of each database are used for feature extraction. First, the average power spectral density (PSD) in C3 and C4 channels was calculated, in order to provide an effective reference in wavelet decomposition stage.
3.2.1. Waveletfeatures
According to the EEG signals of motor imagination and power spectrumin C3 and C4 channels, were chosen five levels of decomposition and the mother wavelet Daubechies 10. Table II shows the frequency bands obtained for each level of wavelet decomposition, with 128Hz and 100Hz sampling frequency for the respective datasets. The extracted wavelet coefficients provide the distribution of motor imagination signal in time and frequency.
First, we apply EMD to each EEG signal. Subsequently, we determined by PSD, which IMFs are on the same frequency band of the rhythms in order to group it.
By grouping the IMF signals at different levels that show similar spectral behavior, the Hilbert transform is applied to each level shown in TableIII. In this case, after applying Hilbert transform given by (3) to the signals formed in each level, we obtain the real component of the amplitude of the analytic signal.
To characterize the brainrhythms and represent the distribution of the frequency and amount of changes in it, were calculated two statistical functions on the dataset obtained from the wavelet decomposition and datasets extracted through EMD for each frequency level. These features are Standard Deviation and Relative Energy. Each statistical function is applied to the respective sub-levels of decomposition (6 DWT coefficients and 4 EMD levels), for both C3 and C4 channels. Thus,24 and 16 statistical features of DWT and EMD were respectively obtained.
3.2.3. Results and discussion
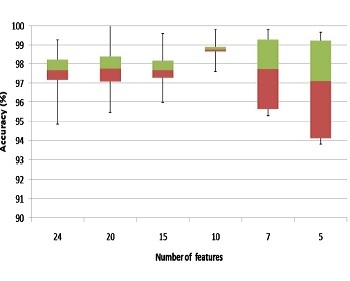
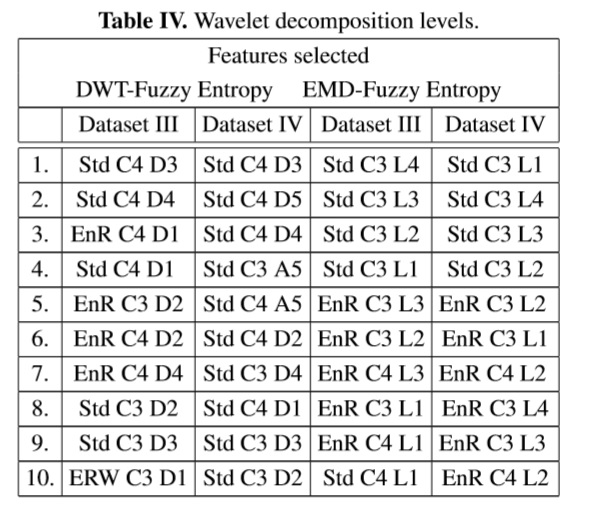
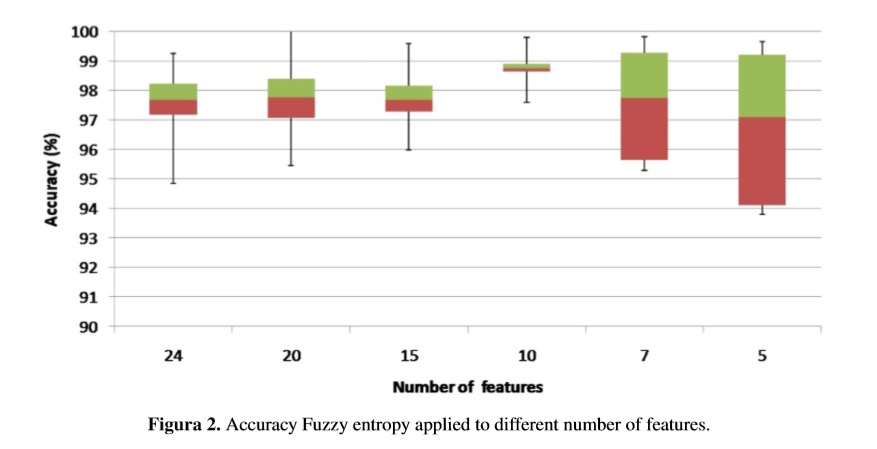
We use the function fuzzy c-means of MATLAB ®, to construct the fuzzy membership values for the features obtained of the two databases; each of these reflects the degree of membership of the sample for each of the two classes. Combining the membership values obtained µik and equations (5), (6) and (7), were calculated the fuzzy entropy on specific features space. Table IV details the number of features, in order, with the lowest value of fuzzy entropy that identifies patterns with greater information content. Figure2 shows the box plots of the average evaluation of fuzzy entropy algorithm applied to different numbers of selected features. In this way, to reduce the space dimensions, the ten features with less fuzzy entropy value were trained and classified by cross- validation (10 fold cross-validation) for k−nn classifiers and support vector machines (SVM).
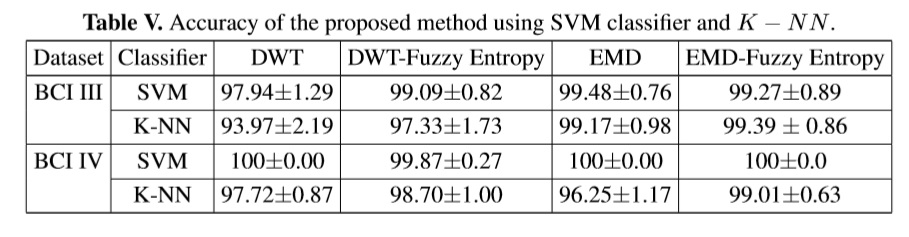
Classification results of the features extracted by the proposed method are shown in TableV for k−nn (k = 3) and SVM classifier with linear kernel function to map the training points to a higher-dimensional space.
The results of classification based on the characterization by wavelet transform and fuzzy entropy widely evident that the SVM classifier has better results than k-nn classifier in most occasions when validation is performed. However, the feature extraction based on the EMD and fuzzy entropy, both classifiers tend to show the same results in accuracy, which makes them generally have the yield potential for use in pattern recognition tasks of motor imagination.
Generally, the method of fuzzy entropy maintains or improves the accuracy of the feature of EMD and DWT where it was evaluated for the database Competition BCI 2003. The results,using fuzzy entropy, show greater impact when evaluated using k-nn classifier, increasing by up to 3.36% of accuracy using less features.
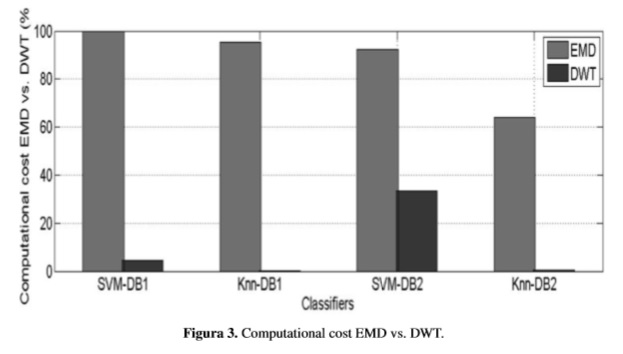
Figure 3 shows the computational cost of the training in EMD and DWT in both databases. It is worth to notice that DWT takes less than 70% time to obtain the results with similar accuracy. Determining the computational cost is achieved by running each of the proposed algorithms using Matlab ® on a laptop with Intel second generation Core i5 processor and 4GB RAM. The time of highest execution was considered 100%, and by rule of three, the remaining percentages were made.
Other feature methods applied to the databases used in this work show lower results, as in [17] with accuracy 90% using wavelet coefficients and autoregressive parameters; also, Qiao [18] obtained accuracies of 90% applying entropy coefficients Wavelet Packet (WEP). Fang et al. [19] used Approximate Entropy (ApEn) and linear classifier LDA with accuracy results of 91.4%, and Zouetal. [6] obtained 3.94% misclassification using DWT and SVM classifier.
4. Conclusions
In this paper we proposed and compared two methods for feature extraction of EEG signal for motor imagery of right and left hand, based on DWT and EMD. Also, the fuzzy entropy algorithm was used to select the most relevant features. The methodology described in this paper enable the automated recognition of motor imagery in BCI systems. Obtained results are very close in EMD and DWT decompositions;howeverthecomputationalcostofDWTis less than 70% of EMD.
We have analyzed the signals electroencephalography contained in datasets Competition 2003 dataset III and dataset IV, according to the classification results obtained effectively check the signals extracted through electrodes positioned on the C3 and C4 channels contain information interest concerning rhythms engines left and right hand.
The classification of patterns extracted through the wavelet decomposition methods and EMD, experienced two different data sets, has yielded good results accuracy. Also, by applying the fuzzy entropy algorithm, the classification accuracy is maintained using alower dimensionality space.The fact of using different data bases and different methods of characterization of EEG signals in addition to optimal classification results, makes the fuzzy entropy algorithm,a technique that could be extrapolated to other data sets and characterization techniques for used in tasks of motor imagination through BCI systems.
5. Acknowledgment
This work is supported by project P13259 from Instituto Tecnológico Metropolitano de Medellín-Colombia, and also Master thesis project “Diseño de una metodología para la extracción de características de electroencefalografía en sistemas con interfaz cerebro-computador”.
References
-
T. M. Vaughan, “Guest editorial brain-computer interface technology: a review of the second international meeting,” IEEE Transactions on Neural Systems and Rehabilitation Engineering, vol. 11, no. 2, pp. 94– 109, Jun. 2003.
-
J. Wang, G. Xu, L. Wang, and H. Zhang, “Feature extraction of brain- computer interface based on improved multivariate adaptive autoregressive models,” 2010 3rd International Conference on Biomedical Engineering and Informatics, pp. 895–898, Oct. 2010.
-
D. Croz-Baron, J. M. Ramirez, M. Baker, V. Alarcon-Aquino, and O. Carrera, “A BCI motor imagery experiment based on parametricfeature extraction and Fisher Criterion,” CONIELECOMP 2012, 22nd International Conference on Electrical Communications and Computers, pp. 257–261, Feb. 2012.
-
C. Chen, W. Song, J. Zhang, Z. Hu, and H. Xu, “An Adaptive Feature Extraction Method for Motor-Imagery BCI Systems,” 2010 International Conference on Computational Intelligence and Security, pp. 275–279, Dec. 2010.
-
D. Hu, W. Li, and X. Chen, “Feature extraction of motor imagery EEG signals based on wavelet packet decomposition,” The2011IEEE/ICMEInternationalConferenceonComplexMedicalEngineering,pp.694–697, May 2011.
-
L. Zou, X. Wang, G. Shi, and Z. Ma, “EEG feature extraction and pattern classification based on motor imagery in brain-computer interface,” 9th IEEE International Conference on Cognitive Informatics (ICCI0010), pp. 536–541, Jul. 2010.
-
P. F. Diez, V. Mut, E. Laciar, A. Torres, and E. Avila, “Application of the empirical mode decomposition to the extraction of features from EEG signals for mental task classification,” Conf. Proc. IEEE Eng. Med. Biol. Soc., vol. 2009, pp. 2579–82, Jan. 2009.
-
C. Parameswariah, S. Member, M. Cox, and S. Member, “Frequency Characteristics of Wavelets,” vol. 17, no. 3, pp. 800–804, 2002
-
N. E. Huang, Z. Shen, S. R. Long, M. L.Wu, H. H. Shih, Q. Zheng, N. C.Yen, C. C. Tung, and H. H. Liu,“The empirical mode decomposition and Hilbert spectrum for nonlinear and non stationary time series analysis,” Proc. R. Soc. London A, vol. 454, pp. 903–995, 1998
-
HU Guang-shu, “Digital Signal Process-Theory, Algorithm, and Realization” [M]. Beijing: Tsinghua University Press, 120, 1997, (in Chinese).
-
R. Gray. Entropy and Information Theory (1st ed.) New York: Springer Verlag, 1990.
-
A. De Luca and S. Termini, “A definition of a nonprobabilistic entropy in the setting of fuzzy sets theory,” Inf. Control, vol. 20, no. 4, pp. 301–312, May 1972.
-
RN. Khushaba, S. Kodagoda, S. Lal, and G. Dissanayake, “Driver Drowsiness Classification Using Fuzzy Wavelet Packet Based Feature Extraction Algorithm,” IEEE, 2011.
-
RN.Khushaba,A.Al-Jumaily,A.Al-Ani, “Novel feature extraction method based on fuzzy entropy and wavelet packet transform for myoelectric Control,” 2007 Int Symp Commun Inf Technol., pp. 352–357, 2007.
-
B.Blankertz,K.Müller,G.Curio,T.M.Vaughan,G.Schalk,J.R.Wolpaw,A.Schlögl,C.Neuper,G.P furtscheller, T. Hinterberger, M. Schröder, and N. Birbaumer, “The BCI Competition 2003 : Progress and Perspectives in Detection and Discrimination of EEG Single Trials,” vol. 51, no. 6, pp. 1044–1051, 2004.
-
Benjamin Blankertz, Gabriel Curio and Klaus-Robert Müller, Classifying Single Trial EEG: Towards Brain Computer Interfacing, In: T. G. Diettrich and S. Becker and Z. Ghahramani (eds.), Advances in Neural Inf. Proc. Systems 14 (NIPS 01), 2002
-
A. Zhang, B. Yang & L. Huang. Feature Extraction of EEG Signals Using Power Spectral Entropy. 2008 International Conference on BioMedical Engineering and Informatics, 435–439, 2008.
-
X. Qiao, Y. Wang, and D. Li, “Feature extraction and classifier evaluation of EEG for imaginary hand movements,” 2010 Sixth Int. Conf. Nat. Comput., no. Icnc, pp. 2112–2116, Aug. 2010
-
Y. Fang, M. Chen, X. Zheng, and R. F. Harrison, “Feature Extraction of Motor Imagery in BCI with Approximate Entropy,” vol. 6, no. March, pp. 2485–2491, 2012.
Boris Medina Salgado
Recibió su grado de Ingeniero Electrónico de la Universidad Pedagógica y Tecnológica de Colombia, en Octubre de 2002. Obtuvo su título de Maestría en Automatización y Control Industrial en el Instituto Tecnológico Metropolitano de Medellín, en Mayo de 2014. Su principal interés de trabajo investigativo está en el área de reconocimiento de patrones en señales biomédicas. Actualmente se desempeña como profesor catedrático en el área de Ingeniería de la Universidad Nacional Abierta y a Distancia - UNAD, Colombia.
e-mail: boris.medina@unad.edu.co
Leonardo Duque Muñoz
Recibió su grado de Ingeniero Electrónico de la Universidad Nacional de Colombia, sede Manizales en el año 2009. En el año 2012 obtuvo el grado de Maestría en Ingeniería - Automatización Industrial en la misma Universidad. Actualmente realiza sus estudios de doctorado en Ingeniería Electrónica en la Universidad de Antioquia. El principal interés de trabajo docente e investigativo está en las áreas inteligencia computacional, aprendizaje de máquina y algoritmos de optimización, aplicados a la identificación y reconocimiento de patrones en señales biomédicas.
e-mail: leonardoduque@titm.edu.co
This work is authorized by an Attribution-NonCommercial-NoDerivs CC BY-NC-ND license.
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.

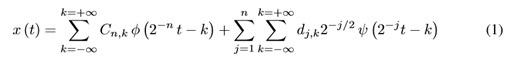


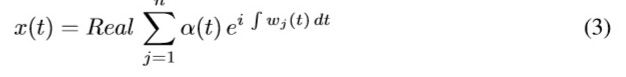
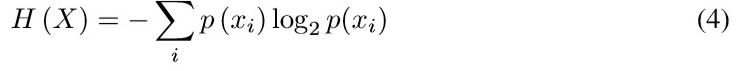
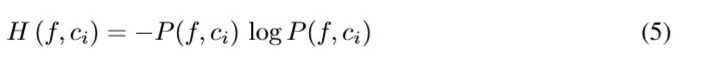


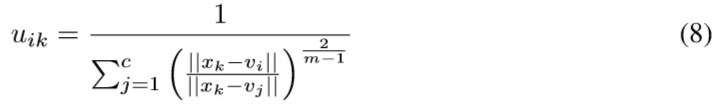



2.jpg)