DOI:
https://doi.org/10.14483/23448393.18734Publicado:
2023-04-29Número:
Vol. 28 Núm. 2 (2023): Mayo-agostoSección:
Ingeniería IndustrialEl problema de localización y ruteo con múltiples objetivos: una revisión de literatura
Multi-objective Location and Routing Problem: A Review
Palabras clave:
logística, optimización multiobjetivo, problema de localización y ruteo, metaheurísticas (en).Palabras clave:
logistics, multi-objective optimization, location and routing problem, metaheuristics (es).Descargas
Referencias
D. Liu, Z. Deng, W. Zhang, Y. Wang y E. I. Kaisar, “Design of sustainable urban electronic grocery distribution network”, Alexandria Eng. J., vol. 60, no. 1, pp. 145-157, 2021. https://doi.org/10.1016/j.aej.2020.06.051 DOI: https://doi.org/10.1016/j.aej.2020.06.051
S. B. Ebrahimi, “A stochastic multi-objective location-allocation-routing problem for tire supply chain considering sustainability aspects and quantity discounts”, J. Clean. Prod., vol. 198, pp. 704-720, 2018. https://doi.org/10.1016/j.jclepro.2018.07.059 DOI: https://doi.org/10.1016/j.jclepro.2018.07.059
G. Nagy y S. Salhi, “Location-routing: Issues, models and methods”, Eur. J. Oper. Res., vol. 177, no. 2, pp. 649-672, 2007. https://doi.org/10.1016/j.ejor.2006.04.004 DOI: https://doi.org/10.1016/j.ejor.2006.04.004
R. B. Lopes, C. Ferreira, B. S. Santos y S. Barreto, “A taxonomical analysis, current methods and objectives on location-routing problems”, Int. Trans. Oper. Res., vol. 20, no. 6, pp. 795-822, 2013. https://doi.org/10.1111/itor.12032 DOI: https://doi.org/10.1111/itor.12032
C. Prodhon y C. Prins, “A survey of recent research on location-routing problems”, Eur. J. Oper. Res., vol. 238, no. 1, pp. 1-17, 2014. https://doi.org/10.1016/j.ejor.2014.01.005 DOI: https://doi.org/10.1016/j.ejor.2014.01.005
M. Drexl y M. Schneider, “A survey of variants and extensions of the location-routing problem”, Eur. J. Oper. Res., vol. 241, no. 2, pp. 283-308, 2015. https://doi.org/10.1016/j.ejor.2014.08.030 DOI: https://doi.org/10.1016/j.ejor.2014.08.030
S. T. W. Mara, R. J. Kuo y A. M. S. Asih, “Location-routing problem: A classification of recent research”, Int. Trans. Oper. Res., vol. 28, no. 6, pp. 2941-2983, 2021. https://doi.org/10.1111/itor.12950 DOI: https://doi.org/10.1111/itor.12950
C. Rueda-Clausen, C. Villa-Roel y C. Rueda-Clausen, “Indicadores bibliométricos: origen, aplicación, contradicción y nuevas propuestas”, MedUNAB, vol. 8, no. 1, pp. 29-36, 2005. https://revistas.unab.edu.co/index.php/medunab/article/view/208
M. Rabbani, S. A. Sadati y H. Farrokhi-Asl, “Incorporating location routing model and decision making techniques in industrial waste management: Application in the automotive industry”, Comput. Ind. Eng., vol. 148, 2020. https://doi.org/10.1016/j.cie.2020.106692 DOI: https://doi.org/10.1016/j.cie.2020.106692
S. Salhi y G. K. Rand, “The effect of ignoring routes when locating depots”, Eur. J. Oper. Res., vol. 39, no. 2, pp. 150-156, 1989. https://doi.org/10.1016/0377-2217(89)90188-4 DOI: https://doi.org/10.1016/0377-2217(89)90188-4
S. Salhi y G. Nagy, “Consistency and robustness in location-routing”, Stud. Locat. Anal., no. 13, pp. 3-19, 1999. https://kar.kent.ac.uk/5249/
E. von Boventer, “The relationship between transportation costs and location rent in transportation problems”, J. Reg. Sci., vol. 3, no. 2, pp. 27-40, 1961. https://doi.org/10.1111/j.1467-9787.1961.tb01276.x DOI: https://doi.org/10.1111/j.1467-9787.1961.tb01276.x
F. E. Maranzana, “On the location of supply points to minimize transport costs”, OR, vol. 15, no. 3, pp. 261-270, 1964. https://doi.org/10.2307/3007214 DOI: https://doi.org/10.1057/jors.1964.47
M. Rabbani, H. Farrokhi-Asl y B. Asgarian, “Solving a bi-objective location routing problem by a NSGA-II combined with clustering approach: application in waste collection problem”, J. Ind. Eng. Int., vol. 13, pp. 13-27, 2017. https://doi.org/10.1007/s40092-016-0172-8 DOI: https://doi.org/10.1007/s40092-016-0172-8
F. Qiu et al., “A novel multi-objective model for the cold chain logistics considering multiple effects”, Sustain., vol. 12, no. 19, 2020. https://doi.org/10.3390/su12198068 DOI: https://doi.org/10.3390/su12198068
E. M. Toro, J. F. Franco, M. G. Echeverri y F. G. Guimarães, “A multi-objective model for the green capacitated location-routing problem considering environmental impact”, Comput. Ind. Eng., vol. 110, pp. 114-125, 2017. https://doi.org/10.1016/j.cie.2017.05.013 DOI: https://doi.org/10.1016/j.cie.2017.05.013
F. M. Safari, F. Etebari y A. P. Chobar, “Modeling and optimization of a tri-objective transportation-location-routing problem considering route reliability: Using MOGWO, MOPSO, MOWCA, and NSGA-II”, J. Optim. Ind. Eng., vol. 14, no. 2, pp. 83-98, 2021. https://doi.org/10.22094/JOIE.2020.1893849.1730
K. Zografos y S. Samara, “A combined location-routing model for hazardous waste transportation and disposal”, Transp. Res. Rec., vol. 1245, pp. 52-59, 1989. https://eprints.lancs.ac.uk/id/eprint/86566
G. List y P. Mirchandani, “An integrated network/planar multiobjective model for routing and siting for hazardous materials and wastes”, Transp. Sci., vol. 25, no. 2, pp. 99-174, 1991. https://doi.org/10.1287/trsc.25.2.146 DOI: https://doi.org/10.1287/trsc.25.2.146
C. ReVelle, J. Cohon y D. Shobrys, “Simultaneous Siting and Routing in the Disposal of Hazardous Wastes” Transp. Sci., vol. 25, no. 2, pp. 99-174, 1991. https://doi.org/10.1287/trsc.25.2.138 DOI: https://doi.org/10.1287/trsc.25.2.138
K. Govindan, A. Jafarian, R. Khodaverdi y K. Devika, “Two-echelon multiple-vehicle location-routing problem with time windows for optimization of sustainable supply chain network of perishable food”, Int. J. Prod. Econ., vol. 152, pp. 9-28, 2014. https://doi.org/10.1016/j.ijpe.2013.12.028 DOI: https://doi.org/10.1016/j.ijpe.2013.12.028
S. Alumur y B. Y. Kara, “A new model for the hazardous waste location-routing problem”, Comput. Oper. Res., vol. 34, no. 5, pp. 1406-1423, 2007. https://doi.org/10.1016/j.cor.2005.06.012 DOI: https://doi.org/10.1016/j.cor.2005.06.012
O. Yilmaz, B. Y. Kara y U. Yetis, “Hazardous waste management system design under population and environmental impact considerations”, J. Environ. Manage., vol. 203, pp. 720-731, 2017. https://doi.org/10.1016/j.jenvman.2016.06.015 DOI: https://doi.org/10.1016/j.jenvman.2016.06.015
M. Rabbani, R. Heidari, H. Farrokhi-Asl y N. Rahimi, “Using metaheuristic algorithms to solve a multi-objective industrial hazardous waste location-routing problem considering incompatible waste types”, J. Clean. Prod., vol. 170, pp. 227-241, 2018. https://doi.org/10.1016/j.jclepro.2017.09.029 DOI: https://doi.org/10.1016/j.jclepro.2017.09.029
J. Current y S. Ratick, “A model to assess risk, equity and efficiency in facility location and transportation of hazardous materials”, Locat. Sci., vol. 3, no. 3, pp. 187-201, 1995. https://doi.org/https://doi.org/10.1016/0966-8349(95)00013-5 DOI: https://doi.org/10.1016/0966-8349(95)00013-5
I. Giannikos, “A multiobjective programming model for locating treatment sites and routing hazardous wastes”, Eur. J. Oper. Res., vol. 104, no. 2, pp. 333-342, 1998. https://doi.org/10.1016/S0377-2217(97)00188-4 DOI: https://doi.org/10.1016/S0377-2217(97)00188-4
M. Zhang, Y. Ma y K. Weng, “Location-routing model of hazardous materials distribution system based on risk bottleneck”, Proceedings of ICSSSM ’05. 2005 International Conference on Services Systems and Services Management, pp. 362-368. https://doi.org/10.1109/ICSSSM.2005.1499496 DOI: https://doi.org/10.1109/ICSSSM.2005.1499496
R. Caballero, M. González, F. M. Guerrero, J. Molina y C. Paralera, “Solving a multiobjective location routing problem with a metaheuristic based on tabu search. Application to a real case in Andalusia”, Eur. J. Oper. Res., vol. 177, no. 3, pp. 1751-1763, 2007. https://doi.org/10.1016/j.ejor.2005.10.017 DOI: https://doi.org/10.1016/j.ejor.2005.10.017
J. Zhao y J. Zhao, “Model and algorithm for hazardous waste location-routing problem”, ICLEM 2010: International Conference of Logistics Engineering and Management, vol. 387, pp. 2846-2852, 2010. https://doi.org/10.1061/41139(387)398 DOI: https://doi.org/10.1061/41139(387)398
Y. Zhang y J. Zhao, “Modeling and solution of the hazardous waste location-routing problem under uncertain conditions”, ICTE 2011 - Third International Conference on Transportation Engineering, pp. 2922-2927, 2011. https://doi.org/10.1061/41184(419)483 DOI: https://doi.org/10.1061/41184(419)483
F. Samanlioglu, “A multi-objective mathematical model for the industrial hazardous waste location-routing problem”, Eur. J. Oper. Res., vol. 226, no. 2, pp. 332-340, 2013. https://doi.org/10.1016/j.ejor.2012.11.019 DOI: https://doi.org/10.1016/j.ejor.2012.11.019
J. Zhao y L. Huang, “An augmented ϵ-constraint algorithm to the hazardous waste locationrouting problem”, ICTE 2015 - Fifth International Conference on Transportation Engineering, pp. 2847-2857, 2015. https://doi.org/10.1061/9780784479384.362 DOI: https://doi.org/10.1061/9780784479384.362
J. Zhao, L. Huang, D.-H. Lee y Q. Peng, “Improved approaches to the network design problem in regional hazardous waste management systems”, Transp. Res. Part E Logist. Transp. Rev., vol. 88, pp. 52-75, 2016. https://doi.org/10.1016/j.tre.2016.02.002 DOI: https://doi.org/10.1016/j.tre.2016.02.002
J. Zhao y V. Verter, “A bi-objective model for the used oil location-routing problem”, Comput. Oper. Res., vol. 62, pp. 157-168, 2015. https://doi.org/10.1016/j.cor.2014.10.016 DOI: https://doi.org/10.1016/j.cor.2014.10.016
H. Yu y W. D. Solvang, “An improved multi-objective programming with augmented ε-constraint method for hazardous waste location-routing problems”, Int. J. Environ. Res. Public Health, vol. 13, no. 6, 2016. https://doi.org/10.3390/ijerph13060548 DOI: https://doi.org/10.3390/ijerph13060548
J. Zhao y L. Huang, “Multi-period network design problem in regional hazardous waste management systems”, Int. J. Environ. Res. Public Health, vol. 16, no. 11, 2019. https://doi.org/10.3390/ijerph16112042 DOI: https://doi.org/10.3390/ijerph16112042
M. Jamali, “Presenting a location-routing problem for multi-vehicle hazardous materials transport, considering the cost dependent to the amount of materials loaded”, Int. J. Supply Chain Manag., vol. 8, no. 3, pp. 1079-1100, 2019.
F. Delfani, A. Kazemi, S. M. SeyedHosseini y S. T. A. Niaki, “A novel robust possibilistic programming approach for the hazardous waste location-routing problem considering the risks of transportation and population”, Int. J. Syst. Sci. Oper. Logist., vol. 8, no. 4, pp. 383-395, 2021. https://doi.org/10.1080/23302674.2020.1781954 DOI: https://doi.org/10.1080/23302674.2020.1781954
H. Yu, X. Sun, W. D. Solvang, G. Laporte y C. K. M. Lee, “A stochastic network design problem for hazardous waste management”, J. Clean. Prod., vol. 277, 2020. https://doi.org/10.1016/j.jclepro.2020.123566 DOI: https://doi.org/10.1016/j.jclepro.2020.123566
X. Yu, Y. Zhou y X. F. Liu, “The two-echelon multi-objective location routing problem inspired by realistic waste collection applications: The composable model and a metaheuristic algorithm”, Appl. Soft Comput. J., vol. 94, 2020. https://doi.org/10.1016/j.asoc.2020.106477 DOI: https://doi.org/10.1016/j.asoc.2020.106477
H. Hu, X. Li, Y. Zhang, C. Shang y S. Zhang, “Multi-objective location-routing model for hazardous material logistics with traffic restriction constraint in inter-city roads”, Comput. Ind. Eng., vol. 128, pp. 861-876, 2019. https://doi.org/10.1016/j.cie.2018.10.044 DOI: https://doi.org/10.1016/j.cie.2018.10.044
H. Farrokhi-Asl, A. Makui, A. Jabbarzadeh y F. Barzinpour, “Solving a multi-objective sustainable waste collection problem considering a new collection network” Int. J. Oper. Res., vol. 20, pp. 1977-2015, 2020. https://doi.org/10.1007/s12351-018-0415-0 DOI: https://doi.org/10.1007/s12351-018-0415-0
F. Delfani, A. Kazemi, S. M. Seyedhosseini y S. T. A. Niaki, “A green hazardous waste location-routing problem considering the risks associated with transportation and population”, Int. J. Eng. Trans. B Appl., vol. 33, no. 11, pp. 2272-2284, 2020. https://doi.org/10.5829/IJE.2020.33.11B.18 DOI: https://doi.org/10.5829/ije.2020.33.11b.18
M. Nikzamir y V. Baradaran, “A healthcare logistic network considering stochastic emission of contamination: Bi-objective model and solution algorithm”, Transp. Res. Part E Logist. Transp. Rev., vol. 142, 2020. https://doi.org/10.1016/j.tre.2020.102060 DOI: https://doi.org/10.1016/j.tre.2020.102060
A. Saeidi, S. Aghamohamadi-Bosjin y M. Rabbani, “An integrated model for management of hazardous waste in a smart city with a sustainable approach”, Environ. Dev. Sustain., vol. 23, pp. 10093-10118, 2020. https://doi.org/10.1007/s10668-020-01048-7 DOI: https://doi.org/10.1007/s10668-020-01048-7
Z. Ziaei y A. Jabbarzadeh, “A multi-objective robust optimization approach for green location-routing planning of multi-modal transportation systems under uncertainty”, J. Clean. Prod., vol. 291, 2021. https://doi.org/10.1016/j.jclepro.2020.125293 DOI: https://doi.org/10.1016/j.jclepro.2020.125293
D. Raeisi y S. Jafarzadeh Ghoushchi, “A robust fuzzy multi-objective location-routing problem for hazardous waste under uncertain conditions”, Appl. Intell., vol. 52, pp. 13435-13455, 2022. https://doi.org/10.1007/s10489-022-03334-5 DOI: https://doi.org/10.1007/s10489-022-03334-5
M. Rabbani, A. Nikoubin y H. Farrokhi-Asl, “Using modified metaheuristic algorithms to solve a hazardous waste collection problem considering workload balancing and service time windows”, Soft Comput., vol. 25, pp. 1885-1912, 2021. https://doi.org/10.1007/s00500-020-05261-4 DOI: https://doi.org/10.1007/s00500-020-05261-4
E. B. Tirkolaee, P. Abbasian y G.-W. Weber, “Sustainable fuzzy multi-trip location-routing problem for medical waste management during the COVID-19 outbreak”, Sci. Total Environ., vol. 756, 2021. https://doi.org/10.1016/j.scitotenv.2020.143607 DOI: https://doi.org/10.1016/j.scitotenv.2020.143607
J. Zhao, B. Wu y G. Y. Ke, “A bi-objective robust optimization approach for the management of infectious wastes with demand uncertainty during a pandemic”, J. Clean. Prod., vol. 314, 2021. https://doi.org/10.1016/j.jclepro.2021.127922 DOI: https://doi.org/10.1016/j.jclepro.2021.127922
M. Nikzamir, V. Baradaran y Y. Panahi, “Designing a logistic network for hospital waste management: A benders decomposition algorithm”, Environ. Eng. Manag. J., vol. 19, no. 11, pp. 1937-1956, 2021, [Online]. http://www.eemj.icpm.tuiasi.ro/pdfs/vol19/no11/2_603_Baradaran_19.pdf DOI: https://doi.org/10.30638/eemj.2020.184
K. Govindan, A. K. Nasr, P. Mostafazadeh y H. Mina, “Medical waste management during coronavirus disease 2019 (COVID-19) outbreak: A mathematical programming model”, Comput. Ind. Eng., vol. 162, 2021. https://doi.org/10.1016/j.cie.2021.107668 DOI: https://doi.org/10.1016/j.cie.2021.107668
G. Kordi, P. Hasanzadeh-Moghimi, M. M. Paydar y E. Asadi-Gangraj, “A multi-objective location-routing model for dental waste considering environmental factors”, Ann. Oper. Res., 2022. https://doi.org/10.1007/s10479-022-04794-1 DOI: https://doi.org/10.1007/s10479-022-04794-1
K. Govindan, S. Nosrati-Abarghooee, M. M. Nasiri y F. Jolai, “Green reverse logistics network design for medical waste management: A circular economy transition through case approach”, J. Environ. Manage., vol. 322, 2022. https://doi.org/10.1016/j.jenvman.2022.115888 DOI: https://doi.org/10.1016/j.jenvman.2022.115888
H. Farrokhi-Asl, R. Tavakkoli-Moghaddam, B. Asgarian y E. Sangari, “Metaheuristics for a bi-objective location-routing-problem in waste collection management”, J. Ind. Prod. Eng., vol. 34, no. 4, pp. 239-252, 2017. https://doi.org/10.1080/21681015.2016.1253619 DOI: https://doi.org/10.1080/21681015.2016.1253619
J.-B. Sheu, “Challenges of emergency logistics management”, Transp. Res. Part E Logist. Transp. Rev., vol. 43, no. 6, pp. 655-659, 2007. https://doi.org/10.1016/j.tre.2007.01.001 DOI: https://doi.org/10.1016/j.tre.2007.01.001
S. Rath y W. J. Gutjahr, “A math-heuristic for the warehouse location-routing problem in disaster relief”, Comput. Oper. Res., vol. 42, pp. 25-39, 2014. https://doi.org/10.1016/j.cor.2011.07.016 DOI: https://doi.org/10.1016/j.cor.2011.07.016
A. Nedjati, G. Izbirak y J. Arkat, “Bi-objective covering tour location routing problem with replenishment at intermediate depots: Formulation and meta-heuristics”, Comput. Ind. Eng., vol. 110, pp. 191-206, 2017. https://doi.org/10.1016/j.cie.2017.06.004 DOI: https://doi.org/10.1016/j.cie.2017.06.004
H. Adrang, A. Bozorgi-Amiri, K. Khalili-Damghani y R. Tavakkoli-Moghaddam, “Planning for medical emergency transportation vehicles during natural disasters”, J. Optim. Ind. Eng., vol. 13, no. 2, pp. 185-197, 2020. https://doi.org/10.22094/JOIE.2020.688.1455
S. Mohammadi, S. Avakh Darestani, B. Vahdani y A. Alinezhad, “A robust neutrosophic fuzzy-based approach to integrate reliable facility location and routing decisions for disaster relief under fairness and aftershocks concerns”, Comput. Ind. Eng., vol. 148, 2020. https://doi.org/10.1016/j.cie.2020.106734 DOI: https://doi.org/10.1016/j.cie.2020.106734
S. Long, D. Zhang, Y. Liang, S. Li y W. Chen, “Robust optimization of the multi-objective multi-period location-routing problem for epidemic logistics system with uncertain demand”, IEEE Access, vol. 9, pp. 151912-151930, 2021. https://doi.org/10.1109/ACCESS.2021.3125746 DOI: https://doi.org/10.1109/ACCESS.2021.3125746
S. Khanchehzarrin, M. Ghaebi Panah, N. Mahdavi-Amiri y S. Shiripour, “A bi-level multi-objective location-routing optimization model for disaster relief operations considering public donations”, Socioecon. Plann. Sci., vol. 80, 2022. https://doi.org/10.1016/j.seps.2021.101165 DOI: https://doi.org/10.1016/j.seps.2021.101165
H. Wang, L. Du y S. Ma, “Multi-objective open location-routing model with split delivery for optimized relief distribution in post-earthquake”, Transp. Res. Part E Logist. Transp. Rev., vol. 69, pp. 160-179, 2014. https://doi.org/10.1016/j.tre.2014.06.006 DOI: https://doi.org/10.1016/j.tre.2014.06.006
B. Vahdani, D. Veysmoradi, N. Shekari y S. M. Mousavi, “Multi-objective, multi-period location-routing model to distribute relief after earthquake by considering emergency roadway repair”, Neural Comput. Appl., vol. 30, no. 3, pp. 835-854, 2018. https://doi.org/10.1007/s00521-016-2696-7 DOI: https://doi.org/10.1007/s00521-016-2696-7
H. M. Saatchi, A. A. Khamseh y R. Tavakkoli-Moghaddam, “Solving a new bi-objective model for relief logistics in a humanitarian supply chain using bi-objective meta-heuristic algorithms”, Sci. Iran., vol. 28, no. 5, pp. 2948-2971, 2021. https://doi.org/10.24200/sci.2020.53823.3438 DOI: https://doi.org/10.24200/sci.2020.53823.3438
H. Beiki, S. M. Seyedhosseini, L. W. W. Mihardjo y S. M. Seyedaliakbar, “Multiobjective location-routing problem of relief commodities with reliability”, Environ. Sci. Pollut. Res., 2021. https://doi.org/10.1007/s11356-020-11891-w DOI: https://doi.org/10.1007/s11356-020-11891-w
M. Khorsi, S. K. Chaharsooghi, A. H. Kashan y A. Bozorgi-Amiri, “Pareto-based grouping meta-heuristic algorithm for humanitarian relief logistics with multistate network reliability”, OR Spectrum, vol. 43, pp. 327-365, 2021. https://doi.org/10.1007/s00291-021-00630-3 DOI: https://doi.org/10.1007/s00291-021-00630-3
P. Ghasemi, F. Goodarzian y A. Abraham, “A new humanitarian relief logistic network for multi-objective optimization under stochastic programming”, Appl. Intell., vol. 52, pp. 13729-13762, 2022. https://doi.org/10.1007/s10489-022-03776-x DOI: https://doi.org/10.1007/s10489-022-03776-x
A. Bozorgi-Amiri y M. Khorsi, “A dynamic multi-objective location-routing model for relief logistic planning under uncertainty on demand, travel time, and cost parameters”, Int. J. Adv. Manuf. Technol., vol. 85, pp. 1633-1648, 2016. https://doi.org/10.1007/s00170-015-7923-3 DOI: https://doi.org/10.1007/s00170-015-7923-3
B. Zhang, H. Li, S. Li y J. Peng, “Sustainable multi-depot emergency facilities location-routing problem with uncertain information”, Appl. Math. Comput., vol. 333, pp. 506-520, 2018. https://doi.org/10.1016/j.amc.2018.03.071 DOI: https://doi.org/10.1016/j.amc.2018.03.071
L. Shen, F. Tao, Y. Shi y R. Qin, “Optimization of location‐routing problem in emergency logistics considering carbon emissions”, Int. J. Environ. Res. Public Health, vol. 16, no. 16, 2019. https://doi.org/10.3390/ijerph16162982 DOI: https://doi.org/10.3390/ijerph16162982
A. M. Fathollahi-Fard, K. Govindan, M. Hajiaghaei-Keshteli y A. Ahmadi, “A green home health care supply chain: New modified simulated annealing algorithms”, J. Clean. Prod., vol. 240, 2019. https://doi.org/10.1016/j.jclepro.2019.118200 DOI: https://doi.org/10.1016/j.jclepro.2019.118200
E. M. Toro, J. F. Franco, M. G. Echeverri, F. G. Guimarães y R. A. Gallego Rendón, “Green open location-routing problem considering economic and environmental costs”, Int. J. Ind. Eng. Comput., vol. 8, pp. 203-216, 2016. https://doi.org/10.5267/j.ijiec.2016.10.001 DOI: https://doi.org/10.5267/j.ijiec.2016.10.001
K. Alamatsaz, A. Ahmadi y S. M. J. Mirzapour Al-e-hashem, “A multiobjective model for the green capacitated location-routing problem considering drivers’ satisfaction and time window with uncertain demand”, Environ. Sci. Pollut. Res., vol. 29, pp. 5052-5071, 2022. https://doi.org/10.1007/s11356-021-15907-x DOI: https://doi.org/10.1007/s11356-021-15907-x
A. Heidari, D. M. Imani, M. Khalilzadeh y M. Sarbazvatan, “Green two-echelon closed and open location-routing problem: application of NSGA-II and MOGWO metaheuristic approaches”, Environ. Dev. Sustain., 2022. https://doi.org/10.1007/s10668-022-02429-w DOI: https://doi.org/10.1007/s10668-022-02429-w
J. Zarean Dowlat Abadi, M. Iraj, E. Bagheri, Z. Rabieipakdeh y M. R. Dehghani Tafti, “A multiobjective multiproduct mathematical modeling for green supply chain considering location-routing decisions”, Math. Probl. Eng., 2022. https://doi.org/10.1155/2022/7009338 DOI: https://doi.org/10.1155/2022/7009338
L. F. Galindres, F. G. Guimarães y R. A. Gallego-Rendón, “Multi-objective sustainable capacitated location routing problem formulation in sustainable supply-chain management”, Eng. Optim., 2021. https://doi.org/10.1080/0305215X.2021.2014476 DOI: https://doi.org/10.1080/0305215X.2021.2014476
H. X. Zhang y C. M. Zhang, “Multiobjective green time-dependent location-routing problem and algorithms”, Adv. Oper. Res., 2022. https://doi.org/10.1155/2022/1811689 DOI: https://doi.org/10.1155/2022/1811689
I. Meidute-Kavaliauskiene, N. Sütütemiz, F. Yıldırım, S. Ghorbani y R. Činčikaitė, “Optimizing multi cross-docking systems with a multi-objective green location routing problem considering carbon emission and energy consumption”, Energies, vol. 15, no. 4, 2022. DOI: https://doi.org/10.3390/en15041530
H.-K. Chen, C.-F. Hsueh y M.-S. Chang, “Production scheduling and vehicle routing with time windows for perishable food products”, Comput. Oper. Res., vol. 36, no. 7, pp. 2311-2319, 2009. https://doi.org/10.1016/j.cor.2008.09.010 DOI: https://doi.org/10.1016/j.cor.2008.09.010
B. Aghaei Fishani, A. Mahmoodirad, S. Niroomand y M. Fallah, “Multi-objective location-allocation-routing problem of perishable multi-product supply chain with direct shipment and open routing possibilities under sustainability”, Concurr. Comput. Pract. Exp., vol. 34, no. 11, 2022. https://doi.org/10.1002/cpe.6860 DOI: https://doi.org/10.1002/cpe.6860
K. Khalili-Damghani, A.-R. Abtahi y A. Ghasemi, “A new bi-objective location-routing problem for distribution of perishable products: evolutionary computation approach”, J. Math. Model. Algorithms Oper. Res., vol. 14, pp. 287-312, 2015. https://doi.org/10.1007/s10852-015-9274-3 DOI: https://doi.org/10.1007/s10852-015-9274-3
P. Li, H. Lan y F. Saldanha-Da-Gama, “A Bi-objective capacitated location-routing problem for multiple perishable commodities”, IEEE Access, vol. 7, pp. 136729-136742, 2019. https://doi.org/10.1109/ACCESS.2019.2941363 DOI: https://doi.org/10.1109/ACCESS.2019.2941363
I. Meidute-Kavaliauskiene, F. Yıldırım, S. Ghorbani y R. Činčikaitė, “The design of a multi-period and multi-echelon perishable goods supply network under uncertainty”, Sustain., vol. 14, no. 4, 2022. https://doi.org/10.3390/su14042472 DOI: https://doi.org/10.3390/su14042472
F. Navazi, A. Sedaghat y R. Tavakkoli-Moghaddam, “A new sustainable location-routing problem with simultaneous pickup and delivery by two-compartment vehicles for a perishable product considering circular economy”, IFAC-PapersOnLine, vol. 52, no. 13, pp. 790-795, 2019. https://doi.org/10.1016/j.ifacol.2019.11.212 DOI: https://doi.org/10.1016/j.ifacol.2019.11.212
L. Leng, J. Zhang, C. Zhang, Y. Zhao, W. Wang y G. Li, “Decomposition-based hyperheuristic approaches for the bi-objective cold chain considering environmental effects”, Comput. Oper. Res., vol. 123, 2020. https://doi.org/10.1016/j.cor.2020.105043 DOI: https://doi.org/10.1016/j.cor.2020.105043
Z. Wang, L. Leng, S. Wang, G. Li y Y. Zhao, “A hyperheuristic approach for location-routing problem of cold chain logistics considering fuel consumption”, Comput. Intell. Neurosci., 2020. https://doi.org/10.1155/2020/8395754 DOI: https://doi.org/10.1155/2020/8395754
L. Leng, J. Zhang, C. Zhang, Y. Zhao, W. Wang y G. Li, “A novel bi-objective model of cold chain logistics considering location-routing decision and environmental effects”, PLoS One, vol. 15, no. 4, 2020. https://doi.org/10.1371/journal.pone.0230867 DOI: https://doi.org/10.1371/journal.pone.0230867
L. Leng, C. Zhang, Y. Zhao, W. Wang, J. Zhang y G. Li, “Biobjective low-carbon location-routing problem for cold chain logistics: Formulation and heuristic approaches”, J. Clean. Prod., vol. 273, 2020. https://doi.org/10.1016/j.jclepro.2020.122801 DOI: https://doi.org/10.1016/j.jclepro.2020.122801
I. A. Martínez-Salazar, J. Molina, F. Ángel-Bello, T. Gómez y R. Caballero, “Solving a bi-objective transportation location routing problem by metaheuristic algorithms”, Eur. J. Oper. Res., vol. 234, no. 1, pp. 25-36, 2014. https://doi.org/10.1016/j.ejor.2013.09.008 DOI: https://doi.org/10.1016/j.ejor.2013.09.008
M. Rabbani, F. Navazi, H. Farrokhi-Asl y M. H. Balali, “A sustainable transportation-location-routing problem with soft time windows for distribution systems”, Uncertain Supply Chain Manag., vol. 6, pp. 229-254, 2018. https://doi.org/10.5267/j.uscm.2017.12.002 DOI: https://doi.org/10.5267/j.uscm.2017.12.002
Y. Wang, K. Assogba, Y. Liu, X. Ma, M. Xu y Y. Wang, “Two-echelon location-routing optimization with time windows based on customer clustering”, Expert Syst. Appl., vol. 104, pp. 244-260, 2018. https://doi.org/10.1016/j.eswa.2018.03.018 DOI: https://doi.org/10.1016/j.eswa.2018.03.018
J. Du, X. Wang, X. Wu, F. Zhou y L. Zhou, “Multi-objective optimization for two-echelon joint delivery location routing problem considering carbon emission under online shopping”, Transp. Lett., vol. 00, no. 00, pp. 1-19, 2022. https://doi.org/10.1080/19427867.2022.2112857 DOI: https://doi.org/10.1080/19427867.2022.2112857
R. Tavakkoli-Moghaddam, A. Makui y Z. Mazloomi, “A new integrated mathematical model for a bi-objective multi-depot location-routing problem solved by a multi-objective scatter search algorithm”, J. Manuf. Syst., vol. 29, no. 2-3, pp. 111-119, 2010. https://doi.org/10.1016/j.jmsy.2010.11.005 DOI: https://doi.org/10.1016/j.jmsy.2010.11.005
J. Liu y V. Kachitvichyanukul, “A Pareto-based particle swarm optimization algorithm for multi-objective location routing problem”, Int. J. Ind. Eng. Theory Appl. Pract., vol. 22, no. 3, pp. 314-329, 2015. https://doi.org/10.23055/ijietap.2015.22.3.1553
S. T. W. Mara, A. M. Sri Asih y R. J. Kuo, “Solving a multi-objective location-routing problem with minimum cost and total time balance”, Int. J. Inf. Manag. Sci., vol. 30, no. 3, pp. 249-269, 2019. https://doi.org/10.6186/IJIMS.201909_30(3).0004
N. Ghaffari-Nasab, M. S. Jabalameli, M. B. Aryanezhad y A. Makui, “Modeling and solving the bi-objective capacitated location-routing problem with probabilistic travel times”, Int. J. Adv. Manuf. Technol., vol. 67, pp. 2007-2019, 2013. https://doi.org/10.1007/s00170-012-4627-9 DOI: https://doi.org/10.1007/s00170-012-4627-9
L. Leng, Y. Zhao, J. Zhang y C. Zhang, “An effective approach for the multiobjective regional low-carbon location-routing problem”, Int. J. Environ. Res. Public Health, vol. 16, no. 11, 2019. https://doi.org/10.3390/ijerph16112064 DOI: https://doi.org/10.3390/ijerph16112064
A. M. Golmohammadi, S. A. Bonab y A. Parishani, “A multi-objective location routing problem using imperialist competitive algorithm”, Int. J. Ind. Eng. Comput., vol. 7, pp. 481-488, 2016. https://doi.org/10.5267/j.ijiec.2015.12.002 DOI: https://doi.org/10.5267/j.ijiec.2015.12.002
E. J. Mamaghani y S. Davari, “The bi-objective periodic closed loop network design problem”, Expert Syst. Appl., vol. 144, art. 113068, 2020. https://doi.org/10.1016/j.eswa.2019.113068 DOI: https://doi.org/10.1016/j.eswa.2019.113068
X. Wang, F. Yang y D. Lu, “Multi-objective location-routing problem with simultaneous pickup and delivery for urban distribution”, J. Intell. Fuzzy Syst., vol. 35, no. 4, pp. 3987-4000, 2018. https://doi.org/10.3233/JIFS-169721 DOI: https://doi.org/10.3233/JIFS-169721
S. Validi, A. Bhattacharya y P. J. Byrne “An evaluation of three DoE-guided meta-heuristic-based solution methods for a three-echelon sustainable distribution network”, Ann. Oper. Res., vol. 296, no. 1, pp. 421-469, 2021. htttps://doi.org/10.1007/s10479-020-03746-x DOI: https://doi.org/10.1007/s10479-020-03746-x
S. Validi, A. Bhattacharya y P. J. Byrne, “Sustainable distribution system design: a two-phase DoE-guided meta-heuristic solution approach for a three-echelon bi-objective AHP-integrated location-routing model”, Ann. Oper. Res., vol. 290, pp. 191-222, 2020. https://doi.org/10.1007/s10479-018-2887-y DOI: https://doi.org/10.1007/s10479-018-2887-y
C. Chen, R. Qiu y X. Hu, “The location-routing problem with full truckloads in low-carbon supply chain network designing”, Math. Probl. Eng., 2018. https://doi.org/10.1155/2018/6315631 DOI: https://doi.org/10.1155/2018/6315631
V. R. Ghezavati y M. Beigi, “Solving a bi-objective mathematical model for location-routing problem with time windows in multi-echelon reverse logistics using metaheuristic procedure”, J. Ind. Eng. Int., vol. 12, pp. 469-483, 2016. https://doi.org/10.1007/s40092-016-0154-x DOI: https://doi.org/10.1007/s40092-016-0154-x
N. Eskandari, R. Tavakkoli-Moghaddam, P. Memari y F. Jolai, “A new mathematical model of a waste collection problem with social issues”, 47th International Conference on Computers & Industrial Engineering (CIE 47), 2017
M. Rabbani, M. Mokhtarzadeh y H. Farrokhi-Asl, “A new mathematical model for designing a municipal solid waste system considering environmentally issues”, Int. J. Supply Oper. Manag., vol. 5, no. 3, pp. 234-255, 2018. https://doi.org/10.22034/2018.3.4
Y. Wang, Y. Sun, X. Guan y Y. Guo, “Two-echelon location-routing problem with time windows and transportation resource sharing”, J. Adv. Transp., 2021. https://doi.org/10.1155/2021/8280686 DOI: https://doi.org/10.1155/2021/8280686
Y. Wang, Y. Sun, X. Guan, J. Fan, M. Xu y H. Wang, “Two-echelon multi-period location routing problem with shared transportation resource”, Knowledge-Based Syst., vol. 226, 2021. https://doi.org/10.1016/j.knosys.2021.107168 DOI: https://doi.org/10.1016/j.knosys.2021.107168
R. Kian et al., “Logistics planning of cash transfer to Syrian refugees in Turkey”, Eur. J. Oper. Res., vol. 296, no. 3, pp. 1007-1024, 2022. https://doi.org/10.1016/j.ejor.2021.04.054 DOI: https://doi.org/10.1016/j.ejor.2021.04.054
L. Yang, J. Guo, C. Zhang, P. Wan y H. Li, “Optimization of location-routing for the waste household appliances recycling logistics under the uncertain condition”, Teh. Vjesn., vol. 29, no. 1, pp. 127-138, 2022. https://doi.org/10.17559/TV-20210623085943 DOI: https://doi.org/10.17559/TV-20210623085943
Y. Ma, W. Zhang, C. Feng, B. Lev y Z. Li, “A bi-level multi-objective location-routing model for municipal waste management with obnoxious effects”, Waste Manag., vol. 135, pp. 109-121, 2021. https://doi.org/10.1016/j.wasman.2021.08.034 DOI: https://doi.org/10.1016/j.wasman.2021.08.034
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Recibido: 27 de octubre de 2021; Revisión recibida: 29 de septiembre de 2022; Aceptado: 11 de noviembre de 2022
Resumen
Contexto:
El problema de localización y ruteo constituye una de las principales temáticas en el área de logística e investigación de operaciones con un enfoque hacia la minimización de los costos totales del sistema. Sin embargo, en la gestión de la cadena de suministro, que actualmente presenta una tendencia hacia la sostenibilidad, la mayoría de las decisiones involucra la optimización simultánea de diversos objetivos, incluyendo perspectivas económicas, sociales y ambientales, de lo cual surge el problema de localización y ruteo con múltiples objetivos.
Método:
Se realiza una revisión sistemática de la literatura sobre el problema de localización y ruteo con múltiples objetivos, consultando las bases de datos Scopus y Web of Science. De acuerdo con unos criterios de selección específicos, se identifican 99 artículos científicos asociados a la temática durante el periodo comprendido entre 1989 y 2022, los cuales se clasifican según el tipo de aplicación.
Resultados:
Se describen las características más importantes para cada una de las aplicaciones del problema de localización y ruteo con múltiples objetivos en la literatura y se realiza una revisión de las investigaciones según sus objetivos de estudio y métodos de solución, para finalmente identificar las oportunidades de investigación principales.
Conclusiones:
En primer lugar, la mayoría de los estudios sobre el problema de localización y ruteo multiobjetivo han estudiado la gestión de residuos, la distribución de elementos de socorro, los productos perecederos, el problema de localización y ruteo verde, la cadena de frío y la distribución de bebidas. El objetivo de optimización de mayor implementación es la minimización de costos, combinado con otros objetivos: minimización de riesgos, impactos ambientales, minimización de tiempo, maximización de la satisfacción del cliente, balance de carga de trabajo y confiabilidad rutas. Por otra parte, se aplican métodos exactos y aproximados multiobjetivo para dar solución al problema, siendo los algoritmos evolutivos los más usados para modelos de mayor complejidad. Finalmente, las investigaciones actuales están orientadas al desarrollo de modelos bajo condiciones de incertidumbre y estocásticos, múltiples periodos, ventanas de tiempo, múltiples escalones y flota heterogénea.
Palabras clave:
logística, optimización multiobjetivo, problema de localización y ruteo, metaheurísticas.Abstract
Context:
The location and routing problem is one of the main issues in logistics and operations research oriented to minimize the system's total costs. However, in the supply chain management trend towards sustainability, most decisions introduce the optimization of several objectives simultaneously, including economic, social, and environmental perspectives, from which the multi-objective location and routing problem arises.
Method:
This study reviews 99 scientific articles about the multi-objective location and routing problem published between 1989 and 2022 in Scopus and Web of Science databases. The papers are selected according to specific criteria and classified based on their application.
Results:
This paper describes the most important characteristics of each application of the multi-objective location and routing problem in the literature. It reviews the articles according to their study objectives and solution methods to identify future research opportunities.
Conclusions:
First, most papers on the multi-objective location and routing problem have studied waste management, relief distribution, perishable products, green location and routing problems, cold chain, and beverage distribution. Cost minimization is the most implemented optimization objective, in combination with other goals: risk minimization, environmental impact, time minimization, customer satisfaction maximization, workload balance, and route reliability. Additionally, the problem is solved using exact and approximate multi-objective methods, with evolutionary algorithms being the most suitable for complex models. Finally, current research is oriented toward developing models under uncertainty and stochastic problems, multiple periods, time windows, multiple echelons, and heterogeneous vehicle fleets.
Keywords:
logistics, multi-objective optimization, location and routing problem, metaheuristics..Introducción
El problema de localización y ruteo, o LRP (location routing problem), como su nombre lo indica, considera simultáneamente las decisiones sobre la ubicación de instalaciones y el diseño de las rutas que serán asignadas a una determinada flota de vehículos. El objetivo de estudio principal de este problema corresponde a la minimización de los costos totales del sistema 1. Sin embargo, en la actualidad, el interés por el desarrollo de cadenas de suministro sostenibles ha planteado la combinación de componentes económicos, sociales y ambientales para dar solución al LRP 2. Lo anterior convierte el problema en un modelo de optimización multiobjetivo. Teniendo en cuenta la necesidad de determinar la localización óptima de las instalaciones, la distribución de las rutas de entrega o recolección y, a su vez, optimizar diversos objetivos, se requiere la formulación de modelos matemáticos complejos resueltos con técnicas de solución robustas.
Diversos autores han estudiado los avances en la literatura del LRP para analizar sus características y variantes. 3 plantean un estado del arte que define los principales conceptos del problema con un enfoque hacia los métodos utilizados para su solución desde los inicios hasta el año 2006. Más adelante, 4 proponen una taxonomía por niveles en donde la primera fase se centra en las características del LRP y la segunda en las estrategias de solución y el número de objetivos de optimización. Este trabajo identifica por primera vez la necesidad de investigar el LRP multiobjetivo con mayor detalle. Por otro lado, 5 extienden el estudio presentado por 3 hasta el año 2014, evaluando las nuevas extensiones de esta línea de investigación. De igual manera, 6 realizan una revisión que detalla las características de cada una de las variantes del problema. Estos dos últimos estudios, de manera similar, analizan los avances en formulaciones multiperiodo, multiescalón, multiobjetivo, problemas estocásticos, inventarios, metodologías y algoritmos novedosos. Recientemente, 7 actualizaron la literatura sobre el LRP, cuya conclusión se enfoca en el crecimiento exponencial en la publicación de artículos que formulan modelos con múltiples objetivos como un esfuerzo para involucrar el concepto de sostenibilidad en la logística.
A pesar de que estos estudios analizan el LRP multiobjetivo, la investigación en esta área debe abordarse detalladamente. Por esta razón, este artículo presenta una revisión sistemática de la literatura que permite analizar la intensidad de la investigación sobre LRP con múltiples objetivos a lo largo de los años. Los propósitos del estudio incluyen: (a) determinar las principales aplicaciones del problema, (b) definir los objetivos de optimización utilizados de acuerdo con su aplicación, (c) identificar los métodos implementados para dar solución al LRP multiobjetivo y, por último, (d) evaluar las oportunidades de investigación que se presentan en esta temática.
El contenido de este artículo se organiza de la siguiente manera: la segunda sección describe la metodología de investigación; la tercera sección presenta la definición del LRP; el cuarto apartado expone hallazgos bibliográficos, aplicaciones, objetivos de estudio y métodos de solución para el problema multiobjetivo; la quinta sección plantea la discusión de resultados; y, finalmente, la secciones sexta y séptima detallan oportunidades de investigación y conclusiones.
Metodología
Para la realización de este artículo, se llevó a cabo una revisión sistemática de literatura enfocada en el problema de localización y ruteo con múltiples objetivos. La metodología de investigación inicia con la definición de los términos de búsqueda que incluyen las palabras clave “location” y “routing”. Por otra parte, considerando que la investigación aborda el problema multiobjetivo, se limita la exploración a artículos que incorporan las expresiones “multi-objective”, “multiobjective” o “bi-objective”. Los términos anteriores permiten obtener la ecuación de búsqueda que es aplicada en las bases de datos Scopus y Web of Science. Posteriormente, se aplican, como criterio de filtración para la selección de documentos, artículos de carácter científico únicamente en idioma inglés, sin considerar una ventana de tiempo, con el fin de identificar las investigaciones iniciales asociadas a esta temática hasta la fecha actual, obteniendo 334 artículos. Estos documentos son revisados de acuerdo con su título y resumen, con el propósito de seleccionar únicamente aquellos artículos que se encuentren dentro de los parámetros definidos para el estudio, considerando los siguientes criterios de exclusión:
-
Artículos en los cuales la formulación del problema se lleve a cabo por etapas, es decir, primero se resuelva el problema de localización de instalaciones y posteriormente el problema de ruteo de vehículos.
-
Estudios en los que se implemente el problema de localización, ruteo e inventarios o ILRP (inventory location-routing problem), debido a que el enfoque del estudio se relaciona solo con las decisiones de localización y enrutamiento.
-
Documentos en los cuales se desarrollen modelos para sistemas de transporte diferentes al terrestre, por ejemplo, marítimo, férreo y aéreo.
-
Artículos con modelos matemáticos mono-objetivo y aquellos que impliquen solo decisiones de localización o solo de ruteo de vehículos.
-
Artículos que incluyen los términos clave, pero no están asociados a la temática.
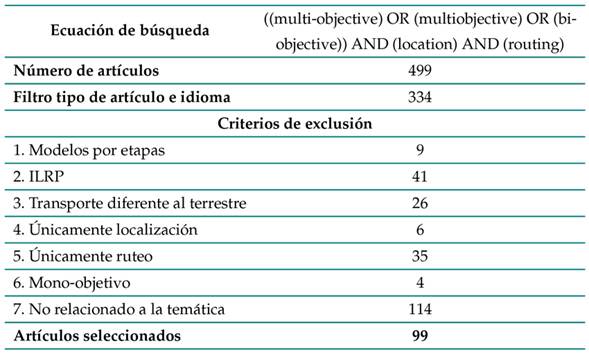
De acuerdo con los criterios de exclusión, se consolida un total de 99 documentos sobre el problema de localización y ruteo multiobjetivo para ser analizados. La Tabla I detalla la metodología descrita en esta sección. Adicionalmente, con el objetivo de evaluar la actividad literaria de la temática de investigación, se realiza un análisis bibliométrico para los artículos encontrados, el cual permite estimar el impacto científico y proporciona información respecto a la evolución y la visibilidad de la línea de conocimiento de interés 8. Finalmente, se efectúa un análisis de contenido de los documentos seleccionados, planteando la estructura de la revisión según los siguientes enfoques: aplicaciones, objetivos de estudio, métodos de solución y tendencias de investigación para la formulación de modelos matemáticos asociados al problema de localización y ruteo multiobjetivo.
Tabla I: Proceso de selección de artículos
Problema de localización y ruteo
El problema de localización y ruteo constituye una de las temáticas de mayor interés en el área de logística e investigación de operaciones 9. En el LRP, las decisiones de localización y el diseño de las rutas de distribución son consideradas simultáneamente. De este modo, el LRP corresponde a una combinación del problema de localización de instalaciones o FLP (facility location problem) y el problema de ruteo de vehículos o VRP (vehicle routing problem), integrando las decisiones estratégicas, tácticas y operativas asociadas a estos problemas 10. El FLP pertenece al nivel estratégico, en el cual las decisiones se tienen en cuenta por un periodo de largo plazo, mientras que el VRP implica un nivel de decisión táctico u operativo, asociado a periodos cortos de tiempo 11.
Los primeros investigadores que cuestionaron la independencia de estos dos tipos de decisiones fueron 12 y 13. Este último asegura en su estudio que la ubicación de fábricas y puntos de suministro que atienden a clientes distribuidos en una red ejerce un impacto en los costos de transporte. Sin embargo, fue hasta 1989 cuando 10 publicaron un estudio en el cual evalúan el efecto de ignorar las decisiones de enrutamiento al ubicar depósitos, demostrando así que la mejor solución luego de la etapa de localización de instalaciones no genera necesariamente la solución de menor costo cuando se lleva a cabo el proceso de ruteo. El problema de localización y ruteo clásico consiste en abrir una serie de instalaciones, tales como plantas de producción, almacenes o centros de distribución, dentro de un conjunto de localizaciones potenciales, asignando clientes a estas instalaciones y seleccionando las rutas para una flota de vehículos determinada 14. Lo anterior se realiza con el objetivo de garantizar la minimización de los costos de abrir instalaciones y el costo total de las rutas establecidas. De este modo, el LRP busca responder dos preguntas específicas:
- ¿Qué instalaciones deben abrirse dentro de un conjunto finito o infinito de posibles opciones establecidas?
- ¿Qué rutas de vehículos deben construirse para atender un conjunto de clientes y en qué secuencia un vehículo de una flota determinada debe visitar cada uno de ellos? 6.
Con el fin de acercar el problema a condiciones de la vida real, la mayoría de los estudios abordan el LRP con restricciones de capacidad para los depósitos y vehículos, lo cual se denomina problema de localización y ruteo capacitado o CLRP (capacitated location-routing problem) 5 , 7 definen el CLRP como una red de nodos V = I ∪ J, donde I = {1, 2, . . . , m} hace referencia al conjunto potencial de depósitos con capacidad Wi , y J = {1, 2, . . . , n} está relacionado con el grupo de clientes que deben ser atendidos, los cuales requieren una demanda dj . Existe una flota de vehículos homogénea K con una capacidad Q y un costo fijo F que se asigna por cada vehículo usado. La apertura de cada depósito representa un costo Oi y la asignación de una determinada ruta equivale a un costo de viaje cij . La solución del problema consiste en determinar qué depósitos I deben abrirse, asignando a cada cliente J un depósito abierto y construyendo rutas de vehículos para cada depósito y sus clientes, de acuerdo con las siguientes restricciones:
-
La capacidad de un depósito abierto no puede ser excedida.
-
Todas las rutas deben iniciar y finalizar su recorrido en el mismo depósito.
-
Cada vehículo realiza, como máximo, un viaje.
-
No se permiten entregas divididas, es decir, cada cliente es atendido por un solo vehículo.
-
La capacidad de un vehículo no puede ser excedida.
Adicionalmente, diferentes variantes del problema se pueden encontrar en la literatura, tales como LRP con recogida y entrega simultánea, LRP con ventanas de tiempo, LRP con flota de vehículos heterogénea, LRP multi-escalón y LRP con demandas estocásticas 15.
Problema de localización y ruteo con múltiples objetivos
Los problemas de optimización con múltiples objetivos involucran un proceso computacional de mayor complejidad que aquel en el cual se implementa un solo objetivo de estudio. Esto, debido a que no es posible generar una solución que optimice todos los objetivos del problema simultáneamente, los cuales, por lo general, están en conflicto entre sí. Para ayudar a la toma de decisiones en este tipo de casos, se genera un conjunto de soluciones que, al intentar mejorar un objetivo, afectan a los demás. Estas se denominan soluciones óptimas de Pareto 16
Tal como se mencionó en la sección anterior, el objetivo económico es usualmente considerado en el LRP. Sin embargo, en la gestión de la cadena de suministro y los procesos de distribución, la mayoría de decisiones involucra la optimización de diversos objetivos conjuntamente 17. Por consiguiente, las investigaciones recientes han planteado otros objetivos adicionales a la minimización de costos, tales como la minimización de riesgos, la minimización de impactos ambientales, el balance de carga de trabajo y la maximización de la satisfacción del cliente. Lo anterior se traduce en un elevado crecimiento en el número de publicaciones asociadas al problema de localización y ruteo multiobjetivo a lo largo de los años, tal como se observa en la Fig. 1 (resultado del análisis bibliométrico).
Figura 1: Proceso de obtención de los residuos para mezcla
Los primeros estudios fueron publicados en el año 1989 por 18 y en 1991 por 19 y 20. Sin embargo, la mayoría de las publicaciones en la temática empieza a realizarse a partir del año 2014, cuando se evidencia un crecimiento continuo de la literatura hasta la actualidad, representado en el 86,9 % de los documentos analizados. Por el contrario, en el intervalo de tiempo entre 1991 y 2014 se presenta poco desarrollo científico. No obstante, durante este periodo se destacan las investigaciones con mayor impacto, considerando el número de citaciones. La investigación realizada por 21 ocupa el primer lugar con 334 citaciones, seguido de 20 con 196 citaciones y de 22, cuyo trabajo cuenta con 191 citaciones. Con respecto a la contribución literaria por país, la nación con la productividad científica más alta es Irán, cuya línea de investigación principal se enfoca en problemas de optimización para la gestión de residuos peligrosos; en segundo lugar, está China, seguida de Estados Unidos, el Reino Unido y Turquía.
A continuación, se expone una recopilación de los resultados obtenidos de la revisión sistemática realizada sobre el problema de localización y ruteo multiobjetivo en referencia a sus principales aplicaciones, objetivos de estudio y métodos de solución.
Aplicaciones
El enfoque de la presente revisión implica en primera instancia la categorización de los documentos seleccionados según su aplicación. La Tabla II permite observar la distribución porcentual de los 99 documentos analizados de acuerdo con la red de distribución o cadena de suministro para la cual se desarrolla el modelo matemático. El problema de localización y ruteo multiobjetivo es abordado en la literatura principalmente para las siguientes aplicaciones: recolección de residuos (waste collection), distribución de elementos de socorro (relief distribution), productos perecederos (perishable products), el problema de localización y ruteo verde (GLRP, green location routing problem), cadena de frío (cold chain) y distribución de bebidas (beverage distribution). En menor medida, se desarrollan trabajos asociados a la distribución de neumáticos (tire supply chain) y ventas en línea (online shopping). Adicionalmente, se identifican algunas investigaciones que no se atribuyen a ninguna área de aplicación específica, pero que constituyen problemas relacionados con la temática, cuyas formulaciones matemáticas pueden ajustarse a cadenas de suministro reales.
Tabla II: Porcentaje de artículos científicos por aplicación

Tal como se observa, existe una alta incidencia en la implementación del GLRP multiobjetivo a las características de los procesos relacionados con la recolección de residuos, teniendo en cuenta que el 44 % de los artículos están enfocados en este sector. A su vez, del porcentaje de publicaciones sobre recolección de residuos, el 84 % de las mismas hacen referencia a estudios vinculados a la gestión de residuos peligrosos (hazardous waste management).
Objetivos de estudio
A continuación, se describen los principales hallazgos respecto a las aplicaciones relacionadas con la temática de investigación, con énfasis en los objetivos de estudio del problema y resaltando algunas características del sistema.
Recolección de residuos
El proceso de transporte de residuos inicia con la etapa de recolección, que consiste en retirar los residuos del lugar de almacenamiento para luego trasladarlos a su destino final. Sin embargo, además de construir las rutas de recolección, para el diseño de un adecuado sistema de distribución, es necesario especificar la ubicación de instalaciones, tales como depósitos, almacenes, puntos de eliminación y centros de tratamiento de residuos 14. Con el propósito de garantizar la viabilidad técnica y económica, así como la seguridad para las personas y el medio ambiente durante los procesos de recolección de los residuos, diversos autores han implementado modelos de optimización para realizar una selección cuidadosa de las instalaciones de procesamiento o eliminación de estos desechos y, del mismo modo, determinar las rutas de transporte que generen el menor riesgo 23. Como se mencionó anteriormente, la gestión de residuos peligrosos constituye la línea de investigación más importante en el área.
Se conoce como residuos peligrosos a aquellos desechos que poseen propiedades como toxicidad, corrosividad, inflamabilidad y reactividad química, los cuales presentan una amenaza tanto para el ser humano como para el medio ambiente 22. Debido al peligro asociado a estos desechos, se requiere un control adecuado para su recolección, transporte, tratamiento, reciclaje y eliminación. El problema de localización y ruteo con múltiples objetivos para los residuos peligrosos ha tenido dos enfoques de optimización principales: minimización de costos y minimización de riesgo. Este último objetivo se caracteriza por ser abordado por los investigadores desde diferentes puntos de vista, tales como riesgo de localización, riesgo de transporte y equidad de riesgo. El concepto de riesgo asociado a las localizaciones o instalaciones está relacionado con la cantidad de residuos depositados en cada sitio y el número de personas dentro de una distancia cercana al punto, mientras que el riesgo de transporte vincula linealmente la cantidad de residuos transportados con el número de personas expuestas a lo largo de la ruta 24. Por su parte, la equidad de riesgo constituye una medida que se calcula como el riesgo máximo de la zona por unidad de población 25 y busca garantizar que el riesgo se distribuya uniformemente 26.
El primer trabajo publicado en esta temática fue desarrollado en el año 1989. En lugar de considerar el objetivo económico, plantea la elaboración de un sistema para la minimización de tres objetivos: riesgo de localización, riesgo de transporte y tiempo de viaje, con el propósito de establecer la ubicación de los sitios de disposición y las diferentes rutas para la recolección de los residuos 18. La mayoría de los estudios posteriores ha considerado el factor de los costos como objetivo principal en la formulación matemática. Los conceptos mencionados previamente en relación con el riesgo fueron implementados en los trabajos realizados por 20, 25 y 26. No obstante, estas investigaciones se caracterizan por el hecho de que sus modelos utilizan un solo tipo de residuos peligrosos, lo cual no es usual para la recolección de estos desechos.
19 desarrollan el primer modelo multiproducto, el cual considera diferentes clases de residuos peligrosos y múltiples tipos de tecnologías para el tratamiento de estos, con los siguientes objetivos de estudio: minimización del riesgo total (riesgo de transporte y riesgo de localización), minimización de los costos y maximización de la equidad del riesgo. Este último objetivo fue aplicado también por 27, pero dejó de implementarse debido a que, con el fin de distribuir uniformemente el riesgo, se aumentaba el número de instalaciones seleccionadas con una tasa de utilización más baja 22. Un aporte importante sobre esta temática fue desarrollado por 22, quienes consideran por primera vez condiciones que habían sido ignoradas en los estudios anteriores, como es el caso del tipo de tecnología utilizada en cada sitio de tratamiento y la compatibilidad que debe existir entre los residuos y dicha tecnología. Durante la época se publicaron investigaciones con énfasis en residuos sólidos de animales 28, riesgos para instalaciones fijas 29 y contribuciones bajo condiciones de incertidumbre 30.
En el año 2013, 31 plantea un diseño para la red de distribución considerado como uno de los más completos de la literatura, el cual incluye generación, tratamiento, reciclaje, nodos de disposición y rutas entre ellos, con el propósito de minimizar el costo total, el riesgo de transporte y el riesgo al que se expone la población cercana a los sitios de disposición de residuos. A partir de entonces aumentan las investigaciones relacionadas con esta temática, con el desarrollo de los estudios propuestos por 32)(35 y 23. Posteriormente, 24 desarrollan una formulación matemática que asocia por primera vez una flota de vehículos heterogénea e imponen restricciones vinculadas al concepto de compatibilidad entre residuos, los cuales, por sus características, no deben recolectarse conjuntamente. Adicional a esto, una brecha no abordada en la literatura fue contemplada por 36, quienes evaluaron horizontes de planificación de periodos múltiples en sus modelos.
Algunos otros trabajos han sido publicados en los últimos tiempos para modelar problemas orientados a la minimización de costos y riesgo con características como la consideración del consumo de combustible y la depreciación del vehículo en la función de costos 37, la presencia de incertidumbres 38, 39, modelos matemáticos de dos escalones 40 y aplicaciones a sectores específicos que generan residuos peligrosos, como lo es la industria automotriz 9. En 2019 se desarrolla un modelo matemático que, adicional al aspecto económico y de riesgo, introduce la maximización de la satisfacción del cliente como tercera función objetivo a optimizar 41. Desde otro punto de vista, algunas investigaciones recientes han contemplado temáticas medioambientales dentro sus objetivos. 42 inician esta práctica evaluando, dentro del campo económico, los costos asociados al uso del combustible de los vehículos y las emisiones de CO2. Sin embargo, son 43 quienes introducen el concepto de problema de localización y ruteo verde o GLRP para los residuos peligrosos, en el cual proponen un estudio que minimiza simultáneamente costos, riesgo de transporte y localización y emisiones de CO2 dentro de sus objetivos. Este enfoque hacia la minimización de emisiones ha sido evaluado en estudios posteriores: 44, 47.
Por otra parte, 48 proponen el único trabajo para residuos peligrosos que plantea, dentro de su modelo, la función objetivo de balance de carga de trabajo. En este problema, los autores discuten la importancia de aumentar la productividad en los empleados, la cual se encuentra directamente relacionada con el equilibrio de la carga laboral de los mismos. Como una problemática que se ha incrementado debido a la pandemia del Covid-19, 49 proponen un modelo de localización y ruteo para la gestión de residuos médicos, que se categorizan como residuos peligrosos. Diversos autores han publicado estudios similares para minimizar los costos y el riesgo asociado a la recolección de esa clase de residuos, cuya generación aumenta en épocas de crisis sanitaria 50, 54.
Para el caso de los estudios en los cuales no se consideran residuos peligrosos, sino desechos como plástico, vidrio, botellas, comida o papel, algunos autores han implementado el objetivo de riesgo como un concepto de carácter social, desarrollando formulaciones matemáticas en las que se busca maximizar la distancia entre los clientes y los puntos de disposición de los desechos, considerando que la exposición a estos sitios es peligrosa 14, 55.
Distribución de elementos de socorro
La logística de emergencia es definida como el proceso de planificación, gestión y control eficiente del flujo de recursos desde un lugar de emergencia hasta el punto donde se encuentran las personas afectadas a las cuales se les debe brindar atención 56. Las víctimas de un desastre natural deben recibir elementos de socorro, lo cual puede incluir alimentos, medicinas y productos de higiene, garantizando su entrega oportuna a la mayor cantidad de personas afectadas. Es por esto que maximizar la demanda atendida es uno de los objetivos de los modelos de optimización de carácter humanitario 57, 58. Algunos autores interpretan la satisfacción de la demanda como la optimización del tiempo de entrega, por lo cual formulan modelos matemáticos para asegurar la minimización del tiempo de viaje 59) (62.
Garantizar la seguridad durante el proceso de transporte en un entorno post-desastres, como es el caso de los eventos sísmicos, es de vital importancia. Para esto se han desarrollado estudios con el objetivo de maximizar la confiabilidad de las rutas como una alternativa para reducir el riesgo al que se puede ver enfrentado el personal de transporte. Aplicando este objetivo, se han propuesto modelos con entregas divididas 63, múltiples periodos 64, multiescalón 65 y escenarios bajo incertidumbre 66, 68.
Las condiciones inciertas de la logística de emergencia hacen que la optimización estocástica sea uno de los enfoques de interés en este tipo de redes de distribución. Diversos autores modelan el problema de localización y ruteo con múltiples objetivos para la distribución de elementos de socorro mediante el uso de parámetros de entrada de carácter estocástico, tales como niveles de demanda y costos o tiempos de viaje 69, mientras que, recientemente, algunas investigaciones exponen la incertidumbre asociada a un nuevo objetivo de estudio en esta temática: la minimización de las emisiones de CO2 70, 72.
GLRP
El problema de localización y ruteo asociado a la logística verde se ha planteado bajo la necesidad de disminuir la contaminación y las consecuencias de efecto invernadero ocasionadas por consumo de combustible utilizado para la industria del transporte 16. La logística se centra en los costos económicos. Sin embargo, tener en cuenta los impactos negativos sobre el medio ambiente ha sido una línea de investigación que ha incrementado su atención en los últimos años. Por esta razón, los modelos matemáticos para la localización y ruteo verde se caracterizan por minimizar costos y, a su vez, las emisiones de CO2, convirtiéndose así en problemas multiobjetivo. Algunas variantes estudiadas para estos modelos GLRP bi-objetivo incluyen: enrutamiento abierto 73, ventanas de tiempo 74, multiescalón 75 y multiproducto 76. Asimismo, otros estudios han evaluado la inclusión de nuevos objetivos tales como el balance de carga de trabajo para incorporar el impacto social al sistema 77, la minimización del tiempo 78 y la minimización del makespan o tiempo de espera en la secuencia de transporte de los vehículos 79.
Productos perecederos
Las cadenas de suministro para alimentos perecederos buscan garantizar la calidad de los productos, la cual disminuye a medida que se incrementa el tiempo del proceso de distribución.
Las investigaciones asociadas a la localización y ruteo con múltiples objetivos para estos productos describen modelos matemáticos principalmente con restricciones de ventanas de tiempo, generalmente establecidas por el cliente para recibir sus productos en las mejores condiciones posibles 80.
En relación con los objetivos de estudio, la minimización de costos constituye la meta principal para los problemas planteados. Este enfoque económico ha sido acompañado en diversas investigaciones por objetivos como la minimización del impacto medioambiental causado por las emisiones de CO2 21, 81, el balance de la carga de trabajo de los centros de distribución 82, la minimización del tiempo de recorrido 83 y la maximización de la satisfacción del cliente 84. Por otra parte, un estudio similar al presentado en 21 propone la maximización de la utilidad del personal y los clientes, además del impacto económico de la apertura de un centro de distribución, en la creación de empleo para una cadena de distribución de alimentos perecederos 85.
Cadena de frío
La cadena de frío corresponde al transporte de productos para los cuales es fundamental conservar una temperatura baja con el fin de mantener su calidad 86. Por tal razón, los modelos matemáticos formulados generalmente buscan, además de minimizar costos, garantizar la satisfacción del cliente. No obstante, la interpretación asociada a este concepto ha sido estudiada desde diferentes puntos de vista, como por ejemplo la minimización del tiempo de distribución 87, la minimización del daño asociado a los tipos de carga (cargas generales, cargas refrigeradas y cargas congeladas) 86, 88, la minimización del tiempo de espera del cliente y los vehículos para asegurar la eficiencia de la cadena de frío 89.
La logística de la cadena de frío se caracteriza por tener un alto consumo energético y elevadas emisiones de carbono. En consecuencia, 15 introducen una nueva función objetivo al sistema: la minimización de las emisiones totales de CO2, CH4 y N2O, como una estrategia para enfrentar esta problemática. Las restricciones asociadas a ventanas de tiempo, flota heterogénea, recogida y entrega simultánea y transporte mixto se evalúan en este estudio para integrar las condiciones reales de distribución de los productos de la cadena de frío.
Distribución de bebidas
La distribución de productos embotellados ha sido modelada en la literatura como un problema de transporte, localización y ruteo o TLRP (transporting location routing problem), considerado como una extensión del problema de localización y ruteo de dos escalones 90. Para este tipo de productos, la red de transporte está conformada por varias plantas de producción y un conjunto de clientes dentro de una ciudad, los cuales pueden ser hoteles, restaurantes o supermercados. Cada planta de producción cuenta con una flota de vehículos encargada de distribuir los productos. Sin embargo, no puede haber una conexión directa entre dichas plantas y los clientes debido a las regulaciones de tráfico pesado de la ciudad. Lo anterior implica la necesidad de incluir centros de distribución en la red, de donde son enviados los productos que serán entregados al cliente.
Este problema es presentado como un modelo LRP multiobjetivo por primera vez en el año 2014, con la finalidad de minimizar costos y asegurar el balance de la carga de trabajo de los conductores en la etapa de enrutamiento 90. Las investigaciones posteriores enfrentan el problema multiproducto teniendo en cuenta las condiciones normales de una planta de producción en donde se producen diferentes tipos de bebidas embotelladas. Las restricciones asociadas a ventanas de tiempo impuestas por los clientes con objetivos de optimización, como la minimización de las emisiones de CO2 91 y la maximización de la satisfacción del cliente 92, han sido estudiadas en este tipo de distribución.
Distribución de neumáticos y ventas en línea
Estas aplicaciones han sido estudiadas en menor medida para el problema de localización y ruteo multiobjetivo. 2 plantea un modelo estocástico para una red cerrada asociada a la cadena de suministro de la industria de los neumáticos, el cual considera aspectos de sostenibilidad y busca minimizar costos y emisiones de CO2, así como maximizar la capacidad de respuesta de la red integrada. Mientras tanto, 93 diseñan un modelo matemático de dos escalones con el propósito de reducir los costos de operación y las emisiones de carbono junto con la maximización de la satisfacción del cliente como estrategia de competitividad para las empresas de ventas en línea.
Otras aplicaciones
Adicionalmente, el estudio del problema de localización y ruteo con múltiples objetivos también ha sido discutido en la literatura mediante el planteamiento de modelos matemáticos que no tienen ningún tipo de producto o cadena de distribución establecido para su aplicación. No obstante, estos trabajos involucran diversos objetivos de optimización, características y restricciones al problema, los cuales contribuyen a la evolución de esta temática de investigación, presentándose como puntos de referencia para su implementación en las diferentes redes de distribución asociadas a la logística de localización y transporte. El planteamiento de las formulaciones matemáticas es variado, puesto que depende de las necesidades del sistema que se pretende modelar. Junto con la minimización de los costos totales, en estos estudios se destacan otros objetivos, tales como la maximización de la demanda total atendida 94 ,95, el balance en la carga de trabajo del sistema de distribución 96, la minimización del tiempo máximo de entrega de los productos al cliente 97, la minimización del tiempo de espera del cliente 98, la maximización de la confiabilidad de las rutas 17, la minimización de la diferencia entre la distancia recorrida por los vehículos 99, la maximización del nivel de servicio 100),(101 y la minimización de las emisiones de CO2 102) , (104.
Métodos de solución
Para resolver el problema de localización y ruteo con múltiples objetivos, se han aplicado diversas técnicas de solución en la literatura que incluyen tanto métodos exactos como aproximados. Las soluciones exactas han encontrado mayor aceptación para optimizar problemas pequeños 24. Por lo tanto, considerando la naturaleza NP-Hard de este problema y la existencia de varios objetivos contradictorios en las formulaciones multiobjetivo, se han desarrollado numerosos algoritmos evolutivos para resolver los problemas a gran escala en un tiempo computacional aceptable.
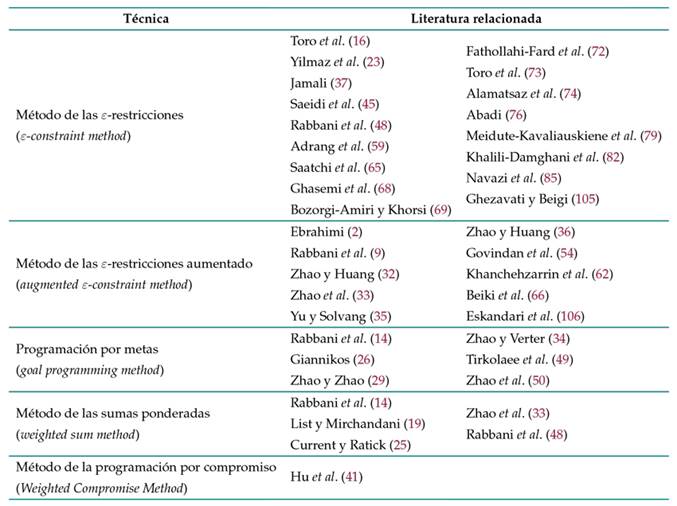
Para el caso de los métodos exactos multiobjetivo propuestos, 20 utilizan el método de las ponderaciones como una de las primeras propuestas de solución al problema. Más adelante, se llevan a cabo estudios que resuelven los modelos planteados por medio de otras técnicas, tal como se describe en la Tabla III, la cual presenta un resumen de los métodos utilizados y la literatura relacionada para cada uno de ellos. El método de las ε-restricciones corresponde la estrategia de mayor frecuencia para dar solución al LRP multiobjetivo. Cabe resaltar que esta técnica ha sido mejorada, dando como resultado el método de las ε-restricciones aumentado, metodología que, de igual manera, ha despertado interés en los autores por esta temática. En menor medida, se han utilizado métodos como la programación por metas, las sumas ponderadas y la programación por compromiso.
Tabla III: Métodos exactos multiobjetivo implementados
Si bien los procedimientos exactos han sido ampliamente implementados, la complejidad computacional de estos problemas constituye un esfuerzo elevado para brindar soluciones eficientemente. Por esta razón, se han desarrollado los algoritmos evolutivos multiobjetivo, o MOEA (multiobjective evolutionary algorithms), los cuales, basados en técnicas metaheurísticas, permiten obtener resultados favorables en un menor tiempo. El primer estudio en implementar estas técnicas es desarrollado por 28 en el año 2007 y utiliza una metaheurística multiobjetivo con procedimiento de memoria adaptativa, o MOAMP (multiobjective metaheuristic with adaptative memory procedure) para dar solución a un problema de localización y ruteo para la eliminación de desechos sólidos animales.
Años más tarde, 94 desarrollan un algoritmo multiobjetivo de búsqueda dispersa MOSS (multiobjective scatter search) para resolver un modelo matemático bi-objetivo de localización de múltiples depósitos y enrutamiento.
Debido al incremento continuo de estudios asociados al LRP multiobjetivo, y dada la complejidad asociada a las nuevas características que se le incluyen al problema, la mayoría de los investigadores se ha inclinado por el desarrollo de diversos algoritmos, con el fin de obtener resultados factibles. La Tabla IV expone un resumen de los métodos más utilizados en la literatura. En el año 2014 se introduce el algoritmo genético no dominado II, o NSGA-II (non-dominated sorting genetic algorithm II) 90. El NSGA-II constituye el método más utilizado en este tipo de investigaciones, y es uno de los más populares en la optimización multiobjetivo, tal como se puede observar en la tabla. A su vez, se ha implementado recientemente el algoritmo genético no dominado III o NSGA-III (non-dominated sorting genetic algorithm III) como una extensión del NSGA-II 45. El algoritmo de optimización por enjambres de partículas multiobjetivo, o MOPSO (multiobjective particle swarm optimization), también ha tenido una importante aceptación, así como el algoritmo evolutivo de fuerza de Pareto o SPEA-II (strength Pareto evolutionary algorithm II), la técnica de recocido simulado multiobjetivo, o MOSA (multiobjective simulated annealing), el algoritmo competitivo imperialista multiobjetivo, o MOICA (multiobjective imperialist competitive algorithm), y la optimización de lobo gris multiobjetivo o MOGWO (multiobjective grey wolf optimizer).
Tabla IV: Algoritmos evolutivos multiobjetivo implementados

Otros autores han optado por técnicas utilizadas en menor frecuencia, como por ejemplo el algoritmo genético y cultural híbrido multiobjetivo, o MOHCGA (multiobjective hybrid cultural and genetic algorithm) 42, el algoritmo evolutivo multiobjetivo basado en descomposición, o MOEA/D (multiobjective evolutionary algorithm based on decomposition) 47, 62, el algoritmo de selección por envolvente de Pareto II, o PESA-II (Pareto envelope-based selection algorithm II) 48, 68, el algoritmo de optimización de maleza invasiva multiobjetivo, o MOIWO (multiobjective invasive weeds optimization algorithm) 47, el algoritmo de flujo de agua multiobjetivo, o MOWFA (multiobjective water flow-like algorithm) 44, y el algoritmo del ciclo del agua multiobjetivo, o MOWCA (multiobjective water cycle algorithm) 17.
Adicional a ello, se han desarrollado estrategias mejoradas para los algoritmos evolutivos existentes, con la finalidad de establecer comparaciones entre los resultados obtenidos y evaluar, a partir de diversas métricas el comportamiento de los algoritmos, como es el caso de 40, quienes desarrollan un algoritmo genético de clasificación no dominado (NSGA-II) mejorado con búsqueda local, que se designa INSGA-dLS (non-dominated sorting genetic algorithm with directed local search). El algoritmo propuesto puede lograr un mejor rendimiento que el obtenido por NSGA-II y MOPSO para resolver un problema de localización y ruteo de dos escalones aplicado a la recolección de residuos peligrosos.
Discusión de resultados
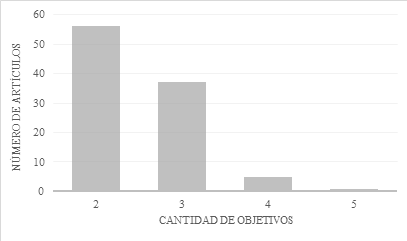
Considerando la importancia de vincular los aspectos económicos con temáticas sociales y ambientales en los procesos logísticos, el problema de localización y ruteo clásico ha evolucionado hacia la implementación de múltiples objetivos en los modelos matemáticos, que permiten a los tomadores de decisiones establecer estrategias que favorecen diferentes factores de manera equilibrada. La Fig. 2 representa el número de artículos de acuerdo con la cantidad de objetivos utilizados para formular el LRP multiobjetivo a lo largo de los años. Según el análisis, el número de artículos bi-objetivo alcanza un 56,6 % de la muestra (56 documentos), mientras que, con tres objetivos se vincula el 37,4 % (37 documentos). Por otro lado, los estudios con cuatro y cinco objetivos han sido formulados en menor medida con porcentajes del 5,1 (5 documentos) y 1 % respectivamente.
Figura 2: Número de artículos por cantidad de objetivos
La información contenida en la Tabla V expone una recopilación de la literatura del LRP multiobjetivo de acuerdo con las principales aplicaciones del problema. Los estudios se describen según año de publicación, objetivos de optimización, tipo de estudio y clase de método de solución. En cuanto a los objetivos implementados, se incluyen principalmente la minimización de los costos, la minimización de los riesgos, la minimización del impacto ambiental, el balance de carga de trabajo, la maximización de la satisfacción del cliente, la minimización del tiempo y la maximización de la confiabilidad de las rutas. Tal como se observa, la mayoría de las investigaciones relacionadas con el LRP multiobjetivo, independientemente de su tipo de aplicación, incluyen el aspecto económico dentro de los modelos matemáticos formulados. Sin embargo, existen algunos objetivos que se emplean en mayor medida para ciertas aplicaciones específicas, debido a las características que impone el sistema.
Nota. La tabla presenta las siguientes abreviaciones: referencia bibliográfica (Ref.), costo (C), riesgo (R), ambiental (A), balance de carga de trabajo (B), satisfacción del cliente (S), tiempo (T), confiabilidad de las rutas (RB), académico (AC), caso de estudio (CE), exactos (E) y aproximados (A).
Tabla V: Resumen de la literatura del LRP multiobjetivo
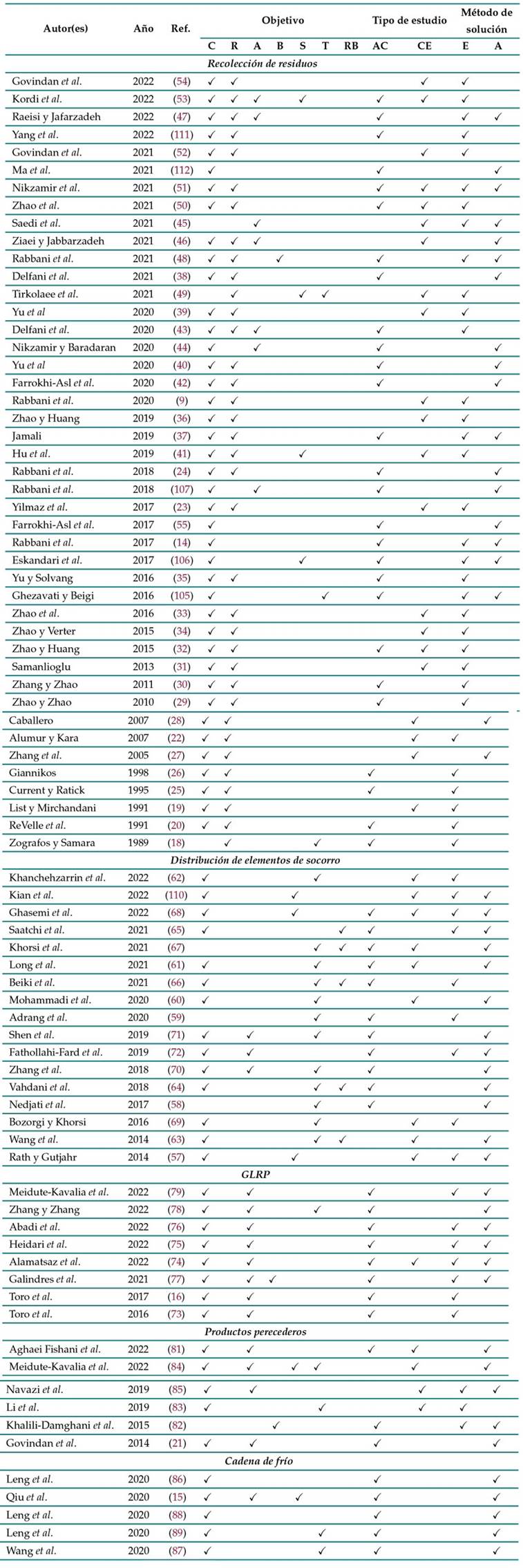
La recolección de residuos se relaciona con la minimización del riesgo, objetivo que se ha interpretado generalmente como el riesgo de localización de las instalaciones de tratamiento, reciclaje o disposición final, el riesgo de transporte asociado a las rutas de recolección y el riesgo total del sistema que vincula los dos mencionados anteriormente 24. Por el contrario, la distribución de elementos de socorro se concentra en la minimización del tiempo como una actividad vital en situaciones de emergencia, debido a que el tiempo de llegada de los productos de socorro a las áreas afectadas impacta negativamente la tasa de supervivencia de las personas 110, de modo que garantizar el menor tiempo de entrega es necesario. Adicionalmente, la maximización de la confiabilidad de las rutas es un objetivo adoptado para estos sistemas, en especial en aquellos en casos en que ocurren desastres naturales que alteran la estabilidad de las carreteras. En lo referente al GLRP, como su nombre lo indica, su propósito es minimizar el impacto ambiental, por lo cual reducir las emisiones de CO2 y consumo de combustible de los vehículos constituyen los temas de mayor alcance. Este objetivo también ha tenido aceptación en los estudios relacionados con la distribución de productos perecederos, mientras que en la cadena de frío ha sido aplicada la minimización del tiempo y los costos totales.
Por otra parte, en relación con el tipo de estudio implementado, un 55,6 % de los documentos analizados proporciona soluciones a sus modelos matemáticos mediante el uso de datos sintéticos o instancias de prueba, en comparación con un 32,3 % que lleva a cabo el desarrollo de casos de estudio. Un 12,2 % de los artículos emplea ambos tipos de datos, generalmente desarrollando instancias de pequeña escala para la validación del modelo mediante métodos exactos, mientras que los casos de estudio tienen mayor aplicabilidad para los algoritmos evolutivos, teniendo en cuenta que se incrementa la complejidad del problema si se usan datos reales en la implementación.
Finalmente, respecto a las técnicas de solución, la Tabla V indica el tipo de método empleado por los autores: exacto o aproximado. El uso de técnicas aproximadas para enfrentar el problema constituye la mayor participación, con un 46,5 % de los documentos, mientras que los métodos exactos equivalen al 33,3 %; el 20,2 % de las investigaciones adopta ambas técnicas. Aunque gran parte de los estudios emplea métodos exactos, en los trabajos recientes ha tenido más relevancia el uso de algoritmos evolutivos multiobjetivo.
Oportunidades de investigación
El problema de localización y ruteo con múltiples objetivos ha sido ampliamente estudiado teniendo en cuenta diferentes características y variantes, con el propósito de simular las verdaderas condiciones del proceso. Desde la revisión realizada por 3 en 2007, el LRP multiobjetivo se considera una línea de investigación de gran alcance. Este estudio demuestra la considerable evolución que ha tenido esta temática a lo largo de los años y la importante atención que se le ha atribuido en la literatura.
Con respecto a las sugerencias propuestas por 5 y 6, la comunidad académica relacionada con la optimización multiobjetivo para el problema de localización y ruteo de vehículos ha abordado algunos temas importantes poco estudiados anteriormente:
-
El desarrollo de versiones más realistas del problema, involucrando aspectos como fluctuaciones de la demanda y condiciones de incertidumbre en los parámetros. Para esto, varios estudios recientes han mostrado interés por la formulación de modelos estocásticos 2, 39, 44, 68 y enfoques de optimización robusta 38, 46, 50, 61.
-
La extensión de variantes al problema como ventanas de tiempo 48, 74, 92 y múltiples escalones 92, 105.
-
La integración del problema en otros contextos de la logística. En la metodología para la selección de documentos de la presente revisión se hallaron 41 artículos que asocian el problema de inventarios con el LRP multiobjetivo, evidenciando la incorporación de otros procesos logísticos a esta área de investigación. Lo anterior se propone como una dirección de investigación para posteriores revisiones.
-
El acercamiento del problema a contextos reales. Es posible observar el interés de la comunidad científica por vincular los problemas de localización y ruteo a aplicaciones como recolección de residuos, distribución de elementos de socorro, productos perecederos o cadenas de frío. Existe un enfoque hacia la implementación de casos de estudio que proporcionan los datos de sistemas reales para resolver el problema.
De igual manera, otras vertientes han sido recomendadas por estos autores. Sin embargo, se han llevado a cabo pocos estudios relacionados. Aspectos como la implementación de horizontes de planeación con múltiples periodos, considerando condiciones de incertidumbre 61, 84, y el desarrollo de metaheurísticas unificadas para evitar la proliferación de variantes muy similares constituyen líneas de investigación que deben ser estudiadas en mayor medida en el futuro. Algunos trabajos han implementado el desarrollo del algoritmo NSGA-II 93, 112 o el MOPSO 109 mejorado con características de otros algoritmos. Cabe resaltar que el uso de metaheurísticas cooperativas también se establece como una estrategia importante para dar solución a los modelos formulados, los cuales cada vez representan mayor complejidad debido al incremento de las variantes del LRP. Adicional a esto, se han desarrollado múltiples técnicas metaheurísticas multiobjetivo, pero el estudio de métodos exactos continúa siendo limitado. Si bien esto tiene su justificación en la complejidad de los problemas, corresponde a un tema con amplias oportunidades de investigación.
Respecto a los objetivos de optimización, la minimización de costos continúa siento la meta principal para el LRP desde sus inicios. Por consiguiente, mantener la iniciativa de combinar otros objetivos de carácter ambiental y social se considera como una alternativa eficiente para satisfacer las condiciones de las cadenas de suministro actuales. Adicionalmente, (5) propone el estudio de problemas en donde es imposible atender a todos los clientes como es el caso de la industria de servicios, por ejemplo, en actividades de mantenimiento y reparación, y en logística de desastres. Algunos autores han intentado abordar este aspecto mediante el desarrollo de modelos matemáticos, con el objetivo de maximizar la demanda atendida 110 y minimizar la cantidad total de demanda perdida 58. Sin embargo, son pocos los estudios relacionados. Finalmente, el análisis de variantes importantes como el LRP de recogida y entrega simultánea o LRPSPD (LRP with pickup and delivery) y el LRP con entregas divididas o SDLRP (LRP with split delivery) aplicado a la optimización multiobjetivo representa líneas de investigación que pueden ser ampliadas. Asimismo, se puede continuar con el desarrollo de modelos con flota de vehículos heterogénea que acerquen el proceso a condiciones de la realidad.
Conclusiones
La optimización multiobjetivo permite la integración de diferentes objetivos de estudio que incluyen perspectivas económicas, sociales y ambientales, de manera que su combinación con el problema de localización y ruteo se considera un punto de partida hacia el desarrollo de cadenas de suministro sostenibles. El análisis de los estudios relacionados con esta temática permite determinar sus principales tendencias de investigación. Considerando lo anterior, este artículo propone una revisión de literatura sobre el problema de localización y ruteo con múltiples objetivos, en la cual se evalúan 99 publicaciones que involucran formulaciones matemáticas referentes a este tipo de modelos dentro de una ventana de tiempo que comienza en 1989 y termina en 2022.
A partir de la revisión, se evidencia que estos modelos han sido aplicados a diferentes cadenas de suministro, teniendo en cuenta la naturaleza de los productos y las necesidades del diseño de la red de distribución, dentro de las cuales se identifican las siguientes: recolección de residuos, distribución de elementos de socorro, localización y ruteo verde, productos perecederos, cadena de frío y distribución de bebidas. Sin embargo, la mayoría de las investigaciones sobre este problema está enfocada en la gestión de residuos, más precisamente desechos peligrosos, por el riesgo que su incorrecta recolección y disposición final implican tanto para el ser humano como para el medio ambiente.
El LRP con múltiples objetivos ha tenido como propósito general la minimización de los costos. Según el tipo de cadena de suministro, se han evaluado diferentes funciones objetivo, dentro de las que se destacan las siguientes: minimización de riesgos, aspectos ambientales, minimización de tiempo, satisfacción del cliente y balance de carga de trabajo. De igual manera, los estudios actuales han presentado mayor interés por acercar el problema a las condiciones reales, por lo cual se han incorporado distintas características como flota heterogénea, vehículos con múltiples compartimentos, ventanas de tiempo, problemas multiperiodo y desarrollo de modelos bajo incertidumbre.
Con respecto a la solución del problema, se han utilizado diversas técnicas multiobjetivo exactas y aproximadas. Con referencia a los métodos exactos, han tenido una amplia aceptación la programación por metas y el método de las ε-restricciones clásico y su versión mejorada. Sin embargo, la mayoría de los estudios se ha orientado hacia la construcción de algoritmos evolutivos multiobjetivo que permitan dar solución a modelos de gran escala. El algoritmo genético no dominado II, o NSGA-II, la optimización por enjambres de partículas multiobjetivo, o MOPSO, y el algoritmo evolutivo de fuerza de Pareto, o SPEA-II, han sido las técnicas de mayor frecuencia.
El problema de localización y ruteo multiobjetivo constituye una línea de investigación activa, con un alcance amplio en número de investigaciones enfocadas en las diferentes aplicaciones, variantes de los modelos matemáticos y diversas técnicas de solución que determinan numerosas alternativas de estudio y grandes desafíos para la comunidad científica asociada a esta temática.
Referencias
Licencia
Derechos de autor 2023 Paula Andrea Cabrales-Navarro, Javier Eduardo Arias-Osorio, Julio Cesar Camacho-Pinto

Esta obra está bajo una licencia internacional Creative Commons Atribución-NoComercial-CompartirIgual 4.0.
A partir de la edición del V23N3 del año 2018 hacia adelante, se cambia la Licencia Creative Commons “Atribución—No Comercial – Sin Obra Derivada” a la siguiente:
Atribución - No Comercial – Compartir igual: esta licencia permite a otros distribuir, remezclar, retocar, y crear a partir de tu obra de modo no comercial, siempre y cuando te den crédito y licencien sus nuevas creaciones bajo las mismas condiciones.






2.jpg)