DOI:
https://doi.org/10.14483/23448393.2669Publicado:
2007-11-30Número:
Vol. 13 Núm. 2 (2008): Julio - DiciembreSección:
Ciencia, investigación, academia y desarrolloSimuladores Dinamicos Computacionales, Principios de Operación
Computerized 3D Modeling Systems Principles Of Operation
Palabras clave:
Simulación dinámica, colisiones, modeladores (es).Descargas
Referencias
C. Murilo G. Dynamic Simulations of Multibody Systems. Editorial Springer. 2001.
M., Francis C. Applied Dynamics. Editorial John Wiley & Sons, Inc. 1998.
E., David. Dynamic Collision Detection using Oriented Bounding Boxes, Disponible: http://www.magicsoftware.com/Documentation/dynacoll.pdf , Magic Software
G., M. C. Lin y D. Manocha 1996. OBB-Tree: A Hierarchical Structure for Rapid Interference Detection. Disponible: http://citeseer.nj.nec.com/gottschalk96obbtree.html
H., Phillip M. 1995 Collision detection for interactive graphics applications. Disponible:http:// citeseer.nj.nec.com/hubbard95collision.html
D., Mintz. Octree Spatial Partitioning for Real-Time 3D Hidden Surface Removal. Disponible: http:// silcon.silcon.com/~brink/papers/octrees.html
I., P., Carles. 2001 portal Rendering. Disponible: http://www.macedoniamagazine.com/
BSP Tree Frequently Asked Questions. Información relacionada con los árboles BSP. Disponible: http:// www.xs4all.nl/~smit/whole.htm
Universidad Complutense de Madrid. 2000. Curso de desarrollo de juegos por ordenador.
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Ciencia Investigación Academia y Desarrollo
Ingeniería, 2008-00-00 vol:13 nro:2 pág:45-54
Simuladores dinamicos computacionales, Principios de operación
Computerized 3D modeling systems principles of operation
Luís Fernando Vargas Tamayo
Magíster en Ingeniería - Materiales y Procesos. Universidad Nacional de Colombia. Docente Facultad de Ingeniería UDFJC. Director del grupo de investigación DIMSI.
Leonardo Emiro Contreras Bravo
Magíster en Ingeniería - Materiales y Procesos. Universidad Nacional de Colombia. Docente Facultad de Ingeniería UDFJC. Director del grupo de investigación DIMSI.
Resumen
Los sistemas de modelamiento computacional en 3D de la actualidad, han alcanzado tal grado de realismo y definición que ya no se restringen a aplicaciones de entretenimiento y diversión como los videojuegos y las animaciones, hoy en día son el eje de desarrollo de una industria en constante crecimiento. La simulación llamada realidad virtual tridimensional, se usa en campos diversos y muy específicos, como son la arquitectura, los simuladores de vuelo, de cirugía, etc. Especialmente el interés para este trabajo consiste en una aplicación de dichos software al modelamiento de sistemas mecánicos y dinámicos, mecanismos y maquinaria; en este aspecto reviste interés el modelamiento tridimensional, el control de solidez y ensamble de las piezas y en algunos casos las interacciones de objetos en movimiento como cuando se analizan sistemas dinámicos virtualmente.
Palabras clave:
Simulación dinámica, colisiones, modeladores
Abstract
Computerized 3D modeling systems have reached such degree of realism and definition that it is not only restricted to entertainment applications such as videogames and animation. Today, they are the development backbone of a constantly growing industry. Simulations called Tridimensional Virtual Reality are used in a variety of specific fields, such as architecture, flight simulations (aviation), surgery, etc. Special interest in the application of such software consists in the modeling of mechanic and dynamic systems, mechanisms and machinery. Aspects like tridimensional modeling, solidity control, assembly of parts and in somecases the interaction of moving objects are of great importance when they are analyzed in a virtually dynamic system.
Key Words:
Simulation, dynamics, collision, modeling.Luís Fernando Vargas Tamayo1
1. INTRODUCCIÓN
El modelamiento basado en la física de los sistemas y en las interacciones entre sus partes es particularmente atractivo, pues no se restringe a un modelamiento de un análisis en un simple dominio, por el contrario, las simulaciones son extremadamente útiles cuando pueden extenderse a varios dominios logrando un análisis multidominio del sistema; un ejemplo de esto puede ser una combinación de análisis térmico y pruebas de esfuerzo en los materiales usados en la manufactura de las partes de un ensamble; con las fuerzas ejercidas en cada una de ellas obtenidas de un análisis de contacto mecánico.
El reto de realizar análisis combinados en multidominios está en el desarrollo de modelos matemáticos del sistema para cada uno de los dominios de interés, requiere además el desarrollo de modelos matemáticos especializados capaces de expresar las interacciones que concuerden con el correcto comportamiento del sistema; en muchos casos, esos modelos matemáticos especializados, son implementados usando diferentes métodos numéricos que pueden no ser compatibles entre sí.
La escogencia del modelo a usar depende de los objetivos de la simulación que deban ser alcanzados, así como de la eficiencia computacional requerida. Por ejemplo una simulación dinámica de un muro cayéndose por una explosión en un video juego no necesita un modelo de alta precisión para representar la estructura interna del muro, será suficiente con un modelo que recree la escena con autenticidad. Sin embargo, esta misma simulación en el contexto de una operación militar puede necesitar un modelo muy preciso del muro para que el arma apropiada pueda ser escogida para cumplir la tarea.
1.1. Sistemas de partículas y de cuerpo rígido
Los sistemas de cuerpo rígido y de partícula son considerados los mas importantes y comúnmente utilizados en los modelos físicos de simulaciones dinámicas. En los primeros se toma en cuenta la forma y la distribución de masa de los objetos a ser simulados siendo especialmente recomendados en la simulación de sistemas donde se presenten flexiones internas, compresiones o tensiones que no cambien la for ma del objeto durante la simulación. La presunción de rigidez en los cuerpos simplifica los cálculos, y hace que las fuerzas aplicadas en algún punto del objeto sean equivalentes a un par fuerza - torque en el centro de masa, lo cual puede ser fácilmente calculado.
Los sistemas de partículas incluyen desde implementaciones básicas de sistemas de masa puntual como los que usan partículas discretas para representar el movimiento de un gas o fluido, hasta sistemas especializados que usan mecánica de fluidos computacional para simular dicho gas o liquido en condiciones de flujo turbulento, una ráfaga de viento, un remolino de vapor e inundaciones, por nombrar unos pocos.
Los cuerpos rígidos pueden ser combinados en sistemas de elementos articulados, donde los cuerpos están unidos a otros mediante juntas o articulaciones. Existen diversos tipos de uniones que pueden ser usados para conectar cuerpos, y estos difieren entre sí por el número de grados de libertad de movimiento que se permiten. Un cuerpo sin restricciones tiene seis grados de libertad, tres de traslación y tres de rotación en los ejes coordenados.
2. ESTRUCTURA DE LOS MOTORES DE SIMULACIÓN
La figura 1 muestra el diagrama de bloques que representa el ciclo principal de un simulador de dinámica, el programa toma inicio en t0, y avanza por pasos de tiempo, llamados "frames", ejecutando cuatro pasos explicados a continuación:
2.1 Primer paso del proceso de simulación (movimiento)
El motor de simulación mueve todos los objetos desde la posición inicial hasta el final del lapso de tiempo en curso, ignorando cualquier posible colisión que pueda suceder durante el movimiento. Este paso consiste en determinar el estado dinámico del sistema (dado por todas las posiciones angulares y lineales, velocidades y aceleraciones, así como los pares externos de fuerza - torque que actúan sobre cada cuerpo) al comienzo del intervalo y usar esa información para solucionar las ecuaciones diferenciales ordinarias (EDOs) de movimiento de cada objeto. Las únicas variables que deben ser calculadas o tenidas en cuenta en los cálculos de esta etapa son los pares externos de fuerza - torque. Ejemplos de fuerzas externas actuando sobre un objeto, son la fuerza de la gravedad, las de contacto, restricciones debidas a los tipos de unión entre cuerpos de un sistema articulado, entre otras.
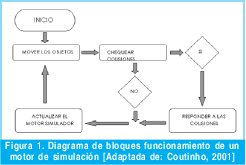
2.2 Segundo paso de la simulación (Control de colisiones)
El segundo paso controla las colisiones que pueden ocurrir entre dos o mas objetos durante la simulación, estos choques son detectados frecuentemente mediante comprobaciones geométricas buscando intersecciones entre los objetos representados. Se lleva a cabo en dos fases: la primera estructura auxiliar a considerar, se usa para ganar velocidad en la tarea de comprobar si los objetos chocaron al realizar el movimiento (trayectorias), la segunda estructura considerada, consiste en descomponer cada objeto en un árbol jerárquico de estructuras simples que puedan ser rápidamente revisadas buscando intersecciones; estas estructuras simples pueden ser: esferas, cubos, cilindros, o en general cualquier polígono convexo.
Como lo muestra la figura 1, si no se detectan colisiones, el movimiento de los objetos para el espacio de tiempo actual es válido y sus nuevas posiciones y orientaciones son enviadas al motor de renderizado, el cual se encarga de hacer los cambios gráficos en la simulación para mostrar las nuevas posiciones; por otro lado si una colisión es detectada, el programa se mueve al tercer paso.
2.3 Tercer paso de la simulación (Condición de solidez)
El establece la restricción de no penetrar en el cuerpo para todos los contactos y colisiones detectadas en el paso anterior; consiste en responder a las colisiones que puedan ocurrir entre dos o más cuerpos durante el movimiento. El punto de colisión, las velocidades normal y relativa de colisión asociadas con el choque más recientemente detectado, son computados desde el desplazamiento geométrico relativo de los objetos que chocaron, así como desde su estado dinámico justo antes de la colisión. Esta información es comunicada al algoritmo de respuesta a colisiones para calcular los impulsos de colisión así como las fuerzas de contacto.
La diferencia entre colisión y contacto es determinada frecuentemente por la medición de la velocidad relativa de los objetos que se encuentran justo antes de que suceda el choque, si la velocidad relativa es menor que un cierto valor de umbral, la colisión es asumida como un contacto. Solucionar las colisiones requiere mover los objetos hacia atrás en el tiempo para colocarlos en el lugar que estaban justo antes del choque detectado, el procesador de simulación necesita recalcular el estado dinámico de los objetos involucrados para el tiempo restante de ese "frame" de modelamiento, esto es hecho reiniciando la integración numérica usando el nuevo estado dinámico del objeto justo después del choque.
2.4 Cuarto paso de la simulación (Actualización del renderizado)
Consiste en comunicar la posición y orientación final de cada objeto en el sistema al motor de renderizado que se esté usando. El procesador de simulación, que ha realizado todas las tareas matemáticas para determinar el estado dinámico del sistema al finalizar ese paso, mantiene una constante comunicación con el motor de renderizado que en últimas es quien muestra los resultados gráficos de todo el proceso y sirve de interfaz con el usuario.
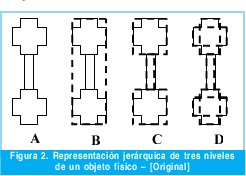
3. REPRESENTACIÓN JERÁRQUICA DE POLIEDROS TRIDIMENSIONALES
Un objeto cualquiera se puede representar con varios volúmenes simples, en la figura 2, se muestra un ejemplo de objeto que se desea descomponer en volúmenes simples, en un primer nivel se usa un solo poliedro que contiene todo el objeto (figura 2 B); posteriormente se llega a un nivel intermedio en el que los volúmenes son más pequeños y definen mas cercanamente el objeto original (figura 2 C); finalmente lo que se podría considerar las "hojas" del árbol jerárquico, son poliedros simples tan pequeños como sea necesario para definir exactamente el objeto, sin dejar regiones vacías que estén dentro de la representación, pero que no sean parte del objeto físico (figura 2); las fronteras de estos volúmenes serán entonces las primitivas del cuerpo inicial.
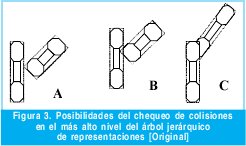
El chequeo de colisiones se hace entonces usando las representaciones jerárquicas de los objetos para rápidamente determinar cuáles no se intersecan o para reducir el número de pares de primitivas que deben ser chequeadas buscando los choques.
Por ejemplo, si el volumen representativo de más alto nivel de cada uno de los objetos que forman un par que se está verificando, no se intersecan entonces podemos estar seguros que los objetos en sí, no colisionaran (figura 3 A); por otro lado si esas representaciones de más alto nivel si se chocan, entonces debemos movernos un nivel más abajo en el árbol jerárquico para chequear si sus "hojas" colisionan o no. Si no, entonces los objetos no están en conflicto (figura 3 B), si por el contrario las "hojas" o niveles intermedios chocan entonces podemos asegurar que los objetos si colisionaron (figura 3 C).
Este proceso continuará hasta que se llegue al más bajo nivel del árbol jerárquico (hojas del árbol), en el que los volúmenes de representación sean los más pequeños posibles, o hasta que en algún nivel se detecte no colisión. En la práctica, existen dos importantes aspectos a considerar cuando se usan representaciones jerárquicas en un motor de simulaciones.
El primero es que la prueba de intersección de los volúmenes representados debe ser considerablemente más rápida que hacer una prueba de intersección con los objetos originales. De esta manera, la representación jerárquica de los objetos debe ser realizada mediante poliedros simples, que no representen un reto más complicado que el mismo objeto. Lo que restringe la utilización a volúmenes sencillos como esferas y cubos, los cuales pueden ser rápidamente examinados buscando las colisiones; en algunos casos se pueden utilizar algunos poliedros convexos o triángulos, siempre que el chequeo sobre estos sea más rápido que sobre la figura original.
El segundo aspecto a tener en cuenta, tiene que ver con el movimiento de los objetos y de sus representaciones jerárquicas; como es lógico cuando el objeto se mueva dentro de la simulación, la representación jerárquica de esta, que como se había dicho antes se basa en su sistema local de coordenadas, debe acompañar al objeto a su nueva posición, sin demoras y sin perder la relación con las primitivas del objeto original.
3.1 Tipos de representaciones jerárquicas
Como se mencionó anteriormente las representaciones jerárquicas se limitan a poliedros sencillos, generalmente cubos y esferas. No es claro cuál representación jerárquica es la mejor, la detección de colisiones es altamente dependiente del desplazamiento relativo de los objetos a considerar, y de esta manera en algunos casos los cubos representarán de una manera más fiel el objeto y en otros casos con las esferas se obtendrá mejor resultado. A continuación se explican algunas de las presentaciones jerárquicas más utilizadas.
3.1.1 Cubos con fronteras alineadas a los ejes
Conocida como AABB por sus siglas en inglés Axis Aligned Bounding Boxes. En la representación jerárquica que utiliza cubos con fronteras alineadas a los ejes, el árbol jerárquico es construido con cubos de frontera en donde las primitivas asociadas con ellos, tales como los ejes de los cubos están alineados con los ejes del sistema local de coordenadas del objeto.
En la figura 4 se ilustra la construcción de un árbol para un objeto sencillo en dos dimensiones. Inicialmente, el cubo de más alto nivel es construido con aristas tangentes a los vértices del objeto, manteniendo las trayectorias en los mínimos y máximos valores a lo largo de los ejes del sistema coordenadas local del objeto. Los valores mínimos y máximos definirán las esquinas inferior izquierda y superior derecha del cubo respectivamente.
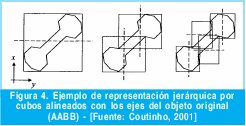
Un plano de partición es entonces seleccionado para que divida el volumen en dos regiones a lo largo de su eje más largo, el punto de intersección entre plano de partición y el eje más largo es escogido de tal manera que las dos regiones sean lo más balanceadas posibles, esto es, que más o menos el mismo número de primitivas sean asignadas a cada región de la subdivisión.
En un nivel subsiguiente, el cubo intermedio es construido desde las primitivas asociadas a él; unos nuevos planos de partición son creados para dividir los cubos en dos regiones, las primitivas son entonces asignadas a cada región y el proceso continúa recursivamente hasta que solamente una primitiva es asignada a cada región de la subdivisión.
3.1.2 Cubos con fronteras orientadas
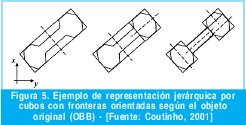
Este tipo de representación también es conocido por sus siglas en inglés Oriented Bounding Boxes (OBB); el árbol jerárquico es construido con cajas que se ajustan estrechamente a las primitivas asociadas a ellas, en este caso los cubos tienen una orientación diferente a los ejes del sistema coordenadas local del objeto, de esta manera su alineación dependerá del desplazamiento geométrico de sus primitivas.
En efecto la estructura de árbol OBB provee una representación jerárquica más ajustada si se compara con la estructura AABB, claramente esto representaría una ventaja para estructura OBB cuando se verifica colisiones entre objetos cercanos; esto reducirá el número de pruebas sobre las primitivas que se lleven a cabo. Sin embargo la construcción de un árbol OBB es mucho más compleja que en el caso AABB, ya que la orientación de cada cubo intermedio deberá ser calculado desde el grupo de primitivas asociadas con él.
3.1.3 Esferas de frontera
En la representación por esferas (BS por Bounding Spheres) el árbol jerárquico es construido por esperas que encapsulan las primitivas asociadas con ellas, estas esferas deberán ser de radio mínimo. La representación BS es de pobre calidad en comparación con sus contrapartes AABB y OBB. Sin embargo la prueba de traslape entre las esferas es la más fácil y rápida de efectuar de los casos considerados hasta ahora, dando una ventaja sobre las demás por la rapidez de las pruebas de colisión.

4. DETECCIÓN DE COLISIONES
4.1 Contextualización
Como se mencionó anteriormente el paso a seguir en la simulación es la verificación de posibles colisiones que se puedan presentar entre los objetos, posterior a representar los objetos mediante boundings adecuados según la aplicación especifica, es necesario comprobar que estos posean una dinámica coherente y real; es decir, detectar las colisiones entre los objetos y responder a estas colisiones de la misma manera que ocurriría en la vida real.
4.2 ¿Por qué detectar colisiones?
Actualmente cualquier sistema de animación interactivo contiene una gran cantidad de entidades virtuales que se mueven e interactúan entre ellas. En estas animaciones no se puede predecir con anterioridad cuál será el comportamiento del usuario y dichas entidades, por lo que será imprescindible ir creando la animación en tiempo de ejecución.
Teniendo en cuenta que para que el usuario acepte la animación como una simulación a tiempo real la imagen mostrada tiene que actualizarse por lo menos unas 50 veces por segundo, deja, en el mejor de los casos, sólo 20 milisegundos para realizar la actualización de todas las entidades de la simulación y representar la escena. No cabe duda que una aplicación de este tipo tiene que disponer de un sistema de visualización muy rápido; sin olvidar que la aplicación contiene una gran cantidad de entidades que necesitan ser actualizadas constantemente y cuyo comportamiento no se puede predecir al ser una aplicación interactiva. Con el tiempo estas entidades pueden llegar a penetrar unas con las otras, dando una muy mala simulación al usuario. Por lo tanto la aplicación deberá tener un sistema de tratamiento de colisiones lo suficientemente rápido como para no arruinar el rendimiento a tiempo real deseado.
Este sistema de tratamiento de colisiones se divide en dos componentes. El primero es un algoritmo de detección de colisiones, el cual es el responsable de encontrar aquellas entidades cuyas superficies hayan empezado a penetrar. Si el algoritmo de detección encuentra alguna entidad en este estado, entonces el sistema de tratamiento de colisiones llama al segundo componente, un algoritmo de reacción a las colisiones. Este algoritmo tiene la función de corregir el comportamiento de las entidades de for ma que dejen de penetrar. Esta corrección puede requerir la aplicación de ciertas leyes de la dinámica, como por ejemplo hacer que una entidad rebote.
4.3 Tareas especificas de un algoritmo de detección de colisiones
Los algoritmos diseñados para detectar las colisiones de los objetos en el mundo simulado deben llevar a cabo ciertas operaciones que garanticen el cumplimiento de los siguientes tres objetivos primarios:
a. Comprobar las colisiones regular y continuamente con incrementos de tiempo constantes: fixed-timestep weakness.
b. Comprobar las intersecciones entre todas las parejas de objetos de la escena: all-pairs weakness.
c. Determinar si las superficies de dos objetos se intersecan: pair-processing weakness.
4.3.1 Fixed-timestep weakness
El hecho de comprobar si dos objetos se interseccionan cada instante de tiempo puede hacer que algunas colisiones no se detecten. La figura es un claro ejemplo de una situación en que dos objetos habrían tenido que colisionar pero no se ha detectado.
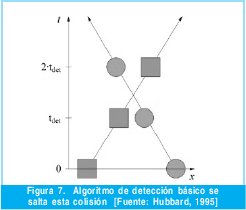
En el ejemplo los dos objetos se mueven en sentido contrario a lo largo del eje x, mostrando su posición a cada incremento de tiempo tdet. Debido a que las comprobaciones de intersección sólo se realizan cada tdet no se detecta la colisión que se produce durante el intervalo entre tdet y 2tdet. En consecuencia los dos objetos se atraviesan el uno al otro durante la simulación.
Se podría pensar en disminuir el valor de tdet para reducir la posibilidad de que aparezca este error, pero esto conllevaría a un empeoramiento en el rendimiento del algoritmo, pues se incrementaría el número de iteraciones realizadas en un mismo intervalo de tiempo.
En este punto, lo que interesa es un método para poder buscar colisiones por todo el intervalo de tiempo y no sólo en ciertos momentos. Aquí es donde entra en escena lo que se llama bounding de movimiento. La palabra bounding viene del inglés y hace referencia a un envoltorio. ¿Y qué es este "envoltorio" de movimiento? Es un embalaje que contiene todo el espacio ocupado por el objeto durante el intervalo de tiempo.
Ahora, en cada proceso de detección de colisiones se generan los boundings de movimiento y la prueba de intersección se hace entre estos en vez de entre los objetos. Si se produce una intersección se sabe que en algún momento del intervalo de tiempo se ha producido una colisión. En la siguiente figura se han generado los boundings de movimiento para los objetos del caso anterior y ahora sí se detecta la colisión.
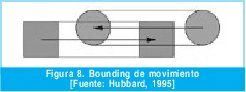
Otra ventaja de utilizar boundings de movimiento es que no hace falta subdividir el intervalo de tiempo, pues con este se cubre todo el intervalo, reduciendo el número de iteraciones necesarias a una sola.
Se tiene que tener en cuenta que constantemente se deberán generar boundings de movimiento y comprobar intersecciones entre ellos. Esto conlleva a que el tipo de envoltorio elegido tenga que ser muy simple, con el problema adicional de no representar con exactitud el espacio ocupado por el objeto.
La condición para detectar todas las colisiones es que el bounding de movimiento sea lo suficientemente grande como para contener todo el espacio ocupado por el objeto, por lo que tendrá una región que no corresponderá al mismo. Si la intersección entre dos boundings se produce en esta región, la colisión detectada será falsa. Para solucionar esto, después de detectar una intersección entre dos boundings es imprescindible comprobar si realmente los dos objetos colisionan en algún momento del intervalo de tiempo.
En un sistema sin boundings de movimiento esta operación sería demasiado costosa debido a la gran cantidad de objetos en la escena, pero los boundings de movimiento descartan rápidamente muchas parejas de objetos, reduciendo el número necesario de este tipo de operaciones. Este problema se ejemplifica en la figura 9, donde se ha utilizado una caja con sus caras paralelas a los planos del mundo como bounding de movimiento.
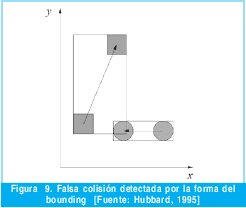
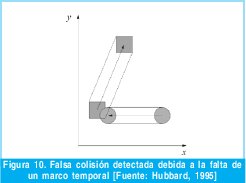
La operación que soluciona el problema anterior también sirve para solucionar otro caso de detección de colisiones falsas. Los boundings de movimiento sólo guardan información espacial del objeto, y no la temporal. Por lo tanto, incluso si el envoltorio elegido aproxima a la perfección el espacio ocupado por el objeto, éste no retiene la posición donde se encontraba el objeto en distintos instantes de tiempo, con lo cual se puede detectar una colisión en el espacio que no se debería producir si se tiene en cuenta el aspecto temporal.
Pero gracias a la operación que soluciona el caso anterior ya queda resuelto también este problema. En la figura 11 se han utilizado envoltorios exactos para mostrar que no es una condición suficiente para afirmar que la colisión detectada es verdadera.
4.3.2 All-pairs weakness
Las simulaciones de hoy contienen muchos objetos, por lo que realizar la operación de intersección entre todas las parejas de objetos representará una cantidad enorme de estas operaciones. Ya hemos visto como la utilización de boundings de movimiento sencillos aumenta el rendimiento del algoritmo de detección, pues el algoritmo de intersección entre los boundings será mucho más rápido que el de intersección entre objetos y pronto se descartarán muchas parejas de objetos, con lo que la operación de intersección entre objetos ya no se realiza para todas las parejas. Pero por más rápido que sea el algoritmo de intersección entre boundings, a medida que la escena va creciendo en número de objetos, la gran cantidad de comprobaciones de intersección que se realizarán hará que el sistema deje de funcionar a tiempo real.
Una característica común entre la gran mayoría de escenas es que los objetos que la componen suelen estar distribuidos en un espacio muy grande en relación al tamaño de estos. Esto hace que se comprueben intersecciones entre boundings de movimiento de objetos que están muy lejanos el uno del otro, siendo muy pocas las que generarán una intersección. Aquí lo interesante sería tener una estructura que nos organice los objetos de for ma que se pueda descartar cualquier posibilidad de colisión entre muchos de los objetos sin tener que realizar la prueba de intersección. Una buena solución es dividir el espacio en regiones más pequeñas, con lo que los objetos estarán en diferentes espacios y se puede afirmar que no colisionarán.
Normalmente esta estructura es compartida con el sistema de visualización del motor de la aplicación; por lo tanto no dependerá sólo del sistema de detección de colisiones el hecho de elegir la estructura más adecuada. Tener una estructura separada de la utilizada por el sistema de visualización puede agilizar la detección de colisiones, pero antes de implementar esta solución es importante estudiar el costo añadido que supondrá para la aplicación tener que mantener otra estructura, tanto por el impacto en el rendimiento como por la memoria extra que necesitará.
4.3.3 Pair-processing weakness
Debido a la complejidad en la forma que un objeto puede tener, diseñar un algoritmo que compruebe si las superficies de dos objetos se intersecan en un momento dado de la simulación implicará que el algoritmo tenga que contemplar una gran multitud de casos en que estas superficies pueden inter seccionar, con lo que el algoritmo será muy poco eficiente.
Si los objetos tuviesen formas más simples entonces se reduciría automáticamente el número de casos en que las superficies de estos podrían interseccionar, pudiendo así diseñar un algoritmo más rápido. Por lo tanto, con el objetivo de acelerar esta fase, se aproximarán los objetos a formas más simples, de forma que el algoritmo compruebe las intersecciones entre estas formas y no entre los objetos.
Cabe mencionar que esta aproximación implica que los objetos utilizados por el sistema de visualización y el de colisiones serán diferentes; por lo tanto, para evitar que el usuario se sienta desconcertado entre lo que ve y lo que realmente colisiona, será necesario llegar a un compromiso entre la complejidad de la forma utilizada para aproximar los objetos y la eficiencia del algoritmo de intersección. Un ejemplo de este error se muestra en la figura 11, donde se ve como se detecta una colisión antes de que el objeto visualizado realmente haya colisionado.
Igual que con la solución dada para la fixed-timestep weakness aquí también se propone la utilización de un envoltorio para aproximar el objeto. Como ya se ha dicho con anterioridad,la ventaja de utilizar un bounding sencillo es que comprobar intersecciones entre ellos es muy eficiente. También cabe mencionar que normalmente será un buen criterio que el envoltorio contenga el objeto en su totalidad, pues de otra forma el usuario podría ver como algunas partes de los objetos penetran sin detectarse una colisión.
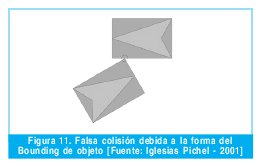
Cada tipo de bounding tiene sus ventajas e inconvenientes; pero, por regla general, como mejor se aproxima al objeto más lento será su algoritmo de intersección. Una aplicación usará el tipo de bounding que más le convenga, algunos de los más utilizados son las esferas (figura 12), las cajas alineadas con el mundo (en inglés axis-aligned bounding box -- AABB) y las cajas orientadas (en inglés oriented bounding box -- OBB) (figura 13).

4.3.4 Boundings más usuales en la detección de colisiones
Inicialmente introduzcamos los distintos tipos de boundings. Éstos se muestran en la figura 14 desempeñando la función de bounding de objeto.
Esfera (bounding sphere): esfera normal.
Caja alineada al mundo (axis aligned bounding box -- AABB): como su nombre indica, es una caja que siempre mantiene la misma orientación que la de los ejes del mundo, de modo que cada cara es paralela a alguno de los planos definidos por los ejes del mundo y perpendicular a los otros dos.
Caja orientada (oriented bounding box -- OBB): a diferencia de la caja alineada al mundo, ésta puede tener una orientación diferente a la de los ejes del mundo.

5. REACCIÓN A LAS COLISIONES
5.1 Introducción
Para que un sistema de colisiones resulte realista después de detectar una colisión se debe variar el comportamiento de las entidades de forma convincente. Idealmente esto implicará aplicar leyes de la dinámica que correspondan con nuestra aplicación, con toda la matemática que eso conlleva.
En otras aplicaciones sólo se necesita implementar una aproximación lo suficientemente realista a algunas de las reacciones más comunes, sin tener necesidad de entrar en el complejo mundo de la dinámica. A continuación se mostrará cómo simular de manera sencilla dos de las reacciones más usuales: el deslizamiento y el rebote.
La gravedad está presente en la mayoría de este tipo de aplicaciones, por lo que también se necesitarán un par de métodos muy sencillos para simularla y hacerla interactuar con las dos reacciones anteriores.
5.2 Deslizamiento
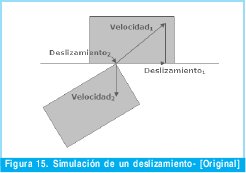
La solución propuesta es muy simple. Antes que nada es necesario hallar el plano de deslizamiento, que corresponde con el plano de colisión. Éste pasará por el punto de colisión y su orientación dependerá de la posición, velocidad y for ma de los objetos que colisionen. Una vez hallado el plano de deslizamiento se proyecta en él, el trozo del vector de velocidad que se encuentre después del punto de colisión (si un objeto se mueve según su vector de velocidad, dicho trozo indicará el espacio que le falta por recorrer al objeto; se podría considerar algo así como la energía restante en el momento de la colisión). Ahora sólo falta reducir esta proyección con el factor de fricción que elijamos y el vector resultante indicará hacia donde y cuanto es necesario desplazar el objeto para simular una reacción de deslizamiento. La figura muestra este procedimiento gráficamente, sin el factor de fricción para mayor claridad.
Con esta reacción podremos hacer que un objeto suba automáticamente ciertos obstáculos y pendientes y se deslice por las paredes, que de otra forma harían que el objeto se detuviera al mínimo contacto. Además eligiendo factores de fricción diferentes para tipos de superficies distintas podemos simular el comportamiento de los objetos en superficies como la arena o el hielo.
5.3 Rebote
Por lo que respecta al rebote, la solución propuesta es tan simple como la propuesta para el deslizamiento, pues sigue un método muy parecido. De hecho, las únicas diferencias son que en lugar de proyectar el trozo restante del vector de velocidad sobre el plano de colisión, ahora es necesario reflejarlo, y que el vector reflejado se reduce con un factor de amortiguamiento en lugar de un factor de fricción. En la figura se muestra un ejemplo.
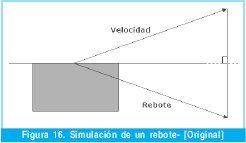
Cabe mencionar que para un rebote se deseará que modifique no sólo el vector de velocidad durante el instante de la colisión sino que lo haga de forma permanente para que el objeto mantenga una nueva trayectoria a partir del momento de la colisión. Esto implicará que se deban modificar aquellos parámetros de la aplicación que sean los responsables de generar el vector de velocidad, de modo que a partir del momento de la colisión den una velocidad reflejada a la anterior. Pero esto ya depende de la implementación de cada aplicación.
Referencias bibliográficas
[1] C. Murilo G. Dynamic Simulations of Multibody Systems. Editorial Springer. 2001.
[2] M., Francis C. Applied Dynamics. Editorial John Wiley & Sons, Inc. 1998.
[3] E., David. Dynamic Collision Detection using Oriented Bounding Boxes, Disponible: http://www.magic-software.com/Documentation/dynacoll.pdf , Magic Software
[4] G., M. C. Lin y D. Manocha 1996. OBB-Tree: A Hierarchical Structure for Rapid Interference Detection. Disponible:http://citeseer.nj.nec.com/gottschalk96obbtree.html
[5] H., Phillip M. 1995 Collision detection for interactive graphics applications. Disponible: http://citeseer.nj.nec.com/hubbard95collision.html
[6] D., Mintz. Octree Spatial Partitioning for Real-Time 3D Hidden Surface Removal. Disponible: http://silcon.silcon.com/~brink/papers/octrees.html
[7] I., P., Carles. 2001 portal Rendering. Disponible: http://www.macedoniamagazine.com/
[8] BSP Tree Frequently Asked Questions. Información relacionada con los árboles BSP. Disponible: http://www.xs4all.nl/~smit/whole.htm
[9] Universidad Complutense de Madrid. 2000. Curso de desarrollo de juegos por ordenador.
Luís Fernando Vargas Tamayo
Ingeniero Mecánico Universidad Nacional de Colombia. Magíster en Ingeniería - Materiales y Procesos. Universidad Nacional de Colombia. Docente de planta facultad de Ingeniería UDFJC. Director del grupo de investigación DIMSI. lfvargast@udistrital.edu.co
Leonardo Emiro Contreras Bravo
Ingeniero Mecánico Universidad Francisco de Paula Santander. Magíster en Ingeniería - Materiales y Procesos. Universidad Nacional de Colombia. Docente de planta facultad de Ingeniería UDFJC. Director del grupo de investigación DIMSI. lecontrerasb@udistrital.edu.co.
Creation date:
Licencia
A partir de la edición del V23N3 del año 2018 hacia adelante, se cambia la Licencia Creative Commons “Atribución—No Comercial – Sin Obra Derivada” a la siguiente:
Atribución - No Comercial – Compartir igual: esta licencia permite a otros distribuir, remezclar, retocar, y crear a partir de tu obra de modo no comercial, siempre y cuando te den crédito y licencien sus nuevas creaciones bajo las mismas condiciones.




2.jpg)