Ingeniería, 2004-00-00 vol:9 nro:1 pág:52-56

Síntesis con Agrupaciones Circulares de Dipolos

DIPOLE CIRCULAR ARRAYS SYNTHESIS

Carlos A. Suárez Fajardo, Miguel Ferrando Bataller, Alejandro Valero,
Departamento de Comunicaciones, Universidad Politécnica de Valencia.
Elvis E. Gaona
Miembro del Grupo de Comunicaciones, Universidad Distrital Francisco José de Caldas.

Resumen

Este artículo describe la síntesis de los patrones de radiación con arreglo de antenas circulares usando el dipolo finito frente al cilindro metálico infinito. La técnica usada puede ser Fourier y un método de síntesis de patrón de radiación con un arreglo de antenas de N dipolos uniformemente espaciados en un anillo circular de radio (b) frente a un cilindro de radio (a). La corriente de excitación requerida se determina de una formula deducida en este artículo.

Palabras Clave:
Arreglos, Agrupaciones circulares, Síntesis de antenas, dipolo.

Abstract

This article describes the synthesis of radiation patterns with circular antenna arrays using the finite dipole in front of a metallic infinite cylinder. The used technique will be that of Fourier, and a method for synthesizing the radiation pattern with antenna array of N dipoles uniformly disposed around a circular ring of radio (b) an in front of a cylinder of radio (a) is proposed. The required excitation currents are determined from a deduced formula in the paper.

Key Words:
Arrays, Circular Array, Antenna Synthesis, Dipole

I. INTRODUCCIÓN

Las agrupaciones de antenas, donde los elementos están situados sobre un círculo o un cilindro circular se han utilizado en diversos sistemas de telecomunicación tales como: radar, navegación aérea, espacial y marítima, así como en estaciones base para telefonía móvil entre otras.

Las agrupaciones circulares son especialmente interesantes para la formación adaptativa de haces, en la búsqueda de señales deseadas, control de ruido no deseado y en diseño de sistemas de antenas inteligentes. Un amplio estudio teórico con aplicaciones prácticas de estas agrupaciones se encuentra entre otros en [1]. En [2] se presenta un método de proyecciones ortogonales para la síntesis con agrupaciones circulares utilizando antenas isotrópicas. En [3]-[4] se encuentran estudios particulares de síntesis con agrupaciones circulares de antenas mediante métodos analíticos basados en técnicas de Fourier,por otra parte los método de síntesis basados en algoritmos genéticos o Simulated Annealing son ampliamente utilizados como en [5] donde se presenta una solución mediante la aplicación de algoritmos genéticos. En [6] se estudia el efecto de la separación entre los elementos y el tipo de diagrama del elemento básico utilizado. En [7] se utilizan las agrupaciones circulares en la generación de múltiples haces para aplicaciones en sistemas móviles en la estación base. Se conocen pocas referencias de síntesis de agrupaciones de dipolos que tengan en cuenta la estructura de soporte [8], [9].

Los diagramas obtenidos con este tipo de agrupaciones ofrecen ventajas como: un amplio cubrimiento angular (360º) con un pequeño cambio en el ancho de banda o nivel de lóbulos laterales, una gran flexibilidad en su forma permitiendo haces tipo pincel direccionables, múltiple pincel, formas como: sectoriales, omnidireccionales y otras formas. El poco desarrollo obtenido en el pasado pudo ser ocasionado por la dificultad de excitar la agrupación circular con los valores apropiados de fase y amplitud que son en general más complejos que en las agrupaciones lineales, hoy en día este problema es superado con la optimización en el diseño de las redes de conformación de haz [10].

Otras características adicionales son: los efectos de los lóbulos de difracción no son tan pronunciados como en agrupaciones planas, ciertos elementos pueden no ser visibles en ciertas direcciones lo cual permite desconectarlos afectando la radiación en los lóbulos secundarios sin consecuencias graves para el diagrama final.

La simetría básica de una agrupación circular ofrece otras ventajas adicionales a las ya expuestas como es la de permitir compensar los efectos del acoplamiento mutuo entre los elementos de la agrupación mediante la escogencia apropiada de la excitación de la agrupación en una serie de componentes espaciales simétricos.

Algunos investigadores han estudiado el problema de síntesis de diagramas de radiación con agrupaciones circulares o cilíndricas, utilizando elementos directivos y en particular algunos han estudiado las agrupaciones cilíndricas de dipolos frente a cilindros, pero la mayoría ha utilizado para su estudio el diagrama directivo teórico dado por E= 1 + cos(Φ), [1], [11], [12].

El uso de elementos con diagramas de radiación directivos permite una mejora adicional como es la de presentar una estabilidad en la amplitud de los modos ante la variación en frecuencia como se muestra en [1], [12].

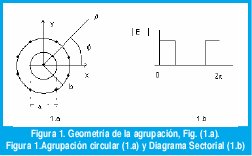
En este artículo se analizará el problema de una agrupación con N dipolos sobre un anillo de radio b, frente a un cilindro metálico de radio α=, figura 1.a calculando inicialmente el campo de radiación E_z (sin considerar el acoplamiento entre dipolos), para posteriormente utilizarlo en aplicaciones de síntesis de diagramas de radiación deseados E_d; en particular se sintetizarán los siguientes diagramas de radiación: sectoriales figura 1.b, polinomios uniformes, triangulares y síntesis de Chebyshev.

II. SÍNTESIS CON AGRUPACIONES CIRCULARES DE DIPOLOS FRENTE A CILINDRO METALICO.

La capacidad de las agrupaciones para modificar el diagrama de radiación de la antena básica puede aprovecharse para sintetizar un diagrama de radiación que cumpla con determinadas especificaciones mediante la selección apropiada de la amplitud y fase de las corrientes.

Los métodos de síntesis de diagramas de radiación han mostrado una constante evolución y se puede notar que hasta el año 1970 aproximadamente, las técnicas más utilizadas eran analíticas y a partir de este año las técnicas preferidas son las numéricas. En una revisión de las publicaciones hasta hoy, se puede concluir que sigue en constante estudio el problema de síntesis, con un incremento notorio en los últimos años de los artículos sobre este aspecto [14].

Como se demostró en [8], el campo de radiación para un dipolo finito frente a un cilindro infinito, y para θ=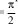 está dado por:

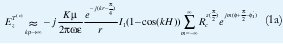
donde

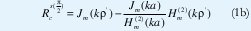
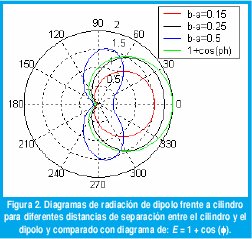
La figura 2 muestra el comportamiento del campo radiado por el dipolo frente al cilindro, para diversas separaciones entre el dipolo y el cilindro y se comparan los resultados contra el caso del diagrama generado por un cardioide.

Generalizando para N dipolos sobre un anillo circular de radio (b) y frente a un cilindro de radio (a) se tiene la siguiente expresión:

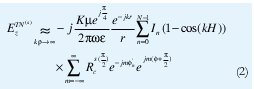
Donde la ubicación de la fuente sobre el anillo está dada por: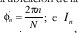; e I_n representa la amplitud y fase de la corriente en cada dipolo y p' = b.

La expresión final para el campo lejano (E^T_zn) Normalizado (para un dipolo dado y una distancia específica), generado por N dipolos sobre un anillo circular de radio (b) frente a un cilindro de radio (a) está dada por:

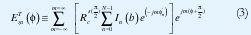
La expresión (3) se interpreta como expansión en serie de Fourier del campo E^T_zn:

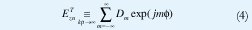
Donde los coeficientes de Fourier D_m están dados por:

Dado que el patrón deseado E_d es periódico, se puede expandir en serie de Fourier como se nota a continuación:

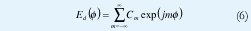
Donde los coeficientes C_m son determinados por:

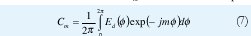
La series infinitas (4) y (6) se truncarán a 2M + 1 términos por razones prácticas en cuanto al número máximo de elementos que se pueden utilizar y el espaciamiento mínimo entre elementos y por otra parte para obtener una única solución.

Igualando las series del patrón deseado y la agrupación y truncándolas a 2M+1 términos se tiene:

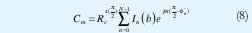
Igualando (7) y (8) se tiene:

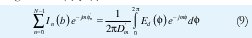
Donde el término D_m está dado por:

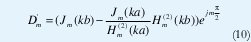
Multiplicando a ambos lados de la ecuación (9) por el término: e_jmΦn y sumando las ecuaciones en (m) al lado derecho se tiene:

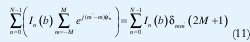
Donde 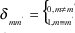es el delta Kronecker. La expresión final para las corrientes es dada por:

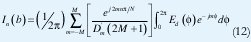
Para: n= 0,1,2....N - 1 .

III. RESULTADOS NUMÉRICOS

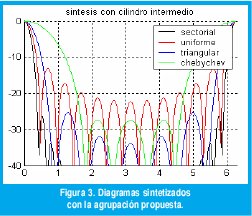
Una vez definida la expresión del campo(E_d) que se desea radiar con la agrupación, se expande en serie de Fourier con los valores de los coeficientes de expansión dados por (C_m) en (7), lo cual permite a través de la expresión en (12), aplicar las corrientes necesarias a la agrupación , para tener el diagrama radiado deseado (E_d). La técnica expuesta se muestra aplicada en la síntesis de diagramas sectorial, la síntesis generada por polinomios uniforme, triangular y síntesis de Chebyshev (en orden de aparición de izquierda a derecha) como se nota en la figura 3; sintetizados por una agrupación con N = 23 elementos, cilindro intermedio de radio a = 0.75λ, dipolos sobre anillo circular de radio b = 1λ.

En el proceso de Síntesis circular con agrupaciones de dipolos frente a cilindro metálico infinito con una separación optima de 0.25 como se nota en figura 2 y en [8], se encontró que los parámetros que tienen incidencia en el diseño de una agrupación de esta naturaleza son:

El tamaño de el radio b del anillo sobre el que están ubicados los dipolos el cual incide directamente en la elección apropiada de el número mínimo de modos M (y número de antenas N) dado que afecta el término 1b ver [8].

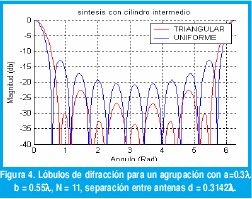
Para agrupaciones con radio b inferior a 0.75λ es difícil mantener una separación mayor o igual a 0.5l entre antenas (para evitar efectos de acoplamiento) sin ocasionar problemas de lóbulos de difracción como se nota en la figura 4, donde se muestra el resultado de una síntesis con radios a = 0.3, b = 0.55λ M = 5, N = 11 y con una separación de 0.3142λ ya se tienen lóbulos de difracción.

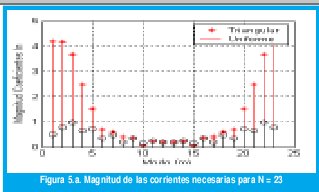
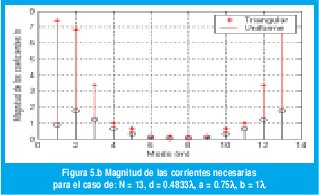
El número de modos M a considerar puede ser inferior al necesario para evitar recorte del término 1b (ocasionando distorsión en el diagrama de un solo dipolo frente al cilindro como se demuestra en [8], ver figura 3), sin embargo el efecto que esto ocasiona desde el punto de vista de síntesis es que la magnitud de los coeficientes crece en la medida que se tomen menos modos M, lo cual se muestra en la figura 5.a para una agrupación con: a = 0.75, b = 1λ, N = 23, d = 0.3722λ comparada con la agrupación con los mismos valores anteriores de los radios pero con N = 13, b = 0.4833λ ver figura 5.b.

La separación entre los dipolos y el cilindro intermedio es óptima en 0.25λ y en la medida en que se aumenta este valor, los coeficientes necesarios para la síntesis son de mayor magnitud.

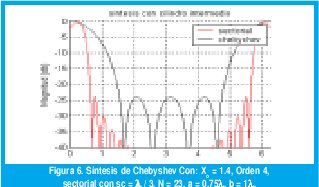
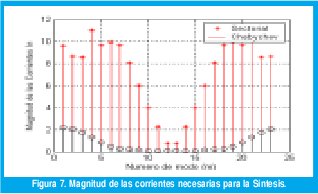
La magnitud de los coeficientes de las corrientes es igualmente afectada por el tipo de diagrama a sintetizar como se nota en la figura 5.a para el caso de un polinomio triangular es mayor la magnitud de los coeficientes que para un polinomio uniforme. Este mismo efecto se nota en las figuras 6 y 7 para el caso de síntesis sectorial y de Chebyshev.

Una de las posibles soluciones que satisfacen los requerimientos de separación entre antenas mayor o igual a 0.5 con el menor número de antenas posible sin ocasionar lóbulos de difracción puede ser para: a = 2.5λ, b = 2.75λ, N = 35.

IV. CONCLUSIONES

Se ha presentado el desarrollo analítico de las ecuaciones de síntesis con agrupaciones circulares que utilizan elementos directivos, tomando el caso de un dipolo frente a cilindro el cual genera una diagrama de elemento muy similar al modelo que tradicionalmente se utiliza para este tipo de estudios como es el de tipo cardioide, sin embargo el estudio presentado aquí, al tomar el diagrama exacto del elemento, nos permite verificar en forma más apropiada el comportamiento de la agrupación, mostrando resultados que no se pueden ver al utilizar el modelo aproximado.

La síntesis de diagramas con este tipo de agrupaciones muestra resultados que dependen de parámetros como: radios de la agrupación y del cilindro interior, número de antenas, así como el tipo de diagrama a sintetizar, hecho que está directamente relacionado con los términos necesarios para efectuar la expansión en serie de Fourier de la función que representa el diagrama a sintetizar.

El problema del efecto de la separación entre los elementos en una agrupación circular, utilizando el modelo tipo cardioide, muestra serios problemas al utilizar separación entre elementos cercana a 0.5l sin embargo con el modelo exacto desarrollado aquí, se corroboran los resultados obtenidos en diversos montajes experimentales usando separaciones cercanas o iguales a 0.5λ

La separación entre las antenas debe ser seleccionada teniendo en cuenta no solamente la separación deseable de 0.5 sino que aparte de esto se debe tener en cuenta el hecho que al truncar la serie infinita que define el campo radiado por la agrupación 1.a esto afecta el término 1.b que depende precisamente de los valores de los radios y su efecto es más notorio para radios pequeños.

REFERENCIAS BIBLIOGRÁFICAS

[1] A. W. Rudge, et al, The Handbook of Antenna Design. London: IEE pres. 1986.

[2] R. Vescovo, "Constrained and Unsconstrained Synthesis of Array Factor For Circular Arrays". IEEE Trans. Antennas Propagation. volt 43. No12, pp .1405-1410, December 1995.

[3] F. I. Tseng, and D. K. Cheng, "Pattern Synthesis of Circular Arrays with Many Directive Elements", IEEE Trans. Antennas Propagation, vol. AP-10, pp. 758-759, nov. 1968.

[4] C. Suárez, M. Ferrando y A. Valero, "Síntesis de Diagramas de Radiación con Agrupaciones Cilíndricas Aplicables en Sistemas 3G UMTS". Revista facultad de Ingeniería, U. Distrital "FJC", No 28, junio 2003.

[5] F. J. Ares, J. A. Rodríguez, E. Villanueva, and S. R. Rengarajan, "Genetic algorithms in the design and optimization of antenna array Patterns," IEEE Trans. Antennas Propagation. Vol. AP-47, pp. 506-510, March 1999.

[6] C. Suárez, M. Ferrando, A. Valero, "Pattern Synthesis of Uniform Circular Arrays with Directive Elements," 2004 IEEE, AP-S/URSI Symposium, Monterrey California, June 20, 2004.

[7] C. Suárez, M. Ferrando, A. Valero, "Pattern Synthesis with Circular Arrays for Multiple Beam Systems," COST 273/284,Workshop on Antennas and Related Systems Aspects in Wire Less. Com. Gothenburg, Sweden, June 10, 2004.

[8] C. Suárez, M. Ferrando y A. Valero, "Radiación de Dipolos Frente a Cilindro Metálico Infinito" URSI, U. La Coruña, España, Septiembre 10, 2003.

[9] John C. Herper, et al. "Element pattern of an Axial Dipole in a Cylindrical Phased Array". IEEE Trans AP-33, No. 3, March 1985, p. 259-272.

[10] Butler, Lowe."Beam forming Matrix Semplifies Design of Electronically Scanned Antennas" .Electronic Design. 1961.

[11] B. Sheleg, "A Matrix-Fed circular Array for Continuous Scanning", IEEE, Proc. Vol. 56, No. 11, November, 1968, p. 2016-2027.

[12] T. Rahim, "Directional pattern synthesis in circular arrays of directional antennas", Ph. D. dissertation, London Univ, 1980.

[13] Lars. Josefsson, H. Steyskal. Methods and Software Tools for the Design of Antennas and Arrays, Advanced Short Course,Universidad de Santiago de Compostela, España, sept. 4, 2002.

Carlos A. Suárez Fajardo
Ingeniero Electrónico, Universidad Distrital Francisco José de Caldas. Especialista en Instrumentación. Adelanta estudios de Doctorado en la Universidad Politécnica de Valencia.

Miguel Ferrando Bataller
Ingeniero. Ph.D. en Comunicaciones. Profesor Titular, Universidad Politécnica de Valencia.

Alejandro Valero
Ingeniero. Ph.D. en Comunicaciones. Profesor Titular, Universidad Politécnica de Valencia.

Elvis E. Gaona
Ingeniero Electrónico, Universidad Distrital Francisco José de Caldas. Miembro del Grupo de Comunicaciones, Universidad Distrital Francisco José de Caldas.