DOI:
https://doi.org/10.14483/23448393.2821Publicado:
2001-11-30Número:
Vol. 7 Núm. 2 (2002): Julio - DiciembreSección:
Ciencia, investigación, academia y desarrolloEl diseño digital y lógica mixta
Palabras clave:
Diseño Digital, Diseño Lógico, Técnica Digital. (es).Descargas
Referencias
Hayes J., "Diseño de Sistemas Digitales y Microprocesadores", McGraw-Hill,1986.
TTL Logic, Standard TTL, Schottky, Low Power Schottky, Texas Instruments Inc., 1988
Mano M., "Digital Design", Prentice Hall, 1991
Hayes J., "Digital Logic Design", Addison Wesley, 1993
Tocci R., "Circuits numériques; Theorie et applications ", Reinal Goulet Inc., 1992.
Porat D. , Barna A., "Introduction to Digital Techniques", Wiley, 1987
Bernard J. et Hugon J., " Pratiques des circuits logiques", Eyrolles, 1987.
Wakerly J., "Digital Design Principles and Practices", Prentice Hall, 1994
Pellerin D., Holley M, " Practical Design Using Programmable Logic ", Prentice Hall, 1991.
Tocci R., "Digital Systems - Principles and Applications", 6th ed., Prentice Hall, 1995.
Pellerin D. and Holley M, " Digital Design using ABEL ", Prentice Hall, 1991.
Peatman J., "Digital Hardware Design ", Mc-Graw-Hill, N.Y., 1980
Sawan M, Fréchette P.," Systemes Logiques II ", Ecole Polytehnique de Montreal, 1992.
Simoni M, " Computer and Digital Fundamentals ", Georgia Institute of Technology, 1998.
Saravia Y., " Conception et Verification des Circuits VLSI ", Editions de Ecole Polytechnique de Montreal, 1994
Gima T.,"Digital Systems Design",College of Computing Sciencies and Engineering, U. of North Florida , 2003
Fletcher W., "An Engineering Approach to Digital Design", Prentice-Hall, 1980
Prosser F. ,Winkel D.E., " The Art of Digital Design ", Prentice Hall, 1987.
Breeding K., "Digital Design Fundamentals", Prentice Hall, 1989
Tinder R., "Digital Engineering Design A Modern Approach", Prentice Hall, 1991
Comer J.D., " Digital Logic and State Machine Design " Saunders College Publisher, 1995.
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Ingeniería, 2002-00-00 vol:7 nro:2 pág:73-78
El diseño digital y lógica mixta
Alvaro Betancourt Uscátegui
Miembro grupo de investigación LAMIC de la Universidad Distrital Francisco José de Caldas.
Resumen
Un buen estilo de diseño de hardware debe ser fácil de entender y aprender, forza al diseñador a pensar a través del diseño total antes de emprender su contrucción. La metodología de lógica mixta presenta cierta resistencia y se prefiere las técnicas de diseño de la lógica positiva o lógica negativa. La combinación de las dos lógicas da nacimiento a la lógica mixta y representa una excelente solución. Aunque la técnica es antigua, su potencia no ha sido suficientemente explotada. Este artículo presenta una descripción de los conceptos de la lógica mixta y muestra algunas de las ventajas de su utilización.
Palabras Clave:
Diseño Digital, Diseño Lógico, Técnica Digital.
Abstract
A good design style should be easy to understand and to learn, force the designer to think through the total design before the construction. Mixed logic methodology still meet some resistance and is prefered the positive and negative logics design techniques. Although the technique is older, but the power has not been widely appreciated. The paper presents the basic idea of mixed logic concepts and its utility.
Key words:
Digital design, Logic Design, Digital Technique.
I. INTRODUCCIÓN
Los cambios a los cuales se enfrenta el ingeniero en diseño digital varían dramáticamente en la medida en que la tecnología avanza. Ello hace que los diseños sean más rápidos, se utilice un gran número de compuertas y físicamente sea más pequeño. Sin embargo las bases que sustentan el diseño no han cambiado y no parece que cambiara en un futuro cercano. La concepción de circuitos lógicos combinatorios en lógica mixta merece una particular atención dada la realización y construcción de circuitos más simples, claros y eficaces. El diseño digital es cambiante y para los diseñadores, la eficiencia puede estar influenciada por las diferentes técnicas utilizadas para desarrollar e implementar el diseño. Las operaciones lógicas AND, OR y NOT son herramientas familiares de aplicación diaria en el diseño de actividades; de ahí, la motivación para que el diseñador digital desarrolle lógica combinatoria en términos de esas familiares primitivas. De otra parte, los diseñadores frecuentemente desean utilizar componentes o dispositivos físicos como NAND y NOR. La Lógica mixta ofrece mejora significativas sobre los métodos convencionales.
Durante años grupos de diseñadores han usado una colección de técnicas de diseño las cuales forman parte de un "estilo" de diseño para encontrar una solución. El estilo incluye una manera conveniente para representar un algoritmo de solución del problema como un diagrama de flujo de hardware. El tiempo utilizado, la claridad de la documentación y la exactitud de los resultados es en cierta forma un estilo de diseño en hardware. La notación de la lógica mixta proporciona un mecanismo simplificado para el análisis y el diseño de circuitos digitales. El uso correcto de dicha notación, proporciona las expresiones y diagramas lógicos de cada uno.
Si bien dicha técnica se integra en los cursos sobre digitales en programas de ingeniería electrónica y afines, las técnicas de la lógica positiva y negativa son utilizadas con mayor frecuencia en libros de textos y manuales sobre digitales. Además, la confusión e ideas no claras relacionadas con la lógica mixta se debe a que tanto en los libros como en los manuales se refieren a las puertas en términos de funcionalidad de la "lógica positiva" [ 1,2].
La puesta en funcionamiento de un circuito lógico combinatorio necesita de una parte, determinar la expresión lógica de la función de la ecuación y en segundo lugar, la realización de dicha función mediante puertas lógicas respetando los diferentes parámetros eléctricos (voltajes, velocidad de propagación, etc.). La complejidad de un circuito se mide por el grado de dificultad que se presenta luego del paso de la ecuación algebraica a un esquema lógico y viceversa.
El paso bidireccional debe hacerse idealmente, sin transformaciones suplementarias, basándose en las diferentes leyes del algebra de Boole (De Morgan y otras). En otras palabras, es necesario que el análisis del circuito lógico sea simple y de fácil comprensión. Dicha simplicidad se apoya en una elección de la lógica de representación de tensiones (voltajes), en los diferentes tipos de componentes a utilizar y en obtener sin retardo razonable la evaluación de la salida de un circuito lógico a partir de las condiciones y combinaciones en sus entradas.
La combinación de las dos lógicas (negativa y positiva) da nacimiento a la lógica mixta y representa una excelente solución. Se destaca la claridad o facilidad de lectura de los esquemas y el pasaje de la ecuación booleana a un diagrama lógico así como la optimización en cuanto a la reducción del número de circuitos integrados y una mejora de la velocidad y retardo de propagación.
El artículo se organiza de la siguiente manera. En la segunda parte se presentan los principios de la lógica mixta, la equivalencia de las puertas lógicas y la simbología. En la tercera parte se presenta un análisis de circuitos lógicos mixtos. A continuación se muestra la conversión de un circuito lógico estándar a uno en la lógica mixta y finalmente las conclusiones.
II. PRINCIPIOS DE LA LÓGICA MIXTA
Los métodos convencionales enfatizan en un paralelo entre la lógica y el voltaje. La lógica mixta por el contrario enfatiza la distinción entre los dos, eliminando la confusión que se introduce al forzar la relación entre el voltaje y la lógica. De ahí que, sobre el diagrama se usa un circulo pequeño unido tanto a la entrada como una salida si hay lugar como se verá mas adelante.
La lógica mixta permite separar la convención (positiva, negativa) y el estado (activo, inactivo) que no se desarrolla en la lógica tradicional. La resistencia para aceptar completamente este método gira alrededor de la comprensión de la notación del "uno" y el "cero" así como del uso alternado de las representaciones de la puertas. Su utilidad viene dada en la medida que aumenta la claridad de un esquema o diagrama , optimiza la utilización de los circuitos integrados y es mas rápida en razón a que hace un mayor uso de compuertas NAND y NOR.
Así por ejemplo, la operación lógica OR de dos entradas : A y B presenta como salida Y tal que Y es activo si A es activo o B es inactivo; A está en lógica positiva (activa Alto) mientras que B está en lógica negativa (activa Bajo). El circuito en lógica tradicional no indica si las entradas son activas en Alto o Bajo. En lógica mixta, la información sobre A y B se muestra por completo (entrada B negativa e inactiva). Recordemos entonces las convenciones y definiciones utilizadas en lógica positiva y negativa.

La lógica mixta toma prestada las convenciones de la lógica positiva y negativa. Además está basada sobre tres funciones lógicas como lo son : AND, OR y el OR exclusivo, cuyas operaciones son realizadas por tres componentes: la puerta lógica AND, la puerta lógica OR y el "NON" . La puerta NON (inversor) tiene como función invertir una tensión (ó voltaje) más nó la lógica de una variable. Esto hace que la puerta AND pueda ser representada por seis símbolos como se muestran en la figura No. 1 y que las puertas lógicas XOR y XNOR puedan estar representadas por los símbolos mostrados en las figuras No. 2 y No. 3 respectivamente.
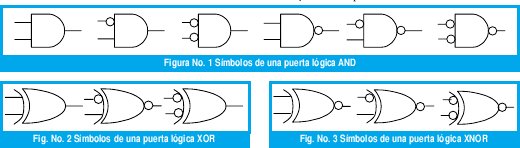
2.1 Equivalencia de las puertas lógicas
Conviene también tener presente que el uso de la lógica mixta permite ver las tablas de verdad de una forma más general que cuando se utiliza la lógica positiva o negativa. A continuación se presentan las tablas de verdad de cada lógica así como las tablas de las tensiones (o voltajes).
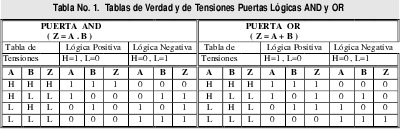
Donde H significa Alto, L significa Bajo. También para " NON " (Z = A) tenemos que :
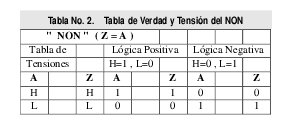
Con base en las tablas anteriores, podemos constatar que una puerta AND en lógica positiva es equivalente a una puerta OR en lógica negativa;
Z = A+ B (1)
A lo largo del artículo se utiliza para la notación anterior como Z=A + B luego Z = A.B (2) ó en general X=X
También se aprecia que una puerta OR en lógica positiva es equivalente a una puerta AND en lógica
negativaZ = A. B (3)
luego Z=A+B (4)
Nótese que de conformidad con lo expresado anteriormente, la notación general X X
2.2 Puertas estándares y sus equivalentes
Los esquemas que representan las puertas lógicas estándar y sus equivalentes dentro de la lógica negativa y lógica positiva se presentan en la Tabla No. 3
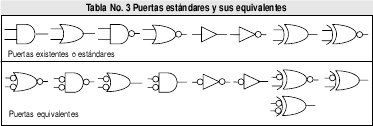
El inversor, la XOR y la XNOR son casos particulares.
Se requieren tres etapas para encontrar la equivalencia de una puerta elemental en una lógica dada aotra lógica. A nivel de la puerta AND tenemos:
a) cambiar la puerta AND en una puerta OR
b)omitir en la puerta OR, los círculos pequeños de las variables que existían en la puerta AND
c) adicionar los círculos pequeños en la puerta OR para las variables que no existían en la puerta AND Debe haber paridad a nivel de los círculos, (es decir a lado y lado) ó nada (no haya círculos).
En el caso de una puerta OR, los mismos procedimientos se deben ejecutar para realizar la conversión a una puerta AND.
2.3 Inversión lógica e Inversión de tensión o voltaje
El inversor no cambia la lógica de una variable pero sí invierte la tensión de la señal. Es decir, el inversor no cambia la convención. Es esta la razón por la cual para evitar el uso peligroso del término "inversor " a la puerta NON se le conoce como función " oops ". La lógica mixta diferencia la inversión lógica de la inversión física.
Es así como la función "oops" implica que la lógica de la señal es satisfactoria pero el nivel de voltaje o tensión debe ser conmutado. La ilustración puede verse al considerar la ecuación A = B o C, donde B es una señal disponible solo en bajo, es decir BL . El circuito correspondiente es:
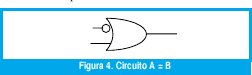
Pero si el diseñador no dispone del circuito, puede utilizar la puerta NOR y tendrá
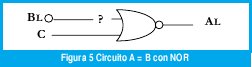
Como BL debe ser cambiado a B, el diseñador inserta la función " oops" y el circuito quedará :
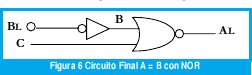
2.4 Simbología
Una variable en lógica positiva está representada por su nombre o por su nombre seguido de (H). Sin embargo , si la variable es activa en lógica negativa, estará representada por su nombre seguido de una barra ó estrella ó bien por (L). A nivel de los esquemas lógicos, un trazo simboliza la variable activa en lógica positiva y un circulo pequeño al inicio del trazo tiene como fín representar la variable en lógica negativa, es decir:
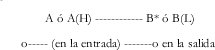
En cuanto a otros símbolos, la inversión acompañada de un cambio de convención esta esquematizada por un a barra oblicua, mientras que la función "oops" invierte la representación física, o sea la tensión (cambia el voltaje). En la figura No. 7 se muestra un resumen de dichos símbolos:
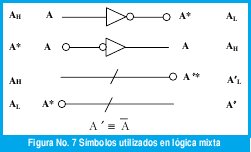
Varios libros de texto sobre digitales muestran la equivalencia de los símbolos alternos disponibles para varias funciones de la lógica positiva [3,4,5,6,7,8,9,10,11,12 ]. Sin embargo no todos utilizan completamente la lógica mixta para el diseño y la documentación para expresar una función prevista.
2. 5 Análisis de circuitos en lógica mixta
Los procedimientos básicos para el análisis de un circuito en lógica mixta, tal como se presentan en [13,14] entre otros, se resumen de la siguiente manera:
a) inscribir sobre el esquema lógico las salidas de las funciones AND y OR a partir de sus puertas respectivas,
b)complementar una expresión si el trazo ó línea que le representa posee una barra oblicua,
Se trata de despreciar, de una parte, la presencia de los pequeños círculos y de otra el hecho que la variable está presentada en lógica negativa o positiva
En la figura No. 8 se presenta al análisis de un circuito diseñado en lógica mixta
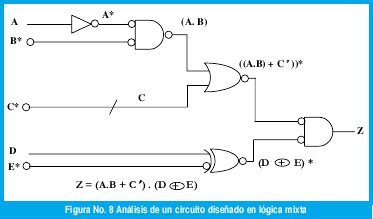
2.6 Síntesis de funciones en lógica mixta
Las etapas de síntesis o implementación de una función lógica a partir de la ecuación algebraica booleana son:
a) ignorar las " complementaciones " y diseñar un diagrama que realice las relaciones lógicas AND y OR
b)transformar el circuito con el objeto de utilizar las puertas estándares específicas solicitadas (NAND, NOR, XOR), de ser necesario
c) adicionar los círculos pequeños y las barras oblicuas para " complementar " las variables, guardando la paridad respectiva a nivel de los círculos, (es decir a lado y lado) ó nada (no haya círculos).
Es claro que una ecuación booleana puede ser representada de diferentes formas.
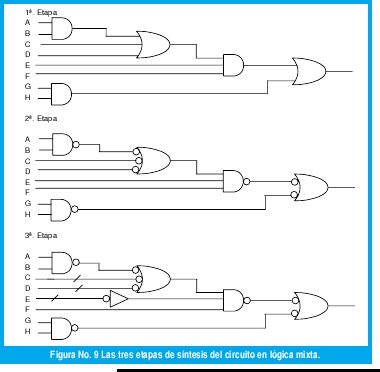
Veamos entonces las tres etapas de la síntesis de un circuito en la lógica mixta. Tomemos el ejemplo de realizar la función que cumpla Z= (AB+C +D)EF+GH. Asumimos que todas las entradas están disponibles en lógica positiva (activa en nivel alto) y que adicionalmente se desea utilizar solamente puertas NAND, [13].
El seleccionar puertas NAND y NOR es aconsejable porque: 1) disminuye el número de piezas de circuitos integrados o sea reduce el costo de concepción; 2) hay optimización de la velocidad de funcionamiento; 3) las puertas son componentes universales, es decir que un circuito lógico se puede realizar con uno u otro tipo de puertas. En la figura No. 9 se muestran las tres etapas de síntesis del circuito en lógica mixta.
III. CONVERSIÓN DE UN CIRCUITO LÓGICO A LA LÓGICA MIXTA
Una vez visto los conceptos de la lógica mixta, se trata ahora de efectuar la conversión de los circuitos existentes de la lógica positiva en lógica mixta. La conversión facilita la lectura y la comprensión y por tanto el mantenimiento del sistema. El esquema lógico debe reflejar la ecuación algebraica que representa. Así que, los elementos de base del esquema, AND y OR, deben corresponder a los elementos de base de la ecuación algebraica (*,+). Las cuatro etapas que se siguen para la conversión son:
1. Convertir la puerta de la etapa de salida en una puerta equivalente, de forma tal que su salida corresponda al nivel de lógica solicitada de acuerdo con la disponibilidad de la señal (Alto ó Bajo);
2. Convertir la(s) puerta(s) que alimentan la última etapa de tal forma que el número de pequeños círculos sobre un trazo ó línea que unen una salida de una puerta a una entrada de otra puerta, es par (es decir a lado y lado) ó nada (no haya círculos);
3. Completar las otras etapas una a la vez de la misma forma que se lleva a cabo la segunda etapa de conversión;
4. Colocar barras oblicuas y las funciones " oops", que dependen del estado de las variables y de las puertas presentes a la entrada del circuito.
En la figura No. 10 se presenta la conversión de un circuito de lógica estándar a uno en la lógica mixta.
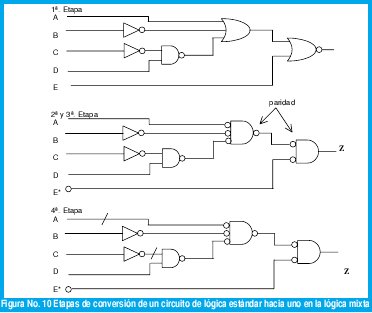
La puerta de salida es reemplazada por una puerta AND (donde Z es activa en el nivel alto ó lógica positiva). Todas las entradas están activas en el nivel alto a excepción de E. Es la razón por la cual se coloca una barra oblicua tanto en A como en C.
IV. DISEÑO DE UN CIRCUITO EN LÓGICA MIXTA
A continuación se presenta la realización de un esquema en lógica mixta a partir de una ecuación determinada y teniendo en cuenta, las señales de entrada disponibles, la señal de salida requerida y las puertas o módulos disponibles. El procedimiento a utilizar es realizar en primer lugar el esquema o circuito imagen para luego transformarlo, siendo este último el esquema ó circuito final.
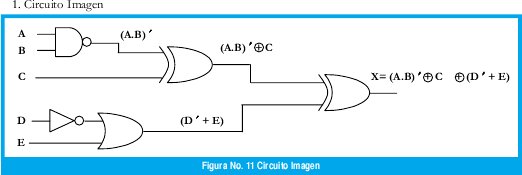
El diseño que se muestra a continuación tiene por objeto realizar el diagrama en lógica mixta de la siguiente ecuación:
X= (A.B) + ⊕ C ⊕+ (D + E)
Señales disponibles : A* , B, C*, E
Salida activa Baja
Módulos ó puertas disponibles:
7486 (XOR 2 entradas)
7400 (NAND 2 entradas)
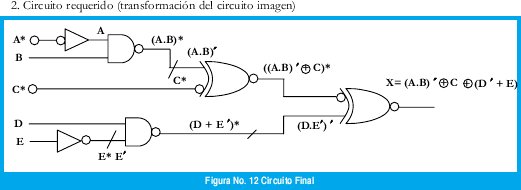
En las figuras 11 y 12 se muestran los circuitos imagen y final respectivamente.
La lógica mixta también provee ventajas en áreas relacionadas con el diseño VLSI CMOS, en las máquinas de estado finito. [15,16]. La realización y documentación de los circuitos es de mayor claridad.
IV. CONCLUSIONES
La lógica mixta es una técnica muy útil para el diseño lógico en razón a que el resultado es un circuito que visualiza claramente la intención original y facilita las tareas de mantenimiento y modificación del hardware. El análisis y la documentación del circuito se aprecia con mayor claridad, exactitud y comprensión del diseño digital. La mayoría de nosotros hemos sido entrenados primero en la lógica positiva y aunque es necesario un periodo de familiarización y aprendizaje, como sucede con cualquier nueva herramienta de simplificación del diseño, la lógica mixta le permite al diseñador concentrarse en su lógica y preservar toda la información alrededor de la implementación física. El autor ha enseñado los conceptos de la lógica mixta en cursos de control y digitales, una vez experimentada la lógica mixta por los estudiantes se aprecian las bondades y ventajas.
Se han presentado los principios de la lógica mixta, su análisis, conversión y realización de un circuito lógico.
Es importante que dicha técnica se extienda tanto a la industria como a la academia Para quienes tengan interés en un estudio adicional de la lógica mixta se recomienda las referencias [14,17,18,19,20,21]. En la gran mayoría de casos, la lógica mixta no solo es un estilo de diseño más claro sino que requiere menos hardware.
REFERENCIAS
[1] Hayes J., "Diseño de Sistemas Digitales y Microprocesadores", McGraw-Hill,1986.
[2] TTL Logic, Standard TTL, Schottky, Low Power Schottky, Texas Instruments Inc., 1988
[3] Mano M., "Digital Design", Prentice Hall, 1991
[4] Hayes J., "Digital Logic Design", Addison Wesley, 1993
[5] Tocci R., "Circuits numériques; Theorie et applications ", Reinal Goulet Inc., 1992.
[6] Porat D. , Barna A., "Introduction to Digital Techniques", Wiley, 1987
[7] Bernard J. et Hugon J., " Pratiques des circuits logiques", Eyrolles, 1987.
[8] Wakerly J., "Digital Design Principles and Practices", Prentice Hall, 1994
[9] Pellerin D., Holley M, " Practical Design Using Programmable Logic ", Prentice Hall, 1991.
[10] Tocci R., "Digital Systems - Principles and Applications", 6th ed., Prentice Hall, 1995.
[11] Pellerin D. and Holley M, " Digital Design using ABEL ", Prentice Hall, 1991.
[12] Peatman J., "Digital Hardware Design ", Mc-Graw-Hill, N.Y., 1980
[13] Sawan M, Fréchette P.," Systemes Logiques II ", Ecole Polytehnique de Montreal, 1992.
[14] Simoni M, " Computer and Digital Fundamentals ", Georgia Institute of Technology, 1998.
[15] Saravia Y., " Conception et Verification des Circuits VLSI ", Editions de Ecole Polytechnique de Montreal, 1994
[16] Gima T.,"Digital Systems Design",College of Computing Sciencies and Engineering, U. of North Florida , 2003
[17] Fletcher W., "An Engineering Approach to Digital Design", Prentice-Hall, 1980
[18] Prosser F. ,Winkel D.E., " The Art of Digital Design ", Prentice Hall, 1987.
[19] Breeding K., "Digital Design Fundamentals", Prentice Hall, 1989
[20] Tinder R., "Digital Engineering Design A Modern Approach", Prentice Hall, 1991
[21] Comer J.D., " Digital Logic and State Machine Design " Saunders College Publisher, 1995.
Alvaro Betancourt Uscátegui
Ingeniero Electrónico, Universidad Distrital, Especialista en Telecomunicaciones Móviles, Universidad Distrital, Msc. Ciencias Financieras y de Sistemas, Universidad Central, Magister en Ingeniería, Informatique Appliquée, Ecole Polytechnique Université de Montreal, Canadá, Profesor Facultad de Ingeniería, Universidad Distrital, Coordinador de la Especialización en Telecomunicaciones Móviles abetancourt@ atlas.udistrital.edu.co
Creation date:
Licencia
A partir de la edición del V23N3 del año 2018 hacia adelante, se cambia la Licencia Creative Commons “Atribución—No Comercial – Sin Obra Derivada” a la siguiente:
Atribución - No Comercial – Compartir igual: esta licencia permite a otros distribuir, remezclar, retocar, y crear a partir de tu obra de modo no comercial, siempre y cuando te den crédito y licencien sus nuevas creaciones bajo las mismas condiciones.




2.jpg)