DOI:
https://doi.org/10.14483/23448393.2278Published:
2001-11-30Issue:
Vol. 7 No. 1 (2002): January - JuneSection:
Science, research and developmentAlgoritmos Genéticos en el Despacho de Energía Eléctrica
Keywords:
Inteligencia Computacional, Algoritmos Genéticos, Despacho de Energía. (es).Downloads
References
Proceedings of International Conference on Genetic Algorithms,San Mateto, California, USA, vol. 2 no. 1, 1995.
Proceedings of the Second International Conference on Genetic Algorithms,San Mateo, California, USA,vol. 1no. 1,1987.
Proceedings of the Third International Conference on Genetic Algorithms, San Mateo, California, USA, vol. 1 no. 3,1989.
Proceedings of the Forth International Conference on Genetic Algorithms, San Mateo, California, USA, vol. 3 no. 2, 1991.
Proceedings of the Fifth International Conference on Genetic Algorithms, San Mateo, California, USA, vol. 1 no. 1,1993.
Davis, L., " Handbook of Genetic Algorithms," first ed., Boston, USA, International Thomson Computer Press., 1996.
Tanomar, J., " Motivacao Fundamentos e Aplicacoes de Algoritmos Genéticos", II Congreso Brasileriro de Redes Neurais Relatorio da Conferencia, Brasil, 1994.
Federal Energy Regulatory Commision," Notice of Proposed Rulemakink : Docket No. RM93-3", Congressional Record, USA, vol.2 no. 1, 1993.
Federal Energy Regulatory Commision," Notice of Proposed Rulemakink : Docket No. RM95-8-000 ", Congressional Record, USA, vol.15 no. 3, 1995.
Michalewicz Z., Genetic Algorithms+Data Structures= Evolution Programs, New York, USA., 1996.
Wood A.J., y Woldberg B.F., " Power Generation, Operation and Control "New York, USA. ,1984.
Kazarils S.A., Bakirttz A.G., Pertridis V., " GA Genetic Algorithm solution to the unit commitment problem", IEEE, Transaction Power System, USA, vol. 11, no.1, 1996.
Goldberg, D.E., "Genetic Algorithms in Search, Optimization & Machine Learning ", Massachusets, USA., 1989.
Sheblé G.B et al, " Unit Commitment by Genetic Algorithm with Penalty Methods and a Comparaison of Langrangian search and Genetic Algorithm Economic Dispatch Example", USA, vol. 2 no. 1, 1996.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Ingeniería, 2002-00-00 vol:7 nro:1 pág:91-95
Algoritmos genéticos en el despacho de energía eléctrica
Alvaro Betancourt Uscátegui
Resumen
Se presenta en este artículo una aplicación de inte- ligencia computacional para resolver un problema de despacho de energía, mostrando cómo los algoritmos genéticos pueden ser útiles en la solución de problemas de optimización combinacional. El problema investigado es complejo. Incluye limitaciones y restricciones relacionadas con el generador y los requerimientos de carga. Básicamente, el objetivo es la selección de un conjunto de generadores los cuales pretenden cubrir totalmente la demanda horaria impuesta por la carga con un mínimo costo.
Palabras Clave:
Inteligencia Computacional, Algoritmos Genéticos, Despacho de Energía.
Abstract
In this paper, we present an application of computational intelligence to resolve a problem of energy dispatch, showing how genetic algorithms can be useful in the solution of combinatorial optimization problems. The investigated problem is complex. It includes constraints related to the generator and the requirements of the load. Basically, it aims the selection of a set of generators, wich attempts to fully reach the hourly demand imposed by the load with a minimum cost.
Key Words:
Computational Intelligence, Genetic Algorithms, Energy Dispatch.
PRESENTACIÓN
Son varias las razones que motivan el tema que se trata a continuación. Una primera, es que si bien dentro del contexto de despacho de energía en el sector eléctrico colombiano, la Constitución Política de 1991 abrió la posibilidad a la participación del sector privado y a la competencia en la prestación de los servicios públicos y que la reforma del sector eléctrico en sus leyes 142 y 143 llevan a un sistema de bolsa de energía en donde el precio de la energía transada en la bolsa se determina por el precio de equilibrio entre las ofertas de venta y la demanda real del sistema, puede ser interesante e importante para la empresa generadora en particular, la optimización de la demanda horaria de carga a un mínimo costo mediante la aplicación de la inteligencia computacional, tema de actualidad en diferentes áreas. Una segunda, es la reciente visita a la facultad de ingeniería por parte del CNA para analizar la apertura del programa de ingeniería eléctrica, en donde el mayor soporte fue nuestro reconocido programa de ingeniería electrónica, su infraestructura y el grupo de docentes. Las principales recomendaciones, giraron alrededor de plantear un plan estudios de ingeniería eléctrica que incorpore nuevos temas, aplicaciones y muestre diferencias comparativas pero al mismo tiempo que lo diferencie claramente del programa de ingeniería electrónica. Por ello, se selecciona un artículo de importancia y pertinencia para en el sector eléctrico que muestra investigación y desarrollo y se realiza su traducción. Sus autores, Biondi L, Chiganer L., y Fukuda H., y su título Algoritmos genéticos no despacho de energía electrica. El artículo que presentan los autores mencionados acomete de manera estructurada y a profundidad, la solución a un problema de ingeniería eléctrica por parte del sector académico; el soporte puntual a nivel bibliográfico muestra el uso de diversas técnicas y enriquece el tratamiento del tema, que por su conveniencia se incluye en su totalidad. Es claro que, el tipo de problema planteado motiva al sector académico para que plantee soluciones de optimización que redunde en un beneficio social, dentro del contexto Universidad - Empresa.
I. INTRODUCCION
El sistema eléctrico investigado está compuesto de seis (6) unidades generadoras, cada una con capacidades limitadas de generación de energía eléctrica entre un número mínimo y máximo de potencia y con su consecuente costo por MW de energía diferenciado citados por [1,2,3]. Una demanda a ser atendida, es suministrada diariamente, hora a hora, durante un total de 24 periodos de muestreo.
La metodología usada en la solución del problema realiza una investigación adaptativa, basada en los procesos biológicos y la selección natural (adaptada a los seres vivos), estudiada por Darwin para un aspecto biológico y luego adaptada por Holland como se cita en [4,5] para la utilización en procesos artificiales denominados Algoritmos Genéticos (AGs).
En el caso de estudio, cada cromosoma es representado, matricialmente por 144 genes, esto es, seis generadores para cada uno de los 24 periodos de muestreo. Cada gen representa una potencia despachada por una unidad generadora en un período dado. Estos individuos son generados aleatoriamente, pero deben obedecer a restricciones preestablecidas para que efectivamente representen una solución viable del problema. Las poblaciones creadas están formadas por un conjunto de cromosomas y para cada cromosoma se determina su aptitud, directamente ligada al costo de generación de cada unidad [6].
Posteriormente, esas aptitudes individuales son normalizadas a través de un proceso de selección, que privilegia a los individuos más aptos. Estos se seleccionan para sufrir la acción de los operadores genéticos de recombinación y mutación, generando los descendientes que irán a conformar la próxima generación. Un proceso iterativo para cada nueva generación verifica que la aptitud vaya mejorando, así como también que el costo de generación vaya decreciendo, hasta un sistema que converge para un cromosoma que contempla las potencias óptimas de seis (6) unidades generadoras por periodos de muestreo, en la situación de costo mínimo[7].
II. MODELAMIENTO DEL PROBLEMA
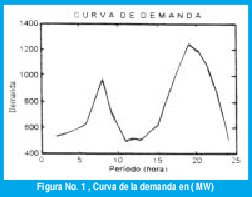
El caso investigado consiste en atender una demanda horaria como se muestra en la figura 1, que representa una necesidad de energía eléctrica tomada en intervalos de una (1) hora [8,9]. Un despacho de energía eléctrica se realizará a través de seis generadores térmicos, cuyas características se muestran en la tabla 1.
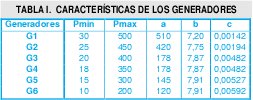
Pmin- Capacidad mínima generada (MW)
Pmax - Capacidad máxima generada (MW)
a,b,c - coeficientes de curva de los generadores
El problema presenta básicamente, las siguientes restricciones [8,9]:
- La demanda horaria debe ser atendida plenamente por los generadores
- La potencia generada por cada generador debe ser como mínimo igual a Pmin
- La potencia generada por cada generador debe ser como máximo Pmax.
Se considera además que:
n=6 : Cantidad de generadores
k=24 : Cantidad de periodos de muestreo
Pmax (i) : Capacidad máxima del generador i
Pmin (i) : Capacidad mínima del generador i
D (j) : Demanda horaria exigida en el periodo j
P (i,j) : Energía despachada P(i,j) por el generador i en el periodo j
costo (i,j) : Costo referente al despacho P(i,j) considerado en el estudio unitario
f(i,j) : Función de costo
El objetivo, obedeciendo a dichas restricciones, es atender una demanda horaria a un costo mínimo de despacho de energía [10,11,12], sin considerar los límites de capacidad de transmisión:
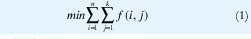
donde,
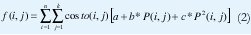
Obedeciendo a las siguientes restricciones:
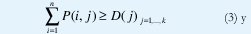
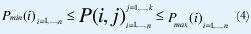
III. REPRESENTACION DEL CROMOSOMA
De conformidad con el análisis hecho en el modelaje del problema, el caso de estudio involucra la necesidad de atender una demanda horaria en un periodo de k=24 horas, usándose n=6 generadores. Eso sugiere un cromosoma, de forma matricial con dimensiones (n*k), donde cada gen, es representado por un número real, que indica la potencia a ser despachada por cada unidad generadora (i) para atender la demanda exigida en el periodo (j). Así mismo, el cromosoma propuesto en el artículo será una representación de lo seguido en [6,7], pudiendo también ser adoptada una versión dada por la matriz transpuesta correspondiente. En la tabla II se muestra la representación cromosómica.


Teniendo en cuenta la naturaleza compleja del problema y con visión a incorporar conocimientos específicos en la representación cromosómica, es necesario establecer la r utina específica de inicialización [10] como se muestra en la figura No. 2. El propósito es crear una población válida de cromosomas, compuesta de individuos que obedecen rigurosamente a las restricciones impuestas por el problema, so pena de generar descendientes con características genéticas defectuosas, esto es, que no representen efectivamente una solución al problema. En la rutina anterior, Ger(i) representa las potencias de los generadores y Dem (j) las demandas exigidas por la carga.
IV. CALCULO DE APTITUD
La idoneidad del cromosoma se define por la función de costo, señalada anteriormente. Como el objetivo es evitar problemas relativos al cálculo, la validación hecha, adopta técnicas de normalización líneal [13] que básicamente minimiza los siguientes efectos:
1. Acción de superindividuos (cromosomas con aptitud elevadísima) que tienen pocas posibilidades de recombinarse con otros miembros de la población, tornándose así en elementos dominadores.
2. Problemas relativos de competición próxima (cromosomas con aptitud semejantes), que en el análisis disminuye la presión selectiva entre los mejores.
V. SELECCIÓN DE LOS PROGENITORES
La selección de los progenitores es hecha por el método de la ruleta viciada[13], privilegiándose la función de aptitud de los individuos más aptos. El método consiste en:
- Calcular la sumatoria de aptitudes de todos los cromosomas de población AT.
- Generar un número aleatorio n entre 0 y AT.
- Seleccionar primero un miembro de la población con la sumatoria de aptitudes mayores o iguales a "n"
Una vez seleccionados los progenitores sufren una acción de los operadores genéticos para generar descendientes, a saber: - Recombinación (crossover) actúa como acelerador del proceso de búsqueda, recombinando parte de los cromosomas.
- Mutación introduce modificaciones a la información genética, generando diversidad de individuos.
VI. OPERADORES GENÉTICOS
6.1 Recombinación
Inicialmente, se escoge una tasa de recombinación 0<=PCROS <=1, cuya función es definir si se va o nó a realizar la recombinación al par de progenitores seleccionados[13]. Se genera un número aleatorio N RAND entre 0 y 1, adoptándose el siguiente criterio:
- Si NRAND es menor o igual que PCROS entonces la recombinación se realiza entre los descendientes y estarán compuestos de partes de progenitores.
- Si NRAND es mayor que P CROS entonces la recombinación no se realiza y se hace una copia idéntica de los progenitores para los respectivos descendientes.
Los descendientes DESC1 y DESC2 se determinan de la siguiente forma:
- Se crean las matrices auxiliares denominadas DIV y REM[10].
- DIV = div(i,j) , que representa un valor medio entre los genitores seleccionados y
- REM= rem(i,j), que representa el resto de la división por 2 (mod 2 ) de la suma de los progenitores e indica los redondeos necesarios . Así tenemos;
- div(i,j) = [ P(i,j)1 + P(i,j)2 ]/2
- rem(i,j) = [ P(i,j)1 + P(i,j)2 ]mod 2
La matriz REM muestra una característica importante, debido al hecho de representar un número par de elementos de valor 1 en cualquier línea o columna de su conformación. Debido a esa propiedad es posible transformar la matriz REM en dos matrices de modo que:
REM = REM1 + REM2 y consecuentemente afirmar que:
Ger REM1 ( i ) = Ger REM2 ( i ) = Ger REM ( i )/2 , para i= 1,...,n
Dem REM1(j ) = Dem REM2 ( j ) = Dem REM ( j )/2 , para j= 1,...,k
Finalmente, se crean dos nuevos descendientes [10],DESC1 y DESC2 de la siguiente forma:
DESC1 = DIV + REM1
DESC2 = DIV + REM2
6.2 Mutación
Similar a la recombinación, se escoge una tasa de mutación de 0,001<=PMUT<=0,1 , normalmente mucho menor que la tasa de recombinación [10,13]. Se genera un número aleatorio N RAND entre esa nueva tolerancia o variación, obedeciendo a las siguientes reglas:
1) Si NRAND <= PMUT la mutación se realiza y el descendiente se compone para generar diversidad,por la modificación gen a gen del cromosoma.
- Una sub-matriz aleatoria denominada Mut(i,j) se selecciona de la matriz descendiente obtenida de la operación de recombinación.
- La diversidad se crea sobre esa sub-matriz a través de una rutina similar a la usada en la inicialización cromosómica, generándose una nueva sub-matriz denominada NEW_Mut(i,j) y que lógicamente, satisface las restricciones impuestas por el problema.
- Finalmente, la sub-matriz NEW_Mut(i,j) se reubica en la misma posición de donde fue retirada la matriz Mut(i,j), generando así un nuevo descendiente.
2) Si NRAND es mayor que PMUT entonces la mutación no se realiza y el descendiente es una copia fiel del cromosoma seleccionado y es afectado apenas por la recombinación.
Una nueva población de individuos se compone de los descendientes obtenidos a través de las operaciones genéticas de recombinación y mutación, preservándose el mejor individuo (menor costo) de la población anterior a la población siguiente.
VII. RESULTADOS
Las pruebas iniciales fueron realizadas bajo las siguientes condiciones: 10 corridas del algoritmo, 50 generaciones cada una con una población que varía de 10, 20 y 50 individuos. Tasa de recombinación de 0,75 y tasa de mutación 0,0001. La evolución de la curva de costo, figura 3, representa la curva media de las 10 corridas del algoritmo.
Inicialmente, ocurre una caída brusca del costo (recombinación), y para las siguientes generaciones cae suavemente debido a la acción de mutación. En las pruebas, prácticamente no se presenta diferencia del desempeño para los casos de poblaciones con 20 o 50 individuos, aún cuando la curva sugiere que el sistema todavía puede converger hacia un costo más bajo.
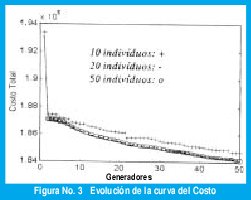
Tratando de mejorar los resultados de las pruebas preliminares, se realizaron las siguientes modificaciones en los parámetros, que llevan el costo hacia 1.82x 105: 10 corridas con 100 generaciones para cada población de 50 individuos, la tasa de recombinación de 0,75 y la tasa de mutación de 0,01.
VIII. CONCLUSIONES
La solución al problema de despacho de energía eléctrica se resume en determinar un conjunto de unidades generadoras que satisfagan una necesidad de demanda y la forma más económica posible. En la búsqueda de esa solución óptima diversas técnicas se emplearon.
Una solución clásica usa las funciones de Lagrange para imponer las restricciones (características de los generadores) al problema[14]. Actualmente, una solución más común para el problema de despacho se concentra en el uso de la programación dinámica. Lo cierto es que, cuando el número de generadores a ser despachado crece, el tiempo de ejecución del algoritmo de programación dinámica se torna muy grande. Frente a los resultados alcanzados, no sólo lo expuesto en este artículo, sino también en diversos artículos divulgados para el sector eléctrico, parece que los AGs representan una técnica bastante adecuada para la solución del problema en cuestión. Finalmente, es importante señalar que los algoritmos genéticos se convierten fácilmente en programas para ser ejecutados en máquinas paralelas. En estos casos, al realizar varias corridas del algoritmo, el tiempo de ejecución se torna rápido.
IX. COMENTARIOS FINALES DEL TRADUCTOR
Es supremamente enriquecedor ver cómo el sector académico puede dar respuesta a necesidades del medio externo a través de investigación y desarrollo a un problema de generación de energía. Es precisamente la generación de energía eléctrica uno de los campos de acción de los programas de reconocido prestigio académico en ingeniería eléctrica, complementado con los de distribución y transmisión. A nivel de posgrado podría perfectamente y así se han venido ofreciendo programas serios de formación en cada uno de los campos específicos mencionados. La investigación y aplicación presentada por los autores muestra diferencias comparativas con otros programas.
REFERENCIAS
[1] Proceedings of International Conference on Genetic Algorithms,San Mateto, California, USA, vol. 2 no. 1, 1995.
[2] Proceedings of the Second International Conference on Genetic Algorithms,San Mateo, California, USA,vol. 1no. 1,1987.
[3] Proceedings of the Third International Conference on Genetic Algorithms, San Mateo, California, USA, vol. 1 no. 3,1989.
[4] Proceedings of the Forth International Conference on Genetic Algorithms, San Mateo, California, USA, vol. 3 no. 2, 1991.
[5] Proceedings of the Fifth International Conference on Genetic Algorithms, San Mateo, California, USA, vol. 1 no. 1,1993.
[6] Davis, L., " Handbook of Genetic Algorithms," first ed., Boston, USA, International Thomson Computer Press., 1996.
[7] Tanomar, J., " Motivacao Fundamentos e Aplicacoes de Algoritmos Genéticos", II Congreso Brasileriro de Redes Neurais - Relatorio da Conferencia, Brasil, 1994.
[8] Federal Energy Regulatory Commision," Notice of Proposed Rulemakink : Docket No. RM93-3", Congressional Record, USA, vol.2 no. 1, 1993.
[9] Federal Energy Regulatory Commision," Notice of Proposed Rulemakink : Docket No. RM95-8-000 ", Congressional Record, USA, vol.15 no. 3, 1995.
[10] Michalewicz Z., "Genetic Algorithms+Data Structures" Evolution Programs, New York, USA., 1996.
[11] Wood A.J., y Woldberg B.F., " Power Generation, Operation and Control "New York, USA. ,1984.
[12] Kazarils S.A., Bakirttz A.G., Pertridis V., " GA Genetic Algorithm solution to the unit commitment problem", IEEE, Transaction Power System, USA, vol. 11, no.1, 1996.
[13] Goldberg, D.E., "Genetic Algorithms in Search, Optimization & Machine Learning ", Massachusets, USA., 1989.
[14] Sheblé G.B et al, " Unit Commitment by Genetic Algorithm with Penalty Methods and a Comparaison of Langrangian search and Genetic Algorithm- Economic Dispatch Example", USA,vol. 2 no. 1, 1996.
Alvaro Betancourt Uscátegui
Ingeniero Electrónico, Universidad Distrital. Especialista en Telecomunicaciones Móviles, Universidad Distrital. Msc. Ciencias Financieras y de Sistemas, Universidad Central. Magister en Ingeniería, Informatique Appliquée, Ecole Polytechnique Université de Montreal, Canada. Profesor Facultad de Ingeniería, Universidad Distrital. Coordinador de la Especialización en Telecomunicaciones Móviles. abetancourt@ atlas.udistrital.edu.co
Creation date:
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.





2.jpg)










