Ingeniería, 2002-00-00 vol:7 nro:2 pág:101-103

Vibraciones elásticas en presencia de una serie de dislocaciones de tornillo

Hugo Aya Baquero
Miembro grupo de investigación Optoelectrónica, Universidad Distrital Francisco José de Caldas.
Valeri Gachevski
Fundador del grupo de investigación PERSEO, Colciencias.

Resumen

Las tensiones elásticas producidas por una serie de dislocaciones son significativamente mayores que las producidas por una dislocación aislada y su efecto sobre las vibraciones elásticas también es mayor. En el presente artículo se analizó el espectro de vibraciones en el campo de tensiones elásticas relacionadas con una serie infinita de dislocaciones de tornillo y los resultados se compararon con los resultados correspondientes a una dislocación aislada.

Palabras claves:
Dislocación, oscilaciones, espectro.

Abstract

Elastic tensions resulting from a dislocation array are significantly higher than those from an isolated dislocation. Therefore their influence on elástic vibrations is higher too. In this paper elastic vibration spectra in elastic field yielded by an infinite array of screw dislocations was analyzed and compared with the spectra of vibrations in the elástic field of an isolated screw dislocation.

Key words:
Dislocation, oscillations, spectrum.

I. INTRODUCCIÓN

Por muchos años se han desarrollado investigaciones sobre la influencia de las dislocaciones en las características de diferente tipo de materiales [1-3]. Se han llevado a cabo investigaciones teóricas sobre las vibraciones elásticas en un campo de tensiones relacionadas con una dislocación aislada [4-6]. En las estructuras multicapas de dispositivos electrónicos aparecen grupos de dislocaciones causadas por la diferencia de los parámetros de la red cristalina y de los coeficientes de dilatación térmica de los materiales de las capas. Las tensiones elásticas relacionadas con las series de dislocaciones son mayores en comparación con las tensiones causadas por una dislocación aislada. Es lógico suponer que la influencia de la serie de dislocaciones en vibraciones elásticas también es mayor. En el presente artículo se calcula el espectro de vibraciones elásticas en el campo de tensiones relacionadas con una serie infinita de dislocaciones de tornillo.

II. DEFINICIÓN DEL PROBLEMA

Tomamos una serie infinita de dislocaciones de tornillo idénticas y paralelas una a la otra con vector Burgers b= (0,0,b) localizada a lo largo del eje Y en un sistema de coordenadas cartesiano, donde las líneas de las dislocaciones son paralelas al eje Z y una de ellas coincide con este eje. Las dislocaciones están separadas por una distancia y₀.

El objetivo del trabajo es calcular el espectro de vibraciones en el campo de tensones elásticas relacionadas con dicha serie.

III. METODOLOGÍA Y SOLUCIÓN DEL PROBLEMA

Teniendo en cuenta la complejidad del problema la solución se realiza basado en un modelo escalar en el que los átomos solamente se pueden desplazar en una única dirección. La dislocación tipo tornillo genera desplazamientos con una única componente paralela a la línea de dislocación. Tomamos dicha componente como la dirección de desplazamiento de los átomos.

Los desplazamientos de los átomos se pueden describir con la suma de dos funciones: u0(x,y,z) es la función de desplazamientos estáticos de la posición de equilibrio de los átomos en el campo de tensiones elásticas producidas por las dislocaciones, y u (x,y,z,t) es la función de pequeños desplazamientos de los átomos que oscilan alrededor de sus posiciones de equilibrio.

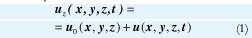
De acuerdo con [5] la ecuación para las oscilaciones es la siguiente:

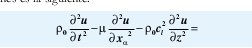
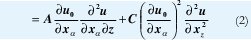
donde µ=pu₀c²_t y 0 c l2 son los módulos de elasticidad de segundo orden, A es el módulo de elasticidad de tercer orden y C es el módulo de elasticidad de cuarto orden; α corresponde al índice de la sumatoria con valores 1 y 2,p₀ es la densidad del material, c_t es la velocidad de las ondas transversales y c_l es la velocidad de las ondas longitudinales

La función de desplazamientos estáticos producidos por una dislocación de tornillo con vector Burgers b= (0,0,b) localizada en el origen de coordenadas se puede escribir de la siguiente manera:

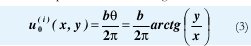
En el caso de una serie de dislocaciones la función de desplazamientos U₀ será la suma de los desplazamientos U₀ producidos por las dislocaciones de la serie. Entonces, las derivadas de U₀ quedarían así:

donde i es el índice de la sumatoria y η= mod _y0 (y)

Asumimos la solución de la ecuación (2) en un sistema de coordenadas polares de la forma:

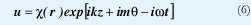
donde r² = x²+y² y m es un número entero.

Realizando separación de variables de la ecuación (2) se obtiene la siguiente ecuación para la parte radial de desplazamiento χ:

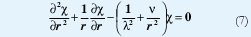
donde λ²= c²_t(c²_t- ω²)

El valor de v se calcula con:

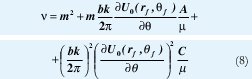
donde A, C y µ son constantes de la ecuación (2)

La formula (8) se escribe asumiendo que según el análisis realizado las funciones (4) y (5) cambian muy lentamente en el espacio con excepción de las regiones muy cercanas a las líneas de dislocaciones. Las variaciones de dichas funciones son pequeñas en los límites de las oscilaciones de los átomos. En tales circunstancias, es posible reemplazar la función U₀(r,θ) con su valor U₀(r_∫, θ_∫) tomado en el punto de la posición de equilibrio de los átomos con coordenadas r∫ y θ∫.

La ecuación (7) corresponde a la ecuación de Schrödinger para la parte radial de la función de onda de una partícula en las coordenadas cilíndricas, con la constante de Planck igual a 1 y la masa de la partícula es 1/2. Dicha partícula está localizada en el campo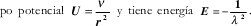

Cuando m = 0 la ecuación (7) puede describir el movimiento de una partícula en un pozo quántico bidimensional. En este caso existe un número infinito de los estados. Según el análisis cuasiclásico la fórmula para las frecuencias de las oscilaciones es la siguiente:

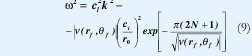
donde r₀ es el radio del tubo de la dislocación y N es un número entero.

Las ondas que se propagan lo largo de la serie de dislocaciones perpendicularmente a las líneas de dislocaciones, o sea a lo largo del eje Y, son de carácter transversal. Además, la expresión (2) conduce a ω²=c²_t k² bajo las condiciones ya mencionadas y en los límites del modelo escalar.

IV. RESULTADOS

El análisis de (9) muestra que el espectro de frecuencia depende de las coordenadas X y Y. La frecuencia de las vibraciones cambia periódicamente en la dirección de la coordenada Y, y cuando la distancia hasta la serie de dislocaciones crece, las perturbaciones sobre la red cristalina disminuyen. En consecuencia el efecto de las dislocaciones sobre el espectro también disminuye.

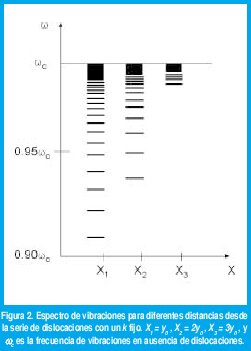
La Figura 2 muestra los resultados de cálculo numérico de tres espectros de vibraciones en los puntos con las distancias iguales a y₀ , 2y₀ y 3y₀ desde la serie de dislocaciones. La separación entre las frecuencias en los espectros discretos decrece con el incremento de la distancia.

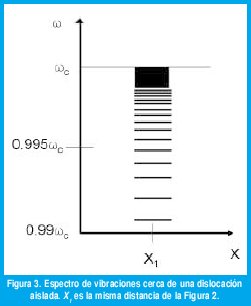
La Figura 3 muestra el espectro de vibraciones en el campo de tensiones elásticas de una dislocación de tornillo aislada en el punto con la distancia y₀ desde la línea de dislocación. Se observa la diferencia entre este espectro y el primer espectro de la Figura 2. En el caso de la dislocación aislada la variación máxima de la frecuencia es aproximadamente 1% de la frecuencia en ausencia de dislocación. Las tensiones elásticas relacionadas con la serie de dislocaciones producen una variación de la frecuencia hasta del 8%.

La simplicidad del espectro de vibraciones transversales se explica a partir de las propiedades del modelo usado. Los átomos se mueven a lo largo del eje Z y las distancias entre las capas atómicas cuando se propagan las ondas permanecen sin alteración comparadas con las distancias entre los átomos del material no deformado. Sin embargo, se puede apreciar como efecto particular que la energía potencial depende de las coordenadas. Por tanto, la amplitud de las oscilaciones cambia con la variación de las coordenadas.

V. CONCLUSIONES

Los resultados obtenidos muestran que la influencia de una serie de dislocaciones en vibraciones elásticas es significativamente mayor en comparación con la influencia de una dislocación aislada. Las fórmulas deducidas permiten calcular los espectros de vibraciones con mayor exactitud y forman la base de investigación de la influencia de series de dislocaciones en la interacción excitón-fonón y en propiedades ópticas del material.

REFERENCIAS

[1] H. Booyens and J.S.Vermaak, J. Appl. Phys. 48, 7 (1977).

[2] A. Gavallini, P. Gondi and A. Castaldini, Phys. Stat. Sol. (b) A43, 2 (1977).

[3] V. M. Chernov and V. V. Ivanov, Cryst. Res. and Technol. 19, 6 (1984).

[4] I. M. Lifshitz and A. M. Kosevich, Rept. Progr. Phys., 29 (1966).

[5] A. M. Kosevich, Low Temperature Physics, 4, 902 (1978).

[6] A. A. Maradudin, Nat. Bur. Stand. (US) Spec. Publ. 317, 205 (1970).

Hugo Aya Baquero
Ingeniería Electrónica, Profesor Facultad de Ingeniería Universidad Distrital Francisco José de Caldas. haya@udistrital.edu.co

Valeri Gachevski
Ingeniería de Sistemas, Profesor Facultad de Ingeniería Universidad Distrital Francisco José de Caldas. vgachevs@uniandes.edu.co