DOI:
https://doi.org/10.14483/23448393.15530Published:
2020-07-03Issue:
Vol. 25 No. 2 (2020): May - AugustSection:
Systems EngineeringAlgoritmo de Encriptación para Imágenes a color basado en Sistemas Caóticos
Encryption Algorithm for color Images based on Chaotic Systems
Keywords:
Criptografía, Cifrado de imágenes, Caos, Lorenz, Arnold, Chen (es).Keywords:
Cryptography, Image Encryption, Chaos, Lorenz, Arnold, Chen (en).Downloads
References
S. Nagaraj, G.S.V.P. Raju, K. Koteswara Rao. (2015). Image Encryption Using Elliptic Curve Cryptograhy and Matrix, Elsevier, International Conference on Intelligent Computing, Communication & Convergence, pp. 276-281. https://doi.org/10.1016/j.procs.2015.04.182
A. Bakhshandeh, Z. Eslami. (2013). An authenticated image encryption scheme based on chaotic maps and memory cellular automata, Elsevier, Optics and Lasers in Engineering, pp. 665-673. https://doi.org/10.1016/j.optlaseng.2013.01.001
M. H. Al-Mashhadi, Q. I. Abduljaleel. (2017) . Color Image Encryption using Chaotic Maps, Triangular Scrambling, with DNA Sequences. International Conference on Current Research in Computer Science and Information Technology (ICCIT), Slemani - Iraq, IEEE, pp. 93-98. https://doi.org/10.1109/CRCSIT.2017.7965540
X. Wu, B. Zhu, Y. Hu, Y.Ran (2017) . A novel color image encryption scheme using rectangular transform enhanced chaotic tent maps, IEEE, Vol 5, pp. 6429-6436. https://doi.org/10.1109/ACCESS.2017.2692043
Biham Eli, Shamir Adi (1991). Differential cryptanalysis of DES-like cryptosystems, Springer-Verlag Berlin Heidelberg, pp.3-72. https://doi.org/10.1007/BF00630563
Mostafa I. Soliman and Ghada Y. Abozaid (2008) . Hardware visualization of the advanced encryption standard (AES ) algo-rithm, ICCTA Alexandria Egypt, pp 85-93. https://www.researchgate.net/conference event/ICCTA_International-Conference-on-Computer-Theory-andApplications_2008/14101
Thakur J., Kumar N. (2011). DES, AES and Blowfish: Symetric key Crytography algorithms Simulation Based Performance Analysis, International Journal of Emerging Technology and Advanced Engineering - IJETAE, Volumen 1, número 2, pp. 6-12. Website: www.ijetae.com
] Verma A., Guha P., Mishra S. (2016). Comparative study of different cryptographic algorithms, International Journal of Emerging Trends of Technology in Computer Science-IJETTCS, Volumen 5, número 2, pp 58-63. Website: www.ijettcs.org
Lucena Manuel. (2011). Criptografía y Seguridad en Computadores, tercera edición. Universidad de Jaén. Libro electrónico gratuito disponible en http://wwwdi.ujaen.es/~mlucena/lcripto.html .
C. Fu, W. Li, . Z. Meng, Wang and P. Li,(2013). A Symmetric Image Encryption Scheme Using Chaotic Baker map and Lo-renz System, Ninth International Conference on Computational Intelligence and Security, IEEE,pp.724- 728. https://doi.org/10.1109/CIS.2013.158 .
Hou J., Rui Xi, P. Liu, T. Liu. (2017). The Switching Fractional Order Chaotic System and Its Application to image Encryp-tion. IEEE/CAA Journal of Automática Sinica, Vol. 4, No. 2, pp. 381-388. https://doi.org/10.1109/JAS.2016.7510127
Liu W., K. Sun, C. Zhu. (2016). A fast image encryption algorithm based on chaotic map, Optics and Lasers in Engineering 84, ELSEVIER, journal homepage: www.elsevier.com/locate/optlaseng , pp. 26-36. https://doi.org/10.1016/j.optlaseng.2016.03.019
Zhou Y., Bao L., C.L. Philip Chen. (2014). A new 1D chaotic system for image encryption, Signal Processing 97, ELSEVIER, pp. 172-182. https://doi.org/10.1109/ICSSE.2012.6257151
Ying Qian Z., Xing Yuan W.(2015). A new image encryption algorithm based on non-adjacent coupled map lattices, Applied Soft Computing, journal homepage: www.elsevier.com/locate/asoc , ELSEVIER, pp. 10-20. https://doi.org/10.1016/j.asoc.2014.09.039
Xu L., Li Z. , Li J., Hua W.(2016). A novel bit-level image encryption algorithm based on chaotic maps, Optics and Lasers in Engineering 78, ELSEVIER, journal homepage: www.elsevier.com/locate/optlaseng, pp. 17-25. https://doi.org/10.1016/j.optlaseng.2015.09.007
Acosta Del Campo O. R., C. Ortega Corral, C. Cruz Hernández, y otros (2016). Encriptado de imagen basado en permutación-difusión y sistemas caóticos fraccionarios, Congreso Internacional. Ing. Electromecánica, ELECTRO, vol. 38, pp. 235-240, Chihuahua, Chih., México. Recuperado de http://electro.itchihuahua.edu.mx/memorias_electro/MemoriaElectro2016.zip
Murillo Escobar M.A., Cruz Hernandez C., Abundiz Pérez F. y otros. (2015). A RGB image encryption algorithm based on total plain image characteristics and chaos, Signal Processing, Volumen 109, pp. 119-131. https://doi.org/10.1016/j.sigpro.2014.10.033
Jiménez Rodríguez M., Flores Siordia O., González Novoa M. G.(2015). Sistema para codificar información implementando varias órbitas caóticas, Ingeniería Investigación y Tecnología Volumen XVI, número 3, ISSN 1405 7743 FI- UNAM, pp. 335-342 https://doi.org/10.1016/j.riit.2015.05.004
Pérez Abundiz F., C. Cruz Hernández, M.A. Murillo Escobar., y otros. (2014). Encriptado de imágenes utilizando caos y secuencia de ADN, Memorias del XVI Congreso latinoamericano de control autómatico. Cancún México. https://publons.com/p/16059288/
Yaghoobi Roohbakhs M. (2015). Color Image Encryption using Hyper chaos Chen, International Journal of Computer Appli-cations, vol. 110 Número 4, pp. 9-11. https://www.researchgate.net/deref/http%3A%2F%2Fdx.doi.org%2F10.5120%2F19303-0752
Zhang J. (2015). An Image Encryption Scheme Based on Cat Map and Hyperchaotic Lorenz System, International Conference on Computational Intelligence & Communication Technology, IEEE, pp. 78-82. https://doi.org/10.1109/CICT.2015.134
Ye G., Zhao H., Chai H.(2016). Chaotic image encryption algorithm using wave-line permutation and block difusión, Nonlinear Dyn, springer, pp. 2067-2077. https://doi.org/10.1007/s11071-015-2465-7
Hua Zhongyun, Zhou .Yicong, Pun Chi-Man, C.L. Chen Philip. (2015). 2D Sine Logistic modulation map for image encryp-tion. ScienceDirect, ELSEVIER, vol 297, pp. 80-94. https://doi.org/10.1016/j.ins.2014.11.018
Xingyuan Wang, Suo Gao, Longjiao Yu, Yuming Sun, Huaihuai sun. (2019). Chaotic Image Encryption Algorithm Based on Bit-Combination Scrambling in Decimal System and Dynamic Diffusion, , IEEE, Vol 7, pp. 103662-103677. https://doi.org/10.1109/ACCESS.2019.2931052
Xiancheng Hu, Liansuo Wei, Wei Chen, Qiqi Chen, Yuan Guo. (2020). Color Image Encryption Algorithm Based on Dynamic Chaos and Matrix Convolution, IEEE, Vol 8, pp. 12452-12466. https://doi.org/10.1109/ACCESS.2020.2965740
Devaney R. L. (1948). An introduction to chaotic dinamical systems. Boston University, Addison- Wesley Publishing Com-pany.
Kathleen T. Alligood, Tim D. Sauer, James A. Yorke. (1997). Chaos An Introduction To Dynamical Systems, Springer. https://doi.org/10.1007/0-387-22492-0_3
Taylor G. A., I. Pisica, S. Grenard, A. Yunta Huete. (2011). Recent developments towards novel high performance computing and communications solutions for smart distribution network operation, IEEE PES Int. Conf. and Exh. on Innovative Smart Grid Technologies (ISGT Europe). https://doi.org/10.1109/ISGTEurope.2011.6162812
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Recibido: 8 de noviembre de 2019; Revisión recibida: 13 de abril de 2020; Aceptado: 30 de abril de 2020
Resumen
Contexto:
Aprovechando los fundamentos de la teoría de sistemas dinámicos no lineales, se propone un modelo de encriptación para imágenes a color basado en sistemas caóticos que satisface estándares de seguridad acordes con los desafíos a que se enfrenta la sociedad.
Método:
Se propone un algoritmo simétrico utilizando el sistema caótico Cat de Arnold para la permutación y para la difusión el sistema hipercaótico de Chen o el sistema hipercaótico de Lorenz. En la implementación se utiliza programación paralela para reducir los tiempos de ejecución.
Resultados:
e aplican métricas de desempeño para evaluar la seguridad del modelo criptográfico propuesto. Se encuentra que los indicadores obtenidos se enmarcan dentro de los publicados en artículos recientes que abordan el problema de la seguridad a través del caos.
Conclusiones:
Los resultados obtenidos permiten confirmar que el uso de la teoría del caos, como herramienta para el fortalecimiento de los esquemas de seguridad en comunicaciones, es una buena alternativa, particularmente cuando se hace referencia a la transferencia de imágenes.
Palabras clave:
Arnold, caos, Chen, cifrado de imágenes, criptografía, Lorenz..Abstract
Context:
Taking advantage of the foundations of the theory of non-linear dynamic systems, we propose an encryption model for color images based on chaotic systems, which satisfies security standards in accordance with the challenges faced by society.
Method:
A symmetrical algorithm is proposed using Arnold’s chaotic Cat system for permutation and for diffusion Chen’s hyperchaotic system or Lorenz’s hyperchaotic system, a parallel programming in implementation is used to reduce execution times.
Results:
Performance metrics are applied to evaluate the security of the proposed cryptographic model, finding that the indicators obtained are framed within those published in recent articles that address the problem of security through chaos.
Conclusions:
The results obtained confirm that the use of chaos theory as a tool for strengthening security schemes in communications is a good alternative, particularly when referring to image transfer.
Keywords:
Arnold, chaos, Chen, cryptography, image encryption, Lorenz.Introducción
Con la evolución de las nuevas tecnologías y la necesidad creciente de compartir información a través de las redes, es necesario desde las instituciones académicas de educación superior promover comunidades interesadas en fomentar el desarrollo de esquemas de seguridad que eviten que personas no autorizadas accedan a contenidos de tipo privado, pues ello genera riesgos económicos y sociales a nivel personal, institucional o estatal. La criptografía proporciona mecanismos de seguridad mediante el ocultamiento de la información a través de diferentes técnicas. Sin embargo, los métodos que se utilizan para cifrar textos, en general, no son apropiados cuando se desean aplicar a imágenes, audios o videos, principalmente por el gran volumen de información que ellos manejan. Frente a este inconveniente han surgido varias tendencias de seguridad tales como las que se basan en curvas elípticas, computación cuántica, código ADN, autómatas celulares o en sistemas dinámicos caóticos. Este último es el eje de desarrollo de este artículo [1]-[3].
La importancia de utilizar sistemas dinámicos caóticos para generar estrategias de cifrado radica en la analogía que existe entre las características comportamentales de un sistema caótico, tales como ergodicidad, propiedades de mezcla, dependencia sensitiva de los parámetros y condiciones iniciales, con respecto a las propiedades ideales de sistemas de cifrado para imágenes, audios o videos, basados en los procesos de difusión y permutación [4].
Los algoritmos criptográficos se clasifican en simétricos (clave secreta) y asimétricos (clave pública). Los algoritmos simétricos utilizan una clave para cifrar y descifrar los datos, mientras que los algoritmos asimétricos utilizan dos claves, una pública para cifrar y una privada para descifrar. En criptografía simétrica se han destacado los algoritmos DES (por sus siglas en inglés de Data Encryption Standard) y AES (por sus siglas en inglés de Advanced Encryption Standard). DES fue adoptado como estándar por la National Boureau of Standards en noviembre de 1976, Biham y Shamir hacen un criptoanálisis diferencial de DES en 1991 [5]. AES fue seleccionado por el National Institute of Standard and Technology (NIST) como estándar de encriptación en octubre de 2000 y en este mismo año se publicó una implementación en hardware para visualizar el algoritmo AES [6].
Se han registrado muchos ataques exitosos contra DES que lo hacen un algoritmo inseguro de cifrado; por otro lado, el único tipo de ataque efectivo contra AES ha sido el ataque de fuerza bruta, pero AES se sigue considerando como un método de cifrado seguro [7], [8]. En la criptografía asimétrica el algoritmo más utilizado es el RSA, llamado así en honor a sus inventores R. L. Rivest, A. Shamir y L. Adleman, el cual, debido a su robustez, sigue siendo vigente. Este algoritmo basa su cifrado en el producto de dos números primos de gran tamaño, aritmética modular y en la función indicatriz de Euler [9].
Se describen a continuación algunos referentes científicos tomados como base para el desarrollo de este trabajo, basados en sistemas caóticos, tanto continuos como discretos, de dimensión 1, 2 o más y de orden fraccionario, con indicadores de seguridad que garantizan la viabilidad de sus esquemas criptográficos.
En el 2013 se plantea en [10] una estrategia para aplicaciones prácticas de cifrado de imágenes en tiempo real. Los autores desarrollan un algoritmo simétrico para cifrado de imágenes en escala de grises, utilizan el sistema dinámico generado por la función del panadero para el esquema de permutación e implementan la fase de difusión de pixeles mediante el atractor caótico de Lorenz, obteniendo un mecanismo de cifrado con una fuerte impredictibilidad y un espacio de clave amplio.
En [11], mediante un sistema caótico de Chen de orden fraccionario, con propiedades muy buenas dentro del contexto del caos, generan dos subsistemas caóticos que utilizan para proponer un algoritmo simétrico de cifrado de imágenes a escala de grises o a color. Una sucesión caótica es utilizada como la secuencia de claves, definiendo el mecanismo de cifrado por medio de la operación XOR implementada entre los valores de los pixeles de la imagen y los valores de dicha sucesión caótica. Con lo anterior se logran buenos indicadores tanto de seguridad como de velocidad de ejecuci ón, con un amplio espacio de clave igual a 10182.
En la misma dirección, Liu, Sun y Zhu [12] presentan un sistema dinámico caótico para encriptaci ón de imágenes en escala de grises a partir de un sistema hipercaótico planteado por los autores, el cual comparan con los utilizados en otros artículos, entre ellos el presentado en Hou et al. [11], señalando que su sistema caótico presenta mejores propiedades de aleatoriedad y entropía. Los autores implementan las etapas de difusión y permutación de línea de onda, las cuales se definen a partir de los valores de la sucesión caótica generada por el atractor hipercaótico. Sugieren una forma de extensión de esta metodología a imágenes a color mediante la separación de las capas RGB y la aplicación de la función logística. Las pruebas de desempeño presentadas permiten concluir que el algoritmo tiene buenas propiedades alusivas a seguridad, sensibilidad a la clave inicial, tiempo de ejecución y resistencia a ataques estadísticos [12].
Por otra parte, Zhou, Bao y Chen [13] presentan un sistema caótico para cifrar imágenes en escala de grises, el cual se puede extender a imágenes a color a partir de una combinación no lineal de dos sistemas caóticos unidimensionales que los autores denominan mapas semillas, obteniendo sistemas con propiedades referentes a comportamiento caótico de mayor complejidad que las obtenidas por aparte en cada sistema unidimensional. Muestran que para los casos en que se utiliza la función logística, tienda o senoidal, se obtienen sistemas con exponentes de Lyapunov mayores que los correspondientes exponentes de Lyapunov para los sistemas semilla de manera individual. Como caso de estudio, los autores consideran un sistema caótico definido a partir de la combinación de la función tienda y la función logística, notado como sistema LTS (por sus siglas en inglés de Logistics Tent System), y lo utilizan para generar un sistema de encriptación de imágenes en multimedia. Encuentran buenas propiedades de aleatoriedad, impredictibilidad, resistencia a ataques de fuerza bruta y un amplio el espacio de clave de 1084 [13].
Otro trabajo destacable en el campo del caos y la criptografía se presenta en [14]. Los autores, basados en el sistema de malla acoplado CML (por sus siglas en inglés de coupled map lattices) definido a partir de la función logística y la función Cat de Arnold, generan un nuevo sistema de malla acoplado no adyacente NCML (por sus siglas en inglés de non-adjacent coupled map lattices), el cual tiene propiedades dinámicas más complejas que el CML y que utilizan para implementar la etapa de difusión en un algoritmo de encriptación de imágenes en escala de grises, cuyo mecanismo de permutación afecta todos los bits de cada pixel. Los resultados mostrados indican que el espacio de clave es mayor que 10120, con una buena sensibilidad a la clave inicial y una baja correlación entre pixeles adyacentes de la imagen cifrada.
En [15] se reporta un algoritmo de encriptación de imágenes en escala de grises a partir de un método de descomposición de la imagen en planos de bits, generando dos sucesiones binarias del mismo tamaño a las que les implementan una estrategia de difusión mutua. Para la permutación emplean una sucesión generada por un atractor caótico a trozos que los autores definen. Además, acuden a otros algoritmos propuestos en la literatura enfocados al uso de sistemas caóticos para comparar las medidas de desempeño de estos con las del algoritmo que ellos proponen, evidenciando como fortaleza que en un solo ciclo obtienen mejores indicadores.
Por otra parte, en [16] utilizan un atractor caótico de orden fraccionario para diseñar un mecanismo de encriptación en tiempo real de imágenes a color basados en el algoritmo para encriptación de imágenes publicado en [17]. El atractor de orden fraccionario surge de una modificación de un sistema hipercaótico de Lorenz y presenta dos exponentes de Lyapunov positivos que implican mejores características caóticas. El objetivo es realizar los procesos de difusión y permutación pixel a pixel. El espacio de clave que obtuvieron es de 128 bits e incluyen en este el orden de la derivada. Las pruebas de desempeño muestran robustez del esquema planteado.
En [17], a partir de las características de la imagen plana y de la función logística unidimensional, proponen un esquema de encriptación de imágenes a color para ser usado en tiempo real, utilizando un algoritmo desarrollado por los autores previamente. Obtienen buenos resultados con una sola ronda de difusión y de permutación. Utilizan una clave de 128 bits para generar las condiciones iniciales y el valor del parámetro de la función logística. Los indicadores de desempeño y seguridad muestran que el algoritmo propuesto es altamente seguro.
A partir de un sistema discreto caótico definido mediante la función logística, en [18] obtienen tres órbitas distintas generadas por diferentes condiciones iniciales y parámetros, las cuales emplean con el fin de diseñar un sistema de encriptación que sirve para codificar cualquier tipo de información con solo dividirla en bloques de 8 bits. Como caso de estudio lo aplican para imágenes a color utilizando siete claves para cifrar.
En [19] combinan código ADN con sistemas caóticos para proponer un esquema de cifrado de imágenes a color, esto tiene el propósito de aprovechar las ventajas de ambas metodologías y obtener un sistema más robusto. Utilizan una secuencia ADN para modificar las propiedades de color de los pixeles de la imagen original. Con base en un sistema dinámico caótico definido por medio de la función de Henón, construyen dos sucesiones que son utilizadas para modificar las posiciones de los pixeles de la imagen. Finalmente, diseñan un software para encriptación de imágenes desarrollado en el entorno Guide de MatLab. Los análisis de resultados muestran una baja correlación entre los pixeles de la imagen encriptada, un espacio de clave amplio e igual a 1054, así como una alta sensibilidad a la variación de la clave.
Yaghoobi [20] desarrolla un algoritmo para encriptación de imágenes a color utilizando el atractor Cat de Arnold en dos dimensiones para la etapa de permutación con siete iteraciones y para la fase de difusión usa un atractor hipercaótico de Chen de cuatro dimensiones que combina con la operación XOR. El algoritmo es evaluado con las pruebas convencionales de desempeño para encriptación de imágenes, concluyendo que es un esquema de encriptación robusto [20].
De la misma manera, Zhang [21] propone un algoritmo para encriptación de imágenes en escala de grises, inicialmente utilizando solo permutación, a través de una estrategia basada en el sistema caótico Cat de Arnold. Logra muy buenos resultados con una y dos iteraciones, aunque con propiedades estadísticas muy deficientes con respecto a seguridad; por ello, consideran necesario implementar, además, la etapa de difusión de pixeles, para la cual emplea un atractor hipercaótico de Lorenz. Este, por su alto nivel de complejidad, fortalece el proceso de cifrado y logra buenos indicadores de seguridad [21].
Otro trabajo que ha contribuido en el campo de la criptografía caótica es el de Ye, Zhao y Chai [22]. Plantean un algoritmo para encriptación de imágenes en escala de grises basado en la función hash SHA-3, utilizan la técnica de permutación de línea de onda e implementan un mecanismo de difusión por medio del atractor caótico Cat de Arnold de dimensión 2, el cual soporta también la fase de permutación. Los aspectos positivos que destacan en este algoritmo son: el tama ño del espacio de clave de 1056, buenos indicadores de seguridad según los valores obtenidos de NPCR (por sus siglas en inglés de number of changing pixel rate), UACI (por sus siglas en inglés de unified averaged changed intensity), entropía y correlación de pixeles [22].
De manera similar, en [23], utilizando un sistema caótico en dos dimensiones llamado función modulación logística 2D, el cual se define a partir de una combinación no lineal de los sistemas caóticos unidimensionales obtenidos por una función senoidal y la función logística, se propone un esquema de encriptación de imágenes. Este muestra que tiene mayor complejidad que los atractores de origen y se resaltan sus ventajas en cuanto a seguridad y velocidad de ejecución, gracias a las características de complejidad caótica del atractor que proponen y a la sencillez de la estrategia de permutación formulada.
En [24], los autores desarrollan un algoritmo de encriptación de imágenes basado en la combinaci ón de bits en el sistema decimal y en la utilización de tres sistemas dinámicos caóticos: los generados por función logística, el mapeo de Arnold y un sistema en dos dimensiones definido a partir de la función seno. Inicialmente consideran una imagen en escala de grises, asumen los valores de los pixeles en escala decimal y los dividen en tres grupos: unidades, decenas y centenas de dígitos. A cada grupo le realizan diferentes iteradas con el sistema dinámico caótico de Arnold. Los parámetros y la cantidad de iteradas del mapeo de Arnold están determinados por la imagen original. Una vez hecho este proceso, la imagen permutada se genera por combinación y luego se le aplica la fase de difusión, la cual puede comenzar desde cualquier posición del valor de un pixel en la imagen original utilizando una secuencia caótica obtenida a partir de la función logística o el sistema definido en términos de la función seno para realizar la operación XOR. Esto facilita que si la imagen tiene N pixeles, existan N maneras diferentes de realizar el proceso de difusión. Los autores extienden el algoritmo sobre imágenes a color, llevando a cabo el proceso descrito en cada uno de sus canales RGB, aplican pruebas de seguridad y desempeño, y concluyen que su propuesta es altamente segura.
Recientemente, en [25] se reportó un algoritmo para encriptación de imágenes a color utilizando un modelo caótico basado en un generador de números pseudoaleatorios y en el sistema caótico de Fibonacci, esto con el fin de aumentar la complejidad caótica, generar múltiples conjuntos no correlacionados de secuencias dinámicas caóticas y aumentar el tamaño del espacio clave. Utilizan la operación XOR y las secuencias obtenidas para difundir los pixeles de la imagen a color. Para el proceso de permutación, recurren a la operación convolución de matrices en redes neuronales. Los autores concluyen que el algoritmo propuesto es resistente contra ataques de texto plano y tiene una buena seguridad, lo cual está soportado a partir de las pruebas experimentales y análisis de desempeño que presentan.
La propuesta que se presenta en este trabajo busca incentivar a que otros académicos se interesen por esta línea de trabajo y que se unan esfuerzos en pro de articular el área de los sistemas dinámicos, particularmente los de comportamiento caótico, con la criptografía, lo anterior para crear esquemas de cifrado acordes con las exigencias impuestas por el avance y desarrollo de las redes de intercambio de información. En este artículo se propone un algoritmo de encriptación de imágenes a color, la permutación se realiza con el algoritmo de línea de onda definido a partir del sistema caótico Cat de Arnold y el proceso de difusión se realiza mediante un sistema hipercaótico de Chen o un sistema hipercaótico de Lorenz.
Buscando reducir tiempos de ejecución se hace uso de programación paralela, evidenciando efectivamente menor tiempo de cifrado. Las pruebas de seguridad confirman que el algoritmo es altamente fiable. Como estrategia pedagógica, para hilar y esquematizar de forma comprensible la fundamentación y desarrollos presentados en este artículo, se presentan algunos conceptos de sistemas dinámicos enfatizando en los atractores utilizados, se describe el algoritmo propuesto, se analizan los resultados experimentales, se realizan los análisis de desempeño, se contextualizan los resultados obtenidos frente a otros algoritmos encontrados en literatura reciente y se dan las consideraciones importantes a manera de conclusiones.
Marco teórico
Un sistema dinámico es un proceso que varía con el paso del tiempo de acuerdo con una regla de evolución que puede ser de tipo discreta o continua, el objetivo del estudio de los sistemas dinámicos es predecir su comportamiento a largo plazo. Cuando se está en presencia de sistemas dinámicos no lineales es probable que existan comportamientos enmarcados dentro de las carácter ísticas de los sistemas caóticos. La definición de sistema caótico que se adopta en este artículo es la presentada en [26].
En la literatura existen muchos modelos de sistemas dinámicos que exhiben caos. En este trabajo se hace uso de los sistemas Cat de Arnold, Chen y Lorenz, los cuales se utilizan para formular el algoritmo de encriptación.
La función Cat de Arnold, llamada así en honor a Vladimir Arnold, quien usó la imagen de un gato y analizó su transformación a partir de una aplicación lineal del toro en sí mismo, se define por medio de la ecuación (1).
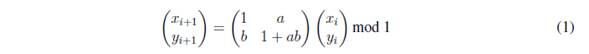
Donde xi y yi están en el intervalo (0; 1), a y b son los parámetros del sistema y mod denota la operación módulo. Esta función es invertible en tanto tiene determinante 1, el conjunto de puntos con órbitas periódicas es denso en el toro, es topológicamente transitiva y tiene dependencia sensitiva a las condiciones iniciales. Para los parámetros a y b positivos tiene un exponente de Lyapunov positivo, características que se ajustan dentro de la definición adoptada de caos. Una descripción de las propiedades de los sistemas dinámicos que exhiben caos se puede encontrar en [27].
El sistema de Arnold se utiliza en el algoritmo que se propone en este trabajo con el fin de generar una sucesión de iteradas que sirven para definir la forma de permutación de línea de onda aplicada en el algoritmo.
El sistema hipercaótico de Chen está dado por las ecuaciones (2).
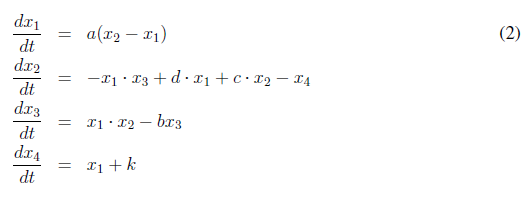
Siendo a, b, c, d y k los parámetros del sistema. Gracias al comportamiento dinámico complejo que tiene este sistema se adapta muy bien para definir el mecanismo de difusión de pixeles. El sistema hipercaótico de Lorenz está dado por las ecuaciones (3).
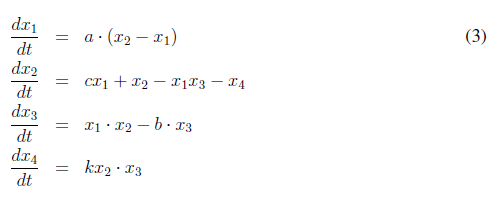
Donde a, b, c y k son los parámetros del sistema. Para ciertos valores de los parámetros el sistema de Lorenz tiene muy buenas características dentro del caos, en este contexto se utiliza para difundir los pixeles, aunque también se puede elegir el atractor de Chen.
Como estrategia de trabajo se recurrió a la programación en paralelo, lo cual se puede hacer a nivel de hardware dependiendo de la cantidad de núcleos del equipo y a nivel de software de acuerdo con el número de tareas que se programen para ejecutarse al mismo tiempo, es decir, del número de hilos que se definan [28].
Metodología del algoritmo propuesto
Debido a que el objetivo de este trabajo de investigación es aprovechar las características inherentes a los sistemas caóticos para proponer un nuevo modelo de criptografía, la fase inicial fue el estudio de la fundamentación teórica de los sistemas dinámicos caóticos y la identificación de las propiedades de estos que se aplican dentro de las estrategias de encriptación de imágenes. Lo anterior tiene el fin de especificar los requerimientos de diseño, teniendo como base la revisión bibliográfica consultada sobre trabajos desarrollados en seguridad con enfoque en caos.
En consonancia con lo anterior, se propone un algoritmo para encriptación de imágenes a color con buenos indicadores de velocidad de ejecución y seguridad. El algoritmo se evaluó aplicando técnicas de criptoanálisis diferencial y estadístico; además, se midió el nivel de desorden de los pixeles en la imagen cifrada, el cual es dado por el valor de entropía, y se hizo análisis de sensibilidad de clave, comparando de esta forma los resultados obtenidos con otros algoritmos con el enfoque en caos. Con esto último se evidencian buenas propiedades de seguridad y desempeño.
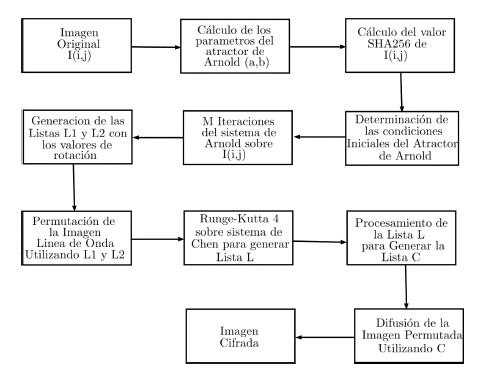
Para una imagen a color I(i; j) de tamaño NxM pixeles en formato RGB se implementan las etapas de permutación y difusión sobre cada capa RGB. La permutación se realiza con el algoritmo de línea de onda basado en el sistema caótico Cat de Arnold y el proceso de difusión se hace con el sistema hipercaótico de Chen o con el sistema hipercaótico de Lorenz, esto se decidió explorando varios algoritmos con el enfoque en caos encontrados en la literatura y generando una propuesta propia enmarcada dentro de la hipótesis de alta seguridad y rendimiento. Se propone un esquema de permutación que se válida para varios números de iteraciones de la función de Arnold, y se generan dos mecanismos de difusión: uno a partir de un atractor hipercaótico de Chen y el otro a partir de un sistema hipercaótico de Lorenz. Como caso de estudio se presentan los resultados obtenidos considerando tres iteraciones para la permutación.
Para la imagen a color IN x M, se consideran las capas RGB y se realizan las fases de permutación y difusión para cada capa. Las etapas del proceso de permutación para una capa se presentan a continuación.
1. Se suman todos los valores de los píxeles de la capa en consideración y se almacena en una variable llamada “S”, dada en la ecuación (4).

2. Se calculan los parámetros a y b del atractor Cat de Arnold por medio de las expresiones dadas en (5).

3. Se calcula el SHA 256 de la imagen a color, este genera un arreglo de 32 bytes, es decir, 256 bits que se almacenan en el arreglo {Hi }, como se indica en la ecuación (6).

4. Se divide el arreglo fHig en dos grupos de 16 bytes y se suman los bytes en base 10 de cada grupo para almacenarlos en las variables S1 y S2 respectivamente, como se muestra en la expresión (7).
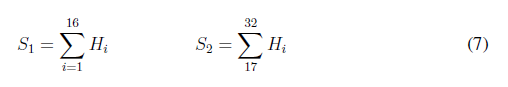
5. Se calculan las condiciones iniciales para la función Cat de Arnold (x0; y0) de acuerdo con las expresiones dadas en (8) y (9).
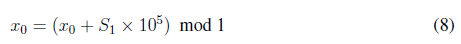
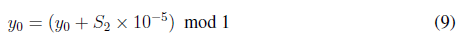
Siendo x0 y y0 valores incluidos en la clave.
6. Partiendo de la condición inicial obtenida en elpunto anterior se aplica el sistema Cat de Arnold “M -1” veces para obtener cols parejas (xi; yi) dadas por las ecuaciones (10) y (11).
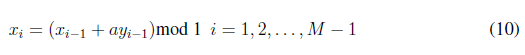
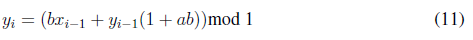
Las listas de valores para las coordenadas (xi; yi) obtenidas anteriormente se modifican de acuerdo con las expresiones (12) y (13).
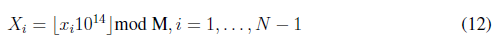
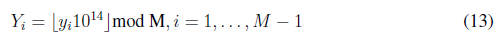
Donde [x] denota la función parte entera generando dos listas L1 y L2, formadas por los valores Xi y Yi, respectivamente.
7. Los valores almacenados en L1 y L2 se utilizan para definir las rotaciones circulares que se hacen por medio del procedimiento de línea de onda.
8. Se rotan las columnas utilizando el siguiente proceso. El número de columnas “M” de la imagen se encuentra en el rango [0; 1; 2; : : : ;M - 2;M - 1]; se recorren las columnas así: si la columna “i”, con i > M/2 se hace una rotación L1[i] hacia abajo, donde, L1[i] representa el valor generado en la iterada número i mediante el proceso descrito en los puntos 7 y 8; por otro lado, si el número de columna es menor o igual que M/2 la rotación se hace hacia arriba.
9. Se rotan las filas de manera similar al procedimiento utilizado para las columnas. El número de filas de la imagen “N” se encuentra en el rango [0; 1; 2; : : : ;N - 2;N - 1] Se recorren las filas así: para la fila “j”, con j > N/2 , se hace una rotación L2 [j] hacia la derecha, siendo L2[j] el valor generado mediante el proceso descrito en los puntos 7 y 8. Si el número de fila es menor o igual que N/2 , la rotación se hace hacia la izquierda.
Los procesos descritos en 8 y 9, se pueden efectuar varias veces.
Partiendo de la imagen generada para cada capa en el proceso de permutación se realiza el proceso de difusión, el cual consta de los pasos mencionados a continuación.
-
Se obtienen los valores de Chen o de Lorenz con las condiciones iniciales x1; x2; x3; x4 dadas en la clave por medio del método de Runge Kutta 4, obteniendo NxM valores que se almacenan en una lista L. Con estos valores se procede a realizar el proceso de cambio del valor de los píxeles de la imagen permutada.
-
Por cada pixel de la imagen en cada capa se coge un elemento de la lista L llamado l i . De l i se toman los últimos tres dígitos y al número formado por estos dígitos se le calcula el módulo 255. Este valor se almacena en una lista C.
-
El nuevo valor de cada pixel en cada capa de la imagen será (RNi;GNi;BNi), dados por las expresiones definidas en (14).
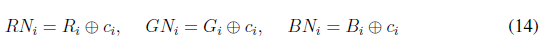
Siendo R i , G i , B i los valores de los pixeles de la imagen permutada, c i la variable i de la lista C. De esta forma se completa el proceso de cifrado. Los procesos de permutación y difusión se resumen en el diagrama de flujo que se muestra en la Figura 1.
Figura 1: Diagrama de flujo del algoritmo propuesto.
Para la implementación del algoritmo se empleó procesamiento en paralelo con el fin de reducir el tiempo de ejecución del programa. Los pasos 2 y 3 del proceso de difusión se implementaron en paralelo. El algoritmo propuesto se desarrolló en C++.
Análisis de resultados experimentales
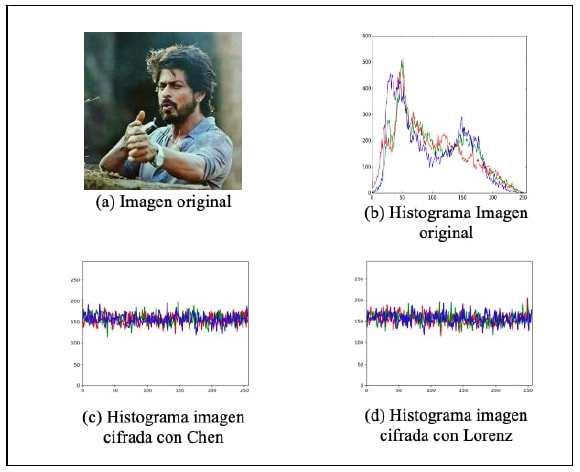
Para las pruebas del algoritmo se utilizaron los siguientes valores en los parámetros de los atractores de Chen y Lorenz: a = 36, b = 3, c = 28, d = -16, k = 0; 2. Se ejecutaron varias rondas de permutación, obteniendo un buen desempeño con tres iteraciones. En la Figura 2 se presentan secuencialmente los resultados de la aplicación del algoritmo para una imagen en estudio de 200 x 200 pixeles, aplicando tres iteraciones para el proceso de permutación de línea de onda. Se observa que la imagen original se oculta perfectamente.
Figura 2: Proceso de encriptación.
Para el proceso de desencriptación se aplican las operaciones inversas sobre la imagen cifrada, logrando recuperar completamente la imagen original.
Para validar y evaluar el algoritmo propuesto se realizaron pruebas de seguridad y velocidad de ejecución. Las pruebas de seguridad se implementaron en Python y las pruebas de velocidad de ejecución se realizaron en C++, utilizando un equipo con procesador Intel Core i7-4700MQ CPU @ 2.40GHz x 8.
Los histogramas de frecuencia para la imagen real y la imagen encriptada con tres iteraciones para el proceso de permutación, según se aplique Chen o Lorenz para la difusión, se muestran en la Figura 3, destacando que las distribuciones de los histogramas de la imagen cifrada son bastante uniformes tanto con el atractor de Chen como con el de Lorenz.
Figura 3: Histograma de frecuencias.
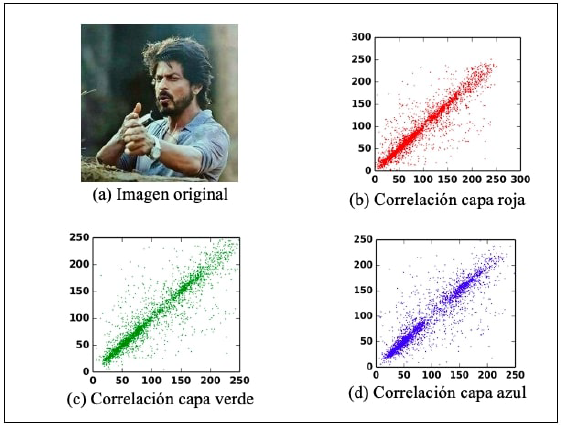
Se calcularon los valores de correlación de pixeles de la imagen original para cada capa y se muestran en la Tabla I, evidenciando que en las tres capas estos son próximos a 1, como se esperaba.
Tabla I: Consideraciones de potencia de los equipos empleados en los diferentes procesos analizados.
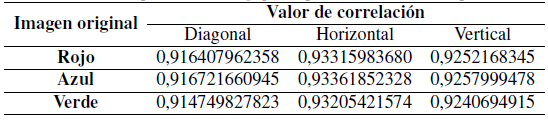
Los gráficos de correlación de pixeles de la imagen original para cada capa se muestran en la Figura 4, situación coherente con la fuerte correlación existente entre pixeles adyacentes.
Figura 4: Correlación de pixeles de la imagen original por capas.
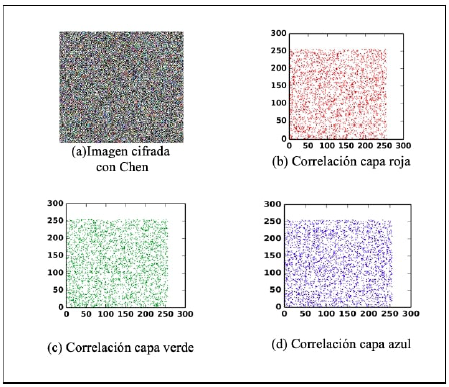
En la Tabla II y la Tabla III se presentan los valores de correlación de pixeles para la imagen encriptada con la función Cat de Arnold y para la difusión con el atractor de Chen o con el atractor de Lorenz. Estos valores de correlación se obtienen tomando las parejas posibles en las direcciones horizontal, vertical y diagonal, en este caso un total de 158.802 pixeles fueron obtenidos para generar dichos valores.
Tabla II: Valores de correlación imagen cifrada con Chen.
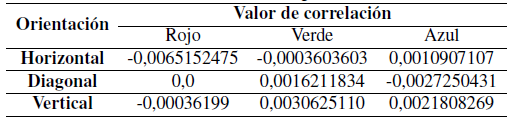
Tabla III: Valores de correlación imagen cifrada con Lorenz.
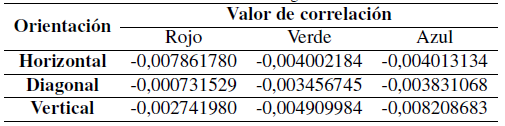
Se observa que los valores de correlación de la imagen cifrada tanto con el atractor de Chen como con el atractor de Lorenz son muy cercanos a cero, que es lo deseable. Estos resultados se pueden apreciar en las Figura 5, tras aplicar tres iteraciones para la función Cat de Arnold y utilizando para la fase de difusión el atractor de Chen, los cuales son muy coincidentes con los provistos por el atractor de Lorenz.
Figura 5: Correlación pixeles imagen cifrada por capas.
Se calcularon los indicadores NPCR y UACI, los cuales se muestran en la Tabla IV y la Tabla V.
Tabla IV: Valores NPCR por capas.

Tabla V: Valores UACI por capas

Como se esperaba, los resultados del indicador NPCR son muy cercanos al 100% y los de UACI están por encima del 30 %, estos son acordes con los estándares de seguridad y garantizan que el algoritmo propuesto en este trabajo es robusto ante ataques diferenciales.
Se calcularon los valores de entropía en cada capa de la imagen cifrada, mostrados en la Tabla VI, según se aplique el atractor de Chen o Lorenz. Estos valores indican el nivel de desorden que hay entre los pixeles de las imágenes cifradas y deben ser cercanos al valor ideal 8.
Tabla VI: Valores de entropía.

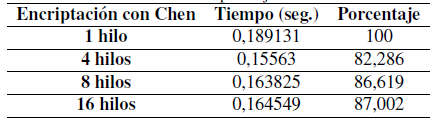
El tiempo de ejecución con la implementación en paralelo se calculó usando la librería de hilos POSIX de Linux pthread.lib. Los resultados se muestran en la Tabla VII, evidenciando que con cuatro hilos es posible disminuir el tiempo de ejecución del algoritmo en un 17% aproximadamente.
Tabla VII: Tiempo de ejecución
Con respecto al tamaño del espacio de clave, es importante precisar que la clave K se compone de las condiciones iniciales y parámetros de los atractores de Arnold, Lorenz y Chen, es de la forma mostrada en (16).
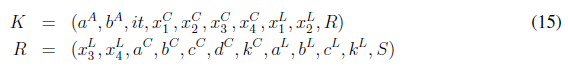
Donde it denota el número de iteraciones de Arnold; los superíndices A, C, L se refieren a Arnold, Chen y Lorenz respectivamente; xi denota las condiciones iniciales de los atractores; a, b, c, d son los valores de los parámetros de los sistemas en consideración, y S indica el tipo de atractor utilizado para la difusión. Como cada uno de los valores de la clave se representa en binario, el espacio total de clave es de tamaño igual a 2641, considerando que cada una de las primeras 20 condiciones iniciales se representan en 32 bits y la ultima en un solo bit.
Se realizó el análisis de sensibilidad de la clave aplicando el algoritmo propuesto de encriptación para una misma imagen con tres iteraciones de la función Cat de Arnold y con los atractores de Chen y Lorenz, con la clave correcta y con la clave modificada infinitesimalmente en una de las condiciones iniciales, obteniendo en cada caso dos imágenes cifradas diferentes, como se observa en la Figura 6. Lo anterior indica una alta sensibilidad a las condiciones iniciales, ya que además no se logra recuperar la imagen original con la clave modificada.
Figura 6: Sensibilidad de la clave.
Para corroborar la robustez del algoritmo que se propone en este trabajo, los resultados obtenidos aplicando tres iteraciones con el atractor de Arnold se compararon con otros trabajos con el mismo enfoque, resaltando los siguientes aspectos:
-
Los valores de correlación de la imagen cifrada que se obtienen en este trabajo, con los atractores de Chen y Lorenz, son muy próximos a 0 y equiparables a los presentados en [17]- [19], [23], [24] y [25]. Asimismo, los valores de NPCR son mejores que los de [17], [23] y [25], pese a que en estas referencias reportan mejores valores de UACI. Además, aunque en este trabajo se obtuvieron unos valores de entropía muy próximos al valor ideal 8, es de resaltar que dichos valores de entropía son inferiores a los reportados en [24].
-
En [19] obtienen para cada capa RGB un valor de NPCR óptimo igual al 100 %, pero el UACI no corresponde a los estándares, ya que está alrededor del 0,8% .
-
El tamaño del espacio de clave obtenido en el algoritmo propuesto es de 2641 y supera a varias referencias tales como [17], [22], [24] y [25].
Conclusiones
Con la ejecución de este trabajo, se aprovecharon las características de los sistemas dinámicos caóticos para consolidar un algoritmo de encriptación de imágenes a color, utilizando en el proceso de permutación el atractor caótico generado por la función Cat de Arnold con el algoritmo de línea de onda y los atractores de Chen y Lorenz para la fase de difusión, logrando ocultar con éxito la imagen original y recuperando dicha imagen sin ninguna alteración. Se llevaron a cabo una serie de análisis y pruebas para validar la seguridad y la validez del algoritmo propuesto, los indicadores de seguridad obtenidos son satisfactorios para el propósito, así como el tiempo de ejecución, comparables con varios artículos científicos recientes con el mismo fin. Se destaca que la clave presenta sensibilidad, el espacio de clave es amplio y que gracias al paralelismo se obtienen tiempos de ejecución pequeños. Este trabajo motiva a seguir explorando con otros sistemas caóticos, así como la fusión con otras técnicas tales como las basadas en código ADN y autómatas celulares, esto con miras a contribuir desde lo académico a soluciones que puedan ser aplicables en entornos reales de seguridad.
Referencias
License
Copyright (c) 2021 Isabel Amaya Barrera, César Augusto Suárez Parra, Daniel Santos Bustos

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.







2.jpg)










