DOI:
https://doi.org/10.14483/23448393.2096Published:
2006-11-30Issue:
Vol. 12 No. 1 (2007): January - JuneSection:
Science, research, academia and developmentProceso de Reconocimiento de Objetos, Asistido por Computador, Aplicando Gases Neuronales y Técnicas Data Mining
Keywords:
Gases Neuronales, C , reconocimiento, visión artificial (es).Downloads
References
. B.M del Brio, "Redes Neuronales y sistemas difusos" 2da ed. Vol 1. Ed. Zaragoza España: Alfaomega Ra-Ma 2002.
. J.R Hilera "Redes Neuronales Artificiales" 1ra ed. Vol 1. Ed Madrid España: Alfaomega Ra-Ma 2000.
. Nilson "Inteligencia artificial" 1ra ed. Vol 1. Ed Madrid España: Alfaomega Ra-Ma 2000.
. Ph.d Revuelta "Modelo de representación y procesamiento de movimiento en tiempo real" Universidad de Alicante. España, 2001.
. Orallo "introducción a la minería de datos" 1ra ed. Vol 1. Ed Madrid España 2004: Pearson (Prentice Hall).
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Ingeniería, 2007-00-00 vol:12 nro:1 pág:22-27
Proceso de reconocimiento de objetos, asistido por computador, aplicando gases neuronales y técnicas data mining
Juan Diego Gómez Valencia
Ingeniería Biomecánica y análisis de Imágenes.
Instituto MEM Research Center.
Resumen
El presente artículo desarrolla un modelo de reconocimiento de objetos basado en la forma de los mismos. Para dicho fin se estudian y comparan muchas técnicas de inteligencia artificial que son potenciales herramientas para resolver el problema; demostrando así la efectividad única que posee para dicho fin una de las más recientes tendencias en IA, desarrollada principalmente en trabajos doctorales de la Universidad de Alicante y Valladolid (España), como lo son los growing neural gas. Finalmente se enuncian las posibilidades tangibles que esta técnica abre no solo para reconocer formas, sino también, texturas, colores y movimiento (visión completa).
Palabras clave:
Gases Neuronales, C++, reconocimiento, visión artificial.
Abstract
The present work develops a model of recognition of objects based on its form. For this end, many techniques of Artificial Intelligence that are potential tools to solve the problem are studied and compared; demonstrating the best answer given for the most recent tendencies in IA, developed mainly in doctoral works of the University of Alicante and Valladolid (Spain), like the growing neurals gases. Finally it is showed in the article that this technique is not just useful to recognize the forms, but it can recognize textures, colors and movement too.
Key Words:
Growing neural gas, recognition, artificial vision.
1. Introducción
En la desesperada búsqueda que en los últimos años ha emprendido el hombre, para desarrollar poderosos sistemas computacionales basados en modelos de otras áreas del conocimiento como la medicina bajo el nombre de una disciplina llamada Inteligencia Artificial [3]; se ha encontrado con miles de retos al desarrollar algoritmos humanizados como las redes neuronales, sistemas expertos, algoritmos genéticos etc. Pero ningún reto más motivador y exigente, como el de sustituir el ojo humano por una maquina, o al menos dotarla del sentido de la visión (el más complejo).
El desarrollo de diferentes técnicas con este fin alrededor del mundo, sigue evolucionando de forma exponencial, más sin embargo, es un hecho que aun hay mucho camino por recorrer, para llegar a concebir un sistema 100% eficiente en este campo, y que involucre toda la gama de posibilidades y complejidades que el mismo conlleva. Puesto que no hace falta enumerar las dificultades que acarrea el intento de generar un sistema de visualización computarizada perfecto, y en el momento podemos simplemente asumir que son demasiadas, ya que tampoco pretendemos solucionarlas todas en este artículo. Es necesario enfocarse en tratar de resolver una necesidad básica, primordial y altamente compleja de dicho sistema, como lo es, aprender a reconocer formas de objetos para poder clasificarlos correctamente. Tratando de desarrollar esta solución mediante una técnica que sea eficiente, confiable y que no se desmesure constante u ocasionalmente en el coste computacional (sistema estable).
2. Planteamiento del problema
El problema de reconocer la forma de un objeto para su debida clasificación, por medio de un computador, se puede solucionar, o por lo menos así se intentó solucionar en el presente artículo, mediante la aplicación de la siguiente secuencia de pasos (algoritmo global):
1) Fotografiar el objeto (no blanco), estático,en fondo blanco, con buena luz, y totalmente solo (sin sombras).
2) Escalar la foto a blanco y negro, mediante un algoritmo computacional discriminante,cuyo objetivo es: todo píxel de la foto de color blanco o casi blanco lo vuelva negro y cualquier otro píxel lo convierta a blanco.
3) Considerar la parte blanca de la foto como un subespacio de entrada, de R2, tal que alguna técnica de IA se adapte topologicamente a él.
4) Luego, que la técnica usada puede representar la topología del espacio de entrada (la forma del objeto). Hallar los patrones y características que este posee, para tratar de clasificarlo con una técnica de data mining como es el clustering o clausterización (mediante cluster's naturales).
Nótese que el meollo del problema está en encontrar la técnica que se adapte topologicamente a un subespacio de entrada para poder representarlo. Razón por la cual este artículo se dedica a continuación, exclusivamente a dicho propósito.
3. Potenciales herramientas
Las siguientes técnicas neuronales de inteligencia artificial, que se van a enunciar, utilizadas comúnmente en data mining, son denominadas auto-organizadas y no supervisadas, esto quiere decir a grosso modo que poseen elementos que se adaptan o tratan de imitar el espacio que se introduce a la entrada patrón a patrón. Por lo tanto el sistema a partir de un proceso de autoorganización proporcionará cierto resultado, el cual será el reflejo de las relaciones de similitud existente entre dichos patrones de entrada [2].
3.1. Redes neuronales de Kohonen
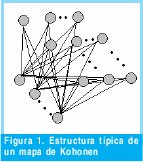
Podríamos referirnos a los mapas autoorganizados de Kohonen [1], como la técnica de clausterización más usada. Esta red se compone de dos capas de neuronas una lineal y otra matricial, Figura 1, la primera de ellas (capa de entrada), tiene tantas neuronas como dimisiones tenga el espacio de entrada, y la segunda, que se ajusta después del entrenamiento a los patrones de entrada, tiene tantas neuronas como deseemos, tal que, la adaptación sea total o por lo menos abarquemos la mayor parte del espacio de entrada (cantidad de patrones de entrenamiento). El proceso de entrenamiento de esta red es competitivo [1], pero no es preciso detallarlo en este momento, en verdad es más importante revisar de que manera puede resolver nuestro problema.
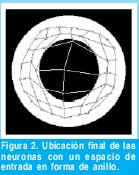
Se utiliza entonces para una prueba, como espacio de entrada, un subespacio de R2, el cual se compone de todos los puntos blancos de la Figura 2, (no todos, pero si un gran numero), lo cual supone que nuestra red posee 2 neuronas en la capa de entrada y un numero suficiente de neuronas en la capa de salida, luego de un entrenamiento exhaustivo de la red, finalmente las neuronas de la capa de salida, quedan ubicadas (autoorganizadas) y conectadas, tal y como se ve en la Figura 2.
Estas redes son comúnmente utilizadas para reducción de dimensiones, reconocimiento de texto, reconocimiento de voz, cuantificación vectorial... Y podemos observar que son también especialmente prácticas paranuestro cometido, ya que se adaptan de manera aceptable a nuestro subespacio de entrada, como lo muestra la Figura 2. El cual sería, en nuestro caso la silueta (rellena), del objeto a reconocer.
3.2. Growing cell structures
Este modelo posee una estructura flexible, con un número variable de neuronas, y una topología k-dimensional donde k es escogido arbitrariamente y a priori. Las neuronas están conectadas entra sí,formando hipertetraedros. En el caso más usual en el que la red es bidimensional, las neuronas están unidas formando triángulos [4].
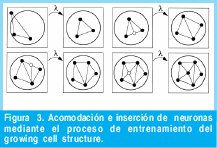
Tampoco podemos detallar en el proceso de entrenamiento de la red, ya que entre otras cosas, es común [4]. Es suficiente con decir, que inicia con una cantidad determinada de neuronas y dependiendo de un error que calcula con los patrones de entrada, va acomodando e insertando nuevas neuronas para reducir dicho error. Algo muy importante y que la hace más optima que la red de Kohonen, es el hecho que puede formar subredes totalmente independientes.
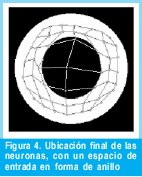
La red reaccionó a la misma prueba de anillo que se le hizo a nuestra anterior red, de la forma que se observa en la Figura 4.
3.3. Gases neuronales
Indudablemente esta técnica que apenas surge en el campo del desarrollo en sistemas de inteligencia artificial, además de innovadora, es demasiado efectiva, razón por la cual se hace mayor hincapié en ella, además también por haber sido la más apta para la solución. Este modelo abarca varias características de otros modelos autoorganizados como [4]:
Realizan su proceso de adaptación según una función de energía (espacio de los vectores de entrada) a diferencia de Kohonen, en el que viene determinado por la estructura de la red. Convergen rápidamente a errores de cuantización pequeños, menores que los obtenidos con los modelos anteriores. Estos modelos pretenden evitar la restricción de los modelos anteriores, donde se requiere un conocimiento a priori sobre la dimensión topológica del espacio de los vectores de entrada. Por ello no preestablecen ninguna topología de red, sino que es durante el aprendizaje cuando las neuronas se conectan o desconectan reajustando su red de interconexión.
3.3.1. Neural gas
Este modelo (simple) posee todas las características mencionadas anteriormente, pero posee la gran desventaja de tener que predeterminar el tamaño de la red, o sea el número de neuronas con que este contará. Ha sido empleada en la predicción de series temporales, control de robots, clasificación de escrituras.
La mejor manera de ver su evolución o comportamiento es viendo la Figura 5, en donde el gas neuronal simple, se adapta o toma la forma de una estructura en tres dimensiones, después de su entrenamiento.
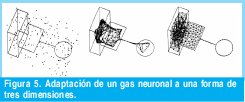
Ahora, el método de entrenamiento de este gas si es de nuestra incumbencia pero no lo esbozaremos por dos razones: Primero, se le debe hacer un detenido estudio que nos llevaría otro artículo entero, segundo se esbozará más adelante uno casi igual, que pertenece a la siguiente técnica a tratar.
3.3.2. Growing neural gas
Por fin una técnica que satisface todas nuestras necesidades, necesidades que explicaremos más adelante. Valiéndose de las bondades del neural gas y de la growing cell structure, surge el gas neuronal creciente, en el que no se establece topología de unión entre las neuronas y tampoco el numero de neuronas de la red, sino que a partir de dos neuronas, el gas se va reproduciendo y ubicando, generando y uniendo neuronas hasta que toma la forma exacta del espacio de entrada, y a nuestro parecer esta es la mayor flexibilidad que se puede obtener en un sistema, además de la rapidez y disminución en error a comparación con otras técnicas.
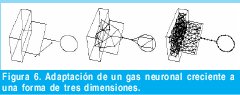
Este modelo es utilizado comúnmente en la robótica e identificación de gestos, y en la Figura 6 podemos ver su evolución para el mismo cuerpo tridimensional como espacio de entrada.
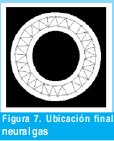

Luego de ver estos dos métodos en acción, es justo observar su comportamiento para el ejercicio que veníamos haciendo con los anteriores modelos (anillo), Figuras 7,8. Podrán notar que lo hace mejor el gas neuronal simple pero más adelante podremos intuir porqué de manera global, es mejor y más útil el gas creciente. Para finalizar esta sección esbozaremos el algoritmo en pseudocódigo y totalmente en español (difícil de encontrar) para un gas neuronal creciente.
3.3.3 Algoritmo de entrenamiento en pseudocódigo para un growing neural gas
• Inicio: Cree 2 neuronas de gas, aleatoriamente sobre la dimensión a la que pertenece el espacio de entrada (Rn) inícielas con error local acumulado (error k) igual a 0, únalas con conexión de edad igualmente en 0.
• Genere una señal de entrada X a (Rn), que conforma la distribución del espacio de entrada.
• Localice las dos neuronas (s,t) mas parecidas a la señal X de entrada. O sea aquellas 2 neuronas con vectores de pesos asociados Ws y Wt, cuya distancia euclidiana con X, ||Ws-X||2 y ||Wt-X||2, sea la mas pequeña y la segunda más pequeña respectivamente, de las k neuronas que hallan en ese momento.
• La neurona ganadora (s) debe actualizar su error local, para lo cual le sumaremos a este la distancia euclidiana entre el vector de entrada y su vector de peso:
errors = errors + ||Ws-X||2
•Mueva la neurona ganadora s, y a todos sus vecinas (todas aquellas que tengan conexión con s) hacia la señal de entrada X, en factores de sus distancias de es y en así (es ,ena [0,1]):
Ws=Ws+es(X-Ws)
Wn=Wn+en(X-Wn)
Para todo n que sea vecina de s
- Incremente la edad de todas las conexiones de la neurona s con sus vecinas topológicas.
- Si la neurona s y t están conectadas ponga a esa conexión edad 0, si no existe pues entonces créela.
- Si hay alguna conexión con edad mayor a amax, destrúyala, si después de esto alguna neurona esta totalmente desconectada también elimínela.
- Si la iteración actual es un múltiplo entero de ë, y la cantidad máxima de nodos aun no se ha alcanzado, entonces inserte una nueva neurona r, así:
- busque la neurona u, con el error local acumulado mas grande
- Entre los vecinos de u, busque la neurona v con el error mas grande
- Inserte la nueva neurona r entre u y v asi:
Wr = (Wu+Wv) / 2. - Cree conexiones entre u y r y entre v y r, retire la conexión entre u y v.
- Disminuya el error de u y v y ponga el error local de r:
erroru = á erroru
errorv = á errorv
errorr = erroru
- Disminuya el error de todas la neurona s j, por un factor â:
errorj = errorj - â errorj
- Si el criterio de parada aun no se da entonces repita el algoritmo, un criterio puede ser el numero máximo de nodos.
4. Cuál es la mejor técnica
El mejor criterio de evaluación para las técnicas expuestas se basa en dos requisitos: Primero la técnica que mejor preserve la topología [4], y segundo, teniendo en cuenta que el sistema es un sistema en tiempo real, también es vital el coste computacional de la técnica o el consumo de tiempo que esta requiera para converger. Por lo cual se debe realizar un balance entre estos dos ítems y decidir cual de las técnicas proporciona mejor desempeño. Para este fin, podemos sustentarnos en la siguiente Tabla I, que resume los entrenamientos y pruebas a las que se sometieron las técnicas.

Concluyamos entonces: Que para todas las figuras anteriores o espacios de entrada (estrella, círculo...) y otros adicionales definitivamente el más veloz de todos los métodos, fue el de growing cell structures, pero como vimos en el caso de los anillos no es el que mejor se adapta o conserva la topología (aunque no lo hace mal), Podemos verificar sin duda para todos los casos, incluyendo el anillo, que el método que mejor preserva la topología o se adapta es el del gas neuronal simple, pero también es evidentemente, que es el que más tiempo consume en todos los casos. Así que si observamos el método de growing neural gas o gas neuronal creciente, este está totalmente balanceado y es el optimo, ya que fue el segundo método que mejor preservo la topología, y también el segundo método que consumió menos tiempo (aunque casi igual al mejor). Por este motivo, y la secuencia de pruebas adicionales que se le hicieron en tiempo real y con figuras o espacios complejos, concluimos que este es el mejor método para representar topológicamente un espacio de entrada en tiempo real.
5. Paso a seguir: del gas al grafo
Es evidente que después del entrenamiento neuronal, lo que obtenemos es un complejo grafo (nodos=neuronas, aristas=conexiones), que tiene la forma de nuestro objeto. Pero momentáneamente, es solo importante para nosotros, la silueta del objeto (para reconocer su forma) y podemos obviar el interior o relleno del grafo, para quedarnos simplemente con un grafo de contorno del grafo original. Para esto utilizamos un algoritmo simple que cumple con el siguiente lema: Dado un grafo, se define como su grafo de contorno el conjunto de aristas que pertenecen únicamente a un polígono (las demás se destruyen, al igual que los nodos totalmente desconectados). La aplicación de esta técnica para obtener el grafo silueta se muestra en la figura No 9.
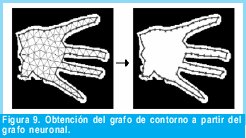
Después de obtener este grafo de contorno podemos hacerle más tratamiento como reducción de nodos con detección de esquinas (teoría de grafos). Sin embargo lo que en verdad nos interesa es que este grafo guardará características únicas de su forma (la forma del objeto), tal que nos permitirán distinguirlo o clasificarlo agrupadamente (con data mining "clustering") con grafos que tengan características similares (objetos de la misma especie o con la misma forma). Algunas características se enuncian a continuación para un grafo, de manera resumida [4]
Dado un grafo de contorno, el diámetro se define como la distancia máxima existente entre dos vértices (neuronas) cualesquiera del mismo. Esta medida es invariante con rotaciones o traslaciones.
Dado un grafo de contorno, se define su longitud como la suma de las longitudes de todas las aristas que le conforman. Esta medida es igualmente invariante a rotación o traslación.
La Curvatura de un grafo de contorno, viene dada por el ritmo de la variación de las pendientes de sus aristas, comenzando siempre desde el mismo punto. Con esta característica se pueden hallar las esquinas del grafo y los segmentos rectos. En la Figura 10, se muestra la función de curvatura para varios elementos de dos clases, puede verse que cada clase conserva un patrón similar de curva.
La Firma del grafo, se obtiene calculando la distancia de cada uno de los vértices al centro del grafo, Igual que en la curvatura se debe partir del mismo punto para todos los grafos. Si se divide esta medida por la distancia entre el nodo más lejano y el centro, se obtiene una medida invariante a al rotación y traslación.
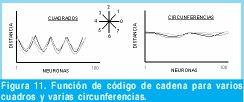
Los Códigos de Cadena se emplean para representar un contorno mediante una sucesión de segmentos de dirección especificada. Usualmente se basa en segmentos de conectividad cuatro u ocho. En la Figura 11, se muestra la función de código de cadena para varios elementos de dos clases, empleando conectividad ocho.

Existe más variedad de características de grafos como los momentos, pero en aras de resumir, es suficiente con lo expuesto hasta el momento.
6. Proceso de clasificación
Luego de obtener el respectivo grafo de contorno de un objeto, con toda la respectiva información que este nos puede brindar, información que es exclusiva de cada grafo y que debe guardar un alto grado de similitud, con grafos parecidos o grafos que representan objetos con igual forma. Nos valemos de esto para clasificarlos o agruparlos, Creando un sistema de clustering, que al recibir la información de un nuevo grafo, le clasificará en un grupo (manzanas, bananos, estrellas...) basándose en la similitud de información que el grafo tenga con este.
Para este proceso de clasificación, que es multidimensional, en donde inclusive se deben tratar de agrupar funciones con características similares, se debe utilizar una convencional técnica de minería de datos [5] o data mining, que cumpla con dicho propósito. Por lo tanto se ha implementado una red neuronal autoorganizada de Kohonen, de igual forma se pudo utilizar nuevamente un gas neuronal, pero en aras de la versatilidad y merma en la complejidad del sistema, se opto por la primera opción. Este mapa de Kohonen, que se implementa es de alta dimensionalidad, ya que los patrones a clasificar (grafos) a sí lo son. Puesto que un patrón P (grafo), no se componen de dos o tres dimensiones, sino, de varias funciones f(x), g(x)... y números reales a, b... Como su curvatura y su diámetro etc. ( P [f(x), g(x),....,a,b...] )
7. Resultados y conclusiones
Hemos querido que los resultados se basen en la Figura 12, la cual representa resumidamente lo obtenido de un ejemplo de clasificación del sistema, para varios objetos reales de diferentes clases.

Esta figura muestra los cuatro grupos que el sistema formo después de haberle introducido fotos de aleatoriamente de diferentes tipos de zapatos, copas, manzanas y sombreros. Cabe resaltar que estos mismos grupos se generaron después de ingresar los elementos varias veces en órdenes diferentes y aleatorios.
Es importante en este momento aclarar, que la técnica de los gases neuronales no llega a dar su máximo potencial en este ejemplo de reconocimiento y clasificación basado en formas, puesto que no debemos olvidar que de los resultados de acoplamiento a la topología o espacio de entrada, que resultaron ser un grafo, han sido inexplorados en un 90%, ya que eliminamos todo el interior del grafo para obtener el grafo de contorno. Pero en verdad este grafo completo, genera mucha más información de la que pensamos y al hacer un tratamiento especial de esta, podemos obtener características de texturas, sombras, colores... Inclusive con secuenciación de entrenamientos a ráfagas de fotos en tiempo real se puede obtener información, sobre una escena, y los movimientos que hay en ella. En fin este estudio es apenas una pequeña muestra de la capacidad de esta técnica.

En la Figura 13, las fotos reales de los elementos clasificados por el sistema, con el fin de observar en detalle el buen desempeño del mismo.
Finalmente concluimos que la técnica aplica de una manera formidable para la resolución del problema planteado y que además esta es susceptible a cambios y modificaciones heurísticas que pueden mejorar su desempeño notablemente. También se debe concluir la capacidad computacional tan alta que el sistema requiere para su optimo desempeño, esto nos sugiere maquinas y procesadores de alta velocidad, lo que refleja un impedimento actual, mas aun si pensamos en el sistema como un sistema portable pues los avances tecnológicos respecto a dispositivos portátiles están poco desarrollados actualmente.
Referencias bibliográficas
[1]. B.M del Brio, "Redes Neuronales y sistemas difusos" 2da ed. Vol 1. Ed. Zaragoza España: Alfaomega Ra-Ma 2002.
[2]. J.R Hilera "Redes Neuronales Artificiales" 1ra ed. Vol 1. Ed Madrid España: Alfaomega Ra-Ma 2000.
[3]. Nilson "Inteligencia artificial" 1ra ed. Vol 1. Ed Madrid España: Alfaomega Ra-Ma 2000.
[4]. Ph.d Revuelta "Modelo de representación y procesamiento de movimiento en tiempo real" Universidad de Alicante. España, 2001.
[5]. Orallo "introducción a la minería de datos" 1ra ed. Vol 1. Ed Madrid España 2004: Pearson (Prentice Hall).
Juan Diego Gómez Valencia
Ingenierio en sistemas y computacion. Universidad Tecnológica de Pereira, Colombia. Actualmente perfeccionamiento en ingenieria biomecánica y análisis de imágenes. Instituto MEM Research Center.
Creation date:
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.





2.jpg)










