DOI:
https://doi.org/10.14483/23448393.2285Published:
1998-11-30Issue:
No 1 (1999)Section:
Science, research, academia and developmentAvances en comunicaciones por fibra óptica: Acopladores ópticos pasivos en estrella.
Last advances in optical fiber communications Passive optical star couplers
Keywords:
Acoplador óptico, difracción de Bragg, simulación, fibras ópticas. (es).Downloads
References
Tabiani et al. An efficient NxN Passive Optical Star Coupler. IEEE Photonics Technology Letters. Vol. 2 No. 11. Nov. 1990. 826-829
Tabiani et al. Theory of An Efficient NxN Passive Optical Star Coupler. Journal of Lgthwave Technology. Vol 9. No. 4. Apr. 1991. 448-455.
Dragone, C. Integrated Optics NxN Multiplexer on Silicon. IEEE Photonics Technology Letters. Vol. 3. No. 10 . Oct. 1991. 896-899.
Cheng et al. Determination of Coupling Length in Directional Couplers from Spectral Response. IEEE Photonics Technology Letters. Vol. 2 No. 11. Nov. 90. 823-825.
Jeruchim, M. et al. simulation of communications Systems. Plenum Publishing Corporation.New York, 1992.
Okamoto, K. et al. Fabrication of large Scale Integrated-Optic NxN Star Couplers. IEEE Photonics Technology Letters. Vol. 4. No. 9. Sep. 1992. 1032-1035.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Investigación y Ciencia
Ingeniería, 1999-00-00 vol: nro:1 pág:36-42
Avances en comunicaciones por fibra óptica.
Acopladores ópticos pasivos en estrella.
Last advances in optical fiber communications Passive optical star couplers
Andrés Lombo Carrasquilla
Resumen
Uno de los principales componentes de las nuevas redes de fibra óptica que soportan múltiples servicios, son los acopladores ópticos. Se presenta un estudio detallado de la estructura de reflexión dentro de un acoplador óptico en estrella, teniendo en cuenta los patrones de radiación de ondas electromagnéticas y las condiciones de difracción de Bragg. Se analizan los campos electromagnéticos producidos de acuerdo a la geometría del acoplador y se presenta un ejemplo sencillo de un acoplador transmisivo.
Palabras Clave:
Acoplador óptico, difracción de Bragg, simulación, fibras ópticas.
Abstract
The optical couplers are one of the main components of the new optical fiber nets that support multiple services. It is presented a detailed study of the reflection structure within an optical star coupler taking into account the electromagnetic wave pattern radiation and the Bragg diffraction conditions. They are analyzed the electromagnetic fields produced according to the geometry of the coupler and is presented a simple example of a transmissive coupler.
Key Words:
Optical coupler, Bragg diffraction, simulation, optical fibers.
INTRODUCCIÓN
La tendencia de las comunicaciones en los últimos 10 años presenta a la fibra óptica como el medio de transmisión de mayor crecimiento en cuanto a cantidad y calidad de servicios transportados por kilómetro instalado. Ya no solo se usa para el transporte de conversaciones telefónicas en rutas troncales internacionales; servicios como la televisión por cable, internet, redes bancarias y empresariales hacen uso de esta tecnología cada vez más cerca del escritorio mismo del usuario final. Los acopladores ópticos surgen igualmente como uno de los elementos indispensables en cualquier red de fibra óptica. La necesidad de obtener un alto desempeño en los puntos de conmutación de la red y donde se requiera combinar múltiples servicios a altas velocidades y con la mejor calidad posible, hace necesario reeemplazar las formas puramente electrónicas y reemplazarlas por medios de acople que tengan la misma naturaleza de los medios de transmisión. Los acopladores ópticos permiten la interacción simultánea de múltiples señales ópticas sobre el mismo medio (fibra óptica) siempre y cuando estas tengan una longitud de onda diferente. Esta idea ha sido ampliamente explotada en los actuales sistemas de multiplexación por longitud de onda (WDM- Wavelenght Division Multiplexing).
Como parte de la línea de investigación en Comunicaciones &Oacuxte;pticas del Laboratorio de Aplicaciones Optoelectrónicas de la Universidad Distrital, este trabajo es un esfuerzo más hacia la desarrollo del currículo de la Maestría en Aplicaciones Optotlectrónicas. En el presente artículo se analizan los factores de propagación dentro de un acoplador óptico, con el fin de obtener pautas para su diseño y posterior simulación asistidos por computador.
FUNCIONAMIENTO BÁSICO DEL ACOPLADOR ÓPTICO EN ESTRELLA
La construcción de acopladores ópticos en estrella se ha venido desarrollando con el fin de dar solución a una gran variedad de aplicaciones dentro del mundo de las redes de área local (LAN), en donde quiera que se necesite integrar varios servicios (voz, vídeo, datos, etc.) simultáneamente, y en donde se establezcan conexiones simultáneas todos contra todos a grandes velocidades. Inicialmente se tendió a realizar combinaciones de acopladores 2x2 para alcanzar el número deseado de puertos [1], [2], pero el resultado es cada vez más complicado cuando hay un gran número de estaciones para conectar. De esta forma se hace necesario construir un dispositivo económico que tenga un número mayor de puertos, con menos interconexiones y una mínima pérdida de potencia.
La estructura básica de un acoplador en estrella está compuesta por una región de entrada/salida por la cual se dirigen los haces de entrada cada uno con una longitud de onda diferente y una región de incidencia común de dichos haces que tiene como particularidad un índice de refracción variable. Esta última zona de índice de refracción variable puede estar dispuesta de dos formas según las cuales se caracteriza el acoplador:
Acopladores Transmisivos NxN: aquellos que poseen en forma separada una región de entrada y otra de salida; en medio de estas dos se encuentra una región en la cual se mezclan las señales provenientes de las N entradas y que es atravesada por todos los rayos incidentes obteniendo una muestra de cada una de las señales de entrada en todas las N salidas indistintamente.
Acopladores Reflectivos N: son aquellos que poseen N puertas de entrada cuyos rayos inciden sobre una región central de índice de refracción variable; los puertos de entrada son también de salida gracias a que en medio de la región central se dispone de una superficie especular que refleja en dirección contraria a la de entrada la señal resultante de la combinación de todas las entradas.
En particular se puede ver que el uso de acopladores reflectivos disminuye el número de fibras de interconexión, sinembargo se hace más difícil su construcción y la posterior disposición de equipos duales de transmisión y recepción.
PROPAGACIÓN DE LAS ONDAS DENTRO DEL ACOPLADOR
A continuación se presenta un modelo de propagación que permite obtener expresiones matemáticas muy acertadas de las ondas que viajan a través del acoplador [3]. Se debe tener en cuenta inicialmente el principio físico y después proponer un modelo matemático apropiado
La Difracción de Bragg:
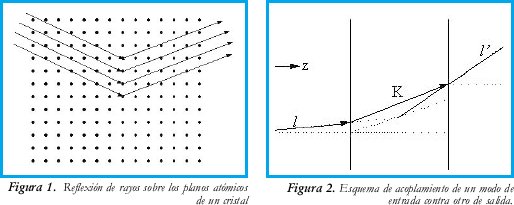
William Henry Bragg y su hijo trabajaron la relación existente entre la longitud de onda y las posiciones de los máximos de interferencia en estructuras cristalinas. El fenómeno se ubica dentro de una estructura cristalina tal como la que puede ser encontrada en la región intermedia de un acoplador óptico. Un cristal se puede observar como una red de átomos muy regularmente distribuidos en planos perfectos sobre los cuales inciden rayos luminosos con direcciones definidas. En la figura 1. se ilustra la forma de incidencia de los rayos sobre los planos atómicos del cristal. El fenómeno que se produce es de interferencia tanto constructiva como destructiva. Las longitudes de onda que experimentan interferencia constructiva son aquellas que pueden atravesar exitosamente el cristal y lo hacen con unos ángulos de incidencia determinados por la longitud d de separación interatómica. Bragg comprobó que se produce interferencia constructiva entre los rayos reflejados únicamente con ángulos en los que Φ es un múltiplo de 2π:
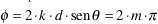
Esta relación se conoce comúnmente como la ley de Bragg:
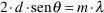
Igualmente Bragg estableció que las dimensiones de d deben estar dentro de la siguiente condición:
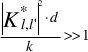
En el caso del acoplador en estrella se trata de acoplar inicialmente un modo l de entrada a un modo l de salida. Para este primer caso la función del índice de refracción va a ser de la forma:
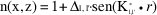
donde D es el coeficiente de acoplamiento entre la entrada l' y la salida l, r, son las dimensiones en el espacio y K es el vector formado de la suma de los vectores de las ondas incidentes y reflejadas de los modos l y l'. La figura 2 muestra gráficamente la formación del vector K en el espacio.
Patrón de Radiación.
Una vez obtenido un modelo simplificado se le puede dar aplicación al caso real en el cual se van a tener varias señales incidentes. De esta forma se va a formar un patrón de radiación que determine la dirección y magnitud de los vectores resultantes de acoplar una entrada a todas las salidas y todas las entradas a todas las salidas [4].
Acople del l-ésimo modo de entrada a N=2M+1 modos de salida: en este caso se debe tener en cuenta que el índice de refracción debe ser de tal forma que cumpla la condición de reflexión expuesta arriba simultáneamente para todos los N modos de salida; entonces se debe cumplir que:
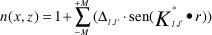
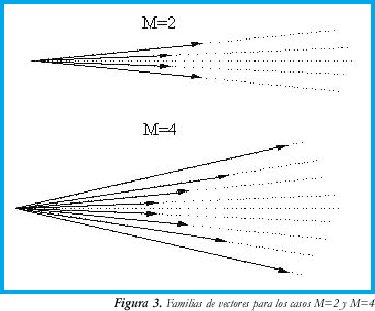
Con esta expresión se pueden evaluar varios casos para diferentes valores de M. Se nota claramente que la construcción típica de un acoplador puede ser 3x3, 5x5, 7x7, etc. Tomando el caso de M=2 y M=4 se tiene una familia de vectores K mostrados en la figura 3.
Con estos casos se observa la formación de una familia de vectores cuyas terminaciones son arcos de sucesivas circunferencias que determinarán el patrón de radiación dentro del acoplador.
Acople de N=2M+1 modos de entrada con N=2M+1 modos de salida: de manera similar, pero teniendo en cuenta el acoplamiento simultáneo tanto en la entrada como en la salida, se tiene que el índice de refracción dentro del acoplador debe ser:
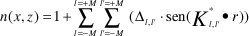
Con esta última expresión se puede determinar la forma de propagación de las ondas luminosas dentro de la región de índice de refracción variable con la cual se debe cumplir la ecuación de Maxwell:
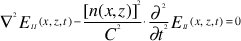
La solución de esta ecuación debe ser de la forma:
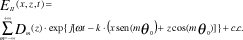
donde c.c. es el complejo conjugado del exponencial de la expresión, &thta;o es el valor del ángulo de separación entre las entradas del acoplador que es la misma diferencia entre los ángulos de incidencia de ondas adyacentes y Dm(z) es el coeficiente de la m-ésima onda en la región central. En una forma similar se pueden expresar los campos resultantes en las regiones de entrada y salida del acoplador.
Para encontrar los valores del coeficiente Dm(z) se reemplazan los valores del índice de refracción n(x, z) y del campo E en la región II, en la ecuación de Maxwell. De ahí se obtienen los valores del coeficiente para los diferentes casos de refracción:
a. Para el caso marginal: cuando se acopla la entrada m # 0
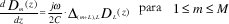
b.Para el caso de la entrada central: cuando se acopla a la salida m=0
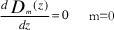
De esta forma se pueden configurar varios ejemplos:
Cuando M=2: se forma una acoplador 5 x 5 y se necesitan 5 ondas E1, E2, E3, E4 y E5. El procedimiento debe ser acoplar o mezclar primero E1 con las restantes 4, luego E2 con las restantes 3, luego E3 con las restantes 2 y finalmente E4 con E5. De aquí se ve que se forman 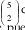 combinaciones de ondas, que en general se pueden ver como
combinaciones de ondas, que en general se pueden ver como 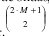 combinaciones para cualquier valor.
combinaciones para cualquier valor.
Valores típicos de Mθn deben ser mucho menores de π para asegurar una adecuada mezcla de las ondas dentro de la región central del acoplador y para no requerir que dicha región se haga muy extensa. Construcciones ya realizadas obtuvieron buenos resultados con un espesor d=3.4875 mm usando una longitud de onda λ=1550 nm. Básicamente la relación se puede generalizar como d= 2250λ como máximo para obtener un patrón de radiación definido sin llegar a solapar o producir interferencia entre una longitud de onda y otra.
SIMULACIÓN
En la actualidad se cuenta con varias herramientas de simulación; sinembargo, más allá de que sea una herramienta u otra, lo importante es el método matemático empleado en el programa simulador. Se debe tener en cuenta que son varias las etapas y por tanto varios los métodos empleados.
A grandes rasgos se encuentran dos métodos matemáticos para la simulación de componentes ópticos, entre ellos las fibras ópticas y los acopladores: un método en el dominio del tiempo y otro en el dominio de la frecuencia [5]. Con ellos se pretende dar una solución a las ecuaciones de Maxwell en cada una de las zonas del acoplador. En esta labor se encuentra que la solución de campo óptico contiene dos componentes: L es un operador lineal responsable de la dispersión del pulso, y N es un operador no lineal que cuantifica el efecto Kerr y otros efectos no lineales. Cada método se diferencia en la for ma como el operador L es calculado. N siempre se calcula en el dominio del tiempo.
El método en el Dominio del Tempo por Pasos Separados (TDSS Time Domain Siplt-step) calcula L como un producto de convolución de muestras en el tiempo de la señal por una respuesta impulso; en tanto que su homólogo en el dominio de la frecuencia FDSS (Frecuency Domain Split-step) calcula la Transformada Rápida de Fourier (FFT) de la señal muestreada en el tiempo y la multiplica por la FFT del impulso, y el resultado es nuevamente convertido al dominio del tiempo aplicando la transformada inversa FFT.
Para el presente caso se escogió la forma TDSS, dado que el error intrínseco al método FDSS al calcular la convolución, conllevaría un efecto de superposición de soluciones al convertirlas al dominio del tiempo.
Resta todavía calcular las variaciones del índice de refracción dentro del acoplador en estrella, para lo cual, observando la ecuación para n(x,z) se escogió el método de diferencias finitas. Este método es empleado es varios simuladores construídos en diversos países, entre ellos: BeamProp® de Rsoft Inc. y la Universidad de Columbia, y BPM-CAD® de Optiwave Corporation, Canadá, el cual fué adquirido por la Universidad Distrital. De esta forma se simula exactamente la propagación del haz óptico a través de una región de índice de referacción variable.
RESULTADOS
Se simuló un acoplador transmisivo teniendo en cuenta el ejemplo de acople de 2M+1 con 2M+1 modos para un acoplador con ocho entradas y ocho salidas, longitud de onda λ=1550 nm y un espesor de la región de acoplamiento de d=0.650 mm.
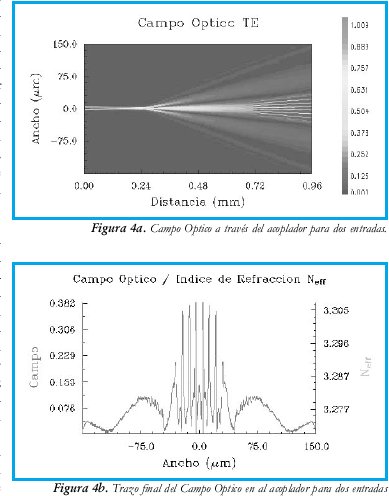
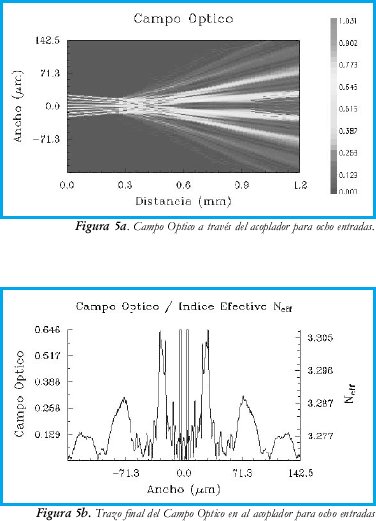
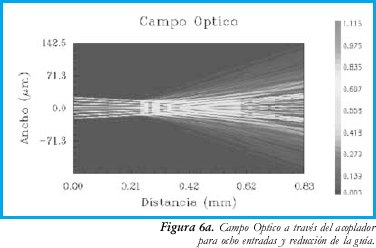
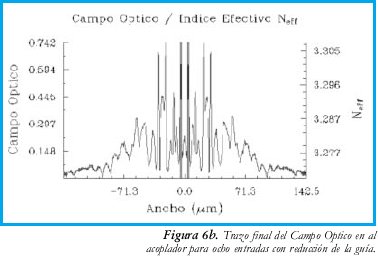
El análisis tuvo en cuenta el campo óptico TE para todos los casos. Inicialmente se obtuvo la respuesta del acoplador para las dos entradas centrales. En la figura 4a y 4b se aprecian las magnitudes campo óptico sobre un corte longitudinal de todo el acoplador y un corte transversal del extremo final del mismo, respectivamente. Posteriormente se consideran todas las 8 entradas; en la figura 5a y 5b se aprecian las magnitudes campo óptico sobre un corte longitudinal de todo el acoplador y un corte transversal del extremo final del mismo, respectivamente para este caso. Finalmente, en la figura 6a y 6b se aprecian las magnitudes campo óptico sobre un corte longitudinal de todo el acoplador y un corte transversal del extremo final del mismo, respectivamente recortando en 0.3 mm en la longitud de la región de acople.
CONCLUSIONES
El trabajo aquí reportado forma parte de un proceso de aprendizaje en el modelamiento y simulación de dispositivos optoelectrónicos dentro de la línea de investigación en Comunicaciones Opticas del Laboratorio de Aplicaciones Optoelectrónicas de la Universidad Distrital Francisco José de Caldas. Se ha desarrollado un análisis matemático de la propagación de la onda a través del acoplador apoyándose en una solución de las ecuaciones de Maxwell y teniendo en cuenta que dentro del acoplador se encuentra una región de índice de refracción variable. Los resultados obtenidos al llevar el diseño a una herramienta de simulación permiten concluir lo siguiente:
•Las aproximaciones y consideraciones realizadas demuestran un buen resultado en aquellos casos en los cuales hay excitación del acoplador por un número reducido de entradas. Para el caso mostrado, la distribución de potencia en la salida del acoplador fue uniforme tal como se muestra en la figura 4 para los 6 canales centrales; se aprecia una atenuación alrededor de 3 dB para los canales de los extremos, con relación a los canales centrales.
•Hay un porcentaje no muy significativo de potencia que se desvía dentro de la región de índice de refracción variable y que no llega a las guías de onda de salida.
•Conservando la geometría del experimento anterior, pero considerando la interacción de las 8 entradas (figura 5), el perfil de potencia a la salida del acoplador no se conserva en forma homogénea; por el contrario la mayor densidad de potencia se observa hacia las salidas extremas.
•La anterior conclusión hace pensar que se debe reducir la longitud de la región central de acople. En la figura 6 se muestra el efecto de reducir esa región en 0.3 mm, con lo cual se recupera el perfil de distribución de potencia sobre las 8 salidas.
Estas conclusiones y otros diseños posibles conforman material adicional para continuar el proceso investigativo dentro de la línea de investigación de Comunicaciones Opticas.
BIBLIOGRAFÍA
[1] Tabiani et al. An efficient NxN Passive Optical Star Coupler. IEEE Photonics Technology Letters. Vol. 2 No. 11. Nov. 1990. 826-829
[2] Tabiani et al. Theory of An Efficient NxN Passive Optical Star Coupler. Journal of Lgthwave Technology. Vol 9. No. 4. Apr. 1991. 448-455.
[3] Dragone, C. Integrated Optics NxN Multiplexer on Silicon. IEEE Photonics Technology Letters. Vol. 3. No. 10 . Oct. 1991. 896-899.
[4] Cheng et al. Determination of Coupling Length in Directional Couplers from Spectral Response. IEEE Photonics Technology Letters. Vol. 2 No. 11. Nov. 90. 823-825.
[5] Jeruchim, M. et al. simulation of communications Systems. Plenum Publishing Corporation.New York, 1992.
[6] Okamoto, K. et al. Fabrication of large Scale Integrated-Optic NxN Star Couplers. IEEE Photonics Technology Letters. Vol. 4. No. 9. Sep. 1992. 1032-1035.
Andrés Lombo Carrasquilla
Ing. Electrónico U.D. M.Sc. U.Andes Profesor T.C. Fac. Ingeniería U.D. Miembro del Grupo de Optoelectrónica y Microelectrónica Universidad Distrital. laoe@udistrital.edu.co
Creation date:
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.





2.jpg)










