DOI:
https://doi.org/10.14483/23448393.2310Published:
2005-11-30Issue:
Vol. 11 No. 1 (2006): January - JuneSection:
Science, research, academia and developmentImplementación de Lógica Difusa para realizar Pruebas de Hipótesis Estadísticas Univariadas
A Fuzzy Logic Approach to Test Univariate Statistical Hypothesis.
Keywords:
Lógica Difusa Tipo I, Pruebas de Hipótesis Estadísticas, Test No- Paramétricos, Test Paramétricos. (es).Downloads
References
JAMES J. BUCKLEY., «Fuzzy Statistics: hypothesis testing». Soft Computing A Fusion of Foundations , Methodologies and Applications, Volumen 9, Número 7, Julio de 2005, pp 512-518.
JAMES J. BUCKLEY., «Fuzzy statistics: regression and prediction». Soft Computing A Fusion of Foundations , Methodologies and Applications, Vol. 9, Número 6, Mayo de 2005, pp 769-775.
JAMES J. BUCKLEY., «Fuzzy Probabilities: New approach and applications». Physica-Verlag, Vol. 4, Número 1, 2003a, pp 196-212.
JAMES J. BUCKLEY., Fuzzy Statistics. Editorial SpringerVerlag, 2004.
A. Mohammadpuor y A. Mahammad.Djafari. «On Classical, Bayesian and Fuzzy Hypothesis Testing», 25th International Workshop on Bayesian Inference and Maximum Entropy Methods in Science and Engineering. 2005
B. F. Arnold. «An approach to Fuzzy Hypothesis Testing», Metrika, Vol. 44, Número 2, 1996, pp. 119-126.
MOOD, ALEXANDER M.; GRAYBILL, FRANKLIN A. & BOES, DUANE C. Introduction to the Theory of Statistics. McGraw Hill Book Company, 1974.
CANAVOS, GEORGE C, Probabilidad y Estadística; Aplicaciones y Métodos. McGRAW HILL, 1988.
THODE, HENRY C: Jr. Testing For Normality. Marcel Drecker Inc. New York, Basel, 2002.
WILKS. Mathematical Statistics. John Wiley and Sons, New York, 1962.
KLIR, GEORGE J. & FOLGER, TINA A. Fuzzy Sets, Uncertainty and Information. Prentice Hall, 1992.
KLIR, GEORGE J. & YUAN, BO. Fuzzy Sets and Fuzzy Logic: Theory and Applications. Prentice Hall, 1995.
WANG, LI-XING. Adaptive Fuzzy Systems and Control, Design and Stability Analysis. Prentice Hall, 1994.
MENDEL, JERRY. Uncertain Rule-Based Fuzzy Logic Systems: Introduction and New Directions. Prentice Hall, 1994.
CARLOS ANDRES PEÑA REYES, «Coevolutionary Fuzzy Modeling», Tesis Doctoral para Ph.D, Sección de Informática, Escuela Politécnica Federal de Lausanne, Suiza, 2002.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Ciencia, Investigación, Academia y Desarrollo
Ingeniería, 2006-00-00 vol:11 nro:1 pág:51-61
Implementación de Lógica Difusa para realizar Pruebas de Hipótesis Estadísticas Univariadas
A Fuzzy Logic Approach to Test Univariate Statistical Hypothesis.
Juan Carlos Figueroa García
Miembro Grupo de Investigación LAMIC (Laboratorio de Automática, Microelectrónica e Inteligencia Computacional, Universidad Distrital). Coinvestigador Grupo de Investigación MMAI (Modelos Matemáticos Aplicados a la Industria, Universidad Distrital).
Luis Eduardo Campos Trujillo
Miembro Grupo de Investigación LAMIC (Laboratorio de Automática, Microelectrónica e Inteligencia Computacional, Universidad Distrital).
Camilo Caquimbo Tabares
Miembro Grupo de Investigación LAMIC (Laboratorio de Automática, Microelectrónica e Inteligencia Computacional, Universidad Distrital).
Resumen
El siguiente artículo muestra un acercamiento de la lógica difusa a las pruebas de hipótesis estadísticas, las cuales son una herramienta inferencial para determinar si una afirmación del valor de un parámetro de una población debe ser rechazada o no. Las técnicas estadísticas clásicas para realizar pruebas de hipótesis poseen una limitante importante, ya que no se muestra algún grado de cumplimiento de la muestra utilizada frente a la población de interés. La aplicación difusa pretende brindar, a quien evalúa una muestra de una población, un valor que indique el grado de cumplimiento de la afirmación, con el fin de tomar decisiones acerca de la muestra.
Palabras clave: Lógica Difusa Tipo I, Pruebas de Hipótesis Estadísticas, Test NoParamétricos, Test Paramétricos.
Abstract
This paper shows a fuzzy logic approach to univariate statistical hypothesis testing. This tests are an inferential tools to determine whether a statement about the value of a population's parameter should be rejected or not. Classical statistical techniques used in hypothesis testing have an important limitation, because does not show the fulfillment level of the used sample faced with the population of interest. The fuzzy application wants to offer, to the appraiser of a sample of a population, a value that indicates the fulfillment level of the statement, in order to improve the decisions making about the sample.
Key words: Non-parametric tests, Parametric tests, Statistical hypothesis test, Type I Fuzzy Logic.
1. INTRODUCCIÓN
Este artículo muestra una forma de realizar pruebas de hipótesis estadísticas usando lógica difusa. Las pruebas de hipótesis estadísticas consisten en determinar, con base en una muestra (Usualmente n ≥ 30 ) de un proceso, si una afirmación del valor de un parámetro (peso, tamaño, velocidad, rendimiento, etc.) de una población debe ser rechazada o no de forma excluyente, pero sin encontrar un valor del grado de cumplimiento de la afirmación. De lo anterior se puede observar que la conclusión tiene un carácter booleano, el cual, en algunas ocasiones, puede conducir a errores Tipo I o Tipo II(1). El objetivo principal de este artículo es describir cómo, usando lógica difusa, se puede obtener un valor del grado de cumplimiento de una afirmación, el cual lo podría usar un observador o sistema automático para compararlo con un grado de cumplimiento predeterminado como objetivo. Se definió el máximo cumplimiento en 100% y, por tanto, se espera que el observador tome decisiones graduales para alcanzar este valor, partiendo de la información que la técnica difusa entrega con base en la muestra.
Otros autores han diseñado métodos que utilizan números difusos para comparar las hipótesis de interés, como James J. Buckley, quien diseñó un método de comparación de los intervalos de confianza para las medias de la Hipótesis Nula y de la muestra a través de sus funciones de pertenencia, el cual mantiene la característica de decisión Booleana, para mayor referencia se puede consultar [1] y en base a sus estudios diseño un método de regresión difusa bajo el supuesto de no-incertidumbre en la matriz de datos X, el cualse puede estudiar en [2], basado en otros resultados que Buckley denomina como «Probabilidades Difusas» cuyo desarrollo se referencia para el lector en [3] y [4].
Otros Autores han trabajado formalmente el asunto bajo el supuesto de utilizar números difusos mediante la utilización de técnicas clásicas usando los intervalos de incertidumbre de cada variable a probar, como es el caso de A. Mohammadpuor y A. Mahammad.Djafari en [5] y Arnold en [6]. Los resultados obtenidos son bastante interesantes ya que se muestra la equivalencia entre la mejor prueba difusa con información a-priori y las pruebas a diferentes niveles del parámetro de interés utilizando el lema de Neyman-Pearson para la búsqueda de la mejor prueba en las pruebas clásicas. El enfoque utilizado por dichos autores se diferencia del presentado en este artículo ya que el que se presenta se basa no sólo en el uso de conjuntos difusos sino en la utilización de Lógica Difusa para la prueba.
La idea de usar lógica difusa, para dar con una solución a éste problema, surge debido a que un experto, basado en los conocimientos que tiene sobre un problema y en estudios sobre el comportamiento del mismo, puede establecer universos, con sus respectivos conjuntos de pertenencia, adecuados para la descripción del problema. En el caso de la técnica propuesta, los conjuntos de pertenencia debían describir en forma gradual el cumplimiento de una afirmación, de tal forma que el menor valor posible de cumplimiento fuera 0% y el máximo 100%, lográndose extraer información adicional e involucrando la incertidumbre relacionada con las diversas situaciones presentadas por las diferentes variables no controlables en los procesos estocásticos subyacentes al desarrollo de las variables de estudio mediante el diseño de una prueba de hipótesis de forma difusa.
El artículo se divide en 4 secciones principales, en donde la primera es una introducción y motivación al tema, la Sección II muestra una introducción a la teoría de las pruebas de hipótesis paramétricas(2) asumiendo que la población y la muestra provienen de una distribución normal, un vistazo a las pruebas de hipótesis no paramétricas y una revisión de los principales inconvenientes presentados por éstas técnicas y los efectos de la violación de los supuestos subyacentes en la construcción de las mismas, en la Sección III se desarrolla una enfoque metodológico para el diseño de un motor de inferencia difuso Mamdami Tipo I basándose en ciertas características generales de los datos muestrales y el conocimiento de la población y en la Sección IV se muestran 2 casos de aplicación para luego entrar a la Sección V con las conclusiones del estudio.
2. PRUEBAS DE HIPÓTESIS ESTADÍSTICAS
2.1. Definición Estadística
En general, la prueba de hipótesis se puede usar para determinar si se debe rechazar o no una afirmación acerca del valor de un parámetro de población. En la prueba de hipótesis se comienza proponiendo una hipótesis tentativa acerca de un parámetro poblacional. Esta hipótesis tentativa se llama hipótesis nula y se representa con Ho. A continuación se define otra hipótesis, llamada hipótesis alternativa, que es la opuesta de lo que afirma Ho y se denota Hα. Usualmente se debe conocer uno o varios de los parámetros poblacionales para poder realizar una prueba de hipótesis, pero en general se debe tener un buen estimador poblacional de la media y en base al supuesto de distribución que se trabajará en la sección 2.2 se pueden realizar tests con varianza conocida o desconocida, utilizando un «buen» estimador. En este tipo de prueba, la hipótesis nula se define como:
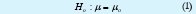
Y la hipótesis alterna como:
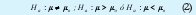
Donde:
- µ: Media Muestral estimada(3).
µo: Media Poblacional.
El rechazar o no la hipótesis nula depende de un estadístico de prueba, que en general hace un test sobre alguna característica de una muestra respecto a una población y de acuerdo con la inferencia realizada sobre la distribución asintótica de esa característica se acepta o no el valor observado en la muestra con un grado de confiabilidad denominado α. Las pruebas de hipótesis Paramétricas y No Paramétricas más utilizadas en la práctica se basan en la aplicación del Teorema Central del Límite, el cual demuestra que la convolución de n muestras de cualquier distribución con media µ y varianza δ2, tiende a ser una variable normalmente distribuída, conforme n tiende a infinito, de manera más formal tenemos:
Sean X1, X2,..., Xn, n variables aleatorias iid(4) con una distribución de probabilidad no especificada y que tienen una media y varianza 2 finita. El promedio de las muestras:
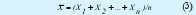
Tiene una distribución con media µ y varianza δ2/n conforme n tiende a infinito. Si centramos la variable y estandarizamos respecto a la varianza esperada obtendremos sin pérdida de generalidad una variable Normal estandarizada, la cual teóricamente se demuestra que está distribuída con media Cero y Varianza Uno, esto es, N [0;1]:
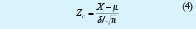
Donde:
Zc: Valor calculado del parámetro estandarizado, Distribuido normalmente N [0;1].
De esta forma se puede observar que gran cantidad de los test estadísticos utilizan este resultado con el fin de establecer estadísticos de prueba o una medición de alguna característica de la población y de la muestra.
Dentro de los test más utilizados encontramos la estadística Z para poblaciones Normalmente distribuídas, la Prueba Chi-Cuadrado para comparación de varianzas de poblaciones Normalmente distribuídas, la prueba t-Student para poblaciones Normales con varianza desconocidas, la Prueba F para comparaciones múltiples, el estadístico de Levenne para comparación de varianzas bajo el supuesto de normalidad en la variable respuesta, la prueba de Mann-Whitney, la prueba de tendencias de Wald-Wolfowitz (5), la prueba de signos de Wilcoxon, la prueba de Kruskal-Wallis, la prueba de Friedman para k muestras igualadas, la prueba de coeficientes de Spearman, la prueba de Anderson-Darling, entre otras, las cuales en su mayoría se basan en la aplicación de este importante Teorema fundamental de la estadística moderna.
2.2. Pruebas Estadísticas bajo el supuesto de una Población Normalmente Distribuida.
Siendo una de los campos de mayor estudio en el último siglo, el supuesto de que una población está normalmente distribuída es tal vez uno de los conceptos más aplicados en diferentes situaciones en donde se practican test de hipótesis con el fin de comparar alguna característica de una muestra contra una población de referencia, tanto en el caso univariado como en el multivariado.
En el presente artículo se pretende hacer una aplicación de la lógica difusa introducida por Lotfi A. Zadeh en 1975 como un enfoque alternativo y complementario al test de una característica respecto a un parámetro de referencia, que inicialmente se considerará como proveniente de una distribución Normal con parámetros conocidos, siendo el caso ideal ya que se posee información completa acerca de la característica a comparar.
Muchas de las aplicaciones prácticas de test de hipótesis se realizan utilizando el supuesto propuesto en el Teorema Central del Límite, es decir, asumir que tanto la muestra como la población de interés son iid con f.d.p.(6) Normal, por lo que generalmente se utiliza el estadístico Z o t para distribuciones Normales estandarizadas(7).
Para nuestro caso en particular utilizaremos test de hipótesis basados en poblaciones y muestras Normalmente distribuídas, en donde el parámetro crítico de comparación es la media de la muestra. Para mayor referencia sobre su aplicación y metodología se puede consultar Mood, Alexander M.; Graybill, Franklin a. & Boes, Duane C. [7] y Canavos, George C. [8].
2.3. Supuestos principales de las pruebas estadísticas basadas en Poblaciones Normalmente Distribuídas.
Los principales supuestos de los test de Hipótesis desarrollados bajo el supuesto de Poblaciones Normalmente Distribuídas son los siguientes:
- La muestra es iid con fdp Normal.
- La distribución de los datos alrededor de su media es simétrica, es decir, su Asimetría debe ser de cero y su Curtosis Relativa deber ser de 3.
- El 95% de los datos están contenidos en el intervalo de ±2δ, alrededor de la media de la población.
- Su desarrollo es asintótico, esto es, existe la probabilidad de que ocurra cualquier valor en el intervalo [-∞,∞].
- Los parámetros de forma de esta distribución son la medida de tendencia central µ y la desviación estándar δ de la población.
De esta forma, todos estos supuestos son la clave en la utilización de una herramienta cuya base sea la suposición de normalidad en las mediciones o aún en alguno de los desarrollos del test como tal, y la violación del supuesto principal de Normalidad constituye un gran problema en la estimación y cálculo que se desean realizar, que en muchos casos introduce un sesgo muy importante en los test realizados y aumenta considerablemente la incertidumbre relativa al método de inferencia utilizado.
De manera general, el estadístico Z y T-Student indican la cantidad de desviaciones estándar que dista  de µo. El uso de z se debe a que siempre que el tamaño de la muestra es grande (n ≥ 30), la distribución muestral de se puede aproximar mediante una distribución normal de probabilidad, mientras que el estadístico t es muy utilizado cuando se desconoce la varianza de la población o se poseen menos de 30 datos de la muestra. Así, al realizar la prueba se puede determinar si se desvía lo suficiente con respecto a µo para justificar el rechazo de la hipótesis nula. Si los datos de la muestra indican que no se puede rechazar Ho, las pruebas estadísticas no respaldan la conclusión de que no se encuentra cerca del valor de referencia. Por otro lado, si los datos de la muestra indican que si se puede rechazar Ho, se puede concluir que no se encuentra cerca del valor de referencia. Una excelente ampliación del estudio sobre los supuestos de Normalidad en las muestras y en el desarrollo de tests de hipótesis se encuentra desarrollado en Thode, Henry C: Jr. [9] y Wilks [11].
de µo. El uso de z se debe a que siempre que el tamaño de la muestra es grande (n ≥ 30), la distribución muestral de se puede aproximar mediante una distribución normal de probabilidad, mientras que el estadístico t es muy utilizado cuando se desconoce la varianza de la población o se poseen menos de 30 datos de la muestra. Así, al realizar la prueba se puede determinar si se desvía lo suficiente con respecto a µo para justificar el rechazo de la hipótesis nula. Si los datos de la muestra indican que no se puede rechazar Ho, las pruebas estadísticas no respaldan la conclusión de que no se encuentra cerca del valor de referencia. Por otro lado, si los datos de la muestra indican que si se puede rechazar Ho, se puede concluir que no se encuentra cerca del valor de referencia. Una excelente ampliación del estudio sobre los supuestos de Normalidad en las muestras y en el desarrollo de tests de hipótesis se encuentra desarrollado en Thode, Henry C: Jr. [9] y Wilks [11].
2.4. Errores Tipo I Y Tipo II.
La hipótesis nula y alterna son aseveraciones sobre la población que compiten entre sí. O la hipótesis nula es verdadera, o lo es la hipótesis alterna, pero no ambas. En este tipo de prueba no siempre son posibles las condiciones correctas. Esto se debe a que la prueba de hipótesis se basa en información de muestra. La Tabla I muestra en que momento se hacen conclusiones correctas y cuando se cometen errores de tipo I o de tipo II. En el renglón donde se muestra lo que puede pasar cuando la conclusión es aceptar Ho se puede observar que si Ho es verdadera, esta conclusión es correcta, pero si Ha es verdadera, entonces se ha cometido un error de tipo II, es decir, se acepto Ho siendo falsa. En el renglón donde se muestra lo que sucede cuando la conclusión es rechazar Ho se puede observar que, si Ho es verdadera, se ha cometido un error de tipo I, pero si Ha es verdadera, se ha hecho la conclusión correcta.
En la practica, la persona que efectúa la prueba de hipótesis especifica la máxima probabilidad permisible, llamada nivel de significancia (α), de cometer un error de tipo I. Sin embargo, aunque en la mayoría de las aplicaciones se controla la probabilidad de cometer un error de tipo I, no siempre se controla la de incurrir en un error de tipo II. Debido a la incertidumbre asociada con cometer un error de tipo II, en estadística se recomienda usar la redacción "no rechazar Ho " en lugar de "aceptar Ho". Por tanto, sólo hay dos conclusiones posibles: No rechazar Ho o Rechazar Ho.

2.5. Violación de Supuestos.
Como se vio en la sección anterior, existe una serie de supuestos en los cuales se basa la aplicación de las pruebas Z y T-Student, cuya violación presenta una serie de problemas como se reseña a continuación:
- Las estimaciones de la varianza muestral podrían no corresponder a la poblacional y viceversa.
- Dependiendo de la distribución real de los datos de la muestra, puede ser significativo el efecto de datos que aparentemente no son atípicos.
- El sesgo introducido por la diferencia entre las estimaciones de las varianzas de la distribución muestral y poblacional modifica el valor del parámetro de tendencia central de la muestra, pudiendo ser muy significativo en algunos casos.
- Las probabilidades de ocurrencia de los datos de la muestra pueden diferir considerablemente de las probabilidades de la población, cuyo efecto inmediato se da en la estimación de las medidas de tendencia central y dispersión de la muestra.
- Los estadísticos de prueba fueron desarrollados para muestras grandes, pero en muchas aplicaciones prácticas no se posee un gran número de muestras para realizar la prueba, por lo que la convergencia y confiabilidad de algunos test se ve comprometida al tamaño de la muestra.
- En muchas situaciones y campos de aplicación no se hace inferencia muestral para conocer cuál es la distribución de los datos y evaluar la conveniencia de aplicar o no un test determinado.
- Al entenderse la desviación de 1 dato respecto a la media como una distancia euclidiana, podría no ser adecuada esta medida de distancia entre los datos y la media, subvaluando medidas cercanas a la media o sobrevaluando medidas muy distantes de la misma.
Estos son los efectos más importantes que posee el tener una muestra pequeña, los datos atípicos y el efecto de la no-normalidad en las estimaciones realizadas.
La implementación difusa que se planteará en las siguientes secciones muestra un enfoque alternativo que hace un test de hipótesis similar al estadístico, con la gran ventaja de involucrar la incertidumbre presente tanto en la medición de la variable como en la incertidumbre presente en las estimaciones y aplicaciones de test estadísticos cuya distribución muestral se desconoce o no corresponde a una fdp Normal, además de considerar una exigencia sobre la desviación presente en los datos, reduciendo el efecto de los datos atípicos y el de considerar las distancias entre los datos y la media como euclidiana, mediante la aplicación de lógica difusa en la construcción de la prueba utilizando sentencias lingüísticas.
3. VENTAJAS DE UN ENFOQUE DIFUSO EN LA CONSTRUCCIÓN DE TEST DE HIPÓTESIS
La lógica difusa es una alternativa que nos permite corregir, aunque no completamente, algunos de los problemas mencionados anteriormente. No se trata de hacer una técnica que reemplace la técnica estadística, pero sí una que aporte más información sobre los parámetros en evaluación y la complemente con el fin de hacer una buena toma de decisiones. Además, la técnica propuesta, toma conceptos de la estadística para su construcción, pero, a la vez, evita los supuestos hechos por ésta, ya que se basa en la definición de reglas lingüísticas a partir del conocimiento de la situación problema. A continuación se presentan las principales ventajas que presenta la técnica difusa frente a la técnica estadística:
- Involucra la Incertidumbre: Aunque se sabe que es muy difícil conseguir mediciones de manera perfecta en muchas situaciones, siempre existe la posibilidad de que se hayan cometido errores al recolectar los datos de la muestra a la cual se le quiere realizar la prueba de hipótesis y por lo tanto, se puede incurrir en los errores de aceptar o rechazar hipótesis aunque la conclusión real sea la contraria. La técnica difusa permite manejar la incertidumbre en dos flancos: La evaluación de la cercanía al punto deseado en los conjuntos de los universos entrada y en el cumplimiento de la hipótesis en los conjuntos del universo de salida.
Numerosos autores han hecho importantes aclaraciones y discusiones sobre el concepto de incertidumbre y sus clasificaciones, entre los cuales se destacan Jerry Mendel, George Klir y en el campo de los sistemas adaptativos se destaca LiXing Wang, para ampliación de estos temas se recomienda consultar [11], [12], [13] y [14]. - Salida: la información que proporciona la técnica difusa, al realizar la prueba de hipótesis a un dato o conjunto de datos, se ha concebido como un apoyo para la toma de decisiones, pues dice cual es el grado de cumplimiento del dato o la muestra de la hipótesis, más que mostrar si cumple o no con ésta. Claro que si alguien desea, puede comparar el grado de cumplimiento de la muestra con uno establecido como deseado, pero este paso depende de la persona que realiza la prueba y el criterio utilizado para definir este grado y en la forma de agregación utilizada en el sistema difuso. Es de notar, sin embargo, que redundaría en el mismo problema de la técnica estadística.
- Flexibilidad: El experto, dependiendo de las exigencias del estándar, puede modificar los conjuntos difusos para permitir una mayor o menor pertenencia de los datos dentro de los conjuntos de los universos de entrada, de tal forma que aumente o disminuya el grado de cumplimiento de la muestra, añadiendo mayor exigencia o no en la medición de la dispersión y del cumplimiento de la muestra respecto a la población.
- Como se mostró anteriormente, la técnica estadística hace supuestos sobre los datos de las muestras, los cuales no siempre se cumplen. Además, es necesario que los datos se ajusten a la distribución normal en la mayoría de los casos, pero la realización de la prueba de normalidad es a la vez compleja y susceptible a errores. La técnica difusa no se encuentra restringida a las muestras de datos ajustados a la distribución normal y evita, por tanto los supuestos relacionados con este aspecto. Así, la técnica difusa se puede aplicar para obtener información acerca del proceso y depende de lo exigente del mismo para su definición.
En ésta primera etapa se ha querido que la técnica difusa tenga sencillez y, como se verá más adelante, tanto las reglas de la técnica como los universos de entrada y de salida se basan en la experticia en las variables a probar.
4. PRUEBA DE HIPÓTESIS ESTADÍSTICA (LÓGICA DIFUSA)
Este método pretende aplicar la lógica difusa de tal modo que entregue unos resultados bastante fiables acerca del cumplimiento que tiene un producto con respecto a un valor de referencia de una de las características de dicho producto. Propiamente, los resultados deben acercarse a los entregados en estadística con la prueba de hipótesis, solo que, si se quiere, se puede evaluar más de una característica de un producto con respecto al valor de referencia respectivo a la vez. En la tabla II se muestran los elementos que la técnica va a utilizar.

4.1. Universos de Entrada
Los universos de entrada, en lógica difusa, son definidos de acuerdo al conocimiento del experto y, por tanto, a cada problema le corresponden sus propios universos. Sin embargo, para la realización de pruebas de hipótesis, es posible definir dos factores cuya evaluación arroja un resultado lo suficientemente confiable para concluir acerca del cumplimiento o no de la hipótesis nula. Para cada característica que se desee evaluar en la prueba es necesario definir dos universos de entrada, los cuales corresponden a los factores descritos a continuación.
- Promedio con Respecto al Valor de Referencia: este factor es importante ya que el promedio de la muestra debe estar cerca del valor de referencia para poder concluir que se esta cumpliendo con la hipótesis nula. Se plantean dos Pruebas de Hipótesis:
· Si se desea hacer una Prueba de Hipótesis Bilateral se deben Plantear dos Conjuntos de Entrada como Promedio Cercano (Φc) y Promedio No Cercano (Φnc), el cual es el complemento del segundo.
En términos generales, si el valor muestral es cercano al poblacional o el estándar, tendrá alta pertenencia, de lo contrario será baja.
- Si se desea Hacer un Prueba de Hipótesis Unilateral, se deben plantear 3 Conjuntos de Entrada como Promedio Cercano (Φc), Promedio Inferior (Φu) y Promedio Superior (Φs), con el fin de establecer la base de reglas adecuada para la prueba de la Hipótesis.
En términos generales, si el valor muestral es cercano al poblacional, tendrá alta pertenencia, si la Hipótesis alterna es Ha: µ > µo, entonces la base de reglas deberá especificar que los valores superiores al valor poblacional sean deseables, mientras que si la Hipótesis alterna es Ha: µ < µo, entonces la base de reglas deberá especificar que los valores inferiores al valor poblacional sean deseables.
Cabe anotar que los conjuntos difusos deben mantener la condición de transformar los valores de entrada en Números Difusos ya que deben ser conjuntos Normalizados.
- Desviación con Respecto la medida de tendencia central de la Muestra: La importancia de este factor recae en que la muestra debe tener homogeneidad, o de lo contrario, aunque tenga un promedio igual al valor de referencia, no permite afirmar la hipótesis nula, siendo deseable que la muestra no sea tan dispersa y además se acerque al valor poblacional. La desviación se ha definido con respecto al valor del promedio de la muestra, pues lo que realmente se desea saber es como varia la muestra. Para el análisis objetivo se definen 2 tipos de Pruebas de Hipótesis:
- Si se desea realizar una Prueba de Hipótesis Bilateral se deben definir 2 Universos de Entrada como Desviación Baja (δb) y su complemento Desviación Alta (δa). En términos generales, si la muestra es muy dispersa, aunque esté cercana al valor poblacional no tendrá una pertenencia muy alta debido a que es deseable una muestra poco dispersa y cercana al valor poblacional.
- Si se desea hacer una Prueba de Hipótesis Unilateral se deben definir 3 Universos de Entrada como Desviación Nula (δn), Desviación por Encima (δs) y Desviación por Debajo (δu), con el fin de ponderar la orientación de la desviación de los datos en la base de reglas.
En términos generales, si el valor de desviación es nulo, se tendrá una variable poco dispersa y deseable, si la desviación es superior y la Hipótesis alterna es Ha : >o, es deseable ésta dispersión, caso contrario con la Hipótesis alterna Ha: µ < µo, si la desviación es Inferior y a Hipótesis alterna es Ha: µ < µo, es deseable ésta condición, caso contrario en la Hipótesis alterna Ha: µ > µo, lo cual se debe ver reflejado en la base de reglas.
4.2. Universo de Salida
Mediante el procesamiento del universo de salida se hallan valores de interés para el experto. En este caso, solo se desea hallar un valor: El Porcentaje de cumplimiento de la hipótesis nula. Para cualquier prueba de hipótesis se puede usar el universo definido a continuación.
Cumplimiento de la Hipótesis Nula: Se plantean tres conjuntos: Bajo cumplimiento (φb), Medio cumplimiento (φm) y Alto cumplimiento ( φa). Se definieron estos tres conjuntos de pertenencia debido, principalmente, a que para los universos de entrada, y sus respectivos conjuntos de pertenencia, se definen una base de reglas apropiada para cada caso, dependiendo de si se hace una Prueba de Hipótesis Unilateral o Bilateral. Los intervalos y las formas de los conjuntos se definieron con base en pruebas comparativas entre la técnica estadística y la técnica difusa. Es recomendable dar una simetría adecuada a estos porcentajes de cumplimiento, aunque la opinión de los expertos en el tema tratado podría dar alguna pauta de interés en la exigencia de la prueba y modificarlos.
4.3. Base de Reglas.
Las reglas se definen para especificar como los universos de entrada condicionan a los universos de salida. Para cada Prueba de Hipótesis se establecen una serie de reglas como sigue a continuación:
- Pruebas de Hipótesis Bilateral, Ha:µ ≠ µo

- Prueba de Hipótesis Unilateral, Ha: µ > µo:
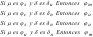
- Prueba de Hipótesis Unilateral, Ha: µ < µo:

4.3.1. Pasos de la Prueba de Hipótesis
Los pasos que se deben seguir para realizar la prueba de hipótesis usando lógica difusa son:
- Definir las hipótesis nula y alterna adecuadas para el caso.
- Definir, con base en las funciones generales de los conjuntos de pertenencia, los conjuntos para el problema.
- Reemplazar los datos proporcionados por la estadística descriptiva en las funciones de los conjuntos de pertenencia de los universos de entrada, teniendo en cuenta que se debe evaluar la Hipótesis con ±ns para observar el comportamiento de los datos alrededor de la media.
- Con los valores obtenidos en el paso 2, realizar las intersecciones definidas por las reglas generales para pruebas de hipótesis. Se recomienda usar como T-Norma el mínimo.
- Realizar las implicaciones definidas por las reglas. Se recomienda usar la implicación de Kleene-Dienes o el Método del Mínimo por su sencillez y bajo consumo computacional.
- Hacer la agregación de las reglas en el universo de salida, se recomienda el método del máximo por su sencillez computacional.
- Realizar el proceso de Defuzificación, se recomienda el método del centroide dado que es un método que da peso a todas las reglas utilizadas.
Para mayor información acerca de la implementación de lógica difusa se pueden consultar importantes autores que han trabajado intensivamente el campo, como Jerry Mendell, George Klir y Li-Xing Wang, para mayor referencia se proponen como textos de consulta [11], [12], [13] y [14], en donde se encuentran las bases y teoría subyacente al diseño de sistemas difusos, al igual que Peña [15] en el campo del modelamiento de sistemas difusos.
5. RESULTADOS DE LA APLICACIÓN DE LA TÉCNICA
A continuación se muestra los resultados obtenidos al aplicar la técnica basada en lógica difusa en comparación con los obtenidos usando la técnica estadística. Los ejemplos siguen todas las pautas presentadas anteriormente.
5.1. Prueba Unilateral bajo Ha: µ > µo
Se han recogido datos del promedio Total de 883 estudiantes de un determinado programa de estudios, con los siguientes estadísticos descriptivos:
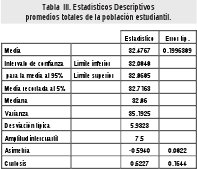
Hipótesis de interés:
Ho: El promedio estudiantil debe ser µo=3.25
Ha: El promedio estudiantil es menor que el estándar mínimo exigido µa < 3.25.
5.1.1. Solución Estadística:
Dado que se trata de una prueba Unilateral, se utilizará un α=0.05, de lo cual obtenemos:

Conclusión: como t < t0.05;882 no se puede rechazar Ho, es decir, no existe evidencia estadística para rechazar la Hipótesis de que los estudiantes tienen promedio total de 3,25.
5.1.1.1. Pruebas de Normalidad.
Se realizaron una serie de Pruebas de Normalidad evaluando los supuestos bajo los cuales trabaja la Hipótesis Estadística, resumidas en la Tabla IV.
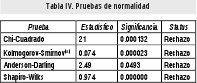
Esta tabla rechaza el Supuesto básico de Normalidad en la variable. De esta forma se utilizará un enfoque difuso para obtener mayor información de los Datos.
5.1.2. Solución Usando Lógica Difusa
Para la definición de los conjuntos de entrada y de salida, se escogieron 3 Tipos de funciones de pertenencia a utilizar, Gaussiana, Polinómica hacia la derecha (S-Shaped Spline) y Polinómica hacia la Izquierda (Z-Shaped Spline), definidos así:
- Función de pertenencia Gaussiana:
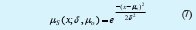
Donde:
x: Variable de evaluación.
δ: Desviación estándar permisible de la población.
µo: Medida de tendencia central poblacional.
S: Variable lingüística que define el Conjunto Difuso.
- Función de pertenencia Polinómica hacia la izquierda (Z-Shaped Spline):
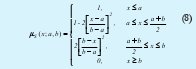
Donde:
x: Variable de evaluación.
a: Constante de modificación del polinomio.
b: Constante de modificación del polinomio.
S: Variable lingüística que define el Conjunto Difuso.
- Función de pertenencia Polinómica hacia la derecha (S-Shaped Spline):
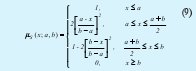
Donde:
x: Variable de evaluación.
a: Constante de modificación del polinomio.
b: Constante de modificación del polinomio.
S: Variable lingüística que define el Conjunto Difuso.
5.1.2.1. Conjuntos de pertenencia:
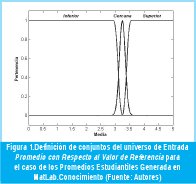
- Media con respecto a la referencia (Fig. 1)
· Función de Pertenencia para Promedio Inferior, µφu(Χ): Z-Shaped Spline de la forma µφu(χ;2.95,3.95).
· Función de Pertenencia para Promedio Cercano µφc(Χ): Gaussiana de la forma µφc(χ;0.1;3.2 5).
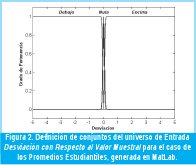
· Función de Pertenencia para Promedio Superior µφs(Χ): S-Shaped Spline de la forma µφs(χ;3.25;3.55). - Desviación con respecto a la Muestra (Fig. 2)
· Función de Pertenencia para Desviación por debajo µ∂u(∂): Z-Shaped Spline de la forma µ∂u(χ;-0.15,0.0).
· Función de Pertenencia para Desviación Nula µ∂n(∂): Gaussiana de la forma µ∂n(χ;0.05,0.0).
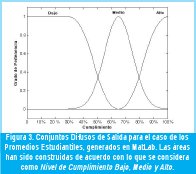
· Función de Pertenencia para Desviación por Encima µ∂s(∂): S-Shaped Spline de la forma µ∂s(χ;0.0,0.05). - Conjuntos de Salida (Fig. 3):
· Función de Pertenencia para Cumplimiento Bajo µφb(χ, ∂): Z-Shaped Spline de la forma µφb (χ, δ;30,50). - Función de Pertenencia para Cumplimiento Medio µφm(χ, ∂): Gaussiana de la forma µφm(χ, δ;5,65).
- Función de Pertenencia para Cumplimiento Alto µφa(χ,∂): S-Shaped Spline de la forma µφa(χ, δ;80,100).
5.1.2.2. Implicaciones y Agregación.
Las implicaciones se han hecho utilizando el mínimo para el operador AND y el máximo para el operador OR, utilizando el método de implicaciones de Kleene-Dienes, por su sencillez y bajo costo computacional, la Agregación de las reglas se realizó utilizando el método del máximo.
5.1.2.3. Defuzzificación.
El método elegido fue el del Centroide, ya que es un método que pondera el resultado de todas las reglas y sus valores, adecuado ya que en estos casos no existe un rendimiento totalmente satisfactorio ni un rendimiento totalmente deficiente para el valor de la muestra frente al de referencia.
El resultado de la Defuzificación de las reglas para una Media de 3.247 y desviación de 0.593, un cumplimiento de 94.4%, mientras que para una desviación de -0.593, el cumplimiento es de 65%. En la Figura 4 se muestra la superficie de respuesta resultante de la base de reglas y las implicaciones realizadas.

5.1.2.4. Conclusión del estudio.
Dada la información obtenida por la técnica difusa, podemos considerar que si el rendimiento estudiantil no tuviera varianza, el cumplimiento de la Hipótesis sería alto, de igual forma los estudiantes que se encuentran en el intervalo superior a dicho valor, es decir, alrededor de 3 o más desviaciones estándar superior a la media, mientras que los estudiantes que se encuentran alrededor de 3 o más desviaciones de la media tendrían un cumplimiento medio e inclusive inferior, lo cual no es deseable en este caso.
De esta forma es posible clasificar a cada uno de los estudiantes en una de las zonas de rendimiento definidos como Bajo, Medio y Alto. Por otra parte la técnica difusa muestra además como valores extremos se ubican en las diferentes zonas de cumplimiento y los valores típicos de rendimientos estudiantiles se ubican cerca de la medida de tendencia central de la muestra lo que no significa que estén cerca del valor de referencia, situación que debería ser deseable en cualquier caso.
Mediante la utilización de la técnica propuesta se muestra claramente el efecto que tiene una alta dispersión en los rendimientos estudiantiles, la distancia que existe entre los bajos, altos rendimientos, respecto al de referencia y el muestral y el nivel de cumplimiento que en promedio tiene la muestra extraída frente al valor de referencia.
6. CONCLUSIÓN
La aplicación de la lógica difusa obtiene información cualitativa a través del análisis de datos estadísticos, en términos del conjunto de salida el cual muestra la ubicación de la muestra en uno de los conjuntos definidos por la variable lingüística, en este caso el grado de cumplimiento.
El método propuesto es fácilmente aplicable para el análisis de datos que están en 1, 2 o 3 desviaciones estándar dispersos frente a su medida de tendencia central lo que da información acerca del cumplimiento que ofrecen valores cercanos y lejanos a ésta medida, teniendo en cuenta el valor de referencia y el valor muestral obtenido, dando importancia a la dispersión de los datos y a la cercanía de los mismos frente al valor de referencia, no sólo a la dispersión de los datos frente a la Hipótesis Nula como en el método estadístico.
Por otra parte es importante notar que el método difuso da relevancia no sólo a la cercanía de la muestra frente a la hipótesis en términos de la media y varianza de la muestra sino que da prelación a muestras con varianza baja cercanas a la Hipótesis Nula utilizando funciones de pertenencia y una base de reglas estándar.
El método propuesto es útil en casos donde se está muy cerca de la zona de rechazo de las técnicas clásicas de pruebas de hipótesis ya que en ningún caso rechaza la prueba sino que establece el grado en el cual una muestra cumple una hipótesis de interés. Por ser un método no-paramétrico no es sensible al supuesto de distribución y es robusto frente a datos atípicos.
7. REFERENCIAS BIBLIOGRÁFICAS
[1] JAMES J. BUCKLEY., «Fuzzy Statistics: hypothesis testing». Soft Computing - A Fusion of Foundations , Methodologies and Applications, Volumen 9, Número 7, Julio de 2005, pp 512-518.
[2] JAMES J. BUCKLEY., «Fuzzy statistics: regression and prediction». Soft Computing - A Fusion of Foundations , Methodologies and Applications, Vol. 9, Número 6, Mayo de 2005, pp 769-775.
[3] JAMES J. BUCKLEY., «Fuzzy Probabilities: New approach and applications». Physica-Verlag, Vol. 4, Número 1, 2003a, pp 196-212.
[4] JAMES J. BUCKLEY., Fuzzy Statistics. Editorial SpringerVerlag, 2004.
[5] A. Mohammadpuor y A. Mahammad.Djafari. «On Classical, Bayesian and Fuzzy Hypothesis Testing», 25th International Workshop on Bayesian Inference and Maximum Entropy Methods in Science and Engineering. 2005
[6] B. F. Arnold. «An approach to Fuzzy Hypothesis Testing», Metrika, Vol. 44, Número 2, 1996, pp. 119-126.
[7] MOOD, ALEXANDER M.; GRAYBILL, FRANKLIN A. & BOES, DUANE C. Introduction to the Theory of Statistics. McGraw Hill Book Company, 1974.
[8] CANAVOS, GEORGE C, Probabilidad y Estadística; Aplicaciones y Métodos. McGRAW HILL, 1988.
[9] THODE, HENRY C: Jr. Testing For Normality. Marcel Drecker Inc. New York, Basel, 2002.
[10] WILKS. Mathematical Statistics. John Wiley and Sons, New York, 1962.
[11] KLIR, GEORGE J. & FOLGER, TINA A. Fuzzy Sets, Uncertainty and Information. Prentice Hall, 1992.
[12] KLIR, GEORGE J. & YUAN, BO. Fuzzy Sets and Fuzzy Logic: Theory and Applications. Prentice Hall, 1995.
[13] WANG, LI-XING. Adaptive Fuzzy Systems and Control, Design and Stability Analysis. Prentice Hall, 1994.
[14] MENDEL, JERRY. Uncertain Rule-Based Fuzzy Logic Systems: Introduction and New Directions. Prentice Hall, 1994.
[15] CARLOS ANDRES PEÑA REYES, «Coevolutionary Fuzzy Modeling», Tesis Doctoral para Ph.D, Sección de Informática, Escuela Politécnica Federal de Lausanne, Suiza, 2002.
Notas
(1) En la sección II del presente artículo se muestra una introducción a la medición del error en pruebas de hipótesis estadísticas.
(2) Conocidas en el ambiente estadístico como Libres de Distribución
(3) Para efectos de este artículo se concidera como mejor estimador insesgado y consistente de al promedio de la muestra, para mayor referencia consultar Mood. Alexander M.; Graybill, Franklin a. & Boes, Duane C. [7].
(4) Independientes Estadísticamente e Idénticamente Distribuidas.
(5) También conocida como prueba de Rachas.
(6) Función de Distribuciòn de posibilidad.
(7) Una variable de Normal Estandarizada es una variable Normal con media cero y varianza conocida, esto es, N (0, δ2).
Juan Carlos Figueroa García.
Ingeniero Industrial de la Universidad Distrital Francisco José de Caldas, de Bogotá, Colombia. Candidato a Magíster en Ingeniería Industrial de la Universidad Distrital Francisco José de Caldas, de Bogotá, Colombia. Actualmente se desempeña como profesor en el área de Estadística y Modelamiento Matemático en la Universidad Distrital en Bogotá, Colombia y como Docente en el área de Procesos Estocásticos, y Simulación en la Universidad Católica de Colombia en Bogotá.e-mail: jcfigueroag@udistrital.edu.co
Luis Eduardo Campos Trujillo
Estudiante de X semestre de Ingeniería de Sistemas de la Universidad Distrital Francisco José de Caldas, de Bogotá, Colombia. Es miembro del Grupo de Investigación LAMIC lcampos3285@yahoo.com
Camilo Caquimbo Tabares
Estudiante de X semestre de Ingeniería de Sistemas de la Universidad Distrital Francisco José de Caldas, de Bogotá, Colombia. Es miembro del Grupo de Investigación LAMIC. ingcamiloc@yahoo.com
Creation date:
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.





2.jpg)










