DOI:
https://doi.org/10.14483/23448393.2693Publicado:
2002-11-30Número:
Vol. 8 Núm. 2 (2003): Julio - DiciembreSección:
Ciencia, investigación, academia y desarrolloControlador Difuso Inteligente para un Cargador de Baterías de Plomo-ácido
Intelligent fuzzy controller for a lead-acid battery charger
Palabras clave:
Difuso, Plomo-Ácido, Inferencia, Microcontrolador, Centroide, Fuzzificacion (es).Descargas
Referencias
Chuen Chien Lee, 1990, "Fuzzy logic in control systems: Fuzzy logic controller - part I and II", IEEE Trans. Syst. Man, Cybern., vol. 20, no. 2, pp. 404 - 435
Palo Mattavelli, Leopoldo Rossetto, 1997, " General - purpose fuzzy controller for DC -DC converters", IEEE Trans. Power Electronics, vol. 12, no.1, pp. 79 - 85.
Stefan Teoharov, 1995," Microprocessor controller for charging Led - acid batteries", MSc. Thesis, Technical University of Sofia, Bulgaria.
L. A. Zadeh, 1973, "Out line of a new approach to the analysis of complex systems and decision process ", IEEE Trans. Syst. Man, Cybern., vol. SMC -3, no. 1, pp. 28 - 44.
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Ciencia, Investigación, Academia y Desarrollo
Ingeniería, 2003-00-00 vol:8 nro:2 pág:62-67
Controlador difuso inteligente para un cargador de baterías de plomo-ácido
Intelligent fuzzy controller for a lead-acid battery charger
Javier Antonio Guacaneme Moreno
Profesor Ingeniería Electrónica Universidad Distrital - Miembro LIFAE
Danny Alejandro González Beltrán
Ing. Electrónico Universidad Distrital - Miembro LIFAE
César Leonardo Trujillo Rodríguez
Ing. Electrónico Universidad Distrital - Miembro LIFAE
Resumen
Durante los últimos diez años, el Control Difuso se ha convertido en el método más popular en el control de procesos no lineales, debido a la simplicidad de su implementación, su robustez y su independencia de una presentación matemática rigurosa. En este artículo se analiza un control difuso para un cargador de baterías de plomo-ácido. El control efectivo del proceso de carga es complejo debido a la relación exponencial entre la corriente de carga y el tiempo de carga. Los algoritmos de control clásico son difíciles de implementar debido a que no se conoce el valor del coeficiente de descarga en la relación exponencial corriente-tiempo. Se desarrolla una arquitectura digital basada en microcontrolador la cual se encarga de regular la carga de la batería a través de un sistema de inferencia difusa cuya salida corrige el tiempo de disparo de un interruptor de potencia.
Palabras clave: Difuso, Plomo-Ácido, Inferencia, Microcontrolador, Centroide, Fuzzificacion.
Abstract
Abstract-During the last ten years, Fuzzy Control has become the most popular method for controlling non-linear processes, due to its implementation simplicity, robustness and lack of a rigurous mathematic presentation. A fuzzy controller for a lead acid battery charger is studied in this paper. Effective control of the charging process is complex because of the exponenetial relationship between the charging time and current. Classic control algor ythms are difficult to implement because the value of the discharge coefficient is unknown in the current-time exponenetial relationship. A microcontroller based digital architecture is developed; its task is to regulate the battery charging process through a Fuzzy Inference System which output changes the trigger angle of a Power Switch.
Key words: Fuzzy, Lead-acid, Inference, Microcontroller, Centroid, Fuzzification.
I. INTRODUCCIÓN
Las baterías recargables tienen una gran variedad de aplicaciones no solo en la industria automotriz sino también en telecomunicaciones, industria energética, medicina, aplicaciones de defensa y casi en todas las aplicaciones industriales, donde se requiere un suministro de potencia ininterrumpido. Los métodos para cargar dichas baterías varían dependiendo de su composición química, su capacidad, los métodos usados para su construcción y la manera en que son aprovechadas. La eficiencia de los algoritmos de carga también depende de la corriente usada durante este proceso, de los niveles de oscilación en ésta, de los niveles de voltaje de carga, del tiempo de carga y de las fluctuaciones de temperatura durante el proceso de carga.
En el diseño discutido en este artículo se diseña un cargador inteligente, en el cual el algoritmo de control es implementado con lógica difusa. La arquitectura digital inteligente se implementa con el microcontrolador de 8 bit. Motorola MC68HC908JK3, el microcontrolador además de permitir implementar el sistema de inferencia difusa, posee los conversores A/D necesarios para obtener los valores de voltaje y corriente, así que el hardware de control externo al microcontrolador es mínimo.
El algoritmo de control difuso lleva a cabo el proceso de carga en dos fases. Durante la primera fase el voltaje se mantiene por debajo de un máximo valor posible para el tipo de batería a cargar y la corriente se regula a un valor que esta íntimamente relacionado con la capacidad de la batería. La segunda fase comienza cuando el voltaje de la batería alcanza un valor especifico, durante esta fase la variable controlada es el voltaje y la corriente decrece hasta un valor que es la propia corriente de subcarga de la batería, éste valor depende también de la capacidad de la misma.
II. CONCEPTOS FUNDAMENTALES DE CARGA Y DESCARGA DE BATERÍAS
Hay dos modos básicos de aprovechamiento de las baterías:
- Modo Continuo de aprovechamiento
- Modo de aprovechamiento Stand by o flotante
En el primer modo la batería es conectada al dispositivo de carga solo después de que ya no es capaz de suministrar la energía requerida a la carga como resultado de un gran periodo de consumo. La batería se desconecta de la carga durante el proceso de carga y consume energía del dispositivo cargador. En el segundo modo de operación la batería se conecta al dispositivo cargador y a la carga simultáneamente.
El dispositivo de carga tiene dos tipos diferentes de funciones durante este modo de operación. Primero, el dispositivo de carga funciona como una fuente de corriente, inmediatamente después de la descarga de la batería. La corriente inicial alta caracteriza a este modo y asegura una carga rápida de la batería al comienzo del ciclo, donde se carga del 80 al 90% de la capacidad total. El dispositivo de carga entra a la segunda fase cuando el voltaje llega al valor requerido. El dispositivo cargador funciona como fuente de voltaje en esta fase, regulando el voltaje en el valor en que el dispositivo cambió de fase. La batería consume entonces solo una cantidad de corriente que es necesaria para culminar el proceso de carga. Por consiguiente la corriente decrece gradualmente y se estabiliza en un valor que se denomina "Current of the Under Charge" o corriente de sostenimiento de carga. Esta pequeña corriente compensa la corriente de autocarga de la batería.
Hay varios métodos para cargar baterías (Teoharov) [3],
- Carga con corriente constante.
- Carga con corriente semiconstante
- Carga con voltaje constante
- Carga multietapa de acuerdo a la regla del Amperio-Hora y ciclo de carga de dos etapas el cual simplifica el método multietapa, donde el ciclo de carga es primero con corriente constante y luego con voltaje constante.
El primer método es raramente usado en aplicaciones en general, pero es muy efectivo cuando se carga un gran número de baterías conectadas serialmente. Este método tiene un pequeño coeficiente de eficiencia y un efecto adverso sobre las características y la durabilidad de la batería, mientras que el segundo método tiene una arquitectura muy simple, la cual consiste en un transformador, un puente rectificador y un resistor limitador de corriente como se muestra en la Figura 1.
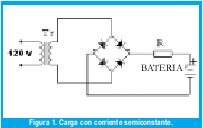
Con este método las baterías son normalmente sobrecargadas debido a la gran corriente y por consiguiente se ve reducida su vida útil. Este método también se caracteriza por un bajo coeficiente de eficiencia debido al resistor y además se requiere limitación de la corriente inicial. En el tercer método (Figura 2) la corriente de carga inicial es muy alta, pero se mantiene por debajo de cierto nivel (10% 25% de la capacidad de la batería) a fin de proteger la batería. La corriente gradualmente decrece hacia el final del ciclo de carga. El voltaje de carga se debe ajustar dependiendo de la capacidad de la batería y de sus características de temperatura.
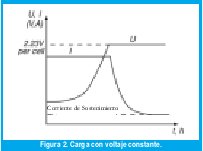
El cuarto método es ampliamente aceptado como el mejor y es discutido mas adelante en detalle. Este método es recomendado para cargar la batería de Plomo-Ácido en corto tiempo y manteniendo a la batería en modo Stand By.
III. REGLA DEL AMPERIO-HORA (REGLA Ah)
Es importante mencionar la regla del Amperio-Hora, establece que en cualquier momento del ciclo de carga la corriente de carga expresada en amperios no debe exceder la capacidad de la batería en ese momento, expresada en Amperio-Horas.
Esta regla expresa matemáticamente la corriente de carga como:
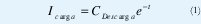
Donde Icarga - corriente de carga en amperios, CDescarga - Capacidad descargada de la batería, t - tiempo de carga. La Figura 3 (Balogh, 1998), muestra algunas curvas de carga para un numero de baterías de Plomo-Ácido.
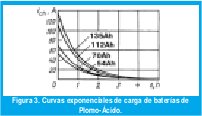
Las curvas anteriores se derivan asumiendo que las baterías están completamente descargadas. Integrando ambos lados de la Ecuación (1) y multiplicando por dt la ecuación queda:
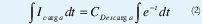
El miembro izquierdo de la ecuación (2) representa la capacidad de la batería durante el ciclo de carga. Al resolver la anterior ecuación se tiene que c - constante de integración, puede encontrarse de las condiciones iniciales: t=0, Cbat = 0; así c = CDescarga; entonces Cbat puede expresarse como:

La tabla I muestra la importancia de la regla del Amperio-Hora cuando se cargan baterías de PlomoÁcido. Los porcentajes obtenidos experimentalmente son el porcentaje de carga de la capacidad total de la batería, cuando se carga de acuerdo a la regla anteriormente mencionada.

La aplicación de la regla del Amperio-Hora para cargar baterías de plomo-ácido puede ser considerado como el método mas eficiente, cuando se consideran el tiempo y la energía ahorrados. La implementación de este método se muestra brevemente en la Figura 4.
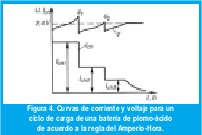
La técnica de carga dada en la Figura 4 puede ser simplificada a un ciclo de carga con dos etapas, donde el tiempo de carga puede ser reducido a cerca del 50% sucediendo lo mismo con la energía requerida para cargar la batería, mientras se conservan todas las ventajas del método. Esta implementación mas simple de la regla del Amperio-Hora se prueba con el algoritmo difuso y se evidencia una vez mas la efectividad del método a través de un montaje experimental. La Figura 5 muestra las características del dispositivo de carga. Durante la primera fase la corriente de carga se controla a cierto valor y el voltaje de la batería gradualmente crece, pero se mantiene por debajo de un nivel máximo determinado el cual se define de acuerdo a las características de la batería. El dispositivo ingresa a la segunda fase cuando el voltaje alcanza cierto valor definido de acuerdo al tipo de batería.
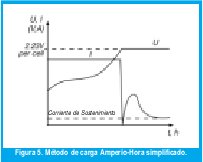
El voltaje de la batería debe ser ahora regulado a un valor que debe ser mas pequeño que el valor en el cual el dispositivo cambio de fase y la corriente gradualmente comienza a descender, ya que la batería se ha cargado hasta cerca del 90% de su capacidad total durante la primera fase del ciclo de carga. El hecho de entrar en la segunda fase también protege a la batería de sobrecargas. Los valores de salida deben estar dentro de los siguientes limites en este modo (Tabla II):

IV. CONTROL DIFUSO
Cualquier controlador difuso abarca tres grandes pasos. Fuzzificacion, evaluación de reglas y defuzzificacion [1] [2]. La arquitectura de un sistema de control basado en lógica difusa se muestra en la Figura 6.
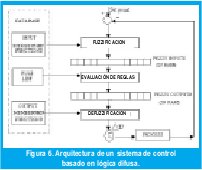
La aplicación que se trata en este articulo es un sistema difuso de dos entradas y una salida, así que el diseño de un motor de inferencia para este controlador se discute en detalle.
A. Diseño de la base de datos de las funciones de pertenencia.
Las entradas al sistema son el error (ek) y el cambio del error (ek) los cuales se calculan como:
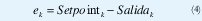
Donde k es el k-esimo tiempo de muestreo.
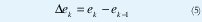
Primero las variables de control deben ser divididas en un conjunto de regiones difusas, a las cuales se les asignan etiquetas, dentro del dominio de las variables. En nuestro caso las etiquetas son: Negativo, Cero y Positivo. Cada uno de estos conjuntos esta definido por ciertos parámetros que son sus limites dentro del universo en general. La pertenencia de cada etiqueta se calcula en el paso de fuzzificacion. El universo en discusión en nuestro caso esta limitado por -255 (FF) y 255 (FF) que es rango posible de las operaciones aritméticas al interior del microcontrolador y además por que la longitud de la palabra de la CPU y del conversor A/D es de 8 bit. Los conjuntos difusos para el voltaje quedan definidos entonces como:

Para la tendencia del error (Dek) los conjuntos difusos son:

Con lo anterior quedan entonces definidos los conjuntos para las dos variables de entrada y para este caso se usan seis reglas que se describirán mas adelante.
Para el caso de la corriente los conjuntos difusos son los mismos por esto no es necesario profundizar en este aspecto para la fase en que se regula corriente. Las funciones de pertenencia tienen una amplitud de 1 en el mundo difuso, a fin de poder realizar los cálculos en el microcontrolador, se asigna una altura de 156 (9CH) para la altura máxima de las funciones, este numero nace de la razón de que se dispone de operaciones de 8-bit, y si se usara 255 como altura, implicaría generar rutinas de 16 bit que hacen que el controlador responda mucho mas lento a un cambio en la salida, cosa que es inconveniente ya que de por si la carga computacional que genera un control como el de esta aplicación es grande.
B. Fuzzification
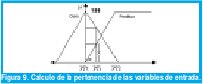
En la fase de fuzzificacion los valores de entrada reales son mapeados a funciones de pertenencia difusas. Para este caso se utiliza un fuzzificador singleton, luego, cualquier valor real cae en dos funciones de pertenencia en la región donde estas se solapan, en las otras regiones vale 0 o vale 1 su pertenencia, entonces para la región donde las funciones se solapan, se calcula la pertenencia usando el principio de los triángulos semejantes, por ejemplo asumamos que la variable error (ek) toma el valor 20 decimal (PTi), de acuerdo a la figura, la pertenencia de la variable Error = 20 en la función de pertenencia Positivo se calcula como sigue:
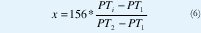
Aquí x toma un valor decimal que dentro del microcontrolador es un valor hexadecimal, finalmente la pertenencia de la variable Error = 20 en la función de pertenencia Cero seria 156-x de acuerdo al principio de ortogonalidad de triángulos.
C. Diseño y evaluación de la base de reglas
La evaluación de las reglas es el elemento central de un sistema de control basado en lógica difusa. Este paso procesa una lista de reglas a partir de una base de conocimiento usando los actuales valores difusos de entrada que se encuentran en la memoria RAM. Estas salidas difusas se pueden entender como sugerencias acerca de lo que el sistema debe hacer de acuerdo a las condiciones actuales de la salida del proceso.
El diseño de reglas para el control difuso implica el hecho de escribir oraciones que relacionen las variables de entrada con las propiedades de los conjuntos de salida. Estas reglas se expresan como declaraciones Si - Entonces (IF-THEN) y la sintaxis es como sigue:
Si error es positivo y tendencia del error es negativa entonces la salida de control es tiempo alto positivo.
Un grupo de las anteriores declaraciones forman lo que se denomina una base de reglas difusa.
Antes de enunciar las reglas que rigen el comportamiento de este sistema es necesario conocer los conjuntos de salida, ya que con ellos se construyen los consecuentes de las mismas. Para el caso de esta aplicación, la variable a controlar es el tiempo de disparo del tiristor que regula la cantidad de potencia que se entrega a la carga, luego la salida del controlador es una corrección al tiempo actual de disparo, es decir, corregirlo para disminuirlo o para aumentarlo, en este caso un aumento en el tiempo de disparo implica menor potencia entregada a la carga y un tiempo mayor lo contrario.
Con lo anterior se definen los conjuntos de salida como singleton situados en ubicaciones especificas las etiquetas de las funciones de pertenencia son PA (Positivo Alto), PM (Positivo Medio), Z (Cero), NA (Negativo Alto), NM (Negativo Medio).
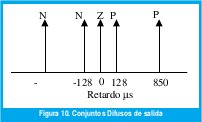
Con el conocimiento del universo de salida, es ahora conveniente enunciar las reglas que rigen al sistema, para este caso son seis, la Tabla III muestra la base de reglas del controlador implementado [4].

Las anteriores reglas conectan los antecedentes con el mínimo y este resultado se conecta con el consecuente a través del máximo, es decir el aporte de cada regla a la salida se calcula como:
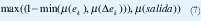
Debido a que los conjuntos de salida son singleton, obtener la ponderación de cada uno de ellos según la regla que aplique requiere realizar sencillamente la operación de mínimo entre el error y la tendencia, con este dato ya es posible conocer el aporte a la salida de esa regla en particular.
D. Defuzzification
El paso final en el controlador difuso es combinar la salida difusa de cada regla para obtener un valor efectivo en el mundo real, y así realizar la acción de control necesaria.
Hay varios métodos para calcular la salida del controlador hacia el actuador, el método del centroide es el utilizado en esta aplicación debido a que brinda mejores resultados. El centroide para esta aplicación, se expresa matemáticamente a través de la ecuación 8:
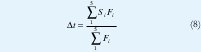
Donde Si es la posición del i-esimo singleton, Fi es el resultado de la operación mínimo entre las pertenencias de ek y Δek en un tiempo de muestreo k y Δt es la corrección que es necesario hacer al tiempo de disparo del tiristor para generar la siguiente respuesta del sistema. Los posibles valores que genera el proceso de defuzzificacion para todas las posibles condiciones de entrada se observan en la superficie de control que se genero con ayuda del editor FIS de MATLAB.
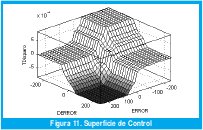
V. MONTAJE EXPERIMENTAL
Para los experimentos se utilizo una batería de 12V 7Ah, y un kit de desarrollo sencillo para el microcontrolador MC68HC908JK3, además de los circuitos que se muestran en las Figuras 12 y 13.
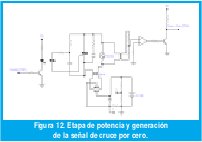
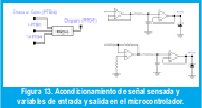
VI. RESULTADOS EXPERIMENTALES
Se implemento el controlador difuso sobre el microcontrolador de 8 bit y se logro optimizar hasta obtener una respuesta del control de 800ms, es decir, la siguiente respuesta del controlador hacia el actuador para un cambio en las condiciones de la salida tarda 800ms en generarse. El sistema efectivamente carga las baterías mas rápido ya que discrimina las regiones de voltaje y corriente constante, se presentan pequeñas oscilaciones de la corriente mas que en el voltaje esto por ende sugiere que para el caso de esta aplicación el filtrado en la etapa de potencia es critico, además se hace notorio que es necesario utilizar un microcontrolador o microprocesador con una capacidad superior por ejemplo que pueda procesar instrucciones de 16 bit. Finalmente el sistema no presenta transientes muy acentuados cuando conmuta de corriente constante a voltaje constante, tal y como se muestra en la figura 14 y 15.


VII. CONCLUSIÓN
Se desarrollo un cargador muy efectivo y de alto rendimiento. Todos los setpoints críticos son independientes del hardware lo que garantiza control preciso. El tiempo de carga con este método se redujo casi a un 50% en comparación a los métodos clásicos, para una batería totalmente descargada el tiempo de carga requerido fue de aproximadamente 3 horas. Este método también evita que la batería se sobrecargue, esto es resultado de la buena sintonización del regulador difuso.
Por otro lado es importante destacar que el control difuso permitió en esta aplicación implementar un sistema de regulación sobre una planta o proceso que presentaba alinealidades evidenciándose así el poder del enfoque difuso en problemas complejos desde el punto de vista matemático. Sin embargo la carga computacional de un controlador difuso es enorme y en especial si este comienza a hacerse denso en su base de reglas, por ello es necesario conocer bien el proceso para poder determinar la resolución que se requiere para el controlador y así diseñar para el óptimo tiempo de procesamiento.
REFERENCIAS BIBLIOGRÁFICAS
[1] Chuen Chien Lee, 1990, "Fuzzy logic in control systems: Fuzzy logic controller - part I and II", IEEE Trans. Syst. Man, Cybern., vol. 20, no. 2, pp. 404 - 435
[2] Palo Mattavelli, Leopoldo Rossetto, 1997, " General - purpose fuzzy controller for DC -DC converters", IEEE Trans. Power Electronics, vol. 12, no.1, pp. 79 - 85.
[3] Stefan Teoharov, 1995," Microprocessor controller for charging Led - acid batteries", MSc. Thesis, Technical University of Sofia, Bulgaria.
[4] L. A. Zadeh, 1973, "Out line of a new approach to the analysis of complex systems and decision process ", IEEE Trans. Syst. Man, Cybern., vol. SMC -3, no. 1, pp. 28 - 44.
Javier Antonio Guacaneme Moreno
Profesor Ingeniería Electrónica Universidad Distrital
jguacaneme@udistrital.edu.co
Danny Alejandro González Beltrán
Ing. Electrónico Universidad Distrital.
sea_harrier@hotmail.com
Cesar Leonardo Trujillo Rodríguez
Ing. Electrónico Universidad Distrital.
operaluna@hotmail.com
Creation date:
Licencia
A partir de la edición del V23N3 del año 2018 hacia adelante, se cambia la Licencia Creative Commons “Atribución—No Comercial – Sin Obra Derivada” a la siguiente:
Atribución - No Comercial – Compartir igual: esta licencia permite a otros distribuir, remezclar, retocar, y crear a partir de tu obra de modo no comercial, siempre y cuando te den crédito y licencien sus nuevas creaciones bajo las mismas condiciones.





2.jpg)