DOI:
https://doi.org/10.14483/udistrital.jour.reving.2013.2.a05Published:
2013-12-06Issue:
Vol. 18 No. 2 (2013): July - DecemberSection:
Special Section: Best Papers "VI Symposium on Optimization".Diseño de cadenas de distribución con demanda bajo incertidumbre: una aproximación de programación lineal difusa
Design of distribution networks under uncertainty demand: A fuzzy linear programming approach
Keywords:
distribution networks, fuzzy linear programming, uncertainty demand. (en).Keywords:
redes de distribución, programación lineal difusa, demanda bajo incertidumbre. (es).Downloads
References
N. C. Nam, T. H. L. An, and P. D. Tao, “A Branch and Bound Algorithm Based on DC Programming and DCA for Strategic Ca-pacity Planning in Supply Chain Design for a New Market Opportunity,” in Operations Research Proceedings 2006, P. D. K.-H. Waldmann and D.-W.-I. U. M. Stocker, Eds. Springer Berlin Heidelberg, 2007, pp. 515–520.
Y. Yin, I. Kaku, J. Tang, and J. Zhu, “Supply Chain Design Using Decision Analysis,” in Data Mining, Springer London, 2011, pp. 121–132.
R. Velásquez, M. T. Melo, and S. Nickel, “An LP-based Heuristic Approach for Strategic Supply Chain Design,” in Operations Research Proceedings 2005, P. D. H.-D. Haasis, P. D.-I. H. Kopfer, and D. J. Schönberger, Eds. Springer Berlin Heidelberg, 2006, pp. 167–172.
T. Seidel, “Rapid Supply Chain Design by Integrating Modelling Methods,” in Build To Order, G. Parry and A. Graves, Eds. Springer London, 2008, pp. 277–295.
S.-H. Liao and C.-L. Hsieh, “Integrated Location-Inventory Retail Supply Chain Design: A Multi-objective Evolutionary Ap-proach,” in Simulated Evolution and Learning, K. Deb, A. Bhattacharya, N. Chakraborti, P. Chakroborty, S. Das, J. Dutta, S. K. Gupta, A. Jain, V. Aggarwal, J. Branke, S. J. Louis, and K. C. Tan, Eds. Springer Berlin Heidelberg, 2010, pp. 533–542.
Z.-J. M. Shen and M. S. Daskin, “Trade-offs Between Customer Service and Cost in Integrated Supply Chain Design,” MSOM, vol. 7, no. 3, pp. 188–207, Jun. 2005.
H. Yan, Z. Yu, and T. C. Edwin Cheng, “A strategic model for supply chain design with logical constraints: formulation and so-lution,” Computers & Operations Research, vol. 30, no. 14, pp. 2135–2155, Dec. 2003.
R. Hammami, Y. Frein, and A. B. Hadj-Alouane, “A strategic-tactical model for the supply chain design in the delocalization context: Mathematical formulation and a case study,” International Journal of Production Economics, vol. 122, no. 1, pp. 351–365, Nov. 2009.
S. Talluri and R. C. Baker, “A multi-phase mathematical programming approach for effective supply chain design,” European Journal of Operational Research, vol. 141, no. 3, pp. 544–558, Sep. 2002.
B. M. Beamon, “Supply chain design and analysis:,” International Journal of Production Economics, vol. 55, no. 3, pp. 281–294, Aug. 1998.
V. Jayaraman and A. Ross, “A simulated annealing methodology to distribution network design and management,” European Journal of Operational Research, vol. 144, no. 3, pp. 629–645, Feb. 2003.
N. V. Sahinidis, “Optimization under uncertainty: state-of-the-art and opportunities,” Computers & Chemical Engineering, vol. 28, no. 6–7, pp. 971–983, Jun. 2004.
A. R. Singh, R. Jain, and P. K. Mishra, “Capacities-based supply chain network design considering demand uncertainty using two-stage stochastic programming,” Int J Adv Manuf Technol, pp. 1–8.
H. Selim and I. Ozkarahan, “A supply chain distribution network design model: An interactive fuzzy goal programming-based solution approach,” Int J Adv Manuf Technol, vol. 36, no. 3–4, pp. 401–418, Mar. 2008.
K. N. Rao, K. V. Subbaiah, and G. V. P. Singh, “Design of supply chain in fuzzy environment,” J Ind Eng Int, vol. 9, no. 1, pp. 1–11, Dec. 2013.
S. Ahmed and N. V. Sahinidis, “An Approximation Scheme for Stochastic Integer Programs Arising in Capacity Expansion,” Operations Research, vol. 51, no. 3, pp. 461–471, May 2003.
M. C. Georgiadis, P. Tsiakis, P. Longinidis, and M. K. Sofioglou, “Optimal design of supply chain networks under uncertain transient demand variations,” Omega, vol. 39, no. 3, pp. 254–272, Jun. 2011.
F. Pan and R. Nagi, “Robust supply chain design under uncertain demand in agile manufacturing,” Computers & Operations Research, vol. 37, no. 4, pp. 668–683, Apr. 2010.
H.-J. Zimmermann, “Fuzzy programming and linear programming with several objective functions,” Fuzzy Sets and Systems, vol. 1, no. 1, pp. 45–55, Jan. 1978.
J. C. Figueroa-García, C. A. Lopez-Bello, and D. Kalenatic, “An iterative algorithm for fuzzy mixed production planning based on the cumulative membership function,” Ingeniería, vol. 16, no. 2, pp. 6–17, 2011.
J. C. Figueroa-García, D. Kalenatic, and C. A. Lopez-Bello, “Multi-period Mixed Production Planning with uncertain de-mands: Fuzzy and interval fuzzy sets approach,” Fuzzy Sets and Systems, vol. 206, pp. 21–38, Nov. 2012.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
DISEÑO DE CADENAS DE DISTRIBUCIÓN CON DEMANDA BAJO INCERTIDUMBRE: UNA APROXIMACIÓN DE PROGRAMACIÓN LINEAL DIFUSA
DESIGN OF DISTRIBUTION NETWORKS UNDER UNCERTAINTY DEMAND: A FUZZY LINEAR PROGRAMMING APPROACH
Eduyn Ramiro López Santana, Universidad Distrital. Bogotá, Colombia. erlopezs@udistrital.edu.co
Germán Andrés Méndez Giraldo, Universidad Distrital. Bogotá, Colombia. gmendez@udistrital.edu.co
Carlos Franco Franco, Universidad Distrital. Bogotá, Colombia. cafra87@gmail.com
Recibido: 30/09/2013 - Aceptado: 30/11/2013
RESUMEN
Este artículo presenta un modelo para el diseño de una red de distribución considerando la demanda bajo incertidumbre en un ambiente de múltiples productos y múltiples periodos. El modelo propuesto integra un problema de localización de instalaciones y un problema de distribución con restricciones difusas en el cumplimiento de la demanda, el cual se resuelve utilizando el método de restricciones suaves propuesto por Zimmermann considerando parámetros difusos en el lado derecho de las restricciones de un problema de programación lineal entera mixta y funciones de pertenecía lineales. Los resultados encontrados muestran como la localización de las plantas y almacenes se puede conservar para en el modelo flexible, mientras se realiza un balance entre el inventario generado y el costo incurrido.
Palabras clave: Redes de distribución, programación lineal difusa, demanda bajo incertidumbre.
ABSTRACT
This paper presents a model for designing a distribution network considering the demand under uncertainty, in a multi-products and multi-periods environment. The proposal model integrates a Facility Location Problem and a Distribution Problem with fuzzy constraints in demands satisfying which is solved using the soft constraints method proposed by Zimmermman, which considers fuzzy parameters in the right hand side of a Mixed Integer Linear Programming problem and linear membership functions. The obtained results show how the localization of the plants and distribution centers can be conserved for different membership degrees, while there is a balance between the inventory and the cost.
Key words: Integration of the supply chain, information technologies, arcs of integration, outsourcing services.distribution networks, fuzzy linear programming, uncertainty demand.
1. INTRODUCCIÓN
El problema de diseño de una red de distribución ha sido ampliamente estudiado en la literatura [1], [2], [3], [4] y [5], busca satisfacer la demanda de un conjunto de clientes utilizando efectivamente los recursos disponibles, suministrando el mejor acceso posible a los clientes teniendo como criterios la distancia, el tiempo, los costos de flete, entre otros aspectos. El problema consiste en dado un conjunto de posibles ubicaciones de plantas (o fábricas) de producción y de almacenes (o centros de distribución) con unas capacidades de producción y almacenamiento, respectivamente; determinar la mejor ubicación de un número determinado de plantas y almacenes con el fin de satisfacer la demanda de un conjunto de clientes minimizando los costos asociados a la apertura de plantas y almacenes y a la distribución de los productos desde las plantas hasta los clientes finales. Por otro lado, determina cuantos productos se deben fabricar y almacenar en las plantas y almacenes, respectivamente. En la mayoría de los problemas estudiados se asume que la información de costos y demandas es conocida y determinística, ignorando que la incertidumbre de dicha información puede resultar en soluciones sub-óptimas cuando se implementan en el sistema debido a que se pueden generar inventarios cuando la demanda real es menor que la pronosticada o déficit de productos en caso contrario [6].
El problema a estudiar en este trabajo se fundamenta en cómo se debe configurar una red de distribución que consiste en un sistema integrado de localización y distribución considerando diferentes instalaciones (etapas) como fábricas, almacenes, centros de consumo y múltiples productos y periodos dentro de un horizonte de planeación. En una red de distribución los almacenes actúan como nodos intermediarios entre los proveedores y sus puntos de venta, por tanto en estos se pueden almacenar productos en inventario con el fin de abastecer demandas futuras. Problemas similares han sido analizados en trabajos como [7], [8], [9], [10] y [11]. Los métodos más sencillos tratan el problema de redes logísticas en donde los parámetros que se usan en el modelo son determinísticos y se pueden formular problemas de programación lineal entera, dadas las condiciones de apertura de plantas y almacenes. En el 2007 se publicó un método de solución para el problema discreto basado en DC Programming [1], en el problema planteado, la configuración de la red se realiza para mercados emergentes o mercados nuevos. Para utilizar está técnica de DC programming, se reformula un problema lineal y luego se solucionan múltiples problemas lineales hasta que se obtiene la solución adecuada. También se han desarrollado métodos heurísticos o aproximados para este problema [3], donde se plantean estrategias de inicialización de las asignaciones y las plantas a utilizar, para obtener una solución inicial, se relaja el problema lineal entero, y se obtienen soluciones aproximadas, luego de esto se proceden a hacer redondeos pero teniendo en cuenta las factibilidades para no alterar la solución. Una vez se obtienen soluciones factibles se realizan perturbaciones o intercambios a la solución para saber si esta mejora.
El trabajo desarrollado en este artículo incorpora múltiples productos y la demanda bajo incertidumbre para el problema del diseño de una red de distribución. Cuando se habla de problemas de toma de decisiones bajo incertidumbre, se tiene un grado de complejidad mayor debido a la presencia de variables de decisión enteras que se modelan en un entorno multi-etapa. Es por esto, que se han propuesto varios modelos para la optimización bajo incertidumbre y una variedad de algoritmos se han desarrollado y utilizado con éxito en muchas aplicaciones [12], [13], [14] y [15]. Algunos de estos algoritmos, permiten aproximar la solución de los problemas a gran escala basados en los métodos de muestreo y aproximaciones de la función de costo, dado que una solución exacta es mucho más difícil y requiere de más recursos computacionales [13] y [16].
Problemas similares con la demanda bajo incertidumbre han sido trabajados por Sofioglou et al. [17] en el cual la demanda tiene un comportamiento estocástico descrito por una función de densidad de probabilidad y lo resuelven mediante unan aproximación por escenarios y por programación estocástica. Pan & Nagi [18] resuelven un problema similar mediante aproximación por programación estocástica y una heurística de solución para este problema. En el trabajo de Singh et al, [13] se propone un modelo de dos niveles, en el primer nivel se tienen en cuenta aquellas variables y restricciones que se incluyen y no están relacionadas con los parámetros estocásticos, por otro lado en el segundo nivel se incluyen las soluciones obtenidas en la primera etapa y se toman en cuenta las restricciones y variables asociadas a los parámetros que presentan incertidumbre. Existen numerosas y diversas aplicaciones sobre el desarrollo de configuraciones de redes logísticas como las presentadas [4], [5] y [13], sin embargo su dificultan es el tratamiento estocásticos de la información y la dificultad para resolver problemas de programación estocástica, en los cuales se recurre a la utilización de heurísticas y meta-heurísticas.
Finalmente existen modelos que involucran incertidumbre mediante el uso de lógica difusa ante la dificultad de la programación estocástica, mediante la aplicación de conjuntos y números difusos para manejar la incertidumbre en algunos parámetros de un modelo de programación lineal como un intervalo. Zimmermann [19] planteo un procedimiento para resolver un problema de programación lineal con coeficientes difusos en el vector del lado derecho, conocido como programación con restricciones suaves (soft constraints programming). En este trabajo se emplearán estas técnicas de programación lineal con coeficientes intervalares en el vector del lado derecho para modelar la demanda. Se pueden encontrar trabajos relacionados como el de Selim y Ozkarahan [14] y el de Rao, Venkata y Singh [15], ambos plantean estrategias de configuración de redes logísticas en ambientes de incertidumbre lingüística. El primer modelo plantea un problema basado en programación meta planteando diversas funciones objetivo, mientras que en el segundo modelo se plantean diversos modelos lineales difusos y se soluciona iterativamente. Trabajos como los de Figueroa, López y Kalenatic [20], [21] presentan aplicaciones de modelos de programación lineal difusa para problemas de planeación de producción en ambientes de múltiples productos y múltiples periodos.
El resto de este artículo es organizado de la siguiente manera. En la sección 2 se establece el modelo general para el diseño de una red de distribución en un ambiente multi-producto y multi-periodo, luego se define la demanda como un conjunto difuso y el enfoque de solución para el problema con restricciones difusas. En la sección 3 se muestra un caso de aplicación del modelo propuesto. En la sección 4 se presentan los resultados, y en la sección 5 las conclusiones de este trabajo y algunas líneas de interés para futuros trabajos.
2. UN MODELO DE PROGRAMACIÓN LINEAL DIFUSA PARA EL DISEÑO DE RED DE DISTRIBUCIÓN
En esta sección se muestra el modelo general para el diseño de una red de distribución en un ambiente multiproducto y multiperiodo, luego se define la demanda como un numero difuso y se establece la función de pertenencia. Finalmente se describe el método de solución para este problema aplicando el procedimiento propuesto por Zimmermann [19].
2.1. Modelo general para el diseño de una red de distribución
El modelo general para el diseño de una red de distribución se basa en un sistema dedicado a la fabricación de diferentes productos para lo cual se consideran unas posibles ubicaciones de sus plantas de producción y una serie de centros de distribución donde se almacenarán sus productos antes de ser transportados a los clientes finales. Por otro lado, se debe evaluar el tipo de tecnología para la producción de las plantas, la cual tiene diferentes consumos y costos. También en los centros de distribución es necesario seleccionar la tecnología más apropiada que garantice un almacenamiento adecuado, dado que los productos deben estar sometidos a ciertas condiciones de almacenamiento. Los supuestos de esta situación se puede resumir como:
- Existe un conjunto de tecnología disponible para el proceso de producción en las plantas; la diferencia entre tipos de tecnología radica en la capacidad y su costo.
- Existe un conjunto de tecnología disponible para el proceso de almacenamiento de los productos en los centros de distribución; la diferencia entre tipos de tecnología radica en la capacidad y su costo.
- Cada producto producido en una planta con una de las tecnologías consume una porción de la tecnología que posee la planta.
- Cada producto almacenado en un centro de distribución consume una porción de la tecnología que posee el centro de distribución.
- No se puede asignar más de un tipo de tecnología a una planta.
- No se puede asignar más de un tipo de tecnología a un centro de distribución.
- Existe una capacidad máxima de producción y envío asociada a cada planta según el tipo de tecnología.
- Existe una capacidad máxima de almacenamiento y envío asociada a cada centro de distribución según el tipo de tecnología.
- Se tiene una demanda para cada uno de los productos en cada periodo de planeación por cada punto de venta.
El objetivo es minimizar los costos de producción y transporte de los productos desde las plantas a los centros de distribución, al igual, que los costos de mantenimiento de inventario y envío entre los centros de distribución a puntos de demanda y los costos fijos de apertura de las plantas y los centros de distribución con la tecnología necesaria para todo el horizonte de planeación. En la Figura 1 se puede ver como se conectan las plantas y almacenes a través de los flujos de productos entre plantas y almacenes, y entre almacenes y puntos de venta, y los últimos suplen los clientes finales.
Conjuntos
L es el conjunto de productos, indexado en l=1...L
I es el conjunto de plantas, indexado en i=1...I
J es el conjunto de Almacenes, indexado en j=1...J
K es el conjunto de puntos de venta, , indexado en k=1...K
P es el conjunto de tecnologías de cada planta, indexado en p=1...P
Q es el conjunto de tecnologías de cada almacén, indexado en q=1...Q
T es el conjunto de periodos, indexado en t=1...T
Parámetros
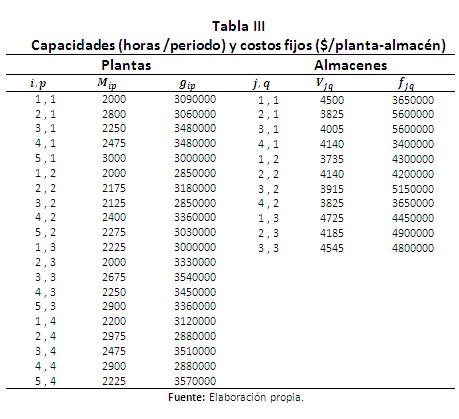
Mipt: Matriz de capacidades máximas (en horas disponibles) para la planta i con tecnología p en el periodo t.
Vjqt: Matriz de capacidades máximas (en horas disponibles) para el centro de distribución j con tecnología q en el periodo t.
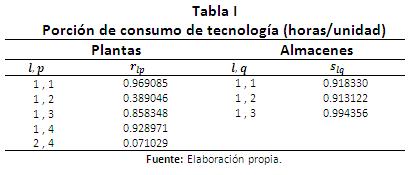
rlp: Porción de tecnología que consume el producto l producido en una planta con una de la tecnología p (en horas por unidad de producto).
slq: Porción de tecnología que consume el producto l almacenado en un centro de distribución con una de la tecnología q (en horas por unidad de producto).
gip: Costo fijo asociado a la apertura de la planta i con el tipo de tecnología p.
fjq: Costo fijo asociado a la apertura del centro de distribución j con el tipo de tecnología q.
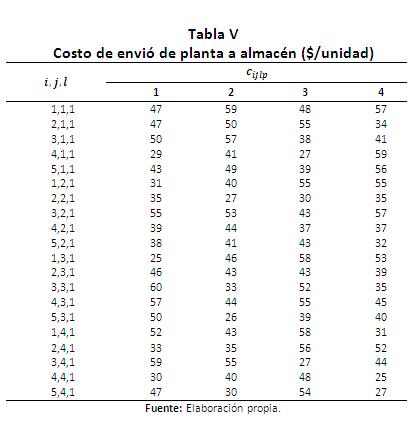
cijlp: Costo unitario asociado al tipo de producto l por ser producido y enviado desde una planta i con una tecnología p a un centro de distribución j.
bjklq: Costo unitario asociado al tipo de producto l por ser almacenado y enviado desde el centro de distribución j con una tecnología q a un punto de demanda k.
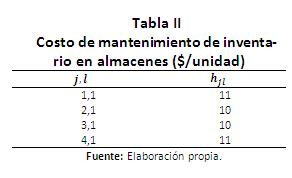
hjl: Costo unitario de mantenimiento de inventario para el producto l en el almacén j.
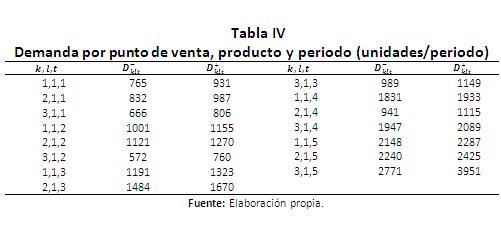
Dklt: Demanda unitaria para todo el periodo de planeación del punto de venta k del tipo de producto l en el periodo t.
Amax: Máximo número de plantas que se pueden abrir.
Bmax: Máximo número de centros de distribución que se pueden abrir.
Variables de decisión
Xijlpt: Cantidad en unidades enviada de la planta i con tecnología p al almacén j del producto l en periodo t.
Yjklqt: Cantidad en unidades enviada del Almacén j con tecnología q al punto de venta k del producto l en el periodo t.
Wjlt: Inventario al final del periodo t del producto l en el almacén j.
Aip: Es una variables binaria donde (1) indica la apertura una planta i con tecnología p, (0) de lo contrario.
Bjq: Es una variables binaria donde (1) indica la apertura un almacén j con tecnología q, (0) de lo contrario.
El modelo de programación lineal entera-mixta (MILP, Mixed Integer Linear Programming) se presenta a continuación:
Para este modelo en (1) se busca minimizar los costos totales de la cadena de distribución. Las restricciones (2) y (3) se refieren al cumplimiento de la capacidad de plantas y centros de distribución en cada uno de los periodos, respectivamente. La restricción (4) se refiere a que cada planta abierta debe tener un solo tipo de tecnología, y la restricción (6) que máximo se puede abrir un número determinado de plantas en todo el horizonte de planeación, (5) y (7) son similares pero para los centros de distribución. La restricción (8) es de balance de productos e inventarios en cada centro de distribución, por cada producto y en cada periodo. La restricción (9) asegura que se debe satisfacer la demanda de cada cliente, producto y en cada periodo. La restricción (10) se refiere a la naturaleza de las variables de decisión.
2.2. La demanda como un número difuso
Respecto a la demanda se tiene que en la realidad esta nunca se conoce con certeza absoluta, inclusive con los métodos más robustos de pronósticos no se puede garantizar que se conocerá exactamente el valor de ésta, es así que la demanda posee una incertidumbre inmersa la cual es necesaria incluir dentro de la toma de decisiones, en otras palabras la demanda posee un carácter de impresisción para cada producto, cliente y periodo que se puede considerar como un intervalo (ver ecuación 11).
Entonces este intervalo se puede considerar como un número difuso tipo I, al cual se le puede asociar una variable lingüística como lo es el nivel de proyección de ventas, indicando que la cantidad de ventas tiene una pertenencia a la variable de ventas pesimistas si es inferior a D-klt, y si es superior a D+klt se considerarían ventas optimistas. El objetivo es determinar dentro del intervalo [D-klt ; D+klt] un valor más preciso (cerrado o pequeño) que garantice un costo mínimo y que sea útil para la planeación de ventas y el diseño de una red de distribución.
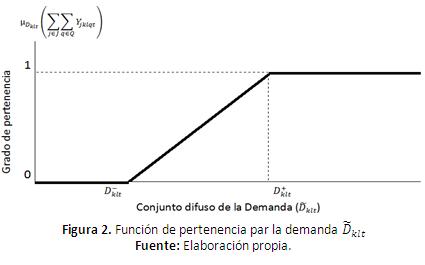
Si la demanda se considera como un conjunto difuso entonces la restricción de cumplimiento de demanda (9) tendría la siguiente función de pertenecía (μDklt (ΣjЄJ ΣqЄQ Yjklqt)) para un conjunto difuso definido sobre un intervalo como se muestra en la Figura 2.
Para D+klt se asocia la máxima pertenencia, es decir un valor de 1, de tal forma que la función representada en la Figura 2 se puede modelar como se muestra en la ecuación (12). Si la demanda es menor que D-klt la pertenecía es cero. Para valores dentro del intervalo la pertenencia se representada mediante funciones lineales.
2.3. Procedimiento de solución de Zimmermann
Zimmermann [19] planteo un modelo conocido como soft constraints model, en donde se busca hallar el valor máximo de las funciones difusas que satisfagan las restricciones, para esto se busca maximizar el grado de satisfacción de los conjuntos difusos. Este método utiliza funciones de pertenencia lineales para un problema dado como 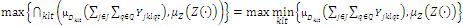 , donde
, donde 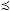 indica que la restricción tiene un orden parcial difuso, que implica una flexibilidad en la restricción,
indica que la restricción tiene un orden parcial difuso, que implica una flexibilidad en la restricción, 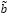 se presenta como un conjunto difuso con una función de pertenencia
se presenta como un conjunto difuso con una función de pertenencia 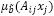 dada por:
dada por:
- Encontrar dos cotas z- y z+ (inferior y superior, respectivamente) para la función objetivo, donde z- es calculada resolviendo el PL con b- y z- es calculada con b+.
- Definir un conjunto difuso lineal para z dado por:
-
Encontrar el máximo nivel de pertenencia sobre la intersección de las funciones de pertenencia para todos los conjuntos difusos
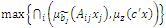 . La intersección de conjuntos difusos se puede representar por el operador min, de tal forma que se desea resolver el problema
. La intersección de conjuntos difusos se puede representar por el operador min, de tal forma que se desea resolver el problema 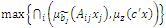 . Este problema no lineal se puede resolver mediante un modelo de programación lineal equivalente definido α como es grado de satisfacción de todos los conjuntos difusos. Este PL esta dado como:
. Este problema no lineal se puede resolver mediante un modelo de programación lineal equivalente definido α como es grado de satisfacción de todos los conjuntos difusos. Este PL esta dado como:
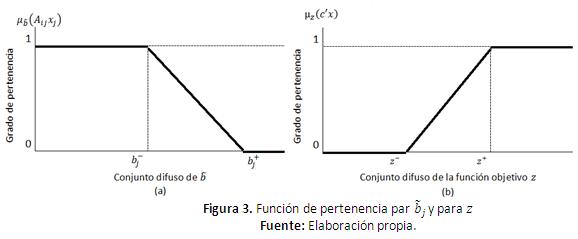
Esta función de pertenencia se puede representar gráficamente por la Figura 3 (b). Cuando los valores de la función objetivo son mayores a la cota superior se asigna una valor de 1 (máxima grado de pertenencia) y cuando son menores a la cota inferior se asigna un valor de 0. Dentro del intervalo se asume una función lineal.
2.4. Procedimiento de solución
El método descrito en la sección anterior se puede aplicar al modelo de MIPL dado por (1)-(10), donde las restricciones (9) son restricciones suaves modeladas como un numero difuso descrito en la sección 2.2. El método para este caso se describe a continuación.
- Encontrar una cota Z-(⋅) para la función objetivo dada por (1), donde Z-(⋅) es calculada resolviendo el MIPL con D-klt en las restricciones (9).
- Encontrar una cota Z+(⋅) para la función objetivo dada por (1), donde Z+(⋅)) es calculada resolviendo el MIPL con D+klt en las restricciones (9).
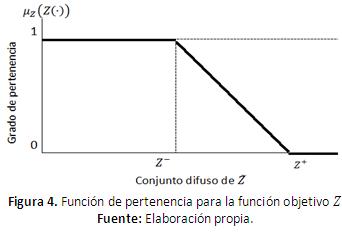
- Definir un conjunto difuso lineal para Z(⋅) dado la ecuación (16). Esta función de pertenencia se puede representar gráficamente por la Figura 4. Se asigna el mayor grado de pertenecía para los valores de la función objetivo menores a la cota inferior, y cero cuando son mayores a la cota superior. En el intervalo se asume una función lineal.
-
Resolver el siguiente modelo de MIPL que equivale a encontrar el máximo grado de pertenencia (α) de
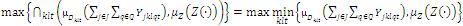
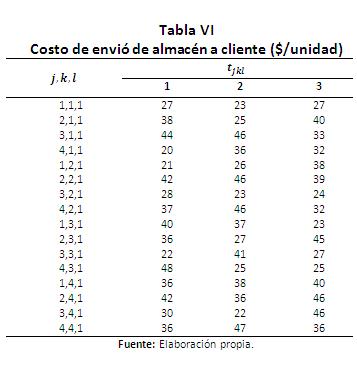
Se presenta el siguiente ejemplo para mostrar la aplicación del modelo propuesto y del enfoque de solución. Se consideran 5 plantas, 4 centros de distribución, 4 clientes, 4 y 3 tipos de tecnología para plantas y centros de distribución respectivamente, 5 periodos de horizonte de planeación y se pueden abrir máximo 2 plantas y 2 centros de distribución. Se fabrican un solo tipo de producto (aunque se puede ampliar a múltiples productos). La información de los parámetros descritos en la sección 2.1 se encuentra en la Tablas I a VI), por facilidad se toma la capacidad de las plantas y de los almacenes constantes en todo el horizonte de planeación.
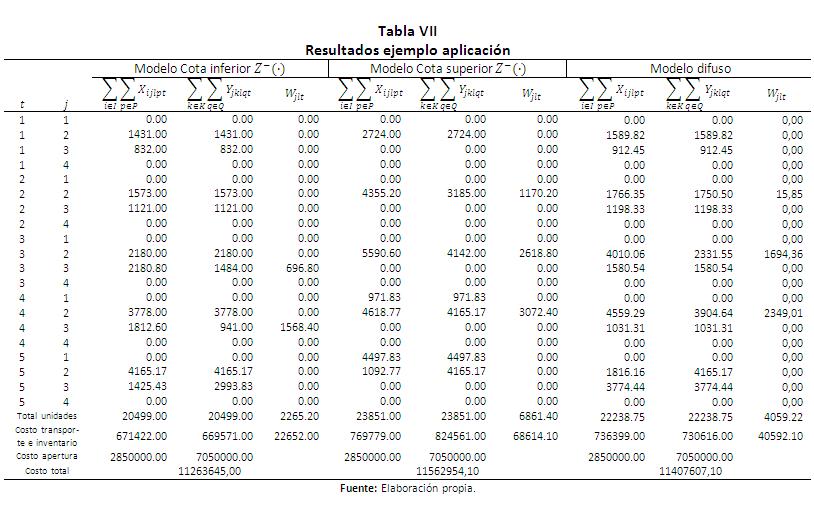
Este problema se ejecutó en Xpress-MP 7.4 en Windows 8 64-bit, con un procesador Intel i5 3337 (2x1.8 GHz) y 6GB de RAM. Los modelos se resolvieron entre 30 y 60 segundos. La Tabla VII muestra los resultados respecto a la cantidad de productos que ingresa y sale de cada almacén en cada periodo y el inventario al final del mismo. También se muestra el total de unidades para estas variables así como su costo de producción, almacenamiento y el costo total. Las 2 primeras columnas presentan el periodo y el almacén. Las columnas 2, 4, y 5 presentan la solución para Z-(⋅), las columnas 6, 7, y 8 para Z+(⋅) y las columnas 9, 10 y 11 para el modelo de programación lineal entera mixta difusa.
En cuanto apertura de plantas en los tres modelos se decide abrir una planta (i=2) con la misma tecnología (p=2), mientras que para los almacenes se puede observar como la decisión de apertura en la cota inferior y del modelo difuso es la misma (almacenes j=2 y 3 con tecnologías q=1 y 2, respectivamente), mientras que para la cota superior la configuración es diferente (almacenes j=1 y 2 con tecnología q=1). Los costos de apertura de plantas y almacenes son los mismos en los tres modelos, la diferencia son los tipos de tecnología utilizados.
Respecto a las cantidades enviadas desde las plantas hacia los almacenes y de estos a los puntos de venta los resultados del modelo difuso están dentro del rango dado por los resultados de la cota inferior y superior. Un comportamiento similar se presenta con el total de unidades en inventario generado en el horizonte de planeación, aunque para el modelo de la cota inferior se incurre en inventario en los periodos 3 y 4, para los otros dos modelos se incurren en los periodos 2, 3, y 4. Los costos de producción y envió desde plantas, de almacenamiento y envió desde almacenes y de inventario presentan las misma tendencia que la unidades, aunque se utilizan distintas tecnologías, el modelo difuso obtuvo un resultado intermedio entre la cota inferior y la cota superior indicando un nivel de ventas que debe satisfacerse con ese grado de satisfacción de las restricciones de los conjuntos difusos.
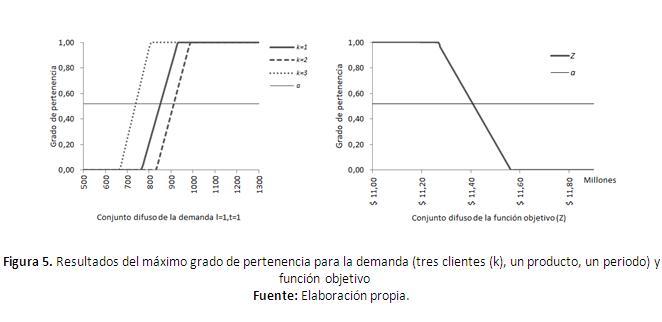
En resumen para esta aplicación, se obtiene un Z-(⋅) de 11’263,645.00, un Z+(⋅) de 11’562,954.10 y Z*(⋅) de 11’407,607.10. El grado de pertenencia obtenido fue de 0.519. En la Figura 5 se observa cómo se encuentra un valor de la demanda para un producto en cada uno de los puntos de venta, también se intenta alcanzar el mínimo costo (cota inferior de los valores de la función objetivo).
5. CONCLUSIONES Y TRABAJOS FUTUROS
En este trabajo se consideraron algunas extensiones a los modelos clásicos de diseño de redes de distribución como los múltiples productos y periodos, la elección entre diferentes tipos de tecnologías para las plantas y almacenes, el almacenamiento de inventario en los centros de distribución y la inclusión de la demanda como un número difuso. Diferentes aplicaciones prácticas pueden tener estas características lo cual hace que el modelo propuesto en este artículo tenga una gran aplicabilidad para implementarlo en el diseño de redes de distribución reales.
El modelo propuesto genera un valor de la demanda que se acota por la función de pertenencia, es decir, que el modelo realiza un balance entre dos cotas de la función objetivo y entre el cumplimiento de la demanda con un costo mínimo, por eso es un modelo flexible. Esto permite hacer un análisis de la variable lingüística asociada, que en este caso es la proyección de ventas, la cual genera valores más confiables acerca de lo que se tiene que vender en cada periodo de tiempo, para minimizar los costos y cumplir con las expectativas planteadas en los escenarios propuestos. El entendimiento de esta variable es fundamental para la comprensión del modelo y sus alcances conceptuales, ya que sin ese entendimiento, el modelo podría no tener ninguna validez teórica ni práctica.
La implementación de este modelo en un contexto real, dentro de una compañía, supone la colaboración de diferentes áreas, como la financiera, donde se encuentran los costos asociados a la cadena de abastecimiento; el área de logística, donde se pueden encontrar las redes asociadas y las necesidades respecto al modelo, y los grupos multidisciplinares (crossfunctional groups) para estimar los escenarios optimistas y pesimistas de la demanda.
Para trabajos futuros se puede considerar otro tipo de funciones de pertenencia y otros parámetros flexibles como los costos, los coeficientes tecnológicos, las capacidades, etc. También la aplicación de conjuntos difusos Tipo II, que permiten medir la incertidumbre de las distintas funciones de pertenencia para un mayor manejo de la incertidumbre en el sistema.
AGRADECIMIENTOS
Agradecemos a Fair Isaac Corporation (FICO) por proveernos licencias de uso académico de Xpress -MP bajo el programa académico (Academic Partner Program) suscrito con la Universidad Distrital Francisco José de Caldas. También agradecemos al revisor por sus valiosos comentarios y sugerencias que ayudaron a presentar mejor el modelo propuesto y los resultados obtenidos.
REFERENCIAS BIBLIOGRÁFICAS
- N. C. Nam, T. H. L. An, and P. D. Tao, “A Branch and Bound Algorithm Based on DC Programming and DCA for Strategic Capacity Planning in Supply Chain Design for a New Market Opportunity,” in Operations Research Proceedings 2006, P. D. K.-H. Waldmann and D.-W.-I. U. M. Stocker, Eds. Springer Berlin Heidelberg, 2007, pp. 515-520.
- Y. Yin, I. Kaku, J. Tang, and J. Zhu, “Supply Chain Design Using Decision Analysis,” in Data Mining, Springer London, 2011, pp. 121-132.
- R. Velásquez, M. T. Melo, and S. Nickel, “An LP-based Heuristic Approach for Strategic Supply Chain Design,” in Operations Research Proceedings 2005, P. D. H.-D. Haasis, P. D.-I. H. Kopfer, and D. J. Schönberger, Eds. Springer Berlin Heidelberg, 2006, pp. 167-172.
- T. Seidel, “Rapid Supply Chain Design by Integrating Modelling Methods,” in Build To Order, G. Parry and A. Graves, Eds. Springer London, 2008, pp. 277-295.
- S.-H. Liao and C.-L. Hsieh, “Integrated Location-Inventory Retail Supply Chain Design: A Multi-objective Evolutionary Approach,” in Simulated Evolution and Learning, K. Deb, A. Bhattacharya, N. Chakraborti, P. Chakroborty, S. Das, J. Dutta, S. K. Gupta, A. Jain, V. Aggarwal, J. Branke, S. J. Louis, and K. C. Tan, Eds. Springer Berlin Heidelberg, 2010, pp. 533-542.
- Z.-J. M. Shen and M. S. Daskin, “Trade-offs Between Customer Service and Cost in Integrated Supply Chain Design,” MSOM, vol. 7, no. 3, pp. 188-207, Jun. 2005.
- H. Yan, Z. Yu, and T. C. Edwin Cheng, “A strategic model for supply chain design with logical constraints: formulation and solution,” Computers & Operations Research, vol. 30, no. 14, pp. 2135-2155, Dec. 2003.
- R. Hammami, Y. Frein, and A. B. Hadj-Alouane, “A strategic-tactical model for the supply chain design in the delocalization context: Mathematical formulation and a case study,” International Journal of Production Economics, vol. 122, no. 1, pp. 351-365, Nov. 2009.
- S. Talluri and R. C. Baker, “A multi-phase mathematical programming approach for effective supply chain design,” European Journal of Operational Research, vol. 141, no. 3, pp. 544-558, Sep. 2002.
- B. M. Beamon, “Supply chain design and analysis:,” International Journal of Production Economics, vol. 55, no. 3, pp. 281-294, Aug. 1998.
- V. Jayaraman and A. Ross, “A simulated annealing methodology to distribution network design and management,” European Journal of Operational Research, vol. 144, no. 3, pp. 629-645, Feb. 2003.
- N. V. Sahinidis, “Optimization under uncertainty: state-of-the-art and opportunities,” Computers & Chemical Engineering, vol. 28, no. 6-7, pp. 971-983, Jun. 2004.
- A. R. Singh, R. Jain, and P. K. Mishra, “Capacities-based supply chain network design considering demand uncertainty using two-stage stochastic programming,” Int J Adv Manuf Technol, pp. 1-8.
- H. Selim and I. Ozkarahan, “A supply chain distribution network design model: An interactive fuzzy goal programming-based solution approach,” Int J Adv Manuf Technol, vol. 36, no. 3-4, pp. 401-418, Mar. 2008.
- K. N. Rao, K. V. Subbaiah, and G. V. P. Singh, “Design of supply chain in fuzzy environment,” J Ind Eng Int, vol. 9, no. 1, pp. 1-11, Dec. 2013.
- S. Ahmed and N. V. Sahinidis, “An Approximation Scheme for Stochastic Integer Programs Arising in Capacity Expansion,” Operations Research, vol. 51, no. 3, pp. 461-471, May 2003.
- M. C. Georgiadis, P. Tsiakis, P. Longinidis, and M. K. Sofioglou, “Optimal design of supply chain networks under uncertain transient demand variations,” Omega, vol. 39, no. 3, pp. 254-272, Jun. 2011.
- F. Pan and R. Nagi, “Robust supply chain design under uncertain demand in agile manufacturing,” Computers & Operations Research, vol. 37, no. 4, pp. 668-683, Apr. 2010.
- H.-J. Zimmermann, “Fuzzy programming and linear programming with several objective functions,” Fuzzy Sets and Systems, vol. 1, no. 1, pp. 45-55, Jan. 1978.
- J. C. Figueroa-García, C. A. Lopez-Bello, and D. Kalenatic, “An iterative algorithm for fuzzy mixed production planning based on the cumulative membership function,” Ingeniería, vol. 16, no. 2, pp. 6-17, 2011.
- J. C. Figueroa-García, D. Kalenatic, and C. A. Lopez-Bello, “Multi-period Mixed Production Planning with uncertain demands: Fuzzy and interval fuzzy sets approach,” Fuzzy Sets and Systems, vol. 206, pp. 21-38, Nov. 2012.
Este trabajo está autorizado por una Licencia Attribution-NonCommercial-NoDerivs CC BY-NC-ND.
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.




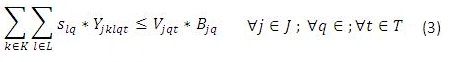
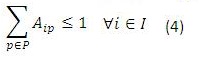
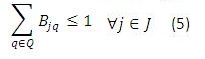
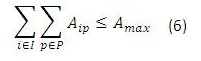
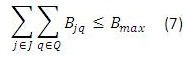
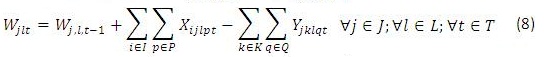
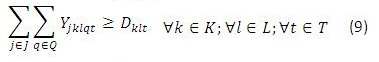
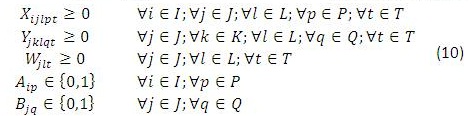
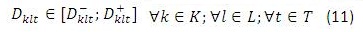
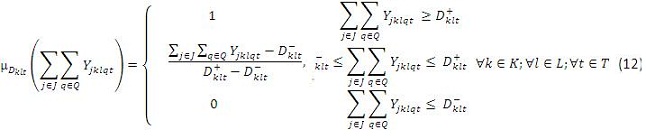

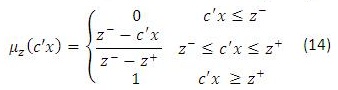
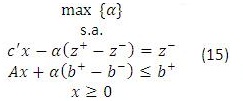
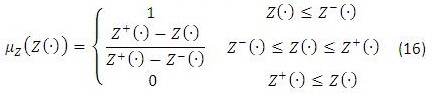
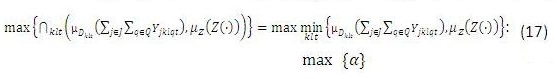
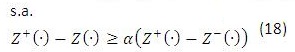
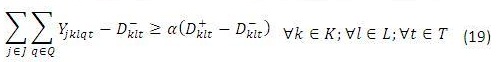
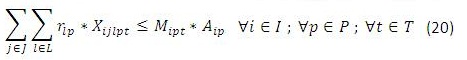
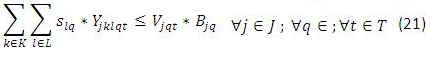
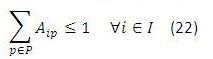
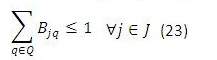
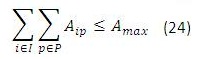
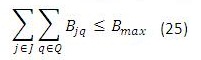
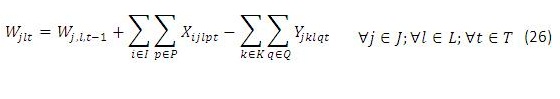
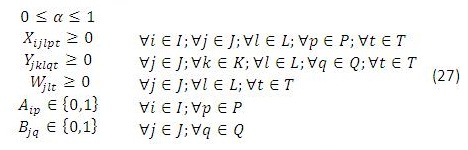




2.jpg)










