DOI:
https://doi.org/10.14483/23448393.2814Published:
2001-11-30Issue:
Vol. 7 No. 2 (2002): July - DecemberSection:
Science, research, academia and developmentPredecibilidad del tráfico en redes modernas de comunicaciones
Keywords:
Predicción óptima, predicción lineal, Tráfico autosimilar, Control de Congestión. (es).Downloads
References
R. Srikant. «Control of Communication Networks». In «Perspectives in Control Engineering», T. Samad, editor. IEEE Press, Piscataway, NJ, 2000.
] Sally Floyd and Van Jacobson. "Random Early Detection Gateways for Congestion Avoidance". IEEE/ACM Trans. On Networking, August 1993
S. Athuraliya, V. H. Li, S. H. Low and Q. Yin. "REM: Active Queue Management", IEEE Network, May 2001.
Wu-chang Feng, Dilip D. Kandlur, Debanjan Saha and Kang G. Shin. "BLUE: A New Class of Active Queue Management Algorithms", U. Michigan CSE-TR-387-99, April 1999.
M. Arlitt and C. Williamson. "Internet Web Servers: workload characterization and performance implications", IEEE/ACM Trans. On networking, Vol.5, N. 5, 1997
M. Crovella and A. Bestavros. "Self-similarity in WWW traffic: evidence and possible causes", IEEE/ACM Trans. On networking, Vol.5, N. 7, 1997
A. Feldmann, A. Gilbert, P. Huang and W. Willinger. "Dynamics of IP Traffic: A study of the role of variability and the impact of control". Proceedings ACM SIGCOMM, 1999.
M. Garret and W. Willinger. "Analysis, modeling and generation of self-similar VBR video traffic". Proceedings ACM SIGCOMM, 1994.
W. Leland, M. Taqqu, W. Willinger and D. Wilson. "On the selfsimilar nature of Ethernet traffic", IEEE/ACM Trans. On networking, Vol.2, N. 1, 1994
A. Feldmann. "Characteristic of TCP connection arrivals". In "Selfsimilar network traffic and performance evaluation", edited by K. Park and W. Willinger, John-Wiley and sons, 2000
Marco Alzate, "Tráfico Autosimilar en Redes de Comunicaciones", Revista INGENIERIA Universidad Distrital, Vol.7 N. 1, 2002.
M. Grossglauser and J. Bolot. «On the Relevance of long-rangedependence in network traffic», Proceedings ACM SIGCOMM, 1996.
T. Tuan and K. Park. "Congestion control for self-similar network traffic". In "Self-similar network traffic and performance evaluation", edited by K. Park and W. Willinger, John-Wiley and sons, 2000
G. He, Y. Gao J. Hou and K. Park. "A case for exploiting selfsimilarity of Internet traffic in TCP Congestion Control", Technical report, Department of Electrical Engineering, The Ohio State University, 2002
Yuan Gao, Guanghui He and Jennifer Hou. "On Exploiting Traffic Predictability in Active Queue Management", IEEE Infocom 2002, New York, June 2002
Yuan Gao, Guanghui He and Jennifer C. Hou. "On Leveraging Traffic Predictability in Active Queue Management", Technical report, Department of Electrical Engineering, The Ohio State University, 2002
T. Gyires, "Using Active Networks for Congestion Control in HighSpeed Networks with Self-Similar Traffic", IEEE Intl. Conf. On Systems, Man, and Cybernetics, 2000, Vol. 1
Lawrence Berkley National Laboratory, The Internet Traffic Archive, http://ita.ee.lbl.gov/html/ contrib/BC.html, April 29, 2000.
G.R.Grimmet and D.R. Stirzaker, "Probability and random processes", Oxford Science Publications, New York, 1992.
G. Gripenberg and I. Norros. "On the Prediction of Fractional Brownian Motion", 1994 <http://citeseer.nj.nec.com/ gripenberg94prediction.html>
Monson H. Hayes. "Statistical Digital Signal Processing and Modeling", John Wiley and Sons, New York, 1996.
Rene K. Boel, Iven M.Y. Mareels and Matthew R. James, "Performance Comparison Of Adaptive And Robust Predictors For Long Range Dependent Signals", 39th International Conference on Decision and Control, Sydney, Australia, December 2000
Fei Xue, "Modeling and Predicting LRD traffic with Farima Processes",
José Félix Vega Stavro, " Acerca de la Aplicación del Efecto de Memoria a Largo Plazo en el Control de Congestión en Redes de Conmutación de Paquetes", Universidad Distrital, Maestría en Teleinformática, por publicar Agosto 2003.
P Abry, D Veitch, Wavelet Analysis of LRD Traffic. IEE Transaction on Informatioin Theory, 1998.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Ingeniería, 2002-00-00 vol:7 nro:2 pág:21-30
Predecibilidad del tráfico en redes modernas de comunicaciones
Marco Aurelio Alzate Monroy
Miembro grupo de investigación en Comunicaciones,
Universidad Distrital Francisco José de Caldas
José Félix Vega Stavro
Candidato a Magister en Teleinformática Universidad Distrital Francisco José de Caldas
Resumen
En este artículo se presentan los resultados de al- gunos experimentos que permiten determinar la predecibilidad de una traza real de tráfico con características fractales. Se concluye que, sin necesidad de ajustar las observaciones a un modelo autosemejante particular, es posible utilizar estadísticas muestrales típicas para predecir con sorprendente exactitud la intensidad de tráfico en el futuro inmediato. Por último, se discute cómo podría explotarse esta característica para mejorar los mecanismos actuales de control de congestión en redes modernas de comunicaciones. Tanto el tratamiento del tema como la presentación de los experimentos se hacen de una manera tutorial. El apartado final presenta algunos resultados de investigación sobre protocolos de control de congestión basados en predecibilidad, obtenidos con el simulador de eventos discretos NS-2.
Palabras claves:
Predicción óptima, predicción lineal, Tráfico autosimilar, Control de Congestión.
Abstract
This paper presents the results of some experiments that allow determining the predictability in a real traffic trace with fractal behavior. The conclusion is that without fitting the trace to any particular self-similar model, is possible to use typical point statistical to predict, with high grade of precision, the traffic intensity in the near future. Finally we discuss about the use of this results for congestion control in modern telecommunications networks. The paper explains, in a tutorial manner, both the theory and the experiments. The final section presents some investigation results about congestion control protocols based on predictability, obtained with the discrete event simulator NS-2.
Key Words:
Optimal Prediction, Linear Prediction, Self Similar Traffic, Congestion Control, NS-2 Simulation.
I. INTRODUCCIÓN
Los procedimientos de control de congestión mediante realimentación entre extremos, como TCP,consisten en que las fuentes de tráfico ajusten su tasa de datos según las medidas de congestión obtenidas de la red. Estas medidas suelen ser indirectas (por ejemplo la ausencia de un reconocimiento o el incremento en el tiempo de "ida-y-vuelta", RTT) y llegan a las fuentes después de un retardo significativo. Inclusive cuando se usa notificación explícita de la congestión (ECN), que es una medida directa que tarda menos en llegar que las medidas indirectas anteriores, el tiempo que transcurre entre la detección de la congestión y su notificación a las fuentes de tráfico es del orden de un RTT, el cual suele ser mucho mayor precisamente durante los períodos de congestión. Este retardo en el camino de la realimentación implica muchas dificultades en el control efectivo de la congestión pues las acciones de control que se toman no corresponden al estado actual de congestión en la red, sino a algún estado previo. Por supuesto, una acción retardada suele traducirse en oscilaciones e inestabilidades que traen efectos desastrosos en la calidad del servicio ofrecido por la red [1].
Muchos esfuerzos de investigación se han concentrado en tratar de mitigar estos efectos negati- vos del retardo en el lazo de realimentación mediante la estabilización de las colas en los nodos congestionados o próximos a congestionarse. Como resultado de estos esfuerzos se han desarrollado diferentes estrategias de administración de la memoria en estas colas, tales como RED, REM, BLUE y todas sus variantes [2,3,4]. Sin embargo, excepto por un posible procedimiento de ajuste del tráfico en los nodos de ingreso (básicamente Leaky Bucket), ninguno de estos mecanismos de control de congestión prestan atención a las características estadísticas de cada flujo de tráfico ni del flujo agregado. De acuerdo con muchas medidas recientes de tráfico en muy distintos contextos [5,6,7,8,9,10], es muy probable que esas características correspondan a un proceso con dependencia de rango largo, LRD, lo cual implica una alta variabilidad y presencia de ráfagas en muchas escalas de tiempo [11]. Este tipo de variabilidad induce extensos períodos de sobrecarga y subutilización que degradan significativamente el desempeño de la red. De hecho, se ha reportado que bajo tráfico LRD los períodos de congestión pueden ser tan extensos y con una pérdida de paquetes tan concentrada que nisiquiera un gingantesco incremento en el tamaño de la memoria podría decrementar la tasa de pérdida de paquetes de una manera notoria [12]. En consecuencia, las técnicas de control por realimentación son poco útiles si el tiempo de respuesta del control no alcanza a considerar las muchas escalas a las cuales se puede presentar la congestión, especialmente en redes en las que el producto retardo´ancho de banda es muy alto [14].
Si bien la variabilidad LRD tiene estos efectos negativos sobre el desempeño, imponiendo serias dificultades a los algoritmos de control de congestión, también es cierto que este tipo de procesos poseen una compleja estructura de correlación que puede ser explotada para "predecir el futuro" [14]. Algunos autores han trabajado en esta idea con promisorios resultados, aunque sus trabajos se han basado en modelos particulares de tráfico en los que la predicibilidad está garantizada por la estructura misma del modelo (básicamente, movimiento browniano fraccional, fbm, sintetizado aproximadamente mediante el multiplexaje de procesos on/off con dis- tribuciones de cola pesada en sus períodos de actividad y/o inactividad) [14, 15, 16, 17, 18]. En este artículo revisamos la predecibilidad de una traza real de tráfico para verificar su aplicabilidad en los esquemas de control de congetión, asignación de recursos,balanceo de carga, etc. En particular, utilizamos la traza BC-pAug89 medida en la red Ethernet de Bellcore en 1989 [19], para la cual ya se ha establecido plenamente su autosemejanza [9].
Puesto que no estamos asumiendo ningún modelo de tráfico, no podemos utilizar técnicas óptimas de predicción basadas en modelos. En cambio de esto utilizaremos dos esquemas en el dominio del tiempo que aprovechan la supuesta dependencia de rango largo: uno es un método particular de estimación de la media condicional [14] y otro es un método tradicional de predicción lineal [16]. En ambos casos, compararemos los resultados de predecibilidad con una traza muestral de un proceso Poisson 'equivalente', esto es, con el mismo tiempo promedio entre llegadas y la misma longitud promedio de los paquetes.
En la sección 2 describimos las trazas muestrales del tráfico. En la sección 3 discutimos la predicción óptima e implementamos un método aproximado de predicción óptima. En la sección 4 describimos la predicción lineal de mínino error cuadrado promedio. Por último, en la sección 5, discutimos la posibilidad de usar estas predicciones para mejorar los mecanismos actuales de control de congestión en redes modernas de comunicaciones, con lo cual concluimos el artículo.
II. TRAZAS DE TRÁFICO
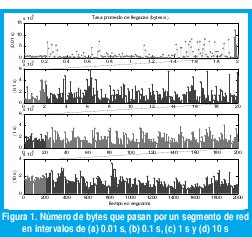
La traza muestral BC-pAug89 [19], medida en una red Ethernet de los laboratorios de investigación Bell (hoy Telcordia technologies) en 1989, corresponde a dos series de tiempo que representan los instantes de llegada y las longitudes de un millón de paquetes, medidos en un lapso de 3142.82 segundos. En promedio llegan 318,185 paquetes por segundo, cada uno con una longitud promedio de 434,29 bytes. Esta traza muestral exhibe alta variabilidad en un amplio rango de escalas de tiempo, como se puede ver en la Figura 1. En efecto, en la figura 1(a) observamos el número promedio de bytes por segundo que llegan durante los primeros 2 segundos, considerando los promedios durante períodos de 0.01 segundos; esto es, la barra que aparece en el instante t de la gráfica corresponde al número de bytes por segundo que, en promedio, pasaron por un segmento de la red en el intervalo [t, t+0.01 s). En la figura 1(b) extendemos el rango de 2 a 20 segundos aumentando la granularidad de los intervalos de 0.01 s a 0.1 s. Este proceso lo repetimos en las figuras 1(c) y 1(d), que tienen granularidades de 1 y 10 segundos respectivamente; esto es, la barra que aparece en el instante t de la figura 1(d) corresponde al número de bytes por segundo que, en promedio, pasaron por ese segmento de la red en el intervalo [t, t+10 s). Se puede observar la presencia de ráfagas en cada una de estas escalas, de manera que la variabilidad parece ser una característica autosemejante en esta traza.
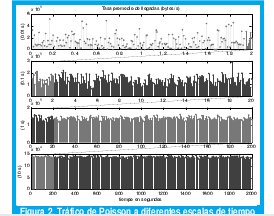
En contraste, la figura 2 muestra el mismo procedimiento de conteo de bytes con diferentes granularidades en el tiempo, pero considerando un proceso de Poisson con longitud de paquetes exponencialmente distribuida. Nótese cómo en este caso, a diferencia de la traza BC-pAug89, cualquier segmento de 10 segundos que consideremos servirá para hacer un adecuado estimativo del número de bytes que llegan por segundo: la presencia de ráfagas sólo se da en un rango muy limitado de escalas de tiempo, en el orden del intervalo promedio entre llegada
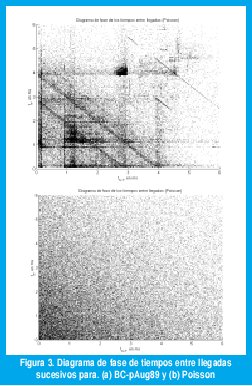
La invarianza a la escala en la traza BC-pAug89 puede explicarse en términos de la rica estructura de autocorrelación que ésta posee. La figura 3(a) muestra, por ejemplo, un diagrama de fase de tiempos entre llegadas sucesivos (tn vs tn-1) para la traza BC-pAug89, donde se aprecian estr ucturas determinísticas tales como líneas horizontales, verticales y diagonales además de alta concentración de puntos en determinadas áreas. La figura 3(b) muestra el mismo diagrama para el tráfico de Poisson, el cual carece de todas estas estructuras.
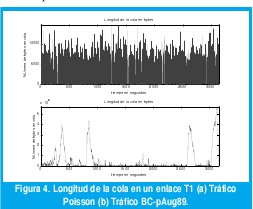
Por supuesto, estas características tan diferentes entre las dos trazas de tráfico deben tener consecuencias significativas en cuanto al desempeño de las redes de comunicaciones por donde ellas transitan. Para verificar esto, introducimos las dos trazas a través de un enlace T1 de 1.544 Mbps y medimos la longitud de la cola como función del tiempo. Es razonable utilizar un enlace T1 pues ambas trazas generan un promedio de 1.105 Mbps, de manera que la utilización del enlace sería de menos del 72% que, en términos de los métodos de diseño sugeridos por el modelo M/M/1 de la teoría de colas, implicaría un retardo promedio en cola de menos de 6 ms. En efecto, como muestra la figura 4(a), la longitud de la cola con el tráfico Poisson nunca excede los 15 Kbytes, donde los picos de máxima ocupación sólo duran algunas pocas fracciones de segundo. El retardo promedio de los paquetes, incluyendo la transmisión, es de menos de 8 ms con un retardo máximo de 85 ms. No hay congestión en ningún instante. Sin embargo, una situación muy diferente ocurre con el tráfico BC-pAug89, como se muestra en la figura 4(b). Necesitaríamos un buffer de 6 Mbytes, 410 veces mayor que el que necesitaríamos con el tráfico de Poisson. Los picos de máxima ocupación duran cientos de segundos, constituyendo largos períodos de fuerte congestión. En promedio, cada paquete tarda 3 s con un retardo máximo de hasta 30 s. Ciertamente, la correlación que exhibe la traza BC-pAug89 durante varias escalas de tiempo resulta desastrosa para el desempeño de la red.
III. PREDICCIÓN DEL TRÁFICO FUTURO MEDIANTE LA ESPERANZA CONDICIONAL
Existen muchas técnicas de predicción óptima, ya sean basadas en modelos específicos o no. En este artículo nos referiremos a dos técnicas sub-óptimas pero prácticas para su implementación en tiempo real. Nuevamente, aquí el tratamiento será de tipo tutorial.
¿Qué es una predicción óptima? Depende del criterio de optimalidad que se escoja. En nuestro caso escogeremos, a priori, el criterio del mínimo error cuadrado medio (MMSE -minimum mean square error-), ya que él nos permite utilizar un principio geométrico muy útil e intuitivamente obvio, como es el principio de ortogonalidad [21]: Si X0 es el número de bytes que llegarán en los próximos T segundos y hemos de escoger el mejor predictor de X0 entre los elementos de un espacio vectorial lineal de posibles predictores, S, obtendremos el mínimo error si proyectamos X0 perpendicularmente sobre dicho espacio, de manera que el error resulte ortogonal a cualquier vector del espacio de predictores. Definiendo la proyección de A sobre B como el producto interno E[AB], el principio de ortogonalidad dice que Y será un predictor óptimo de X0 si
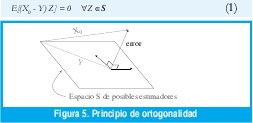
En efecto, supongamos que Y satisface la ecuación (1). Entonces, para cualquier Z que pertenezca al espacio S,
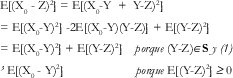
Así pues, E[(X0 - Y)Z] = 0 Z∈S implica
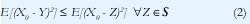
De manera que Y es el mejor predictor en el espacio S. De hecho, se puede demostrar igualmente fácil la implicación en el otro sentido ((2) ⇒ (1)) [21], de manera que (1) y (2) son equivalentes.
Considérese, por ejemplo, el espacio de predictores constituido por todas las constantes reales, S=R, donde R es el conjunto de los números reales. El mejor estimador será Y=y si y minimiza el error cuadrado medio E[(X0- y)2]:
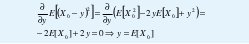
Este resultado se obtiene más directamente del principio de ortogonalidad:
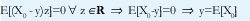
Así pues, en ausencia de mayor información, el mejor predictor de X0 es el valor esperado del número de bytes que llegan en períodos de T segundos. Para construir este predictor debemos estimar E[X0] para lo cual, gracias a la estacionariedad del proceso de incrementos {Xn}, podríamos usar el simple promedio aritmético de los anteriores p períodos. Pero, ya que debemos contar con esa información, sería mejor utilizarla para construir un mejor predictor utilizando un mayor espacio de predictores S sobre el cual proyectar X.
En particular, para el caso de movimiento browniano fraccional, en [22] se sugiere una regla práctica: Utilícese sólo el último segundo para predecir el siguiente segundo, el último minuto para predecir el siguiente minuto, la última hora para predecir la siguiente hora, etc. Así pues, supongamos que queremos predecir el número de bytes que llegarán en los próximos T segundos, X0, basados en la medida obtenida de los últimos T segundos, X-1. Puesto que queremos encontrar un predictor óptimo de la forma Y=f(X-1), es natural escoger el espacio de estimadores S={g(X-1), g:RR}. Un miembro de S es Y=h(X-1)E[X0|X-1], y sea Z=u(X-1) cualquier otro miembro de S. Consideremos la expresión E[(X0 - Y)Z]:
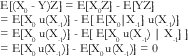
En consecuencia, el método por implementar consiste en predecir X0 mediante la estimación de E[X0|X1]1, pues éste es el predictor óptimo en el sentido del mínimo error cuadrado promedio. Por definición, si el número de bytes que llegaron en los anteriores T segundos es i, el predictor óptimo sería
donde pij es la probabilidad condicional de que lleguen j bytes en los próximos T segundos dado que
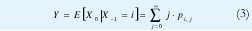
llegaron i bytes en los anteriores T segundos. Por supuesto, no se puede estimar el arreglo pij pues su tamaño sería excesivo (en teoría, tanto i como j pueden tomar valores enteros desde cero hasta ∞). Sin embargo, para utilizar de alguna manera la ecuación (3) en la predicción, vamos a hacer una burda cuantización vectorial de {Xn}: Habiendo medido el máximo y el mínimo volumen de tráfico que han llegado en los anteriores períodos de T segundos, Xmax y Xmin, podemos dividir el rango [Xmin, Xmax] en L intervalos y, con cada nueva medida X-n ir calculando incrementalmente las frecuencias relativas de cada intervalo, dado el intervalo donde cayó la medida anterior, X-n-1. Estas frecuencias relativas serían un estimador de pij, redefinido como pij=Prob[X-n∈ Intervalo j | X-n-1 Intervalo i], la cual sería independiente de n gracias a la estracionariedad del proceso de incrementos {Xn}, y sería mucho más fácil de calcular, pues ahora el rango de valores de i y j sólo sería el intervalo de números enteros [1, L]. Si el centroide del intervalo l∈[1,L] es x(l) º E[X| X∈ intervalo l], y si el número de bytes que llegaron en los anteriores T segundos cayó en el intervalo i, la nueva versión cuantizada del predictor óptimo (3) sería
Este predictor es prácticamente idéntico al utilizado en [14]. En particular, el paso de cuantización se
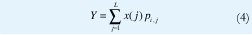
escoje como Δx = (Xmax - Xmin)/L, y los intervalos se definen cómo [0, Xmin+Δx), [Xmin+Δx, Xmin+2Δx), , [Xmin+(L-1)Δx,). Para L=8, los intervalos serían como muestra la figura 6.
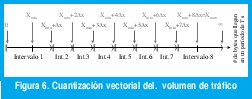
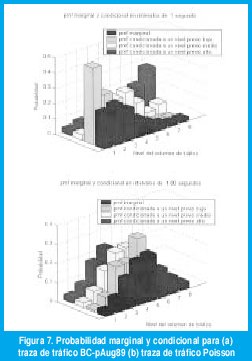
La figura 7(a) muestra la probabilidad marginal pj=Prob[X-n ∈ Intervalo j] y las probabilidades condicionales p1j , p5j y p8j , para 8 niveles de cuantización sobre el tráfico BC-pAug89, con una granularidad T= 1 s. La figura 7(b) muestra las mismas distribuciones para el tráfico de Poisson. Claramente, en este último caso, condicionar en el nivel de tráfico del anterior segundo no ayuda a obtener una mejor estimación del nivel de tráfico en el próximo segundo, pues las probabilidades condicionales son muy parecidas entre sí y casi idénticas a la probabilidad marginal. Para el tráfico BC-pAug89, por el contrario, si el nivel de tráfico durante el anterior segundo fue bajo (o alto), es mucho más probable que el nivel de tráfico durante el siguiente segundo sea también bajo (o alto).
También sería interesante observar el rango de escalas de tiempo para el cual esta propiedad de predicibilidad se cumple. Con este propósito, la figura 8(a) representa las distribuciones p1j y p8j , en azul y rojo respectivamente, para el tráfico BC-pAug89, con diferentes granularidades en el tiempo (10 ms, 100 ms, 1 s y 10 s). Podemos ver que la predicibilidad condicionada a un tráfico previo bajo se mantiene a cualquier escala de tiempo, siendo mejor en escalas más finas. Cuando condicionamos a un tráfico previo alto, la predicibilidad es pobre en las escalas finas de tiempo, pero mejora a medida que incrementamos la escala de tiempo, al menos dentro del rango de escalas seleccionado. La figura 8(b) repite la gráfica anterior para el tráfico Poisson, permitiendo observar que, en este caso, a ninguna escala se podría aprovechar el conocimiento del anterior nivel del volumen de tráfico para mejorar la predicción del siguiente nivel del volumen de tráfico.
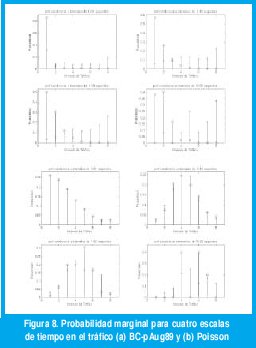
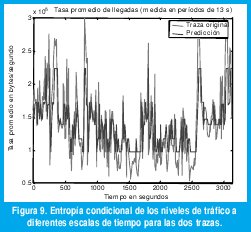
Aunque las figuras 7 y 8 dejan claro la posibilidad de usar este método para predecir el tráfico futuro en la traza BC-pAug89, todavía no queda claro cuánto puede pesar la gran predicibilidad condicionada a un bajo tráfico previo respecto a la relativamente pobre predicibilidad condicionada a un alto tráfico previo. Desearíamos que, dado el conocimiento que tenemos del nivel inmediatemente anterior del tráfico, la probabilidad del próximo nivel del tráfico estuviera concentrada en uno de los intervalos de tráfico de la figura 6. Esto es, quisiéramos disminuir al máximo nuestra incertidumbre o, lo que es lo mismo, la entropía de la distribución. Así pues, una buena medida de la predecibilidad podría ser la entropía promedio de la distribución condicional,
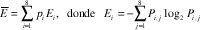
la cual se muestra en la figura 9. En ambos casos la predicibilidad parece ser ligeramente mejor a mayores escalas de tiempo, aunque definitivamente, en el rango de escalas de interés, la predicibilidad del tráfico BC-pAug89 resulta muy superior. Por supuesto, de las figuras 1(d) y 2(d) puede deducirse que, a grandes esclas de tiempo, el tráfico de Poisson es efectivamente más predecible puesto que los intervalos correspondientes de la figura 6 resultan mucho menores para el tráfico Poisson que para el tráfico BC-pAug89, a pesar de que la distribución pueda ser más dispersa entre ellos. Sin embargo, sabemos que ésto no se debe a la estructura particular del proceso sino al hecho simple de que, para una secuencia de variables aleatorias independientes, la media muestral tiende a la media estadística cuando el número de muestras es muy grande (hay ~3200 paquetes por barra en la figura 2(d)).
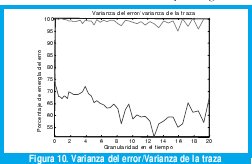
Esta predecibilidad se puede apreciar cuando observamos la varianza del error E[(X0 - Y)2] normalizada respecto a la varianza de la traza E[(X0- E[X0])2], como se aprecia en la figura 10. Esta razón es prácticamente 1 para el tráfico Poisson en cualquier escala, indicando que el mejor estimador sigue siendo el valor promedio incondicional. En cambio, para el tráfico BC-pAug89, esta razón puede ser tan pequeña como 0.5 en algunas escalas de tiempo, indicando que hay una notoria ventaja en predecir el tráfico mediante la esperanza condicional, aunque sea la versión cuantizada que usamos acá.
De hecho, la mínima varianza para la traza BC-pAug89 la obtenemos al predecir el número de bytes por segundo que llegarán dentro de los próximos 13 segundos, dada la tasa de llegadas en los anteriores 13 segundos. Esta escala de tiempo es demasiado grande para hacer control de congestión mediante ajuste de tasa de datos en la fuente, pero puede ser una escala muy adecuada para controlar la congestión mediante la distribución óptima de la carga sobre rutas paralelas independientes (por ejemplo, mediante las capacidades de ingeniería de tráfico que ofrece MPLS). Precisamente, la figura 11 muestra la tasa promedio predicha mediante (4), comparándola con la tasa promedio medida de la traza actual BC-pAug89. Se aprecia que la principal fuente de error en la predicción es la cuantización vectorial, pues mientras el máximo centroide es de sólo 220 Kbytes/segundo, la traza real alcanza picos de hasta 300 Kbytes/segundo cuando se mide en períodos no sobrelapados de 13 segundos. Igualmente, existen períodos de 13 segundos en los que llegan sólo 50 Kbytes/segundo, pero el mínimo centroide de la cuantización vectorial es de 100 Kbytes/segundo.
IV. PREDICCIÓN LINEAL DEL TRÁFICO FUTURO
El predictor anterior, basado en la ecuación (4), sólo utiliza la medición del tráfico en los anteriores T segundos para predecir el tráfico en los siguientes T segundos. Sin embargo, la predicción también se basa en una estimación de las probabilidades condicionales pij, para lo cual necesita observar el tráfico durante muchos períodos de T segundos (recordemos que no estamos suponiendo ningún modelo particular de tráfico). Esto es, para calcular E[X0|X-1] no sólo se usa el valor observado de X-1 sino el de toda la secuencia {X-n, n=1,2,}, hasta donde sea posible extender las observaciones. Esto sugiere la idea de usar un mejor estimador, que es el valor esperado condicionado a las p anteriores observaciones, Y=E[X0 | X-1, X-2, X-p+1, X-p]. La dificultad con este nuevo estimador está en que, en ausencia de un modelo adecuado, la única alternativa para calcular la predicción es usar las probabilidades condicionales de orden p+1, lo cual es prohibitavamente difícil para p>1. Sin embargo podemos hacer las cosas más fáciles si reducimos nuestro espacio de estimadores de S = {g1(X-1, X-2, X-p+1, X-p), g:Rp→R} a S = {a1X-1+a2X-2+ +ap-1X-p+1+apX-p, ai,∈R i=1,2,,p}; esto es, en vez de considerar todas las posibles funciones de p variables reales (como hicimos para llegar a (3) en el caso p=1), sólo vamos a considerar todas las posibles combinaciones lineales de p variables reales. ¿Cuál será el mejor predictor? Por supuesto, el predictor que satisfaga el principio de ortogonalidad
Definamos α= (α1, α2, αp)T y Xp= (X-1, X-2, X-p+1, X-p)T como dos vectores columna de Rp, el primero compuestos por p coeficientes arbitrarios y el segundo compuesto por las anteriores p observaciones de la tasa de tráfico en períodos de T segundos. El predictor Y=αTX será óptimo dentro del espacio de estimadores lineales si
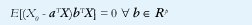
esto es, el error debe ser ortogonal a cualquier vector en el espacio de estimadores o, lo que es lo mismo, el estimador óptimo debe ser la proyección perpendicular de X0 sobre el espacio de todas las combinaciones lineales de {X-1, X-2, X-p+1, X-p}.
Expandiendo (5) y teniendo en cuenta que (αT X)(bTX)=bTXXTα,
bTE[X0X] - bTE[XXT]α= 0 ∀ b ∈ Rp
lo cual no puede ser una identidad para cualquier b a menos que
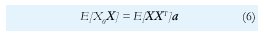
La ecuación (6) es una sistema de p ecuaciones lineales con p incógnitas (los elementos de a) donde los coeficientes y los términos independientes son las funciones de autocorrelación del proceso estocástico {Xn}, E[XiXj] r|i-j|. Esto es, la forma expandida de (6) es
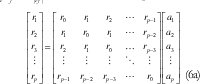
Habiendo observado el tráfico durante N períodos anteriores de T segundos, X-1, , X-N, los términos de la función de autocorrelación se pueden estimar fácilmente mediante el siguiente promedio muestral:
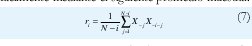
La ecuación (6a) se puede obtener igualmente fácil escogiendo directamente los coeficientes α que minimizan el error cuadrado medio de la predicción,
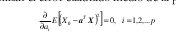
Obsérvese en la ecuación (6a) que la matriz de coeficientes tiene una estructura muy particular, pues es simétrica y todas todos los elementos de cada una de sus diagonales tienen el mismo valor. A este tipo de matrices se les llama Toeplitz y para ellas existen muy eficientes métodos de solución de la ecuación (6) [23], de manera que no es difícil pensar en la implementación de un predictor lineal del tráfico en los nodos de una red moderna de telecomunicaciones. De hecho, éste es exactamente el predictor que se utiliza en [15, 16 y 17].
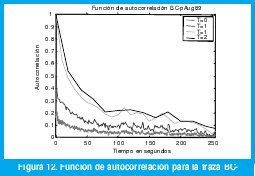
Como es de esperarse, La función de autocorrelación de la traza Poisson, estimada mediante (7), es un impulso en el instante 0 pues, para cualquier otro valor del tiempo, la correlación es cero. La traza BC-pAug89, en cambio tiene una rica estructura de correlación, como ya se intuyó a partir de las figuras 1 y 3, y como se puede verificar con la figura 12. Nótese cómo la autocorrelación persiste a diferentes escalas de tiempo de manera que, independientemente de la escala, los valores significati- vos alcanzan un orden de varias decenas. De hecho, se nota que a cualquier escala la autocorrelación de orden 20 sigue siendo significativa.
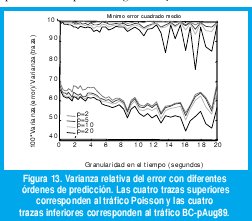
El efecto de estas propiedades se puede observar en la varianza del error, normalizada respecto a la varianza de la traza, E[(X0-Y)2]/E[(X0-E[X0])2], como se muestra en la figura 13. Para el tráfico Poisson todos los órdenes de predicción generan una varianza del error cercano a la varianza de la traza, de manera que el valor medio sigue siendo un predictor casi tan bueno como el predictor lineal óptimo. Para el tráfico BC-pAug89, en cambio, la varianza del error puede ser hasta menos de la mitad de la varianza de la traza de tráfico. Mayores órdenes de predicción podrían arrojar aún mejores resultados, pero puede resultar impráctico calcular predictores de mayor orden en una aplicación de tiempo real dentro de un nodo de conmutación. Por esa razón, escogeremos el orden de predicción p=20.
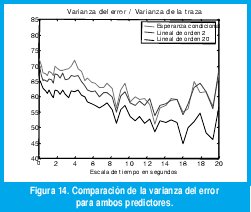
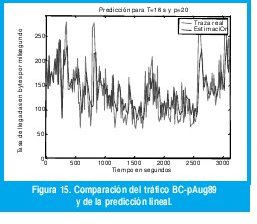
Es de anotar que el estimador lineal resulta mejor que el estimador de esperanza condicional, inclusive con órdenes de predicción muy bajos, según se puede apreciar en la figura 14. Esto no es de extrañar puesto que, mientras la esperanza condicional sólo utiliza la observación inmediatamente anterior, basándose en la estimación de la distribución condicional obtenida a partir de toda la información disponible, el predictor lineal utiliza la misma información global para estimar la función de autocorrelación (que es más exacta que la estimación de la distribución condicional) y, basándose en ella, utiliza p observaciones anteriores para predecir el tráfico futuro. De hecho, es la cuantización vectorial del predictor de esperanza condicional la causante de esta diferencia, como se puede apreciar al comparar las figuras 11 y 15.
V. MODELO DE DISPERSIÓN BASADA EN H.
Una vez que se ha determinado la posibilidad de predecir el tráfico con suficiente grado de exactitud, surge la pregunta de cómo usar esta información para mejorar el desempeño de las redes de datos.
Varios autores proponen usar esta información para anticipar estados de congestión en la red, y tomar medidas correctivas. Aunque se encuentran diversos mecanismos de control de congestión en la literatura [15,16,17,18] escogimos el propuesto en [18] por cuestiones de espacio.
El predictor usado en este trabajo observa el nivel de tráfico de la red en el presente instante y supone que en el siguiente instante dicho nivel será aproximadamente el mismo. Este grado de aproximación se hace más exacto a medida que aumenta el valor H.
El control de congestión se hace por dispersión de tráfico. A manera de ilustración veamos la red propuesta en la figura 16. El nodo N0 (Nodo_Origen) se considera nodo generador de tráfico autosemejante, puede tomarse como el gateway de una red de datos, el nodo N4 es el destino de todos los paquetes, que pueden seguir la ruta N0-N1-N2-N4 (ruta primaria) o la ruta N0-N1-N3-N4 (ruta secundaria). La dispersión se realiza de la siguiente forma: los paquetes siguen la ruta primaria por defecto, cuando el tráfico entre N0-N1 excede cierto valor umbral, calculado como una función del tamaño del buffer primario y de H, el tráfico se dispersa a través del enlace secundario.
La función para el cálculo del umbral es:
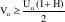
- Vn Nivel de tráfico observado durante el instante
Tn entre N0-N1 - Un Espacio disponible en buffer, en el instante n.
- H Parámetro de Hurst.
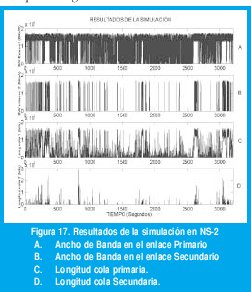
Es decir, si H fuera 1 (máxima autosemejanza) la ruta secundaria entraría en operación cada vez que el nivel de tráfico actual superara el espacio disponible en cola, si H fuera igual a 0.5 (tráfico no autosemejante) el mecanismo de dispersión funcionaría cada vez que el nivel actual de tráfico superara el 75% del espacio disponible en cola, según se muestra en la figura 17
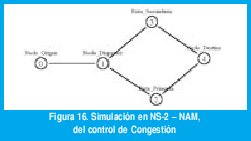

Para evaluar la efectividad del mecanismo de dispersión se realizó una simulación en NS-2 sobre la red de la figura 16, con un tiempo de simulación de 3200 segundos, una longitud máxima en cola primaria de 200Kbytes. La serie de datos que alimenta al nodo origen es la traza BC-89 de la que se habló con anterioridad. El parámetro H=0-86 de la serie BC se obtuvo por el estimador basado en Wavelets propuesto en [32]. El procedimiento de dispersión se efectuó cada 50mS. El enlace primario y el secundario tienen una velocidad T1. El enlace entre N0 y N1 es un enlace a 10 Mbps.
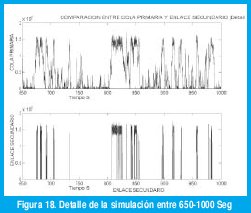
Las figuras 17 y 18 muestran algunos de los resultados de la simulación. La figura 18 muestra un detalle del proceso desde 650 hasta 1000 S. Puede notarse que efectivamente la activación del enlace secundario se anticipa a los periodos de mayor congestión de la cola primaria y la desactivación se produce también de manera anticipada cuando se predice que la congestión va a finalizar.
Estos resultados pueden contrastarse con los de la figura 4b, que muestra la longitud de la cola si la red sólo usara el enlace primario.
Puede concluirse que este método permite anticipar congestión, usando un estimador bastante sencillo. Sin embargo surge otra pregunta, cuál es la efectividad del método de dispersión del tráfico?, qué sucede con el enlace secundario?.
Para el efecto volvamos a las figuras 17 y 18. Observamos que el enlace secundario se ocupa al 100% durante los periodos de congestión en el enlace primario y que la cola secundaria alcanza una longitud que supera los valores máximos de la cola primaria. Es decir, al dispersar el trafico estamos dispersando la congestión también. Es lógico pensar que dispersar la congestión afectará dramáticamente el desempeño del enlace secundario y a los datos de otras fuentes que transitaran por este enlace. Gyires propone afrontar esta situación usando múltiples rutas de dispersión, de manera que el tráfico se enrute proporcionalmente sobre las trayectorias que tengan menor uso, sin embargo, Gyires no demuestra la efectividad de usar esta modificación. En un futuro trabajo evaluaremos este aspecto [31].
VI. CONCLUSIONES
Existen excelentes trabajos sobre la utilización de las propiedades de memoria de rango largo de los procesos estocásticos autosemejantes, todos ellos basados en modelos específicos tales como movimiento browniano fraccional [22], procesos fraccionales autoregresivos integrales de promedios móviles [26,29], etc. Sin embargo, aquí utilizamos sólo algunas estadísticas muestrales para hacer predicción de tráfico sin recurrir a modelos específicos, de acuerdo con los procedimientos usados en [14-17]. Puesto que el ajuste de trazas muestrales a modelos particulares es un proceso computacionalmente complejo debido a la lenta convergencia de los promedios muestrales bajo LRD, no es de esperarse que en un nodo de conmutación se haga ningún tipo de estimación paramétrica y, como se muestra en este artículo, tampoco sería necesario hacerla si el propósito es estimar el tráfico en el futuro inmediato.
En particular, la traza de tráfico seleccionada permite predicciones bastante precisas en un amplio rango de escalas de tiempo que incluye desde las fracciones de segundo hasta las decenas de segundos. En este rango no sólo se encuentran los «tiempos de ida-y-vuelta» (RTT) típicos de las redes modernas de comunicaciones, sino que podría corresponder a un rango de tiempo adecuado para tomar decisiones de ingeniería de tráfico tales como el reenrutamiento de flujos en MPLS para distribuir óptimamente la carga sobre los enlaces de la red.
Habiendo verificado la predecibilidad del tráfico en las redes modernas de comunicaciones, creemos que es posible explotar este conocimiento para mejorar los mecanismos actuales de control de congestión, de manera que las decisiones de regular la tasa de datos en las fuente de tráfico se tomen después de compensar el retardo con que llegan la información ofrecida por medidas indirectas tales como pérdida de paquetes o duplicidad de reconocimientos [14-17, 31]. Pero, más aún, creemos que es posible utilizar esta propiedad del tráfico para definir nuevas arquitecturas de gestión de red que sean capaces de operar en escalas de tiempo tan pequeñas como los milisegundos, pues en estas arquitecturas la predicción compensaría los retardos propios de la notificación de eventos. De esta manera la práctica común de proporcionar exceso de recursos al tráfico en tiempo real (overprovisioning) mientras se controla la tasa de datos del tráfico elástico, podría remplazarse por un método más eficiente que permita una mayor utilización del ancho de banda reservado para el tráfico en tiempo real. Actualmente trabajamos en estos conceptos [31].
REFERENCIAS
[1] R. Srikant. «Control of Communication Networks». In «Perspectives in Control Engineering», T. Samad, editor. IEEE Press, Piscataway, NJ, 2000.
[2] ] Sally Floyd and Van Jacobson. "Random Early Detection Gateways for Congestion Avoidance". IEEE/ACM Trans. On Networking, August 1993
[3] S. Athuraliya, V. H. Li, S. H. Low and Q. Yin. "REM: Active Queue Management", IEEE Network, May 2001.
[4] Wu-chang Feng, Dilip D. Kandlur, Debanjan Saha and Kang G. Shin. "BLUE: A New Class of Active Queue Management Algorithms", U. Michigan CSE-TR-387-99, April 1999.
[5] M. Arlitt and C. Williamson. "Internet Web Servers: workload characterization and performance implications", IEEE/ACM Trans. On networking, Vol.5, N. 5, 1997
[6] M. Crovella and A. Bestavros. "Self-similarity in WWW traffic: evidence and possible causes", IEEE/ACM Trans. On networking, Vol.5, N. 7, 1997
[7] A. Feldmann, A. Gilbert, P. Huang and W. Willinger. "Dynamics of IP Traffic: A study of the role of variability and the impact of control". Proceedings ACM SIGCOMM, 1999.
[8] M. Garret and W. Willinger. "Analysis, modeling and generation of self-similar VBR video traffic". Proceedings ACM SIGCOMM, 1994.
[9] W. Leland, M. Taqqu, W. Willinger and D. Wilson. "On the self- similar nature of Ethernet traffic", IEEE/ACM Trans. On networking, Vol.2, N. 1, 1994
[10] A. Feldmann. "Characteristic of TCP connection arrivals". In "Self- similar network traffic and performance evaluation", edited by K. Park and W. Willinger, John-Wiley and sons, 2000
[11] Marco Alzate, "Tráfico Autosimilar en Redes de Comunicaciones", Revista INGENIERIA Universidad Distrital, Vol.7 N. 1, 2002.
[12] M. Grossglauser and J. Bolot. «On the Relevance of long-range- dependence in network traffic», Proceedings ACM SIGCOMM, 1996.
[14] T. Tuan and K. Park. "Congestion control for self-similar network traffic". In "Self-similar network traffic and performance evaluation", edited by K. Park and W. Willinger, John-Wiley and sons, 2000
[15] G. He, Y. Gao J. Hou and K. Park. "A case for exploiting self- similarity of Internet traffic in TCP Congestion Control", Technical report, Department of Electrical Engineering, The Ohio State University, 2002
[16] Yuan Gao, Guanghui He and Jennifer Hou. "On Exploiting Traffic Predictability in Active Queue Management", IEEE Infocom 2002, New York, June 2002
[17] Yuan Gao, Guanghui He and Jennifer C. Hou. "On Leveraging Traffic Predictability in Active Queue Management", Technical report, Department of Electrical Engineering, The Ohio State University, 2002
[18] T. Gyires, "Using Active Networks for Congestion Control in High- Speed Networks with Self-Similar Traffic", IEEE Intl. Conf. On Systems, Man, and Cybernetics, 2000, Vol. 1
[19] Lawrence Berkley National Laboratory, The Internet Traffic Archive, http://ita.ee.lbl.gov/html/ contrib/BC.html, April 29, 2000.
[21] G.R.Grimmet and D.R. Stirzaker, "Probability and random processes", Oxford Science Publications, New York, 1992.
[22] G. Gripenberg and I. Norros. "On the Prediction of Fractional Brownian Motion", 1994 <http://citeseer.nj.nec.com/ gripenberg94prediction.html>
[23] Monson H. Hayes. "Statistical Digital Signal Processing and Modeling", John Wiley and Sons, New York, 1996.
[26] Rene K. Boel, Iven M.Y. Mareels and Matthew R. James, "Performance Comparison Of Adaptive And Robust Predictors For Long Range Dependent Signals", 39th International Conference on Decision and Control, Sydney, Australia, December 2000
[29] Fei Xue, "Modeling and Predicting LRD traffic with Farima Processes",
[30] José Félix Vega Stavro, " Acerca de la Aplicación del Efecto de Memoria a Largo Plazo en el Control de Congestión en Redes de Conmutación de Paquetes", Universidad Distrital, Maestría en Teleinformática, por publicar Agosto 2003.
[31] P Abry, D Veitch, Wavelet Analysis of LRD Traffic. IEE Transaction on Informatioin Theory, 1998.
Marco Aurelio Alzate Monroy
Ingeniero Electrónico de la Universidad Distrital en 1989 y Master en Ingeniería Electrica en la Universidad de los Andes 1991. Entre 1989 y 1992 fue docente-investigador en la División de Investigación del ITEC Telecom y luego se vinculó a la Facultad de Ingeniería de la Universidad Distrital donde actualmente se desempeña como profesor. En este momento adelanta su disertación doctoral en Ingeniería Electrica y de Computadores en la Universidad de Maryland USA
Jose Felix Vega Stavro
Ingeniero Electrónico de la Universidad Distrital en 1998. Fue asesor en el area de Telecomunicaiones del Ministerio de Agricultura entre 1998 y 2000. Coordinó el proyecto curricular de electrónica en la Universidad Pedagógica Nacional durante 2002. Actualmente se desempeña como docente en la Facultad de Ingeniería Electrónica de la Universidad Central y realiza su Tesis de Maestría en Teleinformática en la Universidad Distrital.
Creation date:
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.





2.jpg)










