DOI:
https://doi.org/10.14483/23448393.22697Published:
2024-09-17Issue:
Vol. 29 No. 3 (2024): September-DecemberSection:
EditorialSolving the Power Flow Problem in Transmission Networks Using Nonlinear complex-domain Modeling Via Julia Software
Keywords:
Complex-variable (en).Downloads
References
O. D. Montoya, C. A. Ramírez-Vanegas, and J. R. González-Granada, “Dynamic active and reactive power compensation in distribution networks using pv-statcoms: A tutorial using the julia software,” Res. Eng., vol. 21, p. 101876, Mar. 2024. https://doi.org/10.1016/j.rineng.2024.101876
X. Bai, H. Wei, K. Fujisawa, and Y. Wang, “Semidefinite programming for optimal power flow problems,” Int. J. Elec. Power Energy Sys., vol. 30, no. 6–7, pp. 383–392, Jul. 2008. https://doi.org/10.1016/j.ijepes.2007.12.003
A. Garcés-Ruiz, W. J. Gil-González, and O. D. Montoya-Giraldo, Introducción a la estabilidad de sistemas eléctricos de potencia. Pereira, Colombia: Universidad Tecnológica de Pereira, 2023. https://doi.org/10.22517/9789587228960
P. Anderson and A. Fouad, Power system control and stability. Piscataway, NJ: Wiley-Interscience, 2003. https://ieeexplore.ieee.org/servlet/opac?bknumber=5264012
J. Bezanson, A. Edelman, S. Karpinski, and V. B. Shah, “Julia: A fresh approach to numerical computing,” SIAM Rev., vol. 59, no. 1, pp. 65–98, 2017. https://doi.org/10.1137/141000671
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Solving the power flow problem for transmission grids is crucial for ensuring the reliable and efficient operation of electrical power systems. Power flow analysis allows engineers to determine the voltage, current, and power flow of a network, which is essential for maintaining system stability and avoiding overloads. Accurate power flow solutions help to identify potential issues such as voltage drops, line losses, and system inefficiency, enabling the proactive maintenance and optimization of the network. This analysis is vital for integrating renewable energy sources, as it ensures effective power distribution even under variable generation conditions. Ultimately, solving the power flow problem enhances the overall resilience, reliability, and economic performance of transmission networks, supporting a stable supply of electricity to consumers.
Complex-variable power flow modeling
For electrical systems, the power flow problem can be formulated as a reproduction complex-variable optimization model 1. This optimization problem takes right holder the following form:
Objective function:
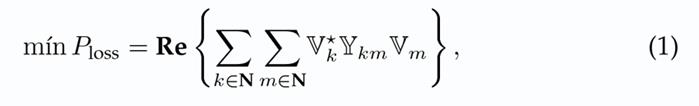
where P
loss represents the active power losses in the transmission system;
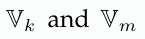correspond to the voltage variables in the complex domain that are assignable to nodes
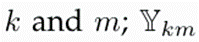; Y
km
is the component of the nodal admittance matrix that relates nodes k and m; and N represents the set that contains all the nodes in the system. Note that the operator
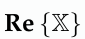obtains the real part of the complex variable
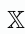, while the operator
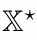obtains its complex conjugate.
Set of constraints:
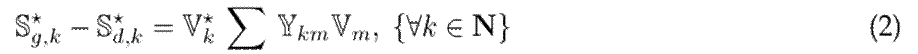
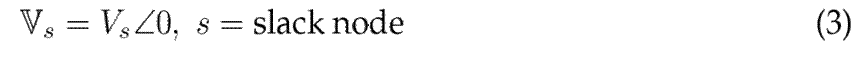
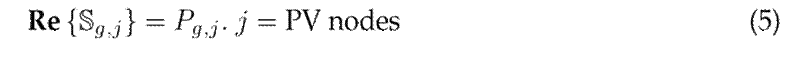
where
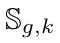corresponds to the complex power injected by the generator connected to node
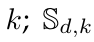represents the complex power demanded at node
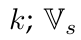denotes the complex voltage assigned to the slack node (reference bus), whose magnitude is V
s
; V
j
corresponds to the magnitude of the voltage assignable to the nodes; and P
g,j
is the active power assigned to these nodes.
It is important to mention that the formulation (1)-(5) can also represent the optimal power flow problem in the complex domain if the active power constraint assigned to the PV nodes is relaxed, allowing them to move within their maximum and minimum capacity limits 2.
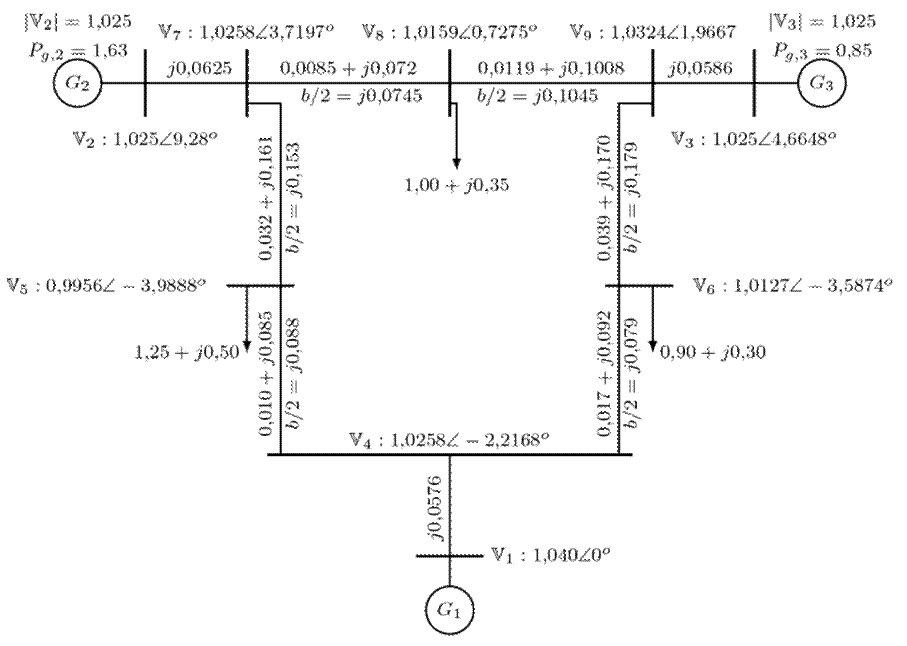
The IEEE-WSCC
To illustrate the solution to the power flow problem in transmission systems according to the formulation (1)-(5), consider the IEEE-WSCC (Western System Coordinating Council) system, whose impedance and nodal voltage data are shown in Fig. 1. Note that the data reported in this figure were obtained by applying the Newton-Raphson method 3.
Figure 1: IEEE-WSCC (adapted from4)
Julia software implementation
This section illustrates the computational implementation of the mathematical model 1)-(5 in the Julia software, using the Ipopt solver in the JuMP optimization environment 5.
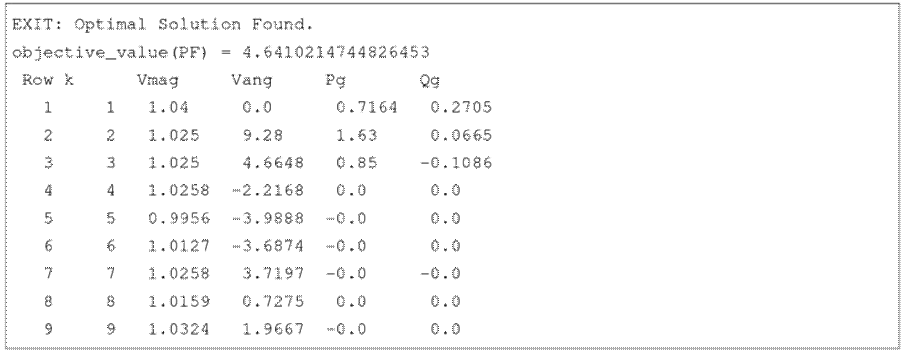
By executing this computational routine, the following results are obtained:
Thus, it is possible to note that:
-
The electrical variables, i.e., the magnitude and angle of the voltages at each of the buses, are equivalent to the solution obtained using the Newton-Raphson method (Fig. 1) 3.
-
Under the given operating conditions, the active power losses for this system amount to 4.6410 MW.
Remark 1. Suppose that the programmer is interested in solving the optimal power flow problem for transmission networks. In this scenario, the active power injection at the PV buses is left unconstrained, allowing the programmer to determine the optimal combination of these power inputs in order to minimize the total grid power losses.
Conclusion
This editorial note provides an easily implementable computational routine to deal with the power flow problem in transmission networks, which can be extended to any single-phase AC grid, using a complex-domain variable formulation. The solution to the power flow problem is obtained via the interior point optimizer (i.e., the Ipopt solver) available in Julia’s JuMP optimization environment. This routine is presented as a tutorial, using the IEEE-WSCC network to demonstrate that the power flow solution is equivalent to the solution reached with the classical Newton-Raphson method
Acknowledgements
Acknowledgment
This research received support from the Ibero-American Program of Science and Technology for Development (CYTED), through the thematic network 723RT0150, i.e., Red para la integración a gran escala de energías renovables en sistemas eléctricos (RIBIERSE-CYTED).
Referencias
License
Copyright (c) 2024 Oscar Danilo Montoya, Edwin Rivas-Trujillo, Walter Gil-Gonz´alez
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.
2.jpg)
