DOI:
https://doi.org/10.14483/23448393.15835Publicado:
2021-05-30Número:
Vol. 26 Núm. 2 (2021): Mayo-AgostoSección:
Ingeniería de SistemasA Metaheuristic Solution for the School Bus Routing Problem with Homogeneous Fleet and Bus Stop Selection
Palabras clave:
metaheurísticas, modelo de optimización, problema de planificación de rutas de autobuses escolares (es).Palabras clave:
metaheuristics, optimization model, school bus routing problem (en).Descargas
Referencias
R. Newton, and W. Thomas, “Design of school bus routes by computer”, Socio-Economic Planning Sciences, vol. 3, no. 1, pp. 75-85, 1969. https://doi.org/10.1016/0038-0121(69)90051-2 DOI: https://doi.org/10.1016/0038-0121(69)90051-2
L. Li, and Z. Fu, “The school bus routing problem: A case study”, Journal of the Operational Research Society, vol. 53, no. 5, pp. 552-558, 2002. https://doi.org/10.1057/palgrave.jors.2601341 DOI: https://doi.org/10.1057/palgrave.jors.2601341
F. Machado, D. Simões, S. Vieira, N. Ramos, “A mixed load capacitated rural school bus routing problem with heterogeneous fleet: Algorithms for the Brazilian context”, Expert Systems with Applications, vol. 56, pp. 320-334, 2016, https://doi.org/10.1016/j.eswa.2016.03.005 DOI: https://doi.org/10.1016/j.eswa.2016.03.005
M. Fonseca, J. Sarubbi, C. Silva, M. Porto, and N. Ramos, “A real geographical application for the school bus routing problem”, 17th International IEEE Conference on Intelligent Transportation Systems (ITSC), 2014. https://doi.org/10.1109/ITSC.2014.6958132 DOI: https://doi.org/10.1109/ITSC.2014.6958132
E. López y J. Romero, “Un aproximación híbrida de generación de columnas y agrupación para resolver el problema de ruteo de buses escolares con ventanas de tiempo”, Ingeniería, vol. 20, no. 1, pp. 111-127, 2015. http://dx.doi.org/10.14483/udistrital.jour.reving.2015.1.a07 DOI: https://doi.org/10.14483/udistrital.jour.reving.2015.1.a07
A. Bock, E. Grant, J. Könemann, and L. Sanità, “The school bus problem on trees”, Algorithmica, vol. 67, pp. 49-64, 2013. https://doi.org/10.1007/s00453-012-9711-x DOI: https://doi.org/10.1007/s00453-012-9711-x
D. Moura, R. de Camargo, S. Conceição, M. Porto, and N. Nunes, “A multi-loading school bus routing problem”, Expert Systems with Applications, vol. 101, pp. 228-242, 2018. https://doi.org/10.1016/j.eswa.2018.02.014 DOI: https://doi.org/10.1016/j.eswa.2018.02.014
E. Talbi, Metaheuristics: From Design to Implementation, John Wiley & Sons, Inc., 2009, p. 500.
J. Park, and B.-I. Kim, “The school bus routing problem: A review”, European Journal of Operational Research, vol. 202, no. 2, pp. 311-319, 2010. https://doi.org/10.1016/j.ejor.2009.05.017 DOI: https://doi.org/10.1016/j.ejor.2009.05.017
W. Ellegood, S. Solomon, J. North, and J. Campbell, “School bus routing problem: Contemporary trends and research directions”, Omega, vol. 95, 2020. https://doi.org/10.1016/j.omega.2019.03.014 DOI: https://doi.org/10.1016/j.omega.2019.03.014
J. Riera-Ledesma, and J. J. Salazar-González, “A column generation approach for a school bus routing problem with resource constraints”, Computers and Operations Research, vol. 40, no. 2, pp. 566-583, 2013. https://doi.org/10.1016/j.cor.2012.08.011 DOI: https://doi.org/10.1016/j.cor.2012.08.011
R. Bowerman, B. Hall, and P. Calamai, “A multi-objective optimization approach to urban school bus routing: Formulation and solution method”, Transportation Research Part A: Policy and Practice, vol. 29, no. 2, pp. 107- 123, 1995. https://doi.org/10.1016/0965-8564(94)E0006-U DOI: https://doi.org/10.1016/0965-8564(94)E0006-U
P. Schittekat, J. Kinable, K. Sörensen, M. Sevaux, F. Spieksma, and J. Springael, “A metaheuristic [1]for the school bus routing problem with bus stop selection”, European Journal of Operational Research, vol. 229, no. 2, pp. 518-528, 2013. https://doi.org/10.1016/j.ejor.2013.02.025 DOI: https://doi.org/10.1016/j.ejor.2013.02.025
X. Chen, Y. Kong, L. Dang, Y. Hou, and X. Ye, “Exact and metaheuristic approaches for a bi-objective school bus scheduling problem”, Plos One, vol. 10, no. 7, 2015. https://doi.org/10.1371/journal.pone.0132600 DOI: https://doi.org/10.1371/journal.pone.0132600
M. Spada, M. Bierlaire, and T. M. Liebling, “Decision-aiding methodology for the school bus routing and scheduling problem”, Transportation Science, vol. 39, no. 4, pp. 443-556, 2005. https://doi.org/10.1287/trsc.1040.0096 DOI: https://doi.org/10.1287/trsc.1040.0096
D.-S. Chen, H. A. Kallsen, H.-C. Chen, and V.-C. Tseng, “A bus routing system for rural school districts”, Computers & Industrial Engineering, vol. 19, no. 1-4, pp. 322-325, 1990. https://doi.org/10.1016/0360-8352(90)90131-5 DOI: https://doi.org/10.1016/0360-8352(90)90131-5
J. Kinable, F. Spieksma, and G. Vanden, “School bus routing: a column generation approach”, International Transactions in Operational Research, vol. 21, no. 3, pp. 453-478, 2014. https://doi.org/10.1111/itor.12080 DOI: https://doi.org/10.1111/itor.12080
S. Ezquerro, J. Moura, Á. Ibeas, and J. Benavente, “Optimization model for school transportation design based on economic and social efficiency”, Transport Policy, vol. 67, pp. 93-101, 2018. https://doi.org/10.1016/j.tranpol.2018.01.015 DOI: https://doi.org/10.1016/j.tranpol.2018.01.015
H. Caceres, R. Batta, and Q. He, “School bus routing with stochastic demand and duration constraints”, Transportation Science, vol. 51, no. 4, pp. 1031-1386, 2017. https://doi.org/10.1287/trsc.2016.0721 DOI: https://doi.org/10.1287/trsc.2016.0721
F. de Souza Lima, D. Pereira, S. da Conceição, and R. Camargo, “A multi-objective capacitated rural school bus routing problem with heterogeneous fleet and mixed loads”, 4OR-A Quarterly Journal of Operations Research, vol. 15, pp. 359-386, 2017. https://doi.org/10.1007/s10288-017-0340-8 DOI: https://doi.org/10.1007/s10288-017-0340-8
J. Pacheco, and R. Martí, “Tabu search for a multi-objective routing problem”, Journal of the Operational Research Society, vol. 57, no. 1, 2006. https://doi.org/10.1057/palgrave.jors.2601917 DOI: https://doi.org/10.1057/palgrave.jors.2601917
A. Corberán, E. Fernández, M. Laguna, and R. Martí, “Heuristic solutions to the problem of routing school buses with multiple objectives”, Journal of Operational Research Society, vol. 53, no. 4, 2002. https://doi.org/10.1057/palgrave.jors.2601324 DOI: https://doi.org/10.1057/palgrave.jors.2601324
L. Sales, C. Sousa, T. de Oliveira, and B. Athayde, “Memetic algorithm for the heterogeneous fleet school bus routing problem”, Journal of Urban Planning Development, vol. 144, no. 2, 2018. DOI: https://doi.org/10.1061/(ASCE)UP.1943-5444.0000454
J. Braca, J. Bramel, B. Posner, and D. Simchi-Levi, “A computerized approach to the New York Cityschool bus routing problem”, IIE Transactions, vol. 29, pp. 693-702, 1997. https://doi.org/10.1023/A:1018526202990 DOI: https://doi.org/10.1080/07408179708966379
G. Astorga, B. Crawford, R. Soto, E. Monfroy, J. García y E. Cortés, “Un enfoque de meta- optimización para resolver el problema de cobertura de conjunto”, Ingeniería, vol. 23, no. 3, pp. 274- 288, 2018. https://doi.org/10.14483/23448393.13247 DOI: https://doi.org/10.14483/23448393.13247
J. Fajardo, “Soft Computing en problemas de optimización dinámicos”, Tesis Doctoral, Universidad de Granada, Granada, 2016, http://hdl.handle.net/10481/42206
R. Lewis, K. Smith-Miles, and K. Phillips, “The school bus routing problem: An analysis and algorithm”, Brankovic L., Ryan J., Smyth W. (eds), Combinatorial Algorithm, vol. 10765, Springer, pp. 287- 298, 2018. https://doi.org/10.1007/978-3-319-78825-8_24 DOI: https://doi.org/10.1007/978-3-319-78825-8_24
E. Toro, A. Escobar, and M. Granada, “Literature review on the vehicle routing problem in the green transportation context”, Luna Azul, vol. 42, pp. 362-387, 2016. DOI: https://doi.org/10.17151/luaz.2016.42.21
D. H. Wolpert, and W. G. Macready, “No free lunch theorems for optimization”, IEEE Transactions on Evolutionary Computation, vol. 1, no. 1, pp. 67-82, 1997. https://doi.org/10.1109/4235.585893 DOI: https://doi.org/10.1109/4235.585893
J. Derrac, S. García, D. Molina, and F. Herrera, “A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms”, Swarm and Evolutionary Computation, vol. 1, no. 1, pp. 3-18, 2011. https://doi.org/10.1016/j.swevo.2011.02.002 DOI: https://doi.org/10.1016/j.swevo.2011.02.002
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Recibido: 23 de enero de 2020; Revisión recibida: 8 de septiembre de 2020; Aceptado: 8 de septiembre de 2020
Resumen
Contexto:
Los problemas de optimización permiten representar situaciones de la vida real, y con un método apropiado se puede llegar a una buena solución del problema. Conceptualmente, el problema bajo estudio se conoce como problema de planificación de ruta de autobuses escolares. El presente trabajo puede ser tomado como punto de partida para la creación de herramientas para este problema.
Método:
En este trabajo se diseñó e implementó un modelo matemático del problema basado en la literatura y se adaptó para su solución usando algoritmos metaheurísticos. Se implementaron tres operadores de mutación y un mecanismo de selección basado en pesos, según las mejoras que brindaba cada uno a la solución. Para evaluar los resultados, se realizó una comparación estadística con otra solución de la literatura a partir de la evaluación de 112 instancias del problema.
Resultados:
En la solución de las 112 instancias del problema se utilizaron los siguientes algoritmos: búsqueda tabú, variantes del escalador de colinas, recocido simulado y un portafolio de algoritmos que incluye a los anteriores. Los resultados reflejaron que el mejor comportamiento lo obtuvo el portafolio con resultados comparables a los de la literatura. Sin embargo, a medida que crece el número de instancias, los resultados tienden a empeorar.
Conclusiones:
Con esta investigación se obtuvo un modelo que permite representar el problema inicial, así como dos algoritmos para la búsqueda de soluciones utilizando metaheurísticas. Según los resultados obtenidos, los trabajos futuros deben encaminarse hacia nuevas formas de construcción de la solución inicial y la implementación de nuevos operadores de asignación y mutación.
Palabras clave:
metaheurísticas, modelo de optimización, problema de planificación de rutas de autobuses escolares..Abstract
Context:
Optimization problems allow representing real-life situations, and, with the right method, a good solution to a problem can be reached. Conceptually, the problem under study is known as the School Bus Routing Problem. This work can be taken as a starting point for the creation of tools for this problem.
Method:
In this work, a mathematical model based on the literature was designed and implemented, and it was adapted to be solved using metaheuristics. Three mutation operators and a selection mechanism based on weights were implemented according to the improvements that each of them offered to the solution. To evaluate the results, a statistical comparison was made with another solution in the literature based on the evaluation of 112 instances of the problem.
Results:
In the solution of the 112 instances of the problem, the following algorithms were used: the Tabu Search, Hill Climbing variants, Simulated Annealing, and an algorithm portfolio that includes the previous ones. The results showed that the best behavior was obtained by the portfolio, with results comparable to those in the literature. However, as the number of instances grows, the results tend to get worse.
Conclusions:
With this research, it was possible to obtain a model that represents the initial problem, as well as two algorithms for finding solutions by means of metaheuristics. According to the results obtained, future work should be directed towards new ways of building the initial solution and the implementation of new assignment operators.
Keywords:
metaheuristics, optimization model, school bus routing problem..Introducción
El problema de planificación de rutas de autobuses escolares (conocido como SBRP, por sus siglas en inglés School Bus Routing Problem) tiene su origen en escuelas que cuentan con una flota de autobuses y tienen un conjunto de estudiantes a los cuales se les debe brindar el servicio de transporte, puesto que la distancia entre sus casas y la escuela excede el límite superior que pueden caminar para llegar a la escuela. En el surgimiento de este problema la mayoría de las escuelas tenía que preparar la planificación de las rutas de autobuses manualmente. Esta actividad resulta costosa en cuanto al tiempo que consumía desempeñarla, además de que requería de talento administrativo por parte de la persona encargada de llevar a cabo esta tarea. Lo que traía consigo que la calidad del resultado final de la planificación estuviera directamente relacionada con la experiencia que tuviera el responsable de realizarla [1]. Con el crecimiento de la población, el aumento de la región que cubren las escuelas y por tanto el incremento de la cantidad de estudiantes que deben ser transportados, fue ganando mayor importancia el estudio de SBRP [1].
El SBRP ha sido objeto de estudio de disímiles investigaciones desde [1], la primera publicación que se conoce acerca del tema. El SBRP se considera un tipo de problema del conjunto de los problemas de planificación de rutas de vehículos (conocido como VRP por sus siglas en inglés) [2]. Además, ha sido aplicado en diferentes escenarios. Uno de estos se plasma en [3], en el cual se resuelve el problema de planificación de rutas de autobuses escolares en un área rural en Brasil y se cuenta con una flota con capacidad limitada. En el mismo se busca disminuir el costo y hacer el recorrido en un tiempo razonable. En [2] se hace un estudio para el desarrollo de un sistema para el servicio de transporte escolar de Hong Kong. El artículo plantea que en este territorio suman más de 600.000 los niños que cursan alguna enseñanza hasta primaria, y la mayoría de ellos utiliza el transporte escolar. En Brasil también, según el estudio realizado por [4], donde se propone una solución para optimizar el transporte de estudiantes usando un modelo SBRP. Para el problema presentado cuentan con 944 estudiantes, 23 escuelas y una red de caminos de toda la ciudad de Brasilia. En [5] se resuelve el problema para una aplicación real en un colegio de Bogotá, Colombia, con 600 estudiantes y 400 nodos localizados en área urbana y rural. En este artículo, se tiene en cuenta las ventanas de tiempo y se utiliza la generación de columnas como método de solución.
El objetivo de SBRP es planificar rutas de autobuses escolares para transportar los estudiantes desde una parada cercana a su casa hasta la escuela, siempre teniendo en cuenta que cada estudiante no debe caminar más que una distancia máxima definida [6].
El presente trabajo se plantea como problema de investigación, ¿cómo resolver el problema de planificación de rutas de autobuses escolares usando algoritmos metaheurísticos? Para dar respuesta al mismo, se propone un modelo que abarca la preparación de los datos, la selección de las paradas de los autobuses y la generación de las rutas de los autobuses. Es un modelo diseñado para problemas de flota homogénea, en el que la capacidad de los autobuses es la misma, se considera una sola escuela como origen y destino final de todos los estudiantes trasladados y no tiene en cuenta la transportación de estudiantes con tratamiento diferenciado. El objetivo del modelo de SBRP propuesto busca minimizar la distancia total recorrida por todos los autobuses, mientras que las restricciones que plantea van dirigidas a garantizar que:
-
Cada parada sea visitada como máximo solo una vez.
-
Cada estudiante pueda alcanzar la parada a la que fue asignado.
-
En cada ruta no se exceda la capacidad del autobús.
-
Cada parada a la que se asigna algún estudiante sea visitada por las rutas de autobuses una y solo una vez.
El valor práctico de este trabajo es la obtención de un modelo y una solución basada en metaheurísticas para el problema de planificación de ruta de autobuses escolares (SBRP). Además, proporciona una base para futuras investigaciones y soluciones que consideren nuevos aspectos de la realidad.
Este trabajo, aparte de presentar el modelo teórico, incluye los detalles de diseño e implementación de una solución metaheurística del mismo, así como un estudio experimental en más de 100 instancias de la literatura. Los resultados obtenidos permiten afirmar que la propuesta es competitiva con el estado del arte en este tema.
Problema de planificación de rutas de autobuses escolares
El problema de planificación de rutas de autobuses escolares es un problema clásico de optimización combinatoria [7]. Por su complejidad, se clasifica como NP-duro y es un tipo específico de los problemas de planificación de rutas de vehículos (VRP, por sus siglas en inglés) [6]. Este grupo tiene como característica que, a pesar de poder ser descrito fácilmente, es muy difícil de resolver. Esto se puede hacer a través de métodos matemáticos exactos, pero no se obtiene la mejor solución en un tiempo polinomial [8].
El SBRP brinda una planificación eficiente de rutas de autobuses escolares, en las que los autobuses deben recoger estudiantes en varias paradas y trasportarlos hasta la escuela que cada uno tiene designada. Para las soluciones que brinda el problema, se debe tener en cuenta el cumplimiento de restricciones que pueden ser de capacidad de los autobuses, del tiempo máximo que pueden estar los estudiantes viajando en el autobús o de los períodos de tiempo de las escuelas, entre otras [1], [4].
En [9] se define que SBRP se divide en cinco subproblemas: preparación de los datos, selección de las paradas de los autobuses, generación de las rutas de los autobuses, ajuste al horario del timbre escolar y programación de las rutas. Según [9], los dos últimos subproblemas del ajuste al horario del timbre escolar y la programación de las rutas son aplicables en casos en los que se debe tener en cuenta más de una escuela como destino final de los estudiantes.
Preparación de los datos: esta etapa prepara los datos para los procedimientos del resto de los subproblemas. En este subproblema son especificados los siguientes datos: estudiantes, paradas de autobuses, autobuses y matriz de costo de origen- destino (OD). Además, se define la red de caminos por los que pueden transitar los autobuses.
De cada estudiante se tiene la localización de la casa donde vive, la escuela a la que se dirige en problemas con múltiples destinos, y el tipo de estudiante en problemas en los que se tiene en cuenta la transportación de estudiantes de educación especial. De las escuelas se puede tener: localización, horario de entrada y salida de estudiantes y tiempo máximo de recorrido que pueden hacer los estudiantes. De los autobuses se incluye la localización de su origen y el tipo de autobús, además de saber la capacidad de cada uno de ellos para estudiantes generales y para estudiantes de educación especial. La matriz OD almacena el menor costo (tiempo, distancia, etc.) del desplazamiento entre cada par de nodos. En los nodos se incluyen las escuelas, la ubicación de los estudiantes y las paradas.
Selección de las paradas de los autobuses: en esta etapa de un problema de planificación de rutas de autobuses escolares corresponde hacer la selección de cuáles paradas se van a visitar y cómo se van a asignar todos los estudiantes entre las paradas seleccionadas. En los SBRP en entornos rurales normalmente cada estudiante es recogido en su casa, pero en entornos urbanos no se comporta de igual forma. En este último caso los estudiantes se dirigen a una parada de autobús a esperar ser recogidos por el mismo. Algunos problemas presentan restricciones de cuál debe ser la distancia máxima entre la casa de los estudiantes y la parada a la que fueron asignados. Los enfoques de las heurísticas de solución en esta etapa se dividen en tres estrategias [10]: la primera conocida como LAR (location-allocation-routing) [11], la segunda conocida como ARL (allocation-routing-location) [12] y la tercera conocida como LRA (location-routingallocation) [13].
La estrategia LAR primero determina el conjunto de paradas que van a ser visitadas por alguna de las rutas y ubica a todos los estudiantes en estas paradas; luego realiza la planificación de las rutas con las paradas previamente seleccionadas [9]. Por otra parte, la estrategia ARL comienza dividiendo en grupos los estudiantes, teniendo en cuenta no exceder la capacidad de los autobuses; luego realiza la selección de las paradas y se genera una ruta para cada grupo; finalmente se ubican los estudiantes en las paradas seleccionadas, teniendo en cuenta la restricción acerca de la distancia máxima entre la casa de los estudiantes y la parada a la que fueron asignados [9]. La estrategia LRA propone identificar en primer lugar el conjunto de paradas a las que cada estudiante puede llegar, luego planifica las rutas considerando solo las paradas del conjunto previamente definido, minimizando el costo total de ejecutar las rutas, y finalmente asigna los estudiantes a las paradas de autobuses seleccionadas [10].
Generación de las rutas de los autobuses: es un clásico problema de planificación de ruta de vehículos. El resultado final de esta etapa son las rutas confeccionadas. Para esto se pueden seguir dos enfoques. Uno plantea crear una gran ruta que incluya todas las paradas y luego se divide en rutas más pequeñas, cumpliendo con la restricción de capacidad de los ómnibus. El otro enfoque lo plantea en sentido contrario, divide a los estudiantes en grupos y planifica las rutas de forma tal que cada ruta responda a un grupo diferente, y todas deben cumplir con las restricciones del problema.
Existen algunos enfoques en los que los subproblemas se trabajan de manera independiente y secuencial, y esto es debido a la complejidad que puede tener el problema a resolver. En gran parte de la literatura solo se consideran para trabajar partes del problema SBRP [9]. Este trabajo plantea un modelo que, según las características que posee, solo abarca la preparación de los datos, la selección de las paradas de los autobuses y la generación de las rutas de los autobuses.
Características del problema
Cantidad de escuelas: el SBRP puede ser diseñado para satisfacer una o varias escuelas. Generalmente el problema se diseña para modelos con múltiples escuelas, pero existe un gran número de artículos en la literatura que lo modelan para una sola escuela. Algunos de los estudiados con estas características son [2], [13], [14].
Los problemas de una sola escuela son muy similares a los problemas clásicos de VRP, donde se planifica una ruta que comienza en el depósito, visita un conjunto de paradas o clientes, y finalmente regresa al depósito. En un modelo de múltiples escuelas, [15] propone dos enfoques, uno basado en las escuelas y otro basado en las casas. En el enfoque basado en las escuelas se planifica un conjunto de rutas para cada escuela, por tanto, un autobús solo recoge estudiantes de una escuela; y estas rutas deben ajustarse a los horarios de la escuela. El enfoque basado en las casas permite la recogida de estudiantes de diferentes escuelas en un mismo autobús y garantiza que todas las escuelas de los estudiantes recogidos sean visitadas. Este enfoque soporta la característica de carga mixta [15].
Área urbana o rural: el enfoque de solución para el SBRP puede ser diferente si el problema se desarrolla en un entorno urbano o rural. Se asume que, en entornos urbanos, los estudiantes deban recorrer cierta distancia para llegar desde sus casas a la parada donde toman el bus. Por otra parte, cuando el problema se desarrolla en entornos rurales, la cantidad de estudiantes a transportar es menor y los estudiantes son recogidos en sus hogares. Por tanto, en un entorno rural el paso de selección de las paradas y asignación de estudiantes a paradas se omite [9].
Algunos autores han planteado que, en entornos urbanos con alta densidad de estudiantes, la capacidad de los autobuses es agotada antes de que el tiempo máximo de estancia de los estudiantes en el autobús sea alcanzado [9]. Esto lleva a que [12] plantee que la restricción acerca del tiempo máximo que pueden estar los estudiantes en el autobús no sea fija para todos los problemas.
En [16] se plantea que los principales aspectos que hacen que se deban diseñar problemas diferentes para cada uno de estos entornos son: densidad de la población, distancia recorrida por ruta, cantidad de paradas por ruta, características de los caminos por los que deben transitar los ómnibus y depósitos donde los autobuses pasan la noche. Flota homogénea o heterogénea: una flota heterogénea es aquella en la que los ómnibus que la componen tienen diferentes características entre ellos. Estas pueden ser: capacidad, máximo de tiempo para una ruta y costo por unidad de distancia recorrida. Mientras que, en una flota homogénea, todos los autobuses son iguales y presentan los mismos valores para cada una de las características mencionadas anteriormente [9].
Por otro lado, la mayoría de los estudios asume que cada capacidad en el autobús es destinada a un solo estudiante. Pero en [12] se considera que esto puede variar para cada estudiante según el espacio que ocupe. Por ejemplo, si un estudiante cursa el primer grado de la primaria, ocupa dos tercios de una capacidad de la guagua. Y en estos casos la cantidad de estudiantes que puede recoger cada ómnibus varía dependiendo de las características de los estudiantes que debe recoger.
Función objetivo: la literatura estudiada muestra que los principales objetivos que se persiguen con el diseño de un SBRP son:
-
Minimizar la cantidad de autobuses: esto implica que, en cada ruta, la capacidad del autobús sea completada. De esta forma se garantiza que queden desocupados, y por tanto desaprovechados, la menor cantidad de capacidades posible [17], [18].
-
Minimizar el costo (distancia o tiempo) total recorrido: se trata de realizar la asignación de los estudiantes y la planificación de rutas de forma tal que se minimice la distancia total a recorrer o el tiempo que consumiría cumplir la planificación de rutas [13], [19].
-
Minimizar el tiempo o la distancia que están los estudiantes en el ómnibus: con esta función objetivo se trata de que desde que se monta un estudiante al autobús, hasta el lugar donde se debe bajar, el tiempo (o la distancia) debe ser el menor posible. Esto trata de evitar que los estudiantes hagan viajes muy largos [18], [20].
-
Minimizar la distancia que deben recorrer los estudiantes para alcanzar la parada a la que fueron asignados: se trata de ubicar a los estudiantes en paradas cercanas a sus hogares, de forma tal que cada mañana deban recorrer la menor distancia posible hasta alcanzar la parada [11].
-
Minimizar el tamaño máximo de la ruta: se busca que la distancia total recorrida por cada ómnibus, en una ruta, sea la menor posible; ya sea visitando menos paradas o visitando paradas cercanas entre sí [21], [22].
Algunos autores como [7], [18], [20], [23] combinan varios de estos objetivos con el fin de encontrar soluciones más apropiadas a entornos particulares y ofrecer un balance entre objetivos económicos y objetivos sociales.
Restricciones: para cada diseño del problema, y dependiendo de la(s) función(es) objetivo(s) que se proponga(n), se puede definir también un conjunto de restricciones. Estas restricciones deben ser garantizadas en la solución brindada. A continuación se muestra una lista con algunas de las restricciones más comunes.
-
Tiempo máximo de recorrido de los estudiantes sobre el ómnibus [7], [14].
-
Distancia máxima o tiempo máximo desde la casa de los estudiantes hasta alcanzar las paradas [19], [20].
-
Hora de recogida más temprana [24].
-
Mínimo de estudiantes para crear una ruta [11].
Los valores que definen cada una de estas restricciones resultan de la información brindada por el cliente que desea obtener una planificación de ruta en una situación específica. Estos valores pueden variar entre diferentes instancias.
Modelo matemático
En esta sección se presenta una formulación matemática del SBRP, que es diferente del presentado en [13], donde se había enfocado esto desde la visión de Programación Lineal Entera. Para poder aplicar el modelo diseñado a la planificación de rutas de autobuses escolares, el problema debe cumplir con las siguientes características:
-
Una sola escuela de origen y destino de todos los estudiantes.
-
Todos los estudiantes son iguales y ninguno requiere de tratamiento especial.
-
Todos los autobuses tienen igual capacidad de transportación y dicha capacidad es fija.
A continuación se presenta el modelo propuesto, el cual, aunque su base conceptual es similar a la formulación de programación entera presentada en [13], tiene un enfoque más orientado a su implementación y solución con un enfoque metaheurístico.
Variables de entrada:
c: capacidad de cada autobús
b: cantidad de autobuses
d: distancia máxima que pueden caminar los estudiantes
P: conjunto de posibles paradas
E: conjunto de estudiantes
C p : conjunto de vectores con pares de coordenadas de posibles paradas
contiene las coordenadas de la escuela
:
: coordenada x de la parada p
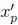
: coordenada y de la parada p
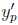
Ce: conjunto de vectores con pares de coordenadas de la casa de cada estudiante
: representa la coordenada x de la ubicación del estudiante e
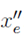
: representa la coordenada y de la ubicación del estudiante e
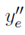
Variables intermedias:
C ij : matriz de costo entre cada par de paradas (i, j)
S pe matriz binaria. 1 si el estudiante e puede alcanzar la parada p y 0 en caso contrario
Se utiliza la fórmula de distancia euclidiana para el cálculo de la matriz de costo entre paradas, pero se puede sustituir por cualquier otra fórmula de distancia.
Variables de decisión:
R km : indica la parada que es visitada por la ruta k en orden m
Z e : indica la parada donde es recogido el estudiante e
La función objetivo (1) minimiza la distancia total recorrida por toda la flota de autobuses. Las ecuaciones (2), (3), (4) y (5) son restricciones que se deben cumplir para que la solución sea factible. La restricción (2) garantiza que cada parada sea visitada como máximo una sola vez, exceptuando la parada p 0 que representa la escuela, destino final de todos los autobuses. La restricción (3) asegura que cada estudiante pueda alcanzar la parada a la que fue asignado para tomar el autobús. La restricción (4) tiene en cuenta que en la ruta de cada autobús no se exceda la capacidad del mismo. La restricción (5) garantiza que cada parada, a la que se asigna al menos un estudiante, sea visitada por un autobús.
Función objetivo:
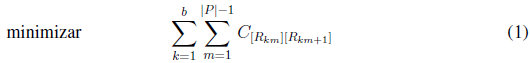
Restricciones:
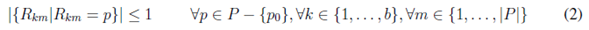

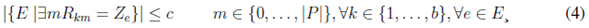
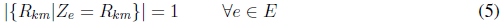
En este artículo se propone un nuevo modelo, y no se utiliza el mismo modelo propuesto en [13]. Esto se debe a que el modelo propuesto en [13] tiene una formulación de programación entera y por este motivo presenta una cantidad mayor de variables de decisión y una mayor cantidad de restricciones. Con el modelo planteado, muchas de las restricciones del modelo de [13] son garantizadas, quedando solo cuatro restricciones para el modelo propuesto.
Solución propuesta
Los algoritmos metaheurísticos son algoritmos aproximados que combinan métodos heurísticos a un nivel más alto para conseguir una exploración del espacio de búsqueda de forma eficiente y efectiva. Varios estudios han demostrado la habilidad de estos métodos para resolver problemas de optimización complejos en un tiempo computacional razonable [8]. Estos algoritmos acoplan procedimientos de mejora local y estrategias a nivel más alto, lo que los hace ser capaces de escapar de óptimos locales [25].
Los algoritmos metaheurísticos pueden ser clasificados según su trayectoria en dos grupos [8]: basados en un punto o algoritmos de trayectoria, y basados en poblaciones de puntos. Los algoritmos basados en una trayectoria son técnicas que parten de un punto inicial y van renovando la solución actual. Por otro lado, los algoritmos basados en poblaciones se caracterizan por trabajar con un conjunto de soluciones en cada iteración [8].
Para encontrar soluciones al modelo planteado, se utilizaron los siguientes algoritmos metaheurísticos basados en un punto, implementados en la biblioteca de algoritmos metaheurísticos Bi- CIAM [26]: escalador de colinas (EC), escalador de colinas con reinicio (ECR), escalador de colinas de mejor ascenso (ECMA), búsqueda aleatoria (BA), recocido simulado (RS), búsqueda tabú (BT) y portafolio de algoritmos (PA).
Implementación del modelo propuesto haciendo uso de BiCIAM: BiCIAM contiene el paquete problem.definition, conformado por las clases que abstraen el problema del algoritmo, permitiendo que sean empleadas para definir cualquier situación o problema. Por ello se implementaron las clases SBRP_Codification (hereda de Codification), SBRP_Model, SBRP_ObjectiveFunction (hereda de ObjectiveFunction), SBRP_Operator (hereda de Operator) y SBRP_Tester.
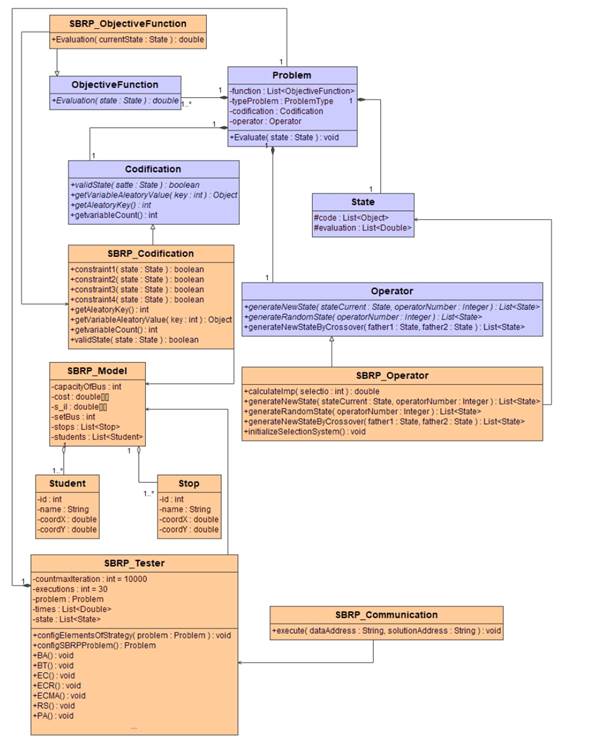
En la Figura 1 se ilustra el diagrama que refleja las clases definidas para la implementación del problema SBRP que hace uso de la biblioteca BiCIAM.
Figura 1: Diagrama de clases del SBRP
Se representan las clases principales del modelo del problema, con sus atributos y métodos más importantes. Las clases que se resaltan en morado son aquellas que pertenecen a la biblioteca BiCIAM.
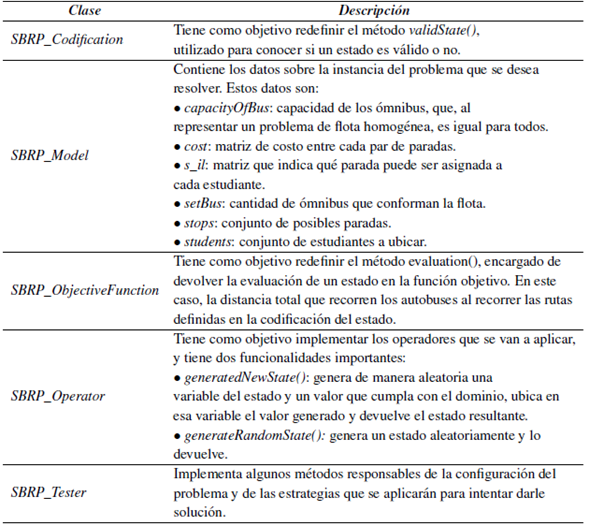
Las principales responsabilidades de estas clases se describen a continuación en la Tabla I.
Tabla I: Descripción de las clases del paquete problem.definition
Construcción de la solución inicial
La construcción de una solución para el problema planteado consta de dos pasos: la selección de las paradas y la asignación de los estudiantes, y la planificación de las rutas. En este caso, se siguió la estrategia LAR comentada anteriormente.
Construcción de la variable studentToStop: para realizar la asignación de los estudiantes a una parada del conjunto de posibles paradas se desarrollaron dos algoritmos: studentToRandomStop () y studentToFirstStop (). A continuación, se brinda una descripción de cada uno de estos métodos.
studentToRandomStop (). para cada estudiante se selecciona un conjunto de paradas
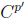 , donde
, donde
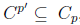 , que contiene las paradas a las que puede ser asignado el estudiante, cumpliendo con la restricción de distancia máxima entre su hogar y la parada. Finalmente se escoge la parada para el estudiante de forma aleatoria del conjunto
, que contiene las paradas a las que puede ser asignado el estudiante, cumpliendo con la restricción de distancia máxima entre su hogar y la parada. Finalmente se escoge la parada para el estudiante de forma aleatoria del conjunto
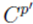 .
.
studentToRandomStop (). para cada estudiante se selecciona un conjunto de paradas
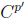 , donde
, donde
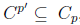 , que contiene las paradas a las que puede ser asignado el estudiante, cumpliendo con la restricción de distancia máxima entre su hogar y la parada. Finalmente se escoge la parada que ocupa la primera posición del conjunto
, que contiene las paradas a las que puede ser asignado el estudiante, cumpliendo con la restricción de distancia máxima entre su hogar y la parada. Finalmente se escoge la parada que ocupa la primera posición del conjunto
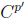 para ubicar al estudiante.
para ubicar al estudiante.
Para ambas formas de construcción inicial, en caso de que la parada seleccionada de forma aleatoria ya tenga asignado un número de estudiantes igual a la capacidad de los vehículos, se intenta insertar al estudiante en alguna de las otras paradas del conjunto
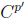 . Esto se realiza respetando el mismo orden que presenta el conjunto, y siempre garantizando que no se asignen a una parada más estudiantes de los que permite un vehículo.
. Esto se realiza respetando el mismo orden que presenta el conjunto, y siempre garantizando que no se asignen a una parada más estudiantes de los que permite un vehículo.
Construcción de la variable routes: para realizar la planificación de las rutas se propuso un único método, que lo hace de forma semialeatoria y garantiza el cumplimiento de las restricciones (2) y (3), llamado stopCompletingFirstRoute(). A continuación, se brinda una descripción del mismo.
stopCompletingFirstRoute(): por cada ruta se selecciona un conjunto de paradas
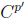 donde
donde
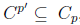 , que contiene todas aquellas paradas donde fue asignado al menos un estudiante y que contienen un número de estudiantes que aún pueden ser insertados a la ruta sin exceder la capacidad de los vehículos. Se van seleccionando de manera aleatoria las paradas para completar la ruta de dicho conjunto, y se va actualizando según la disponibilidad de la capacidad de la ruta. Una vez que el conjunto esté vacío, se debe crear una nueva ruta, la cual se llena siguiendo el mismo procedimiento. Si al satisfacer la capacidad de la última ruta, aún quedan paradas por ubicar, se incorporan en esta ruta y la solución generada no resulta factible.
, que contiene todas aquellas paradas donde fue asignado al menos un estudiante y que contienen un número de estudiantes que aún pueden ser insertados a la ruta sin exceder la capacidad de los vehículos. Se van seleccionando de manera aleatoria las paradas para completar la ruta de dicho conjunto, y se va actualizando según la disponibilidad de la capacidad de la ruta. Una vez que el conjunto esté vacío, se debe crear una nueva ruta, la cual se llena siguiendo el mismo procedimiento. Si al satisfacer la capacidad de la última ruta, aún quedan paradas por ubicar, se incorporan en esta ruta y la solución generada no resulta factible.
Operadores de mutación
Muchas de las variantes de VRP utilizan combinaciones de operadores de vecindad para las habituales búsquedas locales. Los operadores que se combinan pueden introducir cambios en una sola ruta o entre varias de ellas [27]. En el SBRP, como variante de VRP, también es posible aplicar este tipo de operadores.
Para la búsqueda de vecindad fueron implementados los siguientes operadores:
Operador Swap [27]: intercambia dos puntos de recogida de estudiantes. Los puntos de recogida pueden ser seleccionados de una misma ruta [28], o de diferentes rutas [20]. Para implementarlo se seleccionan aleatoriamente dos rutas, R1 y R2, y de cada una de ellas se selecciona aleatoriamente un nodo. Finalmente se intercambian los puntos de recogida obtenidos p 1i y p 2j . Si R1 y R2 son iguales, el cambio realizado involucrará solo una ruta; de otro modo el intercambio será entre dos rutas.
Operador Two-Opt [27]: El resultado de la aplicación de este operador es el intercambio de una subcadena en una ruta. Para la implementación del mismo, inicialmente se escoge de manera aleatoria una ruta R. Luego se seleccionan aleatoriamente dos nodos de la ruta escogida,
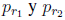 , de forma tal que
, de forma tal que
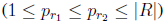 . Finalmente se invierte la cadena
. Finalmente se invierte la cadena
 perteneciente a R.
perteneciente a R.
Operador Section Swap [27]: el objetivo de aplicar este operador es intercambiar dos subcadenas de nodos. Ambas subcadenas tendrán igual tamaño. Para la implementación del operador inicialmente se seleccionan aleatoriamente dos rutas, R
1
y R
2
, garantizando que
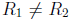 . Luego se selecciona de forma aleatoria la longitud de las subcadenas, teniendo en cuenta que no deben exceder el tamaño de las rutas previamente escogidas. Posteriormente se define en qué posición comenzará la subcadena en cada una de las rutas. Finalmente se intercambia cada uno de los elementos entre ambas subcadenas.
. Luego se selecciona de forma aleatoria la longitud de las subcadenas, teniendo en cuenta que no deben exceder el tamaño de las rutas previamente escogidas. Posteriormente se define en qué posición comenzará la subcadena en cada una de las rutas. Finalmente se intercambia cada uno de los elementos entre ambas subcadenas.
Mecanismo de selección de los operadores
Para la búsqueda local, se aplica un mecanismo que sigue la idea de un sistema clasificador o un portafolio de algoritmos [26], los cuales son “adaptativos”, ya que su capacidad de elegir la mejor acción mejora con la experiencia. Cada operador tiene un peso, y la probabilidad de selección en cada iteración es directamente proporcional a este peso. En cada iteración es seleccionado uno de ellos por probabilidades, y en función del resultado que se obtenga se realizan dos operaciones: se penaliza al operador seleccionado por su utilización, y se premia si obtuvo una mejor solución que la anterior. Con estas operaciones, van siendo modificados los pesos, y por tanto las probabilidades de selección. Siendo en cada iteración más propensa la probabilidad de seleccionar un operador que logra mejoras que otro que no mejora la solución. La función aplicada para actualizar los pesos es la siguiente:
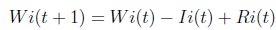
donde:
W i (t + 1) es el peso de la regla en la próxima iteración
W i (t) es el peso actual de la regla
I i (t) es el impuesto que se le cobra a la regla por activarse. t representa el instante de tiempo actual
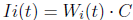
C es la constante de impuesto, con valor entre 0 y 1
Ri(t) es la recompensa que se le da a la regla por su respuesta, 0 si la respuesta es peor que la anterior y Rec si es correcta, donde Rec es una constante positiva, de tal forma que la calidad de la regla varíe de acuerdo a su respuesta.
Para el problema, se definieron los siguientes valores:

Experimentación
Descripción del conjunto de instancias de prueba
En una reciente revisión del estado del arte en este problema se reconoce que son escasas las instancias de prueba que se usan para comparar las soluciones al problema [10]. Los experimentos que aquí se presentan son realizados sobre un conjunto de 112 instancias generadas en [13], que son las que pudieron obtenerse a partir de solicitudes a los autores. Las instancias van desde las más simples con cinco paradas y 25 estudiantes a las más complejas donde se deben ubicar 800 estudiantes en 80 paradas. Las instancias tienen una flota homogénea que puede ser de ómnibus de capacidad de 25 o 50. Es considerado como parámetro de cada instancia el valor de la distancia que se corresponde al máximo que puede ser recorrido por los estudiantes hasta llegar a la parada.
A continuación, la Tabla II muestra de forma resumida las características de las instancias del conjunto de prueba con los valores que pueden tomar.
Tabla II: Características del conjunto de instancias de prueba

Análisis de los resultados
Según el teorema No Free Lunch (NFL, por sus siglas en inglés) planteado en [29], no existe ningún algoritmo de optimización que sea mejor que otro sobre la totalidad de los problemas. NFL plantea que, aplicando los algoritmos de búsqueda a todos los tipos de problemas existentes, todos tienen similar comportamiento en promedio. Debido a esto, se optó por experimentar con varios algoritmos y realizar pruebas no paramétricas para comparar sus resultados, utilizando la prueba estadística de Friedman para conocer si presentan diferencias significativas entre ellos para este problema.
En una primera experimentación se compararon varios algoritmos metaheurísticos para encontrar los que mejor funcionan en este problema. Se experimentó con los siguientes algoritmos: EC, ECR, ECMA, BA, RS, BT, PA. El PA se aplica con la combinación de los siguientes algoritmos: EC, ECR, BA, RSC y BT. Se realizaron, para todos los algoritmos, 30 ejecuciones con 10.000 iteraciones, a partir de la generación de una solución inicial. Para esta experimentación se utilizaron 40 instancias, seleccionadas de manera aleatoria del conjunto de instancias descritas previamente. Cada uno de los algoritmos se probó con las dos formas de construcción inicial para la asignación de estudiantes descritas anteriormente: Random (studentToRandomStop()) y FirstStop (studentToFirstStop()). Se aplicó el test de Friedman [30] para comparar los resultados.
Teniendo en cuenta los resultados del test de Friedman, se puede concluir que la aplicación del portafolio de algoritmos con el método FirstStop para la asignación inicial de los estudiantes a las paradas es el algoritmo que mejores resultados obtiene según el ranking de Friedman (ranking promedio de 4,175) y p-valor de Friedman menor que 0,05, indicando que hay diferencias significativas entre los algoritmos del experimento. A pesar de lo mencionado, se puede observar que los algoritmos ECMA_FS, ECR_FS, EC_FS, BA_FS presentan en los análisis de los post hoc [30], valores de p_valor≥0,05, lo que indica que no presentan diferencias significativas en los resultados obtenidos del portafolio respecto a estos, para un nivel de significancia de α = 0,05.
Además, se puede afirmar que, en promedio, los algoritmos obtienen mejores resultados cuando la asignación inicial de los estudiantes a las paradas se realiza con el método FirstStop previamente descrito, en lugar de aplicar el método Random.
Luego de este análisis se pasó a otra experimentación. En este caso fueron ejecutados los algoritmos que obtuvieron mejores resultados (portafolio de algoritmos y escalador de colinas con mejor ascenso) para cada una de las instancias del conjunto descrito, para ser comparados con el estado de arte en el tema [13]. A continuación, la Tabla III muestra los resultados obtenidos por los algoritmos PA y ECMA. Ambos algoritmos ejecutados con la forma de construcción inicial propuesta en la sección anterior. La tercera columna de la tabla, identificada como MH muestra los resultados obtenidos por [13] con una metaheurística GRASP+VND para las instancias utilizadas.
Tabla III: Resultados del análisis
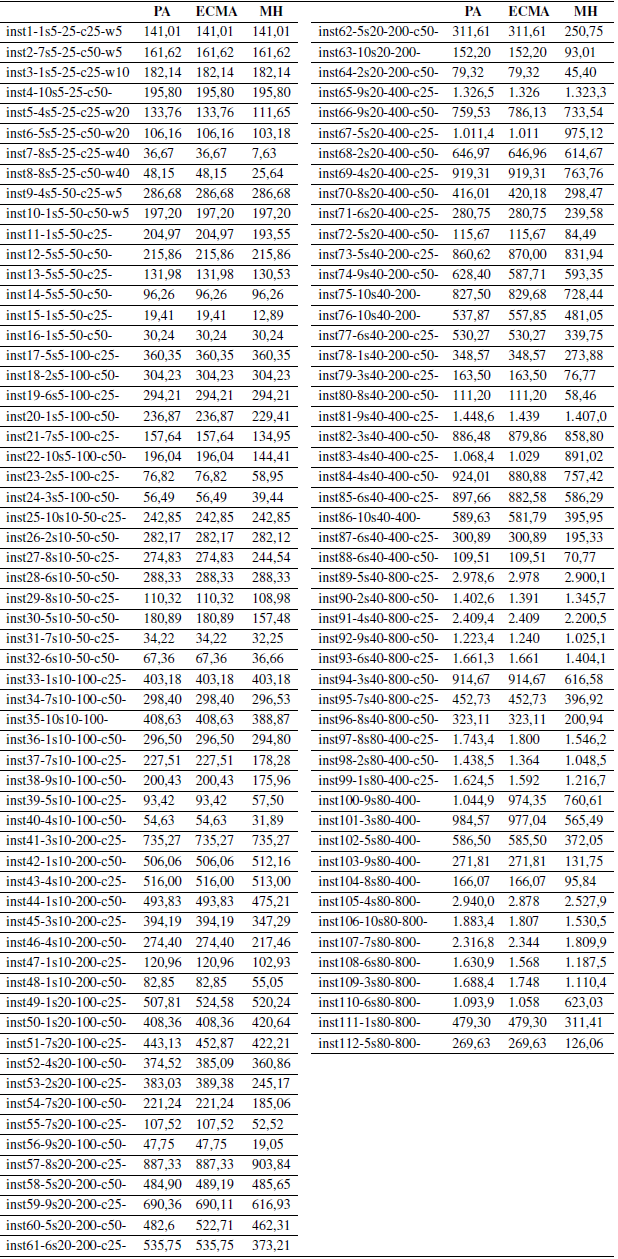
En un análisis de los resultados plasmados en la Tabla III, se puede apreciar que en la mayoría de los casos, los dos algoritmos propuestos en este trabajo obtienen la misma solución, ratificando el resultado obtenido con el Test de Friedman, según el cual ambos algoritmos no presentaban diferencias significativas en los resultados. También es posible apreciar que solo en un 14,2% de las instancias, los algoritmos propuestos alcanzan el mejor valor conocido obtenido en [13]. Como resultado positivo, en un 5,3% de las instancias se obtuvieron resultados mejores que los obtenidos en la fuente previamente mencionada. Es decir, para estas instancias, las soluciones obtenidas en este trabajo no habían sido obtenidas antes con metaheurísticas.
Es importante destacar que los algoritmos propuestos son competitivos respecto al algoritmo planteado en [13], en las instancias en las cuales la distancia máxima que pueden caminar los estudiantes es 5, el menor valor para esta característica en el conjunto de instancias evaluado. Para las instancias en las que esta característica tiene valor 40, se obtienen soluciones hasta dos veces mayores que las obtenidas en [13]. Esto se debe a que en este trabajo no se consideraron operadores que actúen sobre la estructura que representa la asignación de estudiantes a paradas, lo cual indica hacia dónde se debe enfocar la investigación en trabajos futuros. La inclusión de estos nuevos operadores no resultaría una tarea compleja, debido al diseño de la solución, incluido el uso de la biblioteca de clases BiCIAM, mencionada anteriormente.
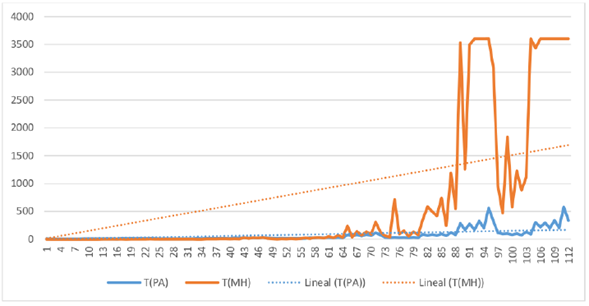
Al hacer un análisis de los tiempos de ejecución de cada uno de los algoritmos, en la Figura 2, se puede apreciar que para las instancias de menor complejidad, aquellas donde la cantidad de paradas es menor que 20 y la cantidad de estudiantes menos que 100, los tiempos de la solución propuesta son más altos que los tiempos del algoritmo de la literatura, aunque la diferencia nunca llega a superar los 20 segundos. Para las instancias de mayor complejidad, aquellas con la cantidad de paradas mayor o igual a 20 y la cantidad de estudiantes mayor o igual a 200, es importante destacar que el algoritmo propuesto obtiene los resultados en tiempos mucho menores que los obtenidos en [13]. El tiempo máximo para obtener resultados en [13] es de una hora (3.600 segundos), mientras que, con la solución propuesta, el tiempo máximo que demora es alrededor de diez minutos. Disminución importante en cuanto al rendimiento de los algoritmos.
Figura 2.: Tiempos de ejecución, en segundos, en las 112 instancias para los algoritmos MH y PA
Por otra parte, el tiempo promedio de diferencia cuando MH es más rápido que PA es de aproximadamente 8 segundos, mientras que el promedio de la diferencia cuando PA es más rápido que MH es de aproximadamente 1,180 segundos (20 minutos). Esto implica que, a mayor complejidad del problema, la solución propuesta logra ahorrar más, llegando a ser diez veces más rápida en varias de estas instancias. Esto resulta muy conveniente cuando se desean utilizar estos algoritmos en aplicaciones prácticas.
En general, los resultados experimentales muestran algunas de las bondades de la solución propuesta:
-
Los resultados obtenidos en seis instancias son los mejores reportados con metaheurísticas y en 16 instancias se igualan las mejores referencias, lo cual muestra que el enfoque es eficaz. De las seis instancias en las que se supera la mejor solución obtenida con metaheurísticas, en una se alcanza el óptimo, mientras que en las restantes cinco los resultados alcanzados pasan a ser referencia para futuras investigaciones.
-
El tiempo de solución del enfoque propuesto es significativamente superior a los previamente reportados en un porcentaje alto de las instancias, y no existen instancias en las que el tiempo de la propuesta sea sustancialmente peor, lo cual demuestra la eficiencia del enfoque propuesto.
-
Se lograron identificar las características de las instancias en las cuales deben enfocarse las mejoras futuras (distancia máxima a caminar por los estudiantes).
-
Al presentarse el diseño flexible de la solución con los artefactos adecuados de lenguaje unificado de modelado (UML, por su sigla en inglés, Unified Modeling Language) permite que estos resultados puedan ser aplicados, reutilizados y mejorados en futuras investigaciones. Por ejemplo, permite de manera simple la inclusión de nuevos operadores que mejoren la eficacia del algoritmo en las instancias que así lo requieran.
Conclusiones y trabajos futuros
En este trabajo se han cumplido con los objetivos propuestos. Se hizo un estudio del estado del arte donde se consultó la literatura principal sobre el problema de planificación de rutas de autobuses escolares (SBRP), y las diferentes variantes para su aplicación. En dicho estudio se puede constatar que el SBRP tiene un amplio campo de aplicación gracias a su flexibilidad y la gran cantidad de variaciones que soporta para ajustarse a muchas situaciones de la vida real. Además, se puede concluir que:
-
El modelo propuesto permite representar el problema y encontrar soluciones para el mismo a través de los algoritmos desarrollados, lo que se puede comprobar a partir de los resultados descritos.
-
La implementación de este modelo, y los algoritmos correspondientes, se simplificó en gran medida, tanto en tiempo como en dificultad de implementación, gracias a la utilización de la biblioteca BiCIAM, la cual aporta un conjunto de funcionalidades reutilizables con este objetivo y permite la utilización de las metaheurísticas ya implementadas.
-
Tanto las metaheurísticas utilizadas, portafolio de algoritmos y escalador de colinas con mejor ascenso, heredadas de BiCIAM, como los operadores desarrollados fueron sencillas de implementar y poseen tiempos de ejecución adecuados en la obtención de los resultados descritos. La utilización de un mecanismo de selección de operadores de mutación, tipo portafolio y basado en una estrategia de penalización-premio, permite que la búsqueda sea dirigida en cada iteración hacia mejores soluciones.
-
Partiendo de los resultados de la literatura en 16 instancias que representan el 14,2% del total se igualaron los resultados obtenidos, mientras que en 6 que representan el 5,3% del total, los resultados aquí alcanzados fueron superiores. Estos porcentajes indican que, a pesar de que es necesario hacer ajustes y mejoras a los algoritmos desarrollados, para algunas instancias es posible obtener buenos resultados.
-
Los resultados alcanzados con los algoritmos propuestos son más competitivos con respecto a la calidad de la solución, en instancias donde la distancia máxima a caminar por losestudiantes tiene su menor valor (5), mientras que los peores resultados se alcanzan cuando esta distancia tiene el mayor valor del conjunto (40).
-
Desde el punto de vista del tiempo de ejecución, en sentido general, la propuesta obtiene muy buenos resultados. Mientras que para instancias de complejidad relativamente simple se obtienen tiempos comparativamente similares, para instancias de gran complejidad, la propuesta ofrece mejores tiempos que los algoritmos de la literatura analizados.
Teniendo en cuenta los resultados y estas conclusiones, el trabajo futuro en esta línea de investigación debe enfocarse en mejorar aún más la calidad de las soluciones obtenidas, para lo cual es necesario implementar estrategias de reparación para las soluciones no factibles, lo que disminuiría notablemente la cantidad de soluciones no factibles exploradas. Asimismo, implementar operadores que actúen sobre la estructura que representa la asignación de estudiantes a paradas, debido a que esto llevaría a un mayor espacio de soluciones, en el cual pudieran existir mejores resultados que los obtenidos. Por último, llevar a cabo la solución del modelo planteado a partir de metaheurísticas poblacionales, pues son de las más utilizadas en la literatura y pueden aportar mejores resultados.
Referencias
Licencia
Derechos de autor 2021 Ana Camila Pérez Pérez, Eduardo, Alejandro Rosete

Esta obra está bajo una licencia internacional Creative Commons Atribución-NoComercial-CompartirIgual 4.0.
A partir de la edición del V23N3 del año 2018 hacia adelante, se cambia la Licencia Creative Commons “Atribución—No Comercial – Sin Obra Derivada” a la siguiente:
Atribución - No Comercial – Compartir igual: esta licencia permite a otros distribuir, remezclar, retocar, y crear a partir de tu obra de modo no comercial, siempre y cuando te den crédito y licencien sus nuevas creaciones bajo las mismas condiciones.

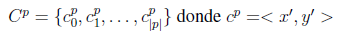
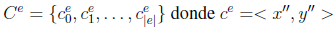
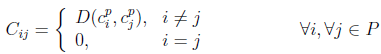
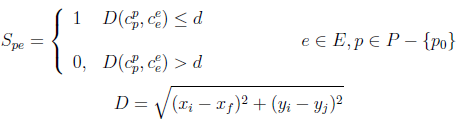



2.jpg)