DOI:
https://doi.org/10.14483/23448393.19303Publicado:
2022-08-12Número:
Vol. 27 Núm. 3 (2022): Septiembre-diciembreSección:
Ingeniería Eléctrica y ElectrónicaSelección óptima de conductores en redes de distribución trifásicas utilizando el algoritmo metaheurístico de Newton
Optimal Selection of Conductors in Three-Phase Distribution Networks using the Newton Metaheuristic Algorithm
Palabras clave:
Algoritmo metaheurístico de Newton, redes de distribución trifásicas, sistemas eléctricos desbalanceados, flujo de potencia trifásico, selección óptima de conductores, optimización combinatorial (es).Palabras clave:
Newton’s metaheuristic algorithm, three-phase distribution networks, unbalanced electrical systems, three-phase power flow, optimal selection of conductors, combinatorial optimization (en).Descargas
Referencias
S. A. A. Kazmi, M. K. Shahzad, A. Z. Khan, and D. R. Shin, “Smart Distribution Networks: A Review of
Modern Distribution Concepts from a Planning Perspective,” Energies, vol. 10, p. 501, apr 2017.
D.-A. Ramirez, A. Garces, and J.-J. Mora-Fl ´ orez, “A Convex Approximation for the Tertiary Control of Unbalanced Microgrids,” Electric Power Systems Research, vol. 199, p. 107423, oct 2021.
A. Garces, “A Linear Three-Phase Load Flow for Power Distribution Systems,” IEEE Transactions on Power Systems, vol. 31, pp. 827–828, jan 2016.
C. Acosta, R. A. Hincapie, M. Granada, A. H. Escobar, and R. A. Gallego, “An Efficient Three Phase Four Wire ´
Radial Power Flow Including Neutral-Earth Effect,” Journal of Control, Automation and Electrical Systems,
vol. 24, pp. 690–701, may 2013.
G. Bakkabulindi, M. R. Hesamzadeh, M. Amelin, and I. P. D. Silva, “Models for conductor size selection in
single wire earth return distribution networks,” in 2013 Africon, IEEE, sep 2013.
M. A. Farrag, A. H. Khalil, and S. Omran, “Optimal conductor selection and capacitor placement in radial distribution system using nonlinear AC load flow equations and dynamic load model,” International Transactions
on Electrical Energy Systems, vol. 30, feb 2020.
S. M. Ismael, S. H. E. A. Aleem, and A. Y. Abdelaziz, “Optimal selection of conductors in Egyptian radial
distribution systems using sine-cosine optimization algorithm,” in 2017 Nineteenth International Middle East
Power Systems Conference (MEPCON), IEEE, dec 2017.
J. F. Mart´ınez-Gil, N. A. Moyano-Garc´ıa, O. D. Montoya, and J. A. Alarcon-Villamil, “Optimal Selection of
Conductors in Three-Phase Distribution Networks Using a Discrete Version of the Vortex Search Algorithm,”
Computation, vol. 9, p. 80, jul 2021.
O. D. Montoya, A. Garces, and C. A. Castro, “Optimal Conductor Size Selection in Radial Distribution Networks
Using a Mixed-Integer Non-Linear Programming Formulation,” IEEE Latin America Transactions, vol. 16,
pp. 2213–2220, aug 2018.
I. Osman, M. A. Rahman, A. R. Mahbub, and A. Haque, “Benefits of optimal size conductor in transmission
system,” in 2014 International Conference on Advances in Electrical Engineering (ICAEE), IEEE, jan 2014.
O. D. Montoya, A. Grajales, and R. A. Hincapie, “Selecci ´ on´ optima de conductores en sistemas de distribuci ´ on´
empleando el algoritmo busqueda tab ´ u,” ´ Ingeniare. Revista chilena de ingenier´ıa, vol. 26, pp. 283–295, jun
H. Falaghi, M. Ramezani, M.-R. Haghifam, and K. Milani, “Optimal selection of conductors in radial distribution
systems with time varying load,” in 18th International Conference and Exhibition on Electricity Distribution
(CIRED 2005), IEE, 2005.
S. Gholizadeh, M. Danesh, and C. Gheyratmand, “A new Newton metaheuristic algorithm for discrete
performance-based design optimization of steel moment frames,” Computers & Structures, vol. 234, p. 106250,
jul 2020.
M. R. Raju, K. V. S. R. Murthy, K. Ravindra, and R. S. Rao, “Optimal conductor selection for agricultural
distribution system - a case study,” in 2010 International Conference on Intelligent and Advanced Systems,
IEEE, jun 2010.
D. Joshi, S. Burada, and K. D. Mistry, “Distribution system planning with optimal conductor selection,” in 2017
Recent Developments in Control, Automation & Power Engineering (RDCAPE), IEEE, oct 2017.
S. Manikandan, S. Sasitharan, J. V. Rao, and V. Moorthy, “Analysis of optimal conductor selection for radial
distribution systems using DPSO,” in 2016 3rd International Conference on Electrical Energy Systems (ICEES), IEEE, mar 2016.
P. Samal, S. Mohanty, and S. Ganguly, “Simultaneous capacitor allocation and conductor sizing in unbalanced
radial distribution systems using differential evolution algorithm,” in 2016 National Power Systems Conference
(NPSC), IEEE, dec 2016.
S. M. Ismael, S. H. E. A. Aleem, A. Y. Abdelaziz, and A. F. Zobaa, “Practical Considerations for Optimal
Conductor Reinforcement and Hosting Capacity Enhancement in Radial Distribution Systems,” IEEE Access,
vol. 6, pp. 27268–27277, 2018.
M. Kumari and R.Ranjan, “Economical Selection of Conductor in Radial Distribution System using PSO,”
Journal of The Institution of Engineers (India): Series B, apr 2022.
T. M. Khalil and A. V. Gorpinich, “Optimal conductor selection and capacitor placement for loss reduction of
radial distribution systems by selective particle swarm optimization,” in 2012 Seventh International Conference
on Computer Engineering & Systems (ICCES), IEEE, nov 2012.
R. S. Rao, K. Satish, and S. V. L. Narasimham, “Optimal Conductor Size Selection in Distribution Systems
Using the Harmony Search Algorithm with a Differential Operator,” Electric Power Components and Systems,
vol. 40, pp. 41–56, nov 2011.
M. Thenepalle, “A comparative study on optimal conductor selection for radial distribution network using conventional and genetic algorithm approach,” International Journal of Computer Applications, vol. 17, pp. 6–13,
mar 2011.
M. Legha, H. Javaheri, and M. Legha, “Optimal Conductor Selection in Radial Distribution Systems for Productivity Improvement Using Genetic Algorithm,” Iraqi Journal for Electrical and Electronic Engineering, vol. 9,
pp. 29–35, jun 2013.
A. Y. Abdelaziz and A. Fathy, “A novel approach based on crow search algorithm for optimal selection of
conductor size in radial distribution networks,” Engineering Science and Technology, an International Journal,
vol. 20, pp. 391–402, apr 2017.
M. Lavorato, J. F. Franco, M. J. Rider, and R. Romero, “Imposing Radiality Constraints in Distribution System
Optimization Problems,” IEEE Transactions on Power Systems, vol. 27, pp. 172–180, feb 2012.
O. D. Montoya, J. S. Giraldo, L. F. Grisales-Norena, H. R. Chamorro, and L. Alvarado-Barrios, “Accurate and ˜
Efficient Derivative-Free Three-Phase Power Flow Method for Unbalanced Distribution Networks,” Computation, vol. 9, p. 61, may 2021.
A. Marini, S. Mortazavi, L. Piegari, and M.-S. Ghazizadeh, “An efficient graph-based power flow algorithm
for electrical distribution systems with a comprehensive modeling of distributed generations,” Electric Power
Systems Research, vol. 170, pp. 229–243, may 2019.
P. D. O.-D. Jesus, M. Alvarez, and J. Yusta, “Distribution power flow method based on a real quasi-symmetric
matrix,” Electric Power Systems Research, vol. 95, pp. 148–159, feb 2013.
S. Aras, H. T. Kahraman, and E. Gedkli, “Determination of the Effects of Penalty Coefficient on the Metaheuristic Optimization Process,” in 2018 International Conference on Artificial Intelligence and Data Processing (IDAP), IEEE, sep 2018.
O. D. Montoya, L. F. Grisales-Norena, L. Alvarado-Barrios, A. Arias-Londo ˜ no, and C. ˜ Alvarez-Arroyo, “Effi- ´
cient Reduction in the Annual Investment Costs in AC Distribution Networks via Optimal Integration of Solar
PV Sources Using the Newton Metaheuristic Algorithm,” Applied Sciences, vol. 11, p. 11525, dec 2021.
J. Castilho Neto and A. M. Cossi, “Alocac¸ao de Cabos em Redes de Distribuic¸ ˜ ao de Energia El ˜ etrica de M ´ edia ´
Tensao (MT) Utilizando Algoritmo Chu-Beasley,” ˜ Energ´ıa, pp. 1–6, 2009.
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Recibido: 21 de abril de 2022; Aceptado: 16 de mayo de 2022
Resumen
Contexto:
El crecimiento acelerado de las ciudades y áreas rurales requiere de la adecuada expansión del sistema eléctrico de distribución para atender de manera eficiente, confiable y segura los requerimientos de energía eléctrica de usuarios comerciales, residenciales e industriales. Para atender a los diferentes usuarios de la red eléctrica, una metodología típica empleada por los operadores de red corresponde a la asignación óptima de los calibres de los conductores asociados a las rutas de distribución, teniendo en cuenta su costo de inversión y operación para un horizonte de planeación determinando.
Método:
Para resolver el problema de selección óptima en redes de distribución trifásicas, se propone la aplicación de un algoritmo de optimización de la familia de las técnicas combinatoriales conocido como algoritmo metaheurístico de Newton (AMN). La principal ventaja del AMN es que emplea reglas de evolución basadas en la primera y segunda derivadas de la función objetivo, las cuales se aplican a cada individuo de la población. Además, las reglas de evolución del AMN hacen que este algoritmo tenga un balance adecuando entre la exploración y la explotación del espacio de soluciones a medida que avanza el proceso iterativo.
Resultados:
Validaciones numéricas en dos sistemas de distribución trifásicos compuestos de 8 y 27 nodos con escenarios de operación balanceada y desbalanceada demuestran que el AMN alcanza la solución óptima reportada en la literatura para el sistema de 8 nodos y mejora los reportes científicos para el sistema de prueba de 27 nodos en ambos escenarios de prueba.
Conclusiones:
Los resultados obtenidos mediante la aplicación del AMN al problema de selección óptima de conductores en sistemas de distribución demuestran la eficacia de la metodología de solución propuesta para problemas de programación no lineal entera mixta en ingeniería eléctrica con tamaños exponenciales del espacio de soluciones. Además, los resultados reportados para los sistemas de prueba de 8 y 27 nodos constituyen un punto de referencia para futuras investigaciones.
Palabras clave:
algoritmo metaheurístico de Newton, redes de distribución trifásicas, sistemas eléctricos desbalanceados, flujo de potencia trifásico, selección óptima de conductores, optimización combinatorial..Abstract
Context:
The accelerated growth of cities and rural areas requires the adequate expansion of electrical distribution systems in order to meet the electrical energy requirements with efficiency, reliability, and safety for commercial, residential, and industrial users. To serve the different users of the electrical network, a typical methodology used by network operators corresponds to the optimal assignment of the calibers of the conductors associated with the distribution routes. This selection is made while considering its cost of investment and operation for a determined planning horizon.
Method:
To solve the problem regarding optimal selection in three-phase distribution networks, the application of an optimization algorithm of the family of combinatorial techniques known as Newton’s metaheuristic algorithm (NMA) is proposed. The main advantage of the NMA is that it uses evolution rules based on the first and second derivatives of the objective function, which are applied to each individual in the population. In addition, the evolution rules of the NMA cause this algorithm to have a proper balance between the exploration and exploitation of the solution space as the iterative process advances.
Results:
Numerical validations in two three-phase distribution systems composed of 8 and 27 nodes with balanced and unbalanced operation scenarios show that the NMA reaches the optimal solution reported in the literature for the 8-node system and improves the scientific reports for the 27-node test system in both test scenarios.
Conclusions:
The results obtained through the application of the NMA to the problem regarding the optimal selection of conductors in distribution systems demonstrate the effectiveness of the proposed solution methodology for mixed integer nonlinear programming problems in electrical engineering with exponential sizes of the solution space. Furthermore, the reported results for the 8-node and 27-node test systems constitute a benchmark for further research.
Keywords:
Newton’s metaheuristic algorithm, three-phase distribution networks, unbalanced electrical systems, three-phase power flow, optimal selection of conductors, combinatorial optimization..Introducción
Contexto general
Al sistema eléctrico de potencia lo componen las etapas de generación, transmisión, distribución y comercialización, cuya función esencial es llevar energía desde las distintas centrales de generación hasta el usuario final en forma segura, cumpliendo los parámetros de calidad de energía, potencia y servicio. Aproximadamente dos terceras partes de la inversión total del sistema de potencia están dedicadas exclusivamente a la etapa de distribución, lo que conlleva a un gran esfuerzo por parte de todos los implicados en el planeamiento, el diseño, la construcción y la operación del sistema de distribución (1, 2. En sistemas de distribución para simplificar el análisis se suele trabajar con equivalentes monofásicos; sin embargo, la realidad operativa de los sistemas de distribución es trifásica y desequilibrada (3. Esta naturaleza operativa de la red, es decir, operación desbalanceada, puede causar corrientes de secuencia negativa provocando problemas en motores, que a su vez provocan corrientes de secuencia cero que pueden causar aumento de las pérdidas del sistema y mal funcionamiento en las protecciones asociadas 4, (5.
Uno de los aspectos fundamentales en la planeación de sistemas de distribución en sistemas trifásicos corresponde a la selección adecuada de los conductores de la red (6, ya que esto compromete aspectos de inversión asociados con el coste de los conductores, y de operación asociados con las pérdidas de energía durante el horizonte de estudio (7. En la actualidad algunos de los trabajos más destacados en la solución eficiente del problema de la correcta y eficaz selección de conductores se encuentran la aplicación de algoritmos heurísticos, técnicas de optimización metaheurísticas como algoritmos genéticos y diversas estrategias evolutivas 8. También es posible encontrar aproximaciones lineales y modelos de programación no lineal para resolver el problema 6). Estos modelos se resuelven a través de técnicas exactas disponibles en paquetes de optimización comercial 9.
El mal dimensionamiento de los conductores causa gastos innecesarios en los sistemas de distribución y el no aprovechamiento efectivo de todas las capacidades de distribución en los mismos 8. Es decir, así como se busca la eficiencia energética, también se debe propender por el beneficio económico para los operadores de red 10. Si bien este problema se ha intentado resolver de a través de diferentes metodologías de solución, en esta investigación se propone una nueva metodología de optimización del tipo maestro-esclavo, en la cual la etapa maestra se encarga de definir los calibres de los conductores a ser instalados, y la etapa esclava evalúa las características operativas de dicha solución.
Motivación
Durante años la energía eléctrica se ha venido expandiendo por todo el mundo; de este modo, la industria está siempre en búsqueda de métodos de optimización en diferentes aspectos que conforman las redes de distribución que permitan atender de manera oportuna toda la demanda requerida por la red, a un menor costo (11. La importancia de las redes trifásicas en los sistemas de distribución se debe a que estas "a diferencia de las monofásicas" resultan más económicas dado a que requieren una cantidad menor de material conductor 8.
Para la planificación de sistemas de distribución se presta especial atención a la reducción de los costos a través de la selección del conductor, para lo cual se han venido utilizado varios métodos metaheurísticos 12. Estos estudios valen la pena, dado que existen trabajos cuya implementación ofrece reducciones hasta del 30 % en el costo de la implementación del tendido eléctrico (11.
Por lo anterior, esta investigación busca aportar a la solución de un problema de la vida real, de amplio impacto para los sistemas de distribución y de interés particular para los operadores de red, que invierten de forma significativa en sus tendidos eléctricos. Para lo anterior, se propone la implementación de un nuevo algoritmo de optimización combinatoria desarrollado durante el 2020 conocido como algoritmo metaheurístico de Newton (AMN) (13, el cual no ha sido explorado para el problema investigado en este trabajo, y se constituye como una oportunidad de investigación para la literatura científica en temas de planeación de sistemas de distribución.
Revisión de la literatura
A continuación se presentan algunas de las estrategias de optimización más comúnmente empleadas en la literatura especializada para resolver el problema de selección óptima de conductores en redes de distribución de energía eléctrica y algunas otras que servirán como punto de partida para el desarrollo del AMN.
Los autores de 14) analizan el problema de selección de conductores en sistemas de distribución, cuya función objetivo es la minimización de las pérdidas con el mínimo costo de conductores considerando la depreciación de la inversión de capital. El modelo usado para tal propósito es un modelo de programación no lineal entero mixto (PNLEM). El estudio fue realizado en un sistema de 22 nodos con 5 diferentes calibres disponibles para los conductores. En (7, los autores emplean el algoritmo de optimización de seno-coseno para la selección óptima de conductores. Esta metodología de solución se aplica en un sistema de distribución real localizado en Egipto. En el modelo matemático se tiene en cuenta una tasa de crecimiento anual de la demanda con una proyección a 10 años; además, los autores emplean un catálogo comercial con 20 opciones de conductor disponible. Los resultados numéricos fueron satisfactorios en términos de la calidad de la solución el tiempo de procesamiento requerido. LOS autores de (15 presentan una estrategia heurística para la selección óptima de conductores en sistemas de distribución a través de la aplicación de un algoritmo de flujo de potencia recursivo que evalúa múltiples flujos de potencia para cada conjunto de calibres disponibles. La metodología propuesta se valida en un sistema de 54 nodos; sin embargo, los autores no presentan comparaciones con otras estrategias de solución disponibles en la literatura. En 9, los autores presentan una metodologia de solucion para el problema de selección óptima de conductores en sistemas de distribución mediante la implementación del modelo de PNLEM en el software de modelado algebraico general conocido como GAMS. Los resultados fueron comparados con un algoritmo genético de Chuy Beasley (AGCB), teniendo un desempeño adecuado. Los autores de (16) describen una metodología de solución basada en optimización por enjambre de partículas discretas para la selección de conductor en el sistema de distribución radial. El objetivo de este trabajo corresponde a la minimización del costo de inversión operación de la red. Para validar la eficiencia de la metodología propuesta se emplean sistemas de prueba de 26 y 32 nodos con 5 posibles conductores a instalar. Los autores de 11 presentan la aplicación del método de búsqueda tabú para seleccionar conductores en sistemas de distribución con naturaleza trifásica. Los resultados obtenidos en sistemas de prueba de 8 y 27 nodos muestran la eficiencia de la metodología propuesta cuando se compara con la solución obtenida por medio de AGCB.
En 17 proponen un enfoque de planificación para sistemas de distribución radial no balanceados. Los autores consideran la ubicación simultánea de bancos de condensadores y la selección óptima de conductores a través de la implementación de un algoritmo de optimización conocido como evolución diferencial. Los resultados numéricos demuestran la eficiencia de la metodología propuesta en sistemas de prueba de 19 y 34 nodos. En 18, los autores presentan la aplicación del algoritmo de optimización de las salpas para seleccionar el conjunto óptimo de conductores en una red real de distribución ubicada en Egipto. La principal característica de esta propuesta es que el modelo matemático desarrollado permite cambiar el calibre de los tramos de red existentes con el fin de aumentar la capacidad de transmisión de energía. Los autores de 8) presentan la aplicación del método de optimización de búsqueda por vórtices al problema de selección óptima de conductores en sistemas de distribución trifásicos balanceados y desbalanceados con tamaños de 8 y 27 nodos. Los autores consideran 8 tipos de conductores disponibles. Los resultados numéricos demostraron la eficiencia del método propuesto cuando se compara el AGCB, el algoritmo de búsqueda tabú y el modelo de PNLEM resuelto en el software GAMS.
Otras metodologías de solución aplicadas al problema de selección óptima de conductores en sistemas de distribución son: el método de optimización por enjambre de partículas 19, 20. el algoritmo de optimización de búsqueda armónica (21, el algoritmo genético convencional (22, (23 y el algoritmo de búsqueda por cuervos (24, entre otros métodos.
Contribución y alcance
De la revisión del estado del arte anterior, es importante notar que todos los métodos de optimización, excepto la solución del modelo de PNLEM en GAMS, son de naturaleza maestro-esclavo, es decir, emplean en la etapa maestra alguna estrategia metaheurística para seleccionar los calibres de los conductores y en la etapa esclava emplean un método de flujo de potencia para evaluar las características operativas de la red (voltajes, corrientes, potencias, etc.). Por lo anterior, en este artículo se presentan las siguientes contribuciones:
-
la aplicación del AMN para la generación de las soluciones candidatas del problema de sección óptima de conductores en sistema de distribución a través de una codificación entera en la etapa maestra.
-
su integración con el método de flujo de potencia trifásico basado en la matriz triangular para sistemas balanceados y desbalanceados con el fin de evaluar las características eléctricas de la solución en la etapa esclava.
Es importante mencionar que el AMN no ha sido aplicado al problema de selección óptima de conductores, con lo cual este trabajo de investigación pretende aportar en el desarrollo de nuevas metodologías de optimización para abordar el problema de planeación de sistemas de distribución.Además, los resultados numéricos en los sistemas de prueba de 8 y 27 nodos muestran que: (i) para el sistema de 8 nodos se obtiene la misma solución reportada por el método de búsqueda por vórtices reportado en 8, y (ii) para el sistema de 27 nodos se mejoran los resultados presentados por dicho método. Por otro lado, es importante tener en cuenta que en este trabajo se considera que las redes eléctricas operan con impedancias balanceadas, y las asimetrías se presentan únicamente en las cargas, las cuales pueden estar conectadas en estrella y en triángulo; además, para el caso de cargas conectadas en estrella, se considera que estas están sólidamente aterrizadas.
Estructura del documento
El resto de este documento está estructurado de la siguiente forma: en la sección 2 se presenta la formulación matemática del problema de selección óptima de conductores en sistemas de distribución, el cual tiene como objetivo la minimización de los costos de inversión y operación para un horizonte de planeación de un año. En la sección 3 se presenta la metodología de solución propuesta, la cual consiste en la integración del AMN en la etapa maestra y el método de flujo de potencia triangular en la etapa esclava. En la sección 4 se presentan las principales características de los sistemas de prueba de 8 y 27 nodos con condiciones operativas balanceadas y desbalanceadas. En la sección 5 se presentan los principales hallazgos numéricos en los sistemas de prueba de 8 y 27 nodos, así como su analisis y discusión; además, se presentan los resultados comparativos con metodologías de optimización disponibles en 8. Finalmente, en la sección 6 se presentan las conclusiones derivadas de esta investigación, así como algunos posibles trabajos de investigación futura.
Formulación matemática
El problema de selección óptima de conductores en sistemas de distribución de energía eléctrica con estructura trifásica se presenta a través de un modelo de programación no lineal entera mixta (PNLEM) 9. En este modelo, las variables enteras (o binarias) están asociadas con el calibre del conductor que se puede asignar a cada tramo de red, mientras que, las variables continuas están relacionadas con la solución del problema de flujo de potencia, p. ej., voltajes, corrientes, y flujos de potencia, entre otras (4. El modelo matemático que describe el problema de selección óptima de conductores en sistemas de distribución se presenta a continuación.
Función objetivo
La función objetivo para el problema de selección óptima de conductores en sistemas de distribución con naturaleza trifásica simétrica y/o asimétrica considera un horizonte operativo de un año para minimizar los costos de inversión en conductores y los costos de las pérdidas de energía anuales. En la formulación matemática (1)-(3), la ecuación (1) representa el valor de la función objetivo, la ecuación (2) representa los costos de las pérdidas de energía para el año de estudio, y la ecuación (3) es la componente asociada con el costo de inversión en conductores.
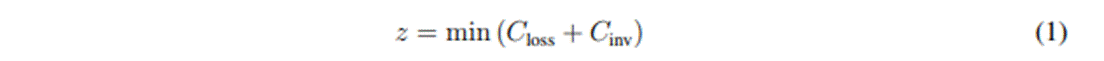
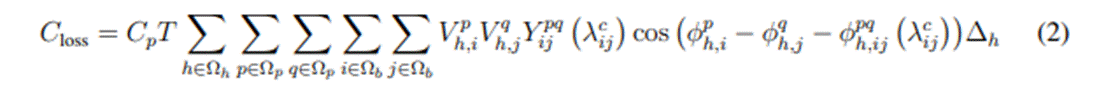
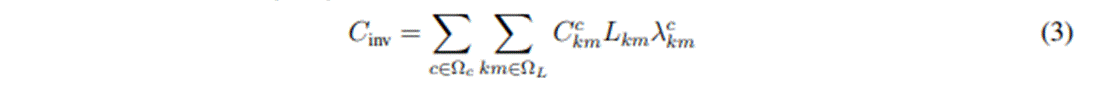
donde
 es la variable asociada con los costos de las pérdidas de energía,
es la variable asociada con los costos de las pérdidas de energía,
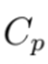 presenta el coeficiente de costo promedio de la energía; T a la longitud del periodo de estudio;
presenta el coeficiente de costo promedio de la energía; T a la longitud del periodo de estudio;
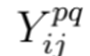 y
y
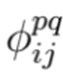 corresponden a las magnitudes de las impedancias que asocian a los nodos i y j en las fases p y q, respectivamente. Nótese que para el problema de selección óptima de conductores en sistemas eléctricos, las variables
corresponden a las magnitudes de las impedancias que asocian a los nodos i y j en las fases p y q, respectivamente. Nótese que para el problema de selección óptima de conductores en sistemas eléctricos, las variables
 y
y
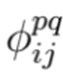 son funciones de la variable binaria
son funciones de la variable binaria
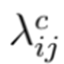 . Esta variable binaria define el calibre tipo c para la ruta que une los nodos i y j.
. Esta variable binaria define el calibre tipo c para la ruta que une los nodos i y j.
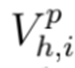 y
y
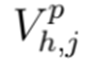 definen las magnitudes de los voltajes en los nodos i y j para el período de tiempo h en la fase p, cuyos ángulos se denotan como
definen las magnitudes de los voltajes en los nodos i y j para el período de tiempo h en la fase p, cuyos ángulos se denotan como
 , respectivamente.
, respectivamente.
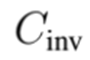 almacena el costo de inversión en conductores, siendo
almacena el costo de inversión en conductores, siendo
 el costo del conductor por kilómetro con calibre tipo c;
el costo del conductor por kilómetro con calibre tipo c;
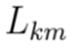 representa la longitud del tramo de red que une los nodos k y m en kilómetros;
representa la longitud del tramo de red que une los nodos k y m en kilómetros;
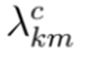 es la variable binaria que define la instalación
es la variable binaria que define la instalación
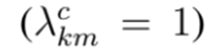 o no
o no
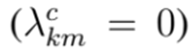 de un conductor con calibre tipo c en el tramo de red que une los nodos k y m. Nótese que
de un conductor con calibre tipo c en el tramo de red que une los nodos k y m. Nótese que
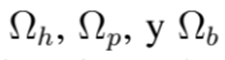 , son los conjuntos que definen los períodos de tiempo del horizonte de planeación, el conjunto de fases del sistema bajo estudio, y el conjunto de nodos de la red, respectivamente.
, son los conjuntos que definen los períodos de tiempo del horizonte de planeación, el conjunto de fases del sistema bajo estudio, y el conjunto de nodos de la red, respectivamente.
Conjunto de restricciones
El problema de selección óptima de conductores en sistemas de distribución con topología desbalanceada está sujeto a las restricciones clásicas de balance de potencia, las capacidades de los conductores, y la regulación de tensión en los nodos, entre otras características. Estas restricciones se presentan desde la ecuación 4 hasta la ecuación 11.
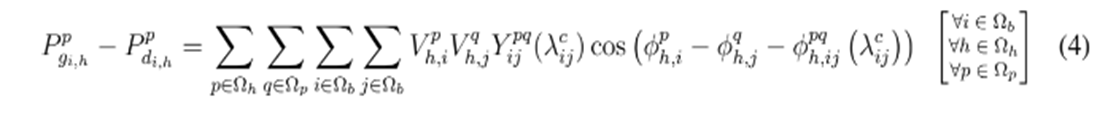
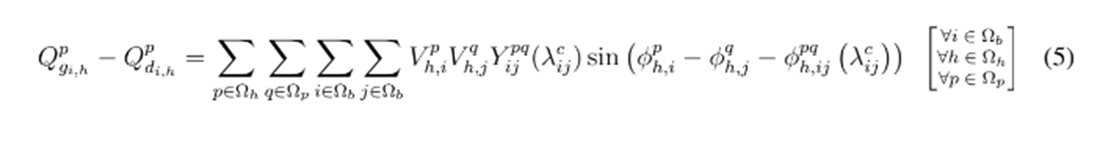
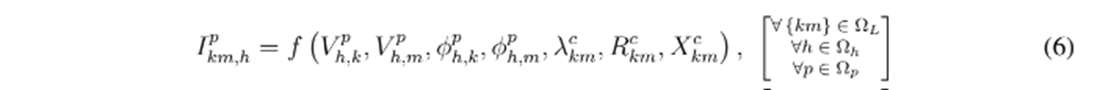
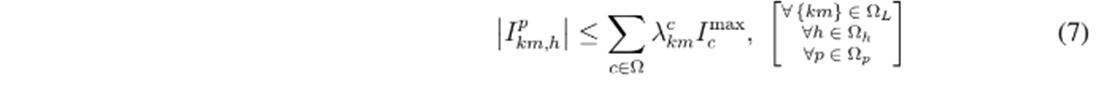
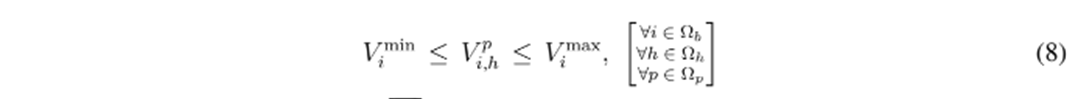
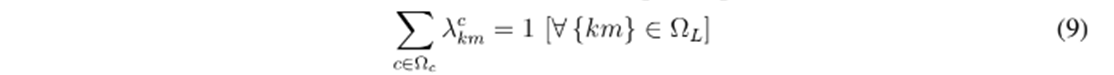
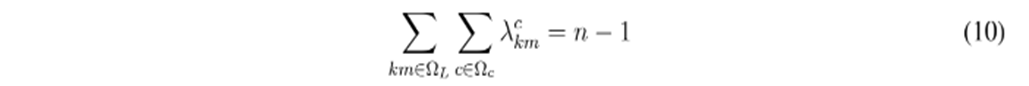
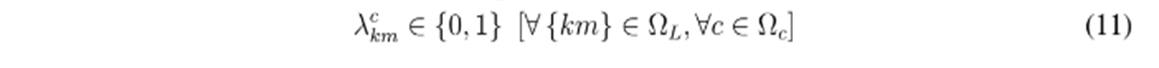
donde las ecuaciones (4) y (5) definen el balance de potencia activa en cada nodo del sistema en cada una de sus clases para cada periodo de tiempo; siendo
 la potencia activa y reactiva proveída por el generador, y
la potencia activa y reactiva proveída por el generador, y
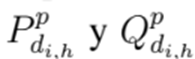 las potencias activas y reactivas demandadas, respectivamente. La ecuación (6) es una función no lineal para corriente
las potencias activas y reactivas demandadas, respectivamente. La ecuación (6) es una función no lineal para corriente
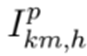 que fluye en la ruta km en el período de tiempo h en la fase p, la cual depende de los voltajes en ambos extremos de la línea en magnitud y ángulo, p. ej.
que fluye en la ruta km en el período de tiempo h en la fase p, la cual depende de los voltajes en ambos extremos de la línea en magnitud y ángulo, p. ej.
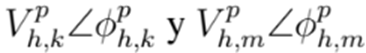 , así como, del tipo de conductor seleccionado
, así como, del tipo de conductor seleccionado
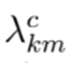 p. ej. de la resistencia
p. ej. de la resistencia
 y la reactancia
y la reactancia
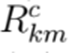 asociadas a este. Nótese que en estas restricciones
asociadas a este. Nótese que en estas restricciones
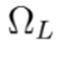 define el conjunto de tramos de red del sistema bajo estudio.
define el conjunto de tramos de red del sistema bajo estudio.
La desigualdad definida en (7) asegura que la corriente que fluye en el tramo de red km en el período de tiempo h sea menor capacidad térmica del conductor tipo c asignado a dicho tramo, p. ej.
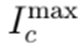 . La restricción (8) asegura que para cada nodo del sistema, en cada período de tiempo y para cada fase se cumpla la regulación de tensión del sistema, la cual se define entre el límite inferior
. La restricción (8) asegura que para cada nodo del sistema, en cada período de tiempo y para cada fase se cumpla la regulación de tensión del sistema, la cual se define entre el límite inferior
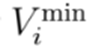 y el límite superior
y el límite superior
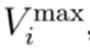 , respectivamente. La ecuación (9) asegura que para la ruta que une los nodos k y m sea seleccionado un único tipo de conductor tipo c además, la ecuación (10) garantiza que el número total de conductores seleccionado sea equivalente al número de nodos de la red n menos 1. Nótese que esto es una condición necesaria para garantizar que la topología de la red sea radial, más no suficiente 25. Por otro lado, la ecuación (11) muestra la naturaleza discreta (binaria) de la variable de decisión asociada con el calibre tipo c que sea asignada a la ruta km.
, respectivamente. La ecuación (9) asegura que para la ruta que une los nodos k y m sea seleccionado un único tipo de conductor tipo c además, la ecuación (10) garantiza que el número total de conductores seleccionado sea equivalente al número de nodos de la red n menos 1. Nótese que esto es una condición necesaria para garantizar que la topología de la red sea radial, más no suficiente 25. Por otro lado, la ecuación (11) muestra la naturaleza discreta (binaria) de la variable de decisión asociada con el calibre tipo c que sea asignada a la ruta km.
Observación 1 El modelo matemático de tipo PNLEM definido entre las ecuaciones (1) a (11) representa la formulación general del problema de selección óptima de conductores para sistemas de distribución con estructura asimétrica 8 . La principal complicación en la solución de este modelo corresponde a la dimensión del espacio de soluciones, para lo cual si se tienen l líneas y c 1
Para hacerse a una idea del tamaño del espacio de soluciones se considera un sistema de 27 nodos, el cual requiere de 26 líneas, p. ej. l = 26, para una configuración radial, además, si el número de calibres disponibles es c= 6, entonces el espacio de soluciones será 626, lo cual implica, un tamaño equivalente a 170581728179578208256, siendo éste alrededor de 170 trillones de posibilidades de solución, lo cual es imposible de evaluar de manera exhaustiva. Lo anterior justifica claramente la aplicación de métodos de optimización combinatorial, con el fin de hallar una solución de buena calidad en tiempos de cómputo razonables (8.
Metodología de solución
Para abordar el problema de selección óptima de conductores en sistemas de distribución balanceados y desbalanceados, definido por el modelo matemático de tipo PNLEM y presentado desde (1) a(11), se propone una metodología de optimización del tipo maestro-esclavo, en el cual la etapa maestra se encarga de asignar los calibres de los conductores, mientras que la etapa esclava evalúa cada configuración de conductores a través de un flujo trifásico desbalanceado 11. Es importante mencionar que en este trabajo, la etapa maestra corresponderá al algoritmo de optimización metaheurístico de Newton 13, mientras que la etapa esclava corresponderá al flujo de potencia trifásico triangular 26.A continuación se presentan las etapas esclava y maestra de la estrategia de optimización propuesta en este trabajo.
Etapa esclava: flujo de potencia trifásico
El problema de flujo de potencia para sistemas eléctricos de naturaleza trifásica desbalanceada requiere de una solución recursiva, ya que este tiene una estructura no lineal de la forma
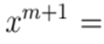
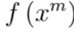 , siendo esta una estructura recursiva donde el valor de la solución en la iteración siguiente m+1 depende explícitamente de la solución en la iteración actual m 3. La metodología de flujo de potencia para sistemas trifásicos fue inicialmente propuesta por Marini et al., en (27, siendo este una mejora del método TRX propuesto en 28. La ventaja del método de flujo de potencia triangular es que es posible demostrar su convergencia para conexiones en estrella según lo reportado en 26, lo cual hace de este un método eficiente y de bajo coste computacional para resolver problemas de flujo de potencia en sistemas trifásicos. La fórmula general para el método de flujo de potencia triangular se define en la ecuación (12).
, siendo esta una estructura recursiva donde el valor de la solución en la iteración siguiente m+1 depende explícitamente de la solución en la iteración actual m 3. La metodología de flujo de potencia para sistemas trifásicos fue inicialmente propuesta por Marini et al., en (27, siendo este una mejora del método TRX propuesto en 28. La ventaja del método de flujo de potencia triangular es que es posible demostrar su convergencia para conexiones en estrella según lo reportado en 26, lo cual hace de este un método eficiente y de bajo coste computacional para resolver problemas de flujo de potencia en sistemas trifásicos. La fórmula general para el método de flujo de potencia triangular se define en la ecuación (12).

donde
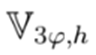 es el vector que contiene todos los voltajes en los nodos de demanda para cada fase en cada período de tiempo
es el vector que contiene todos los voltajes en los nodos de demanda para cada fase en cada período de tiempo
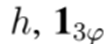 es una matriz rectangular compuesta de matrices identidad;
es una matriz rectangular compuesta de matrices identidad;
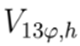 es el vector de voltajes de la subestación para cada periodo de tiempo, el cual en por unidad se representa como
es el vector de voltajes de la subestación para cada periodo de tiempo, el cual en por unidad se representa como
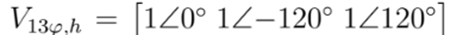 . Por otro lado,
. Por otro lado,
 es la matriz triangular superior en forma trifásica,
es la matriz triangular superior en forma trifásica,
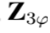 representa la matriz de impedancias primitivas del sistema en forma trifásica, e
representa la matriz de impedancias primitivas del sistema en forma trifásica, e
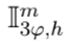 es el vector de corrientes en los nodos de demanda para cada período de tiempo.
es el vector de corrientes en los nodos de demanda para cada período de tiempo.
La principal característica del flujo de potencia trifásico es que la corriente en los nodos de demanda depende específicamente del tipo de conexión de la carga, es decir, cargas conectadas en estrella y cargas conectadas en triángulo. Según lo reportado en 26, para cargas conectadas en estrella, la corriente para un nodo arbitrario k en el período de tiempo h toma la forma (13), mientras que para cargas con conexión en triángulo, esta toma la forma (14).
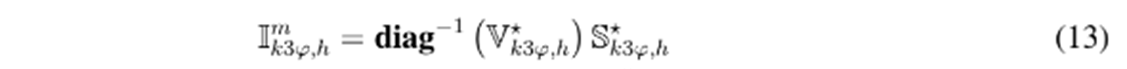
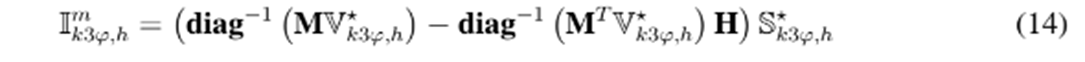
donde las matrices M y H tienen la siguiente estructura,
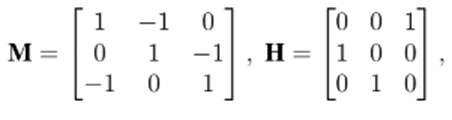
y
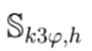 es el vector que contiene las demandas de cada nodo. Nótese que
es el vector que contiene las demandas de cada nodo. Nótese que
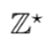 corresponde a la pareja conjugada de la variable/parámetro
corresponde a la pareja conjugada de la variable/parámetro
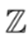 .
.
Una vez construido el vector de corrientes demandadas
 a partir de las ecuaciones (13) y (14), se evalúa la fórmula recursiva partiendo del punto inicial para cada nodo
a partir de las ecuaciones (13) y (14), se evalúa la fórmula recursiva partiendo del punto inicial para cada nodo
 , hasta que se cumpla el criterio de convergencia definido en (15).
, hasta que se cumpla el criterio de convergencia definido en (15).
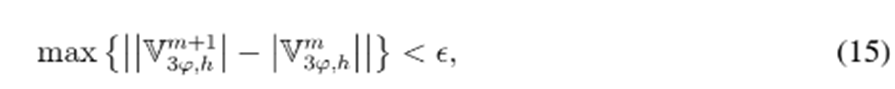
siendo Є el máximo valor de convergencia aceptable para el sistema, el cual se define, según lo recomendado en (26), como Є=1 x 10-10.
Una vez solucionado el flujo de potencia trifásico con la fórmula recursiva (12), se procede al cálculo de las pérdidas de potencia en cada período de tiempo, para lo cual se calculan las corrientes en todas las ramas
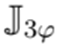 y las caídas de tensión en estas p. ej.
y las caídas de tensión en estas p. ej.
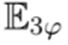 por medio de la matriz triangular.
por medio de la matriz triangular.
Estas variables se definen como en las ecuaciones (16) y (17), respectivamente.


Al combinar estas dos ecuaciones, se tiene la ecuación (18), que representa las pérdidas de potencia aparente en cada período de tiempo, p. ej.
 .
.

Observación 2 Una vez es solucionado el problema de flujo de potencia y halladas las pérdidas de potencia para cada período de de tiempo h, según la ecuación (18), se obtiene la componente de la función objetivo asociada al costo de las pérdidas de energía dada en (2), la cual se puede hallar según (19).
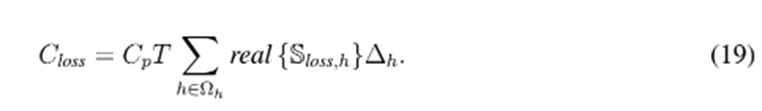
Es importante mencionar que, en el caso de que la solución proveída por la etapa maestra al evaluarse en flujo de potencia tenga problemas de infactibilidad por sobrepaso del límite térmico de los conductores, o baja regulación de tensión (fuera del rango admitido), entonces, la función objetivo será penalizada mediante un factor de ponderación que incrementa las pérdidas totales en función del nivel de incumplimiento de las restricciones 29.
Etapa maestra: algoritmo metaheurístico de Newton
El algoritmo de optimización metaheurística inspirado en el método de solución de sistemas de ecuaciones no lineales de Newton fue recientemente desarrollado por los autores de 13. El objetivo de este desarrollo fue el diseño de estructuras de acero para pórticos. Este algoritmo tiene como ventaja fundamental la fortaleza matemática de su formulación, siendo fácilmente adaptable a problemas con variables enteras y/o binarias, así como, problemas de optimización en el dominio continuo 30. Al igual que la mayoría de algoritmos de optimización metaheurística, el algoritmo metaheurístico de Newlon (AMN), trabaja con una población inicial
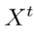 , y un conjunto de reglas de evolución que permiten explorar y explotar el espacio de soluciones. Nótese que t es el contador de iteraciones asignado para el AMN.
, y un conjunto de reglas de evolución que permiten explorar y explotar el espacio de soluciones. Nótese que t es el contador de iteraciones asignado para el AMN.
La estructura de la
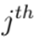 fila de la matriz
fila de la matriz
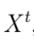 , representa una posible solución candidata del problema estudiado y toma la estructura definida por la ecuación (20).
, representa una posible solución candidata del problema estudiado y toma la estructura definida por la ecuación (20).

donde c representa el mayor calibre disponible en el conjunto de conductores. Además, la dimensión de la matriz asociada con la población inicial
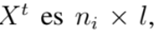 siendo
siendo
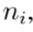 , el número de soluciones candidatas considerando, y l el número de líneas del sistema de distribución.
, el número de soluciones candidatas considerando, y l el número de líneas del sistema de distribución.
Observación 3 Con la solución
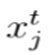 se halla la componente de la función objetivo asociada con los costos de inversión en conductores, es decir, se obtiene la componente
se halla la componente de la función objetivo asociada con los costos de inversión en conductores, es decir, se obtiene la componente
 de la función objetivo definida en (3).
de la función objetivo definida en (3).
La regla de evolución general para el AMN se define en la ecuación (21) (13):
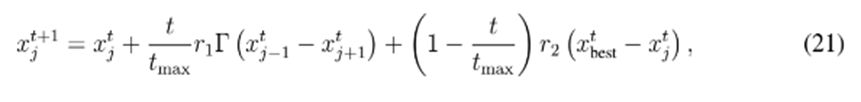
donde
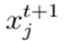 es la
es la
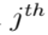 solución en la iteración siguiente, tmax es el máximo número de iteraciones,
solución en la iteración siguiente, tmax es el máximo número de iteraciones,
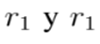 son números aleatorios con distribución uniforme definidos entre 0 y 1,
son números aleatorios con distribución uniforme definidos entre 0 y 1,
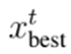 es la mejor solución contenida en la población hasta el momento (solución que provee las mínimas pérdidas para la iteración t), y
es la mejor solución contenida en la población hasta el momento (solución que provee las mínimas pérdidas para la iteración t), y
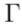 toma la forma definida en la ecuación (22).
toma la forma definida en la ecuación (22).
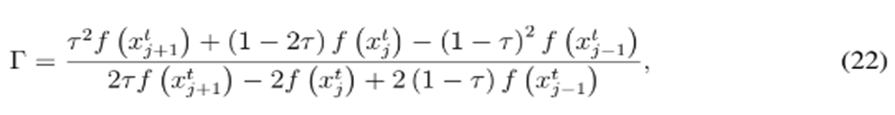
Siendo
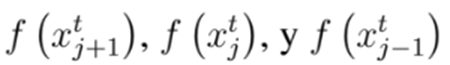 los valores de función objetivo para las soluciones
los valores de función objetivo para las soluciones
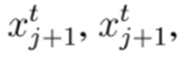 y
y
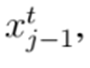 respectivamente; además,
respectivamente; además,
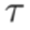 se define según la ecuación (23).
se define según la ecuación (23).

Observación 4 Es importante mencionar que, cada solución candidata generada a partir de
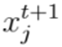 es verificada con el fin de garantizar la factibilidad del espacio de soluciones, es decir que esté compuesta de números enteros entre 1 y c. En caso contrario, esta se corrige mediante el redondeo de los valores decimales que sean generados, y en el caso de estar por fuera del rango admisible, este se eleva su valor admisible más cercano
8
. p. ej. 1 o c respectivamente.
es verificada con el fin de garantizar la factibilidad del espacio de soluciones, es decir que esté compuesta de números enteros entre 1 y c. En caso contrario, esta se corrige mediante el redondeo de los valores decimales que sean generados, y en el caso de estar por fuera del rango admisible, este se eleva su valor admisible más cercano
8
. p. ej. 1 o c respectivamente.
Resumen general de la metodología de solución propuesta
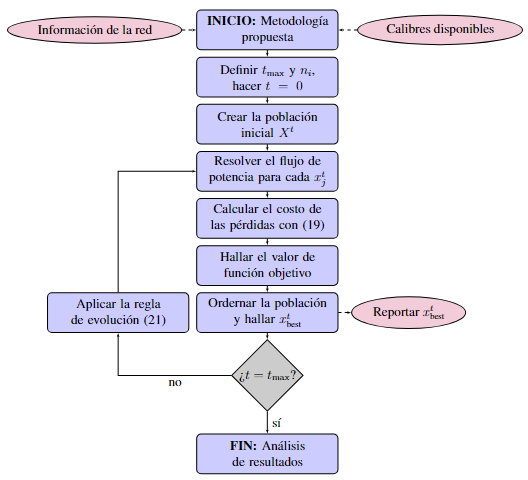
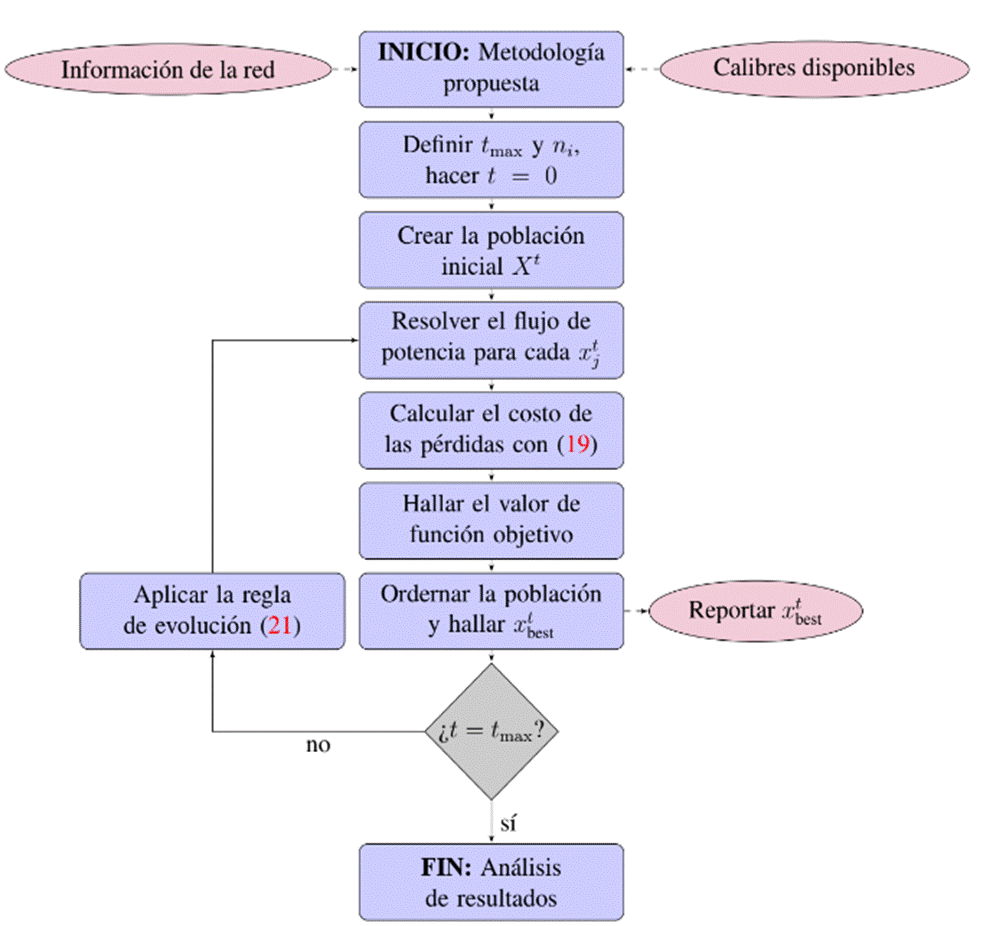
En la figura 1 se presenta en forma general la implementación de la metodología maestro-esclavo, a través de la combinación del AMN y el flujo de potencia mediante el método triangular, para la selección óptima de conductores en sistemas de distribución trifásicos simétricos y asimétricos.
Figura 1: Implementación general de la metodología maestro-esclavo basada en el AMN y el flujo de potencia triangular para la selección óptima de conductores en sistemas de distribución trifásicos.
Sistemas de prueba
Para validar la metodología de solución propuesta se emplean dos sistemas de prueba de la literatura especializada compuestos de 8 y 27 nodos con estructura radial. Para ambos sistemas de prueba se considera el peor escenario de operación (pérdidas máximas), las cuales se dan cuando todas las cargas están conectadas en estrella 8. Además, se considera un escenario de operación en demanda pico, y posibilidad de operación balanceada y desbalanceada. Las características de cada uno de estos sistemas se presenta a continuación.
Sistema de prueba de 8 nodos
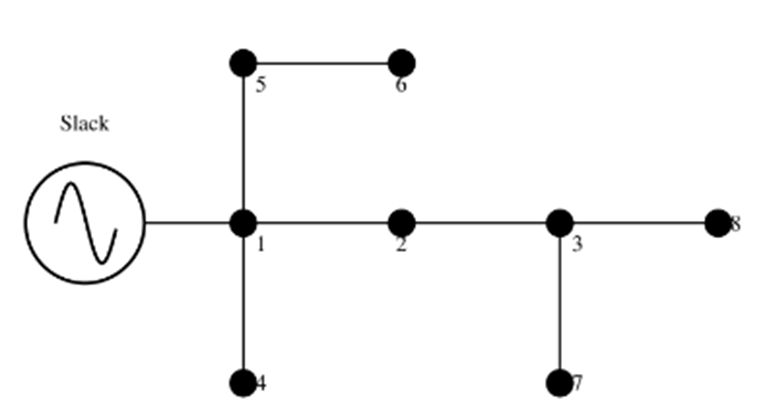
El sistema de prueba de 8 nodos es un sistema radial que opera a una tensión de 13,8 kV entre fase y neutro con topología radial y factor de potencia unitario (8. La configuración inicial de red para este sistema de prueba se presenta en la figura 2.
Figura 2: Diagrama monofásico equivalente para el sistema de prueba de 8 nodos
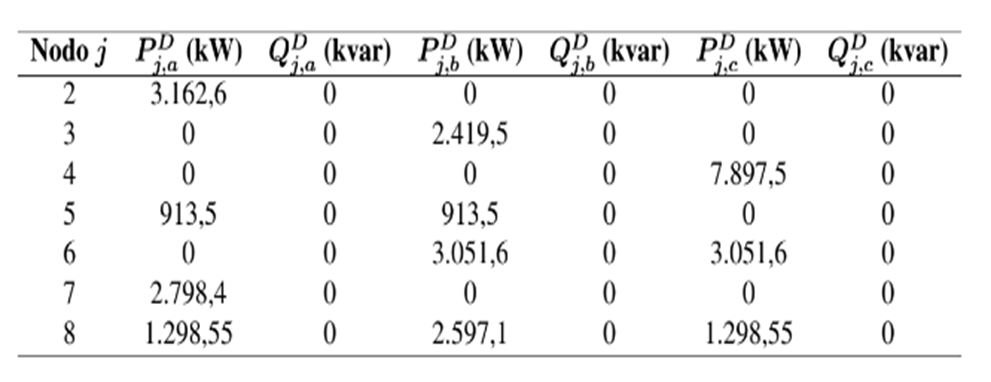
En la tabla I se presenta la información de cargas y longitud de los tramos de red. Es importante mencionar que, la información que se presenta en la tabla I es por fase. Para el caso de operación desbalanceada en el sistema de prueba de 8 nodos se consideran la distribución de demandas que se reporta en la tabla II.
Tabla I: Información de líneas y cargas para el escenario de operación balanceado en el sistema de 8 nodos.
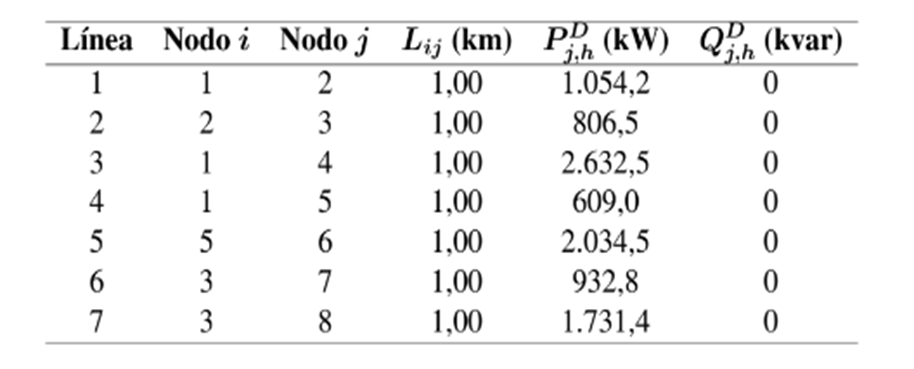
Tabla II: Distribución de cargas para el escenario de operación desbalanceado en el sistema de 8 nodos
Sistema de prueba de 27 nodos
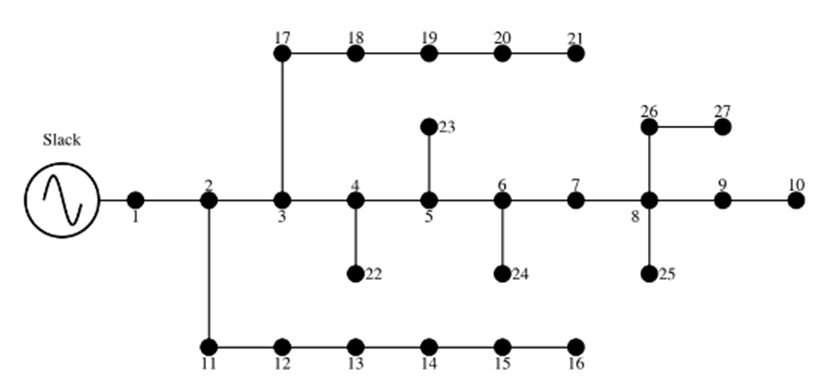
El sistema de prueba de 27 nodos es una red de distribución de topología trifásica de naturaleza radial que opera con una tensión de 13,8 kV en el nodo subestación (ver figura 3). Este sistema de prueba fue inicialmente reportado por los autores de (11, en el cual se aplicó el método de búsqueda tabú para la selección óptima de conductores. En la tabla III se presentan los datos de este sistema de prueba para el escenario de operación balanceado.
Figura 3: Diagrama monofásico equivalente para el sistema de prueba de 27 nodos.
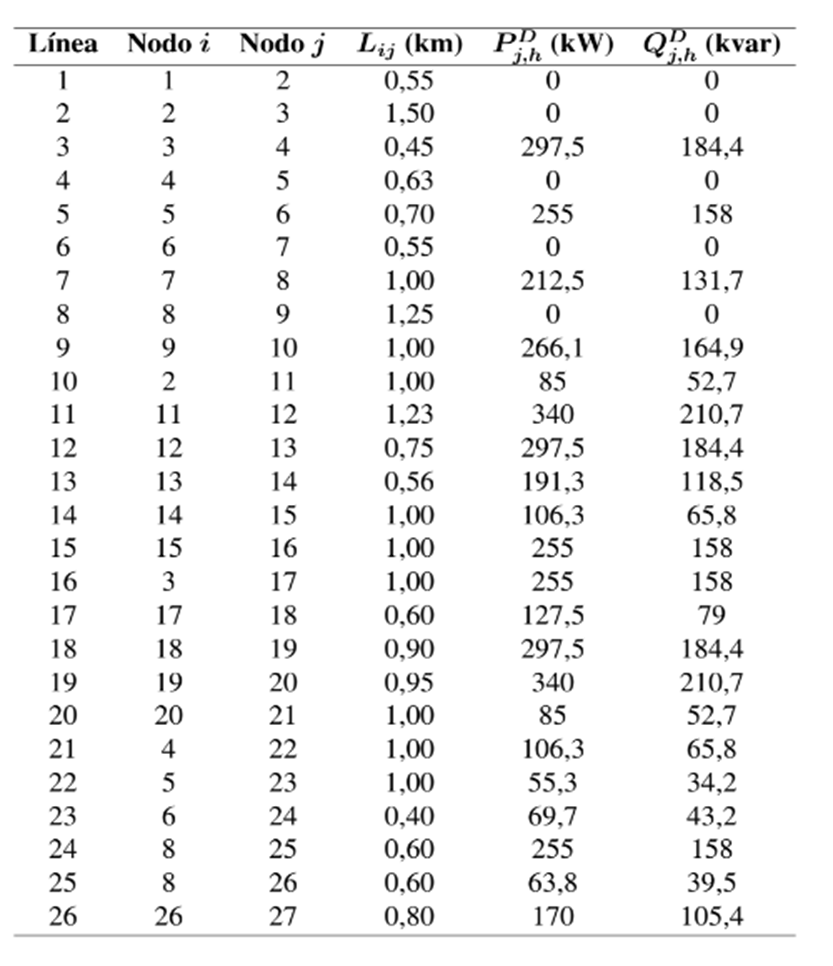
En la tabla III se presenta la información de cargas y longitud de los tramos de red. Es importante mencionar que, la información que se presenta en la tabla III es por fase.
Tabla III: Información de líneas y cargas para el escenario de operación balanceado para el sistema de 27 nodos
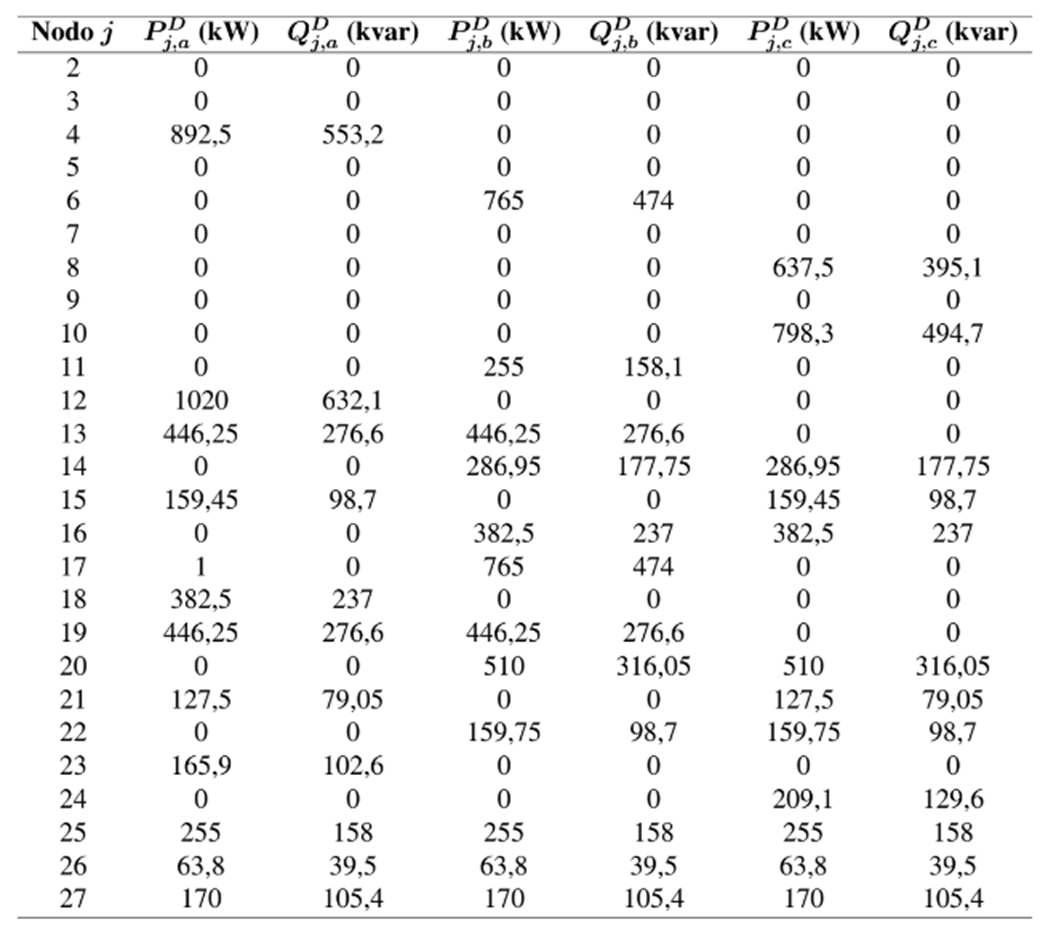
Para el caso de operación desbalanceada se consideran la distribución de demandas que se reporta en la tabla IV.
Tabla IV: Distribución de cargas para el escenario de operación desbalanceado en el sistema de 27 nodos
Conjunto de conductores disponibles
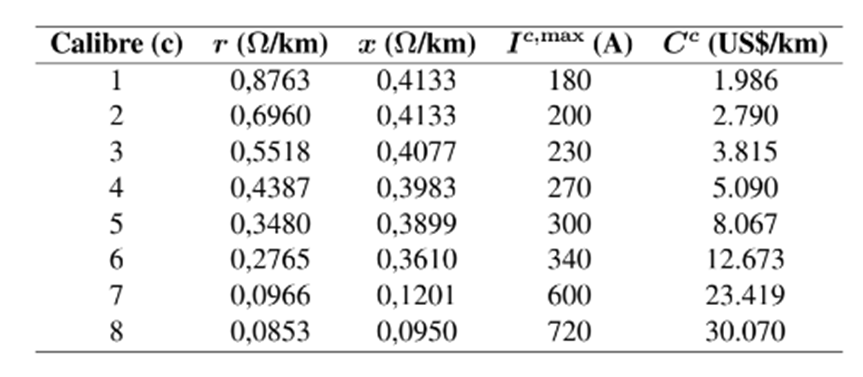
Para la validación de la metodología propuesta se consideran 8 tipos de conductores disponibles para ambos sistemas de prueba (8. La información de estos conductores se presenta en la tabla V, la cual contiene la información de la impedancia promedio de secuencia positiva por kilómetro de red, así como, su respectivo costo.
Tabla V: Conjunto de conductores disponibles para los sistemas de prueba de 8 y 27 nodos
Resultados y discusión
La validación de la metodología de optimización del tipo maestro-esclavo propuesta, en la cual el AMN determine el conjunto de conductores a localizar en la etapa maestra, y el flujo de potencia triangular determine el costo de las pérdidas en la etapa esclava, se realiza en el software MATLAB en la versión 2021b en un computador personal con procesador Intel(R) Core(TM) i5-2410M CPU 2.30GHz, 2301 Mhz, 6 Gb RAM y sistema operativo Windows 10 Home de x64 bits. Para ambos sistemas de prueba se considera un escenario operativo en demanda pico, i.e., T = 8. la demanda siempre está al 100 %. Para estos escenarios de simulación, se considera un costo promedio de la energía C p , equivalente a 0,1390 kWh/año 8. Es importante mencionar que, para implementar el AMN se tiene en cuenta un tamaño de población equivalente a 20 individuos, 100 repeticiones del algoritmo y 1000 iteraciones por repetición.
Resultados en escenario de operación balanceado
En esta sección se presentan los resultados obtenidos para los sistemas de 8 y 27 nodos, cuando se considera el escenario de operación balanceado para ambos sistemas.
Sistema de prueba de 8 nodos
En la tabla VI se presentan la solución alcanzada por el AMN propuesto, así como por los métodos comparativos. Para este escenario de simulación, se consideran como algoritmos de comparación, los siguientes: algoritmo de búsqueda tabú (ABT) 11;algoritmo genético tradicional (AGT) (22); algoritmo genético de Chu y Beasley 31; la solución exacta del modelo de PNLEM en GAMS (9, algoritmo búsqueda por vórtices (ABV) 8.
Tabla VI: Solución obtenida por el AMN y su comparación con los reportes de la literatura
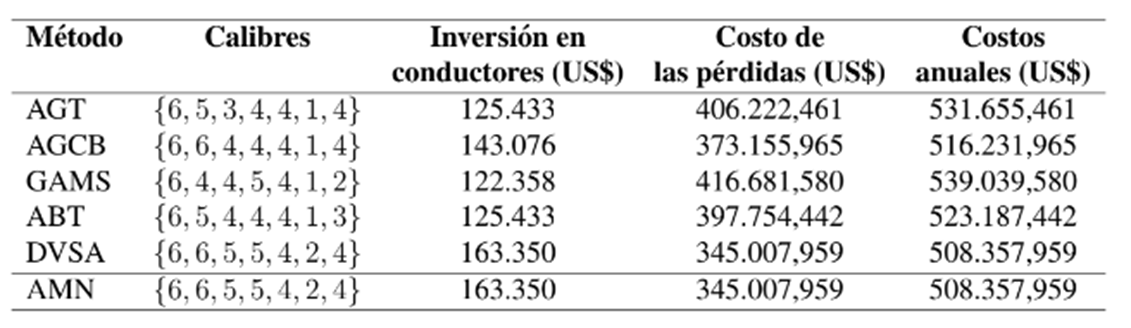
Los resultados presentados en la tabla VI muestran que: (i) la metodología propuesta basada en el AMN alcanza los mismos resultados numéricos que el ABV, con una solución equivalente a US$ 508.357,959, de los cuales el 32,13 % corresponde a los costos de inversión en conductores, y el 67,87 % representa los costos asociados con las pérdidas de energía durante el horizonte de planeación; (ii) la segunda mejor metodología de solución es el AGCB con una función objetivo equivalente a US$ 516.231,965, seguida en tercer lugar por el ABT con un costo anual de US$ 523.187, 442; (iii) debido a la no linealidad y no convexidad del espacio de soluciones, el resultado del modelo PNLEM en el software GAMS se consigue en una solución óptima de naturaleza local, siendo esta la solución de peor calidad presentada en la tabla VI, con un costo anual adicional de US$ 30.681,621: y (iv) es importante mencionar que la solución obtenida por el AMN presenta el mayor nivel de inversión de todos los métodos comparativos al igual que el ABV en términos de calibres de conductores; sin embargo, este costo adicional se ve compensado con el menor nivel de costo en las pérdidas de energía, con lo cual se logra la combinación adecuada para obtener la solución de mejor calidad en este sistema de prueba.
Sistema de prueba de 27 nodos
Para este sistema de prueba en la tabla VI se presentan los resultados comparativos entre el método propuesto y el ABV presentado en (8
Tabla VII: Solución obtenida por el AMN y su comparación con el ABV para el escenario de operación balanceado

Los resultados de la tabla VII muestran que: (i) el AMN propuesto mejora los resultados reportados por el ABV en 8 en US$ 4.329,222, ya que, el AMN logra un costo anual de US$ 557.695,255, mientras que el ABV llega a unos costos finales de US$ 562.024, 477. (ii) la principal diferencia entre las soluciones reportadas por el método propuesto ABV radica en la reducción de los calibres en dos tramos de red, cuando se comparan entre sí. Esto hace que el costo de inversión en conductores del AMN sea menor que el costo alcanzado por el ABV en US$ 6.607,350; aunque esto implica que, el costo de las pérdidas de energía se aumentan, siendo la diferencia entre el ABV y el AMN de US$ 2.278,128; lo cual se traduce en una ganancia neta en favor del AMN.
Resultados en en escenario de operación desbalanceado
En esta sección se presentan los resultados obtenidos para los sistemas de 8 y 27 nodos, cuando se considera el escenario de operación con cargas desbalanceadas para ambos sistemas de prueba.
Es importante mencionar que, para estos sistemas de prueba solo existen reportes en el escenario desbalanceado con el método ABV presentado en 8.
Sistema de prueba de 8 nodos
En la tabla VIII se presentan los resultados comparativos entre el AMN y el ABV. En estos resultados es posible notar que ambas metodologías de solución alcanzan la misma solución óptima, con un costo de inversión y operación anual equivalente a US$ 558.758,394, de los cuales el 51,85 % están asociados a la inversión en conductores, y el 49,15 % están asociados al costo anual de las pérdidas de energía.
Tabla VIII: Solución obtenida por el AMN y su comparación con el ABV para el escenario de operación desbalanceado

Sistema de prueba de 27 nodos
En la tabla IX se presenta la comparación entre los resultados del ABV y el AMN propuesto.
Tabla IX: Solución obtenida por el AMN y su comparación con el ABV para el escenario de operación desbalanceado
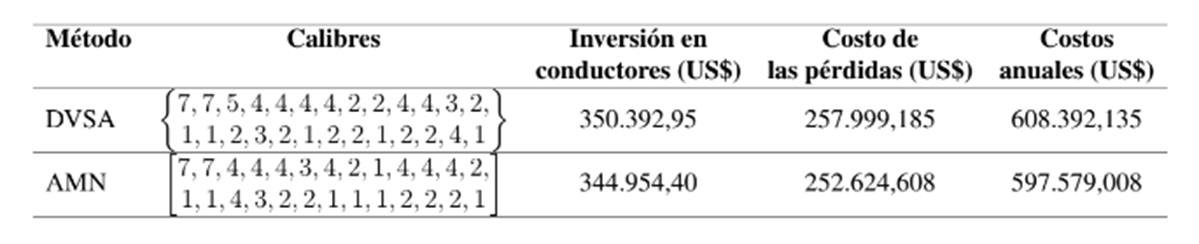
De los resultados de la tabla IX es importante notar que: (i) el costo de inversión en conductores y el costo anual de pérdidas se reducen en la solución obtenida mediante el AMN, siendo estos de US$344.954,40, y US$252.624,608, respectivamente; mientras que los costos obtenidos por el método AVB son en su orden de US$ 350.392, 95, y US$ 257.999, 185. (ii) La ganancia neta obtenida por el AMN en comparación con ABV es de US$10.813,127, de los cuales el 50,30 % se logra por reducción del costo de inversión y el 49,70 % por la reducción en los costos de operación, p. ej. el costo de las pérdidas de energía esperadas durante el horizonte de planeación.
Análisis complementario
Según los resultados en los sistemas de prueba de 8 y 27 nodos para los escenarios de prueba balanceados y desbalanceados, se puede afirmar que:
-
El AMN alcanza los mismos resultados que el ABV para el sistema de 8 nodos en sus versiones balanceadas y desbalanceadas, lo cual permite inferir que para este sistema de distribución, es posible que esta solución corresponda a la solución óptima global. Esto debido a que, para este sistema de prueba la dimensión del espacio de solución es 87 siendo 8 los calibres disponibles, y 7 el número de líneas a asignar, lo que define una dimensión equiva lente a 2.097.152. Este resultado para el sistema de 8 nodos en ambos escenarios de prueba fue corroborado mediante la exploración exhaustiva de todo el espacio de soluciones.
-
El AMN para el sistema de 27 nodos demuestra superioridad numérica en relación con el ABV, llegando a soluciones de mejor calidad, convirtiendo los resultados del AMN en el punto de referencia para futuras investigaciones. El éxito del método propuesto en esta investigación se puede atribuir a las propiedades de exploración y explotación del espacio de soluciones que tiene este método debido a su fortaleza matemática en la construcción de dichas reglas.
-
Como era de esperarse, el costo final de operación e inversión las topologías de 8 y 27 nodos es mayor en el escenario de operación desbalanceado, lo cual se atribuye al hecho de que las pérdidas de energía incrementan por la asimetría en las cargas; además, en todos los casos de simulación, el costo de inversión en conductores aumenta, debido a que la selección del calibre depende de la corriente de mayor magnitud en cada Iínea, independiente de la fase en la que esta se presente.
Con respecto al desempeño numérico después de las 100 ejecuciones del AMN se encontró que el tiempo promedio de solución para el sistema de prueba de 8 nodos fue de 40 s para ambos escenarios de prueba; mientras que para el sistema de prueba de 27 nodos este tiempo fue de 95 s. Estos tiempos son importantes, porque muestran que para dimensiones exponenciales del espacio de solución 826, el tiempo de procesamiento es menor a 2 minutos, encontrando soluciones de muy buena calidad, con las cuales se mejoran los mejores reportes existentes en la literatura especializada.
Conclusiones y trabajos futuros
El problema de selección óptima de conductores en sistemas de distribución trifásicos considerando escenarios de operación bałanceado y desbalanceado fue abordado en esta investigación, mediante la aplicación del algoritmo metaheurístico de Newton a través de una estrategia de optimización del tipo maestro-esclavo. En la etapa maestra, el AMN determina el conjunto de calibres a ser instalado en la red de distribución; mientras que, la etapa esclava evalúa un flujo de potencia trifásico para determinar el costo de pérdidas anuales; así como, el cumplimiento de las restricciones de capacidad de transporte de corriente en los conductores, y la regulación de tensión en todos los nodos del Sistema.
Los resultados numéricos para el sistema de 8 nodos mostró que el AMN alcanza los mismos resultados reportados por el ABV con una función objetivo de US$508.357,959 para el caso balanceado, y US$558.758,394 para el escenario de operación desbalanceado; siendo estos resultados de mejor calidad cuando se compararon el AGT, el AGCB, el ABT y la solución exacta del modelo de PNLEN en el software GAMS. En el caso del sistema de 27 nodos, el AMN mejora los resultados de referencia de la literatura obtenidos con el ABV, siendo esta mejora de US$4.329,222 en el caso de operación balanceado, y US$10.813,127, lo cual convierte al método propuesto en la metodología de referencia para comparar nuevos métodos de optimización aplicables al problema de selección de conductores en sistemas trifásicos.
Respecto a los tiempos de procesamiento, los resultados del AMN muestran que se tarda en promedio 40 s para resolver el problema estudiado en el sistema de 8 nodos, y alrededor de 95 s para el sistema de 27 nodos, lo cual corresponde a tiempos de cómputo excelentes considerando que las dimensiones del espacio de solución para estos sistemas son del orden de 87 y 826, siendo el primero del orden de dos millones de posibilidades, el segundo del orden de trescientos mil trillones, p. ej., 3.0231454903657 X 1023
Como trabajos futuros se proponen los siguientes: (i) el desarrollo de una metodología de optimización para la selección de conductores en sistemas de distribución que tenga en cuenta de manera simultánea el problema de balance óptimo de fases con el fin de reducir los costos de inversión y operación de la red cuando se compare con el caso desbalanceado presentado en este trabajo; y (ii) aplicar el algoritmo de optimización basado en el gradiente al problema de selección óptima de conductores y comparar sus resultados con el AMN.
Acknowledgements
Agradecimientos
Este proyecto de investigación en la modalidad de producción académica ha sido desarrollado por los estudiantes Daniel Julián Nivia Torres y Guillermo Alejandro Salazar Alarcón en el marco de los requisitos de grado del Proyecto Curricular de Ingeniería Eléctrica de la Facultad de Ingeniería de la Universidad Distrital Francisco José de Caldas.
References
Licencia
Derechos de autor 2022 Daniel Julián Nivia Torres, Guillermo Alejandro Salazar Alarcón, Oscar Danilo Montoya Giraldo

Esta obra está bajo una licencia internacional Creative Commons Atribución-NoComercial-CompartirIgual 4.0.
A partir de la edición del V23N3 del año 2018 hacia adelante, se cambia la Licencia Creative Commons “Atribución—No Comercial – Sin Obra Derivada” a la siguiente:
Atribución - No Comercial – Compartir igual: esta licencia permite a otros distribuir, remezclar, retocar, y crear a partir de tu obra de modo no comercial, siempre y cuando te den crédito y licencien sus nuevas creaciones bajo las mismas condiciones.



2.jpg)