DOI:
https://doi.org/10.14483/23448393.3498Published:
1999-11-30Issue:
Vol. 5 No. 1 (2000): January - JuneSection:
Academy and developmentEntropía en VQ-VMF de señal E.C.G
ENTROPY IN VO-VMF OF E. C. G. SIGNAL
Keywords:
código de bloques, entropía, información, cuantificación vectorial, valor medio, clasificador, señal e.c.g. (es).Downloads
References
Carpenter, G., y Grossberg, S. The ART of adaptive pattern recognition by a self-organizing neural network. Computer. 21. 1988.
Grossberg, S. Neural Networks and Natural Intelligence. Cambridge, MA: MIT Press. 1988.
Bradski, G y Grossberg, S. East LearningVIEWNET architectures for recognizing 3-D objects from multiple 2-D views. Technical Report CAS/CNSTR-93-053. Boston University. 1995.
Grossberg, S. y Mingolla, E. Neural dynamics of perceptual grouping; textures, boundaries and emergent segmentations. Perception and Psychophysics. 38. 1985.
Kelly, E, y Grossberg, S. Neural dynamics of 3-D perception: figure-ground separation and lightness perception. Technical Report CAS/CNS TR-98-026. Boston University. 2000.
Cavanagh, P. Image transforms in the visual system. En Fi gural Synthesis. Hillsdale, NJ. 1984.
Carpenter, G. A., et al. A what-and-where neural network for invariant image pre processing. Proceedings of the International Joint Conference on Neural Netwoks. 1992.
Carpenter, G. A., et al. The What-and-Where filter a spatial mapping neural network for object recognition and image understanding. Technical Report CAS/CNS-93-043. Boston University. Junio 1993.
Grossberg, S. Studies of mind and brain. Boston. 1982.
Seibert, M, y Waxman, A. M Spreading activation layers, visual saccades, and invariant representations ofneural pattern recognition systems. 1989.
Carpenter, G. A., y Grossberg, S. A massively parallel architecture for self-organizing neural pattern recognition machine. Computer Vision, Graphics an Image Processing. 37. 1987.
Carpenter, G. A., et al. Fuuzy ART an adapti ve resonance algorithm for rapid, stable classification of analog patterns. Proceedings of the International Joint Conference on Neural Networks. 1991.
Moore, B. ART 1 and pattern clustering. Proceedings of the 1988 Conneccionist Models Summe
Artículo 7
.APARICIO P Lilia Edith, Análisis de Información para transmisión de VQ-VME aplicado a señal E. C. G., Primer Congreso Internacional de Electrónica y Tecnologías de Avanzada, Pamplona, 1999.
.CÁRDENAS BARRERA J. M, LORENZO GINORI J. V Compresión de datos electrocardiogra'ficos empleando cuantificación vectorial. Universidad Central de las Villas. Facultad de ingeniería eléctrica. Santa Clara, Cuba (1998).
PEDROSO VALDES Oscar, PEREZ GARCIA Marcos. Fundamentos de comunicación estadística. Ed Pueblo y educación. Ciudad de la Habana. (1987).
BERNAL Giovanni, SÁNCHEZ Juan Manuel, Análisis de Información para Cuantificación Vectorial, aplicado a ECG, Trabajo de Grado, Universidad Distrital, 1999.
ARANGO E.. Juan, Manual de Electrocardiografia, Corporación para Investigaciones Biológicas, Cuarta Edición, Medellín, 1996
SHANNON C.E. A mathemati cal theory of communications. Bell systems technical journal27p. 379-423.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Academia y Desarrollo
Ingeniería, 2000-00-00 vol:5 nro:1 pág:47-52
Entropía en VQ-VMF de señal E.C.G
ENTROPY IN VO-VMF OF E. C. G. SIGNAL
Lilia Edith Aparicio P.
Profesora Facultad de Ingeniería, Magister en Teleinformática, Candidato a Doctor en Ciencias Técnicas, Directora del Grupo de Investigación en Telemedicina Universidad Distrital. E-mail: medicina@udistrital.edu.co.
Giovanni Alejandro Bernal R.
Ingeniero Electrónico,U. Distrital integrante del grupo de investigación en Telemedicina.
Juan Manuel Sánchez C.
Ingeniero Electrónico, U. Distritalintegrante del grupo de investigación en Telemedicina.
Resumen
Este artículo describe el proceso de medición de la cantidad de información que portan los datos generados a la salida de un cuantificador vectorial Valor Medio Forma de Onda. Se tienen en cuenta los tres datos que entrega el proceso (valor medio, clasificador, índice del libro de códigos) por cada vector conformado por 40 muestras de la señal ECG. El dato valor medio se agrupo en 9 diferentes estados; El dato clasificador e índice se agruparon en conjunto en 29 estados; las pruebas se realizaron con 400 señales ECG.
Palabras Claves:
código de bloques, entropía, información, cuantificación vectorial, valor medio, clasificador, señal e.c.g.
Abstract
This article describes the information measuring process carried by the generated output data from a Wave Shape Mean Value Vectorial Quantifier. Three data delivered by the process are taken into account, i.e., the mean value, the clasifier and the code book index. This is for every 40 samples of the E.C.G. signal. The mean value was grouped in 9 different states, the clasifier and index code book were gruoped together in 29 states. The samples were taken out from 400 E.C.G. signals.
Key Words:
block codes, entropy, information, vector quantization, mean, clasiffier. e.c.g. signal.
INTRODUCCIÓN
Un problema frecuente al analizar y modelar la transmisión de información, es la necesidad de calcular la cantidad de información promedio o entropía que genera una fuente de información; en el caso particular de un cuantificador vectorial con separación del valor medio aplicado a la señal electrocardiográfica, se debe conocer dicha entropía; esta cantidad es un parámetro importante para modelar é sistema de transmisión porque genera información comprimida y es la cantidad que se compara con la transinformación en el canal de comunicaciones y la entropía de recepción. [1].
Para obtener la entropía que posee esta fuente de información, se hace indispensable reconocer los datos que genera el algoritmo y su proceso.El algoritmo propuesto "cuantificación vectorial con separación del valor medio (VQ-VMF)" con clasificación de energía diseñado por Cárdenas Barrera y Lorenzo Ginori [2], cuantifica la forma de onda (para ello se consideran vectores de 40 muestras) de la señal E.C.G por medio de dos libros de código, uno para vectores de alta energía (conformado por 1024 elementos) y otro para vectores de baja energía (64 elementos); la elección del libro de códigos con el cual se hace la cuantificación a un vector dado depende de la energía del mismo, la cual se indica con 1 (uno) para los de alta energía y O (cero) para los de baja energía; la cuantificación del valor medio se realiza escalarmente.
Este algoritmo toma segmentos de la señal ECG con una dimensión de 40 muestras denominado vector, a éste se le calcula su valor medio, con este valor se calcula la forma del vector el cual es: Vector forma = vector -- valor medio del vector, a partir de esto se determina la energía que posee eligiendo el libro con el cual se cuantifica, por último, se indica la posición del vector prototipo que representa al Vector forma con un error mínimo dentro del libro de códigos; este último dato se denomina índice; en consecuencia, la información que genera esta fuente de información está contenida en el valor medio, el indicador (o clasificador) de energía del vector y el índice del vector.
CARACTERÍSTICAS DE LA FUENTE
Inicialmente se caracterizó la fuente de información a la cual pertenece el algoritmo VQ-VMF con clasificación de energía. Para esto se realizaron pruebas, las cuales arrojan los siguientes resultados: debido a que la cuantificación se puede realizar en cualquier momento ya que los resultados de dicho proceso no dependen del momento en que se realice, se dice entonces que la fuente de estudio es estacionaria. Los datos que entrega la fuente dependen fundamentalmente, de la persona a la que se le hace la toma de la señal E.C.G. y de la derivación donde haya sido tomada.
Como la señal E.C.G es cuasiperiódica, posee una alta autocorrelación, debido a esta característica es lógico pensar que los datos que arroja el algoritmo poseen una dependencia estadística en cada uno de los estados que presenta la fuente. Por esto se puede decir que la fuente aquí presentada cumple con un proceso de markov (la probabilidad de un estado depende por lo menos del estado inmediatamente anterior), lo que define la fuente como ergódica [3] .
Debido a que cada uno de los posibles estados han sido analizados con una secuencia de entrenamiento bastante amplia, se tiene, que cada uno de los índices es utilizado al menos una vez durante la compresión. Recuerde que el algoritmo de compresión estudiado entrega los siguientes datos por cada uno de los vectores: (Rm, Clasificador, Rv), Rm es la longitud de bits para describir el valor medio (Rm=8), el clasificador posee un valor de '0' cuando se hace la cuantificación vectorial con el libro de códigos para vectores de baja energía y ' 1 ' para cuantificar los de alta energía con el libro de códigos correspondiente, Rv es la longitud de bits del índice perteneciente al libro de códigos seleccionado, este valor puede ser de 6 para el libro de baja energía y 10 para el de alta energía.
Analizando las posibles combinaciones de cada uno de los valores Rm, Clasificador, Rv se tiene:
2Rm*2*2 Rv Posibles combinaciones para describir a un vector. Así, si el vector es de baja energía se tienen:
28*2*26= 256*1*64= 32768 Posibles vectores de baja energía teóricos y
28*2*26= 256*1 = 524288 Posibles vectores de alta energía teóricos.
Lo anterior da como resultado:
16384 + 262144 = 557.056 Posibles vectores teóricos diferentes.
Si se considerara cada posible vector teórico como un estado, el cálculo de la información que posee cada dato sería casi imposible.
MODIFICACIONES PARA EL CÁCULO DE ENTROPÍA
Para hacer posible el estudio de información promedio (entropía) de los datos a la salida del cuantificador, fue necesario realizar algunas modificaciones, las cuales son el producto de un análisis lógico, basándose en la señal E.C.G.
Para realizar las modificaciones que a continuación se explican, se tomó la decisión de ordenar los dos libros de códigos, de tal forma que los primeros índices indican la posición de los vectores de mayor energía y a medida de que el índice se incrementa, su energía disminuye; por ejemplo, en el libro de alta energía, el índice I=1 tiene una energía de 74, mientras que el índice I=10 tiene una energía de 52 y el índice 1=500 posee una energía de 20. [4].
Modificaciones del dato "índice", el dato "índice" es el que encuentra en el libro de códigos al vector forma de onda (vector prototipo) para la respectiva reconstrucción. Sus valores pueden diferir de (1-64) para el libro de baja energía y de (1-1024) para el libro de alta energía, lo cual da un total de 1088 posibles valores de índices.
Con esta observación se tomó la decisión de agrupar los vectores prototipos de los libros de códigos, en estados dependiendo de sus características. Estas características fueron divididas para cada libro de códigos (de alta o baja energía). Para lograr entender lo que significa la clasificación de los índices en estados realizada, se tuvo en cuenta cada forma de onda mostrada en la figura 1
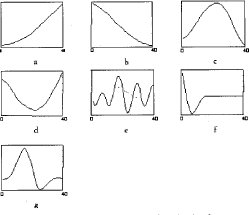
En la figura la se aprecia un "vector ascendente", en la figura l-b - Se observa un "vector descendente", la Figura lc posee un "vector picudo", en la Figura ld se muestra lo que se denominó "depresión", la Figura le presentan señales oscilantes denominadas "ondulaciones", en la Figura lfse muestra la gráfica de una "depresión media", nótese que se trata de una depresión, pero en la parte derecha solo alcanza un nivel medio, en la Figura 1 g se presenta el vector "picos medios" el cual posee una diferencia apreciable gráficamente con el "vector picudo" (figura 1c).
En definitiva se agruparon todos los posibles índices (1024+64=1088 en total) dentro de 29 estados, fue el punto ideal, después de entrenar con muchas posibilidades.
Modificaciones del dato "Valor Medio", cuando se realiza la compresión con el procedimiento (VQVMF), se genera fuera de otros, el dato valor medio.
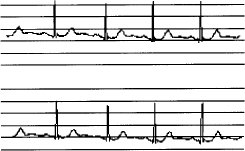
Este como ya se ha explicado se cuantifica de forma escalar uniforme; con este tipo de codificación de 8 bits, se logran valores medios de hasta 256 valores diferentes. Si se analiza detenidamente como se presenta el registro cardíaco en un E.C.G, se puede apreciar que la serial puede comenzar en cualquier posición en la escala vertical sin que afecte su resultado (podría llamarse su valor D.C); en la figura 2 se aprecia este comentario, pues el diagnóstico se basa en magnitudes diferenciales sobre la señal y no en su posición sobre el papel.
Debido a que no se podría determinar este valor, se tomó la decisión de realizar la cuantificación del valor medio de forma diferencial, donde el valor medio diferencial es un incremento o decremento respecto
Por lógica se puede hacer una relación de este valor medio diferencial respecto al estado del índice que se asocia al mismo vector. Así, el código que describe a un vector es determinado por el estado del índice (EI) y el valor medio diferencial (VMD). Este código será (EI,VMD).
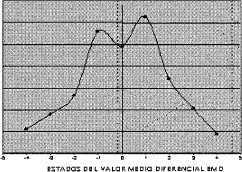
La relación que se puede encontrar depende fundamentalmente de la característica del EI, en el caso de un EI cuya característica sea un vector ascendente, es de esperar, que el valor medio sufra un incremento dependiendo de la pendiente de dicha subida. Por otro lado, si el vector es descendente, es lógico pensar que su valor medio puede decrecer con una alta probabilidad. Debido a estas afirmaciones respecto a la relación existente entre el valor medio y el EI, se decide realizar el análisis para el valor medio en forma diferencial. Con esta modificación se realizaron algunos cálculos de probabilidad para el valor medio diferencial de la señal cardíaca E.C.G tratada con VQ-VMF. (Véase Figura 3).
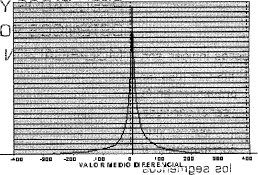
En la figura anterior, se observa que la mayor probabilidad para el valor medio diferencial está cercana a valores próximos a cero, esto se explica debido a que la señal E.C.G en la mayor parte del tiempo no presenta variaciones; las variaciones fuertes tanto de forma de ondá como del valor medio diferencial generalmente sólo se encuentran en el complejo QRS. Debe recordarse que la duración de dicho complejo respecto al período de la señal es muy pequeña [5], por ello el anterior resultado.
También con base en la figura 3, se pueden agrupar estos valores medios diferenciales, al igual que el dato índice, en estados de valor medio diferencial (EMD). Para realizar la cuantificación del valor medio diferencial, se emplearon 11 bits para dicho fin. En conclusión, se tienen 9 estados para el valor medio, esta agrupación fue realizada de esta forma para lograr mayor detalle en valores pequeños de valor medio diferencial (hay gran probabilidad de aparición de este estado), mientras que valores medios diferenciales grandes tienen baja probabilidad de aparición.
Estudio conjunto del EI y del EMD, teniendo en cuenta los dos epígrafes anteriores, se toma el dato completo como el conjunto (EI, EMD), estos dos estados representan en definitiva a un vector en particular y muestra sus características tanto de forma como de valor medio diferencial que éste presenta. Inicialmente se ha dicho que los estados de los índices (FI) son 29 y que los estados del valor medio diferencial (EMD) son 9; en consecuencia, se pueden calcular "Macroestados" (ME) como el conjunto (EI, EMD), con un número de (ME =29x9 =261) posibles combinaciones.
RESULTADOS Y DATOS OBTENIDOS POR LA MODIFICACIÓN
A continuación se muestran las probabilidades de aparición de los diferentes datos modificados por los autores, para luego calcular la información promedio (entropía) que posee esta fuente de información.
Inicialmente se presenta la probabilidad de aparición de los EI, los cuales son los que más aportan información. En la figura 4, se presenta dichoesquema, se aprecia que los estados más bajos (1 ,2,3...,11) son los que presentan una mayor probabilidad de repetición; esto se debe a que precisamente estos estados hacen referencia o contienen a los índices de baja energía; como se ha expresado anteriormente, éstos índices son los que más se presentan en la señal cardíaca puesto que corresponden a los segmentos isoeléctricos y a las ondas (P,T,U); donde estos segmentos son los que mayor duración respecto al período de la señal, entonces, la cantidad de datos promedio de estos segmentos son en comparación con el complejo QRS elevados, los estados correspondientes a los complejos QRS están implícitos desde los EI (12,13...29)
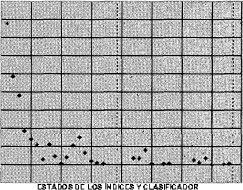
Ahora, el mismo estudio se aplicó para los estados del valor medio diferencial (EMD). La figura 5, muestra la probabilidad de aparición de cada uno de los nueve posibles estados (EMD), se puede apreciar que los estados que corresponden a niveles bajos de valor medio son los que predominan en la gráfica, es el caso de los estados EMD ( - 1,0,1), de igual manera, este resultado es justificado debido a que como los EI que más aparecen son los de baja energía, su variación respecto al valor medio diferencial es muy baja; estos valores medios diferenciales, por lo tanto, corresponderán a los segmentos isoeléctricos y a las ondas (P,T,U). Los EMD (-4,-3,-2,2,3,4) corresponden por lo general a los complejos QRS, los EMD negativos están relacionados con decrementos del valor medio, mientras que los positivos a incrementos de dicho valor.
ENTROPÍA DE LA FUENTE DE INFORMACIÓN
Cada posible vector emitido por la fuente modificada, está representado por un macroestado ME descrito en los epígrafes anteriores, como la combinación de los estados de índice EI, los cuales se cuentan como 29 y los estados del valor medio diferencial EMD que son nueve; como consecuencia ME=(EI, EMD) y son un total de (29*9= 261) posibles macroestados teóricos. Gracias a una extensa secuencia de entrenamiento, se ha determinado experimentalmente que de dichos 261 macroestados teóricos, sólo 232 son los que la fuente de información genera para señales reales; como consecuencia se ha reducido la redundancia de la fuente.
Estos 232 ME reales y posibles son los que conforman la matriz de transición; como ya se sabe su dimensión será de (232*232). Esta matriz es de suma importancia para el cálculo de la entropía en una fuente de markov. Esta matriz se ha formado utilizando secuencias de señales reales aplicadas al algoritmo de compresión propuesto y con ayuda de las modificaciones mencionadas se ha establecido cada una de las probabilidades de transición de un macroestado a otro.
Con dicha matriz se realizaron los cálculos de:
a. Las probabilidades finales de los macroestados.
b. Las probabilidades condicionales de transición entre estados
Las probabilidades calculadas, son los requisitos necesario para calcular la entropía de una fuente de markov cualquiera [6]. Para la determinación de las probabilidades finales de los ME de la fuente, se emplean las ecuaciones que se presentan a continuación:

La primera expresión que debe ser interpretada como:
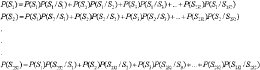
Recuerde que la estructura de la matriz de transición es como se expresa a continuación:

Con ayuda de los datos que se obtienen de la matriz de transición y las probabilidades finales se calcula la entropía de esta fuente de markov por medio de la ecuación que se presenta:
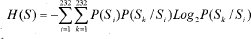
El resultado de la ecuación anterior es:
H(S) = 4.2393 shannon / símbolo
Y la entropía de la fuente adjunta para esta fuente de markov se encuentra con la ecuación:=
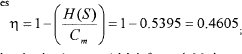
Recuerde que la fuente adjunta es una fuente sin memoria con el mismo alfabeto que la fuente de estudio, las probabilidades son las mismas probabilidades finales encontradas para la fuente de markov estudiada.
Por último debe recordarse que la capacidad del símbolo (Cm) es la máxima entropía que puede posee una fuente y para este caso su valor es:
Cm= Log2 (232) = 7.858 shannon / símbolo
De todo lo anterior se encuentran los siguientes valores:
H(S)/Cm= 4.2393/ 7.858 = 0.5395
La entropía relativa de la fuenté es:; la redundancia es
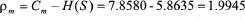
H(S) < H(S)<Log2 (232)
Lo cual significa que la entropía de la fuente de markov es menor o igual a la entropía de su fuente adjunta, ya que al añadir la restricción de la dependencia estadística entre los estados en las secuencias de mensajes, ha disminuido en contenido de información promedio por símbolo; es de esperar que la entropía de la fuente adjunta sea menor a la capacidad del símbolo, ya que las probabilidades finales de la fuente de Markov no son equiprobables.
CONCLUSIONES Y RECOMENDACIONES
Dentro del vector cuantificado, compuesto por valor medio, clasificador e índice; se ha determinado que el último de sus componentes es el que contiene mayor información dentro de éste. Es decir, el índice es el que determina la forma de la señal y por tanto una posible equivocación en él ocasionaría un grave error en la reconstrucción de la señal E.C.G, lo cual sería lamentable para el diagnóstico médico.
Al modelarse los datos generados por el algoritmo de compresión como una fuente de Markov, se aprecia que la entropía de ésta es menor que la entropía de su matriz adjunta. La diferencia entre estas cantidades, indica la pérdida promedio de información por símbolo que se obtiene al inferir una dependencia estadística entre cada uno de ellos y se puede aseverar que existe una mayor redundancia para dicha fuente.
Dado que la redundancia absoluta de la fuente de información analizada es mayor a cero, se puede decir que ésta debe y puede ser eliminada en una futura etapa de codificación para lograr una transmisión óptima.
Debido a que el diagnóstico utilizando la técnica de señal electrocardiográfica no depende sustancialmente de la posición vertical de dicha señal, el tipo de codificación del valor medio utilizado debería hacerse de forma diferencial, ya que limita sus posibles valores respecto a la cuantificación uniforme, el cual toma valores independientes de cualquier otro dato.
REFERENCIAS
(1). APARICIO P Lilia Edith, Análisis de Información para transmisión de VQ-VME aplicado a señal E. C. G., Primer Congreso Internacional de Electrónica y Tecnologías de Avanzada, Pamplona, 1999.
(2) CÁRDENAS BARRERA J. M, LORENZO GINORI J. V Compresión de datos electrocardiogra'ficos empleando cuantificación vectorial. Universidad Central de las Villas. Facultad de ingeniería eléctrica. Santa Clara, Cuba (1998).
(3)PEDROSO VALDES Oscar, PEREZ GARCIA Marcos. Fundamentos de comunicación estadística. Ed Pueblo y educación. Ciudad de la Habana.(1987).
(4)BERNAL Giovanni, SÁNCHEZ Juan Manuel, Análisis de Información para Cuantificación Vectorial, aplicado a ECG, Trabajo de Grado, Universidad Distrital, 1999.
(5) ARANGO E.. Juan, Manual de Electrocardiografia, Corporación para Investigaciones Biológicas, Cuarta Edición, Medellín, 1996
(6)SHANNON C.E. A mathemati cal theory of communications. Bell systems technical journal 27p. 379-423.
Creation date:
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.





2.jpg)










