DOI:
https://doi.org/10.14483/23448393.18468Published:
2022-01-05Issue:
Vol. 27 No. 1 (2022): January-AprilSection:
Sección Especial: Mejores artículos extendidos - WEA 2021A P-Robustness Approach for the Stochastic Inventory Routing Problem
Una aproximación a través del modelo p-robusto para el problema estocástico de ruteo e inventario
Keywords:
problema de ruteo e inventarios, p-robusto, incertidumbre (es).Keywords:
inventory routing problem, p-robustness, uncertainty (en).Downloads
References
L. C. Coelho, J.-F. Cordeau, and G. Laporte, “Consistency in multi-vehicle inventory-routing,” Transp. Res. Part C. https://doi.org/10.1016/j.trc.2012.03.007
C. Franco-Franco and J. C. Figueroa-García, “A column generation-based algorithm for solving combined inventory and routing problems,” Ingeniare, vol. 24, no. 2, 2016, doi: https://doi.org/10.4067/S0718-33052016000200012 DOI: https://doi.org/10.4067/S0718-33052016000200012
E.-H. Aghezzaf, B. Raa, and H. Van Landeghem, “Modeling inventory routing problems in supply chains of high consumption products,” Eur. J. Oper. Res., vol. 169, no. 3, pp. 1048–1063, Mar. 2006, doi: https://doi.org/10.1016/j.ejor.2005.02.008 DOI: https://doi.org/10.1016/j.ejor.2005.02.008
C. Archetti, L. Bertazzi, G. Laporte, and M. G. Speranza, “A Branch-and-Cut Algorithm for a Vendor-Managed Inventory-Routing Problem,” Transp. Sci., vol. 41, no. 3, pp. 382–391, Aug. 2007, doi: https://doi.org/10.1287/trsc.1060.0188 DOI: https://doi.org/10.1287/trsc.1060.0188
L. C. Coelho and G. Laporte, “The exact solution of several classes of inventory-routing problems,” Comput. Oper. Res., vol. 40, no. 2, pp. 558–565, 2013, doi: https://doi.org/10.1016/j.cor.2012.08.012
E. Yadollahi, E. H. Aghezzaf, J. Walraevens, B. Raa, and D. Claeys, “Evaluating approximate solution models for the stochastic periodic inventory routing problem,” J. Manuf. Syst., vol. 50, pp. 25–35, Jan. 2019, doi: https://doi.org/10.1016/j.jmsy.2018.11.001 DOI: https://doi.org/10.1016/j.jmsy.2018.11.001
L. C. Coelho and G. Laporte, “The exact solution of several classes of inventory-routing problems,” Comput. Oper. Res., vol. 40, no. 2, pp. 558–565, 2013, doi: https://doi.org/10.1016/j.cor.2012.08.012 DOI: https://doi.org/10.1016/j.cor.2012.08.012
E. H. Aghezzaf, “Robust distribution planning for supplier-managed inventory agreements when demand rates and travel times are stationary,” J. Oper. Res. Soc., vol. 59, no. 8, pp. 1055–1065, 2008, doi: https://doi.org/10.1057/palgrave.jors.2602444 DOI: https://doi.org/10.1057/palgrave.jors.2602444
L. C. Coelho, J. F. Cordeau, and G. Laporte, “Heuristics for dynamic and stochastic inventory-routing,” Comput. Oper. Res., vol. 52, no. PART A, pp. 55–67, Dec. 2014, doi: https://doi.org/10.1016/j.cor.2014.07.001 DOI: https://doi.org/10.1016/j.cor.2014.07.001
M. Rahimi, A. Baboli, and Y. Rekik, “Multi-objective inventory routing problem: A stochastic model to consider profit, service level and green criteria,” Transp. Res. Part E Logist. Transp. Rev., vol. 101, pp. 59–83, May 2017, doi: https://doi.org/10.1016/j.tre.2017.03.001 DOI: https://doi.org/10.1016/j.tre.2017.03.001
R. Diaz, M. P. Bailey, and S. Kumar, “Analyzing a lost-sale stochastic inventory model with Markov-modulated demands: A simulation-based optimization study,” J. Manuf. Syst., vol. 38, pp. 1–12, Jan. 2016, doi: https://doi.org/10.1016/j.jmsy.2015.09.007 DOI: https://doi.org/10.1016/j.jmsy.2015.09.007
W. J. Bell et al., “Improving the Distribution of Industrial Gases with an On-Line Computerized Routing and Scheduling Optimizer,” Interfaces (Providence)., vol. 13, no. 6, pp. 4–23, Dec. 1983, doi: https://doi.org/10.1287/inte.13.6.4 DOI: https://doi.org/10.1287/inte.13.6.4
Q. J. Yeh, T. P. Chang, and H. C. Chang, “An inventory control model with Gamma distribution,” Microelectron. Reliab., vol. 37, no. 8, pp. 1197–1201, Aug. 1997, doi: https://doi.org/10.1016/S0026-2714(96)00295-8 DOI: https://doi.org/10.1016/S0026-2714(96)00295-8
F. Rayat, M. Musavi, and A. Bozorgi-Amiri, “Bi-objective reliable location-inventory-routing problem with partial backordering under disruption risks: A modified AMOSA approach,” Appl. Soft Comput., vol. 59, pp. 622–643, 2017, doi: https://doi.org/10.1016/j.asoc.2017.06.036 DOI: https://doi.org/10.1016/j.asoc.2017.06.036
L. C. Coelho, J.-F. Cordeau, and G. Laporte, “Consistency in multi-vehicle inventory-routing,” Transp. Res. Part C Emerg. Technol., vol. 24, pp. 270–287, Oct. 2012, doi: https://doi.org/10.1016/j.trc.2012.03.007 DOI: https://doi.org/10.1016/j.trc.2012.03.007
L. C. Coelho and G. Laporte, “Optimal joint replenishment, delivery and inventory management policies for perishable products,” Comput. Oper. Res., vol. 47, pp. 42–52, Jul. 2014, doi: https://doi.org/10.1016/j.cor.2014.01.013 DOI: https://doi.org/10.1016/j.cor.2014.01.013
L. V. Snyder and M. S. Daskin, “Stochastic p -robust location problems,” IIE Trans., vol. 38, no. 11, pp. 971–985, Nov. 2006, doi: https://doi.org/10.1080/07408170500469113 DOI: https://doi.org/10.1080/07408170500469113
C. Franco, V. Augusto, T. Garaix, E. Alfonso-Lizarazo, M. Bourdelin, and H. Bontemps, “Strategic territorial deployment of hospital pharmacy robots using a stochastic p-robust optimization approach,” in 2018 IEEE 14th International Conference on Automation Science and Engineering (CASE), Aug. 2018, pp. 390–395, doi: https://doi.org/10.1109/COASE.2018.8560374 DOI: https://doi.org/10.1109/COASE.2018.8560374
C. Franco Diana Guzmán Cortés Juan Carlos Figueroa García and N. L. Díaz Aldana, “Mathematical model for centralized supply chains with sharing resources decisions,” Ingeniería, vol. 25, no. 3, Oct. 2020, doi: https://doi.org/10.14483/23448393.16921 DOI: https://doi.org/10.14483/23448393.16921
C. Franco and E. Alfonso-Lizarazo, “Optimization under uncertainty of the pharmaceutical supply chain in hospitals,” Comput. Chem. Eng., vol. 135, p. 106689, Apr. 2020, doi: https://doi.org/10.1016/j.compchemeng.2019.106689 DOI: https://doi.org/10.1016/j.compchemeng.2019.106689
F. Morales, C. Franco, and G. Mendez-Giraldo, “Dynamic inventory routing problem: Policies considering network disruptions,” Int. J. Ind. Eng. Comput., vol. 9, no. 4, 2018, doi: https://doi.org/10.5267/j.ijiec.2017.11.001 DOI: https://doi.org/10.5267/j.ijiec.2017.11.001
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Recibido: 15 de agosto de 2021; Aceptado: 15 de septiembre de 2021
Abstract
Context:
Approaches to logistics solutions through mathematical optimization are widely studied in the literature given their importance for business operations and their computational complexity. In this way, studying the uncertainty associated to operations is a key factor in modeling and decision-making.
Method:
A stochastic mathematical model is proposed for the Inventory Routing Problem (IRP), considering scenarios with variation in the demands. To obtain a suitable approach, a p-robustness approach and the reformulation of the classical IRP are presented.
Results:
The performed experiments show the benefits of including uncertainty through a p-robust approach when they are analyzed within an instance of the IRP. Moreover, given the selected modeling, the benefits of combining the approaches can be analyzed.
Conclusions:
The development of stochastic approaches for decision-making applied to the IRP allow analysts to handle uncertainty and also reduce the complexity of decision when combining different types of problems (Routing + Inventory) in the same model.
Keywords:
inventory routing problem, p-robustness, uncertainty..Resumen
Contexto:
Las aproximaciones de soluciones logísticas a través de la optimización matemática son altamente estudiadas en la literatura debido a su importancia en las operaciones de las compañías y su complejidad computacional. En este sentido, el estudio de la incertidumbre asociada a la operación es un factor fundamental del modelamiento y la toma de decisiones.
Método:
Un modelo matemático estocástico es propuesto para el problema combinado de ruteo e inventario (IRP), considerando escenarios de variaciones en la demanda. Para obtener un enfoque adecuado, se presenta una aproximación de p-robusto y la reformulación del problema clásico de aplicación.
Resultados:
Los experimentos realizados muestran los beneficios de incluir la incertidumbre a través de la aproximación de p-robusto cuando se analizan en el marco de una instancia del IRP. También, dado el tipo de modelado seleccionado, se pueden analizar los beneficios de combinar las aproximaciones.
Conclusiones:
El desarrollo de aproximaciones estocásticas de toma de decisiones aplicadas al problema IRP permite a los analistas gestionar la incertidumbre y reducir la complejidad de las decisiones cuando se combinan diferentes tipos de problemas (Ruteo + Inventario) en un mismo modelo.
Palabras clave:
problema de ruteo e inventarios, p-robusto, incertidumbre..Introduction
Setting up all supply chain elements is a key factor that companies face in the short and long term (it is seen as a planning task). Most manufacturing and logistics companies aim to produce and/or distribute goods to final customers, so the role of an efficient supply chain and its distribution network is essential in order to guarantee profits, sustainability, and operability. In this way, the integration of decision-making at different levels becomes a key factor for any supply chain, and the integration of inventory routing decisions integrates tactical problems (inventory management) and operative problems (routing) 1. The integration of both levels into decision-making is known as the Inventory Routing Problem (IRP), inspired by the Vendor Managed Inventory (VMI) strategy, which consists of centralizing inventory-related decision-making.
Thereupon, the IRP implies coordinating two logistic decisions (inventory + routing), whose goal is to minimize the overall costs generated by inventory holding costs plus routing costs over a given planning horizon 2. The decisions to be taken are summarized as follows: when to deliver goods required by each customer, their quantities, and how to ship them all while considering several constraints such as allowable inventory levels and vehicle capacity 3, 4. This model has been widely studied in the literature because of its importance in terms of applicability, where most of its variants deal with different practical issues that require designing appropriate solution methods. Most of the literature deals with deterministic parameters; it considers decision-makers to have complete information beforehand, but several factors have no deterministic behavior, which creates the need to include uncertainty in the analysis (seen as a degree-of-freedom factor). Now, one of the main issues that affects logistic operations over the planning horizon are customer demands, which induce variability/uncertainty since they are hard to estimate in many cases 5.
This paper is organized as follows: Section 2 presents a literature review; in Section 3, the mathematical model of our proposal is presented; Section 4 presents the results in a practical scenario; and Section 5 shows the conclusions of the study.
Literature review
Several approaches deal with the classic inventory routing problem, and their main efforts are steered towards finding optimal solutions within reasonable computing times. One of the main approaches for optimally solving this deterministic problem was presented in (6, while its stochastic version is still a challenge. Some authors have approached solving the stochastic IRP; for instance 7presents an approach for the stochastic IRP considering two uncertainty sources, demands and travel times, which were also considered to be stationary, where the main approach is to solve a robust version of the IRP based on a robust optimal distribution plan solved by a combination of optimization and Monte Carlo simulation methods.
Similarly, 8 developed two approaches for solving two IRP instances: dynamic and stochastic. In the dynamic version, the information is revealed for each time period (i.e., demands which are considered as a source of uncertainty), so decision making happens at the beginning of each period. The stochastic version assumes the involvement of stochastic uncertainty, which affects predictions that are used for decision-making before demands occur. The authors then proposed the use of several heuristics to analyze how a moving horizon period increases computing efforts but does not improve the optimal solution of the problem.
A multi-objective approach is developed in 9, which is based on economic performance, shortage/delivery delays, and environmental footprint as three goals to be evaluated. The authors also considered different uncertainty sources such as the demands and transportation costs. The approach to modeling uncertainty is fuzzy sets and systems, which is divided into two parts: the first is the transformation of the proposed fuzzy mathematical model into an equivalent deterministic/crisp via a fuzzy possibilistic approach, while the second one corresponds to the NSGA-II (Non-Sorting Genetic Algorithm II).
In (10, the authors propose the use of Markov chains along with simulated annealing, pattern search/ranking, and selection procedures to evaluate near-optimal solutions. Authors also solve a periodical stochastic inventory model with auto correlated demands using empirical probability distributions. The proposed method is a simulation-based optimization approach whose results show that inventory performance significantly declines as autocorrelation increases and it is then disregarded.
An interesting IRP application of industrial gases is shown in 11, where the authors propose a Lagrangian relaxation method that obtains an approximate of 8 % in savings. Similarly, 12 presents an inventory control system with periodic review to analyze replenishment decisions by choosing an appropriate replenishment size with different service levels.
Another stochastic IRP is analyzed in 13. The authors propose the use of the order-up-to-level policy, which consists of replenishing when necessary up to the top level of inventory capacity. The main approach here is to penalize stockouts and model the problem as a dynamic programming problem using a hybrid rollout algorithm, which can reduce computing time of large instances to reasonable times, thus constituting an improvement of the benchmark algorithms existing in the literature.
Mathematical approach
The main formulation considers the same basic ideas presented by 1-3 handling stochastic uncertainty through the adaptation of the p-robustness criteria presented in 4 and 5, generating scenarios for modeling uncertainty such as those presented in (6. Therefore, the mathematical model contemplates a set of nodes Vp = 2, . . . , n as the set of customers, where node “1” corresponds to the central depot that distributes products to the network, where, at each time period t ∈ T, there is an amount rtt of product available at the depot.
For each time period, each customer has a demand dtst i that is uncertain and is modeled with the scenario s ∈ S. The variable I st i represents the inventory levels at the depot and the customers, where each has a lower (Li) and upper (Ci) bound to be kept in inventory. Moreover, the depot must decide if there will be a delivery made by a vehicle represented by the set K, which has a specific capacity Qk, and each delivery is modeled with the variable q kt i . Finally, there are the binary variables Xkt ij and Y kt i , which determine if a customer is visited or not. This model considers uncertainty mainly with a two-stochastic optimization approach 19, where first-stage decisions are related to selecting visiting customers, second-stage decisions are related to inventory levels (customers/depot), and the decisions related to the amount of goods to be delivered to each customer per scenario. The mathematical model used is as follows:

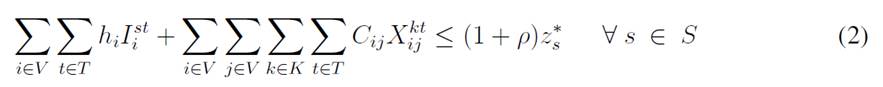
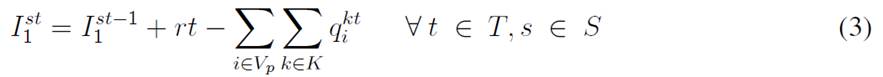

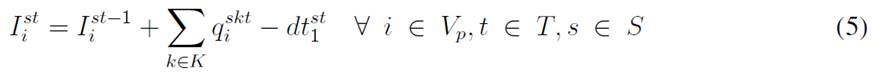
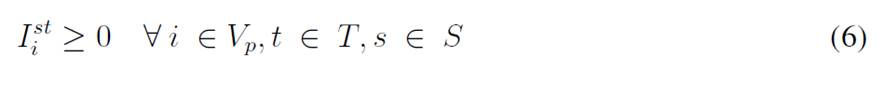
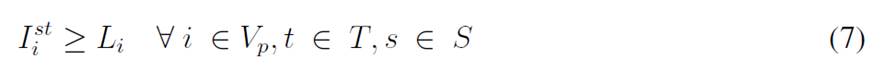
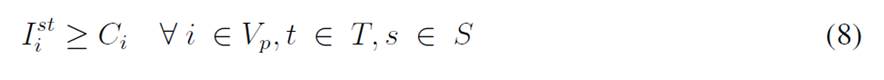
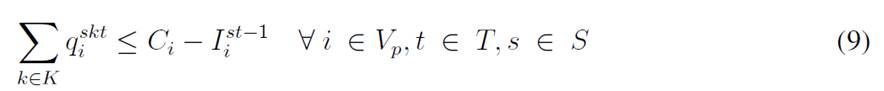
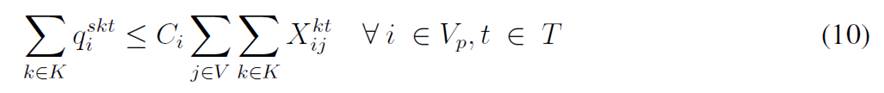
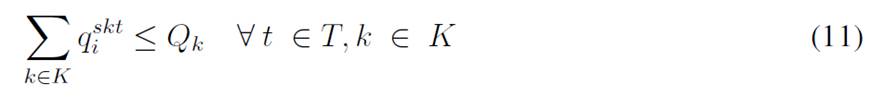
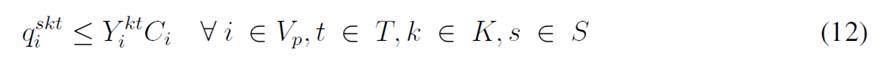
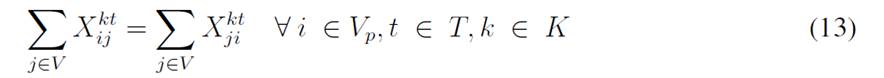
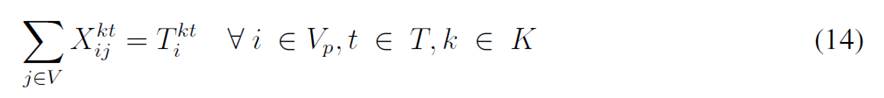
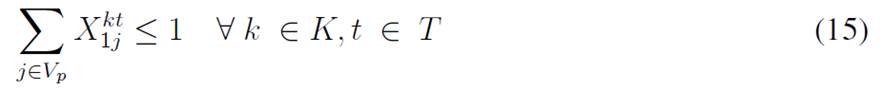
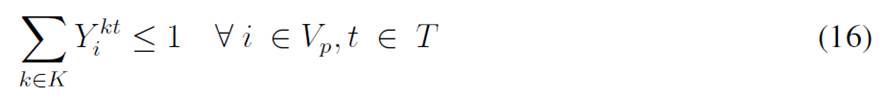
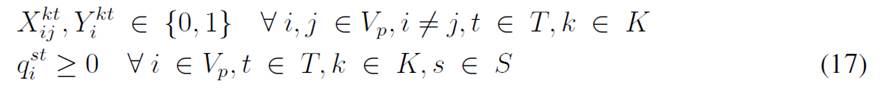
The objective function aims to minimize the expected costs made up by the inventory/holding and transportation costs. Said function is presented in Eq. (1) which represents the overall scenario. Constraint (2) enforces the p-robustness condition, which considers the optimal function for each scenario and a predefined p-robustness. Constraints (3) and (4) determine inventory levels in the depot. Eqs. (5), (6), (7), and (8) determine the upper/lower bounds of inventory levels for every customer. Eq. (9) represents quantities to be delivered to each customer given the maximum capacity allowed by Eq. (10), which also establishes a relationship between integer and binary variables
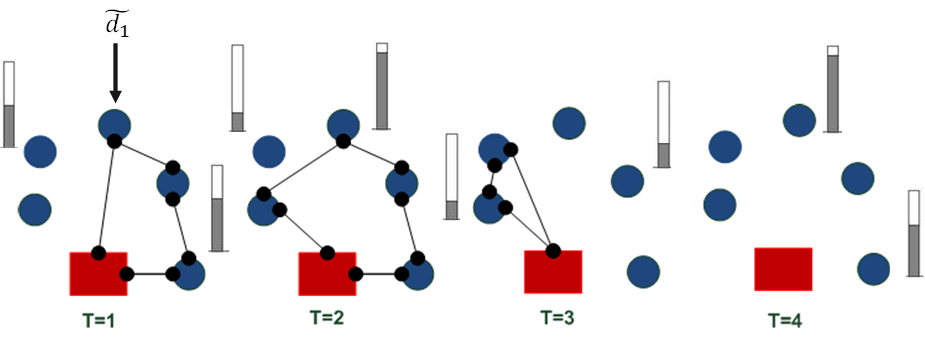
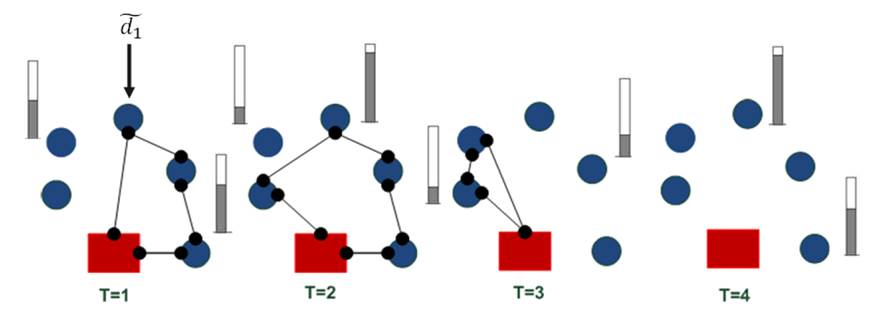
Eq. (11) represents the fixed vehicle capacity, while (12) sets the relationship between the amount of products delivered, the capacity, and a binary variable that activates if a customer is visited. Flow constraints are shown in (13), and the relationship between the two binary variables is presented in (14). Finally, routing constraints are presented in (15) and (16), and (17) sets up the nature of delivering quantities. To get a better understanding of the problem, Fig. 1 presents a graphical description. The example is composed of four different time periods, where a delivery decision must be made for each customer (five in total, as represented by the blue circles). Each customer has their own inventory level constraints (maximum and minimum, represented by the bar) which must be fulfilled. For each time period, from the depot, it must be decided if a replenishment must be done (and the routing process), considering that demand over each time period is stochastic (thus, it is not known beforehand).
P-robustness description
The p-robustness approach 4) is based on a probability-based robustness measure, which is the deviation of a feasible solution provided by a scenario to the global optimal solution. This method proposes the combination of the benefits of stochastic and robust optimization models by the minimization of the expected costs and the min-max cost or regret. The approach then uses a set S of scenarios, where X is a feasible solution of the mathematical model, and a solution is deemed to be robust if the following constraint is guaranteed:

where z ∗ s is the optimal objective function for each scenario s ∈ S; zs(X) is the objective function of a feasible solution X; and ρ is the desired robustness level or maximum allowable regret. To solve the problem, it is mandatory to have the optimal values of each scenario, which are solved as single deterministic problems. The left part of the equation corresponds to the relative regret for each scenario, where the combination of the ρ-robustness version (or constraint) with the minimization of the expected cost (as objective function) generates the stochastic ρ-robustness measure.
Experimentation and results
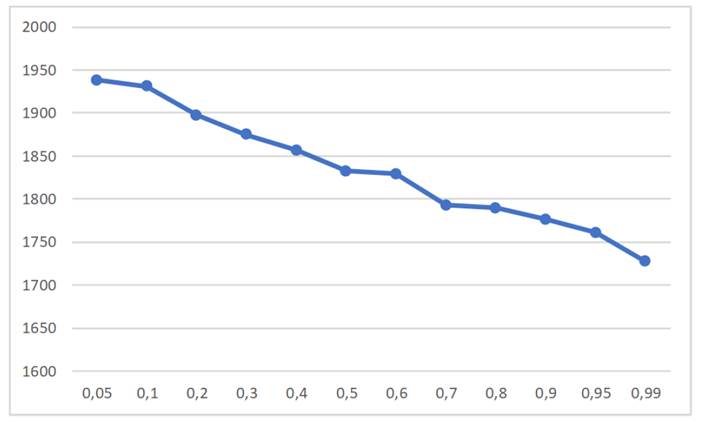
The mathematical model presented in section 3 is tested with the modification of instances presented in different studies 4, 15, 20, considering the scenario generation presented by (18. In this case the scenarios generated are 20, and they aim to analyze the variability of demand, where the model is solved using FICO-Xpress-MP v. 12.1. The analyzed instance has the reference “abs1n5_HC3”, which is composed of 6 customers that have different values of demand over three time periods of the planning horizon (the deterministic version has 65, 35, 58, 24, and 11 units of demand, respectively), and the scenarios are generated according to the behavior of the deterministic demand given variations of ± 20 %. The capacity of each vehicle is fixed to 289 units, and the amount of product available at the depot corresponds to 193 units. In this sense, in Fig. 1, we present the results for a single instance contrasting the variation of the objective function in terms of the p-robustness parameter.
Figure 1: Description of the problem under study
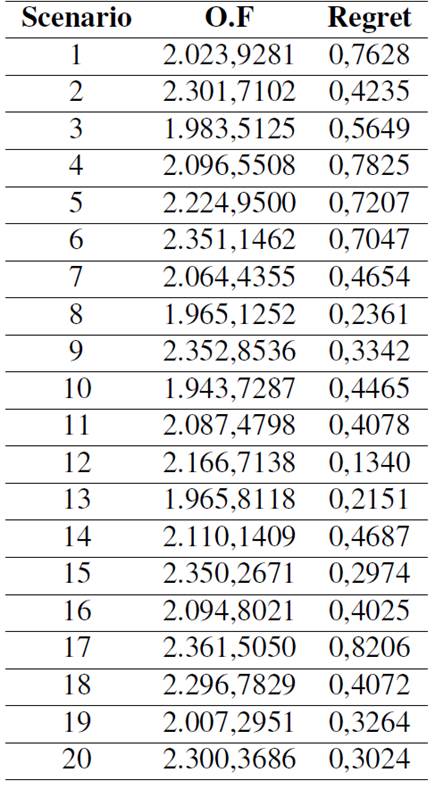
Fig. 2 shows that analyzing the trade-off between the p-robustness and the objective function (which measures the overall logistic costs) shows that, as the p-robustness value increases, the overall objective function decreases. This means that decision-makers can achieve cost reductions by choosing higher values of the p-robust parameter. In order to analyze the behavior of the obtained solution and regret for different scenarios, we have presented the results in Table I, where the first column corresponds to the uncertainty scenario, the second column is its optimal value, and the third column is the regret.
Figure 2: Variation of the objective function in terms of the p-robustness value
Table I shows the overall performance of the regret in every scenario of the optimization model. Roughly speaking, the obtained values are in some cases greater than those obtained by the deterministic model due to the uncertainty of the delivered quantities and the demand used in each scenario. On the other hand, as the regret obtained in different scenarios is somehow small, this model allows analysts to obtain robust solutions in order to deal with uncertain demands and manage logistic costs composed of the inventory holding and routing costs.
Table I: Regret over scenarios
Conclusions
In this paper, we have presented a mathematical model approach for the Inventory Routing Problem with demand uncertainty, where the modeling is carried out through the use of the probustness criteria, which minimizes the worst-case cost or regret and combines the two objectives by minimizing the expected cost while bounding the relative regret in each scenario of uncertainty. The mathematical model contemplates a single-depot and single product but considers several customers within a planning horizon with variations in the demand. The experiments performed allow us to analyze the trade-offs obtained with the objective function contrasted with the parameter of the approach selected. To solve the proposed approach, the p-robustness model requires that several mathematical models are 4solved (given the number of scenarios) for using this information in the general version as a parameter for building the p-robustness criteria (Constraint (2)).
This model can be extended to perform different analyses and increase the complexity of decisions; the impacts of several depots and products can be analyzed, and different types of sources of uncertainty can be considered, such as the transportation and inventory costs and the heterogeneity of vehicles. On the other hand, different methods for solving bigger instances can be proposed, such as heuristics, metaheuristics, or matheuristics, given the computational complexity of the basic problem, which is increased by the uncertainty.
Acknowledgements
Acknowledgements
We would like to thank the Fair Isaac Corporation (FICO) for providing us with Xpress-MP licenses under the Academic Partner Program subscribed with Universidad del Rosario.
References
License
Copyright (c) 2022 Carlos Franco Franco, Juan Carlos Figueroa-García, Juan Sebastían Tenjo-García

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.



2.jpg)