Ingeniería, 2007-00-00 vol:12 nro:1 pág:64-71

Enseñanza de la mecánica de materiales enriquecida con herramientas computacionales

Teaching of the materials mechanics enriched with computational tools

Luis Fernando Vargas Tamayo
Grupo DIMISI Diseño, Modelamiento y Simulación.
Leonardo Emiro Contreras Bravo
Grupo DIMISI Diseño, Modelamiento y Simulación.

Resumen

En el presente trabajo se ilustra la importancia del uso de las herramientas computacionales en el proceso de enseñanza-aprendizaje a nivel universitario, el cual actualmente se ha enfocado en una recopilación, almacenamiento y posible divulgación de información.

El paralelo planteado entre la enseñanza tradicional, la herramienta de la hoja de cálculo y el método de los elementos finitos (MEF) es abordado a partir del desarrollo de un caso puntual de la mecánica de materiales, es decir, desarrollando el concepto de carga axial, esfuerzo y deformación de un elemento hecho de acero. El fin de este articulo es explorar la posibilidad de generar en el estudiante universitario nuevas competencias que faciliten al egresado su actuar profesional a través de la utilizacion de los métodos computacionales y especialmente el método de los elementos finitos (MEF) en los currículos de ingeniería.

Palabras clave:
Método de los elementos finitos, modelado, enseñanza.

Abstract

In this paper illustrates the importance of use of computational tools in teaching-learning process at university level, which currently has focused on a collection, storage and dissemination of information possible.

The proposed parallel between traditional education, the tool of the spreadsheet, and finite element method (MEF) is approached from developing a case in point of the mechanics of materials, ie, developing the concept of load, stress and deformation of an element made of steel. The purpose of this article is the possibility of generating a university student in new powers to afford their graduate professional acting through the importance of using computational methods and especially finite element method (MEF) in engineering curriculum.

Key words:
Finite element method, modeling, teaching.

1. Introducción

El presente trabajo nace de una inquietud frecuente en los docentes encargados de impartir las asignaturas de resistencia de materiales o mecánica de materiales, según es llamada en los currículos universitarios tradicionales de las carreras de ingeniera mecánica, industrial y afines. La práctica de la docencia en este campo del conocimiento ha demostrado que al estudiante le faltan recursos audiovisuales y en especial informáticos de aula para lograr la total comprensión de los fenómenos. Reconocien- do que industrialmente este ejercicio se lleva a cabo de una manera mucho más ágil y que se soporta sobre el poder de cálculo de un computador, se reconoce la necesidad de integrar esta herramienta informática a la pedagogía de aula con el propósito de facilitar procesos de pensamiento encaminados al análisis de fenómenos y no reiterar el conducto habitual de repetición de procedimientos preestablecidos.

La ayuda informática puede utilizarse con múltiples propósitos, en especial cuando se enfoca a sustituir tareas repetitivas e iterativas como la solución de formulas y sus cálculos matemáticos respectivos. Nuestra intención se centra en despertar interés en la exploración de posibilidades pedagógicas soportadas por computador que apunten al desarrollo de competencias de pensamiento y raciocinio, de análisis de fenómenos y de predicción de comportamientos útiles en futuros desarrollos profesionales, y que no centren las consabidas habilidades memorísticas y procedimentales que frecuentemente premian al que de mejor manera recuerde las instrucciones así no comprenda el fenómeno estudiado.

2. Materiales y métodos

Para nuestro estudio fue fundamental la experiencia recogida como estudiantes de ingeniería en el pasado y también como la de docentes en la actualidad, la interacción con estudiantes a niveles en los que se cuestiona no solamente los conocimientos trasmitidos, sino que se indaga la habilidad para poner en situación real lo aprendió, buscando siempre el "saber hacer", y no solo el "saber".

La posibilidad de conocer y trabajar con elementos informáticos cotidianos como la hoja de cálculo y también avanzados como los programas de cálculo de elementos mecánicos basados en el método de los elementos finitos en diversos ambientes y proyectos investigativos, nos permitieron entrelazar la tarea pedagógica con dichas experiencias del pasado.

Adicionalmente, a los recursos tradicionalmente utilizados para la enseñanza en el aula de clase, se conoce de tiempo atrás la aplicabilidad de la hoja de cálculo para modelar situaciones, comprender comportamiento y analizar variables. Reconociendo que la baja complejidad de las ecuaciones a utilizar permite diseñar una hoja de cálculo cuyo objetivo es realizar numerosas iteraciones con el fin de comparar las diferentes variables y facilitar al estudiante el entendimiento del comportamiento. Traspasando aquella frontera que impone el ejercicio del tablero en el que se encuentra resultado a una situación particular sin generalizar el fenómeno.

El método de los elementos finitos (MEF) es otra herramienta que facilita el desarrollo y diseño de diversos productos en diferentes ramas de la ingeniería. El método se desarrolla a través de cinco etapas: Diseño, pre-proceso, enmallado, solución y post-proceso. En cada una de ellas existe la intervención humana en el sentido del diseño y control de las tareas a ejecutar, extrayendo la necesidad de realizar cálculos numéricos en gran número, tarea que se entrega al computador.

En el diseño o etapa inicial, se representa gráficamente y en 3D el objeto o sólido a analizar, es de anotar que esta tarea requiere precisión y exactitud así como un completo conocimiento de formas y dimensiones del caso a analizar. Para cumplir este requerimiento se utilizan frecuentemente programas de modeladores de sólidos como Solid Edge® o SolidWorks® Figura 1, también es frecuente que para piezas o sólidos de geometrías sencillas se utilicen herramientas de dibujo que los programas específicos del MEF traen a su interior.

Posteriormente en el pre-proceso se busca simular la realidad de la situación en la que se encuentra el objeto a ensayar, es decir tratando de alcanzar la realidad virtual del objeto en trabajo. Esto se logra adicionando las cargas, restricciones y propiedades del material a utilizar. Las cargas pueden variar en magnitud, forma de aplicación, sentido y hasta en tipo, pudiendo ser lineales (fuerzas) o aplicadas sobre una cara (presiones) Figura 2. Las restricciones competen a empotramientos o sujeciones a las que este limitado el caso de estudio, estas restricciones según sea el caso pueden ser de movimiento lineal, rotacional, o en general de cualquier grado de libertad. Por otro lado, estos programas generalmente traen una biblioteca con múltiples materiales posibles de aplicar, en los que se encontraran sus principales propiedades físicas y mecánicas, como resistencias, densidades, límites de esfuerzo, constantes de deformación etc. en caso de no encontrar el material a ensayar se pueden editar los valores o crear materiales específicos, con la introducción de dichos valores.

La siguiente etapa llamada enmallado, consiste en dividir el sólido en pequeñas pero finitas porciones de geometrías variables, separas por fronteras en las que identificaran nodos vinculantes, sobre los cuales se aplicaran conjuntos de ecuaciones diferenciales que caracterizan el fenómeno en estudio Figura 3. Estos fenómenos y por ende sus ecuaciones pueden incluir temas como tensiones y resistencias mecánicas, análisis térmicos, estudios de campo electromagnético y de mecánica de fluidos.

La adyacencia de dos nodos implica que el proceso de cálculo es una tarea continua, donde los resultados de una sección o malla, se alimentan como datos de entrada al conjunto de ecuaciones del elemento siguiente, de tal manera se garantiza que los efectos del fenómeno en estudio se analizaran acumulativamente, esto parece una tarea sencilla, sin embargo hay que reconocer que requiere de miles de cálculos matemáticos especializados en los que el computador hará su parte, a esta cuarta etapa se le llama solución.

Por último se debe extraer del proceso de simulación, la información necesaria para entender el fenómeno sucedido, esto es, generalmente implica la representación grafica (Figura 4) de las variables que pertenecen a las ecuaciones que rigen el fenómeno en estudio. De este resultado es donde se basa el ingeniero para emitir un juicio acerca del diseño del sólido u objeto. La representación grafica generalmente incluye una escala graduada con los valores de la variable resultado, es decir, MPa en el caso de esfuerzos y presiones y unidades de longitud como mm cuando se quieren analizar las deformaciones. Estos valores estarán representados por colores o tonalidades de grises para posibilitar la comparación entre la escala y el modelo solucionado.

3. Caso de estudio

Con el fin de llevar a cabo la comparación entre la metodología de enseñanza tradicional de la mecánica de materiales para ingenieros industriales y mecánicos, y una aproximación a la enseñanza enriqueciéndola por medios informáticos se tomó un caso muy elemental que hace parte de la enseñanza del concepto de "Carga y esfuerzo axial", tema que es común en el contenido programático de la asignatura.

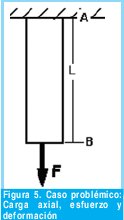
El caso problémico a discutir será como se muestra en la Figura 5, la aplicación de una carga de tipo Puntual de 10000N a una barra de de Acero AISI 1020 de 0.1m. de longitud y que será evaluada para una sección transversal circular de diámetro 10 mm, en donde se pretende que el estudiante adquiera los conocimientos necesarios acerca del concepto de Esfuerzo axial, Deformación axial y Módulo de elasticidad; que son algunas de las propiedades mecánicas importantes que cualquier docente relacionado con el área en cuestión consideraría información indispensable, para que el estudiante produzca, apropie y aplique comprensivamente sus conocimientos en el diseño de una pieza u objeto particular en su campo de acción.

3.1 Metodología de enseñanza tradicional.

La mecánica de materiales define el esfuerzo (σ)como la fuerza (F) aplicada por unidad de área (A):

Por otro lado la deformación longitudinal o alargamiento ( ) que sufre la pieza depende de: la carga (P), la longitud de la barra (L), el área de la sección transversal (A) y el Modulo de Elasticidad (E) típico del material en el que este hecho.

Solucionando las ecuaciones (1) y (2) se obtiene que ó y=1.27E9 Pa y ä=0.64 mm. De estos datos se puede concluir por comparación con los datos del material (esfuerzo de fluencia), si la pieza soportará la carga mencionada o si el esfuerzo es tan alto como para deformarla permanentemente. Adicionalmente se puede predecir la longitud final de la barra después de aplicar la carga.

Como podemos inferir, esta dinámica de clase premia la habilidad memorística recordando ecuaciones y la habilidad matemática en su solución. Olvidando o por lo menos relegando a un segundo plano las conclusiones conceptuales sobre el fenómeno en estudio al que pudiera llegar el estudiante, es decir no relaciona la solución encontrada con un caso de la vida práctica ingenieril, en el cual puede ser necesario elegir un material con menor diámetro, aumentar la carga, variar la sección transversal a cuadrada, rectangular, etc. o por ejemplo incrementar la longitud de la pieza. En ese caso el problema vuelve a "cero" donde el estudiante necesitará una nueva solución matemática (repetición) para poder hacer las predicciones de comportamiento a que haya lugar.

Lo anteriormente expuesto ha sido analizado por múltiples investigadores en enseñanza, por ejemplo según [1] "El problema es que se da con frecuencia el caso de que muchos estudiantes repiten los lenguajes científicos sin comprenderlos y la fuerza de esos lenguajes, que debieran ampliar la mirada, se vuelve contra quienes sólo pueden memorizarlos como cosa ajena para aplicarlos en el campo de las tareas escolares sin establecer conexiones entre su experiencia vital y los contenidos de las ciencias. Si se concibe la enseñanza como transmisión de conocimientos, si se busca transmitir el máximo posible de contenidos y se estimula principalmente el ejercicio de la memoria, es muy posible que las ciencias de la escuela se reduzcan a un elenco de nombres, fechas, lugares, taxonomías, números, fórmulas para rellenar con números o letras y procedimientos mecánicos".

3.2 Metodología usando herramientas computacionales básicas

Retomando ahora nuestras reflexiones iniciales sobre el proceso de aprendizaje de los fenómenos físicos, y en especial de aquellos relacionados con la mecánica de materiales. Se hace evidente que aunque dependen de múltiples variables tanto en número como en "especie" su procedimiento de resolución guarda cierta similitud en muchos casos, es decir, que aunque se presenten variaciones dimensionales, geométricas, de situación o de material empleado, el concepto sobre carga axial y sus efectos (deformación, etc.) para este caso de estudio permanecen inalterados.

Lo expuesto anteriormente tiene como efecto que la iteración de múltiples situaciones con sutiles cambios a cada problema (dimensionales, geométricos, etc) en particular, no aporten significativamente a la comprensión de los fenómenos y por el contrario diluyan el interés de la clase y que por ende las horas de trabajo se inviertan en la memorización de la mecánica de solución del problema puntual.

En algunos casos se encuentran paradigmas contradictorios como aquellos en los cuales al estudiante se le limita la posibilidad de exponer sus preconceptos ya sean erróneos o verdaderos y por el contrario se le encamina a replicar la experiencia en solución de problemas que el profesor propone como metodología de estudio, extrayendo del proceso cualquier análisis racional sobre el fenómeno para potencializar el seguimiento de instrucciones.

La Organización de Estados Iberoamericanos con su programa "Para la Educación, la Ciencia y la Cultura", ha recopilado experiencias docentes de diversos lugares del mundo donde se evidencia esta problemática en la tendencia de enseñanza, en la cual se ha detectado que "Un mínimo análisis de la práctica docente habitual muestra, sin embargo, que los "problemas" son explicados como algo que se sabe hacer, como algo cuya solución se conoce y que no genera dudas ni exige tentativas: el profesor conoce la situación -para él no es un problema- y la explica linealmente, "con toda claridad"; consecuentemente, los alumnos pueden aprender dicha solución y repetirla ante situaciones idénticas, pero no aprenden a abordar un verdadero problema y cualquier pequeño cambio les supone dificultades insuperables provocando el abandono" [2].

Es conocido que la hoja de cálculo dentro de sus múltiples utilidades presenta la ventaja de repetir cálculos matemáticos en gran volumen, adicionalmente a la posibilidad de facilitar dichos cálculos permite la representación gráfica de las relaciones existentes entre las variables implicadas; ya sea a manera de tablas o de gráficas de dispersión.

Teniendo en claro que el estudiante ya solucionó problemas puntuales en los que encontró la relación entre un juego de variables, el paso a seguir será el de demostrar tendencias de comportamiento que relacionen no una pareja, sino múltiples valores para las variables implicadas. En la tabla 1 se muestra un resultado parcial del ejercicio de tomar una hoja de calculo e introducir las relaciones matemáticas necesarias para obtener múltiples resultados para la variación de diámetros desde 1 hasta 10 cm. En este caso se mantuvieron constan- tes las siguientes variables (carga 10000 kN, longitud de la barra 10cms, material de ensayo E=200GPa).

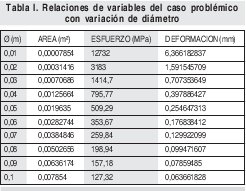
A partir de la Tabla I podremos graficar para el caso particular la relación existente entre las variables diámetro y esfuerzo (Figura 6) y por otro lado diámetro y deformación (Figura 7).

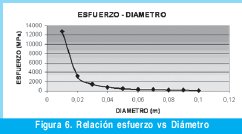
En el campo de trabajo de la ingeniería muy a menudo se presentan casos en los cuales se hace necesario seleccionar un perfil con sección transversal que satisfaga alguna condición de resistencia, llámese resistencia a tensión (en este caso), a compresión, flexión o tal vez fatiga. El estudiante según el ejercicio desarrollado anteriormente por la metodología tradicional probablemente no lograría comprender a cabalidad como se relacionan estas variables; es decir, dar una opinión ingenieril de primera mano acerca de que sección transversal aparte de la circular (hexagonal o cuadrada) es posible incluir en un diseño especifico para que continúe cumpliendo con el requisito de esfuerzo de tensión. Una forma confiable para poder predecir comportamientos en este aspecto, consiste en estudiar la afectación sobre los valores de esfuerzo que tiene el diámetro seleccionado, de esta manera el estudiante se dará cuenta que una modificación en el diámetro tiene incidencia en una disminución drástica del esfuerzo aplicado, efecto que la grafica muestra ampliamente, adicionalmente se podrá analizar en qué proporción se disminuye el esfuerzo cuando el diámetro se duplica, en conclusión además de solucionar rápidamente 10 ejercicios puntuales, se logró encontrar una tendencia de comportamiento que permitirá en casos relacionados formular hipótesis claras sobre la incidencia de estos cambios en la respuesta del material.

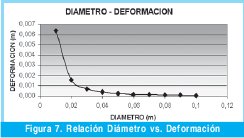
Por otro lado la Figura 7, en la que se muestra la relación entre diámetro y deformación, identifica un comportamiento semejante al de la grafica anterior, esto que pareciera no aportar nada nuevo, reviste importancia cuando se analiza la relación entre la causa y efecto, es decir entre el esfuerzo y deformación.

La segunda parte del análisis por hoja de cálculo incluye la posibilidad de modelar la incidencia de las variaciones de fuerza en las demás cantidades físicas del caso, en este caso se utilizaron cargas desde 1000 hasta 2000 KN, manteniendo las demás características constantes y el diámetro en 10mm.

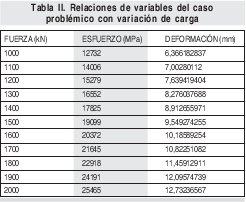
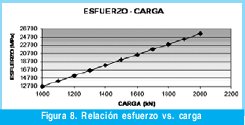
Una de las gráficas que se puede obtener de la anterior tabla, refiere a la relación entre las variables carga y esfuerzo, en esta se resalta su relación lineal, en la que se tiene como constante de proporcionalidad el área de la sección trasversal, que para el caso es constante.

Lo que para el instructor o profesor encargado de realizar esta explicación parece ser evidente, puede que para un estudiante no sea claro hasta que no tenga ante sus ojos un elemento gráfico que lo represente

3.3 Metodología usando herramientas computacionales avanzadas

Por último analizaremos cuales son las facilidades que ofrece la herramienta informática denominada MEF (análisis por el método de los elementos finitos) frente al caso de estudio.

En primera medida a través de esta, la simulación en el software Algor® (en este caso), es posible que el estudiante visualice y reproduzca el efecto del movimiento de cada una de las líneas o secciones que conforman el material en estudio desde el inicio de aplicación de la carga, pasando por la zona elástica, la zona plástica hasta finalizar con el punto de rotura paso a paso como se ve en la Figura 9, adicionalmente, para un instante de tiempo cualquiera es posible obtener valores de deformación y esfuerzo axial en el material, que permitan al estudiante analizar un caso real de diseño de elementos o dispositivos reales conociendo estados dinámicos en puntos particulares y no exclusivamente el máximo ocurrido, esto tendrá utilidad cuando se pretenda aplicar optimización a una pieza determinada, con el conocimiento de esfuerzos locales se puede llegar a diseños esbeltos o aligerados, sin incurrir en sobreesfuerzos.

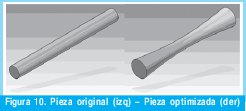
Es decir el estudiante podrá comprender las alternativas de diseño aligeradas que proporciona el conocimiento del comportamiento de esfuerzos puntuales, esto en la vida práctica se ve constantemente en piezas analizadas y optimizadas, como la mostrada en las Figuras 2 y 10.

Esta metodología no solo puede aplicarse a un material especifico, sino que al igual que en una hoja de cálculo es posible modificar las propiedades del material, pero en este caso esa modificación es posible de manera más sencilla ya que estos software poseen bibliotecas o bases de datos de un sin número de materiales típicos ingenieriles, además a diferencia de la hoja de cálculo, esta biblioteca permite el análisis no solo de condiciones elásticas lineal, sino de condiciones híper­elásticas caso imposible de analizar en el aula de clase o tal vez con la hoja de cálculo.

Esta metodología de análisis permitirá al futuro ingeniero optimizar el comportamiento de componentes, reproduciendo los resultados del laboratorio o de campo, pero sin el tiempo y los costes asociados al análisis de fallas real.

Dicha biblioteca mostrada en la Figura 11, permite la rápida selección y por ende la consecución iterativa de soluciones comparables para distintos materiales, dentro de la familia de los metales, polímeros y cerámicos. Además en el caso que se quiera utilizar un material en particular que no se encuentre en la biblioteca, es posible actualizar y alimentar ésta mediante los datos normales de propiedades mecánicas obtenidos de ensayos estandarizados.

4. Conclusiones

Inicialmente se puede entender que el método tradicional de enseñanza de la mecánica de materiales imparte al estudiante la posibilidad de alcanzar la "identificación, comprensión, análisis, decodificación, asociación y representación de textos, símbolos códigos conjuntos algorítmicos, gestuales, graficas y demás metas, lenguajes, expresos o tácitos propios de la ciencia" [3].

La inclusión de la hoja de cálculo dentro del modelo pedagógico, permite además de fortalecer las competencias anteriormente mencionadas, enriquecer la habilidad y capacidad del estudiante para formular hipótesis de comportamiento que expliquen y predigan el resultado de casos puntuales, tal como lo menciona Lara [3] en su documento: "Competencia argumentativa: Desarrollo y fomento de posibilidades, habilidades y saberes orientados a la explicación de conductas, situaciones, condiciones , coyunturas y procesos a partir de los cuales se quiere formular tesis hipótesis o estados de relación con procesos asociados a teorías, diagnósticos".

El método de los elementos finitos, MEF, es una metodología que además de aumentar las competencias señaladas induce ciertas habilidades y capacidades en el estudiante que ayudarán a promover competencias científicas que pueden fomentar la investigación y el avance tecnológico del país. Estas podrían enumerarse de la siguiente manera:

Capacidad de generar conocimiento través de los cuestionamientos de casos de vida real, generando hipótesis que a través del desarrollo de los mismos permitan interpretarlos para generar juicios adecuados.

Proponer diferentes esquemas o modelos matemáticos de situaciones, generando capacidad de análisis crítico de las fuentes de información y de contrastar distintas informaciones con criterios para comprender los conceptos de la mecánica de materiales.

Es claro que el uso de la nuevas y novedosas tecnologías que ofrece la comunidad científica es requerido y debe acoplarse a todo el sistema de educación, y especialmente al ingenieril, ya que es este campo el que más apoya el avance científico y tecnológico del país; generar competencias científicas a través de estas ayudas permite a los estudiantes lograr destrezas y habilidades para emplear sus conocimientos teóricos adquiridos en pro de la mejora de las condiciones de vida, es generar y apuntar hacia un mundo de conocimientos y ventajas competitivas, es facilitar la compresión de su entorno tal como lo dice Posada [4] "El desarrollo de competencias científicas es importante, por una parte, para facilitar a los ciudadanos la comprensión de su entorno y por otra, para contribuir a aumentar la competitividad del sector productivo nacional".

Aunque por ser un país tercermundista, pareciera ser que estamos relegados tecnológicamente, es a través de la enseñanza del aula de clase en la cual incursiona temas y nuevas tecnologías, como es posible generar un avistamiento de mejoras de condiciones de vida; es aquí donde se debe fomentar la generación de conocimientos con técnicas importantes como la mencionada, ya que con la metodología tradicional no se genera o se induce al estudiante a la creación de conocimiento nuevo, se le enseñan técnicas obsoletas que al finalizar el periodo de estudio estarán relegadas no permitiendo apropiarse de tecnologías de punta para generar competencias científicas.

Mediante el uso de las herramientas computacionales y especialmente las de ingeniería el estudiante adquiere una mejor comprensión de la física y matemática de los fenómenos físicos generando posibles soluciones prácticas adaptables al mundo real.

El uso de las tecnologías computacionales es uno de los campos que ha hecho surgir a muchos países del tercer mundo, es por eso que se hace necesario incorporar estas, en los programas curriculares de las universidades, laboratorios y centro de investigación colombianos con el fin de facilitar el progreso científico de nuestro país.

Referencias bilbiográficas

[1] Carlos Augusto Hernández, ¿QUÉ SON LAS "COMPETENCIAS CIENTÍFICAS"?, Profesor de la Facultad de Ciencias. Miembro del Grupo Federici de investigación sobre enseñanza de las ciencias y de la Colegiatura Icfes- Universidad Nacional. Secretaria de educación de Boyacá. Octubre 12 2007. Disponible en http://www.boyaca.edu.co/

[2] Daniel Gil Pérez, Miguel Guzmán Ozámiz. Enseñanza de las Ciencias y la Matemática Tendencias e Innovaciones. Organización de Estados Iberoamericanos Para la Educación, la Ciencia y la Cultura. Editorial Popular. ISBN: 84-7884-092-3

[3] Definición de competencias ­ Acreditación de ingeniería industrial. UDFJC. MSc. Oscar Lara, Bogotá. 2007

[4] Eduardo Posada, Observación, comprensión y aprendizajes desde la ciencia. Septiembre 25 2007, Disponible en : http://menweb.mineducacion.gov.co/altablero/ articulo.asp?sec=3&id=272&num=30

[5] Stephen Timoshenko, Resistencia de materiales, Ed Nº1, Editorial Espasa-Calpe, 2004, Madrid, ISBN: 84-239-63144

[6] Beer. Mecánica De Materiales, 2ª ED, Editorial McGraw- Hill, 1993, ISBN: 958600127X

[7] Elisa López, Manuel Vázquez, El Método De Los Elementos Finitos Aplicado Al Análisis Estructural, Ed Nº1, Ed. Noelia, 2001, Madrid, ISBN: 9788488012067.

[8] Zienkiewicz O.c., Método de elementos finitos, Ed Nº3, Editorial Reverte, 1995, México, ISBN : 8429148949

Luis Fernando Vargas Tamayo
Ingeniero mecánico, Universidad Nacional de Colombia (Bogotá), Magíster en ingeniería - materiales y procesos de manufactura, Universidad Nacional de Colombia. Docente, Universidad Distrital. Pertenece grupo de investigación DIMISI Diseño, Modelamiento y Simulación. lufvargast@udistrital.edu.co

Leonardo Emiro Contreras Bravo
Ingeniero mecánico, Universidad Francisco de Paula Santander (Cúcuta), Magíster en ingeniería - materiales y procesos de manufactura, Universidad Nacional de Colombia. Docente, Universidad Distrital. Pertenece grupo de investigación DIMISI Diseño, Modelamiento y Simulación. lecontrerasb@udistrital.edu.co