DOI:
https://doi.org/10.14483/23448393.2379Published:
2008-11-30Issue:
Vol. 14 No. 2 (2009): July - DecemberSection:
Science, research, academia and developmentEvaluación de funciones de utilidad de GRASP en la programación de producción para minimizar la tardanza total ponderada en una máquina
Evaluation Of Utility Functions For Minimization Of Total Weighted Tardiness In Machine Scheduling Using Grasp
Keywords:
Función de utilidad, GRASP, programación de la producción, tardanza total ponderada. (es).Downloads
References
K. Baker, J. Hayya. "Priority dispatching with operation due dates". Journal of Operations Mangement 2, 167175. 1992.
U. Bilge, M. Kurtulan, F. Kiraç. "A tabu search algorithm for the single machine total weighted tardiness problem". European Journal of Operational Research, 176, 142335. 2007.
W. Bozejko, J. Grabowski, M. Wodecki. "Block Approach Tabu Search algorithm for single machine total weighted tardiness problem". Computers and Industrial Engineering 50, 114. 2006.
R. Britto, G. Mejía, J. P. Caballero-Villalobos. "Programación de la producción en sistemas de manufactura tipo taller con el algoritmo combinado cuello de botella móvil y búsqueda Tabú". Ingeniería y Universidad, volumen 11, No 2, 203 224. 2007.
T. C. E. Cheng, C. T. Ng, J. J. Yuan, Z. H. Liu. "Single machine scheduling to minimize total weighted tardiness". European Journal of Operational Research, 165, 423443. 2005.
F. Chou. "An experienced learning genetic algorithm to solve the single machine total weighted tardiness scheduling problem". Expert Systems with Applications, 36, 38573865. 2009
R. K. Congram, C.N. Potts, S. L. Van de Velde. "An iterated dynasearch algorithm for the single-machine total weighted tardiness scheduling problem". Informs Journal on Computing, 14(1), 5267. 2002.
A. Croes. "A method for solving traveling-salesman problems". Operations Research, 5, 791-812. 1958.
L. M. A. Drummond, L. S. Vianna, M. B. Silva, L. S. Ochi. "Distribution parallel metaheuristics based on GRASP and VNS for solving the traveling purchaser problem". In Proceedings of the 9th International Conference on Parallel and Distributed System, pp. 257263. 2002.
M. L. Fisher. "A dual algorithm for the one machine scheduling problem". Mathematical Programming, 11, 229252. 1976.
F. Glover, G. Kochenberger. "Handbook of Metaheuristics. Kluwer Academic Publishers". 2003.
R. L. Graham, E. L. Lawler, J. K. Lenstra, A.H.G. Rinnooy Kan. "Optimization and approximation in deterministic sequencing and scheduling: A survey". Annals of Discrete Mathematics, 5, 287-326. 1979.
A. Grosso, C. Della, R. Tadei. "An enhanced dynasearch neighborhood for single-machine total weighted tardiness scheduling problem". Operations Research Letters, 32, 6872. 2004.
O. Holthaus, C. Rajendran. "A fast ant-colony algorithm for single-machine scheduling to minimize the sum of weighted tardiness of jobs". Journal of the Operational Research Society, 56, 94753. 2005.
F. Jin, S. Song, C. Wua. "A simulated annealing algorithm for single machine scheduling problems with family setups". Computers and Operations Research, 36, 2133 2138. 2009.
E.L. Lawler. "Efficient implementation of dynamic programming algorithms for sequencing problems". Technical report, BW-106. Amsterdam: Centre for Mathematics and Computer Science. 1979.
F. Jolai, M. Rabbani, S. Amalnick, A. Dabaghi, M. Dehghan, Y. Parast. "Genetic algorithm for bi-criteria single machine scheduling problem of minimizing maximum earliness and number of tardy jobs". Applied Mathematics and Computation, 194, 552560. 2007.
C. Liao, C. Cheng. "A variable neighborhood search for minimizing single machine weighted earliness and tardiness with common due date". Computers and Industrial Engineering 52, 404-413. 2007.
C. Liao, H. Juan. "An ant colony optimization for single-machine tardiness scheduling with sequence-dependent setups". Computers and Operations Research 34. 2007.
T. E. Morton, R. M. Rachamadugu, A. Vepsalainen. "Accurate myopic heuristic for tardiness scheduling". Working paper No. 36-83-84. Pitsburgh: Carnegie-Mellon University. 1984.
M. Pinedo. "Scheduling Theory, Algorithms and Systems". Third edition. New Jersey. Prentice Hall. 2008.
A. H. G. Rinnooy Kan, B. J. Lageweg, J. K. Lenstra. "Minimizing total costs in one-machine scheduling". Operations Research, 25, 908927. 1975.
R. Rios-Mercado, J. Bard. "Heuristics for the flow line problem with setup costs". European Journal of Operational Research 110, 7698. 1998.
T. Sen, J. M. Sulek, P. Dileepan. "Static scheduling research to minimize weighted and unweighted tardiness: a state-of-the-art survey". International Journal of Production Economics, 83, 1 12. 2003.
M. Tasgetiren, Q. Pan, Y. Liang. "A discrete differential evolution algorithm for the single machine total weighted tardiness problem with sequence dependent setup times". Computers and Operations Research, 36, 1900 1915. 2009.
C.A. Vega-Mejía, J.P. Caballero-Villalobos. "Uso combinado de GRASP y Path-Relinking en la programación de producción para minimizar la tardanza total ponderada en una máquina". Ingeniería y Universidad, volumen 14, número 1, 79 96. 2010.
C. Voudouris, Tsang. "Guided Local Search. Handbook of Metaheuristics". Capítulo 7. Kluwer Academic Publishers. 2003.
G. Wan, B.P.C. Yen, "Single machine scheduling to minimize total weighted earliness subject to minimal number of tardy jobs". European Journal of Operational Research 195, 8997. 2002.
X. Wang, L. Tang. "A population based variable neighborhood search for the single machine total weighted tardiness problem". Computers and Operations Research 36, 2105-2110. 2009.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Ciencia, Investigación, Academia y Desarrollo
Ingeniería, 2009-00-00 vol:14 nro:2 pág:51-58
Evaluación de funciones de utilidad de GRASP en la programación de producción para minimizar la tardanza total ponderada en una máquina
EVALUATION OF UTILITY FUNCTIONS FOR MINIMIZATION OF TOTAL WEIGHTED TARDINESS IN MACHINE SCHEDULING USING GRASP
Ángela María Niño Navarrete
Estudiante de Maestría en Ingeniería Industrial de la Pontificia Universidad Javeriana.
Juan Pablo Caballero Villalobos
Profesor Asistente y Director del Grupo de Investigación CIOL, Pontificia Universidad Javeriana. Departamento de Ingeniería Industrial de la Facultad de Ingeniería.
Resumen
Este artículo aborda la minimización de la tardanza total ponderada en un entorno de producción (1|| wj Tj ) que es conocido en complejidad como de tipo NP-hard. El enfoque de solución propuesto utiliza la metaheurística Greedy Randomized Adaptive Search Procedure (GRASP), la cual es reconocida por la correlación existente entre la calidad de las soluciones y la capacidad discriminante de la función de utilidad empleada en su fase constructiva. Este trabajo propone y analiza tres diferentes funciones de utilidad para este problema en particular. El desempeño de estas funciones se evaluó mediante un estudio estadístico que evidenció diferencias significativas en los valores medios de tardanza total ponderada, explicadas por el factor función de utilidad. La fase experimental se desarrolló usando instancias de la librería OR-LIBRARY y permitió obtener soluciones competitivas en calidad con respecto a los mejores valores conocidos para las instancias de este problema. Este trabajo ilustra la potencialidad de uso de métodos GRASP implementados en una hoja de cálculo normal para hallar soluciones a problemas de programación de la producción.
Palabras clave:
Función de utilidad, GRASP, programación de la producción, tardanza total ponderada.
Abstract
This paper considers the total weighted tardiness minimization in a single machine environment (1|| wj Tj ) a scheduling problem which has been proved to be NP-Hard. The solution approach uses the Greedy Randomized Adaptive Search Procedure (GRASP) meta-heuristic known for the quality of the solutions it can generate and the selective ability of its utility function during the construction phase. This work proposes and analyses three different utility functions for the problem in question. A statistical study showed significant differences between the mean values obtained from the proposed utility functions. The computational experiments were carried out using problems instances found in the ORLIBRARY, and the outcome of these experiments were competitive solutions compared to the best known values of the instances involved. This work also shows the ease of developing GRASP methods for solving scheduling problems in a simple spreadsheet software such as MS Excel.
Key words:
Utility function, GRASP, single machine scheduling, total weighted tardiness.
1. INTRODUCCIÓN
El entorno de los negocios actuales caracterizado por la búsqueda de la competitividad en un contexto global y el rápido avance en tecnología y sistemas de información, ha propiciado la orientación de las empresas del sector manufacturero hacia sistemas de producción flexibles. Estos cambios de filosofía, en materia de producción, se evidencian en los cada vez más frecuentes lotes pequeños, en los trabajos bajo pedido (make to order) y en la relevancia creciente del cumplimiento de los tiempos de entrega pactados con los clientes [1] para lograr indicadores de servicio al cliente aceptables y la satisfacción de los mismos.
En este contexto cobra relevancia el problema de minimizar la tardanza ponderada total, catalogado como NP-hard [24, 25] y conocido según la notación de Graham et al. [12] como 1 || ∑ Wj Tj. El problema es formulado de la siguiente manera:
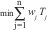
Donde:
wj: es la importancia o prioridad del trabajo j en el conjunto de trabajos.
Tj: max{Cj-Dj,0}, siendo Cj el tiempo de finalización del trabajo j y Dj la fecha de entrega del mismo.
El problema busca la programación de un conjunto de trabajos a procesarse, buscando la minimización de la tardanza total ponderada bajo los siguientes supuestos [28, 29]:
- Se tienen n trabajos (1,2,...,n) a procesarse en una máquina.
- Todos los trabajos están disponibles para ser procesados en el tiempo 0, es decir
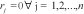
- La máquina puede procesar solo un trabajo a la vez.
- No se permite el desmonte de trabajos.
- Cada trabajo (j = 1,2,...,n) está definido por su pj (tiempo de procesamiento), wj (importancia del trabajo) y Dj (fecha de entrega del trabajo).
Debido a su clasificación, proporciona un ámbito de trabajo desafiante para los algoritmos exactos y enfoques metaheurísticos [29]. Un gran número de estudios se han enfocado en este problema y han experimentado con diversos enfoques entre los que se encuentran los métodos exactos, las reglas de despacho y métodos de intercambio.
Métodos exactos tales cómo algoritmos enumerativos que usan programación dinámica y enfoques de ramificación y acotación fueron descritos para el problema en estudio por Fisher [10], Lawler [16] y Rinnooy et al. [22]. Estos enfoques son una mejora considerable respecto a la búsqueda exhaustiva, pero siguen siendo complejos y sólo son aplicables a problemas relativamente pequeños de máximo 50 trabajos [2, 25, 28].
Los resultados de comparación mostrados por estos algoritmos son computacionalmente ineficientes cuando el número de trabajos es mayor que 50, por lo tanto muchos investigadores se enfocaron en desarrollar heurísticas para obtener soluciones cercanas a las óptimas en tiempos razonables [28, 29].
Las reglas de despacho usadas para construir una solución mediante la fijación de un trabajo en una posición en cada paso, se describen por Cheng et al. [5], Fisher [7] y Morton et al. [20]. Estas heurísticas constructivas son muy rápidas en lo referente a tiempo de respuesta, pero la calidad de las soluciones no es buena [3].
Para problemas de instancias mayores se han utilizado métodos de intercambio como lo presenta Bozejko et al. [3], que parten de una solución inicial y cíclicamente intentan mejorar la solución actual mediante intercambios locales. Para mejorar el desempeño de los algoritmos de búsqueda local se han combinado con metaheurísticas como búsqueda tabú o (tabu Search) [2, 3], Recocido Simulado o (simmulated Annealing) [15], algoritmos genéticos (GA) [6, 17] y optimización de colonia de hormigas o (ant colony optimization) [14, 19]. En la revisión realizada por Wang et al. [29] se muestra el mejor algoritmo para este problema disponible en la literatura, desarrollado por Congram et al. [7] conocido como Iterated Dynasearch, el cual fue mejorado por Grosso et al. [13], al combinarlo con el método de búsqueda en vecindario variable - VNS (variable neighborhood search).
El uso de las metaheurísticas ha permitido alcanzar soluciones exitosas en tiempos de computo razonables para este tipo de instancias (ver p.e. [18],[29]). En el mismo sentido, otros autores han combinado tabu search con VNS [18], GRASP con VNS [9] y GRASP con otra técnica conocida como Path Relinking [26]. El horizonte que plantean estos desarrollos es bastante prometedor en relación a la búsqueda de soluciones competitivas en tiempo y calidad al problema de la tardanza ponderada en instancias de más de 50 trabajos.
2. MARCO TEÓRICO
2.1 Greedy Randomized Adaptive Search procedure (GRASP)
GRASP es una metaheurística que ha logrado buenos resultados en una variedad de problemas de optimización combinatoria [21], en la que cada iteración consta de dos fases: construcción y búsqueda local. La fase de construcción genera una solución factible mediante un proceso de selección y adición de un nuevo elemento de acuerdo a la evaluación de una función de utilidad. La vecindad de esta solución inicial es examinada durante la fase de búsqueda local hasta encontrar un mínimo local. La mejor solución global se mantiene como el resultado [11].
En cada iteración de la fase de construcción se conforma una lista de candidatos con todos los elementos que pueden ser incorporados paso a paso a la solución parcial en construcción, sin destruir la factibilidad de la solución. A partir de esta lista preliminar, se construye un subconjunto de estos elementos denominada la RCL, Lista Restringida de Candidatos, la cual contiene aquellos elementos cuya incorporación a la actual solución parcial resulte en los menores costos incrementales (este es el aspecto codicioso del algoritmo). Esta condición de pertenencia de los candidatos a la RCL se expresa de la siguiente manera:
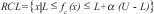
Donde:
- ƒc (χ) es la función de utilidad del elemento χ
- α es un número entre 0 y 1.
- L es el menor valor (caso de minimización) de la función de utilidad encontrado.
- U es el mayor valor (caso de minimización) de la función de utilidad encontrado.
En el paso siguiente se elije un candidato al azar de la RCL (este es el aspecto probabilístico de la heurística) para adicionar a la solución inicial, se actualiza la RCL y los costos incrementales son reevaluados (este es el aspecto adaptativo de la heurística). Este proceso se realiza hasta que se tiene construida la solución inicial. La figura 1 presenta el pseudocódigo del algoritmo descrito:

La etapa de construcción busca generar soluciones iniciales con un grado de diversidad controlado con el fin de permitir explorar diferentes zonas del espacio de solución, sin embargo estas soluciones deben al menos ser tratadas con un algoritmo de búsqueda local, lo que normalmente mejora la solución encontrada [11]. Esta es la segunda etapa de GRASP.
En un algoritmo de búsqueda local se aplica una transformación o modificación parcial denominada como movimiento [4], de forma iterativa a una solución inicial, para encontrar nuevas soluciones alternativas. El algoritmo se detiene cuando se alcance el número de iteraciones predefinido y se guarda la mejor solución encontrada. Un factor que afecta la eficiencia de un algoritmo de búsqueda local es el tamaño de la vecindad. Si se consideran muchos vecinos la búsqueda puede ser muy costosa. Esto es especialmente cierto si la búsqueda toma muchos pasos para alcanzar un óptimo local y/o cada evaluación de la función objetivo, requiere una cantidad significativa de computación [27].
Muchos métodos de mejoramiento se basan en intercambios  -Optimal, que consisten en encontrar soluciones en la vecindad mediante la eliminación de
-Optimal, que consisten en encontrar soluciones en la vecindad mediante la eliminación de  arcos de un grafo dirigido y reconectar la nueva trayectoria del grafo, usando nuevos arcos [11]. Para el caso específico de 2-Optimal, propuesto originalmente por Croes [8], la solución en la vecindad se obtiene de la solución actual mediante la eliminación de dos arcos, reversando una de las trayectorias y reconectando el grafo. Si la solución encontrada es mejor, se toma, de lo contrario se mantiene la mejor encontrada. (Ver pseudocódigo, Figura 2).
arcos de un grafo dirigido y reconectar la nueva trayectoria del grafo, usando nuevos arcos [11]. Para el caso específico de 2-Optimal, propuesto originalmente por Croes [8], la solución en la vecindad se obtiene de la solución actual mediante la eliminación de dos arcos, reversando una de las trayectorias y reconectando el grafo. Si la solución encontrada es mejor, se toma, de lo contrario se mantiene la mejor encontrada. (Ver pseudocódigo, Figura 2).

Una diferencia fundamental entre GRASP y metaheurísticas como búsqueda tabú y recocido simulado, es que GRASP depende de la alta calidad de las soluciones generadas en la fase 1, mientras que los otros métodos no necesariamente requieren buenas soluciones iniciales y gastan la mayor parte del tiempo mejorando la solución inicial e intentando salir de óptimos locales [23]. Finalmente, con la integración de las dos fases se consolida el pseudocódigo de la metaheurística GRASP, que se muestra en la figura 3.

3. DESARROLLO
En esta sección se presenta en detalle el algoritmo implementado para resolver el problema de programación de la producción en una máquina para minimizar la tardanza ponderada total, que consistió en implementar la metaheurística GRASP, con tres diferentes funciones de utilidad y aplicar como método de búsqueda local 2-Optimal (Figura 4). Todos los algoritmos desarrollados fueron implementados en una macro de Excel 2007 en lenguaje Visual Basic para Aplicaciones.
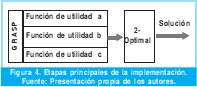
3.1 Parámetros del modelo
El modelo propuesto requiere como datos de entrada: el parámetro α, un valor entre 0 y 1, que indica el porcentaje de elementos que deben adicionarse a la RCL, el número de veces que se ejecutarán la fase constructiva y de búsqueda local de GRASP y la información de cada trabajo (tiempo de proceso pj , importancia Wj y fecha límite de terminación Dj).
La aplicación también puede recibir el valor de la mejor solución encontrada para el problema que se esté procesando, el cual no es obligatorio. Cada trabajo se identifica con un número entero j|j ∈ {1,2,...,n}, donde n es la cantidad de trabajos del problema. Con esta notación cada programa o solución generada será una permutación de los primeros n números enteros.
3.2 Implementación de GRASP con diferentes funciones de utilidad
Un aspecto importante en el desempeño del algoritmo GRASP, es la correcta definición de la función de utilidad, que es el criterio para permitir la adición de un candidato a la lista RCL. En esta investigación se trabajó con tres funciones de utilidad, buscando identificar la más favorable en cuanto a calidad de las soluciones encontradas. En el algoritmo, la función de utilidad de GRASP a utilizar en la ejecución de los problemas se debe seleccionar en la ventana de inicio para poder iniciar la corrida del mismo. Las funciones se especifican a continuación.3.2.1 Función de utilidad basada en WSPT
Para el problema en una máquina 1|| ∑Wj Cj, se ha demostrado que la regla de despacho WSPT (tiempo de proceso ponderado más corto, por sus siglas en inglés), genera la secuencia óptima [21]. Esta regla consiste básicamente en que un trabajo j debería ser procesado antes que un trabajo siempre que se cumpla que:
siempre que se cumpla que:
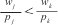
Como en el problema estudiado en este artículo el objetivo es minimizar la tardanza total ponderada, se propone una regla similar como función de utilidad para la metaheurística GRASP, así:

donde t es el tiempo actual del sistema.
3.2.2 Función de utilidad basada en la regla de despacho Earliest Due Date (EDD)
Teniendo en cuenta que para los problemas de 1|| ∑ Lmax y 1|| ∑ Tmax se ha demostrado que la regla de despacho EDD (fecha mínima de entrega, por sus siglas en inglés), genera la secuencia óptima [21], se decide aplicarla de la siguiente forma:

donde t es el tiempo actual del sistema.
3.2.3 Función de utilidad basada en (CR) y (SPT) modificada
Haciendo una modificación de las reglas de despacho CR y SPT (razón crítica y tiempo más corto de procesamiento, respectivamente, por sus siglas en inglés) [21], se propone la siguiente función de utilidad:
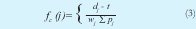
donde t es el tiempo actual del sistema.
La anterior busca utilizar la estructura de las reglas de despacho mencionadas, pero se incluye la importancia del trabajo Wj.
Teniendo presente el objetivo de minimizar la tardanza ponderada total, los elementos que se adicionan a la lista restringida de candidatos RCL, son aquellos que tienen menores valores de ƒc en los tres casos. En la fase posterior se aplica la búsqueda local 2-Optimal, para revisar todos los intercambios posibles de pares de trabajos.
4. RESULTADOS
Se consideraron nueve instancias del problema 1|| ∑ Wj Tj de la librería OR-Library (http://people.brunel.ac.uk/~mastjjb/jeb/info.html) con 40, 50 y 100 trabajos, para medir el desempeño de las diferentes funciones de utilidad propuestas e implementadas en el algoritmo. Por cada instancia el algoritmo se ejecutó en 10 ocasiones, utilizando como parámetro de entrada 10 iteraciones para el procedimiento definido en la Figura 3.
El parámetro α tuvo dos niveles con valores de 0,05 y 0,1. Los parámetros usados en la experimentación fueron fijados en esos valores teniendo en cuenta el número de réplicas necesarias para hacer inferencia estadística de los resultados obtenidos y el comportamiento aleatorizado del método GRASP al utilizar mayores valores de α.
El objeto del estudio era proponer funciones de utilidad diferentes de las obvias para el problema 1|| ∑ Wj Tj e identificar diferencias significativas en la calidad media de las soluciones obtenidas mediante GRASP atribuibles a ellas. Para tal efecto y debido a que la pregunta de interés gira en torno a pruebas de hipótesis de igualdades de medias, se realizaron las pruebas asociadas para realizar dichas evaluaciones.
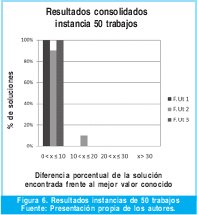
Los resultados obtenidos se presentan en las figuras 5, 6 y 7. La desviación del valor de la función objetivo obtenida por los autores respecto al mejor valor que se conoce en la literatura para cada instancia, se expresa porcentualmente.
En la instancia de 50 trabajos en el 18,7% de las corridas se obtuvo el mejor resultado encontrado en la literatura, y como se observa en la Figura 6, en el 96,7% de los casos la solución estuvo en el rango de desviación de 0% a 10%. Las funciones de utilidad 1 y 3 mostraron mejor desempeño al tener la totalidad de sus soluciones en el rango mencionado anteriormente, mientras que la basada en la regla de despacho EDD, tuvo el 10% de sus soluciones en el rango de 10% a 20% de desviación.
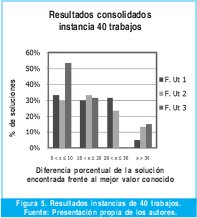
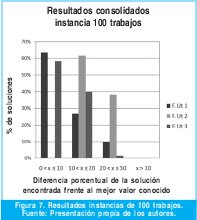
En los problemas estudiados de 100 trabajos en el 40,6% de las corridas, la solución estuvo en el rango de desviación de 0% a 10%, únicamente con soluciones encontradas por las funciones de utilidad 1 y 3, mientras que la basada en la regla de despacho EDD, no tuvo ninguna solución en dicho rango de desviación (Ver Figura 7).
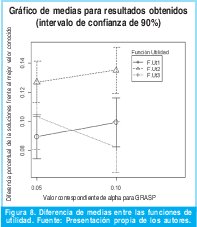
Para concluir sobre la existencia de diferencias en las soluciones obtenidas al usar las tres funciones de utilidad, se realizó una gráfica de diferencia de medias, para todas las instancias del problema, con un nivel de confianza del 90%, que se presenta a continuación:
Analizando la Figura 8 se puede observar que la dispersión de los resultados de la función de utilidad 3 basada en CR y SPT modificada, es mayor que la dispersión de los resultados de las otras dos funciones. Igualmente con un nivel de confianza del 90% hay evidencia que la función de utilidad 1 basada en WSPT para los valores de α seleccionados (0.05, 0.10) obtiene mejores soluciones que la función 2 basada en la regla de despacho EDD. Respecto a las funciones de utilidad 2 y 3 se puede afirmar que con de 0.10, al nivel de confianza del 90% hay evidencia que la función de utilidad 3 basada en CR y SPT modificada, obtiene mejores soluciones que la función 2. En los demás casos estudiados no hay evidencia suficiente para mostrar una diferencia de medias entre las funciones aplicadas.
5. CONCLUSIONES Y RECOMENDACIONES
En este artículo se presentó la implementación de la metaheurística GRASP, con tres diferentes funciones de utilidad propuestas y adaptadas por los autores y la aplicación de 2-Optimal como método de búsqueda local, para resolver el problema de programación de la producción de la tardanza ponderada total en una máquina (SMTWT). Se obtuvieron resultados competitivos en la calidad de las soluciones frente a los mejores valores conocidos de las diferentes instancias de los problemas probados y en tiempos de procesamiento razonablemente cortos. Esto pone a disposición de las empresas una alternativa contundente para solucionar los problemas de programación de producción, solo con contar con MS Excel, sin requerir software más especializado y posiblemente de mayor costo.
En las tres instancias de 40, 50 y 100 trabajos con las que se midió el desempeño del algoritmo en estudio, se encontró con un nivel de confianza del 90% que la función de utilidad 1 basada en WSPT para los valores de α seleccionados (0.05, 0.10) obtiene mejores soluciones que la función 2 basada en la regla de despacho EDD. Mientras que para un α de 0.10, al nivel de confianza del 90% la función de utilidad 3 basada en CR y SPT modificada, obtiene mejores soluciones que la función 2. En los demás casos estudiados no hay evidencia suficiente para mostrar una diferencia de medias entre las funciones aplicadas. Esto permite afirmar que la correcta definición de la función de utilidad es el factor fundamental en el desempeño de la metaheurística GRASP, para obtener buenas soluciones.
Finalmente se observa que en instancias hasta de 40 trabajos la función CR+SPT modificada presentan mayor número de soluciones en el menor rango de desviación. Mientras que en las instancias de 50 y 100 trabajos la función basada en WSPT muestra un mayor número de soluciones en el menor rango de desviación frente al mejor resultado encontrado en la literatura.
En trabajos futuros es importante considerar el estudio de otras funciones de utilidad para solucionar otros problemas como el de minimizar el makespan y comparar la calidad de las soluciones y la influencia del factor α.
REFERENCIAS BIBLIOGRÁFICAS
[1] K. Baker, J. Hayya. "Priority dispatching with operation due dates". Journal of Operations Mangement 2, 167-175. 1992.
[2] U. Bilge, M. Kurtulan, F. Kiraç. "A tabu search algorithm for the single machine total weighted tardiness problem". European Journal of Operational Research, 176, 142335. 2007.
[3] W. Bozejko, J. Grabowski, M. Wodecki. "Block Approach Tabu Search algorithm for single machine total weighted tardiness problem". Computers and Industrial Engineering 50, 114. 2006.
[4] R. Britto, G. Mejía, J. P. Caballero-Villalobos. "Programación de la producción en sistemas de manufactura tipo taller con el algoritmo combinado cuello de botella móvil y búsqueda Tabú". Ingeniería y Universidad, volumen 11, No 2, 203 224. 2007.
[5] T. C. E. Cheng, C. T. Ng, J. J. Yuan, Z. H. Liu. "Single machine scheduling to minimize total weighted tardiness". European Journal of Operational Research, 165, 423-443. 2005.
[6] F. Chou. "An experienced learning genetic algorithm to solve the single machine total weighted tardiness scheduling problem". Expert Systems with Applications, 36, 38573865. 2009
[7] R. K. Congram, C.N. Potts, S. L. Van de Velde. "An iterated dynasearch algorithm for the single-machine total weighted tardiness scheduling problem". Informs Journal on Computing, 14(1), 52-67. 2002.
[8] A. Croes. "A method for solving traveling-salesman problems". Operations Research, 5, 791-812. 1958.
[9] L. M. A. Drummond, L. S. Vianna, M. B. Silva, L. S. Ochi. "Distribution parallel metaheuristics based on GRASP and VNS for solving the traveling purchaser problem". In Proceedings of the 9th International Conference on Parallel and Distributed System, pp. 257-263. 2002.
[10] M. L. Fisher. "A dual algorithm for the one machine scheduling problem". Mathematical Programming, 11, 229-252. 1976.
[11] F. Glover, G. Kochenberger. "Handbook of Metaheuristics. Kluwer Academic Publishers". 2003.
[12] R. L. Graham, E. L. Lawler, J. K. Lenstra, A.H.G. Rinnooy Kan. "Optimization and approximation in deterministic sequencing and scheduling: A survey". Annals of Discrete Mathematics, 5, 287-326. 1979.
[13] A. Grosso, C. Della, R. Tadei. "An enhanced dynasearch neighborhood for single-machine total weighted tardiness scheduling problem". Operations Research Letters, 32, 68-72. 2004.
[14] O. Holthaus, C. Rajendran. "A fast ant-colony algorithm for single-machine scheduling to minimize the sum of weighted tardiness of jobs". Journal of the Operational Research Society, 56, 947-53. 2005.
[15] F. Jin, S. Song, C. Wua. "A simulated annealing algorithm for single machine scheduling problems with family setups". Computers and Operations Research, 36, 2133 - 2138. 2009.
[16] E.L. Lawler. "Efficient implementation of dynamic programming algorithms for sequencing problems". Technical report, BW-106. Amsterdam: Centre for Mathematics and Computer Science. 1979.
[17] F. Jolai, M. Rabbani, S. Amalnick, A. Dabaghi, M. Dehghan, Y. Parast. "Genetic algorithm for bi-criteria single machine scheduling problem of minimizing maximum earliness and number of tardy jobs". Applied Mathematics and Computation, 194, 552-560. 2007.
[18] C. Liao, C. Cheng. "A variable neighborhood search for minimizing single machine weighted earliness and tardiness with common due date". Computers and Industrial Engineering 52, 404-413. 2007.
[19] C. Liao, H. Juan. "An ant colony optimization for single-machine tardiness scheduling with sequence-dependent setups". Computers and Operations Research 34. 2007.
[20] T. E. Morton, R. M. Rachamadugu, A. Vepsalainen. "Accurate myopic heuristic for tardiness scheduling". Working paper No. 36-83-84. Pitsburgh: Carnegie-Mellon University. 1984.
[21] M. Pinedo. "Scheduling Theory, Algorithms and Systems". Third edition. New Jersey. Prentice Hall. 2008.
[22] A. H. G. Rinnooy Kan, B. J. Lageweg, J. K. Lenstra. "Minimizing total costs in one-machine scheduling". Operations Research, 25, 908-927. 1975.
[23] R. Rios-Mercado, J. Bard. "Heuristics for the flow line problem with setup costs". European Journal of Operational Research 110, 76-98. 1998.
[24] T. Sen, J. M. Sulek, P. Dileepan. "Static scheduling research to minimize weighted and unweighted tardiness: a state-of-the-art survey". International Journal of Production Economics, 83, 1-12. 2003.
[25] M. Tasgetiren, Q. Pan, Y. Liang. "A discrete differential evolution algorithm for the single machine total weighted tardiness problem with sequence dependent setup times". Computers and Operations Research, 36, 1900 - 1915. 2009.
[26] C.A. Vega-Mejía, J.P. Caballero-Villalobos. "Uso combinado de GRASP y Path-Relinking en la programación de producción para minimizar la tardanza total ponderada en una máquina". Ingeniería y Universidad, volumen 14, número 1, 79 - 96. 2010.
[27] C. Voudouris, Tsang. "Guided Local Search. Handbook of Metaheuristics". Capítulo 7. Kluwer Academic Publishers. 2003.
[28] G. Wan, B.P.C. Yen, "Single machine scheduling to minimize total weighted earliness subject to minimal number of tardy jobs". European Journal of Operational Research 195, 89-97. 2002.
[29] X. Wang, L. Tang. "A population based variable neighborhood search for the single machine total weighted tardiness problem". Computers and Operations Research 36, 2105-2110. 2009.
Ángela María Niño Navarrete
Ingeniera Industrial de la Pontificia Universidad Javeriana. Actualmente, es estudiante de Maestría en Ingeniería Industrial en la Pontificia Universidad Javeriana. Se desempeña como Coordinador del Sistema Integrado de Gestión en Colcafé S.A.S. anino@javeriana.edu.co
Juan Pablo Caballero Villalobos
Ingeniero Industrial de la Pontificia Universidad Javeriana. Obtuvo su título de Maestría en Ingeniería Industrial en la Universidad de Los Andes. Actualmente se desempeña como profesor asistente y Director del Centro de Investigaciones en Optimización y Logística (CIOL), del departamento de Ingeniería Industrial de la Pontificia Universidad Javeriana, sus intereses de investigación están asociados a técnicas de optimización, problemas de programación de la producción, problemas combinatorios y uso de metaheurísticas. juan.caballero@javeriana.edu.co
Creation date:
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.





2.jpg)