Ciencia, Investigación y Desarrollo

Ingeniería, 2000-00-00 vol:5 nro:1 pág:28-36

El Ruido 1/f

1/f NOISE

Alvaro Betancourt Uscátegui

Profesor Universidad Distrital Francisco José de Caldas, Ingeniero Electrónico Universidad Distrital, Esp. Telecomunicaciones Móviles, Universidad Distrital, Msc. Ciencias Financieras y Sistemas, U. Central, Magister en Informatique Appliquée, Ecole Polytechnique de Montreal, Canada. Profesor y Decano Facultad de Ingeniería, abetancourt@udistrital.edu.co

Resumen

Fluctuaciones de frecuencia bajas que muestran densidad espectral de potencia inversamente proporcional a la frecuencia son observadas en varios sistemas: físicos, técnicos, biológicos y económicos. Se trata de un fenómeno muy particular llamado ruido 1/f o ruido de parpadeo que ha estimulado esfuerzos de investigación de numerosos científicos desde el trabajo pionero de Johnson [1] y Schotty [2].

Palabras Claves:
ruido, ruido 1/f o ruido de parpadeo, fluctuaciones de frecuencias bajas.

Abstract

Low frequency fluctuations showing a power spectral density inversely proportional to the frequency are observed in various physical, technical, biological, and economic systems. This is peculiar phenomemon which is called 1/f noise or flickernoise has stimulated the research efforts of numerous scientists since the early work of Johnson [1] and Schotty [2].

Key words:
noise, 1/f noise or flicker-noise, low frecuency fluctuations

INTRODUCCIÓN

El ruido generalmente implica cualquier perturbación del azar que altera una señal deseada y reduce la certeza con que una observación puede ser medida.

Cuando un voltaje constante es aplicado a través de una resistencia, un componente fluctuante se observa en la corriente además del ruido térmico que también está presente. Similarmente, cuando una corriente constante fluye a través de una resistencia, una fluctuación aleatoria de exceso es observada en la mayoría de las resistencias con la presencia de un voltaje o una corriente d.c. Se muestra que la densidad espectral de potencia varía como 'fi', donde a es más o menos constante y normalmente se encuentra entre 0.8 y 1.4. Esta forma espectral ha sido observada por encima de un ancho rango de frecuencia, variando entre una docena de décadas, de 10-6 hz a 106 hz o mayores en algunos dispositivos de microondas.

De hecho, el ruido que obedece la ley de potencia de frecuencia inversa es conocido hoy día en prácticamente todos los materiales y dispositivos electrónicos, incluso en los dispositivos semiconductores y uniones, en finos metales, en metales líquidos, en soluciones electrolíticas, en superconductores y en uniones Josephson. Ningún amplificador electrónico ha estado libre del ruido 1/f o de parpadeo a bajas frecuencias [3]. Se pretende llevar a cabo a una revisión del ruido 1/f. Se presentan las características generales, sus propiedades y hechos y observaciones experimentales realizadas por diferentes autores.

GENERALIDADES DEL RUIDO 1/f

Diferentes nombres han sido usados en la literatura para este tipo de ruido: el ruido 1/f ha sido llamado como ruido de corriente, ruido de exceso, ruido de baja-frecuencia, ruido de parpadeo (normalmente relacionado con las fluctuaciones en emisión del electrón desde un cátodo termiónico), ruido de semiconductor (antes de que fuera observado y que también apareció en metales y en los electrolitos ) y ruido de contacto (aunque es conocido que el ruido 1/f no es en general un efecto del contacto).

Evidencias muestran que los orígenes del ruido 1/f en diversos tipos de dispositivos pueden ser bien diferentes. La primera observación del ruido 1/en un sistema electrónico fue hecha por Johnson [1], gran parte de este trabajo sobre dicho fenómeno fue descrito por [4], quién también publicó un artículo que incluye otros desarrollos tales como el modelo en términos de función de forma del pulso [5]. Aspectos también interesantes del ruido 1/f se discuten en [6] y a nivel de membranas neurales es conocido que exhiben fluctuaciones 1/f y varias referencias de esta manifestación particular del ruido 1/f se citan en [7].

Varios modelos matemáticos y empíricos propuestos para el ruido 1/f son descritos por [8]. E 1 ruido 1/f es un tipo de fluctuación omnipresente, que aparece no sólo en mediciones de sistemas electrónicos sino también en un diverso rango de observaciones en cualquier parte. Ha sido reportado en terremotos, tormentas y ríos [9] [10], aunque los espectros involucrados en estos casos no son el espectro de potencia en el sentido usual. Los sistemas biológicos exhiben el ruido 1/f: el período normal del latido del corazón humano muestra una fluctuación cuya densidad espectral de potencia varía aproximadamente como 1/1f] a las frecuencias por debajo de 0.3 Hz, y una forma espectral similar se observa en relación con las fluctuaciones de las ondas cerebrales, en particular con el componente de onda alfa del electro - encefalograma (EEG) [11].

Otra área donde el ruido 1/f se encuentra presente es en la música [12]. Voss y Clarke encontraron que la relación entre la intensidad y grado del tono en música clásica como: Mozart, Beethoveen, Bach, Debussy, en música occidental como: los Beatles y el jazz, así como en la música de una variedad de culturas diferentes, el ruido 1/1f 1 es un distintivo. Pero quizás lo más sorprendente es que la percepción individual de la música es influenciada fuertemente por su forma espectral; tres piezas de música 'compuestas' de los números aleatorios con densidades espectrales variaron como 1/1f1 2, 1/Ifi, y 1/1f1 ° (ruido blanco). Dichas piezas fueron juzgados como aburrido (1/1f12), irritante (ruido blanco) y agradable (1/1f]). Se observa que la buena música tiene un espectro 1/1f], probablemente porque su tiempo de correlación no es tan corto como para hacerlo irregular y perturbador ni tan largo como para hacerlo previsible.

El origen físico del ruido 1/f no es claro, excepto quizás en unos pocos casos. De hecho aun en la actualidad no es posible predecir con certeza si el ruido 1/f es originado en la superficie o dentro del volumen de un elemento.

La mayoría de las evidencias sugieren que en algunos tipos de dispositivos es un efecto de superficie, como en el caso del Mosfet donde la interface oxido/semiconductor juega un papel importante; pero en otros dispositivos, como por ejemplo en una resistencia se piensa que el ruido 1/f es un efecto de volumen asociado a una modulación aleatoria, incluyendo una fluctuación bien en el número o en la movilidad de los portadores de carga.

En contraste con muchos datos experimentales sobre el fenómeno, la densidad espectral de potencia del ruido 1/f en materiales homogéneos se comporta más o menos de manera sistemática. Una ley empírica fue formulada por [13] en la que la densidad espectral de potencia varía inversamente con el número total de portadores en el elemento, y aunque no puede ser de validez universal, la ley parece ser bastante representativa de lo observado del espectro de ruido 1/f. Varias teorías ingeniosas se han propuesto encontrándose muchos resultados [14]. El procedimiento resulta de una construcción matemática que da lugar a la forma espectral requerida pero que arroja una pequeña teoría sobre el mecanismo físico responsable del ruido.

Las dos características de 1/f son: correlaciones de tiempo muy largo, y la ausencia de una escala de tiempo [14]. Los tiempos largos serían menos marcados, dado el factor exp[-w/kT]. La idea es que una partícula cargada, que está siendo dispersada por algún centro de fuerza, puede o no emitir un fotón bajo, las dos partes de la función onda que corresponden a estas dos posibilidades suponen una interferencia, debido al hecho que una de ellas tiene una frecuencia ligeramente más baja, habiendo perdido un poco de energía del fotón. Sin embargo, esto viola las reglas fundamentales de la mecánica cuántica [15].

La tabla 1 presenta algunos sistemas en los que fluctuaciones y cantidades de ruido 1/f han sido observadas.

PROPIEDADES

Los fenómenos de fluctuación 1/f en sistemas físicos generalmente pueden ser caracterizados por su densidad de amplitud de distribución gaussiana y por una densidad espectral de potencia S(f) qué sigue una ley f a en un rango ancho de frecuencia f con un exponente a cercano a la unidad. Puede entonces considerarse que 1/f es un proceso aleatorio estacionario gaussiano.

No Varianza de Escala

Como quiera que la potencia del ruido 1/f es inversamente proporcional (K_l,) a la frecuencia, es posible encontrar el ruido contenido en una banda mediante integración de K₁ f^-1 sobre el rango de frecuencia de interés, y tenemos que;

Nf = K₁, In (f_h / f_i)

donde f_h y f₁, son los límites de frecuencia superior e inferior de la banda.

El significado del valor al cuadrado del correspondiente voltaje del ruido es :

Ef² = k n lK(f_h, /f₁,) = Kln (1+Δ f/f1) K Δ f/f₁,

Cuando el ancho de la banda es de un 1-Hz, f_h = f₁, +1 y tenemos: S(f) = K/fV² Hz

siendo ésta la densidad espectral del ruido 1/f .

La potencia del ruido por década del ancho de banda es constante, pero una década desde 0.1 a 1Hz es más angosta que la década de 1 a 10 Hz. Si consideramos el ruido 1/f en un amplificador d.c. existe un límite más bajo a la respuesta de frecuencia por la longitud de tiempo en el que el amplificador ha sido encendido. Así la potencia del ruido total entre décadas de frecuencia es la misma y esta propiedad del ruido 1/f es conocida como no varianza de Escala.

En sistemas realmente físicos se observan desviaciones más significativas de las propiedades ideales y en un juego de sistemas equivalentes los valores reales son estadísticamente distribuidos. Esta situación ha dado lugar a permanente discusiones y controversias ( a veces académicas ) sobre la característica básica del ruido 1/f.

Estacionariedad

Un debate sobre si el ruido 1/f es estadísticamente estacionario ha sido defendido por mucho tiempo en la literatura. Declaraciones sobre el efecto que 1/f es una fluctuación estacionaria es tan común como aquéllos que proclaman que exhibe algún grado de 'non-estacionario'.

Normalmente el significado preciso de estos términos aún no queda claro. Para clarificar la situación dos formas de onda específicas fueron consideradas : ruido 1/f de banda-limitada en el que los componentes de baja frecuencia están ausentes y ruido 1/f de un filtro paso-bajo en que los componentes de baja frecuencia caen a frecuencia cero y están presentes. Estos experimentos que investigan la estacionaridad del ruido 1/f bandalimitado han sido realizados por [16], quién observó fluctuaciones moderadas en la variación del ruido de dos tipos de resistencias de fuente (resistencias de carbón y los transistores bipolares) y los comparó con medidas similares hechas en ruido 1/ f artificial' , cuyos resultados produjeron espectro de potencia del ruido 1/1 f 1 gaussiano estacionario. No encontraron razón alguna para dudar que el ruido 1/f de banda-limitada es estadísticamente estacionario.

En contraste, ruido 1/f de filtro paso bajo es una abstracción teórica y es no-estacionario.

Formas de onda del ruido 1 /f

Se consideran dos formas de onda del ruido 1/f. La primera es un tren de pulsos aleatorios. Schonfeld introdujo la idea que el ruido 1/f podría ser representado por una sucesión aleatoria de pulsos de forma similar y [5] desarrolló el modelo en términos de función de forma del pulso más simple. La segunda representación matemática de un forma de onda del ruido 1/f es basada en la superposición de un gran número de procesos con una cobertura de tiempos constantes [17]. Debido a que relaciona directamente un mecanismo de la superficie para el ruido 1/f, ha recibido mayor credibilidad que la consideración del tren de pulsos aleatorios.

HECHOS EXPERIMENTALES E INTERPRETACIONES

Quizás el rasgo más impresionante de ruido 1/f es su ubicuidad; aparece en todos los tipos de resistencia del carbono, en cristales simples de semiconductores, en los dispositivos de unión de p-n, en estructuras de metal-óxido, en películas de metal continuas y discontinuas, en superconductores.

De otra parte, está ausente en JFET de silicio, dicho fenómeno se atribuye a un mecanismo de la superficie que involucra capturar en otras capas de óxido. A continuación se describen algunos hechos e interpretaciones.

Ruido de contacto

Algunos experimentos fueron diseñados cuidadosamente alrededor cuatro-medidas de prueba, donde dos terminales que mantienen el nivel d.c. son independientes del par que censa la fluctuación [18]. De esta manera son eliminados como una posible fuente del ruido. Por precaución, los chequeos se llevan a cabo con una muestra de control, que es una resistencia de alambre enrollado cuyo valor es conocido y está libre del ruido 1/f , para asegurarse que el experimento por sí mismo no es un generador significante de fluctuaciones 1/f.

Densidad de distribución de amplitud

La distribución de amplitud del ruido 1/f es gaussiana [19]. Aparecen desviaciones que podrían ser explicadas por la interferencia con componentes adicionales de ruido de baja frecuencia , en particular ráfagas de ruido. Aun cuando este es un efecto real en relación con el ruido 1/f, esto representa sólo una distorsión menor en las tallas de la distribución que para propósitos prácticos son ignoradas.

Fluctuaciones de resistencia

Las fluctuaciones de voltaje 1/f observadas en varios tipos de resistencias que incluyen el semiconductor, película delgada de metal, muestran un espectro de potencia que varía como el cuadrado de la corriente d.c. que fluye a través del elemento.

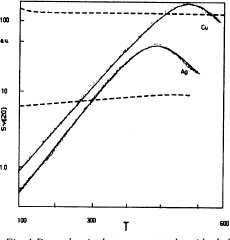
Si una fuente de corriente constante mantiene el nivel d.c., la fluctuación de voltaje v(t) puede derivarse de una fluctuación r (t) en la resistencia de la muestra. Como v(t) = I r (t), donde I es la corriente d.c. , la densidad espectral de potencia de la fluctuación de voltaje es,

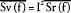
donde Sr(f) es la densidad espectral de potencia de la fluctuación de la resistencia. Este argumento cuenta para la dependencia cuadrática en el nivel de d.c. Aunque ésto no explica el origen del ruido 1/f si llama la atención hacia la resistencia como fuente de la fluctuación. Como la resistencia depende de la densidad y movilidad de los portadores de carga, la conclusión es que el ruido 1/f se deriva del número o fluctuaciones de movilidad.

Cuando una corriente a.c. fluye a través de una resistencia que muestra un ruido 1/f en presencia de corriente de d.c., un ruido parecido a 1/f es producido en las dos bandas laterales de la frecuencia de conducción, fo. Es conocido como ruido 1/ f porque la densidad espectral de potencia en las bandas laterales varía como 1/1fo-f]. Las escalas del ruido 1/ f están en proporción al cuadrado el nivel de la corriente a.c. que también puede interpretarse como debido a una fluctuación áe resistencia.

Fórmula de Hooge

En 1969 Hooge estableció su famosa relación del fenómeno de la densidad espectral de potencia Si(f) de fluctuaciones de corriente o Sr(f) de fluctuaciones de resistencia

Si(f)/I² = Sr(f) / R² = K. 1/f

que describe bien el ruido observado 1/f en metales homogéneos y semiconductores. I y R significan la corriente y resistencia respectivamente. En sistemas con corrientes de densidad homogéneas el factor de intensidad es:

c = α/nV

que solamente depende del número total n.V de los portadores de carga libres donde n es la densidad del portador y V el volumen de la muestra. La menor cantidad del valor a ha sido encontrado empíricamente como una aproximación universal constante 2x10^-3 mostrando sólo una muy débil dependencia a la temperatura.

A pesar del éxito considerable de la ley de Hooge, aumenta la evidencia que a incluso en la forma modificada, no es universalmente representativa del nivel de ruido 1/f en una resistencia homogénea [20]. Es más, Eberhard y Horn midieron el ruido 1/f en películas de plata y cobre y encontraron que el nivel de ruido aumentó rápidamente con la temperatura creciente lo que equivale a decir que a aumentó con la temperatura [21].

Número de Fluctuaciones

Las fluctuaciones observadas de 1/f en materiales homogéneos podrían deberse a fluctuaciones tanto en número o movilidad de los portadores de carga. La dependencia inversa sobre el número total de portadores en la ley de Hooge parecería sugerir una fluctuación en número como el mecanismo responsable para el espectro 1/f. Una cierta cantidad de evidencias experimentales soportan el punto de vista que fluctuaciones de resistencia 1/f no son debidas a una fluctuación de número. El circuito abierto térmico-e.m.f. entre dos elementos del mismo material a temperaturas diferentes depende de la concentración del portador y debería reflejar cualquier fluctuación del número que ocurre. Sin embargo, Hooge [22] no observó ningún ruido 1/f en un circuito abierto termocelda, y [23] no encontró evidencia alguna para soportar la hipótesis del número de fluctuaciones en medidas termoe.m.f. hechas en las muestras de germanio. El número de fluctuaciones no puede ser completamente descartada ya que alguna medida del ruido 1/f en varios tipos de resistencias de silicio fueron interpretadas en términos de número de fluctuaciones [24] y medidas de efecto hall [25] son un indicativo de fluctuación en el número de portadores.

Fluctuaciones de movilidad

La alternativa a una fluctuación en número es una fluctuación en movilidad. Las Fluctuaciones de movilidad podrían explicar las fluctuaciones 1/f en efecto hall. Para explicar el espectro 1/f, las fluctuaciones en movilidad podrían tener características de tiempo libre. El significado de tiempo libre de un portador está en el orden de los picoseconds y los tiempos de tránsito son menos que un milisegundo. Los argumentos físicos parecerían eliminar fluctuaciones de movilidad como una fuente potencial del ruido 1/f , excepto en relación con fluctuaciones de temperatura [7].

Espectros de dependencia de temperatura

Las primeras medidas sistemáticas de la dependencia de temperatura del ruido 1/f en metales fueron reportadas por [21] . Examinaron que el ruido en películas delgadas de plata y cobre, 100-160 de espesor, que fue preparado por evaporación térmica hacia un sustrato de zafiro, y muestra la dependencia de temperatura como se observa en Fig. 1 Sv(f) medida a f=20Hz para películas de metal delgadas.

Nótese la caída rápida en el espectro a medida que disminuye la temperatura por debajo de la temperatura ambiente, y los picos que ocurren aproximadamente a 410 K y 490 K para plata y cobre.

Materiales amorfos y policristalinos

Una de las primeras medidas del ruido 1/f en materiales policristalinos fueron hechas por [26] y desde entonces ha habido numerosos documentos del fenómeno. En [27] .se discute el ruido 1/f en materiales cerámicos para películas de resistencias las cuales tienen aplicación en microelectrónica. En general espectros observados de 1/f en materiales amorfos o policristalinos tienen una precisión proporcional al cuadrado del nivel d.c. y sigue cercanamente la dependencia en frecuencia |f|^-1. En ciertos vidrios el ruido 1/f es independiente de la temperatura.

MECANISMO FISICO Y OBSERVACIONES EXPERIMENTALES

Las propiedades estadísticas del ruido 1/f , la estructura de ciertas formas de onda que muestran el espectro 1/f , y algunas de las evidencias experimentales en el ruido 1/f han sido considerados anteriormente. Se presenta a continuación algunos modelos y mecanismos usados del fenómeno.

Ruido en membranas biológicas

En el progreso de estudios neourofisiológicos del mecanismo del dolor, [28] propuso la 'teoría de la barrera de control' la cual da un conocimiento de la modulación del dolor por estimulación del nervio. El método y los resultados clínicos de la aplicación del ruido 1/f para estimulación eléctrica para el control del dolor fue realizado por [29] en que un tren de pulsos ligeramente - irregular fue producido con la ayuda del computador.

El pulso fue generado a una tasa con la correspondiente secuencia y fue caracterizado estocásticamente por la fluctuación 1/f.

Citan los autores el uso de dos métodos: uno, la generación 1/f que se llevó a cabo en un microprocesador con software de generación seudoaleatoria y un filtro digital 1/f ; el segundo método para obtener fluctuaciones 1/f fue extraer los cambios de períodos largos de frecuencias de la música clásica. En este caso, el estímulo de la música original podría ser aplicado al confort de los pacientes que lo soliciten.

Probaron en pacientes que padecían dolor el uso de un estímulo comercializado y un estimulador de fluctuación 1/f. Las causas de dolor fueron trauma, inflamación principalmente causados por herpes, cáncer, lumbago, dolores de espalda y otros. Cada paciente que había sido estimulado por espacio de más de 10 minutos fue preguntado efectuándose una escala sobre el grado de alivio. Todos los pacientes que usaron ambos estímulos prefirieron el uso el estímulador 1/f.

Luego de un periodo de tratamiento aproximado de treinta minutos fue experimentado que el efecto de alivio del dolor continuó por varias horas aun después de cortar la corriente para terminar el tratamiento de estimulación eléctrica del nervio.

Ruido en pequeños dispositivos electrónicos Los dispositivos electrónicos de dimensiones físicas muy pequeñas son herramientas particularmente eficaces para probar las fuentes microscópicas de ruido situadas bajo el fenómeno del ruido 1/f debido a que las fuentes del ruido son centro de electrones individuales. Los electrones son capturados y emitidos el dispositivo característico es modulado y el ruido entonces producido.

El ruido se procesa en dos tipos particulares de uniones túnel que fueron estudiados por [30]. El primero en uniones túnel Nb/Nb₂, 0₅ /PbInAu, el segundo en uniones Al/SiO₂ /p-Si (MOS).

Los resultados indican que hay muchos flujos de fuentes del ruido microscópicas, el electrón individual atrapado puede llevar a un conjunto de espectro de potencia 1/f. Fueron observados casos donde las solas capturas se comportan de manera no correlacionada estadísticamente, produciendo una contribución espectral Lorentzian, y superpuestos para producir un espectro neto 1/f. También fue mostrado que el espectro que aparece puede estar compuesto de componentes Lorentzian que no necesariamente implican que las fuentes de ruido microscópicas son independientes.

Ruido 1 /f en un condensador descargado

Un condensador descargado puede representarse como una capacitancia C en paralelo con una resistencia R que representa las pérdidas del dieléctrico como se muestra en figura No.2. La resistencia muestra el ruido térmico, representado por el generador de corriente de ruido paralelo In(t) que da lugar a una fluctuación de voltaje de circuito abierto Vn(t) en los terminales. Van der Ziel [31] señaló que la pérdida es independiente de la frecuencia, el voltaje de ruido de salida muestra un espectro 1/f

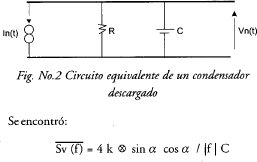
que es una ley 1/ |f| cuando el ángulo de pérdida a es independiente de la frecuencia. Pero para baja frecuencia esta condición no se satisface. La resistencia de pérdida es una medida de la conductibilidad a , del dieléctrico

R = d/αA

independiente de la frecuencia, así el condensador descargado no muestra un espectro 1/|f| a frecuencias muy bajas.

Ruido de baja frecuencia en condensadores polarizados de sólido-tantalium

Los condensadores son usados para acoplar señales mientras bloquea los niveles d.c. proporcionando una baja impedancia en corto circuito a una señal no deseada en circuitos de bajo ruido. Es posible pensar que los condensadores ideales están libres de ruido, aunque en realidad hay pérdidas. El estudio de ruido de baja frecuencia en condensadores sólidos de tantalium fue hecho por [32] y se encontraron niveles significativos de ruido, muy importantes en aplicaciones de bajo ruido.

El ruido se amplificó en una entrada d.c. de un amplificador FET., con la combinación de dos diodos (D1,D2) y un resistencia (R4) para proteger la entrada. El montaje bien realizado estabilizó la temperatura. La salida del amplificador fue pasada a través de los amplificadores adicionales para filtrar y se efectuó la medición del sistema. El circuito usado se muestra en figura No.3.

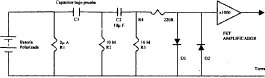
La conclusión fue que un ruido significante es generado por condensadores polarizados de tantalium a muy bajas frecuencias. Esta corriente tiene un espectro 1/f . Para minimizar el ruido es necesario mantener el condensador polarizado tan bajo como sea posible usando condensadores trabajando a un voltaje tan alto como sea factible y efectuar una buena selección de condensadores a los fabricantes.

Teoría cuántica del ruido 1 /f

La ubicuidad del ruido 1/f sugiere que el fenómeno es una característica fundamental e inevitable del transporte de carga La idea fue formalizada por Handel [33] quién desarrolló una teoría cuántica del ruido 1/f en la cual los portadores de carga interactúan con el campo electromagnético cuantizado. Aunque la energía de la emisión de un fotón es sumamente pequeña, es suficiente, según Handel para modular la corriente que fluye en el elemento de tal manera que se produce el ruido 1/f y1/Δf

Validez del modelo de teoría cuántica del ruido 1 /f

Conforme al tratamiento exacto de la teoría cuántica del ruido 1/f el efecto no existe. Fue analizado por [15] para objetar el controversia) modelo de Handel [32] basado en un término de la corrección de la densidad del electrón debido al Brensstrahlung, que ocurre en un proceso de dispersión.

Dos problemas controversiales fueron tratados, primero la manera de derivación de la densidad de probabilidad hecha por Handel y el segundo la influencia en la que el ruido 1 /f es hecha.

La conclusión es que las teorías de Bremsstrahlung aplicadas por Handel son basadas en la electrodinámica lineal, y son inválidas bajo las condiciones de fenómenos no lineales así que la cuántica particular del modelo de ruido 1/f propuesto viola en cierta forma los principios básicos de la teoría cuántica de los sistemas de muchas partículas.

Ruido 1/f para modelamiento de tráfico

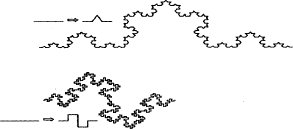
Tal como lo explica [34] si bien para el modelamiento del tráfico multifractal no se requiere una exactitud a nivel de la semejanza propiamente dicha, sí en cambio es necesario una similaridad propia estadística. En estos casos, las figuras correspondientes que son imprevisibles requieren de patrones de ruido particulares. Dichas trazas realizadas a partir de este tipo de ruido son curvas fractales cuya dimensión fractal está directamente relacionada con la pendiente logarítmica de la densidad espectral y en este tipo de movimiento la densidad espectral varía como 1 /f 2. Entonces para el modelamiento, generación y simulación de trafico multifractal, se requiere de la generación de este tipo de ruido 1 /f.

CONCLUSIONES

En dispositivos electrónicos el ruido 1/f está invariablemente presente, como ha sido estudiado durante mucho tiempo. El ruido 1 /f es un fenómeno oscuro y enigmático y su origen no es claro. Diferentes y numerosos experimentos y estudios han revelado sus muchas facetas. Algunos datos experimentales que están disponibles parecen ser contradictorios y están abiertos a interpretación.

Diferentes autores piensan que 1/f es un fenómeno de volumen, otros creen que se origina en la superficie. La ley de Hooge que establece que el nivel del ruido es inversamente proporcional al número total de portadores en la muestra es quizá una indicación del funcionamiento sistemático, aunque esta ley no es universalmente válida.

Desde el punto de vista teórico, no es satisfactorio y aunque existen algunos teorías sólo algunas sobreviven. La dependencia de temperatura del ruido 1/f en películas de metales es compleja de interpretar. Diferentes teorías acerca de la cuántica de 1/f están en discusión y tienen objeciones básicas.

El ruido 1 /f tiene gran aplicación en el modelamiento de tráfico multifractal.

La realidad es que el ruido 1/f se presenta en numerosos sistemas y muchas preguntas todavía están esperando respuesta.

REFERENCIAS

[1]. Johnson JB., The Schottky effect in low frequency circuits, Phys. Rev. 26, 71-85, (1925).

[2] Schottky W., Phys. Rev.28, 74-103, (1926).

[3]. Motchenbacher C.D,Fifchen EC, Low noise Elaytronic Design John Wiley 7, (1973).

[4]. Bell D.A.,Electrical Noise,Van Nostrand, London, chap. 10, (1960).

[5]. Bell D.A., A survey of 1 /fnoise in electrical conductors, J. Phys. Soc., 72, 27-32, (1980).

[6] Van der Ziel A., Flicker noise in electronic devices, Advances in Elect. andPhys., 49, 225-297, (1979).

[7]Weissman M.B., Survey of recent noise theories,Proc. 6th Int. Conf on noise in Physical Systems held at the National Bureau of Standards, Gaithersburg,MD, USA, pp. 133-142, (1981).

[8]. Hooge EIV., 1 /fnoise, Physica, 83 B, 14-23, (1976).

[9]. Machlup S., Earthquakes, thunderstorms and other noises, Proc. 6th Int. Conf on noise in physical systems held at the National Bureau of Standards, Gaithersburg, Md, USA, pp. 157- 160, (1981).

[10]. Gadner M,White and brown music,fractal curves and one-over-f fluctuations,Scientific American, 238(4),16-32 ,(1978).

[11] MushaT, 1/ffluctuations in biological systems, Proc. 6 th Int. Conf on noise in physical systems held at the National Bureau of Standards, Gaithersburg, Md, USA,pp 143-146, (1978).

[12] Voss R.F. and Clarke J., Flicker Ilf noise;equilibrium temperature and resistance fluctuations,Phys. Rev. B, 13, pp. 556-573,(1976). Hooge EN, 1/f noise is no surface effect.,Phys.Lett.A,