Ingeniería, 2005-00-00 vol:10 nro:1 pág:48-54

Compresión de imágenes con Wavelets y Multiwavelets

Samuel Barreto Melo
Profesor de la Facultad de Ciencias y Educación
de la Universidad Distrital Francisco José de Caldas.
Rodrigo Javier Herrera García
Profesor de la Facultad de Ingeniería
de la Universidad Distrital Francisco José de Caldas.

Resumen

Para un mayor rendimiento en la compresión de imágenes, la transformada wavelet requiere de filtros que combinen ciertas propiedades importantes como la ortogonalidad y simetría. Sin embargo, en el diseño de las wavelets tal combinación es limitada, ya que no es posible tener estas propiedades simultáneamente salvo el caso de Haar. El campo de las multiwavelets permite más opciones de diseño y por tanto distintas características simultáneas, tales como: soporte compacto, suavidad, aproximación de orden superior, simetría y ortogonalidad, entre otros. Es necesario por lo tanto establecer parámetros que permitan contrastar el rendimiento de wavelets escalares y multiwavelets. El propósito de este artículo es presentar algunos principios básicos de bancos de filtros, wavelets, multiwavelets y sus conexiones, así como los resultados experimentales obtenidos en la compresión de imágenes de prueba, comparando el rendimiento de cada uno de los sistemas.

Palabras clave:
Transformada wavelet, multiwavelet, compresión de imágenes, bancos de filtros.

Abstract

For best performance in image compression, wavelet transforms require filters that combine some important properties, such as orthogonality and symmetry. However, in the designing of wavelets this combination is limited because to have these simultaneous properties is not possible, except in the Haar case. The multiwavelet system allows more design options than wavelet, and therefore, several simultaneous characteristics such as: compact support, smoothness, higher order approach, symmetry and orthogonality, among others. Therefore, establishing parameters which allow comparing of scalar wavelets and multiwavelets performance, is a necesity. This paper provides an overview of filter banks, wavelets, multiwavelets, basic principles, and connections between each one,in addition to some experimental results from the compression of test images, comparing each system performance.

Key words:
wavelet transform, multiwavelets, image compression, filters banks.

1. INTRODUCCIÓN

En los últimos años, diferentes métodos de compresión de imágenes relacionados con teoría de filtros, análisis espectral y algunos conceptos básicos de probabilidad o estadística han sido objeto de estudio, produciendo nuevos y mejores algoritmos comparados con los métodos ya existentes.

Las técnicas de multiresolución se aplican de manera natural a imágenes, donde las nociones como resolución y escala son cada vez más intuitivas. Una característica importante de tales técnicas en la compresión de imágenes es su propiedad de aproximación sucesiva: en tanto las altas frecuencias sean aumentadas, es posible obtener imágenes de alta-resolución [2]. La codificación de la transformada tiene también una propiedad de aproximación sucesiva formando parte de una amplia clase de técnicas que son caracterizadas por este tipo de aproximación [2].

Las wavelets en las últimas décadas se han convertido en herramientas matemáticas eficientes y efectivas para el análisis tiempo-frecuencia, remplazando en algunos casos al método de Fourier. Sin embargo, con los avances actuales en ciencia y tecnología, existe una necesidad inmediata de extender también las herramientas matemáticas wavelets. Trabajos anteriores plantean razones que justifican el uso de las multiwavelets en lugar de wavelets escalares, en algunas situaciones dentro de la compresión de imágenes [3]. Además en [4] se pueden encontrar una lista de ideas y creaciones matemáticas para otras extensiones de los wavelets que incluyen: Ridgelets digitales y continuos, brushlets, contourlets, eno-wavelets, frames spline-wavelets y los más recientes bandelets de segunda generación.

En la sección 2 se realiza un breve repaso de la transformada wavelet, transformada multiwavelet, y el cálculo de estas transformadas mediante filtros. En la sección 3 se describe el método de compresión empleado para la obtención de los resultados. En la sección 4 se describen los resultados obtenidos para diferentes imágenes de prueba con diferentes tipos de filtros. Finalmente en la sección 5 se presentan algunas conclusiones.

2. FUNDAMENTOS DE BANCOS DE FILTROS, WAVELETS Y MULTIWAVELETS

2.1 Bancos de filtros ortogonales y wavelets:

Cuando se habla de filtraje, usualmente se piensa en un selector de frecuencias. Por ejemplo, un filtro pasa-bajo ideal de tiempo discreto con corte de frecuencia ω_c<ω toma cualquier señal de entrada y la proyecta hacia el subespacio de señales de banda limitada [-ω_c, ω_c]. Los bancos de filtros ortogonales de tiempo discreto realizan una proyección similar, pues basta ver que cualquier secuencia de l 2 (Z ) puede ser escrita como:

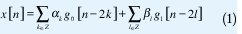
donde

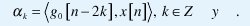
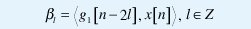
La formula de expansión (1) se puede implementar usando simplemente un banco de filtros multitasa como el de la Figura 1, y teniendo en cuenta que g₀ [n] y g₁[n] son los filtros pasa-bajo y pasa-alto respectivamente.

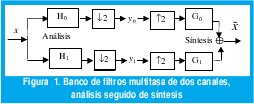
Los filtros de análisis: pasa-bajo H(z) y pasaalto H₁(z) son versiones invertidas en tiempo de G₀(z) y G₁(z), lo que significa: H_i(z) = G_i^(z-1), i = 0,1. El banco de análisis calcula los coeficientes α_i y β_l y el de síntesis realiza la reconstrucción. Considerando la rama análisis/síntesis pasa-bajos se puede verificar que el proceso de filtraje submuestreosupermuestreofiltraje es un operador lineal, autoadjunto, e idempotente, es decir, es una proyección ortogonal del espacio de entrada l₂(Z) hacia el subespacio generado por {g₀ [n-2k]}_k∈Z y denominado V₁ para el cual {g₀ [n-2k]}_k∈Z forma una base ortonormal [5]. De manera similar se puede considerar la rama pasa-alto y ver que esta produce una proyección de l₂(Z) sobre el espacio W₁ generado por {g₁ [n-2l]}_l∈Z. Los espacios V₁ y W₁ son ortogonales y su suma directa formal₂(Z), o l2 (Z) = V₁ ⊕ W₁. Así, un banco de filtro ortogonal divide el espacio de entrada en un espacio V₁ de aproximaciones (gruesas) y su complemento ortogonal W₁ o espacio wavelet (de detalle). Lo anterior es tan solo el primer paso dentro del análisis multiresolución que se obtiene cuando se itera la división pasa-alto/pasa-bajo sobre los pasa-bajo (Figura 2).

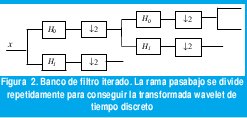
La conexión entre la transformada wavelet discreta y la expansión wavelet de dominio continuo se alcanza de manera precisa a través del análisis multiresolución (MRA) y el isomorfismo entre L₂(R) y l₂(Z).

Las ecuaciones 1 y 2 denominadas ecuación de dilatación y ecuación wavelet constituyen la conexión crucial entre los wavelets (dominio continuo) y los bancos de filtros (dominio discreto).

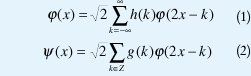
El método de solución más conocido de la ecuación 1 es el algoritmo de cascada, el cual consiste en una iteración infinita con el filtro pasabajo h(k), a partir de una función constante a trozos la cual en cada paso es filtrada y reescalada, reduciéndose en cada iteración. Si la iteración converge a una función límite φ(x) , ésta es solución de la ecuación de dilatación. La ecuación 2 que involucra los coeficientes del pasaalto g(k), genera la función wavelet ψ(x) a partir de la φ(x).

Finalmente cabe mencionar que los bancos de filtros biortogonales que se consideran en secciones posteriores para las pruebas de compresión, convergen a bases biortogonales.

2.2 Transformada multiwavelet

Las wavelets tienen asociada una función de escalado φ(x) y una función wavelet ψ(x) respectivamente dadas por las ecuaciones 1 y 2. Las multiwavelet tienen 2 o más funciones de escalado y wavelet, de forma tal que las funciones vectoriales de multiescalado Φ(x) y multiwavelet ψ(x) vienen dadas por:

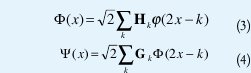
donde {H_k} y {G_k} son filtros matriciales, es decir H_k y G_k son matrices de r x r para cada entero k. Los elementos que conforman este tipo de filtros dan lugar a más grados de libertad que los wavelets escalares. Estos grados de libertad pueden usarse para incorporar propiedades útiles en los filtros multiwavelets, tales como ortogonalidad, simetría, suavidad y aproximación de orden superior [3].

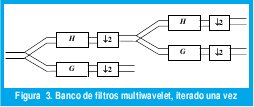
Se han desarrollado métodos para la construcción de multifiltros, los cuales han sido aplicados en trabajos anteriores [8], [9], [10], resaltando que el procesamiento de una señal a través de una estructura multifiltro (Figura 3) es diferente al de un banco de filtros escalar.

3. MÉTODO DE COMPRESIÓN EMPLEADO

3.1 Introducción

La compresión de imágenes es esencial para aplicaciones tales como transmisión y almacenamiento de datos. El propósito de ésta es reducir la tasa de bit, bien sea para transmisión o para almacenamiento, manteniendo una calidad aceptable de la imagen. Una característica común de muchas imágenes es que los píxeles en una vecindad están altamente correlacionados y por lo tanto contienen información redundante. La tarea prioritaria es entonces encontrar una representación de las imágenes en la que los píxeles estén bien de-correlacionados. Redundancia e irrelevancia son dos principios fundamentales usados en la compresión [11]. La compresión puede ser alcanzada transformando los datos, proyectándolos hacia una base de funciones, aplicando umbral y luego codificando esta transformada [12].

3.2 Esquema de compresión

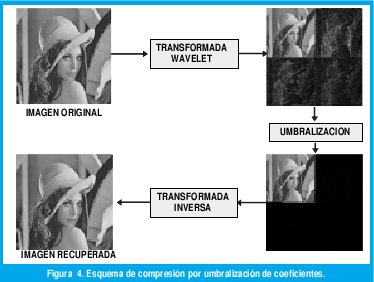
El método de compresión utilizado asocia una transformada wavelet o multiwavelet con un esquema de umbralización. El procedimiento desarrollado para la obtención de los resultados se ilustra en la Figura 4.

El proceso inicia aplicando la transformada wavelet o multiwavelet a la imagen de prueba. Como se sabe, la transformada wavelet decorrelaciona los valores de los píxeles de la imagen original, concentrando la información de la imagen en un número relativamente pequeño de coeficientes. Para la compresión (con pérdida) se aprovecha la propiedad de invarianza de la energía de la transformada wavelet, logrando así niveles de compresión con alta calidad de imagen. Esta propiedad de invarianza afirma que la cantidad total de energía en una imagen no cambia cuando la transformada wavelet se aplica. En otras palabras, lo anterior significa que cualquier cambio realizado a los valores de los coeficientes wavelets, resulta en cambios proporcionales en los valores de los píxeles de la imagen reconstruida, y por tanto en la práctica, se pueden eliminar aquellos coeficientes con magnitudes pequeñas, sin generar distorsión significativa en la imagen reconstruida.

La propiedad de invarianza mencionada anteriormente es la base del proceso de compresión de este trabajo, donde la eliminación de los coeficientes de valor no significativo se implementa aplicando una función de umbralización a la matriz de coeficientes:

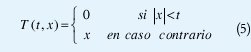
La tasa de compresión (CR) requerida en cada caso se controla variando el parámetro de umbral t. Los valores de las distintas tasas de compresión son producto de la siguiente ecuación:

Se pueden obtener más altas tasas de compresión, cuantificando los coeficientes wavelets no nulos tras la umbralización, en nuestro caso ningún cuantificador es empleado, ya que sólo estamos interesados en comparar la transformada y el desempeño de los diferentes filtros. La implementación del algoritmo de compresión se realiza empleando el paquete de análisis Matlab versión 6.5.

4. RESULTADOS EXPERIMENTALES

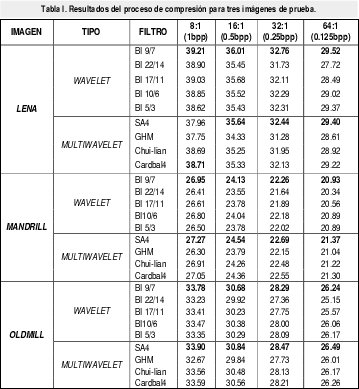
Para la ilustración de los resultados de la aplicación de filtros y multifiltros a la compresión de imágenes, se han seleccionado tres imágenes de prueba con diferentes características, extraídas de la literatura de compresión de imágenes,que permitan evaluar el desempeño de los diferentes bancos de filtros en el proceso de compresión. Estos resultados han sido extraídos como parte de las pruebas realizadas en [6]. Los filtros wavelet empleados (Bi 9/7, Bi 22/14, Bi 17/11, Bi 10/6, y Bi 5/3) son todos del tipo biortogonal y se han escogido, por ser los más representativos dentro del estado del arte de los filtros escalares. De igual manera, los filtros multiwavelet empleados para la prueba (sa4, GHM, Chui Lian y cardbal4) presentan diferentes características de los multifiltros tales como: simetría, antisimetría, balanceo y ortonormalidad, todo lo anterior, con el objeto de dar una mayor validez a los resultados de la prueba.

Los resultados obtenidos se presentan en forma de tabla de valores de relación señal a ruido pico (PSNR), los valores más altos se resaltan con negrita para cada grupo de filtros (wavelet y multiwavelet).

Puesto que todas las pruebas se realizaron sobre imágenes en escala de grises de 8 bits, el valor máximo de la señal es 255. De esta manera los valores de PSNR en dB para una imagen f (x,y) de M x N y su reconstrucción f ( x, y) son calculados mediante:

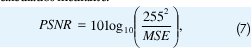
donde el error cuadrático medio MSE está definido como:

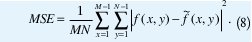
Para cada imagen un número de filtros wavelet y multiwavelet fueron probados y la tasa de compresión variada. Las tasas usadas corresponden a imágenes en escala de grises de 8 bits, por tanto el número de bits por píxel (bpp) es 8 dividido por la tasa de compresión. Los resultados de las pruebas están dados para 1.0 bpp (8:1), 0.5 bpp (16:1), 0.25 bpp (32:1) y 0.125 bpp (64:1). Algunos parámetros de compresión, tales como el nivel de descomposición se mantuvieron fijos (n = 4 para wavelets y multiwavelets).

De acuerdo a la Tabla I, la calidad percibida de las imágenes a altas tasas de compresión no necesariamente corresponde con los valores PSNR. Por ejemplo, comparando la imagen original de Lena (Figura 13) con la imagen reconstruida empleando wavelets escalares (Figura 14) y multiwavelets (Figura 16), visualmente se aprecia una mejor calidad en la imagen reconstruida con wavelet, no obstante el valor de PSNR para los dos casos es muy similar. Además, de acuerdo a los valores de la Tabla I, las imágenes con amplias áreas suavizadas, es decir, que muestran bajos contenidos frecuenciales (como Lena) son más fáciles de comprimir. En contraste, la imagen Mandrill (Figura 5) se caracteriza por la dificultad de compresión que presenta (lo cual se refleja en los valores PSNR obtenidos), al reconstruirse utilizando multiwavelets (Figuras 6 y 8) se obtienen mejores resultados que con filtros escalares, esto se debe a que la textura de la piel del mandril genera un alto contenido frecuencial, distribuido sobre la imagen en general. La capacidad de los multiwavelets para capturar detalles de alta frecuencia, mejor que los wavelets escalares puede verse a través de la Tabla I con los mejores rendimientos para los multifiltros en este tipo de imá- genes. La imagen Oldmill (Figura 9) posee regiones con contenido de baja frecuencia localizada así como regiones con texturas de alto contenido frecuencial. Los resultados ilustran que aunque esta imagen combina las componentes de altas y bajas frecuencias, es mayor el contenido de alta que de baja, de ahí los resultados a favor del multiwavelet. Con respecto a esta imagen y al desempeño de los filtros más largos (Bi22/14 y cardbal4), con una tasa baja el desempeño de los dos es a favor del multiwavelet, mostrando una diferencia de 0.36 dB, en tanto que para la tasa más alta de compresión, la diferencia se inclina a favor del multiwavelet (1.1 dB, ver Tabla I).

5. CONCLUSIONES

El desempeño de las multiwavelets depende en gran parte de las características de la imagen. Como puede verse, para aquellas imágenes con un bajo contenido frecuencial (Lena), los wavelets escalares presentan en general un mejor rendimiento. Sin embargo los multiwavelets aventajan a los wavelets en el sentido de que pre servan mejor los altos contenidos de frecuencia. En especial, las multiwavelets capturan mejor los bordes (o aristas) y patrones de tipo geométrico que ocurren en las imágenes con alto contenido frecuencial como mandrill. Para aquellas imáge nes que contienen simultáneamente áreas de alto y bajo contenido frecuencial (Oldmill), como es común en las imágenes naturales, los multiwavelets presentan un desempeño que es similar al de los wavelets escalares. En efecto, aquellas pruebas sobre imágenes que contienen grandes regiones texturizadas (Mandrill), mues tran que los multiwavelets pueden alcanzar beneficios como el de preservar patrones de alta frecuencia que se pierden para los wavelets escalares.

La relación entre la longitud del filtro y su des empeño es similar tanto para el caso de las wavelets escalares como de las multiwavelets. Los filtros cortos tienden a capturar muy bien deta lles de alta frecuencia ya que ellos no decrecen suavemente a cero en los extremos (o banda de rechazo), y por tanto capturan mejor las discontinuidades locales de las imágenes con alto contenido frecuencial. Por otro lado los filtros largos decrecen más rápidamente a cero y así capturan mejor regiones suaves localmente en imágenes con bajo contenido frecuencial.

Para todas las imágenes de prueba, el valor de los PSNR para cada uno de los filtros y multifiltros probados, disminuye en la medida que la tasa de compresión se aumenta. Este resultado es predecible, puesto que para una alta tasa de compresión la ganancia de codificación de la transformada es sobrecargada por un número insuficiente de bits para la representación.

Si se emplean pocos bits para representar una imagen, la calidad de la reconstrucción es pobre independientemente de la transformada implementada. A bajas tasas de compresión se tiene un número suficiente de bits para la representación, permitiendo a cada una de las transformadas mostrar sus ventajas y desventajas.

REFERENCIAS BIBLIOGRÁFICAS

[1] Strang, G., Nguyen, T. Wavelets and Filter Banks. Wellesley-Cambridge Press. Revised Edition 1997.

[2] Vetterli, M. and Kovacevic, J. Wavelets and subband coding. Secc.,7.1.1, Prentice-hall, 1995.

[3] Martin, M., Bell, A., (2000). New image compression techniques using multiwavelets and wavelet packets. IEEE Transactions on Image Processing, vol. XX.

[4] Welland, G.V. Beyond Wavelets. Studies in Computational Mathematics 10. Academic Press. 2003.

[5] Vetterli, M., Wavelets, Aproximation, and Compression, IEEE Signal Processing Magazine. Sept 2001.

[6] Barreto, S. "Análisis Comparativo de las Multiwavelets y Wavelets Escalares en lo que respecta a los Criterios de Calidad y Compresión de Imágenes". Tesis presentada a la facultad de Ingeniería de la Universidad Distrital Francisco José de Caldas, septiembre, 2004.

[7] Vaidyanathan, P. Multirate Systems and Filter Banks. Prentice Hall. 1993.

[8] Strela V. and Walden, A. T. Orthogonal y Biorthogonal Multiwavelets for Signal Denoising and Image Compression. Proc. SPIE,3391: 96-107, 1998.

[9] Jiang, Q. and Xia, T. Optimal Multifilter Banks: Desing, Related Symmetric Extension Transform and Application to Image Compression. Preprint, 1998.

[10] Strela, V., Heller, P. N., Strang, G., Topiwala, P. and Heil, C. "The Application of Multiwavelet Filter Banks to Image Processing", IEEE Trans. Image Processing, Vol 8, pp.548-562, April. 1999.

[11] Gupta, S., Kaur, L., (2002) Wavelet based imagen compression using daubechies filters. In Proc. 8th National conference in Communications, I.I.T. Bombay.

[12] Antonini, M., Barlaud, M., Mathieu, P., Daubechies, I. (1992) "Image Coding Using Wavelet Transform," IEEE Trans. Image Processing, vol.1 No 2, pp. 205-220.

Samuel Barreto Melo
El profesor Barreto es matemático. En el año 2004 obtuvo el título de Magister en Teleinformática. Se desempeña como docente universitario en la Facultad de Ciencias y Educación de la Universidad Distrital Francisco José de Caldas. Su interés en los últimos años ha estado en las transformaciones de dominio, particularmente en la wavelet. sabame@cale.net.co

Rodrigo Javier Herrera
García El profesor Herrera nació en Bogotá, Colombia. Obtuvo su título como Ingeniero Electrónico en 1987 y como Magíster en Teleinformática en 1999 en la Universidad Distrital Francisco José de Caldas.

Se ha desempeñado como docente universitario desde 1988 en las Universidades Santo Tomás de Aquino y Distrital de Bogotá en las áreas de sistemas digitales y electrónica analógica. A partir de 1997 se vinculó como profesor de tiempo completo en la Facultad de Ingeniería de la Universidad Distrital Francisco José de Caldas. Actualmente, su área de interés es el procesamiento digital de imágenes y dirige el grupo de investigación en Procesamiento Digital de Señales DSP-UD junto con otros profesores. rherrera@udistrital.edu.co.