DOI:
https://doi.org/10.14483/23448393.2674Publicado:
2005-11-30Número:
Vol. 11 Núm. 2 (2006): Julio - DiciembreSección:
Ciencia, investigación, academia y desarrolloGeneración de modelos de caminata bípeda a través de diversas técnicas de modelamiento
Generation of models of biped long walk through diverse techniques of modelling
Palabras clave:
Análisis de marcha Caminata bípeda, Dinámica de marcha, Gráficos de unión. (es).Descargas
Referencias
D.C. Karnopp, D.L. Margolis, y R.C Rosenberg,. System dynamics: a unified approach, 2nd ed., John Wiley & Sons, Inc., New York, NY. 1975
J. Sánchez y J. Prat. Biomecánica de la Marcha Humana Normal y Patológica. Instituto de Biomecánica de Valencia - IBV. 1994.
J. E Pratt (2000). Exploiting inherent robustness and natural dynamics in the control of bipedal walking robots. Ph.D. Thesis, MIT
L. E. Contreras. Modelamiento de la marcha humana por medio de gráficos de unión. Revista Tecnura. ISSN 0123921X Año 2005 Numero 16. Universidad Distrital Francisco José de Caldas.
M. A Roa. Modelamiento y simulación de la caminata bípeda. Tesis de maestría en automatización industrial, Facultad de ingeniería, Universidad Nacional de Colombia Sede Bogotá. 2004.
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Ciencia, Investigación, Academia y Desarrollo
Ingeniería, 2009-00-00 vol:11 nro:2 pág:4-13
Generación de modelos de caminata bípeda a través de diversas técnicas de modelamiento
Generation of models of biped long walk through diverse techniques of modelling
Leonardo E. Contreras Bravo
Ingeniero Mecánico. Profesor Asistente de la facultad de Ingeniería de la Universidad Distrital.
Luís F. Vargas Tamayo
Ingeniero Mecánico. Profesor Asistente de la facultad de Ingeniería de la Universidad Distrital.
Resumen
Muchos investigadores han estudiado el modelamiento y simulación de la marcha humana bajo dos enfoques; modelos de caminata dinámica pasiva, en los que se da gran importancia al efecto de la gravedad sobre el comportamiento de un mecanismo caminador y el enfoque de este articulo en el que se presentarán modelos de caminata dinámica activa, en los que existen actuadores o elementos que proporcionan energía al sistema para lograr la caminata. Se mostrará el análisis el análisis partiendo de modelos simples incrementando su complejidad y exactitud., iniciado con un modelo de péndulo invertido, pasando por un modelo de una pierna hasta llegar a un modelo de cinco eslabones. Para cada uno de los modelos se presentan el análisis dinámico, bajo la técnica de dinámica Lagrangiana y el método de los gráficos de unión.
Los resultados del modelo de cinco eslabones, son validados comparando con los resultados de otras investigaciones.
Palabras Clave: Análisis de marcha Caminata bípeda, Dinámica de marcha, Gráficos de unión.
Abstract
Many researchers have studied the modelling and simulation of the human march under two approaches: models of passive dynamics long walk, in which the gravity occurs to great importance in order that on the behaviour of a walker mechanism and the approach of this article in which active dynamics long walk will be showed, in that exist actuators or elements that will provide energy to the system to obtain the long walk. The analysis will show from the simple thing to the complex, initiated with a model of inverted pendulum, happening through a model of a leg to arriving a five links model. For each one of the models, the dynamics analysis appears under techniques of Langrageana dynamics and the method of the graphs of union.
The results of the five links models are validated comparing with results the others investigations
Key words: biped walking, gait dynamics, gait analysis, biped walking robot.
1. INTRODUCCIÓN
A través del tiempo uno de los problemas básicos de la biomecánica ha sido el poder crear un modelo que permita la representación matemática de los diferentes movimientos que este puede efectuar al caminar, correr, etc. Y en el cual sea posible visualizar una relación entre las diferentes fuerzas y momentos generados en las articulaciones del cuerpo cuando este lleva a cabo los diferentes movimientos.
Es claro que la adaptación de la caminata bípeda cambia en el cuerpo humano desde los primeros años de vida. Caminar es conseguir a través de un proceso de aprendizaje, el entrenamiento de músculos para controlar el cuerpo a la bipedestación y al caminar; razón por la cual no es sorprendente que cada persona tenga sus propias características superpuestas en el patrón básico de la locomoción. Pero el estudio de la misma permite realizar aplicaciones en diferentes disciplinas o ramas entre las cuales se puede destacar: Medicina (diagnóstico de patologías de la marcha, estrategias de rehabilitación, diseño de prótesis y órtesis, etc.), Ciencias de la computación (animación virtual) y Robótica (exploración y generación de robots humanoides, etc.).
La exploración de las diferentes técnicas para realizar el modelamiento y simulación como lo son: la dinámica Lagrangiana, la herramienta Simulink de Matlab® y la técnica de Bondgraphs; parten de los modelos sencillos en los que se ilustra el efecto de las variables principales involucradas en la caminata humana.
A continuación se plantean el modelo de una pierna completa y un modelo de cinco eslabones que, mediante el uso de la dinámica inversa, permiten el estudio de torques en las articulaciones involucradas en la caminata humana, relacionándolos con las fuerzas musculares que permiten el movimiento humano.
2. MATERIALES
Con el fin de validar los modelos realizados a través de las diferentes técnicas de modelamiento, se requirió realizar unas pruebas piloto experimentales realizadas en el Centro Integral de Rehabilitación de Colombia (CIREC).
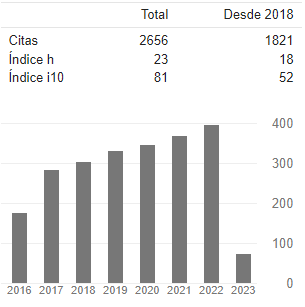
En el laboratorio del CIREC - Centro Integral de Rehabilitación de Colombia (Figura 1) se recurrió al uso de técnicas antropométricas para la medida de segmentos y ángulos de segmentos corporales dependientes de la altura del sujeto. Como técnicas de análisis cinético y cinemático se usaron la plataforma dinamométrica y la fotogrametría respectivamente, por medio de software diseñados por el Instituto Biomecánico de Valencia (IBV), ejecutados en el laboratorio de movimiento del CIREC; dentro de ellos se encuentran Kinescan/ IBV ® y Dinascan/ IBV ®.

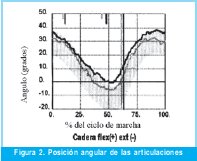
Los resultados de esta experiencia piloto son las curvas de posición (ángulo) relativa para cada una de las articulaciones de la extremidad inferior, las fuerzas de reacción del piso y las curvas de momentos en las articulaciones durante el ciclo de marcha. Los resultados de posición obtenidos por medio del software Kinescan / IBV ® para cada una de las articulaciones del miembro derecho (línea oscura) e izquierdo (línea clara) en el plano sagital (lateral) son mostradas en la Figura 2.
3. METODOLOGÍA DE MODELOS PLANTEADOS
En este documento se presentan la metodología y resultados de algunos de los modelos realizados por medio de la dinámica Lagrangiana, la herramienta Simulink de Matlab® y la técnica de Bondgraphs basado en el planteamiento de Karnoop y Rosemberg [1].
3.1. Dinámica Lagrangiana
Con el fin de obtener la ecuación del sistema analizado, se formula primero la función de Lagrange L, conocida también como potencial cinético o lagrangiano del sistema, y definido por:
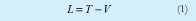
Siendo T la energía cinética y V la energía potencial del sistema. El lagrangiano estaría dando la cantidad de energía transportada de una forma a otra. En forma general, el lagrangiano es función de las coordenadas generalizadas qi, de sus derivadas qi y del tiempo t.
Las ecuaciones de Lagrange, o ecuaciones dinámicas del sistema, pueden obtenerse mediante la denominada formulación de Euler-Lagrange:
Siendo Qi la denominada fuerza generalizada, que corresponde a una fuerza si qi es una coordenada lineal, o a un momento si qi es una coordenada angular. El primer término de la ecuación (1) implica la variación con respecto al tiempo de la velocidad de cambio energética, mientras que el segundo término implica la influencia de la coordenada qi en el cambio en la energía.
3.2. Modelos Multipuertos
Para lograr la ecuación dinámica del sistema se basa en la siguiente secuencia:
- Obtener una definición de cantidades geométricas claves: qk (vector de coordenadas generalizadas), qc (vector de energía potencial C), Vi (representa las velocidades), qI (el vector de desplazamiento de inercia).
- Obtener la matriz de transformación de velocidades
- Obtener la matriz de transformación de entre los vectores qk y Vi
- Establecer la estructura de juntas: Las transformaciones encontradas en los ítems anteriores TCk (qk ) y Tik (qk) pueden ser representadas por juntas tipo O y elementos transformadores modulados (MTF)
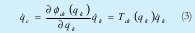
3.3. Modelo 1: Péndulo invertido
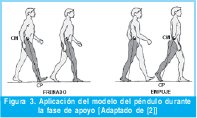
Es el modelo más simple de caminata. El centro de masas del cuerpo será análogo a la masa del péndulo, y el centro de presiones del pie será análogo al pivote del péndulo (Figura 3). A pesar de su sencillez, este modelo permite entender un poco el movimiento durante la fase de apoyo de la marcha. Así, cuando el centro de masa esté en frente del centro de presiones, el péndulo se acelera, y si el centro de masa está detrás del centro de presiones, el péndulo se desacelera. Este primer modelo podría ser útil al tratar de aplicar una fuerza de torsión en el tobillo (punto de sujeción del péndulo).
La Figura 3 muestra el efecto de frenado (desaceleración) que corresponde a la fase inicial de apoyo o de respuesta a la carga (0% - 10% del ciclo de marcha) la cual tiene como propósito principal el mantenimiento de una progresión suave, mediante el rodillo del talón. Seguido a este movimiento seguiría la fase media del apoyo (10% - 30% del ciclo de marcha) en donde el centro de masa del péndulo habrá alcanzado su cénit para luego iniciar el empuje (aceleración) del cuerpo que corresponde a la fase final de apoyo (30% -50% del ciclo de marcha) la cual tiene por objetivos fundamentales proporcionar además de aceleración, asegurar una longitud de zancada adecuada. En el grafico se puede apreciar también la posición relativa entre el centro de presiones (CP) y el centro de masas (CM) que favorece los movimientos indicados.
A partir de la dinámica lagrangiana, se determina la ecuación de movimiento o ecuación de Euler - Lagrange para lo cual se deriva el lagrangiano con respecto al vector coordenadas generalizadas tal como se muestra:
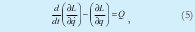
Para este caso Q=0, debido a que no se consideran torques externos.
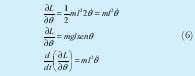
Se define el modelo matemático para el péndulo invertido así:
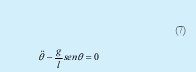
Al momento de simular la ecuación (7), fue necesario utilizar la herramienta simulink de Matlab®; para introducir esta ecuación por medio de diagrama de bloques es necesario despejar la coordenada generalizada.
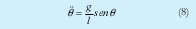
El diagrama a simular utilizando la herramienta simulink de Matlab®; es el mostrado en la Figura 4.
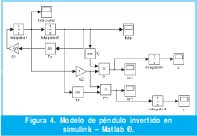
Empleando la metodología de modelos multipuertos, se obtiene el modelo mostrado en la figura 5.
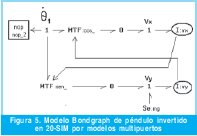
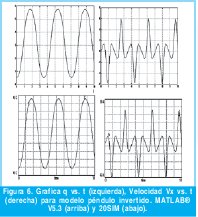
Los resultados obtenidos por los diferentes métodos a través de diferentes herramientas de software fueron muy parecidos y se muestran en la figura 6.
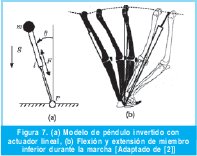
3.4. Modelo 2: Modelo de péndulo invertido con actuador lineal
Ahora se añadirá un actuador lineal a lo largo del péndulo, como se muestra en la Figura 7a. La fuerza en dirección de la longitud del péndulo permitirá un alargamiento y acortamiento de la misma. En la caminata humana la interacción de la rodilla, tobillo y pie (lo que constituye uno de los mecanismos determinantes de la marcha) genera en el contacto mediante el talón un alargamiento efectivo de la pierna en un instante en que la altura de la cadera es mínima. De modo análogo, el despegue mediante el antepié (talón) incrementa también la longitud de la pierna, en un momento en que la altura de la cadera esta disminuyendo suavizando su descenso. La longitud del miembro se reduce durante el apoyo completo del pie mediante una flexión de la rodilla tal como se muestra en la Figura 7b. Dichos movimientos son importantes para los efectos de frenado y aceleración del cuerpo humano en la caminata.
Inicialmente se elige el vector de coordenadas generalizadas; para este caso
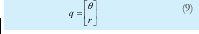
Para que a través de la denominada formulación de Euler - Lagrange se obtengan las ecuaciones dinámicas del sistema:
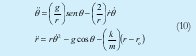
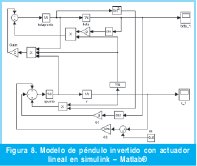
El diagrama del modelo simulado se muestra en la Figura 8.
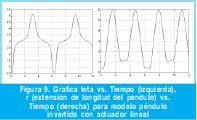
Para este modelo el péndulo inicia su movimiento de oscilación en 0.52 radianes (30º), elevándose el ángulo hasta 5.2 radianes. Luego empieza a oscilar entre estos dos valores al transcurrir el tiempo (s). Según la grafica de la derecha de la Figura 9, el valor de r (longitud del resorte) crece y decrece al transcurrir el tiempo tal como puede ocurrir en el movimiento de los miembros inferiores durante la marcha humana.
3.5 Modelo 3: Modelo de doble eslabón
Los modelos anteriores han considerado que los elementos tienen masa puntual o un elemento inercial; para lograr este modelamiento, los elementos (eslabones) se representan como cuerpos rígidos con un centro de gravedad y un momento de inercia.
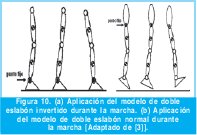
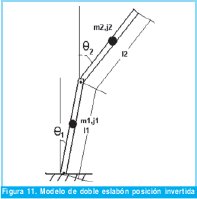
En este modelo cada eslabón representa independientemente muslo y pierna, articulados en el tobillo (fijo), como se muestra en la Figura 10(a). El modelo permitirá apreciar el movimiento de flexión y extensión de rodilla y extensión y flexión de cadera durante la fase de apoyo de la marcha humana. Cuando este modelo se considera en posición de un péndulo normal se entiende el verdadero movimiento de la extremidad inferior durante la fase de balanceo, como se muestra en la Figura 10(b).
Para iniciar con la deducción de las ecuaciones de movimientos por esta técnica se analizó la Figura 11, para la que inicialmente se elige el vector de coordenadas generalizadas como
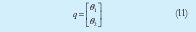
Obteniéndose las ecuaciones diferenciales de segundo orden que definen el movimiento del doble péndulo invertido son:
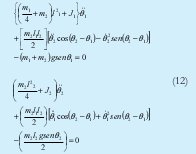
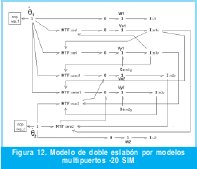
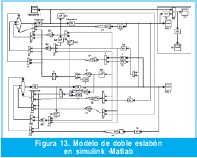
En la Figura 12 y 13 se muestra el modelo en diagrama de bloques usado para simular el doble péndulo invertido con ayuda de Simulink y el modelo multipuertos respectivamente.
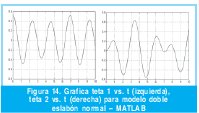
Los resultados de la simulación del modelo de doble eslabón normal para un tiempo de 10 segundos realizado por medio de la herramienta Simulink de Matlab® y el software 20- SIM fueron similares (solo se muestran los resultados de Simulink de Matlab®) en la Figura 14. El error calculado entre los resultados del modelo multipuertos en 20-SIM y la herramienta Simulink de MatlabTM es de 0.02
3.6 Modelo 4: Modelo de una pierna
Para realizar este modelo por medio de la técnica de modelos multipuertos, se realiza un análisis del modelo mostrado en la Figura 15 en donde se muestran las variables geométricas.
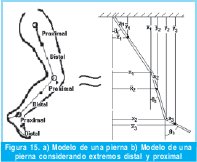
Para este modelo se deben considerar dos grupos de parámetros de entrada al modelo:
- Datos Antropométricos: Comprende la información acerca de los eslabones considerados, tales como longitud, ubicación del centro de gravedad y momentos de inercia respecto al centro de gravedad.
- Datos Cinemáticos: Para este modelo se requieren las posiciones iniciales y velocidades angulares de cada eslabón que conforman la pierna; estos fueron obtenidos a partir del análisis de marcha piloto realizado en el laboratorio de análisis de movimiento del CIREC.
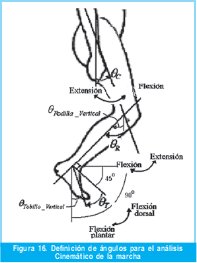
Tal como se muestra en la Figura 16, existe para cada parte de la extremidad inferior una serie de movimientos que reciben desde el punto de vista clínico el nombre de extensión o flexión. Estos términos ayudaran a entender las curvas de posición angular de la cadera, muslo, pierna y tobillo respecto al tiempo durante el ciclo de marcha.
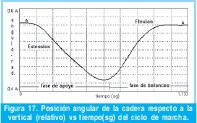
Este modelo proporciona resultados como la trayectoria de movimiento de la cadera en el plano sagital (progresión) durante una zancada normal , extensión en la fase de apoyo y flexión en la de balanceo, produciéndose la inversión en forma gradual tal como se muestra en la Figura 17. El tiempo en la grafica de 1.133 segundos corresponde al 100% del ciclo de marcha normal. Considerando como posición cero la correspondiente al fémur vertical. El intervalo total de movimiento de la cadera es de unos 0.69rad (40 grados).
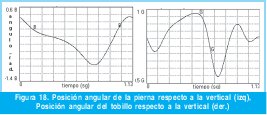
La Figura 18 muestra las curvas de posición angular de la pierna (izq.) y el pie (derecha) respecto a la vertical.
Con el fin de poder comparar los resultados con las graficas de cinemática de la rodilla y tobillo resultado de la experiencia piloto, se hace necesario realizar una conversión de ángulos con el fin de expresar las graficas en posición relativa (respecto a cada eslabón), esta relación se puede apreciar a partir de la Figura 16:
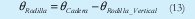
Aplicando las relaciones anteriormente mencionadas se puede determinar el ángulo de la rodilla (relativo) el cual se muestra en la Figura 19.
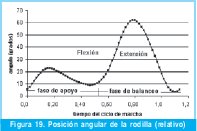
3.7 Modelo 4: Modelo de Cinco eslabones
El modelo anterior representa adecuadamente el comportamiento de una pierna, tanto en balanceo como en apoyo; sin embargo, existe la posibilidad de realizar un modelamiento de las dos piernas y el segmento Head, Arms and Trunk o HAT simultáneamente.
Este modelo desarrollado para el estudio de la caminata consta de cinco grados de libertad. Se considera un cuerpo constituido por 5 eslabones: dos piernas (pantorrillas), dos muslos y un tronco (conocido también como segmento HAT, Head, Arms and Trunk), como se observa en la Figura 20. Los parámetros físicos del modelo incluyen la masa de cada eslabón (m) y su momento de inercia (I), su longitud (l), la distancia entre el centro de masa y la articulación predecesora (α), y el ángulo del segmento con respecto a la vertical (θ).
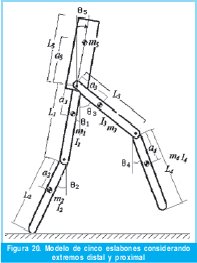
Para construir un modelo dinámico, se requerirán los datos correspondientes a la cinemática del movimiento y de la cinética, obtenidos mediante el software Kinescan / IBV ® y Dinascan/ IBV® en la prueba de laboratorio.
El modelo dinámico se obtiene a partir del planteamiento de un diagrama de cuerpo libre para cada uno de los segmentos involucrados en el análisis como se muestra en la Figura 21 para el caso del pie.
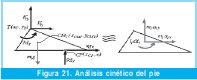
Las incógnitas como las fuerzas de reacción en el tobillo y el momento neto en este (MT), pueden ser calculados por medio de la dinámica newtoniana como sigue:
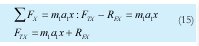
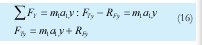
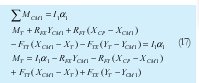
A continuación en la Figura 22, se muestra el modelo en gráficos de unión, desarrollado por el método de modelos multipuestos el cual fue simulado en del software 20- Sim.
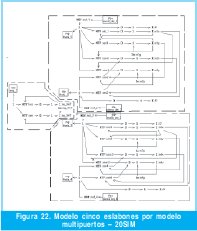
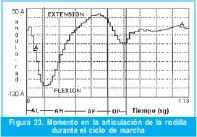
La solución del modelo se lleva a cabo mediante la dinámica inversa la cual expresa las fuerzas y pares que intervienen en función de la evolución de las coordenadas articulares y sus derivadas y proporciona resultados como momentos y potencias en las articulaciones durante el ciclo de marcha de [4], tal como lo muestra la Figura 23.
La solución del modelo de 5 eslabones por método multipuestos también proporciona como se pude apreciar en la Figura 24, la curva del muslo derecho (marcada con letra A) esta desfasada respecto a la del muslo izquierdo (marcada con la letra C); indicando que los movimientos de estos segmentos son alternantes; tal como lo manifiesta [5]. Mientras el muslo derecho presenta un movimiento de extensión, el izquierdo presenta un movimiento de flexión durante la fase de apoyo, lo cual cambia al transcurrir el tiempo en la fase de balanceo. El punto de cruce de las líneas alrededor de 0,26 s. Corresponde al punto donde la pierna derecha se encuentra apoyada recibiendo todo el peso del cuerpo y la izquierda está en la mitad del balanceo, para iniciar su apoyo.
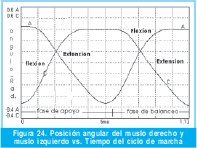
Al igual que la posición angular del muslo derecho e izquierdo respecto al tiempo; es posible determinar la posición de las rodillas (derecha e izquierda) respecto a la vertical para este modelo en cualquier instante de tiempo (en fase de apoyo y fase de balanceo).
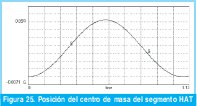
La Figura 25 muestra el desplazamiento vertical del centro de masa del segmento HAT. Como se puede apreciar la forma de la curva es sinusoidal, presentando una amplitud de 0,05m (5 cms aprox.) La existencia de un ciclo de subida (máximo) que corresponde al apoyo monopodal de la pierna derecha y dos mínimos corresponde a los intervalos de apoyo bipodal (inicio y final)
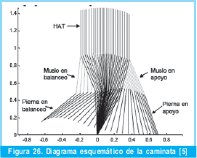
Estos resultados finales pueden contrastarse con los de [5] como se muestra en la Figura 26 desarrollado a través de una interfaz gráfica desarrollada en Matlab® denominada BIPUN, en la cual es posible verificar entre otras cosas la verticalidad del torso (HAT), así como el desplazamiento o posición angular del muslo derecho e izquierdo en balanceo y apoyo.
4. CONCLUSIONES
Los modelos sencillos mostrados en este artículo son una aproximación matemática idealizada al estudio de la marcha humana y proporcionan un mejor entendimiento de la mecánica subyacente en sistemas complejos, con una baja complejidad matemática, ayudando a observar y conceptuar sobre aspectos fundamentales de la mecánica de la marcha.
En los modelos no se considera el efecto de los músculos, el sistema nervioso y el cerebro en la caminata, debido a que el control neurológico de la caminata es un tema aún no entendido completamente. No se tiene certeza total de cómo funcionan los sistemas de retroalimentación del cerebro, ni como es el algoritmo de control que usa el cerebro para controlar la caminata.
La técnica de dinámica Lagrangiana facilita el modelamiento dinámico de sistemas pero presenta dificultades al tratar de modelar sistemas complejos como el de cinco eslabones porque se presentan derivadas de segundo orden que son dependientes unas de otras, lo que resulta en una dificultad para realizar despejes de las mismas con el fin de modelarlas por Simulink-Matlab®.
Al variar los datos antropométricos del modelo de cinco eslabones, el patrón descrito por los ángulos en función del tiempo es muy similar. Este hecho permite justificar una de las hipótesis de trabajo básicas en biomecánica de la marcha [5]: todas las personas, sin importar su longitud de piernas y masas de segmentos corporales, describen la misma trayectoria de ángulos de los eslabones en su ciclo de marcha. Por lo cual este modelo puede usarse para generar patrones de marcha para cualquier combinación de masas y longitudes.
En el modelo de cinco eslabones (que cuenta con pies puntuales), no se usaron los datos de fuerza de reacción del suelo debido a que una posible aplicación de este es el desarrollo de robots bípedos, en donde no se conoce de antemano la fuerza de reacción del piso, además este modelo puede enlazarse con modelos elásticos y/o visco elásticos de los huesos o músculos (resorte-amortiguador) , para predecir de forma más aproximada las cargas existentes sobre los diseño de dispositivos absorbedores de torsión de prótesis y calzado pudiendo realizarse de forma personalizada.
5.REFERENCIAS BIBLIOGRÁFICAS
[1] D.C. Karnopp, D.L. Margolis, y R.C Rosenberg,. System dynamics: a unified approach, 2nd ed., John Wiley & Sons, Inc., New York, NY. 1975
[2] J. Sánchez y J. Prat. Biomecánica de la Marcha Humana Normal y Patológica. Instituto de Biomecánica de Valencia - IBV. 1994.
[3] J. E Pratt (2000). Exploiting inherent robustness and natural dynamics in the control of bipedal walking robots. Ph.D. Thesis, MIT
[4] L. E. Contreras. Modelamiento de la marcha humana por medio de gráficos de unión. Revista Tecnura. ISSN 012-3921X Año 2005 Numero 16. Universidad Distrital Francisco José de Caldas.
[5] M. A Roa. Modelamiento y simulación de la caminata bípeda. Tesis de maestría en automatización industrial, Facultad de ingeniería, Universidad Nacional de Colombia Sede Bogotá. 2004.
Leonardo Emiro Contreras Bravo
Ingeniero Mecánico, Universidad Francisco de Paula Santander (Cúcuta), Magíster en Ingeniería - Materiales y Procesos de Manufactura, Universidad Nacional de Colombia. Docente Universidad Distrital Francisco José de Caldas. Actualmente se encuentra fomentando la creación del grupo DIMSI (Diseño, Modelamiento y Simulación) en el proyecto curricular de ingeniería Industrial lecontrerasb@udistrital.edu.co
Luis Fernando Vargas Tamayo
Ingeniero Mecánico, Universidad Nacional de Colombia (Bogotá), Magíster en Ingeniería - Materiales y Procesos de Manufactura, Universidad Nacional de Colombia. Docente Universidad Distrital Francisco José de Caldas. Actualmente se encuentra fomentando la creación del grupo DIMSI (Diseño, Modelamiento y Simulación) en el proyecto curricular de ingeniería Industrial. lfvargast@udistrital.edu.co
Creation date:
Licencia
A partir de la edición del V23N3 del año 2018 hacia adelante, se cambia la Licencia Creative Commons “Atribución—No Comercial – Sin Obra Derivada” a la siguiente:
Atribución - No Comercial – Compartir igual: esta licencia permite a otros distribuir, remezclar, retocar, y crear a partir de tu obra de modo no comercial, siempre y cuando te den crédito y licencien sus nuevas creaciones bajo las mismas condiciones.




2.jpg)