Ciencia, Investigación, Academia y Desarrollo

Ingeniería, 2001-00-00 vol:6 nro:2 pág:18-23

Análisis del desempeño de modelos en el reconocimiento de la escritura humana

Álvaro Betancourt Uscátegui

Resumen

En el reconocimiento de formas en cuanto hace referencia a la escritura manuscrita se abordan diferentes tendencias. Una de estas técnicas tiene que ver con el fenómeno de la generación de la escritura manuscrita desde el cerebro hasta el brazo. Se presenta en este artículo un análisis comparativo del desempeño de modelos en línea de generación de movimientos simples.

Palabras clave: Reconocimiento formas, escritura manuscrita, modelos.

Abstract

In the pattern recognition of handwriting, different tendencies are approached. One of these techniques is the phenomenon of the generation of handwriting from the brain to the arm. This paper presents a comparative performance analysis of on-line models from the generation of simple movements.

Key words: pattern recognition, handwriting, models.

I. INTRODUCCIÓN

Se puede definir el reconocimiento de formas como el conjunto de técnicas informáticas de representación y de decisión que permiten a las máquinas simular un comportamiento sensible. Fundamentalmente se trata de una parte, de un conjunto de elementos conectados con el computador (micrófono, seguido de convertidores digitales, cámara de video, tabletas digitalizadoras, etc,) y de otra parte de los programas que sean capaces de interpretar las sensaciones recibidas a través de estos captores. La palabra interpretación, significa una categorización percibida de un fenómeno, su identificación y comparación con los fenómenos análogos que se conservan en memoria.

1.1 Los procesos de escritura manuscrita

Se han desarrollado varios modelos físicos y empíricos conceptuales para estudiar la comprensión de la escritura manuscrita. Aunque los modelos pueden diferir mayormente en la descripción de los fenómenos, dependiendo del contexto y propósitos para los que ellos se han planteado, la mayoría coincide en una óptica general normalmente aceptada de procesos involucrados.

Como cualquier proceso motor de escritura rápida, este es considerado como un fenómeno balístico, es decir, un movimiento controlado sin realimentación de la posición instantánea, producto del programa de aprendizaje del proceso motor [1]. Al inicio de un segmento de la escritura, la trayectoria completa de ese movimiento es definida. Ningún control extra es aplicado durante la ejecución. Según este modelo, algunos mecanismos del sistema nervioso central dentro del cerebro, se activan con una intensidad y duración predeterminada de tal manera que la red nerviosa activa los músculos apropiados en un orden predeterminado. El movimiento del lápiz en el papel es el resultado de la contracción o relajación del músculo, siendo ésta, la salida parcial de un trazo que sigue la trayectoria de la punta del lápiz. Un estudio de estos modelos revela que esos esfuerzos de la investigación se concentran en la descripción del sistema matemático nervio-músculo del lápiz sobre el papel, la selección de ecuaciones diferenciales, extracción del parámetro, análisis de movimientos y síntesis.

Diferentes tendencias han sido propuestas para abordar el problema de reconocimiento tales como los métodos estadísticos, no paramétricos, por inteligencia artificial, redes neuronales, lógica difusa, etc. Una de estas técnicas tiene que ver con el fenómeno de la generación de la escritura manuscrita desde el cerebro hasta el brazo. El artículo tiene como base el estudio realizado por [2] [3] y se organiza como sigue. En la segunda sección se describe las ecuaciones básicas. En la tercera sección se aborda la definición del problema y la descripción de los modelos analizados. En la cuarta sección se efectúa el análisis del desempeño de los modelos, pruebas y resultados. En la quinta sección se realiza la discusión y finalmente se presentan algunas conclusiones.

II. ECUACIONES BÁSICAS

Como lo señalan [4] el sistema de la mano-lápizpapel, es representado por un punto de masa M cuyo movimiento a lo largo de la dirección lineal puede describirse como:

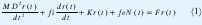
donde:

M masa equivalente del sistema mano-lápiz coeficiente de viscosidad intrínsica de la mano.

K coeficiente de rigidez de la mano.

fe coeficiente extrínseco de fricción entre la punta del lápiz y la superficie de escritura.

N(t) componente de escritura de la presión normal a la superficie de escritura.

Fr(t) fuerza muscular aplicada al punto de masa equivalente.

Se necesitan por lo menos dos ecuaciones de este tipo para producir movimientos bidimensionales de la escritura manuscrita.

En muchos estudios [5] se usan ecuaciones simples de segundo-orden para describir y simular la escritura manuscrita. Una interfaz del nervio-músculo se asume en este caso. En su representación más simple, la interfase puede ser descrita por un sistema de primer orden [6].

III. DEFINICIÓN DEL PROBLEMA

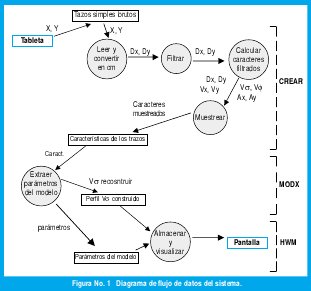
Con base en los datos relacionados con los trazos realizados por un escritor durante la experi encia realizada por [7] en la cual se tiene un archivo que contienen las coordenadas X y Y de trazos simples, se realiza en la presente investigación las etapas descritas por el diagrama de flujo de datos DFD que se presenta en la figura No. 1, en la cual se muestra la manera como se resuelve el problema relacionado con el estudio comparativo de diferentes modelos de generación de movimiento.

3.1 Generación de características del trazado simple

Este módulo tiene por objeto generar a partir de las coordenadas brutas de la tableta todas las características del trazado tales como los respectivos desplazamientos Dx, Dy, las velocidades cartesianas, la velocidad curvilínea y la velocidad tangencial Vx, Vy, Vσ, V]ø, así como las aceleraciones cartesianas Ax, Ay.

3.1.1 Conversión y filtraje de las coordenadas

La tableta suministra las coordenadas X,Y de los puntos a una determinada frecuencia de muestreo. La primera fase que se ha desarrollado es la de convertir estas coordenadas en centímetros [8]. Posteriormente aplicamos un filtro lineal de tercer orden a las mismas coordenadas con el objeto de eliminar la información espúrea y con ruido.

3.1.2 Cálculo de Vx, Vy, Vσ, Vø, Ax, Ay

Para efectuar los cálculos correspondientes, hemos utilizado el método propuesto por [9], que está basado sobre una transformación de la serie de Fourier, para encontrar una función continua de D_X(t) y D_Y(t) a partir de los puntos muestreados D_Xi y D_Yi [10]. Encontradas la funciones correspondientes, efectuamos

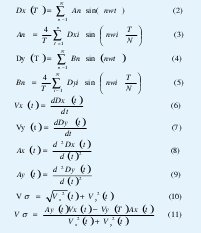
3.1.3 Muestreo de las características del trazo

Obtenidas las funciones anteriores, es necesario efectuar las características discretas del trazo. Para ello, hemos tomado una frecuencia de muestreo del doble del valor inicial, filtramos de nuevo con el mismo filtro lineal de tercer orden y obtenemos las características Dx, Dy, Vx, Vy, Vσ, Vø, Ax y Ay del trazo que se almacenan en una archivo para su tratamiento.

3.1.4 Módulo de reconstrucción de las características

Para realizar la reconstrucción del perfil de la velocidad curvilínea, hemos utilizado para cada uno de los modelos estudiados el método de [11], que consiste en buscar gracias a una técnica iterativa los parámetros de una función paramétrica definida para cada modelo para la cual se aproxima una serie de puntos que provienen del perfil de la velocidad real buscando minimizar el error cuadrático mediano.

3.1.5 Módulo de visualización

Se trata de un programa interactivo que permite al usuario gracias a una serie de menus el ejecutar o bien el módulo CREAR o uno de los módulos MODX, en donde X representa las tres primeras letras del nombre genérico del modelo, así por ejemplo (LGN hace referencia al modelo Log-Normal, etc.) y permite almacenar las diferentes características de cualquier trazo que se haya seleccionado así como el perfil de la velocidad reconstruída.

3.2 DESCRIPCIÓN DE LOS MODELOS

Un modelo de generación de movimiento es una representación matemática del comportamiento temporal del sistema suministrado por el cerebro y la manos humanas. Cada uno de los modelos tiene sus propias características. Sin embargo, podemos clasificarlos en tres grandes familias: Modelos de orientación muscular, Modelos de orientación espacial, Modelos de orientación neuronal.

Los modelos de orientación muscular consideran los músculos como generadores de fuerza, de velocidad o de oscilaciones a partir de un impulsión cerebral. Cada modelo propone una función de transferencia del sistema, el cual tiene por entrada la impulsión cerebral y por salida los desplazamientos de la pluma. Los modelos de orientación espacial centran su interés en los aspectos físicos de la mano que ha generado el trazo, así como en las características intrínsicas del trazo (perfil de velocidad por ejemplo). Los modelos de orientación neuronal proponen una explicación más detallada del fenómeno de la generación del movimiento desde el cerebro hasta la pluma.

Los modelos analizados son, Dos Modelos de orientación neuronal: Modelo Log-normal de Plamondon [12],Modelo VITE de Grossberg y Bullock [13]; Dos Modelos de orientación espacial: Modelo Gaussiano de Plamondon [14], Modelo de Morasso [15]; Tres Modelos de orientación muscular Generadores de fuerza, Modelo de Van Der Gon [16] y de Dooijes [6], Modelo de Yasuhara [1], Modelo de Maarse [3], Un modelo Generador de oscilaciones. Modelo de Eden [17], Mermelstein [18], Hollabach [19], Un modelo Generador de velocidad, Modelo de PlamondonLamarche [20]. Un resumen de cada uno de estos modelos se presenta en la tabla No. 1.

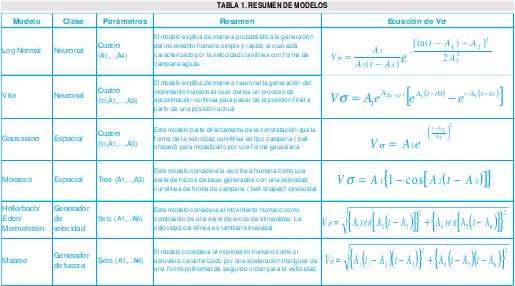
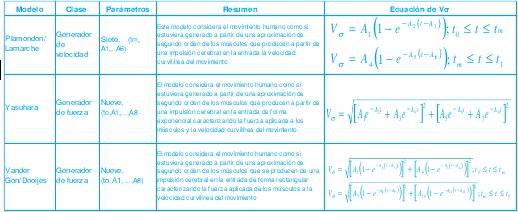
IV. PRUEBAS Y RESULTADOS

Realizada la reconstrucción de los perfiles de la velocidad curvilínea V para los diez trazos y para cada uno de los modelos, se presenta a continuación para dos de los modelos una tabla que resume los valores de los parámetros del modelo para cada trazo así como el error cuadrático mediano. Luego, se muestra una representación gráfica del perfil real y del perfil reconstruído para un ejemplo del trazo a manera representativa de los modelos Lognormal y Gaussiano.

4.1 El Modelo Log-normal

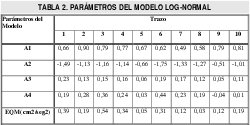
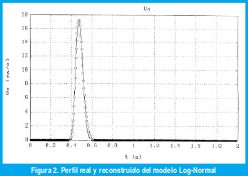
4.2 El Modelo Gaussiano

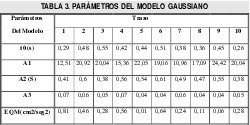
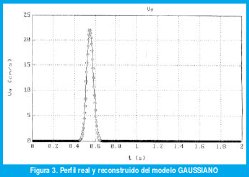
4.3 DESEMPEÑO RELATIVO DE LOS MODELOS

A continuación se presenta una tabla global que resume la clase de cada modelo, el número de parámetros y la mediana sobre los diez (10) trazos del error cuadrático mediano; Tabla No. 4.

Una gráfica que ilustra dichos desempeños se muestra en la figura No. 4

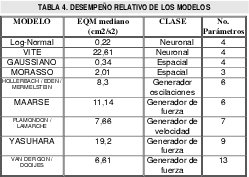
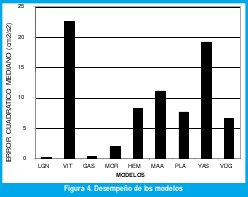
V. DISCUSIÓN

De conformidad con los resultados obtenidos para cada uno de los modelos de acuerdo con sus características y orientación respectiva podemos anotar que el modelo Log - Normal es el mejor desde el punto de vista de exactitud de la reconstrucción de la velocidad curvilínea misma. Los modelos Vite y Yasuhara son los que presentan los peores desempeños, y ello es debido al hecho que proponen perfiles de velocidad exponenciales que están lejos de la realidad. En efecto, el perfil real de la velocidad curvilínea es de tipo campana ( bell-shaped ).

Las ventajas del método de reconstrucción utilizado son de una parte que el método converge hacia la solución óptima con la variación de todos los parámetros. En nuestro caso, se han realizado todos los ensayos para concluir que siempre converge hacia la mejor solución mediante la variación de todos los parámetros, factor determinante en cuanto presenta una ganancia de tiempo enorme. De otra parte, la rapidez con la cual se encuentra la solución de conformidad con la complejidad del problema. En general con una veintena de iteraciones es suficiente.

En cuanto concierne a la modelización de los movimientos humanos simples, se ha probado que este es un camino prometedor. En efecto, el hecho de proponer, comparar y evaluar los diferentes modelos que permiten una reconstrucción del perfil de la velocidad curvilínea la cual es una característica intrínsica del movimiento con tanta exactitud, es un paso bien importante que motiva más trabajo para la reconstrucción del movimiento mismo de la explicación del fenómeno de la escritura y todo lo que pueda derivarse como aplicaciones en (reconocimiento de la escritura manuscrita, verificación de la firma etc.) lo que representará una marcada investigación aplicada.

Los límites del método de reconstrucción utilizado son: el método requiere de gran intervención y supervisión del utilizador para seleccionar bien los valores iniciales de los parámetros que permitan garantizar la convergencia.

En algunos casos existe la convergencia pero hacia una solución óptima local, lo que requiere aumentar la tasa de convergencia y el límite del número de iteraciones en espera de salir de ese mínimo local. Aquellos modelos que presentan un gran número de parámetros como por ejemplo el de Van Der Gon y Dooijes, el tiempo de cálculo para un solo trazo se vuelve muy lento. El método resalta los desempeños de convergencia débiles para aquellos modelos que tienen un perfil exponencial, es decir se muestra las debilidades del modelo mismo, aunque será necesario verificar e investigar aún más que el método como tal no prueba sino ese tipo de debilidades.

En cuanto hace referencia a los modelos que se han probado, es conveniente citar algunas limitaciones en el sentido de que solo modelizan los movimientos simples y rápidos. Permiten reconstruir el desempeño de la velocidad curvilínea; al respecto, será necesario ensayar la reconstrucción del movimiento en su totalidad e integralidad debido a que la reconstrucción de la velocidad V sola no es suficiente para la reconstrucción de la totalidad del movimiento.

VI. CONCLUSIONES

Como resultado del análisis del desempeño de los modelos estudiados para la escritura humana mediante el método planteado podemos concluir que, existen modelos que presentan un error cuadrático mediano aceptable pero dado el gran número de parámetros pueden no ser aconsejables como buenos modelos. Puede afirmarse que una mejor visión de la escritura humana es explicada mediante el modelo Log-Normal el cual confirma también otras experiencias sobre la universalidad de la característica de la velocidad Vσ con forma de campana o bellshaped para todos los movimientos humanos en general y nó solamente para la mano.

Es necesario también confirmar que el modelo Log-Normal prueba así su desempeño para los movimientos simples y rápidos, por supuesto será necesario abordar en otro trabajo si estos desempeños son los mismos para los movimientos más complejos y en especial para aquellos muy lentos que pueden contener retroalimentación visual.

Desde el punto de vista de mejorar y avanzar en la investigación sobre la temática, podemos proponer las siguientes nuevas especificaciones funcionales. Mejorar el programa MODX para cada modelo de tal manera puedan realizar la reconstrucción de manera más automática y eliminar de esta manera al máximo la intervención del utilizador.

Tratar de investigar sobre el número de iteraciones óptimas así como también la tasa de convergencia óptima a partir de las cuales pueda automáticamente parar el método iterativo. Destacar que el presente trabajo se constituirá en la conformación de una línea de investigación en el campo del reconocimiento de formas y en especial de la escritura manuscrita y allí habrá que profundizar sobre aspectos propios tanto de software como de hardware (donde tendrán grandes posibilidades nuestros programas de ingeniería electrónica y de sistemas), temas como la arquitectura de computadores, paralelismo y por supuesto de la matemática aplicada serán de riguroso manejo.

Se ha presentado un estudio sobre el reconocimiento de la escritura humana, en el que a partir de datos de un escritor en particular se han derivado los diferentes parámetros para analizar una característica de fundamental trascendencia como es la velocidad curvilínea Vσ, vía la aplicación sobre un buen número de modelos clasificados en tres tipos de orientación diferente como lo son la orientación neuronal, espacial y muscular que incluye esta última generador de oscilaciones, de fuerza y de velocidad, con el objeto final de analizar cual de todos responde mejor de acuerdo con su desempeño a dicho reconocimiento.

REFERENCIAS

[1] Yasuhara, M , " Experimental studies of handwriting process ", Rep. Univ. Electro-Comm., vol 25, pp. 233-254, 1975.

[2] Betancourt A., " Estudio comparativo y evaluativo de modelos en línea en el reconocimiento de la escritura manuscrita", Reporte Interno, U. Distrital, 2001.

[3] Betancourt A., Alimi A., Boumehdi Y., " Modélisation de l´écriture humaine ", Reporte Interno, École Polytechnique de Montréal, 1990.

[4] Plamondon R., Maarse F., " An evaluation of motors models of handwriting " ,IEEE Transactions on systems, Man, and Cibernetics, vol 19, No.5, 1989.

[5] Stren J.T, " Computer modelling of gross muscle dynamics", J.Biomech., vol7 ,411, 1974.

[6] Dooijes, E.H. " Analysis of handwriting movements", Acta Psicol., vol 454, pp. 99-114, 1983.

[7] Plamondon R., Stelmach G., Teasale N., " Motor Program Coding Representation from a Handwriting Generator Model " Biological Cybernetics; Vol,63 , pp. 443-451,1990.

[8] Nouboud F., Plamondon R., " On line Character Recognition System using a String Comparaison Processor ", Proceedings of 10th. IEEE International conferencie on Pattern Recognition., New Jersey, pp. 460-463,1990.

[9] Burr D. " A Normalising Transform for Cursive Script Recognition ", Proc. of 6th IEEE Int. Conference on Pattern Recognition, Munich, , vol 2, pp. 1027-1030,1988.

[10] Leclerc F.," Validation d´ un modé1e génération de vitesse á profil gaussien sur des signatures manuscrites ", memoire de maitrise, Ecole Polytechnique de Montréal, 1989.

[11]Press, W.H et al, " Numerical Recipes in C " Cambridge University Press, Cambridge, 1989.

[12] Plamondon R., " On the origin of asymetric bell-shaped velocity profiles in rapid-aimed movements ", Tutorials in Motor Neuroscience" , Stelmach Academic Publisher , 1991.

[13] Bullock D., Grossberg S., " Neuronal Dynamics of Planned Arm Movements ", Neural Networks and Natural Intelligence, MIT Press, pp. 553-622, 1987,

[14] Plamondon R., " Handwriting Control a functionnal Model ", Cambridge University Press, pp.553-574, 1989.

[15] Morasso P. , Mussa F., " Trajectory formation and Handwriting " Biological Cybernetics, vol.45, pp.131-142. 1982.

[16] Van Der Gon D., Thuring J., " The guiding of Human Writing Movements " Kybernetik, vol.4 , pp.145, 1985.

[17] Eden M. " Handwriting and Pattern Recognition " IRE Trans. Inform. Theory vol,8, , pp.-160-166, 1962.

[18] Mermelstein , Eden M, " Experiments on Computer Recognition of Connected Handwriting words ", Inf. Centr., vol. 7, , pp.255270, 1964.

[19] Hollerbach, J. " An Oscillation Theory of Handwriting ", Biological Cybernetics, No. 39, , pp. 139-156, 1981.

[20]Plamondon, R, Lamarche F., " Modelisation of Handwriting " Graphomomics Contemporary Reseach in Handwriting, Netherlands, Elseiver Sci., pp,169-183, 1986.

Alvaro Betancourt Uscátegui
Ingeniero Electrónico, Universidad Distrital Especialista en Telecomunicaciones Móviles, Universidad Distrital, Msc. Ciencias Financieras y de Sistemas, Universidad Central, Magister en Ingeniería, Informatique Appliquée, Ecole Polytechnique Université de Montreal, Canada, Profesor Facultad de Ingeniería, Universidad Distrital, Coordinador de la Especialización en Telecomunicaciones Móviles abetancourt@ atlas.udistrital.edu.co