DOI:
https://doi.org/10.14483/23448393.3852Publicado:
2012-12-28Número:
Vol. 17 Núm. 2 (2012): Julio - DiciembreSección:
ArtículosComparación entre un sistema neuro difuso auto organizado y un modelo ARIMAX en la predicción de series económicas volátiles
Comparison between a self organizing neural fuzzy system and an ARIMAX model to forecasting volatile economic series
Palabras clave:
ARIMAX, SONFS, Series Temporales Volátiles. (es).Palabras clave:
ARIMAX, SONFS, Volatile Time Series. (en).Descargas
Referencias
Paul Samuelson y William Nordhaus, Economía. 15 ed. McGraw-Hill, Madrid, España, 1998.
Damodar Gujarati, Basic Econometrics.McGraw Hill, New York City, New York, 2004.
Steven Achelis, Technical Analysis from A to Z. McGraw Hill, New York City, New York, 2000.
Michael Steinberg, Guía para invertir en bolsa.Ediciones Deusto, Bilbao, Portugal, 2001.
Gioqinang Zhang y Michael Y. Hu, “Neural network forecasting of the British Pound/US Dollar exchange rate”. Omega Elsevier Science, Volumen 26, Número 4, Agosto, 1998, pp. 495-506.
André AlvesPortela, Newton CarneiroAffonso y Leandro dos Santos, “Computational intelligence approaches and linear models in case studies of forecasting exchange rates”. Expert Systems with Application Elsevier Science, Volumen 33, Número 4, Noviembre, 2007, pp. 816-823.
Juan Carlos Figueroa y Jose Jairo Soriano, “A comparison on ANFIS, ANN and DBR systems on volatile time series identification”, Annual Meeting of the North American Fuzzy Information Processing Society, 2007, pp. 321-326.
Orlando Greco, Diccionario de Economía. Valletta Ediciones, Buenos Aires, Argentina, 2006.
Bolsa de Valores de Colombia, Ranking por capitalización bursátil, 26 de Julio de 2011, disponible en http://www.bvc.com.co/pps/tibco/portalbvc/Home/Empresas/.
Gordon Alexander, William F. Sharpe y Jeffery V. Bailey, Fundamentos de inversiones: Teoría y Práctica. Pearson Eduacación, México, 2003.
Sheldon M. Ross, Introducción a la estadística. Editorial Reverté, Barcelona, España, 2007.
José Hernandez, Análisis de series temporales económicas II. Esic, Madrid, España, 2007.
George Box y Gwlym Jenkins, Times Series Analysis: Forecasting and Control. Editorial Holden Day, Oakland, California, 1976.
Chia-FengJuang y Yu-Wei Tsao, “A Type-2 Self-Organizing Neural Fuzzy System and Its FPGA Implementation”. IEEE Transactions on Systems, man and cybernetics, Part B, Cybernetics, Volumen 38, Número 6, Diciembre, 2008, pp. 1537-1548.
Chia-FengJuang y Chin-Teng Li, “An on-line self-constructing neural fuzzy inference network and its application”. IEEE Transactions on Fuzzy Systems, Volumen 6, Número 1, Febrero, 1998, pp. 12-32.
Li-Xin Wang and Jerry Mendel, “Back-propagation fuzzy system as nonlinear dynamic system identifiers”, Conference on Intelligent Computing and Intelligent Systems, 2010, pp. 684-688.
Peter A. Brockwell y Richard A. Davis, Introduction to time series and forecasting, Springer-Verlag, New York, New York, 1987.
Armando Aguirre, Introducción al tratamiento de series temporales. Ediciones Díaz de Santos, Madrid, España, 2010.
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
COMPARACIÓN ENTRE UN SISTEMA NEURO DIFUSO AUTO ORGANIZADO Y UN MODELO ARIMAX EN LA PREDICCIÓN DE SERIES ECONÓMICAS VOLÁTILES
COMPARISON BETWWEN A SELF ORGANIZING NEURAL FUZZY SYSTEM AND AN ARIMAX MODEL TO FORECASTING VOLATILE ECONOMIC SERIES
Jose A. Avellaneda G., Universidad Distrital. Bogotá, Colombia. jaavellaneda@correo.udistrital.edu.co
Cynthia M. Ochoa R., Universidad Distrital. Bogotá, Colombia. cmochoar@correo.udistrital.edu.co
Juan Carlos Figueroa García, Universidad Distrital. Bogotá, Colombia. email@email.com
Recibido: 27/08/2012 - Aceptado: 15/11/2012
RESUMEN
En este artículo se presenta el estudio de una acción volátil de la Bolsa de Valores de Colombia la cual es analizada usando un modelo estadístico ARIMAX (Modelo autorregresivo integrado de media móvil con entrada exógena) y un SONFS (sistema neuro difuso auto organizado). Estos métodos son comparados teniendo en cuenta tres características: el menor EMA (Error Medio Absoluto),el residual entendido como un proceso de ruido blanco (evaluado mediante seis pruebas) y el AIC (criterio de información de Akaike); así se elige el modeloque mejor se ajusta para la predicción de la serie.
Palabras clave: ARIMAX, SONFS, Series Temporales Volátiles.
ABSTRACT
This paper presents the selection of a volatile share from Colombian Stock Exchange, which is analyzed using ARIMAX (autoregressive integrated moving ave-rage with exogeneous input) and SONFS (self organizing neural fuzzy sytem) models. These methods are compared using three features: the MAE (mean absolute error), residuals as a white noise process and the AIC (Akaike Information Criterion).
Key words: ARIMAX, SONFS, Volatile Time Series.
1. INTRODUCCIÓN
El mercado bursátil se caracteriza por la alta variabilidad en sus rendimientos, es decir que presenta alto riesgo, pero a su vez entrega mayores rendimientos que otras alternativas de inversión [1]. Por estas razones es importante anticiparse al movimiento de los precios mediante el desarrollo de diferentes métodos en los que se obtengan resultados adecuados de predicción.
Los economistas emplean convencionalmente tres métodos para estimar los precios: modelos econométricos [2], análisis técnico [3] y análisis fundamental [4]. Sin embargo las técnicas de inteligencia computacional han presentado mejores resultados en algunos problemas de predicción de series económicas [5]-[7].
En este artículo se selecciona una acción de la Bolsa de Valores de Colombia que presenta volatilidad, la cual es un caso de estudio interesante dada su complejidad. Luego se compara la predicción de la acción del modelo ARIMAX con la obtenida del sistema neuro difuso auto organizado mediante el EMA y ciertas características que deben encontrarse en los residuales. De este modo se consigue una interpretación del error en las unidades de la serie (peso colombiano, COP) y se determinará si el modelo generaliza o no, así puede esperarse un comportamiento adecuado ante datos desconocidos. Conforme al análisis de los resultados se establecen las ventajas y desventajas de cada uno de los modelos.
2. SELECCIÓN DEL CASO DE ESTUDIO
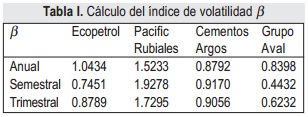
Para escoger la acción volátil de la Bolsa de Valores de Colombia, se consideró la capitalización bursátil correspondiente al producto entre la totalidad de las acciones de un emisor que están en circulación y su precio de cotización [8]. De esta manera se cuantifica la dimensión económica de la empresa y por consiguiente, se toman las acciones más importantes de la lista de capitalización bursátil disponible en el sitio web de la BVC (Bolsa de Valores de Colombia)[9]. Luego cada una de las acciones se graficó para elegir las que presentan variabilidad en sus precios. Finalmente para el caso de estudio se calculó el índice de volatilidad â para los periodos anual, semestral y trimestral, el cual compara la acción con la variabilidad del mercado [10], en este caso representado por el IGBC (Índice General de la Bolsa de Valores), por medio de la ecuación (1).
En la tabla I se muestran los valores del índice β para cuatro de las acciones elegidas. Si éste índice es mayor a 1, se considera que la acción es volátil con respecto al mercado [10].
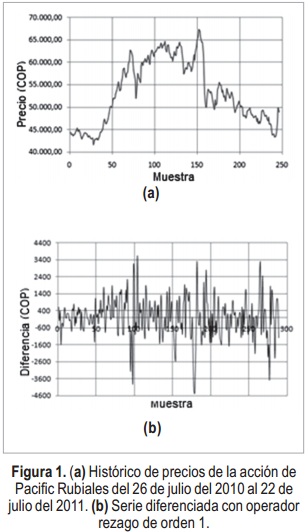
de Pacific Rubiales es la única que presenta mayor volatilidad respecto al mercado en los tres periodos, por esto se escoge esta acción la cual se muestra en la Figura 1 (a), correspondiente a los días comprendidos entre el 26-07-2010 al 22-07-2011, para tener un total de 289 muestras.2.1. Análisis estadístico
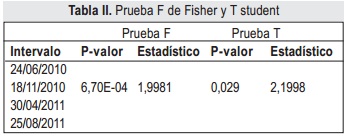
La Figura 1 (a) muestra que la serie de precios no tiene varianza ni media constantes, así se aplica la primera diferencia en la serie para tratar de estabilizarla [7], de este proceso se obtiene la serie diferenciada de la Figura 1 (b). Para comprobar el comportamiento volátil se realiza la pr ueba F de Fisher, ARCH (heteroscedasticidad condicional autorregresiva) y t-Student sobre la serie diferenciada, para determinar si tiene varianza y media constantes [10]. El valor de pro-babilidad y el estadístico respectivo a ambas pruebas se presentan en la tabla II, considerando un valor de significancia (α) de 0.05. De acuerdo a estos resultados, desde el punto de vista estadístico la serie es volátil puesto que rechaza la hipótesis de las pruebas anteriores, lo que indica además un comportamiento no lineal en su media y varianza.
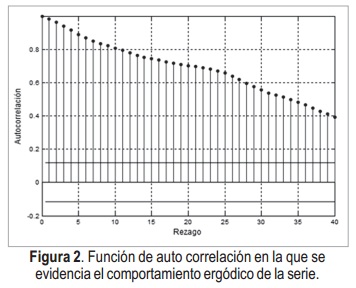
Por otro lado, al tener en cuenta que la serie es ergódica [12], es decir que la influencia entre variables disminuye al aumentar la diferencia temporal entre ellas, como se evidencia en la ACF (función de auto correlación)de la Figura 2 y en base a ésta, se divide la base de datos en 250 muestras para el diseño del modelo ARIMAX y para el entrenamiento del SONFS y 39 muestras para llevar a cabo la validación de ambos modelos.
3. MODELO ARIMAX
Este modelo se obtiene de tres partes: La primera es auto regresiva que relaciona la serie con observaciones de periodos anteriores de ella misma. La segunda parte son medias móviles (MA) que relaciona la serie como una función de una sucesión de errores correspondientes a periodos anteriores ponderados. La tercera parte (X) son las observaciones anteriores de una serie exógena, que en este caso es un indicador técnico de los ocho que comúnmente se utilizan en la economía para estimar los precios [16], estos son: la media móvil, las bandas de Bollinger, el momentum, la tasa de cambio, el índice de fortaleza relativa, la convergencia/divergencia de media móvil, los estocásticos %K y %D y Larry Williams %R.
Adicionalmente, al considerar la serie diferenciada, que se espera que sea estacionaria se obtiene el modelo ARIMAX [13].Para encontrar el orden correcto del modelo ARIMAX, se emplea la metodología propuesta por Box y Jenkins [13] resumida en 5 puntos:
- Identificar el orden del modelo ARIMAX(p,d,q,b).
- Estimar los coeficientes.
- Validar el modelo.
- Verificar el ajuste.
- Seleccionar el mejor modelo disponible.
Así el mejor modelo lineal obtenido con esta metodología es un ARIMAX(6,1,5,7) que emplea el indicador de la tasa de error de cambio para la predicción como entrada exógena U, el modelo es representado por la ecuación:
4. SISTEMA NEURO DIFUSO AUTO ORGANIZADO (SONFS)
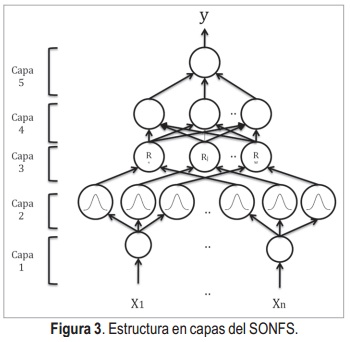
Este sistema es neuro difuso, debido a que el sistema difuso se muestra en una distribución de capas y neuronas. Por otro lado, se denomina auto organizado a causa de la creación de reglas a partir de los datos que entran [14]. Así el SONFS es conformado por cinco capas como muestra el esquema de la Figura 3, las cuales cumplen con di-ferentes funciones como se describe a continuación:
- Capa 1 (entrada): las entradas son valores puntuales, cada entrada debe estar normali-zada, así los nodos en la capa de entrada xi están en los rangos de [-1,1] o [0,1].
- Capa 2 (fuzzificación): Esta capa desempeña la operación de fuzzificación tipo singleton y cada nodo en esta capa define una función de pertenencia gaussiana.
- Capa 3 (Capa de intersección): Cada nodo en esta capa es una regla y desarrolla la operación difusa de intersección usando la t-nor-ma producto. La salida de un nodo es el nivel de activación de la regla denotado como f i.
- Capa4 (capa de normalización): El número de nodos en esta capa es igual al de la capa tres. Cada nivel de activación calculado en la capa anterior es normalizado por la sumatoria de todos los niveles de activación calculados en dicha capa.
- Capa 5 (capa del consecuente): En esta capa se hace la defuzzificación por promedio de centros, de la que se obtiene la salida pun-tual del sistema.
En la Figura 4 se presenta el algoritmo de gene-ración de reglas, donde el criterio para crear una nueva regla es la comparación de un umbral predefinido φTH con el máximo de los niveles de activación [13].
Modificando el trabajo de Juang y Tsao [14] y Juang y Lin [15], se propone la inicialización de la media m y la desviación estándar σ de los antecedentes, y los centros w del consecuente a través de las siguientes ecuaciones:
De acuerdo a lo anterior, sea M un número actual de reglas, la media de una nueva regla corresponderá a un nuevo dato de entrada denotado como xj, cuya desviación estándar está en función de β que es un parámetro predefinido propio del SONFS (diferente al índice de volatilidad β) y por último, el centro se inicializa aleatoriamente. Adicionalmente, para sintonizar estos parámetros se utilizó el algoritmo de gradiente descendente [16].
Las entradas al sistema no son solamente los rezagos de la serie, también ingresan como series adicionales ocho indicadores técnicos. El diseño del SONFS inicia estableciendo el número de rezagos iniciales tanto de la serie que se va a predecir como el de los indicadores técnicos, mediante la ACF y la CCF (Función de correlación cruzada). Posteriormente se sigue una metodología similar a la de Box y Jenkins para buscar el mejor modelo siguiendo los siguientes pasos:
- Cambio de entradas y parámetros del SONFS.
- Entrenamiento del SONFS.
- Validación del modelo.
- Verificación del ajuste del modelo.
- Selección del mejor modelo disponible.
De esta manera se realizan varias pruebas cambiando los parámetros del SONFS incluyendo la tasa de aprendizaje del algoritmo de gradiente descendente, las entradas y rezagos del sistema. Una vez establecidas las características anteriores se entrena y se valida el SONFS. Posteriormente se verifica el ajuste que tiene el modelo a la serie y finalmente se escoge el mejor. El sistema seleccionado generó 38 reglas a través de 1000 iteraciones, como entradas empleó la tasa de cambio y el índice de fortaleza relativa con 3 rezagos de cada una, tiene una tasa de aprendizaje de 0.05, β de 0.8 y un umbral φTH de 0.3.
5. RESULTADOS
5.1. Metodología de selección experimental
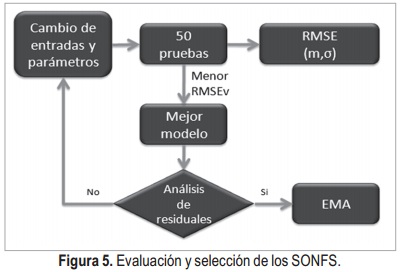
Como se mostró en la Sección 4, el diseño y entrenamiento de un SONFS va en función de sus parámetros que deben ser sintonizados de manera adecuada, a saber: φ, m, σ, w y β. Así pues y dado que la inicialización de los centros es aleatoria, se hicieron una serie de experimentos con el fin de obtener los mejores resultados posibles. La metodología utilizada se muestra en la Figura 5, iniciando con la selección manual de las series que van a ingresar entre los indicadores técnicos y la serie de precios de Pacific Rubiales,
también se seleccionan los rezagos y los parámetros del sistema. Con las características anteriores establecidas, se realizan 50 iteraciones con el fin de obtener una exploración del espacio de búsqueda y finalmente seleccionar el mejor conjunto de parámetros entrenados para cada combinación, teniendo en cuenta el sistema con menor RMSE (Root Mean Square Error). A éste sistema se le analizan sus residuales y si cumple con ciertas características se calcula el EMA o se cambian los parámetros nuevamente.
5.2. Metodología de selección experimental
Uno de los aspectos más álgidos en predicción de series de tiempo es la selección de entradas al modelo, de lo que depende el número de parámetros que los algoritmos de entrenamiento u optimización deben calcular. Esto afecta di-rectamente el costo computacional en la medida que se tendrá mayor número de parámetros para calcular, haciendo que los algoritmos de entrenamiento tengan un tiem-po de convergencia mayor.
La estrategia utilizada en este estudio fue la siguiente:
- Determinar los indicadores técni-cos que presentan correlación entre sí (Usualmente esto se observa a través de la inspección de la definición de cada indicador).
- Determinar las posibles combinaciones de las entradas seleccionadas.
- Realizar pruebas de entrenamiento para cada combinación.
Dicha metodología permite determinar las combinaciones de entradas que podrían ser relevantes para predicción y hacer una búsqueda de parámetros y reglas del SONFS que minimice el error para cada combinación. Evidentemente este proceso puede llegar a ser costoso computacionalmente, pero garantiza una adecuada exploración de la información disponible. De esta manera, se evidencia que aunque este tipo de técnicas puedan parecer costosas computacionalmente, dicho costo se reduce dado el constante incremento en las capacidades de cálculo que existen en la actualidad. Finalmente, los resultados de los mejores modelos encontrados se muestran en el siguiente apartado.
5.3. Resultados de predicción
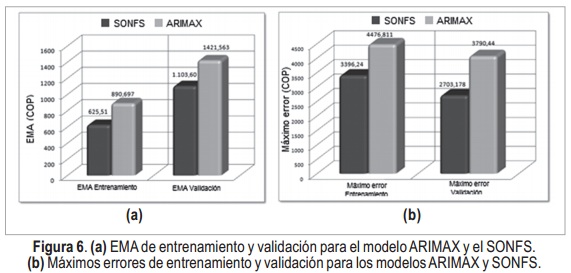
La evaluación de los mejores modelos obtenidos del ARIMAX y del SONFS, se evalúan considerando el EMA obtenido en el entrenamiento y la validación. Estos errores se muestran en el diagrama de barras de la Figura 6 (a), donde se puede ver que tanto para el entrenamiento y la validación hay una disminución del error promedio al pasar del modelo ARIMAX al SONFS correspondiente a una reducción del error de 29,77% y 22,36% para cada conjunto de datos. También al comparar los máximos errores adquiridos expuestos en la Figura 6 (b), se considera que el modelo que tiene menor error es el SONFS.
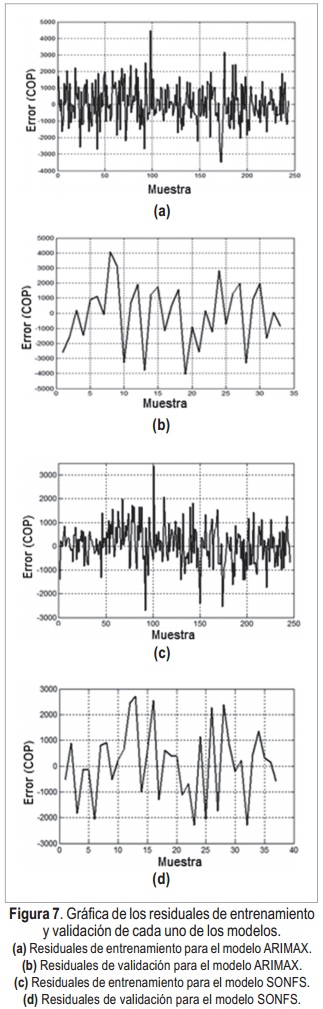
Adicionalmente a la cuantificación del error se realiza un análisis sobre los errores en cada instante de tiempo. A este conjunto de errores se le denomina residuales o residuos, en la Figura 7 se presentan los residuales de cada modelo para cada conjunto de datos.
Lo que se busca es obtener residuos carentes de estructura, es decir que sean ruido blanco ((ε)˜WN (0,σ2)),esto indica que el modelo se ajusta correctamente a la serie y que ha extraído toda la información de ella, implicando que ante nuevos datos va obtener resultados adecuados. Para comprobar si el residual es ruido blanco debe tener las siguientes características [17] [18]:
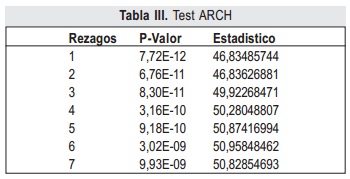
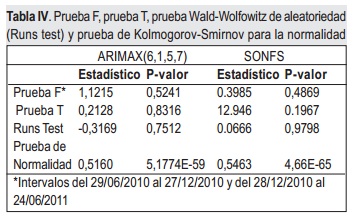
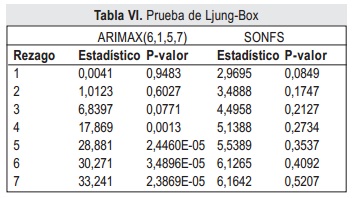
Una serie de pruebas y test pueden verificar cada una de las propiedades sobre el residual del conjunto de entrenamiento. Para la prueba de varianza constante se realiza la prueba F y la prueba ARCH, las siguientes características son evaluadas por las pruebas T, de Wald-Wolfowitz y de Ljung-Box respectivamente, con α de significancia de 0.05. Adicionalmente se realiza la prueba de Kolmogorov-Smirnov para verificar si el residual tiene distribución normal. Cada una de estas pruebas registran su significancia o p-valor y estadísticos (Stat) en las tablas IV a VII para los modelos ARIMAX(6,1,5,7) y SONFS.
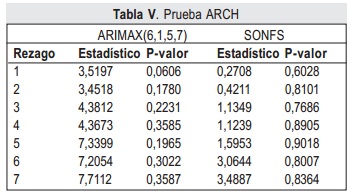
De los p-valores de las pruebas F y ARCH en la tabla IV y tabla V, se determina que ambos mode-los tienen varianza constante.
Adicionalmente, los resultados de la tabla IV indican que los residuales derivados de ambos modelos no tienen distribución normal, aunque ambos residuales son una secuencia de valores aleatorios con media cero y varianza constante. Respecto a ausencia de auto correlación, los residuales del SONFS cumplencon esta característica como indican los p valores de la tabla V y tabla VI, sin embargo el ARMAX presenta correlación serial en los rezagos 5, 6 y 7.
Para resumir estos resultados, el supuesto de normalidad es una propiedad deseable más no necesaria, no afecta considerablemente el comportamiento de los modelos. Así que respecto al análisis de los residuales, el SONFS es una mejor opción para la predicción puesto que cumple con todas las características.
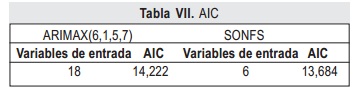
Para finalizar la comparación se calculó el AIC (Akaike Information Criterion), que pondera el ajuste del modelo a la serie teniendo en cuenta su número de variables; se considera que el mejor modelo es el que tenga el AIC más bajo. Según los valores de la tabla VII el SONFS es el que tiene el menor AIC.
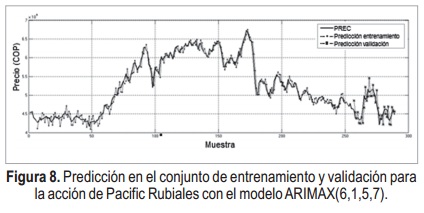
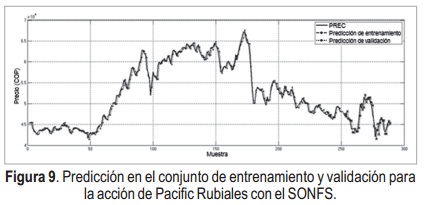
Adicionalmente, los resultados del mejor modelo obtenido, tanto para ARIMAX como para SONFS se muestran representados a través de sus residuales en la Figura 7. Además la predicción resultante en la Figura 8 y Figura 9 respectivamente, donde se observa que el modelo ARIMAX tiende a apartarse del precio real más veces que el SONFS.
6. CONCLUSIONES
En este trabajo se presentó una comparación entre un modelo ARIMAX y un sistema neuro difuso auto organizado aplicado a la predicción de una serie temporal escogida de la Bolsa de Valores de Colombia que expone un comportamiento volátil. De acuerdo al análisis estadístico de la serie seleccionada, se encuentra que el índice de volatilidad revela información útil acerca de las posibles fuentes de incertidumbre que intervienen en una serie temporal.
La inclusión de indicadores técnicos como entradas al SONFS fue importante, debido a que proporcionan información adicional, muestra de ello son las entradas del mejor modelo las cuales fueron la tasa de cambio y el índice de fortaleza relativa. Respecto a los resultados obtenidos, se evidencia que para este caso de estudio el SONFS tiene mejor desempeño que el modelo lineal ARIMAX, como señala la disminución del Error Medio Absoluto (EMA). Además el análisis de los residuos obtenidos de la predicción con cada técnica sugiere que el SONFS cum-ple con todas las propiedades que se espera del residual contrario al modelo ARIMAX, así se puede decir que el SONFS tiene mayor capacidad de generalización. Como un ítem adicional se Figura 8. Predicción en el conjunto de entrenamiento y validación para la acción de Pacific Rubiales con el modelo ARIMAX(6,1,5,7). Figura 9. Predicción en el conjunto de entrenamiento y validación para la acción de Pacific Rubiales con el SONFS. tiene el criterio de información de Akaike es mejor en el modelo obtenido con el SONFS. Este comportamiento es causado por la no estacionaridad de la serie, lo que puede limitar el desempeño del modelo ARIMAX ya que este hace una aproximación lineal de la serie mientras que el SONFS hace una aproximación no lineal adaptándose mejor a la no linealidad expuesta en la varianza y media de la serie. Por las ventajas que ofrece el SONFS se concluye que esta es una mejor opción que el modelo ARIMAX para la predicción del precio de la acción de Pacific Rubiales.
Si bien es cierto que el principal inconveniente de la aplicación de las técnicas de inteligencia computacional respecto a métodos estadísticos es el incremento del costo computacional, se observó en la realización de las pruebas que el SONFS es una técnica que no exige un costo computacional alto, pues tarda en promedio veinte minutos en realizar su sintonización.
REFERENCIAS BIBLIOGRÁFICAS
- Paul Samuelson y William Nordhaus, Economía. 15 ed. McGraw-Hill, Ma-drid, España, 1998.
- Damodar Gujarati, Basic Econometrics.McGraw Hill, New York City, New York, 2004.
- Steven Achelis, Technical Analysis from A to Z. McGraw Hill, New York City, New York, 2000.
- Michael Steinberg, Guía para invertir en bolsa.Ediciones Deusto, Bilbao, Portugal, 2001.
- Gioqinang Zhang y Michael Y. Hu, “Neural network forecasting of the British Pound/US Dollar exchange rate”. Omega Elsevier Science, Volumen 26, Número 4, Agosto, 1998, pp. 495-506.
- André AlvesPortela, Newton CarneiroAffonso y Leandro dos Santos, “Computational intelligence approaches and linear models incase studies of forecasting exchange rates”. Expert Systems with Application Elsevier Science, Volumen 33, Número 4, Noviembre, 2007, pp. 816-823.
- Juan Carlos Figueroa y Jose Jairo Soriano, “A comparison on ANFIS, ANN and DBR systems on volatile time series identification”, Annual Meeting of the North American Fuzzy Information Processing Society, 2007, pp. 321-326.
- Orlando Greco, Diccionario de Economía. Valletta Ediciones, Buenos Aires, Argentina, 2006.
- Bolsa de Valores de Colombia, Ranking por capitalización bursátil, 26 de Julio de 2011, disponible en http://www.bvc.com.co/pps/tibco/ portalbvc/Home/Empresas/.
- Gordon Alexander, William F. Sharpe y Jeffery V. Bailey, Fundamentos de inversiones: Teoría y Práctica. Pearson Eduacación, México, 2003.
- Sheldon M. Ross, Introducción a la estadística. Editorial Reverté, Barcelona, España, 2007.
- José Hernandez, Análisis de series temporales económicas II. Esic, Madrid, España, 2007.
- George Box y Gwlym Jenkins, Times Series Analysis: Forecasting and Control. Editorial Holden Day, Oakland, California, 1976.
- Chia-FengJuang y Yu-Wei Tsao, “A Type-2 Self-Organizing Neural Fuzzy System and Its FPGA Implementation”. IEEE Transactions on Systems, man and cybernetics, Part B, Cybernetics, Volumen 38, Número 6, Diciembre, 2008, pp. 1537-1548.
- Chia-FengJuang y Chin-Teng Li, “An on-line self-constructing neural fuzzy inference network and its application”. IEEE Transactions on Fuzzy Systems, Volumen 6, Número 1, Febrero, 1998, pp. 12-32.
- Li-Xin Wang and Jerry Mendel, “Back-propagation fuzzy system as nonlinear dynamic system identifiers”, Conference on Intelligent Computing and Intelligent Systems, 2010, pp. 684-688.
- Peter A. Brockwell y Richard A. Davis, Introduction to time series and forecasting, Springer-Verlag, New York, New York, 1987.
- Armando Aguirre, Introducción al tratamiento de series temporales. Ediciones Díaz de Santos, Madrid, España, 2010.
Este trabajo está autorizado por una Licencia Attribution-NonCommercial-NoDerivs CC BY-NC-ND.
Licencia
A partir de la edición del V23N3 del año 2018 hacia adelante, se cambia la Licencia Creative Commons “Atribución—No Comercial – Sin Obra Derivada” a la siguiente:
Atribución - No Comercial – Compartir igual: esta licencia permite a otros distribuir, remezclar, retocar, y crear a partir de tu obra de modo no comercial, siempre y cuando te den crédito y licencien sus nuevas creaciones bajo las mismas condiciones.



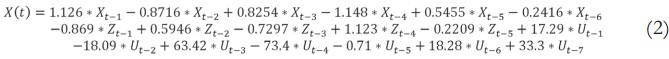

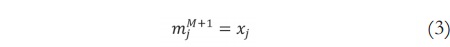
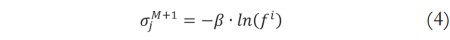
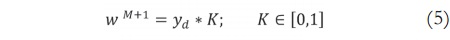



2.jpg)