DOI:
https://doi.org/10.14483/udistrital.jour.reving.2015.1.a03Published:
2015-03-12Issue:
Vol. 20 No. 1 (2015): January - JuneSection:
ArticleOptimización Multiobjetivo en la Gestión de Cadenas de Suministro de Biocombustibles. Una Revisión de la Literatura
Multiobjective optimization in Biofuel Supply Chain Management. A Review of the Literature
Keywords:
supply chain management, biofuels, multi-objective optimization (en).Keywords:
Gestión de la Cadena de Suministro, Biocombustibles, Optimización Multi-objetivo. (es).Downloads
References
A. Dufey, Producción y comercio de agrocombustibles y desarrollo sustentable: los grandes temas, Londres: Instituto Internacional para el Medio Ambiente y Desarrollo, 2006.
A. Demirbas, “Progress and recent trends in biodiesel fuels,” Energy Conversion and Management 50, p. 14–34, 2009.
NACEPT, Strategic Framework for Biofuels Efforts, Estados Unidos: National Advisory Council for Environmental Policy and Technology, 2007.
A. Ajanovic and R. Haas, “Economic challenges for the future relevance of biofuels in transport in EU countries,” Energy 35, pp. 3340 - 3348, 2010.
J. P. Arístegui, “Los agrocombustibles desde la perspectiva del comercio internacional y del derecho de la organización mundial del comercio,” Revista de Derecho (Austral), vol. XXII, núm. 1, pp. 113-134, 2009.
S. Mathur and A. Kenyon, “Creating Value: Shaping Tomorrow’s Business,” Butterworth-Heinemann, 1997.
G. Svensson, “Gestión de la Cadena de Suministro frente a Gestión de la Cadena Sostenible,” EsicMarket, 129, pp. 239-258, 2007.
A. Nikolopoulou and M. G. Ierapetritou, “Optimal design of sustainable chemical processes and supply chains: A review,” Computers and Chemical Engineering 44, p. 94 – 103, 2012.
C. Cambero and T. Sowlati, “Assessment and optimization of forest biomass supply chains from economic, social and environmental perspectives – A review of literature,” Renewable and Sustainable Energy Reviews, p. 62–73, 2014.
S. Liu, M. Leat and M. H. Smith, “State-of-the-art sustainability analysis methodologies for efficient decision support in green production operations,” International Journal of Sustainable Engineering, pp. 236-250, 2011.
M. Ehrgott and M. M. Wiecek, “MULTIOBJECTIVE PROGRAMMING,” in MULTIPLE CRITERIA DECISION ANALYSIS: STATE OF THE ART SURVEYS, Estados Unidos, Springer, 2005, pp. 667-722.
R. Marler and J. Arora, “Survey of multi-objective optimization methods for engineering,” Struct Multidisc Optim 26, p. 369–395, 2004.
J. Lopez, Optimización Multiobjetivo: Aplicaciones a problemas del mundo real, Buenos Aires, Argentina: UNIVERSIDAD NACIONAL DE LA PLATA, 2013.
O. L. De Weck, “Multiobjective optimization: History and promise,” in Third China-Japan-Korea Joint Symposium on Optimization of Structural and Mechanical Systems, Kanazawa, Japan, 2004.
T. Marler and J. S. Arora, “The weighted sum method for multi-objective optimization: new insights,” Struct. Multidisc. Optim. 41, p. 853–862, 2010.
H. O. Alanazi, A. H. Abdullah and M. Larbani, “Dynamic Weighted Sum Multi-Criteria Decision Making: Mathematical Model,” International Journal of Mathematics and Statistics Invention, pp. 16-18, 2013.
M. Ehrgott and S. Ruzika, “Improved ε-Constraint Method for Multiobjective Programming,” Journal
Optim. Theory Appl. 138, p. 375–396, 2008.
C. A. Coello, “Networking and Emerging Optimization,” Septiembre 2002. [Online]. Available:
http://neo.lcc.uma.es/pdf-charlas/MOEA.pdf.
Y. J. Túpac, “Universidad Católica San Pablo,” 23 Noviembre 2011. [Online]. Available: http://www.ucsp.edu.pe/~ytupac/speaks/2011/UNJBG_CIIS_MOGA.pdf.
A. Messac and C. A. Mattson, “ Generating Well-Distributed Sets of Pareto Points for Engineering Using Physical Programming,” Optimization and Engineering Vol. 3, p. 431–450, 2002.
A. Kostin, G. Guillén-Gosálbez, F. Mele, M. Bagajewicz y L. Jiménez, «Design and planning of infrastructures for bioethanol and sugar production under demand uncertainty,» chemical engineering research and design 90, p. 359–376, 2012.
B. Gebreslassie, Y. Yao y F. You, «Design under uncertainty of hydrocarbon biorefinery supply chains: multiobjective stochastic programming models, decomposition algorithm, and a comparison between CVaR and downside risk,» AIChE Journal 58 (7), pp. 2155-2179, 2012.
Y. Huang y W. Pang, «Optimization of Resilient Biofuel Infrastructure Systems under Natural Hazards,» J. Energy Eng., 140(2), 2014.
El-Halwagi, Rosas y Ponce-Ortega, «Multiobjective Optimization of Biorefineries with Economic and Safety Objectives,» AIChE Journal Vol. 59, No. 7, pp. 2427-2434, 2013.
A. Zamboni, N. Shah y F. Bezzo, «Spatially Explicit Static Model for the Strategic Design of Future Bioethanol Production Systems,» Energy Fuels, 23 (10), p. 5134–5143, 2009.
P. Liu, M. Georgiadis y E. Pistikopoulos, «Advances in energy systems engineering,» Ind. Eng. Chem. Res. 50 (9), p. 4915–4926, 2011.
S. Giarola, A. Zamboni y F. Bezzo, «Spatially explicit multi-objective optimisation for design and planning of hybrid first and second generation biorefineries,» Computers and Chemical Engineering, Vol. 35, p. 1782– 1797, 2011.
W. Marvin, L. Schmidt, S. Benjaafar y P. Daoutidis, «Economic and environmental optimization of the biomass-to-biofuel supply chain in the midwest.,» 11AIChE Annual Meeting, Conference Proceedings., 2011.
O. Akgul, N. Shah y L. Papageorgiou, «An optimisation framework for a hybrid first/second generation bioethanol supply chain,» Computers and Chemical Engineering 42, p. 101– 114, 2012.
Čuček, Sabev, Jaromír y Kravanja, «Total footprints-based multi-criteria optimisation of regional biomass energy supply chains,» Energy. Volume 44, Issue 1, p. 135–145, 2012.
Kostin, Guillén-Gosálbez, Mele y Jiménez, «Identifying key life cycle assessment metrics in the multiobjective design of bioethanol,» I&ECR 51 (14), pp. 5282-5291, 2012.
A. Ubando, A. Culaba, K. Aviso, D. Ng y R. Tan, «Fuzzy Multi-Objective Approach for Designing of Biomass Supply Chain for Polygeneration With Triple Footprint Constraints,» ASME 2013 International Mechanical Engineering Congress and Exposition. Volume 12, 2013.
A. Bernardi, S. Giarola y F. Bezzo, «Spatially Explicit Multiobjective Optimization for the Strategic Design of First and Second Generation Biorefineries Including Carbon and Water Footprints,» Ind. Eng. Chem. Res. 52 (22), p. 7170–7180, 2013.
R. Ortiz, S. Giarola y F. Bezzo, «Optimal design of ethanol supply chains considering carbon trading effects and multiple technologies for side-product exploitation,» Environmental Technology. Vol. 34, p. 2189–2199, 2013.
D. Yue, M. Kim y F. You, «Design of Sustainable Product Systems and Supply Chains with Life Cycle Optimization Based on Functional Unit: General Modeling Framework, Mixed-Integer Nonlinear Programming Algorithms and Case Study on Hydrocarbon Biofuels,» ACS Sustainable Chem. Eng. 1 (8), p. 1003–1014, 2013.
F. Xie y Y. Huang, «Sustainable Biofuel Supply Chain Planning and Management Under Uncertainty,» Journal of the Transportation Research Board, pp. 19-27, 2013.
Z. Liu, T. Qiu y B. Chen, «A study of the LCA based biofuel supply chain multi-objective optimization model with multi-conversion paths in China,» Applied Energy 126, p. 221–234, 2014b.
J. Nixon, P. Dey, P. Davies, S. Sagi y R. Berry, «Supply chain optimisation of pyrolysis plant deployment using goal programming,» Energy 68, pp. 262-271, 2014.
Z. Liu, T. Qiu y B. Chen, «A LCA Based Biofuel Supply Chain Analysis Framework,» Chinese Journal of Chemical Engineering, 22(6), p. 669—681, 2014a.
E. Capón, G. Guillén-Gosálbez, L. Jiménez-Esteller y A. Espuña, «Designing the optimal supply chain for biodiesel production in spain,» AIChE 100 Annual Meeting, Conference Proceedings, 2008.
F. You y B. Wang, «Optimal design and operations of cellulosic biofuel supply chains under uncertainty,» 11AIChE Annual Meeting, Conference Proceedings., 2011.
F. You, L. Tao, D. Graziano y S. Snyder, «Optimal Design of Sustainable Cellulosic Biofuel Supply Chains: Multiobjective Optimization Coupled with Life Cycle Assessment and Input–Output Analysis,» AIChE Journal Vol. 58, No. 4, pp. 1157-1180, 2012.
J. Santibañez-Aguilar, J. González-Campos, J. Ponce-Ortega, M. Serna-González y M. El-Halwagi, «Optimal Multi-Objective Planning of Distributed Biorefinery Systems Involving Economic, Environmental and Social Aspects,» Computer Aided Chemical Engineering. Volume 31, p. 470–474, 2012.
L. Turcksin, C. Macharis, K. Lebeau, L. Gorissen y P. L. , «A multi-actor multi-criteria framework to assess the stakeholder support for different biofuel options: The case of Belgium,» Energy Policy 39, p. 200–214, 2011.
A. Halog y Y. Manik, «Advancing Integrated Systems Modelling Framework for Life Cycle Sustainability Assessment,» Sustainability 3 , pp. 469-499, 2011.
S. Zhou, Y. Zhang y X. Bao, «Methodology of Location Selection for Biofuel Refinery Based on Fuzzy TOPSIS,» International Conference on Automation and Logistics - Zhengzhou, China, 2012.
F. Madugu y M. Collu, «Techno-economic modelling analysis of microalgae cultivation for biofuels and co-products,» WIT Transactions on Ecology and the Environment. Volume 190, pp. 1091-1102, 2014.
M. Barón, I. Huertas and J. Orjuela, “Gestión de la cadena de abastecimiento del biodiésel: una revisión de la literatura,” Ingeniería, Vol. 18, Num. 1, pp. 84-117, 2013.
FAO, The state of food security in the world 2008. High food prices and food security: Threats and opportunities, Roma: FAO, 2008.
C. CUE, Evaluación del ciclo de vida de la cadena de producción de biocombustibles en Colombia, Medellín, Colombia: Ministerio de Minas y Energía, 2012.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Optimización multiobjetivo en la gestión de cadenas de suministro de biocombustibles. Una revisión de la literatura
Multiobjective optimization in biofuel supply chain management. A review of the literature
Johan Alexander Aranda Pinilla; Universidad Católica de Colombia. jaaranda@ucatolica.edu.co
Javier Arturo Orjuela Castro; Universidad Distrital Francisco José de Caldas. jorjuela@udistrital.edu.co
Recibido: 11-11-2014. Modificado: 02-03-2015. Aceptado: 12-03-2015
Resumen
La producción de biocombustibles ha tenido un crecimiento constante durante los ultimos años y se espera que este comportamiento se mantenga en el mediano y largo plazo, impulsado principalmente, por las ventajas ambientales que podrían traer en comparación con el combustible fósil, tales como reducción en las emisiones de gases efecto invernadero, balance energético positivo y desarrollo económico para los países productores. Sin embargo, a pesar de sus beneficios, existen preocupaciones por los impactos ambientales y sociales que puede generar su producción y distribución. La teoría de decisión multi-criterio se ha utilizado en los últimos años como marco para integrar los diferentes objetivos en la toma de decisiones en las cadenas de suministro de biocombustibles.
El propósito de este artículo es presentar una revisión de los conceptos y métodos principales de la optimización multiobjetivo, así como la aplicación de éstos en el diseño y planificación de cadenas de suministro de biocombustibles. El estudio muestra que el costo es el objetivo económico más frecuente, las emisiones de efecto invernadero son el objetivo ambiental más utilizado y el número de empleos creados es el criterio social más considerado y se dejan de lado aspectos relevantes como la seguridad alimentaria.
Palabras claves: gestión de la cadena de suministro, biocombustibles, optimización multiobjetivo
Abstract
Biofuel production has had constant growth in recent years and is expected it keeps growing in the medium and long term, mainly driven by the environmental benefits they could bring compared to fossil fuel, such as the reduction of greenhouse gas emissions, positive energy balance and economic development for producer countries. However, despite its benefits, there are concerns about the environmental and social impacts that its production and distribution may generate. The multi-objective or multi-criteria decision theory has been used in recent years as a framework for integrating the various objectives in decision-making on biofuel supply chains. This article aims to present a review of the main concepts and multi-objective optimization methods as well as their application in the design and planning of biofuel supply chains. The study shows that cost is the most frequent economic objective, greenhouse emissions are the most frequently used environmental objective and the number of created jobs is the most considered social criterion, leaving out important aspects such as food safety.
Key words: supply chain management, biofuels, multi-objective optimization.
Recibido: 11-11-2014 Modificado: 02-03-2015 Aceptado: 12-03-2015
1. Introducción
En la actualidad, los biocombustibles son considerados sustitutos parciales del combustible fósil y tienen una creciente proyección de consumo y producción a mediano y largo plazo [1]. Esta creciente proyección se debe principalmente a las ventajas ambientales que podrían presentar los biocombustibles en comparación al combustible fósil [2], al hecho de que se producen a partir de recursos renovables [3] y adicionalmente porque representan una nueva fuente de ingresos para la agricultura. Sin embargo, a pesar de sus beneficios, existen preocupaciones en cuanto a su producción y distribución [1].
Por un lado, los biocombustibles podrían brindar mayores ganancias económicas, desarrollo rural, reducción de la pobreza y menores emisiones de gases con efecto invernadero [1] [4]. En contraste, la producción de biocombustibles podría llevar a un aumento de la deforestación, contaminación del agua, incremento del uso de agroquímicos, problemas sobre la seguridad alimentaria, en lo que respecta a disponibilidad y acceso a los alimentos, y un empeoramiento de las condiciones laborales, entre otras preocupaciones [5]. En este contexto, la toma de decisiones en las cadenas de suministro de biocombustible debe dirigirse a aprovechar al máximo sus beneficios y a reducir los impactos negativos sobre el ambiente y la sociedad.
Las decisiones en las organizaciones se han basado principalmente en el aspecto económico [6] [7]. Sin embargo, la importancia de equilibrar los objetivos sociales, ambientales y económicos ha creado una conciencia cada vez mayor sobre el diseño y planificación óptima sostenible de las cadenas de suministro. En los últimos años, esfuerzos considerables en investigación se han realizado para ampliar los enfoques actuales y equilibrar los objetivos sociales, ambientales y económicos con el fin de garantizar la sostenibilidad a largo plazo [8] [9]. La teoría de la decisión multiobjetivo o multi-criterio (MCDM – Multi-criteria decision making) presenta un marco para integrar múltiples objetivos.
En la literatura se han presentado artículos de revisión sobre técnicas de decisión multicriterio en cadenas de suministro particulares [9] [8] y genéricas [10]. Dentro de éstos, el artículo de revisión desarrollado más cercano a las cadenas de biocombustible es de el de Cambero y Sowlati [9] sobre la cadena de biomasa forestal, como posible fuente de biocombustible. Sin embargo, dicho artículo se centra en describir cómo se han considerado los aspectos técnico-económicos, ambientales y sociales en la cadena, siendo la mayoría de los modelos evaluados mono-objetivo.
En este trabajo se presentar una revisión de los conceptos y métodos principales de la optimización multiobjetivo y la aplicación de éstos en la gestión de cadenas de suministro de biocombustibles. La revisión incluye diferentes fuentes de materia prima, y el análisis se centra en tipos de modelos y técnicas de solución utilizadas. En la sección 2 se presenta la metodología utilizada para el desarrollo del artículo. La sección 3 presenta los conceptos básicos en la optimización multiobjetivo, se hace la clasificación de los métodos de optimización y se exponen los métodos principales. La sección 4 muestra la importancia que ha tenido en los últimos años la optimización multiobjetivo en el diseño y planificación de las cadenas de suministro. El estado del arte de la aplicación de la optimización multiobjetivo en la gestión de cadenas de suministro de biocombustibles se presenta en la sección 5. Finalmente, en la sección 6 se presenta la discusión y en la sección 7, las conclusiones.
2. Metodología
Para el desarrollo del artículo de revisión se realizaron tres búsquedas en las bases de datos Scopus, IEEE y ProQuest. La primera búsqueda tuvo como objetivo hacer una introducción a la optimización multiobjetivo y determinar cuáles son las técnicas más comunes para la solución de este tipo de modelos y su clasificación. Para identificar las técnicas más utilizadas y las tendencias en el uso de las diferentes técnicas, se cuantificó el número de artículos publicados por grupos de años en la base de datos Scopus.
La segunda búsqueda se hizo con el fin observar la importancia que ha tenido la toma de decisiones multi-criterio o multiobjetivo en las cadenas de suministro en general. Se consideraron artículos y ponencias con el criterio de búsqueda “Supply Chain” y posteriormente se limitó la búsqueda a los artículos que tuvieran alguna de las expresiones: “multi-objective”, “multiobjective” y “multi-criteria”. Esta búsqueda se realizó con el fin de analizar la importancia que ha tenido las decisiones multi-criterio o multiobjetivo en las cadenas de suministro en la última década.
Por último, la tercera búsqueda se realizó con el fin de presentar un estado del arte de modelos multiobjetivo en cadenas de suministro de biocombustibles. Para la realización del estado del arte se limitó la búsqueda anterior a los artículos con el criterio “biofuel” o “biodiesel” o “bioetanol” para así considerar las cadenas de suministro de biocombustibles. Posteriormente se hizo la revisión, clasificación y análisis de los artículos seleccionados, considerando tipo y número de objetivos considerados, tipos de modelos y técnicas de solución empleadas.
3. Optimización multiobjetivo
La programación multiobjetivo es una parte de la programación matemática que se encarga de problemas de decisión con múltiples funciones objetivo que deben ser optimizadas sobre un conjunto factible de soluciones [11]. El problema de optimización multiobjetivo general se plantea en la ecuación 1.
Donde k es el número de funciones objetivo, x es el vector de variables de decisión y X el espacio de diseño factible, también llamado el espacio de decisión factible o delimitado por el conjunto de restricciones.
Según Marler y Arora [12], se llama optimización multiobjetivo (MOO) al proceso de optimizar de manera sistemática y simultánea una colección de funciones objetivo. En estos casos no hay una solución global única, sino que es necesario determinar un conjunto de puntos que correspondan a las mejores soluciones, conocido como conjunto de Pareto.
En un problema multiobjetivo no se tiene una única función a optimizar, sino un conjunto de n funciones. En estos casos no hay una solución global única, sino que es necesario determinar un conjunto de puntos que se ajusten a una definición predeterminada de un óptimo. El concepto predominante en la definición de un punto óptimo es el de la optimalidad de Pareto, donde se define que un punto, x* ∈ X, es un óptimo de Pareto si y sólo si no existe otro punto, x* ∈ X, tal que F(x) ≤ F(x*), y Fi(x) < Fi(x*) para al menos una función [12].
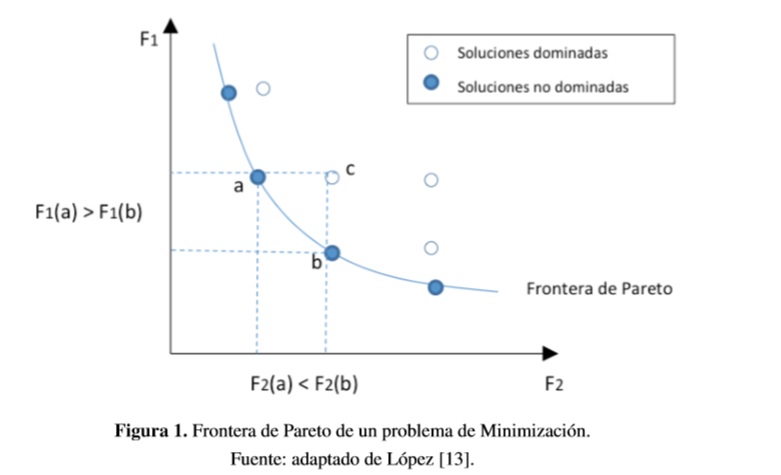
3.1. Optimización de Pareto
El concepto del óptimo de Pareto se presenta gráficamente en la Figura 1. En la figura, la solución “a” pertenece a conjunto de soluciones óptimas (o soluciones no dominadas) dado que no puede encontrarse una solución “b” tal que mejore uno de los objetivos sin empeorar al menos uno de los otros. En este caso, la solución “c” es dominada por “a” y por “b”.
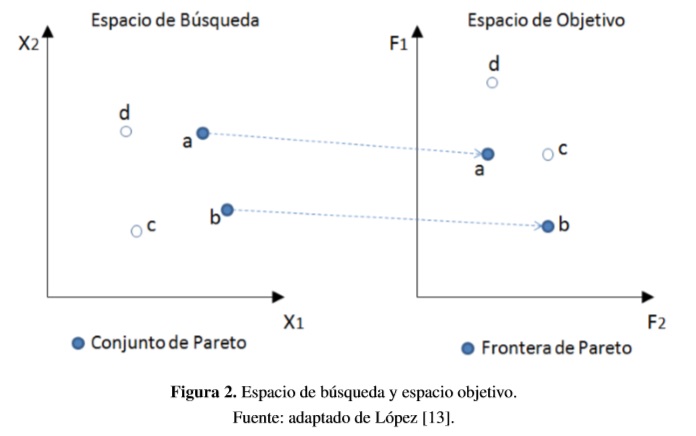
El conjunto de Pareto se define entonces como el conjunto de puntos en el espacio de búsqueda que se corresponden con las mejores soluciones al problema de optimización; y la frontera de Pareto, como el conjunto de soluciones óptimas en el espacio objetivo. Este conjunto de soluciones se integra con aquellos puntos encontrados en el espacio objetivo que se corresponden con las soluciones no dominadas, de acuerdo con el criterio de dominancia de Pareto. El concepto de conjunto de Pareto y frontera de Pareto se representan en la Figura 2.
La frontera de Pareto obtenida puede ser lineal, cóncava, convexa, continua o discontinua dependiendo de las funciones objetivo integrantes del problema. Todas las soluciones pertenecientes a la frontera son igualmente buenas, y no se puede especificar si alguna de las soluciones es preferible a las otras, excepto en aquellos casos en que se haya definido una preferencia a priori.
En la optimización por métodos de Pareto, el desafío es encontrar la frontera de Pareto real, o lograr la mejor aproximación del mismo sujeta a las limitaciones de recursos (tiempo y memoria) existentes. Por esta razón, el proceso de búsqueda utilizado es decisivo.
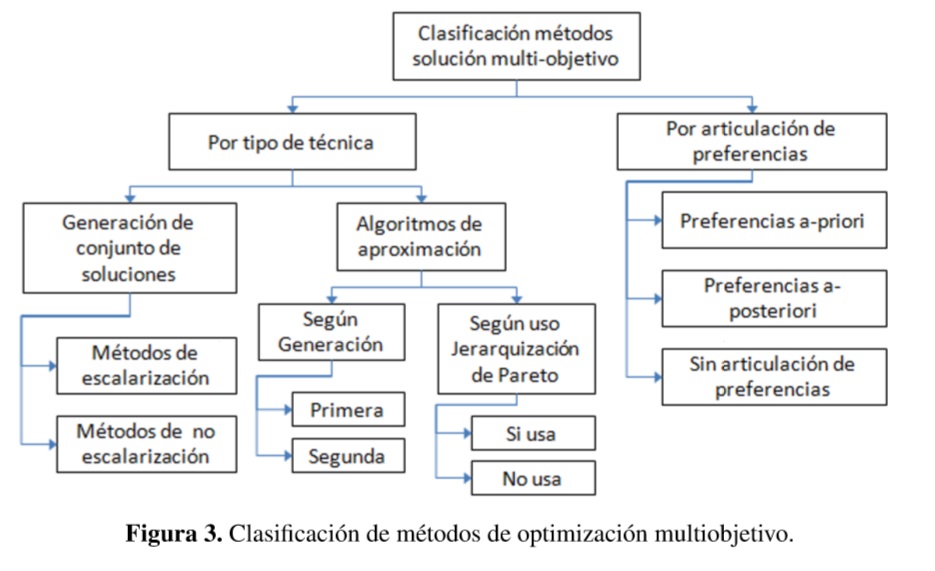
3.2. Clasificación de los métodos de solución de modelos matemáticos multiobjetivo
La clasificación por tipo de técnica se hace en dos grupos: el primero es un conjunto de métodos para generar el conjunto de soluciones, basados en optimización de modelos de programación matemática, y el segundo grupo son algoritmos o heurísticas de aproximación al conjunto de Pareto [11]. A su vez, estos métodos, independientemente del tipo de técnica, pueden clasificarse según la manera en que se expresen las preferencias del tomador de decisiones [14] [12]. La clasificación de los métodos se resume en la Figura 3.
A continuación se exponen los diferentes grupos de métodos de optimización multiobjetivo y se nombran los métodos más comunes de cada grupo. Adicionalmente se presentan los principales métodos para la generación del conjunto de soluciones.
3.2.1. Generación de conjunto de soluciones
Existen dos enfoques para generar conjuntos de soluciones de programación multiobjetivo: los métodos de “escalarización” y los métodos de “no escalarización” [11]. Estas clasificaciones se exponen a continuación:
Métodos de escalarización
Los métodos de escalarización implican la formulación de un modelo mono-objetivo relacionado con el modelo multiobjetivo por medio de una función escalar, de ahí el término escalarización [12]. ésta única función escalar está en términos de las funciones objetivo del modelo multiobjetivo, escalares auxiliares, un vector de variables o un vector de parámetros.
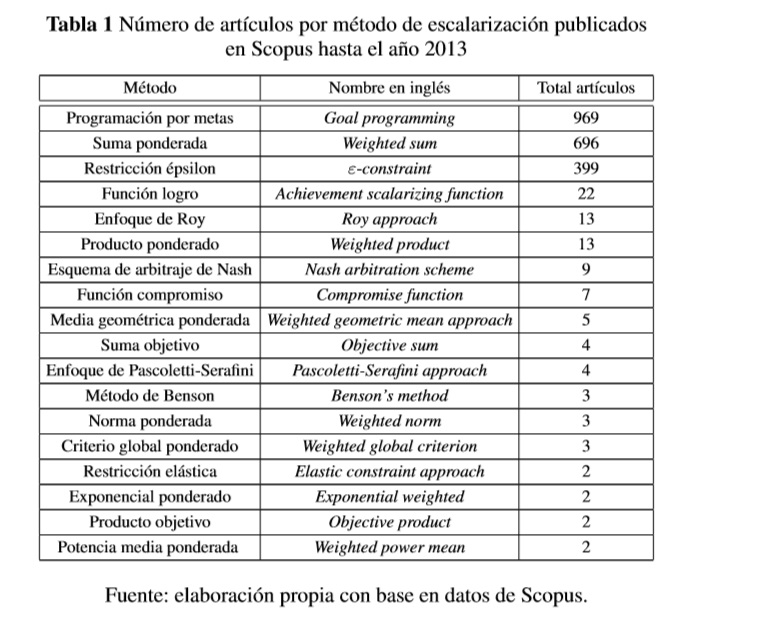
La Tabla 1 presenta métodos de escalarización más utilizados y el número de artículos encontrados en Scopus hasta el año 2013.
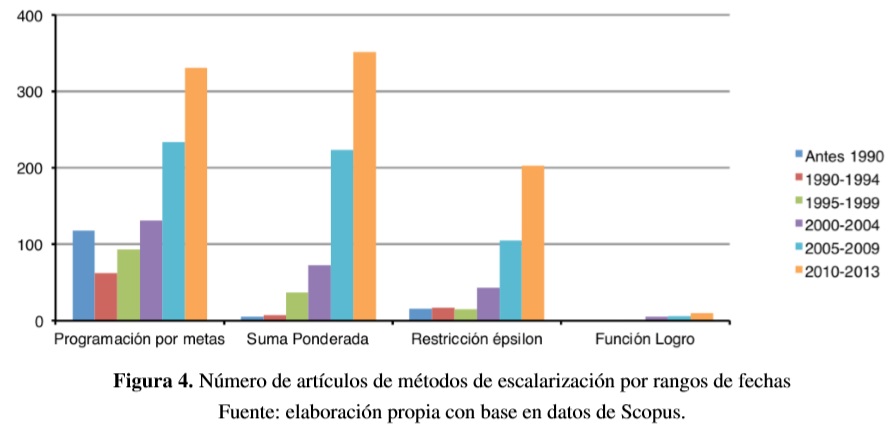
El método de escalarización para modelos con múltiples objetivos con mayor número de artículos es la programación por metas, seguido del método de suma ponderada y de la restricción épsilon (ε-constraint). La Figura 4 muestra los artículos encontrados por rangos de fechas de los cuatro métodos más utilizados. A continuación se presenta una explicación de los métodos de escalarización más utilizados.
En la programación por metas se especifican metas para cada función objetivo y la formulación básica se presenta en la Ecuación 2.
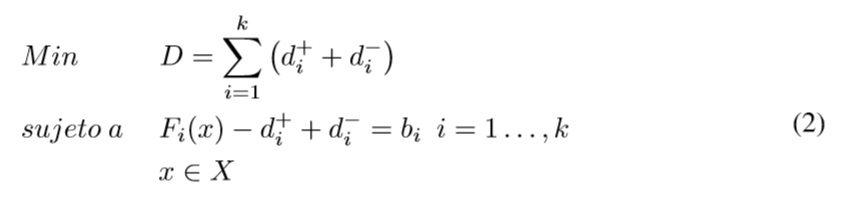
Donde D es la sumatoria total de las desviaciones, las variables d+i y d−i son las desviaciones por encima y por debajo obtenidas para cada meta, bi es la meta definida para cada objetivo, Fi(x) es la i-ésima función objetivo y k es el número de objetivos. El modelo busca minimizar la desviación total de las metas [11].
La programación por metas ponderada (weighted goal programming) constituye una subclase del método de programación por metas, en la que se asignan pesos a la desviación de cada objetivo de su meta respectiva.
El segundo método de escalarización con mayor número de artículos es el de la suma ponderada (U). Este método escalariza el conjunto de objetivos en un solo objetivo multiplicando cada objetivo con un peso definido previamente (ωi). Un modelo multiobjetivo escalarizado con este método tiene la forma presentada en la Ecuación 3.
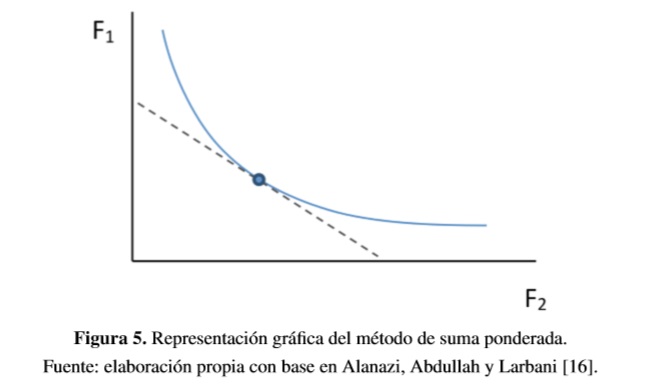
Si todos los pesos son positivos y la frontera de Pareto es convexa, la minimización de la función objetivo establece una condición suficiente para el óptimo de Pareto, es decir, el mínimo de la función siempre será un óptimo de Pareto [15]. Gráficamente, la escalarización y el punto óptimo obtenido se presentan en la Figura 5.
En la Figura 5 se representa la frontera de Pareto de un modelo con dos funciones objetivo. La pendiente de la función objetivo escalarizada (suma ponderada de las funciones objetivo individuales Fi) está determinada por el peso dado cada objetivo. Si se varían dichos pesos, se pueden obtener diferentes puntos de la frontera de Pareto.
El tercer método de escalarización con mayor número de artículos es el de la restricción épsilon (ε-constraint) propuesto por Haimes en 1971, que se basa en una escalarización donde una de las funciones objetivo se optimiza mientras que todas las otras funciones objetivo están limitadas por medio de restricciones adicionales [17]. La formulación tienen la forma de la Ecuación 4.
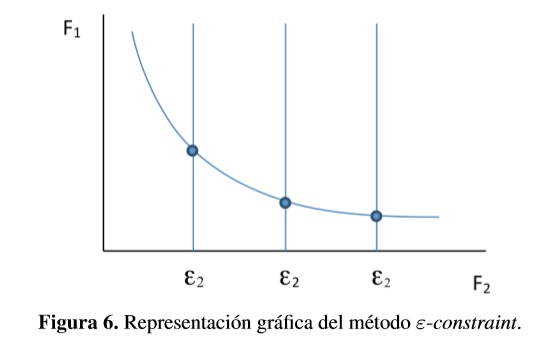
Donde los εi representan los valores de las funciones objetivos y se van alterando para obtener el conjunto óptimo de Pareto en un rango deseado. Gráficamente se observa el procedimiento en la Figura 6.
La Figura 6 describe una frontera de Pareto de un modelo con dos funciones objetivos, donde se minimiza la primera (F1) y se restringe la segunda (F2). El valor ε2 representa el valor al que se restringe F2 y con cada nivel de ε2 se obtiene un punto óptimo de Pareto.
Métodos de no escalarización
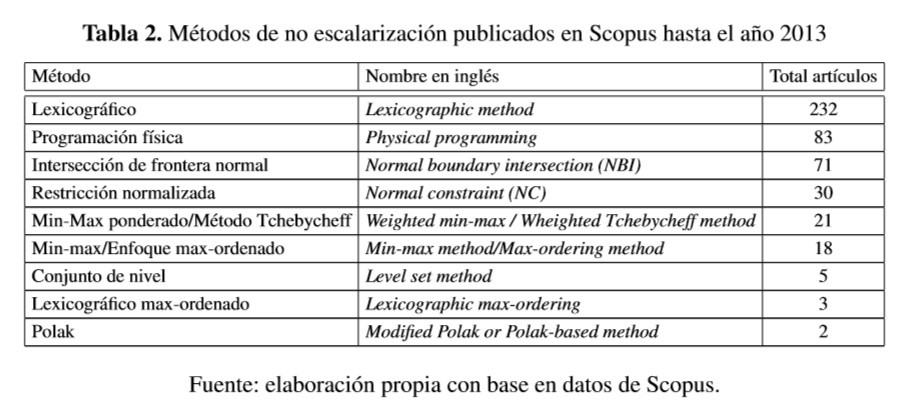
Los métodos de no escalarización, implican un breve tratamiento independiente de cada función objetivo [12]. En contraste con los métodos de escalarización, no utilizan explícitamente una función de escalarización sino que se basan en otros conceptos de optimalidad o conjuntos auxiliares y por lo general se vinculan con conceptos de eficiencia [11]. La Tabla 2 presenta los métodos de no escalarización más utilizados y el número de artículos encontrados en Scopus hasta el año 2013.
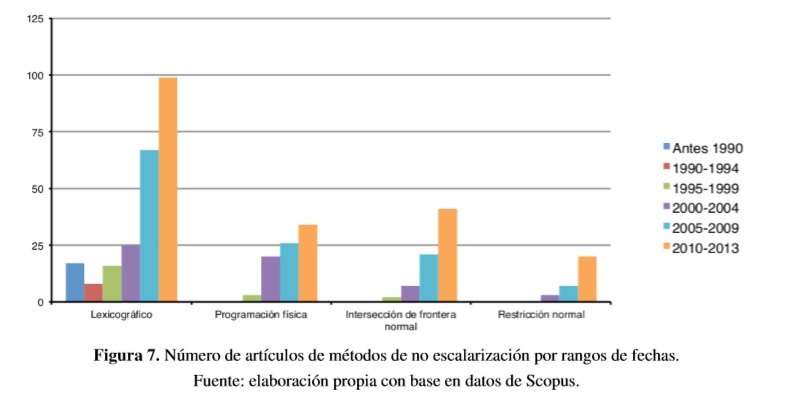
El método con mayor número de artículos publicados es el lexicográfico, seguido de la programación física, intersección de frontera normal (NBI) y restricción normalizada (NC). La Figura 7 muestra los artículos encontrados por rangos de fechas de los cuatro métodos más utilizados. A manera de ejemplo se expone a continuación la técnica de no escalarización más utilizada.
En el método lexicográfico, las funciones objetivo están dispuestas en orden de importancia. Así, posteriormente se resuelve el problema de optimización de un objetivo a la vez siguiendo el orden de importancia. La formulación matemática se presenta en la Ecuación 5.
En este caso, i representa la posición de una función en el orden de preferencia, y F*j (x) representa el óptimo de la función objetivo j-ésima, encontrada en la j-ésima iteración.
3.2.2. Algoritmos de aproximación
En la mayoría de problemas multiobjetivo no es fácil obtener una descripción exacta del conjunto de Pareto debido a que puede abarcar un número muy grande o infinito de puntos. Aunque en teoría es posible encontrar estos puntos exactamente, es computacionalmente difícil y costoso. Considerando lo anterior, una descripción aproximada de este conjunto de Pareto obtenida mediante un algoritmo de aproximación puede resultar conveniente dado que requiere menos esfuerzo y muchas veces puede ser lo suficientemente precisa para desempeñar el papel del conjunto de soluciones y apoyar con eficacia la toma de decisiones [11].
Los enfoques de aproximación emplean un método iterativo para producir puntos que se aproximen el conjunto de Pareto. Algunos enfoques son exactos y se basan en algoritmos que aseguran la obtención de óptimos de Pareto, mientras que otros enfoques se basan en heurísti-cas que no necesariamente aseguran que los puntos encontrados sean óptimos de Pareto.
Existen varios tipos de heurísticas para la solución de problemas multiobjetivo dentro de los que se encuentran los algoritmos evolutivos (EA), recocido simulado (simulated annealing, SA), búsqueda tabú (tabu search, TS), colonia de hormigas (ant colony, AC), aprendizaje por refuerzo distribuido (distributed reinforcement learning, DRL), algoritmos meméticos (memetic algorithms, MA) y técnicas híbridas. Las técnicas más trabajadas en problemas multiobjetivo han sido los algoritmos evolutivos conocidos como MOEA (multi-objective evolutive algorithm) [18].
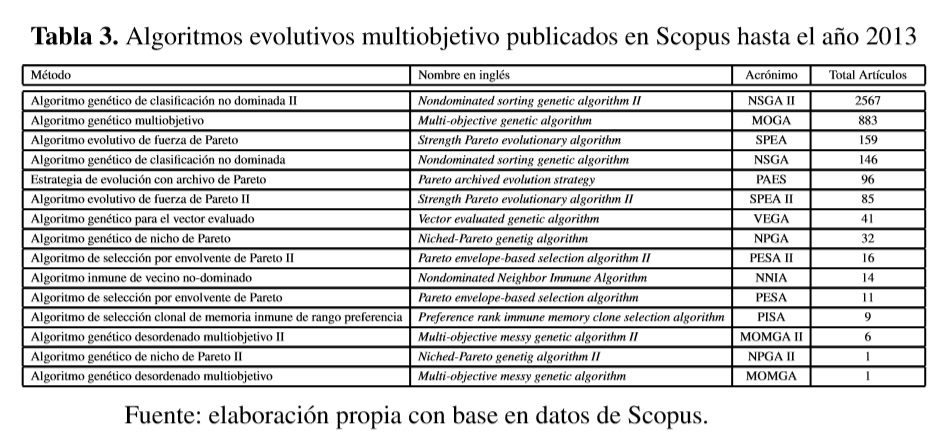
El potencial de los algoritmos evolutivos para resolver problemas de optimización multiobjetivo se remonta a finales de los sesenta en que la tesis doctoral de Rosenberg en 1967 indicó la posibilidad de usar algoritmos genéticos en este dominio. Sin embargo, el primer algoritmo evolutivo para problemas multiobjetivo es el algoritmo genético vector evaluado (VEGA) desarrollado por Schaffer en 1984 [18]. La Tabla 3 presenta los algoritmos evolutivos más utilizados y el número de artículos encontrados en Scopus hasta el año 2013.
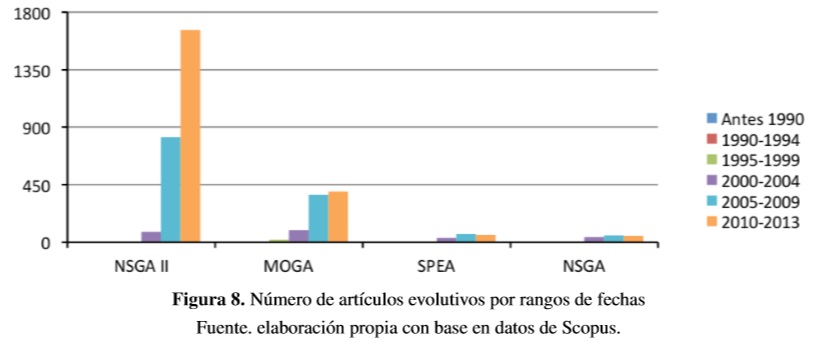
Los cinco algoritmos evolutivos con mayor número de artículos son NSGA II, MOGA, SPEA, NSGA y PAES, que representan el 95% de artículos encontrados. En la Figura 8 se presenta el total de artículos por rangos de fechas de estos métodos.
En la Figura 5 se observa que el número de artículos publicados relacionados con el método NSGA II ha venido creciendo constantemente desde el año 2000. Los demás métodos (MOGA, SPEA y NSGA) han variado poco entre los rangos 2005-2009 y 2010-2013, lo que demuestra una estabilidad en el número de artículos publicados por año. De la investigación, los métodos NNIA, PESA y PISA, a pesar de que tienen pocas publicaciones, han tenido un número creciente de artículos en la última década.
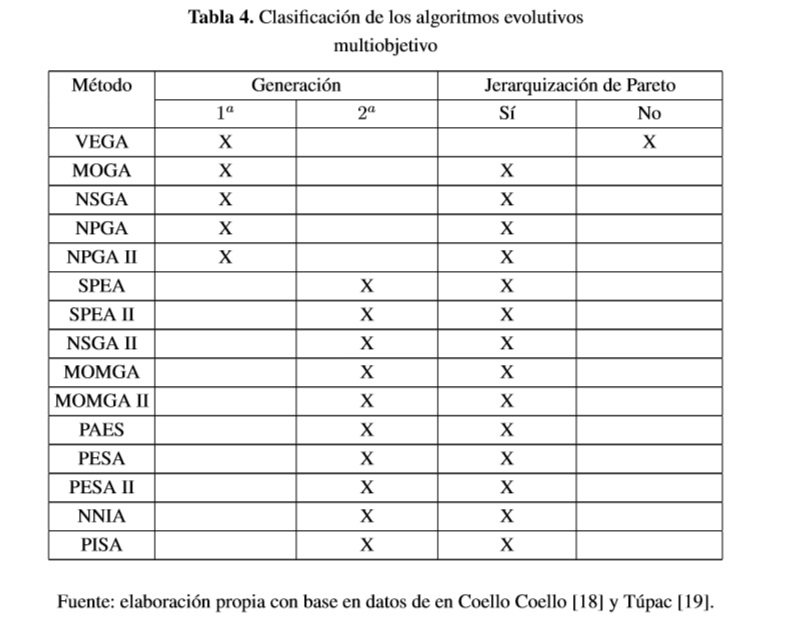
Los MOEA se clasifican en dos tipos: 1) Los algoritmos que no incorporan el concepto de óptimo de Pareto en el mecanismo de selección del algoritmo evolutivo, y 2). Los algoritmos que jerarquizan la población de acuerdo a si un individuo es dominado o no dominado (usando el concepto de óptimo de Pareto).
Adicionalmente, también se puede considerar que ha habido dos generaciones de algoritmos evolutivos multiobjetivo. La primera generación se caracterizada por el uso de jerarquización de Pareto y nichos, y por ser algoritmos relativamente simples [18]. La segunda generación se centra en la eficiencia computacional y se introduce el concepto de elitismo, donde se usan poblaciones secundarias (o externas) para generar soluciones que sean no dominadas y
Adicionalmente, también se puede considerar que ha habido dos generaciones de algoritmos evolutivos multiobjetivo. La primera generación se caracterizada por el uso de jerarquización de Pareto y nichos, y por ser algoritmos relativamente simples [18]. La segunda generación se centra en la eficiencia computacional y se introduce el concepto de elitismo, donde se usan poblaciones secundarias (o externas) para generar soluciones que sean no dominadas y uniformemente distribuidas [19]. En la Tabla 4 se presenta un clasificación de los MOEA por generación y por si usan la jerarquización de Pareto.
3.2.3. Clasificación según la articulación de preferencias
Según De Weck [14], los métodos de optimización multiobjetivo pueden descomponerse en dos categorías: métodos con expresión de preferencias a priori y métodos con expresión de preferencias a posteriori. La diferencia fundamental entre estas categorías es si la información de preferencias de los objetivos es definida antes del proceso de optimización o se realiza después de generar y evaluar el conjunto de soluciones que hacen parte de la frontera de Pareto.
Los métodos con preferencias a priori permiten especificar previamente las preferencias, que pueden ser articuladas en términos de objetivos o de importancia relativa de los diferentes objetivos (pesos). La mayoría de estos métodos incorporan parámetros, que son los coeficientes, exponentes y límites de restricción que pueden estar ajustados para reflejar las preferencias del tomador de decisiones, o ser alterados de forma continua para representar el conjunto óptimo de Pareto completo [12]. Dentro de los métodos con preferencias a priori más conocidos se encuentran los métodos: suma ponderada (weighted sum), ε-constraint, programación por metas (goal programming), método lexicográfico y min-max ponderado.
En otros casos, puede resultar difícil para el tomador de decisiones expresar una aproximación explícita de la función de preferencia. Por lo tanto, resulta conveniente tener un conjunto de soluciones de donde el tomador de decisiones pueda escoger. Para este fin, se utiliza un algoritmo para determinar una representación del conjunto óptimo de Pareto. Estos métodos incorporan una articulación a posteriori de las preferencias, donde se generan primero soluciones y después se elige después la que se considere la mejor decisión [20]. Los métodos con preferencias a posteriori más utilizados son intersección de frontera normal (NBI) y restricción normal normalizada (NC).
Marler y Arora [12] sostienen que existe una tercera categoría que son los métodos que no tienen articulación de preferencias. Estos métodos se aplican cuando en la toma de decisiones no pueden definirse concretamente las preferencias del tomador de decisiones. La mayoría de estos métodos son simplificaciones de los métodos de preferencias a priori con la exclusión de los parámetros del método. En esta categoría se encuentra el método min-max y el método de la función logro (achievement function), entre otros menos difundidos, como producto objetivo y suma objetivo.
4. Modelos de optimización multiobjetivo de la cadena de suministros
En las últimas décadas, se ha prestado atención a la minimización del impacto ambiental en las operaciones industriales a causa de regulaciones ambientales. Como resultado, la gestión de la cadena de suministro (SCM) ha venido pasando de un enfoque específico, centrado en los costos, a un enfoque más amplio que busca la sostenibilidad de la cadena.
La importancia de equilibrar los objetivos sociales, ambientales y económicos en el desarrollo de las empresas ha creado una conciencia cada vez mayor sobre el diseño y planificación sostenible de las cadenas de suministro. En los últimos años, la investigación ha buscado ampliar los enfoques actuales en SCM para capturar estos objetivos con el fin de garantizar la sostenibilidad a largo plazo. La combinación de la gestión ambiental y SCM en un marco único ha dado lugar recientemente a una nueva disciplina conocida como GSCM [8].
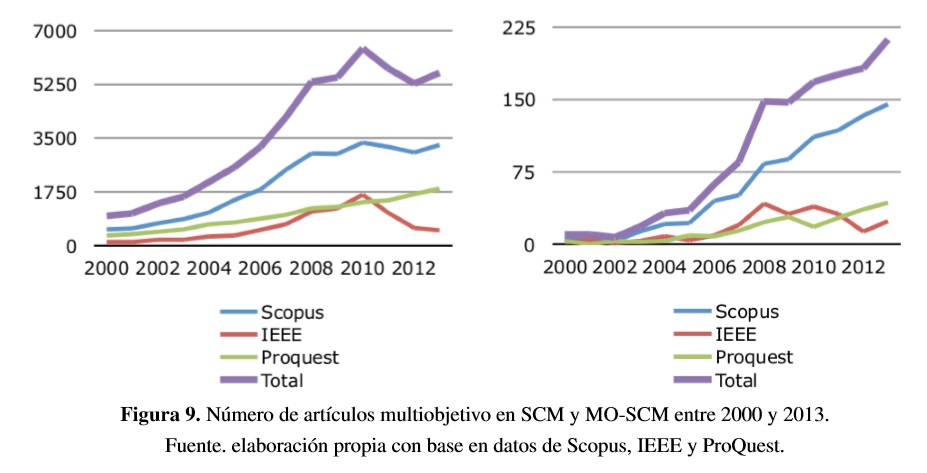
Para observar la importancia que ha tenido la inclusión de múltiples objetivos en las cadenas de suministro, se realizó una búsqueda de artículos y conferencias publicados sobre el tema y se comparó con las publicaciones sobre cadenas de suministro en general. La búsqueda se hizo en las bases de datos Scopus, IEEE y ProQuest utilizando la palabra de búqueda “Supply Chain” . Posteriormente, se limitó la búsqueda a los artículos que tuvieran alguna de las siguientes expresiones: “multi-objective”, “multiobjective”, “multi-criteria” y “multicriteria”. La Figura 9a muestra el número de artículos publicados por año sobre cadenas de suministro en general, mientras las Figura 9b muestra los artículos que tratan de múltiples objetivos en las cadenas.
Las publicaciones sobre cadenas de suministro tuvieron un crecimiento constante desde finales de los años setenta, principalmente a partir del año 2000, hasta el año 2008, lo que evidencia la relevancia del tema en esta época. Sin embargo, después de este año el número de publicaciones se ha estabilizado, con decrecimiento en algunos años.
Por su parte, las publicaciones de cadenas de suministro con múltiples objetivos han venido creciendo constantemente desde el año 2003. Desde el año 2000 hasta final del año 2013 se han publicado un total 1.292 de estos artículos en las bases de datos consideradas, donde el 80% pertenece a los últimos 6 años, lo que muestra la importancia que el tema ha tenido en la última década.
Hasta hace 10 años, el porcentaje de artículos que trataban múltiples objetivos no superaba el 1% sobre el total de artículos de cadenas de suministro. En el año 2013, este porcentaje es cercano al 4% y tiene una tendencia creciente, por lo que se espera que cada vez más se utilicen técnicas multi-criterio en la toma de decisiones en SCM.
5. Modelos multiobjetivo en cadenas de suministro de biocombustibles
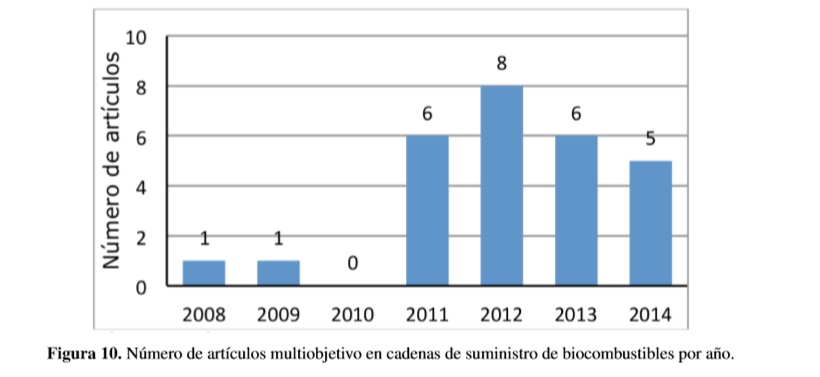
La búsqueda de artículos y artículos de conferencias se realizó en las bases de datos Scopus, IEEE y ProQuest utilizando las palabras de búsqueda “Supply chain”, “Biofuel” y alguno de los siguientes criterios: “multi-objective”, “multiobjective”, “multi-criteria” y “multicriteria”. La búsqueda, que no se limitó en un periodo de tiempo determinado, arrojó un total de 27 artículos. El número de artículos por año se presenta en la Figura 10.
El primer artículo sobre cadenas de suministro de biocombustibles con múltiples objetivos que aparece en las bases de datos se publicó en el año 2008, y la mayoría de artículos (93%) se publicó a partir del año 2011, lo que muestra la reciente importancia que ha tenido el tema.
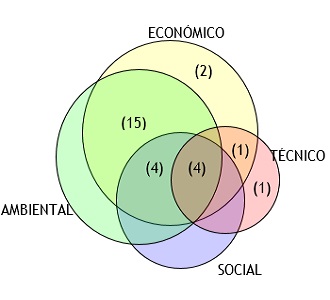
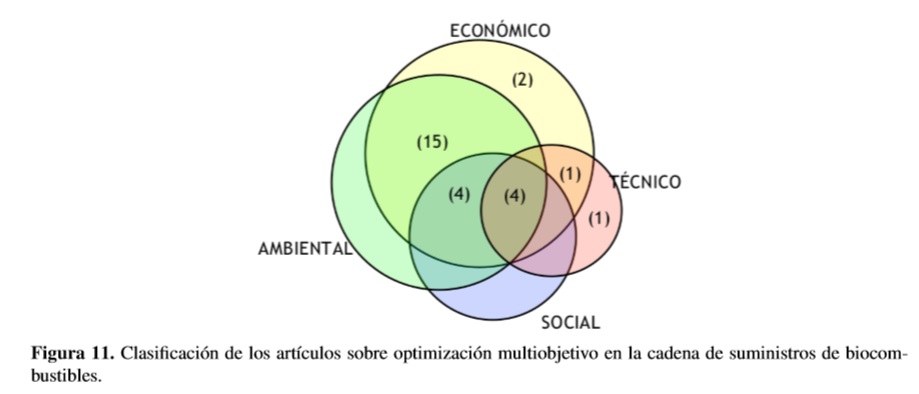
Los artículos presentan objetivos principalmente en cuatro ámbitos (o categorías): técnicos, ambientales, sociales y económicos (en esta última categoría se consideran también los objetivos financieros). En la Figura 11 se presenta cada aspecto como un círculo y el número en paréntesis corresponde al número de artículos que se encontraron en cada categoría o grupos de categorías.
La mayoría de artículos sobre optimización multiobjetivo encontrados en SCM de biocombustibles tienen objetivos en dos categorías que son la económica y la ambiental. Esta combinación de objetivos ocupa el primer lugar con un total de 15 artículos, representando un 55,6% del total de artículos. En segundo y tercer lugar se encuentran los artículos que abarcan los campos económico, ambiental y social (con 4 artículos, correspondiente al 14,8%) o los 4 campos simultáneamente (también con el 14,8%). Posteriormente se encuentran los 2 artículos con múltiples objetivos económicos (7,4%) y finalmente se encuentra un solo artículo con múltiples objetivos técnicos y otro con objetivos técnicos y económicos. Cada uno de estos últimos grupos representa un 3,7% sobre el total de artículos.
En cada uno de los cuatro campos se pueden considerar más de un objetivo, por ejemplo con 2 o más objetivos económico-financieros, como la minimización del costo y del riesgo financiero. El número de objetivos encontrados en los artículos se presentan en la Figura 12.
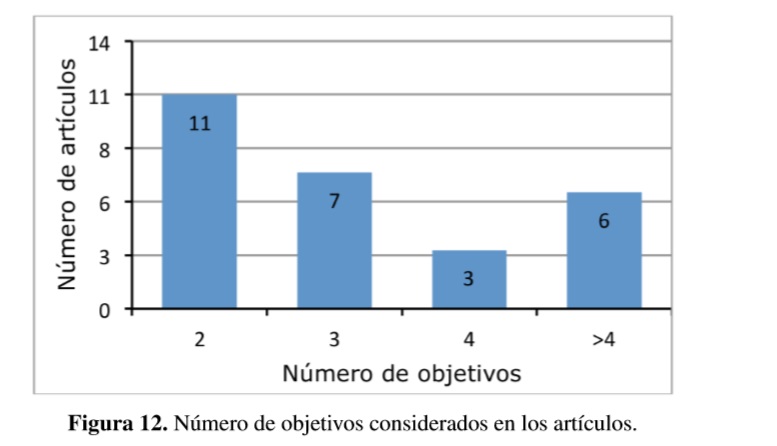
La mayoría de artículos son bi-objetivo (41%), seguido de los artículos con tres objetivos (26%). Los artículos con 3 objetivos representan el 11% del total y el porcentaje restante (22%) corresponde a artículos que manejan más de 4 objetivos.
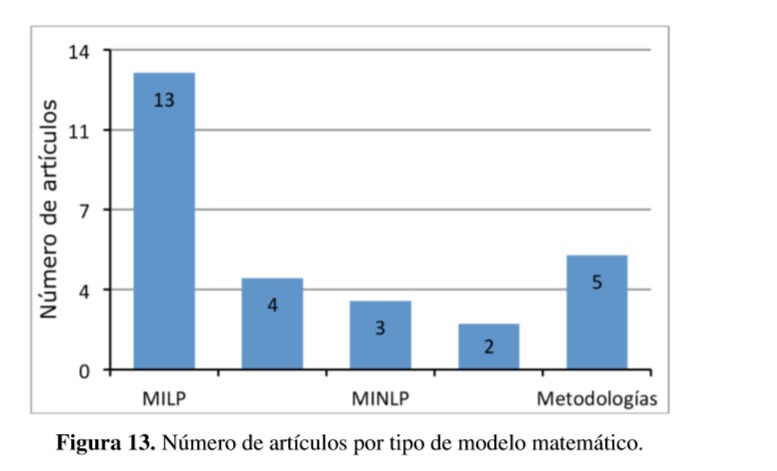
En cuanto a los modelos matemáticos utilizados en los artículos, 27 artículos de los 22 utilizan modelos de programación matemática, en los que se encuentran, principalmente, los modelos de programación lineal entera mixta (MILP), programación lineal entera mixta estocástica (SMILP), programación no lineal entera mixta (MINLP) y programación fraccional lineal entera mixta (MILFP). El número de artículos que utilizaron cada tipo de modelo se presenta en la Figura 13.
Los artículos que contemplan más de 4 objetivos no utilizan modelos de programación matemática, sino metodologías propias del análisis de decisión multi-criterio, como el método TOPSIS (técnica para orden de preferencia por similitud con solución ideal).
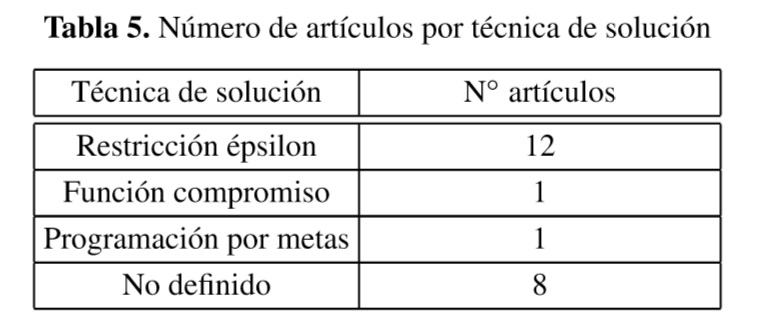
Por otro lado, las técnicas que se utilizaron para solucionar los 22 modelos de programación matemática, ya fuera hallando la frontera de Pareto o un solo punto de solución, son mostradas en la Tabla 5.
La técnica más utilizada es el método de restricción épsilon, con un total de 54,5% de los artículos, para solucionar modelos MILP, MINLP y MILFP. La función compromiso se aplicó para solucionar un modelo estocásticos SMILP y la programación por metas, para solucionar un modelo MINLP. Ocho artículos no definieron el método que utilizaron para encontrar la solución de los modelos.
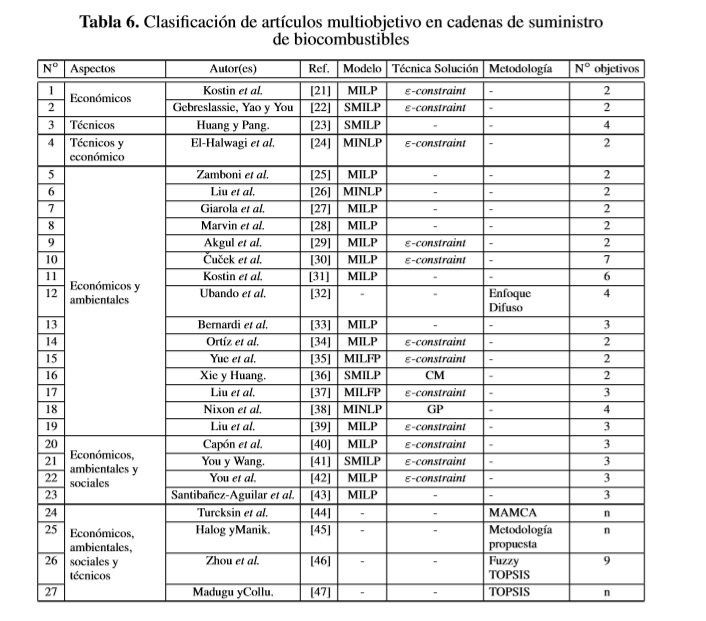
En la Tabla 6 se presentan los datos principales de los artículos revisados, agrupados por los campos, iniciando con los que tienen múltiples objetivos en un solo campo y terminando con los que tienen objetivos en los 4 campos.
MILP: programación lineal entera mixta; SMILP: programación lineal entera mixta estocástica; MINLP: programación no lineal entera mixta; MILFP: programación fraccional lineal entera mixta; CM:Función compromiso; GP: programación por metas.
A continuación se exponen los objetivos de cada modelo siguiendo el orden de agrupación de la Tabla 6.
5.1. Modelos con múltiples objetivos en un solo campo
Kostin et al. [21] plantean un modelo matemático para la cadena de bioetanol de caña de azúcar en la Argentina, donde se busca determinar un plan de ampliación de capacidad, de producción y de inventario considerando dos objetivos en la categoría económica y financiera: maximizar el valor presente neto (VPN) y mitigar riesgos financieros. Gebreslassie et al. [22] también proponen un modelo con dos objetivos en esta categoría: minimizar el costo anualizado y el riesgo financiero. En este caso, el modelo tiene un enfoque estocástico en dos etapas, donde son comparados los resultados de un modelo determinístico con los de un modelo estocástico. El modelo desarrollado busca determinar el diseño óptimo de la red, la selección de la tecnología, la inversión de capital, las operaciones de producción y las decisiones de gestión de la logística. La estructura del modelo propuesto y el algoritmo de solución se aplican en cuatro casos de cadenas de hidrocarburos en el estado de Illinois, en Estados Unidos.
Finalmente, Huang y Pang [23] presentan un modelo matemático para la producción de etanol a partir de residuos de biomasa en California. El modelo busca establecer la infraestructura de sistema de biocombustibles que sea eficaz y resistente contra riesgos potenciales a través de la integración de cuatro objetivos de la capacidad de resiliencia o recuperación: la robustez, la rapidez, la redundancia, y la inventiva.
5.2. Modelos matemáticos con objetivos económicos y técnico
El único artículo revisado en el grupo de modelos que incluyen objetivos económicos y técnicos es de El-Halwagi et al. [24], el cual pretende minimizar el costo de la cadena y a su vez el riesgo acumulado asociado a las etapas clave del ciclo de vida de una biorrefinería, incluyendo el almacenamiento, transporte de biomasa, conversión y almacenamiento de productos. El modelo es no lineal y tiene el propósito de establecer las relaciones entre el costo y los problemas de seguridad en la selección, ubicación y dimensionamiento de una biorrefinería.
5.3. Modelos matemáticos con objetivos económicos y ambientales
El grupo con más artículos es el de modelos con objetivos económicos y ambientales. Cuatro artículos fueron escritos por un mismo grupo de autores, que son Zamboni, Bernardi, Giarola, Bezzo y Ortiz, quienes trabajaron la cadena de bioetanol en el norte de Italia. Zamboni et al. [25] presentaron el primer modelo MILP para la localización de cultivos de biomasa, producción de etanol, asignación de capacidad, así como la optimización del sistema de transporte, buscando la optimización del desempeño económico y ambiental en términos de emisión de gases efecto invernadero (GHG).
Posteriormente, Giarola et al. [27] presentan un modelo MILP donde se optimiza el valor presente neto (VPN) y las emisiones de GHG, considerando en este caso dos materias primas, el grano y el rastrojo de maíz. El modelo permite determinar la mezcla de materia prima, el plan de capacidades y la selección de tecnología de conversión. Así mismo, el modelo considera variables de diseño de la cadena, como la localización de instalaciones, y se enfatiza en el análisis de las relaciones de entre los objetivos de costo y emisiones, así como su relación con las distintas tecnologías y materias primas disponibles.
En compa˜ nía de los autores anteriores, Bernardi [33] presenta un artículo en el cual propone un modelo matemático MILP similar al presentado por Giarola et al. [27]] La diferencia de este modelo es que contempla tres objetivos que son la sostenibilidad económica, la reducción de la huella de carbono y la huella hídrica. Este mismo año, Ortiz et al. [34] presentan también un modelo que complementa el de Giarola et al. [27]. En este caso se considera el valor económico de las emisiones globales de GHG, generado por la introducción del sistema de comercio de emisiones.
Liu et al. [26] en 2011 proponen una estructura genérica de un modelo de optimización bajo incertidumbre y la evaluación del ciclo de vida (LCA). Marvin et al. [28], el mismo año, exponen un modelo matemático MILP con los objetivos de minimizar el VPN y las emisiones de GHG. El modelo matemático tiene como propósito definir un plan de producción que permita cumplir la Norma de Combustibles Renovables (RFS) en Estados Unidos hasta el 2022. El Medio Oeste es elegido como la región de estudio, considerando residuos agrícolas y forestales como fuentes de biomasa.
En 2012, Akgul et al. [29] proponen un modelo para el diseño de la cadena (localización y tamaño de cultivos y plantas) y decisiones logísticas (tasas de cultivo y producción, flujos, medios de transporte) buscando minimizar el costo total diario y el impacto ambiental en términos de emisiones de GHG. El modelo se aplica al caso de producción de bioetanol a partir de biomasa lignocelulósica en Reino Unido. Kostin et al. [31], quienes ya habían presentado un modelo con objetivos económicos y financieros para el diseño de la cadena de bioetanol de caña en Argentina, presenta también un modelo matemático para el diseño de la misma cadena, pero esta vez considerando la optimización del valor presente neto y cinco objetivos ambientales. La medición de los aspectos ambientales evaluados se basa en métricas del análisis del ciclo de vida (LCA, por sus siglas en inglés).
Este mismo año, ˇCuˇcek et al. [30] presentan un modelo para el diseño de cadenas de suministro de biomasa para la conversión de biomasa en energía, buscando la maximización del desempeño económico y la minimización de las huellas ambientales y sociales. Dentro de los aspectos ambientales considerados se encuentran el consumo de energía, el consumo de agua (huella hídrica), las emisiones de CO2, la huella de tierra y la contaminación del agua. Como aspecto social se considera el impacto a la disponibilidad de alimento por el uso de cultivos agrícolas para la producción de energía.
En 2013, Ubando et al. [32] presentan un modelo difuso (fuzzy) que busca maximizar la ganancia manteniendo unos niveles aceptables de huellas de carbono, hídrica y de tierra, mientras Xie y Huang [36] exponen un modelo SMILP para evaluar el impacto económico y ambiental (en términos de emisión de GHG) al establecer una cadena de suministro de etanol celulósico a base de residuos biológicos (como el rastrojo de maíz y residuos forestales) en California como un estudio de caso. También en 2013, Yue et al. [35] proponen un modelo fraccional MILFP para la minimización del costo y la huella de carbono en el diseño sostenible de una cadena de suministro de biocombustible en Illinois, Estados Unidos.
En 2014, Liu et al. [37] [39] presentan dos artículos donde se consideran tres objetivos: el objetivo económico mide la ganancia anual total, el objetivo ambiental medido por emisiones de GHG y el objetivo energético medido en megajulios (MJ) promedio de energía fósil por MJ de biocombustible. Los modelos buscan determinar la localización de las plantas y mercados, la capacidad, tecnología, tasas de producción de materias primas, productos y flujos de éstos en la cadena de biocombustibles en China. El primer artículo es un modelo MILP aplicado a la producción de bioetanol y biodiésel, mientras el segundo es un modelo MILFP que incluye también la producción de biometanol.
Finalmente, el último artículo en este grupo es el de Nixon et al. [38], en el cual se consideran tres metas económicas: costo de capital, la recuperación de la inversión y los costos de producción de bio-aceite y electricidad; como meta ambiental se evalúa la utilización de materia prima (quema de materia prima). El modelo busca determinar la ubicación, tamaño y número de plantas, aplicaciones de energía y cantidades de materias primas procesadas. Es aplicado a pequeña y gran escala en Punjab, India, donde hay una cantidad abundante de residuos de paja. A continuación se describen los modelos que contemplan objetivos económicos, ambientales y sociales.
5.4. Modelos con objetivos económicos, ambientales y sociales
El primer artículo publicado que considera el aspecto social en la cadena de suministro de biocombustibles es el de Capón et al. [40], del año 2008. En este artículo se presenta la estructura matemática de un modelo MILP que busca simultáneamente la minimización de los costos, los impactos ambientales y sociales. El modelo diseña una cadena de suministro que satisfaga la demanda de biodiésel en España, y la frontera de Pareto se obtiene mediante la aplicación de la técnica ε-constraint.
En 2011, You y Wang [41] proponen un modelo matemático SMILP con el objetivo económico de minimizar el costo neto anualizado, el objetivo ambiental de minimizar las emisiones de GHG y adicionalmente un objetivo social de maximizar el número de puestos de trabajo locales acumulados. El modelo se aplica para el diseño, selección de tecnología y decisiones logísticas en la cadena de biocombustible en el estado de Illinois, Estados Unidos, considerando tres tipos de biomasa: residuos de cultivos, cultivos energéticos y residuos de madera. Para la solución del modelo se aplica un algoritmo de descomposición, basado en las técnicas de aproximación de promedio muestral (sample average approximation) y multi-corte en forma de L (Multi-cut L-shaped), y posteriormente el método ε-constraint. En 2012, You et al. [42] vuelven a proponer un modelo aplicado a la misma cadena de biocombustibles, pero en este caso el modelo es MILP (sin considerar demandas inciertas) y es aplicado a dos casos de estudio en la misma zona.
El último artículo en esta categoría es el de Santibañez-Aguilar et al. [43] en el cual presentan un modelo MILP que considera simultáneamente la maximización de las ganancias, la minimización del impacto ambiental, así como la maximización del beneficio del impacto social a través de la generación de empleo en las zonas rurales. El modelo se aplica a un caso de estudio para la planificación de la producción de una biorrefinería en México.
5.5. Modelos con objetivos en los cuatro campos
El último grupo de artículos consideran más de cuatro objetivos, dentro de los cuales se encuentran objetivos económicos, ambientales, sociales y técnicos. Sin embargo, a diferencia de los demás artículos, éstos no presentan modelos de programación matemática, sino metodologías y otras técnicas propias de MCDM. En el caso de Turcksin et al. [44], utilizan la metodología MAMCA (multi-actor multi-criteria analysis) para la evaluación de varias alternativas que puedan contribuir a lograr un 10% de combustibles renovables en el transporte para 2020, como objetivo planteado por la Dirección de Energía Renovable de Bélgica.
El mismo año, Halog y Manik [45] utilizan una metodología integral con un enfoque holístico en evaluación de la sostenibilidad y formulación de políticas para las cadenas de suministro de biocombustibles. La metodología integra diferentes técnicas como el marco de análisis del ciclo de vida (LCA), el análisis de las partes interesadas con el apoyo de análisis de decisión multi-criterio (MCDA), dinámica de sistemas, análisis de la envolvente de datos (DEA) y la teoría de redes de sostenibilidad (SNT).
Posteriormente, Zhou et al. [46] presentan un artículo donde desarrollan una metodología de toma de decisiones para la planificación de las ubicaciones de las biorrefinerías en un entorno difuso basado en el método TOPSIS. La metodología abarca 9 criterios y 32 subcriterios, donde incluye aspectos ambientales, sociales, técnicos y económicos. Finalmente, en 2014, Madugu y Collu [47] desarrollan un modelo de análisis donde se utiliza la técnica TOPSIS para identificar la alternativa más aceptable entre las múltiples rutas y decisiones logísticas relacionadas con toda la cadena de producción de biocombustibles derivados de algas.
5.6. Análisis
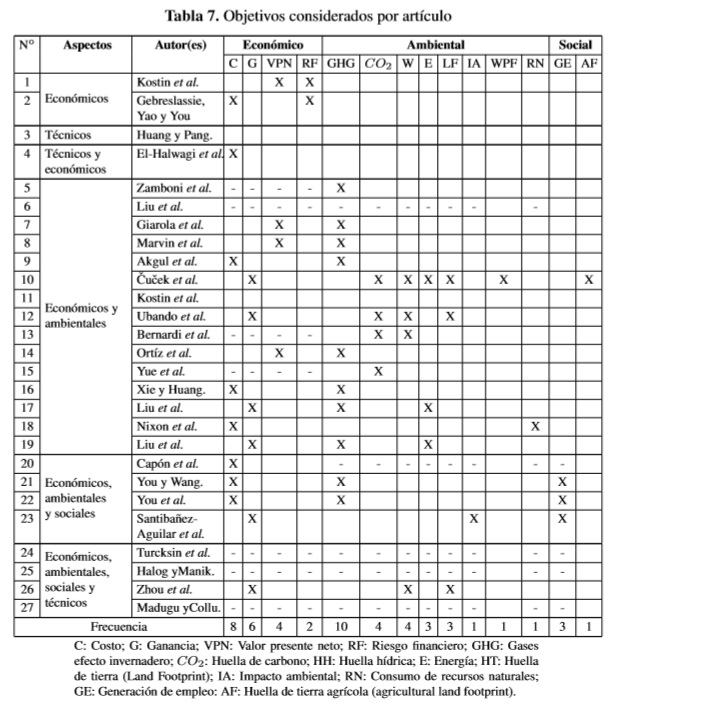
La Tabla 7 presenta el resumen de los objetivos considerados en cada artículo. Las equis representan los objetivos considerados en cada artículo y los guiones representan que no se especificó el objetivo considerado. Por ejemplo, en el modelo de Zamboni et al. [25] se considera un objetivo económico, pero no se especifica si es costo, ganancia, valor presente neto o riesgo financiero.
La revisión de los artículos muestra que el objetivo económico más frecuente en la optimización de cadenas de suministro es la minimización del costo, principalmente en términos de costo anualizado. Por otra parte, el objetivo ambiental más utilizado es la minimización de emisiones de GHG, cuyo cálculo se basa en la metodología LCA, y en segunda instancia la emisión de CO2 (la cual se encuentra incluida en los GHG). El objetivo social más utilizado es la generación de empleo. Los objetivos técnicos no se incluyen dado que son muy variados y dependen de la cadena de suministro en particular considerada.
6. Discusión
En la actualidad, los biocombustibles son considerados sustitutos parciales del combustible fósil y tienen una creciente proyección de consumo y producción a mediano y largo plazo [1]. Esta creciente proyección se debe principalmente a las ventajas ambientales que podrían presentar los biocombustibles en comparación al combustible fósil [48] [2]. Sin embargo, a pesar de sus beneficios, también existen preocupaciones por los impactos ambientales y sociales asociados que pueden causar su producción y distribución [1].
Los biocombustibles se producen a partir de recursos renovables y representan una nueva fuente de ingresos para la agricultura [3], tienen un balance energético positivo y generan menores emisiones GHG que el combustible fósil [1] [4]. En contraposición, la producción de biocombustibles podría llevar a un aumento de la deforestación, pérdida de la biodiversidad, contaminación del agua, incremento del uso de agroquímicos, problemas sobre la seguridad alimentaria, y un empeoramiento de las condiciones laborales, migración, entre otras preocupaciones [1] [5].
La inclusión de los aspectos ambientales y sociales en SCM ha venido ganando mayor relevancia, principalmente en la última década, al aparecer el enfoque GSCM. Por su parte, la optimización con múltiples objetivos ha servido como marco para operacionalizar la inclusión de objetivos ambientales y sociales en GSCM. Esta tendencia no es ajena a la cadena de suministro de biocombustibles, considerando que más del 90% de artículos con múltiples objetivos se han escrito en los últimos 4 años.
Sin embargo, a pesar de los múltiples aspectos ambientales y sociales asociados a la cadena de suministro de biocombustibles, los modelos de optimización multiobjetivo incluyen en su mayoría uno o dos objetivos ambientales (principalmente emisiones GHG y emisiones CO2) y a lo sumo un objetivo social (empleos generados) sin que éstos sean necesariamente los más significativos en este tipo de cadenas. Un mayor número de objetivos han sido considerados con otras técnicas de MCDM, aplicadas a la selección de estrategias entre un número limitado de opciones.
Según la Organización de las Naciones Unidas para la Alimentación (FAO, por sus siglas en inglés) [49], uno de los aspectos sociales más importantes en las cadenas de biocombustibles es el impacto que puede ocasionar en la seguridad alimentaria. En cuanto al aspecto ambiental, un estudio realizado por el Consorcio CUE [50], para el Banco Interamericano de Desarrollo (BID) y el Ministerio Minas y Energía en Colombia, resalta la importancia de considerar el impacto asociado al cambio directo e indirecto del uso del suelo. Estos dos aspectos fueron contemplados solamente en el modelo presentado por ˇCuˇcek et al. [30]. Adicionalmente, otros aspectos importantes como migración y pérdida de biodiversidad, no han sido considerados en los modelos de optimización multiobjetivo encontrados en la revisión del estado del arte, posiblemente debido a su dificultad para cuantificarlos. Por lo tanto, las investigaciones futuras deberían orientarse a definir la forma de cuantificar e incluir estos impactos en los modelos matemáticos, de manera que se facilite su consideración en la toma de decisiones para las cadenas de suministro de biocombustibles.
A pesar de que en la actualidad existen algoritmos como los MOEA, que permiten hallar el conjunto de soluciones óptimas de manera más eficiente, solamente un artículo utilizó un algoritmo de aproximación para generar la frontera de Pareto. En su lugar, la técnica utilizada con mayor frecuencia para hallar el conjunto de soluciones óptimas es el método de la restricción épsilon (ε-constraint). La utilización de técnicas de aproximación (como MOGA, NSGA II, SPEA II) en trabajos futuros permitiría encontrar secciones más grandes y completas de las fronteras de Pareto, así como la inclusión de un mayor número de objetivos y desarrollo de modelos más grandes y complejos para SCM de biocombustibles.
7. Conclusiones
En la última década, la optimización multiobjetivo ha ganado relevancia en SCM dado que permite integrar objetivos sociales, ambientales y económicos en sus decisiones. En este artículo se presentó una revisión de la literatura sobre los tipos de modelos matemáticos, técnicas de solución y su aplicación en cadenas de suministro de biocombustibles. Adicionalmente se realizó un análisis de los tipos de objetivos frecuentemente utilizados en la optimización multiobjetivo de este tipo de cadenas.
Hasta el momento, todos los artículos con modelos de optimización multiobjetivo en cadenas de suministro de biocombustibles han tenido una inclusión parcial de los aspectos ambientales y sociales. Los aspectos económicos, ambientales y sociales más utilizados en el diseño y gestión de cadenas de suministro son la minimización del costo anualizado, la minimización de emisiones de GHG y la generación de empleo. Existe la necesidad de evaluar las técnicas existentes o desarrollar nuevas técnicas que permitan cuantificar los impactos ambientales y sociales más significativos en la cadena de suministro de biocombustibles aún no considerados, así como el desarrollo de modelos matemáticos que permitan optimizarlos.
La inclusión de varios objetivos en las cadenas de suministro de biocombustibles se hace en su mayoría por medio de modelos matemáticos de programación lineal entera mixta (MILP). Hasta el momento, las técnicas más utilizadas para solucionar los modelos matemáticos son las básicas como el ε-constraint. Cuando se considera un mayor número de objetivos, se utilizan diferentes metodologías pertenecientes a la teoría de decisiones multi-criterio (MCDM) en lugar de modelos de programación matemática. La utilización de técnicas de aproximación más recientes permitirá obtener fronteras de solución de manera más eficiente, que a su vez faciliten el análisis de resultados en modelos con un mayor número de objetivos.
Referencias
-
A. Dufey, Producción y comercio de agrocombustibles y desarrollo sustentable: los grandes temas. Londres, Instituto Internacional para el Medio Ambiente y Desarrollo, 2006.
-
A. Demirbas, “Progress and recent trends in biodiesel fuels,” Energy Conversion and Management, 50, pp. 14–34, 2009.
-
NACEPT, Strategic framework for biofuels efforts. Estados Unidos, National Advisory Council for Environmental Policy and Technology, 2007.
-
A. Ajanovic and R. Haas, “Economic challenges for the future relevance of biofuels in transport in EU countries,” Energy, 35, pp. 3340 3348, 2010.
-
J. P. Arístegui, “Los agrocombustibles desde la perspectiva del comercio internacional y del derecho de la organización mundial del comercio,” Revista de Derecho (Austral), 22 (1), pp. 113-134, 2009.
-
S. Mathur and A. Kenyon, “Creating value: shaping tomorrow’s business,” Butterworth-Heinemann, 1997.
-
G. Svensson, “Gestión de la cadena de suministro frente a gestión de la cadena sostenible,” EsicMarket, 129, pp. 239-258, 2007.
-
A. Nikolopoulou and M. G. Ierapetritou, “Optimal design of sustainable chemical processes and supply chains: A review,” Computers and Chemical Engineering, 44, pp. 94 – 103, 2012.
-
C. Cambero and T. Sowlati, “Assessment and optimization of forest biomass supply chains from economic, social and environmental perspectives – A review of literature,” Renewable and Sustainable Energy Reviews, pp. 62–73, 2014.
-
S. Liu, M. Leat and M. H. Smith, “State-of-the-art sustainability analysis methodologies for efficient decision support in green production operations,” International Journal of Sustainable Engineering, pp. 236-250, 2011.
-
M. Ehrgott and M. M. Wiecek, “Multiobjective programming,” en Multiple criteria decision analysis: state of the art surveys, Estados Unidos, Springer, 2005, pp. 667-722.
-
R. Marler and J. Arora, “Survey of multi-objective optimization methods for engineering,” Struct Multidisc Optim, 26. pp. 369–395, 2004.
-
J. Lopez, Optimización multiobjetivo: aplicaciones a problemas del mundo real. Buenos Aires, Argentina, Universidad Nacional de la Plata, 2013.
-
O. L. De Weck, “Multiobjective optimization: History and promise,” en Third China-Japan-Korea Joint Symposium on Optimization of Structural and Mechanical Systems, Kanazawa, Japan, 2004.
-
T. Marler and J. S. Arora, “The weighted sum method for multi-objective optimization: new insights,” Struct. Multidisc. Optim., 41, pp. 853–862, 2010.
-
H. O. Alanazi, A. H. Abdullah and M. Larbani, “Dynamic weighted sum multi-criteria decision making: Mathematical Model,” International Journal of Mathematics and Statistics Invention, pp. 16-18, 2013.
-
M. Ehrgott and S. Ruzika, “Improved ε-constraint Method for Multiobjective Programming,” Journal Optim. Theory Appl., 138, pp. 375–396, 2008.
-
C. A. Coello, “Networking and emerging optimization” septiembre 2002. [Online]. Available: http://neo.lcc.uma.es/pdf-charlas/MOEA.pdf.
-
Y. J. Túpac, “Universidad Católica San Pablo,” 23 de noviembre 2011. [Online]. Available: http://www.ucsp.edu.pe/∼ytupac/speaks/2011/UNJBG CIIS MOGA.pdf.
-
A. Messac and C. A. Mattson, “Generating well-distributed sets of Pareto points for engineering using physical programming,” Optimization and Engineering, 3, pp. 431–450, 2002.
-
A. Kostin, G. Guillén-Gosálbez, F. Mele, M. Bagajewicz y L. Jiménez, “Design and planning of infrastructures for bioethanol and sugar production under demand uncertainty,” Chemical Engineering Research and Design, 90, pp. 359–376, 2012.
-
B. Gebreslassie, Y. Yao y F. You, “Design under uncertainty of hydrocarbon biorefinery supply chains: multiobjective stochastic programming models, decomposition algorithm, and a comparison between CVaR and downside risk,” AIChE Journal, 58 (7), pp. 2155-2179, 2012.
-
Y. Huang y W. Pang, “Optimization of resilient biofuel infrastructure systems under natural hazards,” J. Energy Eng., 140 (2), 2014.
-
El-Halwagi, Rosas y Ponce-Ortega, “Multiobjective optimization of biorefineries with economic and safety objectives,” AIChE Journal, 59 (7), pp. 2427-2434, 2013.
-
A. Zamboni, N. Shah y F. Bezzo, “Spatially explicit static model for the strategic design of future bioethanol production systems” Energy Fuels, 23 (10), pp. 5134–5143, 2009.
-
P. Liu, M. Georgiadis y E. Pistikopoulos, “Advances in energy systems engineering” Ind. Eng. Chem. Res., 50 (9), pp. 4915–4926, 2011.
-
S. Giarola, A. Zamboni y F. Bezzo, “Spatially explicit multi-objective optimisation for design and planning of hybrid first and second generation biorefineries,” Computers and Chemical Engineering, 35, pp. 1782– 1797, 2011.
-
W. Marvin, L. Schmidt, S. Benjaafar y P. Daoutidis, “Economic and environmental optimization of the biomassto-biofuel supply chain in the midwest,” 11AIChE Annual Meeting, Conference Proceedings, 2011.
-
O. Akgul, N. Shah y L. Papageorgiou, “An optimisation framework for a hybrid first/second generation bioethanol supply chain,” Computers and Chemical Engineering, 42, pp. 101– 114, 2012.
-
ˇCuˇcek, Sabev, Jaromír y Kravanja, “Total footprints-based multi-criteria optimisation of regional biomass energy supply chains,” Energy, 44 (1), pp. 135–145, 2012.
-
Kostin, Guillén-Gosálbez, Mele y Jiménez, “Identifying key life cycle assessment metrics in the multiobjective design of bioethanol,” I&ECR, 51(14), pp. 5282-5291, 2012.
-
A. Ubando, A. Culaba, K. Aviso, D. Ng y R. Tan, “Fuzzy multi-objective approach for designing of biomass supply chain for polygeneration with triple footprint constraints,” ASME 2013 International Mechanical Engineering Congress and Exposition, 12, 2013.
-
A. Bernardi, S. Giarola y F. Bezzo, “Spatially explicit multiobjective optimization for the strategic design of first and second generation biorefineries Including carbon and water Footprints,” Ind. Eng. Chem. Res., 52 (22), pp. 7170–7180, 2013.
-
R. Ortiz, S. Giarola y F. Bezzo, “Optimal design of ethanol supply chains considering carbon trading effects and multiple technologies for side-product exploitation,” Environmental Technology, 34, pp. 2189–2199, 2013.
-
D. Yue, M. Kim y F. You, “Design of sustainable product systems and supply chains with life cycle optimization based on functional unit: general modeling framework, mixed-integer nonlinear programming algorithms and case study on hydrocarbon biofuels,” ACS Sustainable Chem. Eng., 1 (8), pp. 1003–1014, 2013.
-
F. Xie y Y. Huang, “Sustainable biofuel supply chain planning and management under uncertainty,” Journal of the Transportation Research Board, pp. 19-27, 2013.
-
Z. Liu, T. Qiu y B. Chen, “A study of the LCA based biofuel supply chain multi-objective optimization model with multi-conversion paths in China,” Applied Energy, 126, pp. 221–234, 2014b.
-
J. Nixon, P. Dey, P. Davies, S. Sagi y R. Berry, “Supply chain optimisation of pyrolysis plant deployment using goal programming,” Energy, 68, pp. 262-271, 2014.
-
Z. Liu, T. Qiu y B. Chen, “A LCA Based Biofuel Supply Chain Analysis Framework,” Chinese Journal of Chemical Engineering, 22 (6), pp. 669—681, 2014a.
-
E. Capón, G. Guillén-Gosálbez, L. Jiménez-Esteller y A. Espuña, “Designing the optimal supply chain for biodiesel production in Spain,” AIChE 100 Annual Meeting, Conference Proceedings, 2008.
-
F. You y B. Wang, “Optimal design and operations of cellulosic biofuel supply chains under uncertainty,” 11AIChE Annual Meeting, Conference Proceedings. 2011.
-
F. You, L. Tao, D. Graziano y S. Snyder, “Optimal design of sustainable cellulosic biofuel supply chains: multiobjective optimization coupled with life cycle assessment and input–output analysis,” AIChE Journal, 58 (4), pp. 1157-1180, 2012.
-
J. Santibañez-Aguilar, J. González-Campos, J. Ponce-Ortega, M. Serna-González y M. El-Halwagi, “Optimal multi-objective planning of distributed biorefinery systems involving economic, environmental and social aspects,” Computer Aided Chemical Engineering, 31, pp. 470–474, 2012.
-
L. Turcksin, C. Macharis, K. Lebeau, L. Gorissen y P. L. , “A multi-actor multi-criteria framework to assess the stakeholder support for different biofuel options: The case of Belgium,” Energy Policy, 39, pp. 200–214, 2011.
-
A. Halog y Y. Manik, “Advancing integrated systems modelling framework for life cycle sustainability assessment,” Sustainability, 3, pp. 469-499, 2011.
-
S. Zhou, Y. Zhang y X. Bao, “Methodology of location selection for biofuel refinery based on fuzzy TOPSIS,” International Conference on Automation and Logistics Zhengzhou, China, 2012.
-
F. Madugu y M. Collu, “Techno-economic modelling analysis of microalgae cultivation for biofuels and coproducts,” WIT Transactions on Ecology and the Environment, 190, pp. 1091-1102, 2014.
-
M. Barón, I. Huertas and J. Orjuela, “Gestión de la cadena de abastecimiento del biodiésel: una revisión de la literatura,” Ingeniería, 18 (1), pp. 84-117, 2013.
-
FAO, The state of food security in the world 2008. High food prices and food security: Threats and opportunities, Roma: FAO, 2008.
-
C. CUE, Evaluación del ciclo de vida de la cadena de producción de biocombustibles en Colombia, Medellín, Colombia, Ministerio de Minas y Energía, 2012.
Johan Alexander Aranda Pinilla
Nació en Bogotá, Colombia. Es Ingeniero Industrial de la Universidad Distrital Francisco José de Caldas, de Bogotá, Colombia. Obtuvo su título de Maestría en Ingeniería Industrial en la Universidad Distrital Francisco José de Caldas, en Bogotá, Colombia. Actualmente se desempe˜na como profesor en las áreas de Logística e Investigación de Operaciones, en la Universidad Católica de Colombia y de la Universidad Distrital Francisco José de Caldas, Integrante del Grupo de investigación GICALyT.
e-mail: jaaranda@ucatolica.edu.co
Javier Arturo Orjuela Castro
Nació en Bogotá, Colombia. Es Ingeniero de Alimentos, Ingeniero Industrial, Especialista en Ingeniería de producción de la Universidad Distrital Francisco José de Caldas, Bogotá, Colombia. Obtuvo su título de Maestría en Investigación y Estadística en la Universidad Tecnológica de Pereira, Colombia. Actualmente estudia el Doctorado en Ingeniería, Industrial y Organizaciones en la Universidad Nacional de Colombia, Se desempe˜na como profesor e investigador en las áreas de Logística en Distrital Francisco José de Caldas, líder del Grupo de investigación GICALyT.
e-mail: jorjuela@udistrital.edu.co

Este trabajo está autorizado por una Licencia Attribution-NonCommercial-NoDerivs CC BY-NC-ND.
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.

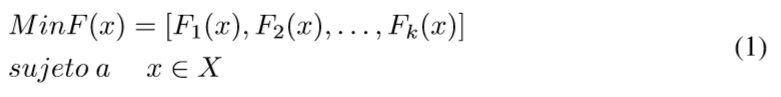
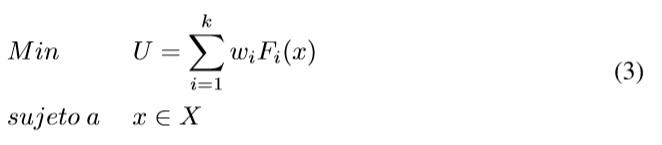
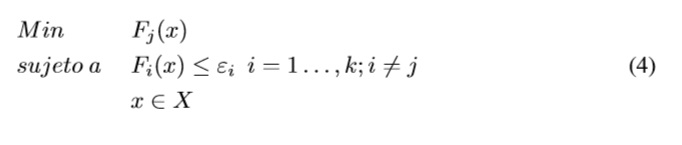
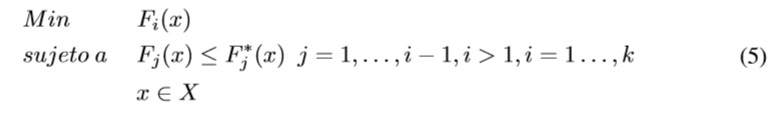



2.jpg)










