Ciencia Investigación y desarrollo

Ingeniería, 2000-00-00 vol:5 nro:1 pág:14-19

Regulación fina de campo magnético por medio de resonancia magnética nuclear pulsada.

Fine Regulation over Magnetic Field by Pulsed Nuclear Magnetic Resonance

Héctor Fernando Cancino De Greiff

Ingeniero Electrónico, Universidad Distrital. Magister en Ingeniería Electrónica, Universidad Central de Venezuela, Candidato a Doctor en Ciencias Técnicas, U. del Las Villas. (Cuba), Profesor Facultad de Ingeniería, Universidad Distrital. Jefe Laboratorio de Electrónica, labelec@udistrital.edu.co

Resumen

En el presente trabajo se desarrolla la modificación a un sistema de control de campo magnético que emplea como elemento sensor una "Punta de Hall" a un nuevo sistema de control discreto, mediante la utilización de un mini-espectrómetro de Resonancia Magnética Nuclear Pulsado (RMN). Considerando que la constante giromagnética de los núcleos resonantes es única para cada elemento químico, manteniendo la frecuencia de excitación estable el campo generado debe mantenerse sin variación. Si el campo de trabajo está cerca de la resonancia de los núcleos de fluor, se genera un batido de frecuencias, que al ser detectadas presenta una forma de onda sinusoidal amortiguada. Empleando un procesamiento digital a la señal detectada, se puede lograr la estabilidad deseada del sistema, controlando el período de esta señal y comparándolo con una medida prefijada para obtener una nueva señal de control que permitirá el comando de la "planta". El sistema retroalimentado presenta una respuesta subamortiguada a estímulos del tipo paso, con una altura de pico razonable que permite la estabilización de campo dentro de un rango de linealidad aceptable.

Palabras claves:
Constante giromagnética, respuesta al escalón, mini espectrómetro RMN, Procesamiento señal RMN.

Abstract

This work is about the magnetic field control system modification that uses a Hall Probe as sensor element to convert it in a new discrete control system through using an NMR spectrometer. Considering that the gyromagnetic constant of resonance nucleus is unique for each chemical element, maintaining stable the excite frequency the obtained field should be supplied without any variation. Employing digital signal processing on detected signal, it is possible to obtain the required stability of the system, controlling the period of this signal and comparing it with a fixed measurement, we get a new control signal that permits the command of the plant. The feedback system presents an damped output to step excitation with reasonable peak that permits stabilization into an acceptable linear range.

KeyWords:
gyromagnetic constant, step excitation, spectrometer, signal processing.

1.INTRODUCCIÓN

Se desea estabilizar el campo magnético generado por un electroimán, capaz de producir un campo máximo de 25 Kgauss, empleando las técnicas de "Resonancia Magnética Nuclear" de Pulsos "RMNP". Para tal efecto, se dispone de un electroimán cuya corriente de alimentación es regulada mediante un servomecanismo que utiliza como elemento sensor un dispositivo basado en el efecto Hall en semiconductores.

La estabilidad obtenida con esta "Punta de Hall" no es satisfactoria para los fines deseados, debido entre otras razones, a la excesiva dependencia del elemento sensor con la temperatura.

El objetivo de este trabajo es la modificación del sistema de regulación mediante el empleo de un mini-espectrómetro de "Spin-Echo" que permite sensar con mayor precisión las variaciones de campo magnético, teniendo encuenta que:

y = w/H (1)

Donde: y= Constante giromagnética del elemento.

w= Frecuencia angular del campo de RF aplicado

H = Intensidad de Campo Externo.

Dado que y es fija, w se mantiene constante, H debe observarse estable. El procesamiento digital de la señal obtenida en el espectrómetro para una muestra patrón colocada en el campo a sensar, dará la información necesaria al sistema de regulación para el ajuste del flujo magnético al valor deseado. [1]

Para lograr la optimización de la respuesta del nuevo sistema, es necesario un estudio detallado del comportamiento del sistema de partida mediante la medición de la salida (campo magnético) teniendo en la entrada un escalón.

Los procedimientos de cálculo posteriores mostrarán un modelo matemático aproximado de la planta, en lazo abierto. Con este esquema se trabajará para determinar un nuevo sistema de control y su adecuada "controlabilidad".

2. BREVE DESCRIPCIÓN DEL SISTEMA DE PARTIDA

La figura 1 muestra un diagrama de bloques del sistema de regulación básico con punta de Hall como sensor de campo magnético.

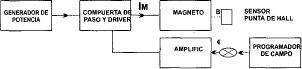
Para la generación del campo magnético se dispone de un electroimán, con campo máximo de 25 Kgauss. La corriente de alimentación es suplida por una fuente capaz de generar hasta 120 amperios.

Dicha corriente es regulada mediante un sistema de control, donde el elemento sensor de campo magnético se basa en el efecto Hall producido por un semiconductor.

La "Punta de Hall" y los circuitos asociados a ella generan una señal proporcional al campo producido por el imán. Esta señal es comparada con una señal referencia que previamente ha sido programada al valor deseado de campo.

El error establecido por el producto de dicha comparación e es amplificado y debidamente compensado a fin de comandar al Driver y la compuerta de Paso. Esta compuerta controla la corriente que alimenta al Magneto.

3. DETERMINACIÓN INICIAL DE UN MODELO DE CONTROL.

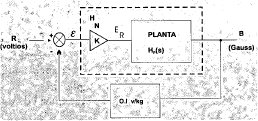
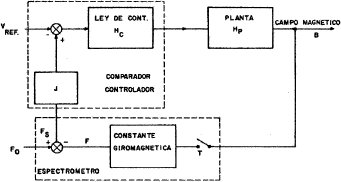
La Figura 2. proporciona un esquema para establecer la función de transferencia en lazo cerrado del sistema de control que emplea el sensor "punta de Hall".

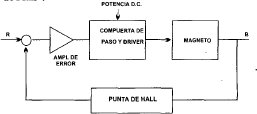
Se desea obtener la relación entre la entrada R y la salida B para encontrar la función de transferencia del sistema.

Para encontrar H(s) se efectúa una identificación del sistema mediante el estudio de la respuesta al escalón. Si se toma la entrada R como un escalar de magnitud K, la transformada de Laplace es:

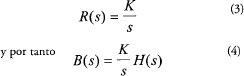
Midiendo la respuesta del electroimán ya descrito, se obtuvo la señal indicada en la figura 3.

Empleando por tanto, una excitación escalón de altura conveniente, se puede establecer el transitorio que se observa en la salida (campo B en gauss). En consecuencia, midiendo la respuesta a un escalón B(s), fácilmente podría determinarse la función H(s) por la ecuación (4).

Modelando éste comportamiento como un sistema de control de 2do. orden [3]descrito en términos de: Q : la razón de amortiguamiento = 0.48. w_n: la frecuencia de oscilación con amortiguación reducida = 19,49 rad/seg.

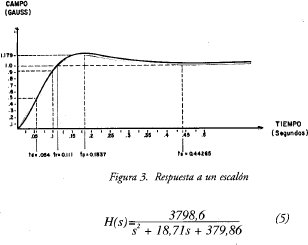
Cuyos polos son: s = -9,3552 ± j 17,098. Se observa que dichos polos se encuentran en el lado izquierdo del plano complejo, confirmando la condición de estabilidad.

4. CALCULO DE LA FUNCIÓN DE TRANSFERENCIA EN LAZO ABIERTO

Considerando el esquema de control (Figura 4) deducido de la arquitectura misma del sistema de l regulación de campo de partida, se puede establecer la función de transferencia en laso abierto que en r adelante se considerará como "la planta".

La ecuación (8) corresponde al modelo de la planta que tiene validez para variaciones de campo alrededor del punto de trabajo. [3]

5. INCONVENIENCIAS DEL SISTEMA DE PARTIDA

A pesar de que la estabilidad para el equipo con regulación por efecto Hall es del orden de 1 ppm, esa especificación sólo se cumple en condiciones muy estables de temperatura y humedad del medio ambiente. En la práctica se observan desviaciones del orden de algunas decenas de gauss, para tiempos de funcionamiento relativamente largos (1 hora o más). El origen de dicho corrimiento puede tener muchas causas, entre las cuales es de destacar la excesiva dependencia del sensor de Hall con la temperatura.

6. PROYECTO DE MODIFICACIÓN

La modificación al Sistema se indica en la figura. 5. Se observa que el lazo de realimentación ahora ha cambiado por un mini-espectrómetro de RMN, un procesador y un comparador que suministra la señal de control que aquí se denomina señal RMN.

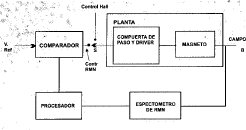
Es de notar que el interruptor S permite conmutar los 2 sistemas, es decir, que en un principio puede usarse el sistema controlado por la punta de Hall hasta llevar el equipo al punto de trabajo determinado y allí conmutarlo al sistema de control por la señal de RMN. Esta función puede desarrollarse en forma automática activando el interruptor una vez obtenida la señal de RMN.

7. MINIESPECTRÓMETRO COMO SENSOR DE CAMPO MAGNÉTICO

Un mini-espectrómetro de RMN permite sensar pequeñas variaciones de campo magnético. La figura 6. ilustra un diagrama de bloques de dicho espectrómetro [2], [6].

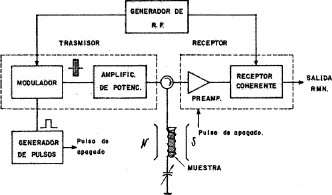
Un generador de pulsos proporciona un tren de pulsos de ancho y periodo variables. El ancho se selecciona según la potencia de transmisor disponible y el tipo de muestra a utilizar, mientras que el periodo se determina optimizando el comportamiento de la regulación en el sistema modificado. El generador de pulsos también suple un tren de pulsos con un periodo igual al anterior pero con ancho mayor para apagar el receptor en caso de que el transmisor esté operando, con el fin de evitar la saturación del receptor cuando aparece el pulso de RF

El generador de RF es el corazón del espectrómetro y genera las frecuencias de trabajo de 90, 100 y 10 Mhz a partir de una frecuencia muy estable controlada por un cristal de 10 Mhz. La precisión del equipo está basada en la estabilidad de este generador, por tanto, hay la posibilidad de introducir una frecuencia externa de 10 Mhz.

La salida del modulador es amplificada para obtener una potencia de salida de 25W e inyectada través de un circulador a una punta de prueba construida por un circuito resonante serie RLC. La muestra patrón (Acido trifluoruroacético con impurezas paramagnéticas de sulfato de cobre y fluoruro de amonio), está localizada dentro de la bobina que a su vez recibe la señal de RMN modulada sobre la frecuencia de precesión de los espines moleculares.

La señal de RMN es preamplificada y detectada mediante un receptor que emplea una frecuencia intermedia de 10 Mhz y un detector sincrónico en la misma frecuencia. Cabe anotar que éste receptor tiene la posibilidad de ser apagado durante la transmisión del pulso modulado, a fin de evitar la saturación del preamplificador.

8. PROCESAMIENTO DE LA SEÑAL DE RMN.

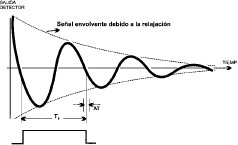
Los núcleos resonantes del ácido trifluoruroacético, que están dentro de la punta de prueba del espectrómetro tienen una frecuencia de precesión diferente a la frecuencia de referencia que emplea el detector sincrónico. Este batido una vez filtrado a través de un amplificador pasabajos, permite obtener una señal que servirá de control y que se muestra en la figura 7.

La frecuencia de la señal detectada debe mantenerse constante en 25.000 Hz a fin de obtener un campo magnético de salida estabilizado. [5]

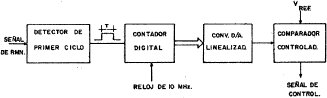
Para medir el periodo de la señal RMN detectada se emplea el montaje con el equipo que se indica en la figura 8.

Con el circuito detector de 1 er ciclo de la señal RMN detectada se obtiene un pulso de ancho T = 1 /fs, siendo fs la frecuencia de dicha señal. Con esta ventana así generada, se abre una compuerta que permite el paso a los pulsos de un reloj de 10 Mhz. La cantidad de pulsos resultantes es registrada en un contador digital en forma decádica. La información digital obtenida es transformada a la forma analógica mediante un conversor D/A.

La señal de salida del conversor es linealizada para lograr una señal que sea proporcional al campo sensado, que a su vez es comparada con una tensión de referencia previamente ajustada y así obtener el error que debidamente compensado permite el control final del sistema.

El experimento se repite con la misma periodicidad del pulso de disparo que comanda al miniespectrómetro, permitiendo nuevas lecturas y estabilizar el error al valor mínimo, convirtiendo al nuevo sistema de control en discreto. Con las consideraciones anteriores, el sistema de regulación final que involucra el procesamiento de la señal RMN es representado en la figura 9.

9.MODELO DE CONTROL MODIFICADO

Con el esquema de control simplificado de la figura 9, se pueden obtener las ecuaciones del sistema de regulación fina de campo donde el sensor de campo magnético es un "espectrómetro de RMN". Además, implica el trabajo de un interruptor con un periodo de T segundos y ciclo útil de 15 Jíseg aproximadamente. Este nuevo elemento transforma al sistema en discreto.

La constante giromagnética aquí empleada es la de los núcleos del flúor del ácido trifluoruroacético:

y = 4,0052034 Khz/Gauss (8)
F. es una frecuencia constante: 90 Mhz proveniente de un cristal mantenido a temperatura constante y
V_ref es la tensión que se ajusta a fin de establecer el punto deseado de trabajo del campo magnético.

La expresión matemática que se ajusta al nuevo modelo de control [1], [3], [8] es el siguiente:

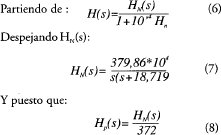
Donde x, y x2 son las variables de estado. Ecuación de salida:

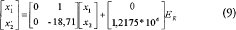
Ecuaciones de estado discretas de la planta son:

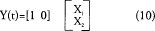
Ecuación discreta de salida:

y (kT). x, (kT) (12)

Complementarias a estas ecuaciones se deducen de la figura. 9 las siguientes igualdades:

F= 0,00540052*y (13)

F,= 90-F (14)
EF= 200Fs (15)
Eo = VR-EF (16)
ER=G*E. (17)

Observe que V_R es la tensión necesaria en la entrada para llevar la salida al punto de trabajo.

CONCLUSIONES:

Los resultados obtenidos con el equipo modificado permiten determinar que la estabilidad obtenida es la deseada para aplicaciones en Resonancia Magnética Nuclear. Estableciendo el error generado por cada uno de los módulos que componen el equipo de regulación se logró determinar que la estabilidad total es del orden de 7,3x10 7 y en consecuencia el proyecto desarrollado permite desviaciones de campo de: ±9,5 m Gauss.

Comparando la estabilidad inicial que era del orden de ± 1 x10-6 ( 1 ppm) con la estabilidad lograda, se obtiene una mejora apreciable, la que se ve reflejada en los beneficios causados al apreciar señales de RMN con una mejor figura de ruido.

REFERENCIAS

(1) Cancino E, "Estabilizador de Campo Magnético por medio de Resonancia Magnética Nuclear de Pulsos" Universidad Central de Venezuela. Caracas. Sept. 1982.

(2) Cadzon James A., Martens Hinrich R., "Discrete Time and Computer Control Systems" Prentice Hall. 1.998.

(3) Ogata Katzuhiho, "Ingeniería de Control Moderno", Prentice Hall Hispanoamericana.1998

(4) Tomizuka M, Auslander D., Takahashi Y, "Simple finite time settli ng Control and manupulatedaariable softening for reverse reaction, Overshoot,and Oscilatory Processes". Asme Winter Annual Meeting, Atlanta, Ga., December 2,1997.

(5) Muller B. Nobble J., Burnett L., "Simple Spin-echo Spectrometer" ASME Journal of Phisics, Volume 42/43, Januaru 1974.

(6) Gilbert, E. G. "Controllability and Observability in Multivariable Control Systems" J Siam Control, Ser. A.1. 1963

(7)Kuo, B. C. "Automatic Control System" 6 1 Ed. Prentice Hall. 1991

(8)Ogata, K "State Space Analysis of Control System" Prentice Hall. 1967

(9)Brogan, W L. " Modern Control Theory" Prentice Hall. 1985

(10)Kreindler, E. And Sarachick, P E. "On the Concepts of Controllability and Observability of Linear Systems" IEEE Transactions on Automatic Control. 1964, pp129-136