DOI:
https://doi.org/10.14483/23448393.2099Publicado:
2006-11-30Número:
Vol. 12 Núm. 1 (2007): Enero - JunioSección:
Ciencia, investigación, academia y desarrolloProbabilidad de Error en el Campo de Suma de Verificación del Protocolo Ip
Probability Of Error In Field Checksum Of Ip Protocol
Palabras clave:
Suma de verificación, combinatoria, complemento a 1's, error, IP, probabilidad, rata de error de bit, TCP (es).Descargas
Referencias
Y. Desaki, K. Iwasaki, Y. Miura y D. Yokota, "Double and Triple Error Detecting Capability of Internet Checksum and Estimation of Probability of Undetectable Error". In Pacific Rim International Symposium on Fault Tolerant Systems, 1997, pp 47-52.
T. Mallory y A. Kullberg, "Incremental Updating of the Internet Checksum", RFC 1141, Internet Engineering Task Force, Enero 1990.
T. Fujiwara, T. Kumasi y S. Lin, "Error Detecting Capabilities of the Shortened Hamming Codes Adopted for Error Detection in IEEE Standard 802.3", IEEE Tran. Communications, vol. 37, No 9, pp. 986-989, Septiembre 1989.
R. Saxena y J. McCluskey, "Analysis of Checksums, Extended-Precision Checksums, and Cyclic Redundancy Checks", IEEE Trans. On Computers, pp. Vol. 39, No 7, Julio, 1990.
A. Tanenbaum, Redes de Computadoras. Tercera edicion, ed. Pearson, México, México, 1997, pp. 187-191.
Braugth G., Signed Binary Numbers. Substraction and Overflow, Dickinson College: Carlisle, 2002.
Plumier W., TCP Checksum Function Design, Bolt Beranek and Newman Inc.: Cambridge, 1978.
Postel J. (Editor), RFC 791: INTERNET PROTOCOL. University of Southern California: Narina del Rey. 1981.
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Ingeniería, 2007-00-00 vol:12 nro:1 pág:48-56
Probabilidad de error en el campo de suma de verificación del protocolo IP
Probability of error in field checksum of IP protocol
Roberto Cárdenas
Director Grupo de Investigación GIRAC, Universidad Distrital.
César Augusto Hernández Suárez
Miembro del Grupo de Investigación Internet Inteligente y ARMOS, Universidad Distrital.
Luis Fernando Pedraza Martínez
Miembro del Grupo de Investigación Internet Inteligente, Universidad Distrital. Y GISSIC, Universidad Militar.
Resumen
En este artículo se presenta el análisis de la probabilidad de error del campo de suma de verificación de IP. Inicialmente se describe la operación matemática complemento a uno, luego se presenta las características del algoritmo del checksum y los patrones de errores no detectables, finalmente se realiza una prueba práctica con el analizador de protocolos de red Ethereal y se muestran los resultados.
Esta investigación tiene por objetivo realizar un análisis claro y preciso de la probabilidad de error que puede llegar a presentar el algoritmo de suma de verificación de IP y además plantea el siguiente interrogante ¿Es realmente necesario el campo de suma de verificación en la cabecera del protocolo IP?
Palabras clave: Suma de verificación, combinatoria, complemento a 1's, error, IP, probabilidad, rata de error de bit, TCP.
Abstract
In this article is presented the analysis of the probability of error of the checksum in IP. Initially is described the mathematical operation complement to one, after is presented the characteristics of the algorithm of the checksum and the pattern of errors undetected, finally is made a practical test with the analyzer of protocols of network Ethereal and the results are shown.
This research has as goal to make a clear and precise analysis of the probability of error that could introduce checksum algorithm of IP and also raises the following question, Is the checksum field really need in the header the IP protocol?.
Key words:
Checksum, combinatorial, one's complement, error, IP, probability, bit error rate, TCP.
1. Introducción
Con la innumerable cantidad de paquetes que circulan a diario por Internet, cual es la probabilidad de que los datos siendo erróneos por algún motivo, sean detectados como correctos?, además ¿Es realmente necesario el campo de suma de verificiacion (checksum) en la cabecera del protocolo IP?
Además de dar respuesta a los interrogantes planteados anteriormente, este articulo tiene por objetivo adicional presentar un análisis claro y metodológico de la probabilidad de error del checksum en el protocolo IP, a fin de ser comprensible para el lector promedio.
Los checksums (sumas de comprobación) son incluidos en paquetes con el objeto de que errores acaecidos durante la transmisión puedan ser detectados. El presente desarrollo utiliza herramientas como el Sniffer Ethereal para capturar paquetes IP y lograr realizar análisis más específicos [2].
Con el objeto de entender como funciona el checksum, se realiza un ejemplo de como se podría construir uno.
Se parte de las siguientes suposiciones:
- Se puede transmitir los dígitos desde 0 hasta ±9 en las tramas de datos de un protocolo.
- Se transmiten los datos A y B dentro de la trama que se muestra en la figura 1.
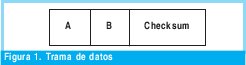
Inicialmente se transmite A=3 y B=5, con estos datos calculamos el checksum como:
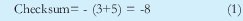
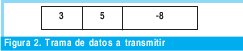
El receptor podrá realizar la siguiente operación para comprobar si hay algún error en los datos recibidos:
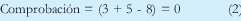
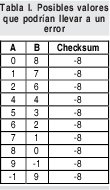
Esta comprobación asumirá que si el resultado es cero, los datos recibidos son correctos. ¿Es esto realmente cierto? Se puede verificar que este mismo resultado se puede obtener como se muestra en la tabla I.
Ahora considérese A=7 y B=9. ¿Cuál seria el checksum? Si se procede como hasta ahora:
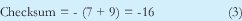
No se puede enviar este checksum ya que solo se puede enviar dígitos de 0 a ±9. Una posible solución es:
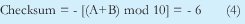
En el receptor se podría realizar la siguiente comprobación:
Comprobación = (A + B + Checksum) mod 10

En este sencillo ejemplo se puede observar la importancia de poder transmitir números positivos y negativos en el checksum. En el siguiente apartado se considera la representación de los números positivos y negativos en forma binaria, ya que en este formato es que se hacen las transmisiones en Internet.
2. Complemento a uno
Una de las formas mas obvias de representar un número positivo o negativo en forma binaria es hacer que con el bit mas significativo se represente el signo de una magnitud y por eso se llama la representación signo-magnitud.
Por ejemplo el número 107 se puede representar como: 107 = 01101011
Y el número -107 en representación signo-magnitud seria: -107 = 11101011
Esta representación tiene dos problemas:
1. El cero podría tener dos representaciones (00000000 y 10000000), lo que hace un poco más difícil la detección de esta condición en los computadores.
2. Con la representación signo-magnitud la suma de números positivos funciona. Por ejemplo 2+ 3 = 0010 + 0011 = 0101 = 5. Pero para números negativos desarrollar una suma de esta forma realmente resulta en una resta. Por ejemplo -3 +1 = 1011 + 0001 = 1100 = -4 ?!?!.
En general las sumas que involucren números positivos y negativos en representación signo-magnitud conducirán a un error.
Existe otra representación en la cual no solo se tiene en cuenta el bit del signo, sino que se da una interpretación a los bits de magnitud. Esta representación se conoce como complemento a uno. Para desarrollar la operación complemento a uno sobre un conjunto de bits, se reemplazan los dígitos ceros con dígitos unos. Por ejemplo el complemento a uno de 01010001 es 10101110.
La representación en complemento a uno de un número positivo se hace de la misma forma que en signo-magnitud, mientras que un número negativo se representa con el complemento a uno del entero positivo con la misma magnitud. Por ejemplo la representación en complemento a uno de 107 es 01101011, mientras que la representación en complemento a uno de -107 es 10010100 es decir se cambian unos por ceros y ceros por unos. Esta es la simplicidad que hace atractiva esta técnica. Nótese que el bit más significativo continúa con su función de bit de signo.
Cabe anotar que en complemento a uno también existen dos representaciones para el cero: +0=0000 y -0=1111. Cuando hacemos operaciones con -0 (1111) se tendrá que tener en cuenta el acarreo.
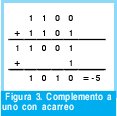
El complemento a uno funciona adecuadamente en la suma de números positivos y la suma de un número positivo en magnitud menor a un número negativo en magnitud mayor [6]. Por ejemplo: 2 + 2 = 0010 + 0010 = 0100 = +4, y -3 + 2 = 1100 + 0010 = 1110 = -1. Sin embargo, la suma de dos negativos o de un negativo en magnitud menor a un positivo en magnitud mayor, generalmente no trabaja en la representación de complemento a uno. Por ejemplo: -3 + -2 = 1100 + 1101 = 1001 = -6?!?! y 3 + -1 = 0011 + 1110 = 1?!?! Estas eventualidades se pueden solucionar considerando el acarreo de cada suma, por ejemplo retomemos el ejercicio de -3 + -2 considerando el acarreo. Como se observa, sumar el acarreo conduce a una respuesta correcta.
Para continuar se define la operación de complemento a uno como: ~.
Ahora retomando el ejemplo 3 + -1, se realiza la siguiente operación:
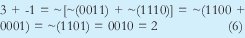
En general se puede comprobar que cuando se suman números (los cuales serian los datos a enviar) usando la representación de los números en complemento a uno, no se incurrirá en un error si hallamos el complemento a uno de la suma de los complementos a uno de los números. Ahora si se usa (6) como checksum, la trama a transmitir seria la que se muestra en la figura 4.
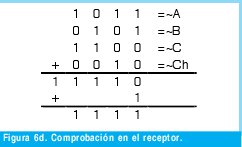
En el receptor se puede desarrollar la siguiente comprobación:
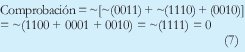
Si se envía como checksum el complemento a uno de (6), seria equivalente a decir que el checksum es la suma de los complementos a uno de los números (datos). En este caso el receptor haría la siguiente comprobación:
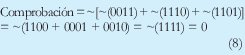
Como conclusión, si se tiene que enviar los datos A y B, el checksum se puede calcular haciendo:
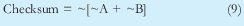
De esta forma es como lo especifica la RFC 791, sin embargo en los múltiples experimentos que realice con el software Ethereal, observe que esta no era la forma en la que realmente se calcula el checksum, sino como lo expresa la ecuación 11, esto se debe seguramente, a que el nivel de procesamiento en el receptor es mayor con 10a o 10b que con 12. La comprobación que debe hacer el receptor cuando se utiliza 9 es:
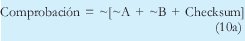
O también como:
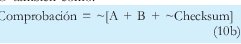
Es decir que como el Checksum es el complemento a uno de las sumas en complemento a uno, el checksum igual a la suma de los datos por lo que en este caso se debería usar (10) o (11) para realizar la comprobación del paquete.
O también se podría calcular el checksum como:
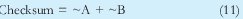
Cuya comprobación en este caso seria:
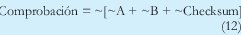
Cuando se realizan estas operaciones, se observa que el resultado (Checksum) es función del acarreo "c" y de algunos bits "m" así:

Esto se puede analizar en la figura 3, donde c=1 y m=1001.
Si c=1 y m=1111, quiere decir que se esta en el estado overflow (desbordamiento), ya que 1111 + 1 = 10000 (numero que ocupa mas de 4 bits). Para evitar este estado se podría definir el checksum como:
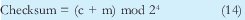
Donde mod significa modulo es decir el residuo de dividir el numero entre 24 (16). Aunque en este caso se escoge 24 debido a que los ejemplos trabajan con 4 bits, para el caso real de IP será 216 porque se trabaja sobre palabras es decir datos de 16 bits.
Y de acuerdo a lo que se ha desarrollado en el presente artículo, se utilizara la ecuación 15 para el cálculo del checksum y la 12 para su comprobación:
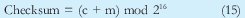
3. Suma de verificación de internet
El algoritmo realizado por el checksum para el cálculo de la detección de errores para un datagrama IP, separa la cabecera del datagrama IP en bloques de 16 bits y los representa en complemento a uno, el campo de checksum es cargado inicialmente con ceros cuyo complemento a uno es FFFF en sistema hexagesimal.
Debido a que el algoritmo de checksum para IP trabaja sobre palabras (16 bits) se utiliza el sistema hexagesimal, pero las operaciones siguen siendo las mismas el lector puede contastarlas realizando las conversiones respectivas. Luego se calcula el checksum como la suma de los complementos a uno de todas las palabras (16 bits) de la cabecera de IP (sumando el acarreo). Este dato es el que se introduce en el campo del checksum para luego transmitir el datagrama IP.
Una operación idéntica se realiza para TCP, solo que aquí el algoritmo del checksum se calcula sobre la cabecera y los datos de TCP [1]. Es decir que el número de bits a considerar ahora son 16 en lugar de 4 como se ha tomado en los ejemplos anteriores.
La figura 5 muestra que la estructura lógica del encabezado IP tiene un ancho de 32 bits y el campo Header Checksum es de 16 bits.
Como el checksum de IP se calcula sobre palabras de 16 bits se podría organizar el encabezado IP con un ancho de 16 bits en lugar de 32 para que le sean aplicadas las operaciones de la suma en complemento a uno.
Si se omite el campo de opciones en la cabecera de IP, el número de palabras de 16 bits que podemos tener es 10. Ahora durante el desarrollo de este artículo se denota:
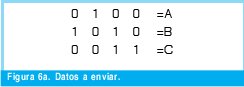
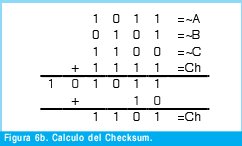
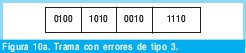
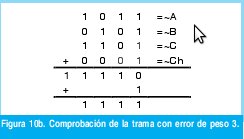
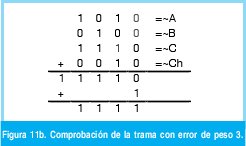
n = Numero de palabras Lo anterior con el fin de desarrollar ecuaciones de calculo de probabilidad de error que sirvan tanto para IP como para TCP, en cuyo caso bastaría con cambiar n por el numero de palabras totales mientras m sigue siendo 16. Donde n=10 y m=16 para IP y Ui para i=6 (U6) representa el campo de checksum, es decir la sexta palabra de 16 bits de la cabecera IP es el campo de checksum, el cual se calcula como: Donde ~ denota la suma en complemento a uno. Para detectar si hubo o no errores en el canal de transmisión, el receptor realiza una verificación del checksum como se muestra en la ecuación (17). Donde U'i denota la iesima palabra en el paquete recibido. Cuando la magnitud de la comprobación en el receptor sea el valor máximo, es decir que |C| = 2m - 1, se corrobora que el paquete llego exitosamente sin ningún error y es aceptado. Para m=16, 2 m-1=FFFF en hexagesimal, cuyo complemento a uno es 0000, comprobando así que la suma en el transmisor es idéntica a la suma en el receptor, sin incluir el campo de checksum. Pero se presenta un problema, el cual radica, en que la comprobación del checksum puede llegar a ser 2m-1, aun cuando ha habido errores durante la transmisión del paquete. Como el objetivo de este trabajo es encontrar la probabilidad de error en el checksum de IP y TCP, se denotan dos vectores como: U = (u1,u2,...,umn), vector transmitido Donde ui y vi son los iesimos bits que conforman el datagrama IP transmitido y recibido respectivamente, para 1 ≤ i ≤ nm. (Note que Ui ui). La distancia hamming d(u,v) es el numero de coordenadas i para las cuales ui#vr un código C de longitud nm y 1≤i≤nm, se define: Donde Bi son los coeficientes que denotan la probabilidad de ocurrencia de patrones de errores indetectables con peso i (i errores). Pero para calcular la probabilidad real de que el algoritmo de checksum no detecte los errores ocurridos durante la transmisión de un paquete IP, es necesario multiplicar los coeficientes Bi por la probabilidad de que ocurran i errores en el canal de transmisión. De esta forma la probabilidad de error en el checksum, viene dada por la función de probabilidad binomial como sigue: Donde en nuestro caso transformaremos 19a en 19b: para las cuales el error no se detecta dividido por el numero de combinaciones totales, es decir que Bi representa la probabilidad de error para i errores y å denota la Rata de Error de Bit (BER) del canal de transmisión. Es fácil deducir que B0=0 y para que un error no sea detectado deben existir por lo menos dos errores para que uno enmascare el error del otro por lo cual un único error será 100% detectable es decir que B1=0. 4. Patrones de error no detectables A continuación se procede a encontrar la probabilidad de que el algoritmo de checksum no detecte dos errores. Debido a que los errores ocurren durante la transmisión de la trama, el campo de checksum ya ha sido calculado por el transmisor, por lo que el receptor no detectara 2 o mas errores, si al realizar el algoritmo de comprobación (ver ecuación 7) el resultado de la suma sigue siendo 0. Por cuestiones de comodidad en el análisis se definirá la última palabra de 16 bits como el campo de checksum. Observe en la Figura 6a, 6b y 6c un ejemplo de una trama enviada sin errores, para 4 nibbles (datos de 4 bits). Observe a continuación un ejemplo de un patrón de error de peso 2 (2 errores) no detectable para el ejemplo anterior, donde los bits rojos son errores (P1 y P2)
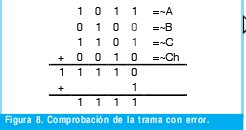
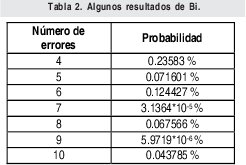
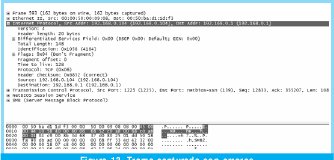
Para probar que este patrón de error de peso 2 no es detectable por el algoritmo del checksum, se realiza la comprobación en el receptor para la trama de la figura 7. Para realizar el análisis de los patrones de error de peso 2, se supone que un vector de error e ∈ {0,1}mn con peso 2 modifica el vector transmitido U ∈ {0,1}mn . Sean P1 y P2 2 bits que pertenecen a e tal que P1 y P2 son los P-iesimos bits donde ocurren los errores ep1 y ep2. De acuerdo con el análisis que realice en el ejemplo de la figura 7 y 8, descubrí con certeza, después de varios ensayos y pruebas que el patrón de error e de peso 2 en el vector U= (u1, u2,..., unm) no es detectado si y solo si: Lo anterior significa que el primer error debe ser equivalente al segundo modulo m, en otras palabras que el primer error debe estar en la misma posición de la palabra correspondiente que el segundo. La segunda condición implica que los errores deben ser distintos es decir que si el primer error fue un cero el segundo debe ser un uno para que de esta forma se logre enmascarar los errores mutuamente y no sean detectados. Ahora se podría pensar que el análisis para errores ocurridos únicamente en los datos es distinto del realizado si uno de ellos ocurriera en el checksum y otro en los datos. Para corroborar que el análisis es el mismo se realizara un análisis por separado de cada caso. Para dos errores, se consideran dos tipos de patrones de errores no detectables (recordar que la última palabra será entendida como el campo de checksum), el primero se da cuando los dos errores se encuentran en los datos y el segundo cuando uno de los errores esta en los datos y el segundo en el campo de checksum (el cual no esta exento de errores). Tipo 1: 1£P1£P2£m(n-1) Tipo 2: 1£P1£m(n-1) y m(n-1)+1£ P2£mn Se denota entonces a B2,i) (m,n) como el numero de patrones de error no detectables con peso dos y de tipo i con 1≤i≤2 [1], para n palabras de m bits cada una. De esta forma se tiene que: Ahora se procede entonces a calcular el número de patrones de error indetectables de cada tipo. Se supone entonces que el vector U transmitido es dividido en n vectores de longitud m. B2,1 esta determinado por el numero de combinaciones de los dos errores ep1 y ep2, tal que ep1 y ep2 ocurran en la misma posición de bit de dos vectores Ui y Vj donde, 1≤i≤j≤n Siendo Ui y Vj vectores de longitud m. Ahora el número de combinaciones para (P1, P2) en n vectores con longitud de un bit (m=1) es: Pero como los errores no detectables de peso dos y tipo 1 se restringen a (P1, P2)=(0,1) ó (1,0), entonces se tiene: B2,2 analiza la ocurrencia de un error en el campo de checksum y otro en cualquiera de los datos, para este caso se tiene 1≤P1≤m(n-1) y m(n-1)+1≤P2mn. Aquí los errores también deben ocurrir en los bits con igual peso de las dos palabras donde ocurren los errores y como una de ellas es fija (checksum) el número de combinaciones para n palabras de un bit es (n-1). Ahora si se toman palabras de m bits, el número de combinaciones es: Para entender lo anterior la figura 9a y 9b muestra un ejemplo de este tipo de error de peso 2. Luego para los dos errores de tipo 2 que no son detectados, se tiene el mismo análisis que el patrón de error de tipo 1 y peso 2. Por lo tanto, no es necesario realizar un análisis por separado para errores ocurridos en el checksum. De los ejemplos propuestos se puede ver que para que los patrones de error de peso 2 no sean detectados, los errores deben tener el mismo peso dentro de la respectiva palabra donde ocurre el error. Entonces para hallar la probabilidad de que un patrón de error de peso 2 no sea detectado por el checksum se debe dividir el número de casos en los que no se detecta sobre el número de casos totales, como se muestra a continuación: En la ecuación 24b se puede analizar que la suma de los resultados obtenidos en las ecuaciones 22b y 23, son equivalentes al numerador de la ecuación 24b, el cual se puede calcular como se hizo con 22b teniendo en cuenta las n palabras. Lo anterior demuestra que no es necesario realizar cálculos independientes para errores ocurridos en el checksum sino que pueden ser tratados de la misma forma. El valor que se obtuvo en 24c se interpretara mas adelante junto al resto de los resultados. Ahora se procede a calcular la probabilidad de patrones para errores no detectables de peso tres (B3(m,n)), es decir para tres errores. Para entender mejor el proceso se muestran a continuación 2 ejemplos (Figuras 10 y 11) de un patrón de error de peso 3 adicionado a la trama del ejemplo de la figura 6c. Para realizar el análisis de los patrones de error de peso 3, se supone que el vector de error e ∈ {0,1}mn con peso tres es adicionado al vector transmitido U ∈ {0,1}mn. Sean P1, P2 y P3 los pesos de tres bits cualquiera en los cuales se presentan los errores con 1d" P1 < P2 < P3d" mn, las relaciones entre las posiciones P1, P2 y P3 de los bits están restringidas al siguiente patrón, el cual obtuve luego de múltiples análisis y ejemplos realizados y comprobados por la herramienta de software Ethereal y por Hping la cual me ayuda a introducir errores en las tramas de IP. El patrón de error e de peso tres en U=(U1, U2,.....,Umn) no es detectado si y solo si: Ya que con estas condiciones los errores se enmascaran entre si. De acuerdo con lo anterior se tiene que para B3(m,n), el número de combinaciones para n palabras de dos bits es: y para n palabras de m bits se tendría: Del mismo modo se procede para hallar los coeficientes Bi para i = {4, 5, 6, 7, 8, 9, 10} errores, cuyos resultados se condensan en la tabla 2. El análisis para i "par" es de la misma forma que para i=2, mientras que para i "impar" es de la misma forma que para i=3, esto se puede apreciar analizando con cuidado las ecuaciones 27 y 28. 5. Resultados En la mayoría de las aplicaciones de transmisión de datos, todos los 2m mensajes de datos posibles son legales, pero debido a la manera en que se configura la trama IP no se usan todas las 2nm palabras códigos posibles [5]. En este desarrollo se tuvo en cuenta que en las tramas IP la primera palabra casi siempre es 4500 por lo que la probabilidad que representa B2,1 se ve decrementada por el factor (n-3)/(n-1)=7/9, B2,2 por el factor (2n-3)/(2n-2)=17/18, por lo que finalmente el coeficiente: Los resultados obtenidos de probabilidad muestran que en gran parte la probabilidad de error del checksum esta determinada por los errores de peso dos, sin embargo vale la pena aclarar que estos valores de probabilidad calculados tienen en cuenta todas las posibilidades que en la realidad no se darán debido a los espacios muéstrales de cada campo los cuales no son de 65.536 datos, por lo que las probabilidades obtenidas en este caso marcan una cota superior para la probabilidad de error del checksum de IP. A continuación se analiza el envío de una trama para corroborar la no detección de un error doble por parte del checksum de IP. El software para el envío de esta trama fue desarrollado en C++ y los datos enviados en hexagesimal inicialmente en este fueron: 4500001410D8400080066852C8A80068C0A80001. Luego se introdujo dos errores, para esto se cambio el primer bit del primer uno en formato binario de 0 a 1 y el primer bit del primer D en formato binario de 1 a 0, como se muestra en la Figura 12. Al capturar la trama con errores en el analizador de protocolos de red «Ethereal», se observa que esta es validada correctamente en el campo de checksum de IP, como se puede ver en la Figura 13, lo cual corrobora los cálculos realizados anteriormente. Este mismo procedimiento fue realizado alrededor de 320 veces, el cual arrojo una probabilidad de error doble del 4.21 %, debido a que el numero de intentos fue bajo. Con los datos calculados para los patrones de error de peso 2, 3, 4, 5, 6, 7, 8, 9 y 10, (ver tabla 2) se estimó dos ecuaciones de tipo exponencial a través de regresión no lineal, que aproximan la probabilidad de error del Checksum para la cabecera de IP para errores pares e impares, las cuales son respectivamente: A partir de este estimativo se obtiene la probabilidad total de error del checksum para la cabecera de IP, la cual es: 6. Conclusiones En el desarrollo de este trabajo se calculó la probabilidad de los patrones de error no detectables por el algoritmo del Checksum para la cabecera de IP, para el calculo de TCP se procede de la misma forma solo que «n» ya no será 10 sino un numero mayor. El calculo de error se desarrollo con base en la distancia hamming. Además se tuvo presente que no todas las 2mn palabras se pueden dar, ya que existen campos que solo pueden tener un determinado numero de combinaciones, durante los cálculos se tuvo en cuenta que la primera palabra es casi siempre es 4500 por lo que la probabilidad para cada error de diferente peso es algo menor a los cálculos realizados habitualmente. También es de tener presente que el campo de protocolo no tiene 256 palabras códigos distintas, sin embargo este calculo no se tuvo presente en este desarrollo. La probabilidad total obtenida en esta investigación se considera para algunos casos como alta, sin embargo vale la pena resaltar el hecho de que no todas las combinaciones se dan y si a esto le sumamos el hecho de que la probabilidad real de error del checksum debe tener en cuenta el BER del canal, lo cual reduce bastante. Para un BER pequeño del orden de 10-3 la probabilidad llega a ser del orden de aproximadamente 4x10-6 % por lo que este algoritmo se puede considerar como no necesario para realizar cualquier transmisión, inclusive sobre medio de transmisión con baja BER. Referencias Bibliográficas [1] Y. Desaki, K. Iwasaki, Y. Miura y D. Yokota, "Double and Triple Error Detecting Capability of Internet Checksum and Estimation of Probability of Undetectable Error". In Pacific Rim International Symposium on Fault Tolerant Systems, 1997, pp 47-52. [2] T. Mallory y A. Kullberg, "Incremental Updating of the Internet Checksum", RFC 1141, Internet Engineering Task Force, Enero 1990. [3] T. Fujiwara, T. Kumasi y S. Lin, "Error Detecting Capabilities of the Shortened Hamming Codes Adopted for Error Detection in IEEE Standard 802.3", IEEE Tran. Communications, vol. 37, No 9, pp. 986-989, Septiembre 1989. [4] R. Saxena y J. McCluskey, "Analysis of Checksums, Extended-Precision Checksums, and Cyclic Redundancy Checks", IEEE Trans. On Computers, pp. Vol. 39, No 7, Julio, 1990. [5] A. Tanenbaum, Redes de Computadoras. Tercera edicion, ed. Pearson, México, México, 1997, pp. 187-191. [6] Braugth G., Signed Binary Numbers. Substraction and Overflow, Dickinson College: Carlisle, 2002. [7] Plumier W., TCP Checksum Function Design, Bolt Beranek and Newman Inc.: Cambridge, 1978. [8] Postel J. (Editor), RFC 791: INTERNET PROTOCOL. University of Southern California: Narina del Rey. 1981. Roberto Cárdenas César Augusto Hernández Suárez Luis Fernando Pedraza Martínez
m = Numero de bits de cada palabra
Ui = La iesima palabra para 1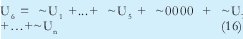
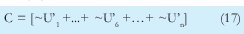
V = (v1,v2,...,vmn), vector recibido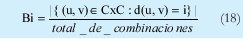
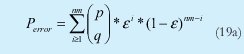
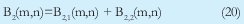


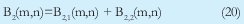
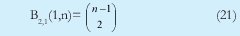
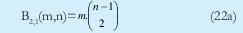
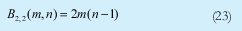



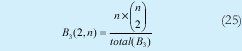



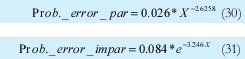

Ingeniero electrónico, Universidad Distrital. Magíster en teleinformática de la Universidad Distrital. Docente de la facultad de Ingeniería ,Universidad Distrital en la maestría y especialización en teleinformática. Actualmente cursa segundo año del doctorado en ingeniería eléctrica en la Universidad Nacional de Colombia. bitek@multi.net.co
Ingeniero electrónico, Universidad Distrital. Especialista en interconexión de redes y servicios telemáticos de la Universidad Manuela Beltrán. Magíster en ciencias de la información y las comunicaciones de la Universidad Distrital. Actualmente adelanta estudios de maestría en economía en la Universidad de los Andes. Se desempeñó como docente investigador en la Universidad Manuela Beltrán durante 3 años donde desarrolló varios proyectos, dentro de los cuales esta Sistema Electrónico Mecánico para la enseñanza de la Lectoescritura del Braille, en curso de patente. Actualmente se desempeña como docente en la U. Distrital. Lctsubasa@Gmail.com
Ingeniero electrónico, Universidad Distrital. Magíster en ciencias de la información y las comunicaciones de la Universidad Distrital. Se desempeño como docente en el área de control en Universidades como Cooperativa de Colombia y Distrital. Es director del grupo de investigación "Semaforización Inteligente". Actualmente se desempeña como docente en la Universidad Militar Nueva Granada. luis.pedraza@umng.edu.co
Creation date:
Licencia
A partir de la edición del V23N3 del año 2018 hacia adelante, se cambia la Licencia Creative Commons “Atribución—No Comercial – Sin Obra Derivada” a la siguiente:
Atribución - No Comercial – Compartir igual: esta licencia permite a otros distribuir, remezclar, retocar, y crear a partir de tu obra de modo no comercial, siempre y cuando te den crédito y licencien sus nuevas creaciones bajo las mismas condiciones.




2.jpg)